ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №797. Докажите, что средняя линия трапеции … – Рамблер/класс
ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №797. Докажите, что средняя линия трапеции … – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
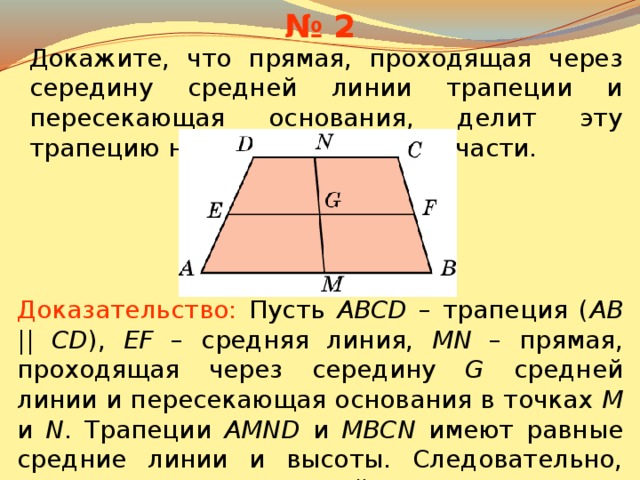
Не могу додуматься, как решить задачу Гл. VIII №797.
VIII №797.
ответы
Надеюсь помогу, задание Гл.VIII №797 решается вот так:
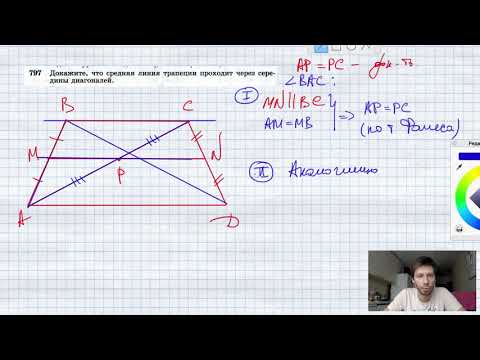
Средняя линия трапеции параллельна основаниям, следовательно она проходит и через средины сторон треугольников образованных из диагоналей трапеции (по теореме Фалеса).
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Психология
Химия
похожие вопросы 5
Не могу додуматься, как решить задачу Гл.VIII №704, необходима помощь.
Окружность с центром О описана около прямоугольного (Подробнее. ..)
..)
ГДЗАтанасян Л.С.Геометрия
Стороны параллелограмма
Стороны параллелограмма находятся в отношении 4:5. Найти стороны параллелограмма если периметр равен 10.8 см (Подробнее…)
ГДЗ
Задание 38 Однородные члены предложения. Что такое однородные члены предложения? Русский язык.4 класс. Канакина В.П., Горецкий В.Г. ГДЗ
Всем привет, поделитесь ответом на задание
Прочитайте.
Рассмотрите условные обозначения однородных членов.
(Подробнее…)
ГДЗРусский языкКанакина В.П.Горецкий В.Г.4 класс
ГДЗ по геометрии 8 класс Атанасян. Гл.IX №780. Докажите, что для любого вектора…
Если не затруднит, объясните задачу Гл.IX №780.
Докажите, что для любого вектора а справедливы равенства: а)1∙͞а = ͞͞͞а; б) (-1) (Подробнее…)
ГДЗАтанасян Л.С.Геометрия8 класс
ГДЗ, русский язык, 8 класс, Ладыженская, упр.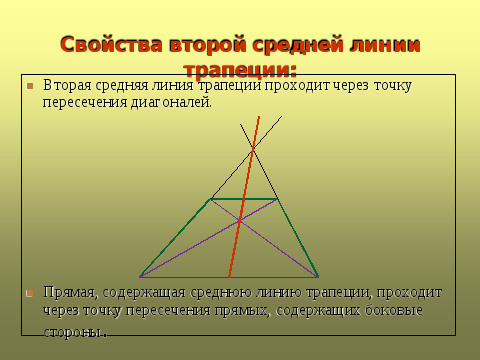
Слова данных частей речи (см. таблицу на с. 22) употребляются только с отрицательной частицей не. Они не образуются с приставкой не-. (Подробнее…)
ГДЗРусский язык8 классЛадыженская Т.А.
Средняя линия трапеции равна половине основания. Трапеция
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
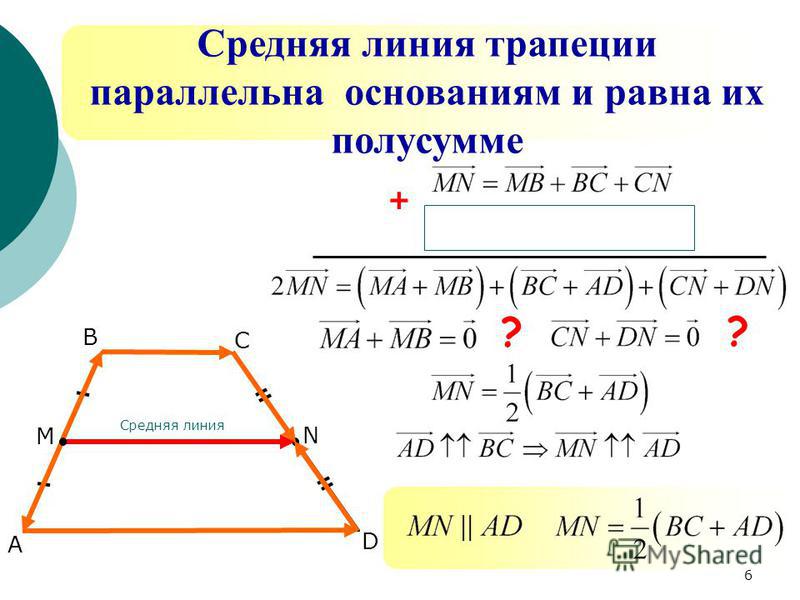
Средняя линия трапеции параллельна основаниям и равна их полусумме.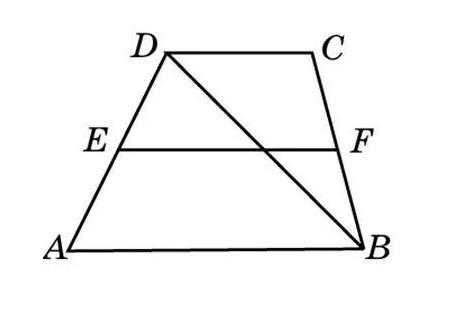
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию.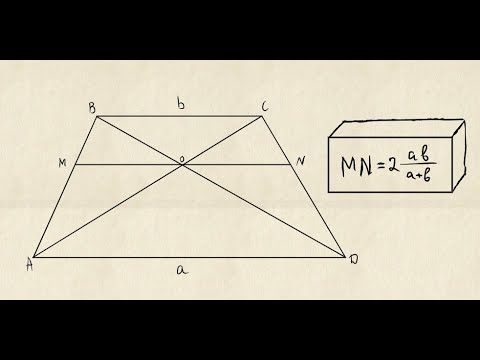 Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок.

- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке.
 Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
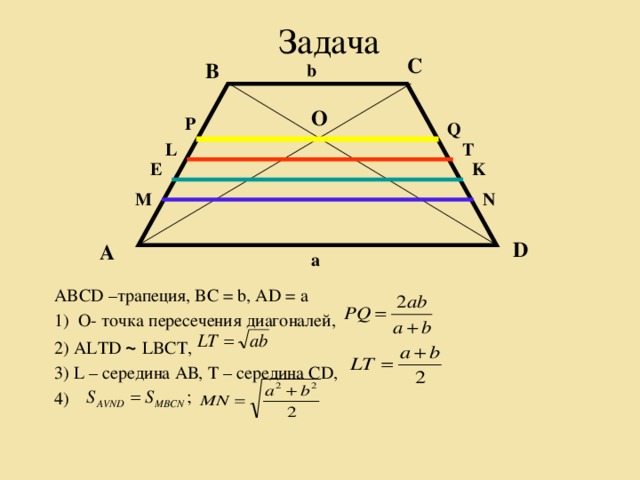
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.

- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.

Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .

- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне.
 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). - Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ .
 Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
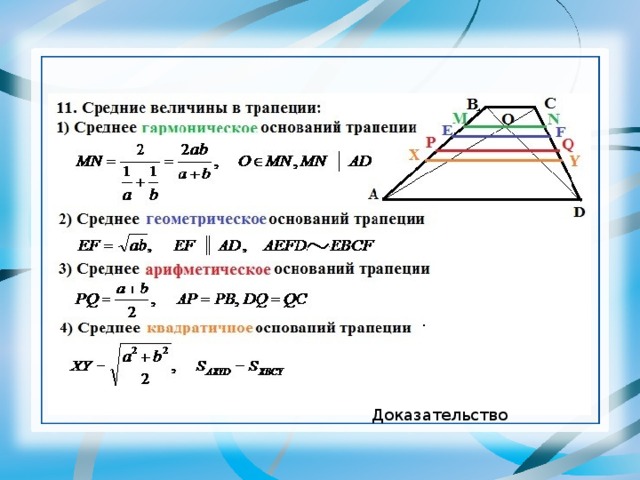
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b.
 Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab . - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.

- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.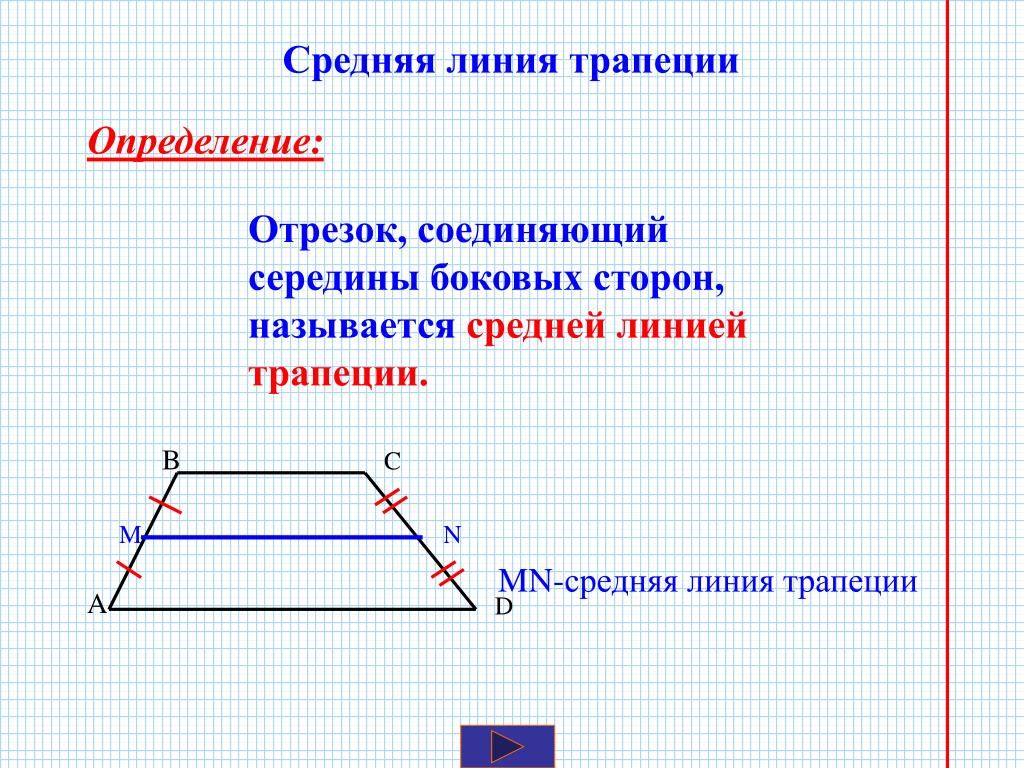
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .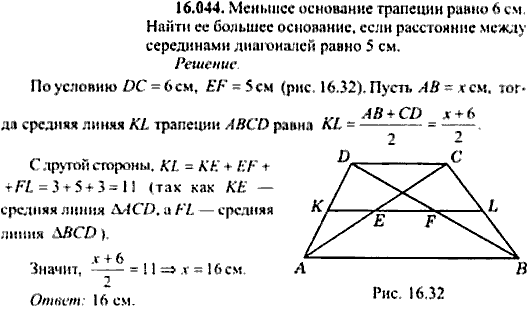
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.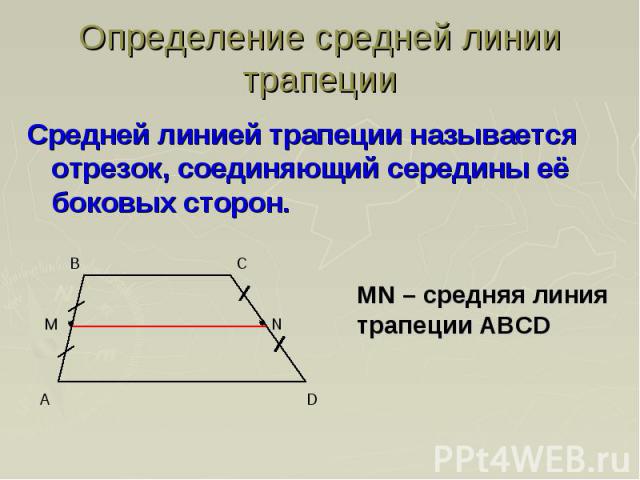
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .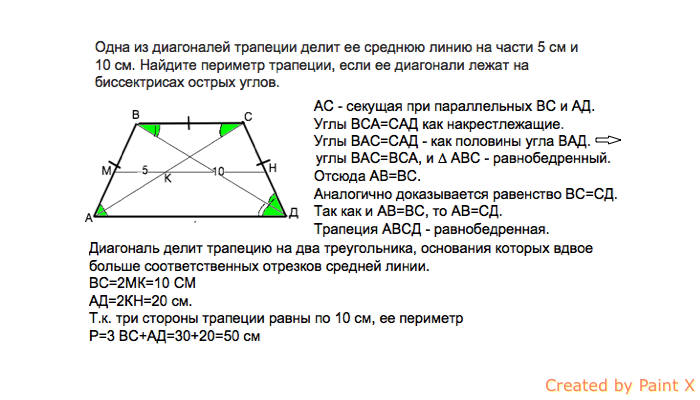
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты.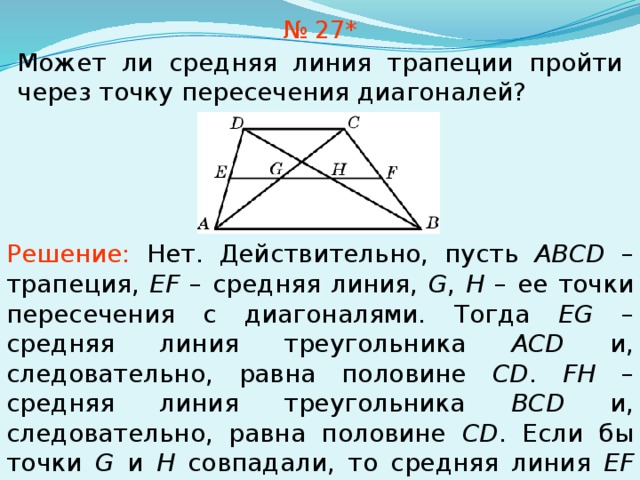 Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .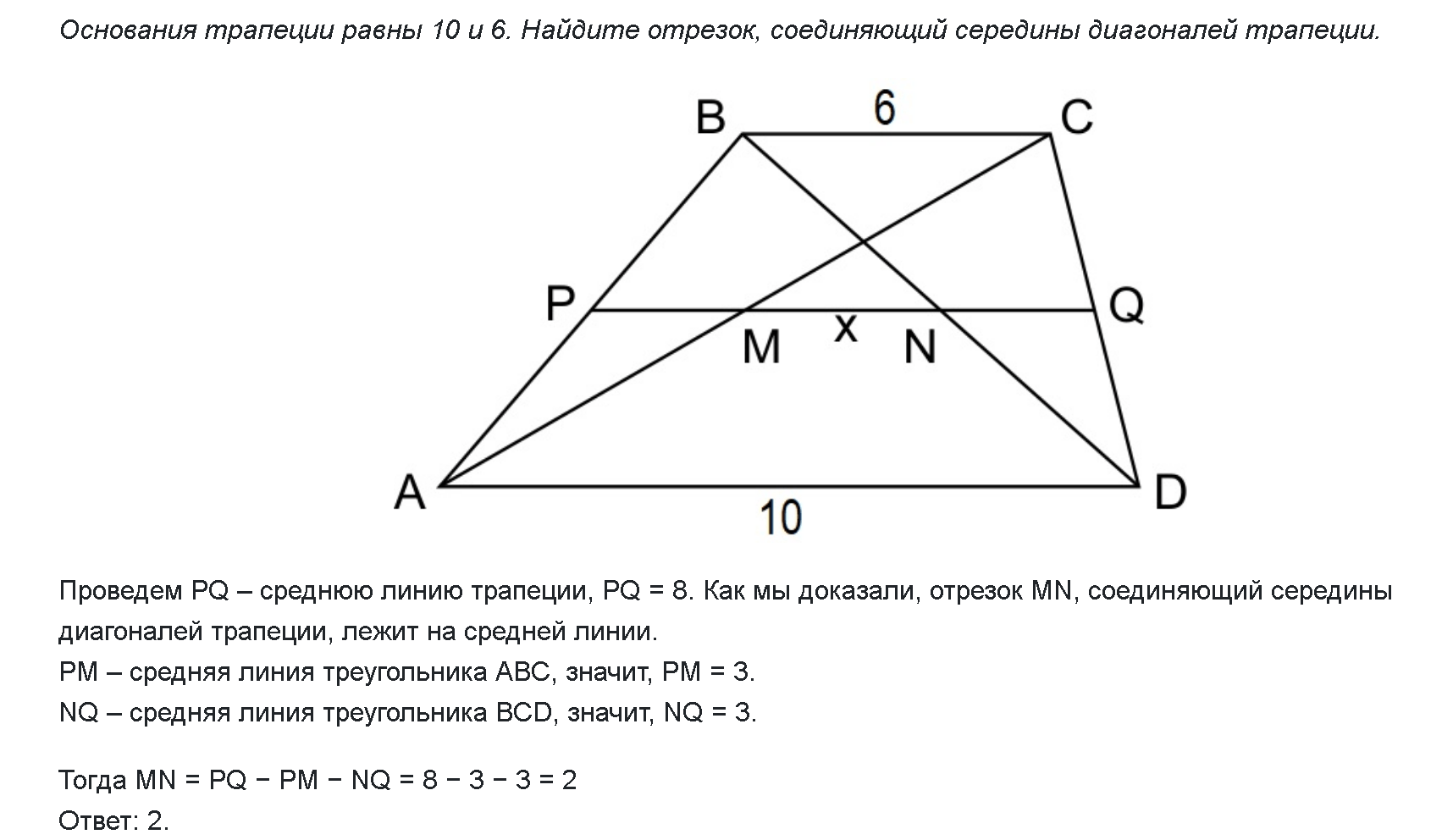
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему.
РЕШЕНИЕ: Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему. Алгебра ->
Настраиваемые средства решения задач Word
-> Геометрия
-> РЕШЕНИЕ: Средняя линия трапеции не совпадает с диагоналями. Объяснить, почему. Войти
Объяснить, почему. Войти
|
|
Раздел 4.5: Трапеции — элементарная геометрия
Section_4_5Теперь обратим внимание на трапеции и на отрезок трапеции, аналог средней линии треугольника.
- Определение: Трапеция это четырехугольник ровно одна пара противоположных сторон параллельна.
Помните, что параллелограмм имеет обе пары противоположных сторон параллельны, тогда как трапеция имеет только одну пару. Параллель стороны трапеции называются основаниями трапеции, а непараллельные стороны — катеты. Углы при основании это пара углов которые имеют одно из оснований трапеции как общую сторону. А трапеция это равнобедренная трапеция если его ноги равны.
- Теорема 4.15:
углы при основании равнобедренной трапеции равны.

| Дано: $ABCD$ — это
равнобедренная трапеция с $\overline{AB}\parallel\overline{CD}$. Доказать: $\угол A\угол \угол B$ и $\угол C \угол \угол D$ | |
Доказательство: (схема): Опустив перпендикуляры из точек $A$ и $B$ на основание $\overline{CD}$, конгруэнтные треугольники (с использованием катета гипотенузы) могут быть сформировался. Это приводит к тому, что углы при основании равны.
- Определение: Медиана трапеции равна отрезок, соединяющий середины катетов трапеции.
Обратите внимание, что медиана трапеции — это не то же самое, что
медиана треугольника; это как средняя линия треугольника.
Некоторые используют выражение «средняя линия трапеции», но «медиана»
является более распространенным термином. Теперь у нас есть основная теорема о
медиана трапеции. Это очень похоже на теорему о средней линии
последний раздел.
- Теорема 4.16: Медиана трапеции параллельна основаниям трапеции и длина медианы равна половине суммы длин базы.
| Дано: $ABCD$ – это
трапеция с медианой $\overline{EF}$. Доказать:
а. $\overline{EF}\parallel\overline{BC}$ и
$\overline{EF}\parallel\overline{AD}$; | |
Доказательство: (Часть
а) Проведите через $F$ прямую, параллельную
$\overline{AB}$. Поскольку $F$ является серединой $\overline{CD}$, мы
иметь $\overline{CF}\cong\overline{FD}$. $\угол CFP \cong \угол DFR$
и $\angle PCF \cong \angle RDF$. Следовательно, $\triangle PCF \cong
\треугольник RDF$ от ASA. Поскольку противоположные стороны $ABPR$ равны
параллелограмм, $ABPR$ — параллелограмм; следовательно, $AB=RP$. $Е$ это
середина $\overline{AB}$, так что $AE=\frac{1}{2}AB$. С
$\triangle PCF \cong \triangle RDF$, имеем
$\overline{RF}\cong\overline{PF}$ и $RF=\frac{1}{2}RP$.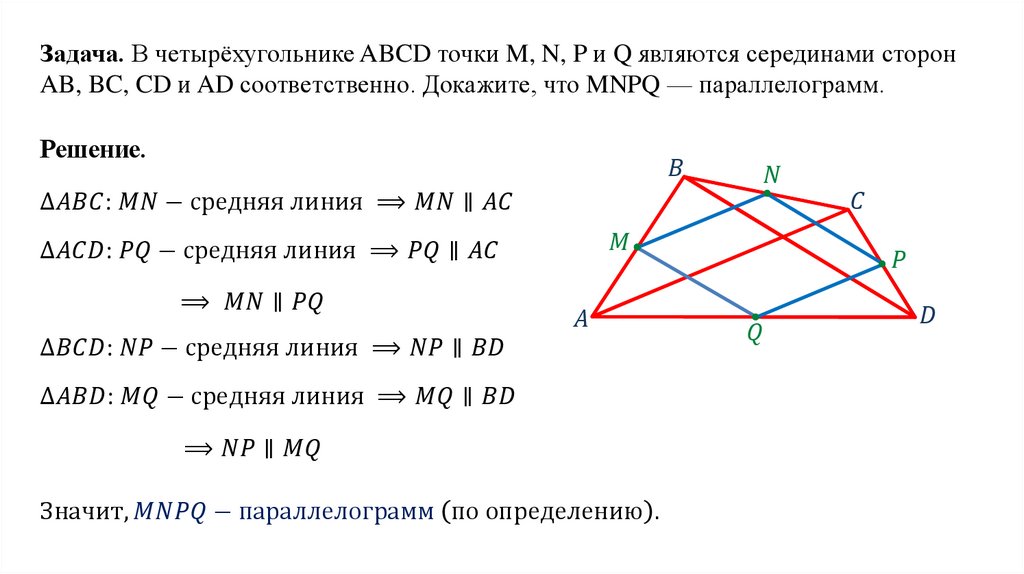


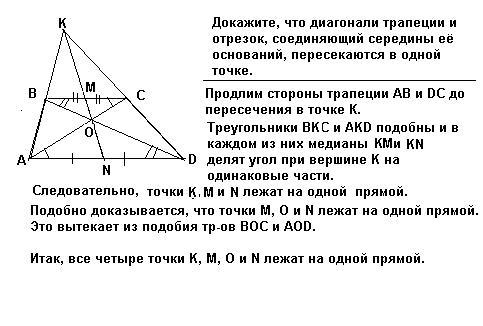 Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.


 Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ). Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.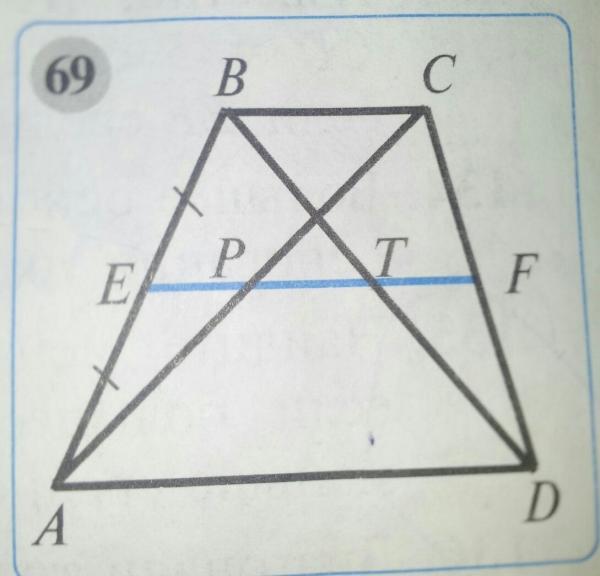 Радиус окружности можно вычислить по формуле: r = √ab .
Радиус окружности можно вычислить по формуле: r = √ab .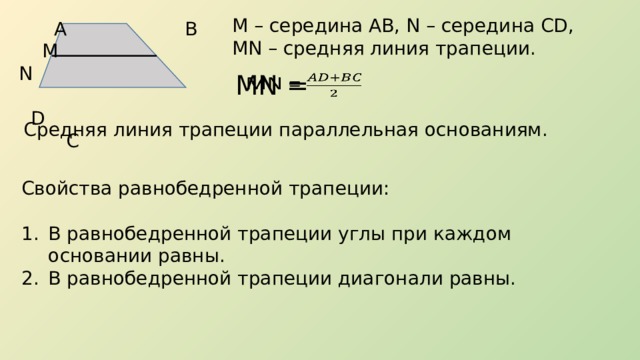
 Объяснить, почему.
Объяснить, почему.  2) Три прямые на плоскости называются параллельными , если они пересекаются в одной общей точке.
Итак, вопрос состоит в том, чтобы объяснить, почему две диагонали трапеции и ее средняя линия НЕ пересекаются в одной общей точке.
Я постараюсь сделать свое объяснение максимально простым.
Пусть трапеция ABCD с основаниями a = AB и b = CD.
Пусть О — точка пересечения диагоналей.
Тогда треугольники AOB и DOC подобны. Это элементарное утверждение, так что возьмем его без доказательств.
Основания этих треугольников, АВ и DC, пропорциональны = .
Далее, поскольку трапеция не является параллелограммом, a =/= b; поэтому не равно 1.
Это означает, что в треугольниках AOB и DOC высоты OE и OF, проведенные из точки O к их основаниям AB и CD,
бывают разной длины.
С другой стороны, средняя линия трапеции ABSD, делит высоту EF трапеции на две конгруэнтные части.
(Это верно для любой трапеции (!) )
Это противоречие объясняет, почему основания трапеции и ее средняя линия не совпадают.
2) Три прямые на плоскости называются параллельными , если они пересекаются в одной общей точке.
Итак, вопрос состоит в том, чтобы объяснить, почему две диагонали трапеции и ее средняя линия НЕ пересекаются в одной общей точке.
Я постараюсь сделать свое объяснение максимально простым.
Пусть трапеция ABCD с основаниями a = AB и b = CD.
Пусть О — точка пересечения диагоналей.
Тогда треугольники AOB и DOC подобны. Это элементарное утверждение, так что возьмем его без доказательств.
Основания этих треугольников, АВ и DC, пропорциональны = .
Далее, поскольку трапеция не является параллелограммом, a =/= b; поэтому не равно 1.
Это означает, что в треугольниках AOB и DOC высоты OE и OF, проведенные из точки O к их основаниям AB и CD,
бывают разной длины.
С другой стороны, средняя линия трапеции ABSD, делит высоту EF трапеции на две конгруэнтные части.
(Это верно для любой трапеции (!) )
Это противоречие объясняет, почему основания трапеции и ее средняя линия не совпадают.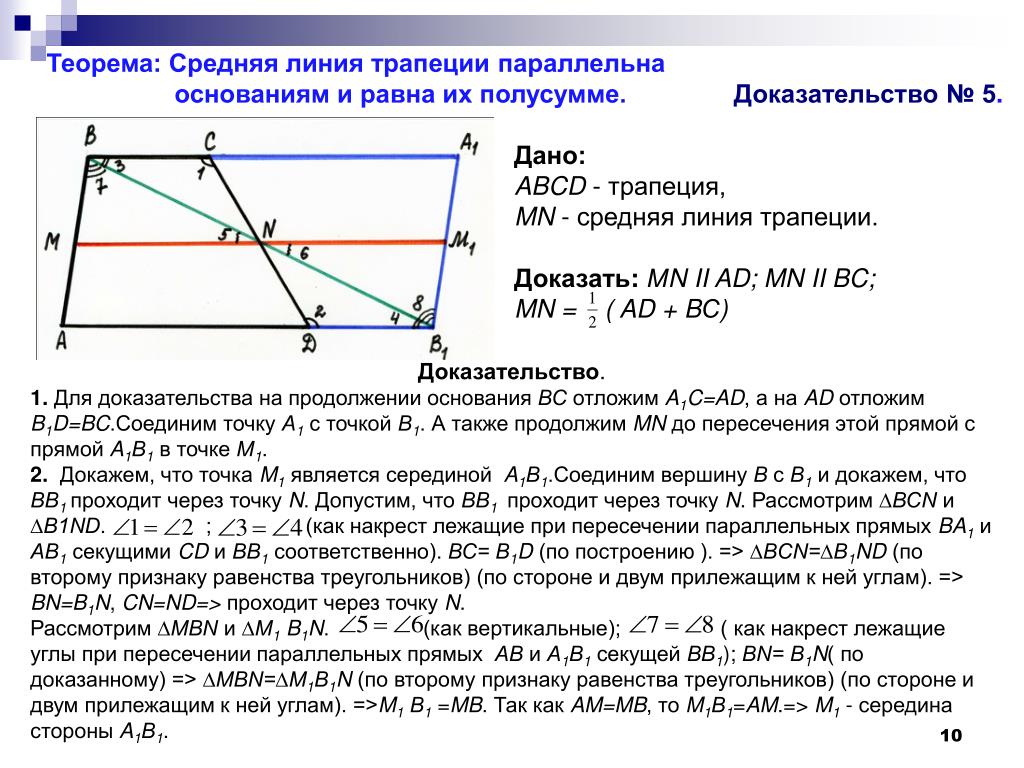

Leave A Comment