Скорость движения в физике, теория и онлайн калькуляторы

Скорость движения в физике, теория и онлайн калькуляторы

Мгновенная скорость движения материальной точки

Пусть положение материальной точки в пространстве задано радиус-вектором $\overline{r}$. При движении этой точки этот радиус-вектор изменяется по величине и направлению. Допустим, что положение материальной точки в момент времени $t_1$ задано при помощи вектора ${\overline{r}}_1$, в момент времени $t_2$ положение этой же точки определяет вектор ${\overline{r}}_2$.

Тогда за время $\Delta t=t_2-t_1$, рассматриваемая нами материальная точка совершает перемещение, равное:

\[\Delta \overline{r}={\overline{r}}_2-{\overline{r}}_1\left(1\right).\]

Тогда предел отношения $\frac{\Delta \overline{r}}{\Delta t}$ при $\Delta t\to 0$ называют мгновенной скоростью ($\overline{v}$):

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta \overline{r}}{\Delta t}\ }\left(2\right). 2_z}\left(5\right).\]

Элементарный путь ($\Delta s$) в общем случае не равен модулю элементарного перемещения ($\left|\Delta \overline{r}\right|$), но если рассматривать отрезки пути и перемещения при $\Delta t\to 0$, то различие между этими параметрами будет тем меньше, чем ближе $\Delta t$ к нулю, поэтому можно считать, что:

\[\overline{v}={\mathop{\lim }_{\Delta t\to 0} \frac{\Delta s}{\Delta t}=\frac{ds}{dt}\ }\left(6\right).\]

Единицей скорости является скорость такого движения, при котором перемещение точки в единицу времени равно единице длины:

\[\left[v\right]=\frac{\left[s\right]}{\left[t\right]}.\]

В Международной системе единиц (СИ) единицей измерения скорости (в том числе и средней скорости) является метр в секунду:

\[\left[v\right]=\frac{м}{с}.\]

Средняя скорость движения тела

Физическая величина, равная отношению перемещения, которое совершило тело к этому промежутку времени движения называют средней скоростью ($\left\langle v\right\rangle $) материальной точки:

\[\overline{\left\langle v\right\rangle }=\frac{\Delta \overline{r}}{\Delta t}\left(7\right). \]

Иногда при вычислении средней скорости используют другое ее определение: среднюю скорость считают равной отношению всего пройдённого пути (s) ко времени (t) движения тела:

\[\left\langle v\right\rangle =\frac{s}{t}\left(8\right).\]

При таком определении средняя скорость — это скалярная величина.

Формулы для вычисления скорости при движении разных видов

Если тело движется равномерно, то его скорость постоянна. Ее вычисляют при помощи выражения:

\[v=\frac{s}{t}\left(9\right),\]

где $s$ — путь; $t$ — время движения. При равномерном прямолинейном движении у скорости постоянным является не только величина, но и направление, то есть можно записать:

\[\overline{v}=const.\]

Если известно ускорение точки как функция от времени ($\overline{a}(t)$) и начальная скорость движения тела (при $t=0$) (${\overline{v}}_0$), то скорость можно найти в любой момент времени применяя формулу:

\[\overline{v}={\overline{v}}_0+\int\limits^{t’}_0{\overline{a}(t)}dt\ \left(10\right). 2+Bt\ \right)=2At+B\ \left(2.3\right).\]

При $t=0$ мгновенная скорость рассматриваемого нами движения равна:

\[v\left(t=0\right)=B\ \left(2.4\right).\]

Конечная скорость при $t=t’$:

\[v\left(t=t’\right)=2At’+B\left(2.5\right).\]

Найдем среднее арифметическое начальной и конечной скоростей на заданном отрезке времени:

\[\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}=\frac{2At’+B+B}{2}=At’+B.\ \]

Ответ: При данном в условии задачи законе движения материальной точки средняя скорость может быть найдена как среднее арифметическое начальной скорости и конечной ($\left\langle v\right\rangle =\frac{v\left(t=0\right)+v\left(t=t’\right)}{2}$).

   

Читать дальше: тело, брошенное под углом к горизонту.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Средняя скорость.

Ускорение | 7 класс Онлайн

Конспект по физике для 7 класса «Средняя скорость. Ускорение». ВЫ УЗНАЕТЕ: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела.  Что такое ускорение. ВСПОМНИТЕ: В каком случае тело движется неравномерно? Что такое путь? Что такое скорость? Каковы единицы скорости? Как определить скорость тела при равномерном движении?

В окружающем нас мире мы крайне редко сталкиваемся с равномерным движением. Обычно скорость тела изменяется с течением времени, и за одинаковые промежутки времени тетю проходит неодинаковые пути. Такое движение является неравномерным. Однако никого не удивляет, когда мы говорим, что ехали на автомобиле со скоростью 60 км/ч, хотя при этом подразумевается, что мы и тормозили, и останавливались перед светофорами, и вновь ускорялись. О какой же скорости тогда идёт речь?

СРЕДНЯЯ СКОРОСТЬ

Для характеристики неравномерного движения вводят понятие средней скорости.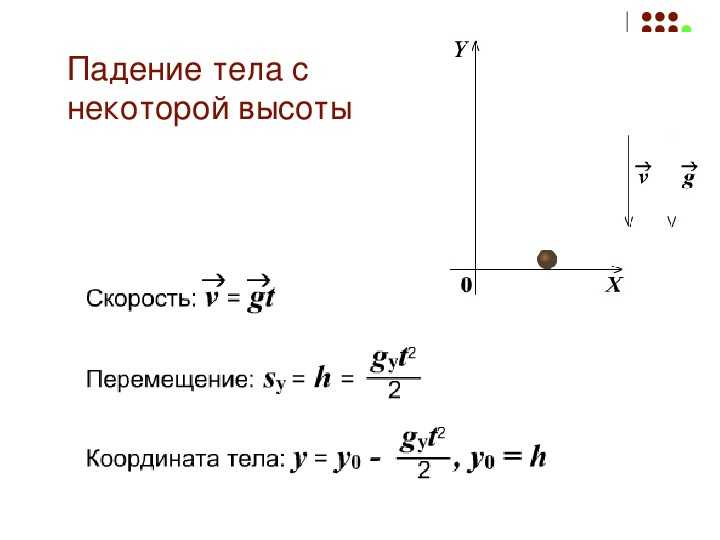 Средняя скорость тела при неравномерном движении находится так же, как и скорость при равномерном движении, т. е. весь пройденный телом путь необходимо разделить на полное время движения тела, включая остановки.

путь
———— = средняя скорость
время

Полученное значение показывает среднюю скорость движения тела на всём пути, и оно может не совпадать со значением скорости в различные моменты времени движения.

Предположим, что автомобиль проехал путь s, состоящий из участков s1, s2, и s3, причём прохождение каждого из них заняло соответственно время t1, t2и t3. Для определения средней скорости движения автомобиля надо весь пройденный путь разделить на общее время движения:
ʋср = (s1 + s2 + s3) / (t1 + t2 + t3)

Зная среднюю скорость движения тела и время движения, можно найти пройденный за это время путь по формуле s = t ʋср.

Если нам известны средняя скорость движения и пройденный путь, мы можем определить время движения по формуле t = s ʋср.

ГРАФИКИ ЗАВИСИМОСТИ ПУТИ И СКОРОСТИ ОТ ВРЕМЕНИ

В отличие от графиков прямолинейного равномерного движения при неравномерном движении графики зависимости скорости и пути от времени могут выглядеть совершенно по-разному в зависимости от конкретной задачи.

Рассмотрим пример. Пусть велосипедист при движении из одного города в другой сначала проехал 8 км за 20 мин. Затем, отдохнув 10 мин, проехал ещё 6 км за 30 мин, а оставшиеся 2,5 км прошёл пешком за 30 мин. Как будут выглядеть соответствующие графики, если в пределах каждого временного интервала велосипедист двигался с постоянными скоростями?

РАВНОПЕРЕМЕННОЕ ДВИЖЕНИЕ

Предположим, в начале определённого отрезка времени мы движемся в автомобиле со скоростью ʋ0.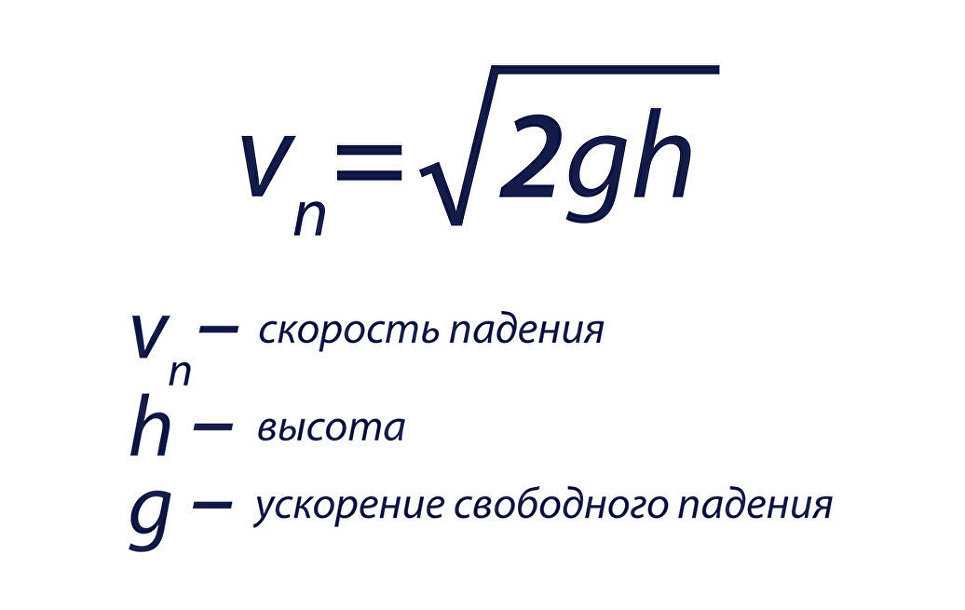 Автомобиль начинает увеличивать скорость, и через время t его скорость становится равной ʋ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.

Прямолинейным равнопеременным движением называется движение, при котором траекторией тела является прямая линия и за любые равные промежутки времени скорость тела изменяется (увеличивается или уменьшается) на одно и то же значение.

УСКОРЕНИЕ

В физике существует величина, характеризующая изменение скорости тела при равнопеременном движении. Она называется ускорением и обозначается латинской буквой а. Для того чтобы вычислить ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло, т. е. от значения его конечной скорости нужно отнять значение начальной скорости и полученный результат разделить на рассматриваемое время движения.

В Международной системе единиц (СИ) за единицу ускорения принимают ускорение такого равнопеременного движения, при котором скорость движущегося тела за время 1 с изменяется на 1 м/с.

Эту единицу называют 1 метр на секунду в квадрате и обозначают 1 м/с2.

Ускорение может принимать как положительное, так и отрицательное значение. Действительно, если скорость тела в начале движения (ʋ0) меньше скорости тела в конце движения (ʋ), то при нахождении ускорения положительное число (ʋ — ʋ0) мы делим на положительное число (t) и получаем положительное значение ускорения. Если же тело замедляется, то значение начальной скорости оказывается больше значения скорости в конце движения, разность ʋ — ʋ0 становится отрицательной и значение ускорения тоже оказывается меньше нуля.

 

Вы смотрели Конспект по физике для 7 класса «Средняя скорость. Ускорение»: Как можно определить среднюю скорость при неравномерном прямолинейном движении тела.  Что такое ускорение. Вернуться к Списку конспектов по физике (оглавление).

Формула скорости

— Что такое формула скорости? Примеры

Формула скорости может быть определена как скорость, с которой объект проходит некоторое расстояние. Скорость можно измерить как расстояние, пройденное телом за определенный период времени. Единицей скорости в СИ является м/с. В этом разделе мы узнаем больше о формуле скорости и ее применении.

Что такое Формула скорости?

Давайте двигаться дальше и больше узнать о формуле скорости в этом разделе. Для выражения скорости могут использоваться различные единицы измерения, такие как м/с, км/ч, мили/ч и т. д. Размерная формула скорости [LT -1 ]. Скорость – это мера того, насколько быстро движется тело. Формула скорости данного тела может быть выражена следующим образом:

Формула скорости

Скорость = расстояние ÷ время

Как использовать формулу скорости?

Формулу скорости можно использовать для определения скорости объектов, учитывая расстояние и время, затраченное на преодоление этого расстояния. Мы также можем использовать формулу скорости для расчета расстояния или времени, подставляя известные значения в формулу для скорости и далее оценивая,
Расстояние = Скорость × Время или Время = Расстояние/Скорость
Давайте кратко рассмотрим пример, показывающий, как использовать формулу для скорости.

Пример:  Какова скорость, если вы проедете 3600 м за 30 минут?

Решение:  Используя формулу для скорости,

Скорость = расстояние ÷ время
Скорость = 3600 ÷ (30 × 60) = 2

Ответ: Ваша скорость, если вы проедете 3600 м за 30 минут, составит 2 м/с.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Заказать бесплатный пробный урок

Примеры формулы скорости

Давайте решим несколько интересных задач, используя формулу скорости.

Пример 1:  Поезд прошел расстояние 120 км за час. Определить скорость поезда в м/с по формуле скорости.

Решение: 

Чтобы найти: Скорость поезда.
Расстояние, пройденное поездом в метрах = 120×1000м = 120000м
Время движения поезда в секундах = 60×60 = 3600 секунд
Использование формулы скорости,
Скорость = Расстояние/Время = 120000/3600 = 33,3 м/с

Ответ: Скорость поезда 33,3 м/с.

Пример 2: Велосипедист проезжает 20 км за 50 минут. Используйте формулу скорости, чтобы вычислить скорость велосипедиста в м/с.

Решение:  Чтобы найти: Скорость велосипедиста.
Расстояние, пройденное велосипедистом в метрах = 20×1000 = 20000м
Время, затраченное велосипедистом в секундах = 50×60= 3000 секунд
Используя формулу скорости,
Скорость = Расстояние/Время = 20000/3000 = 6,67 м/с

Ответ: Скорость велосипедиста равна 6,67 м/с.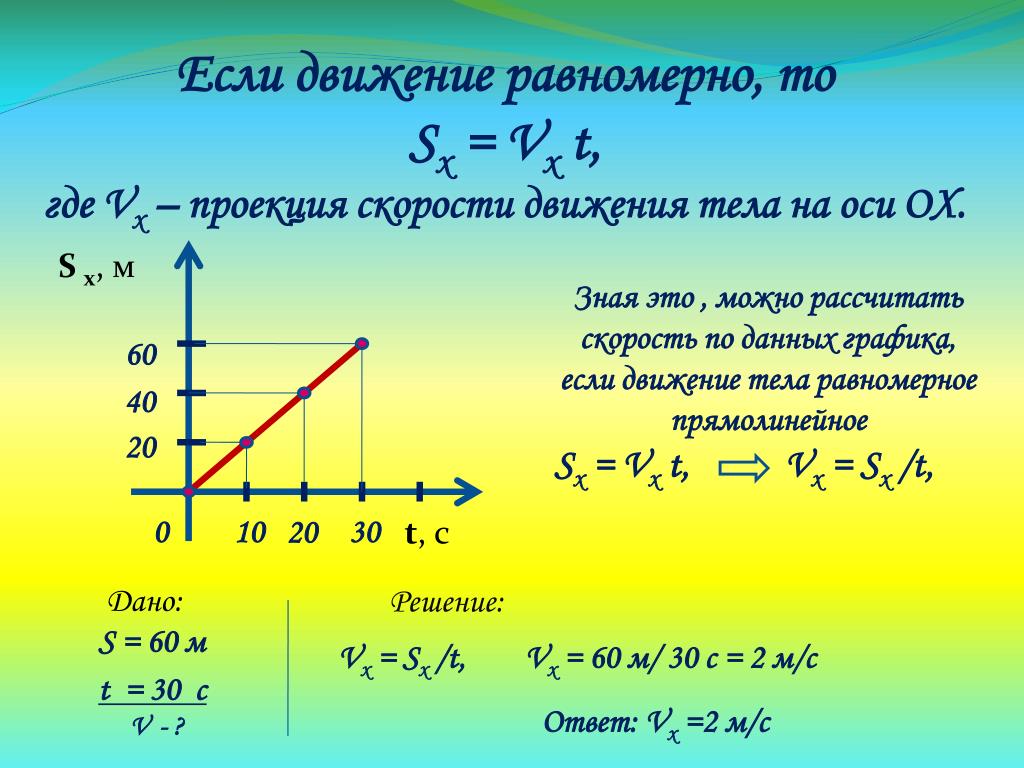

Пример 3: Используя формулу скорости, рассчитайте скорость человека в километрах в час, если расстояние, которое он проходит, составляет 40 километров за 2 часа?

Решение:

Формула для скорости: [Скорость = Расстояние ÷ Время]
Расстояние = 40 км
Время = 2 часа 
Скорость = (40 ÷ 2) км/ч
= 20 километров в час

Ответ: Скорость человека 20 километров в час.

Часто задаваемые вопросы о формуле скорости

Как рассчитать расстояние с помощью формулы скорости?

Формула скорости задается как [Скорость = Расстояние ÷ Время]. Чтобы рассчитать расстояние, формулу скорости можно представить в виде [Расстояние = Скорость × Время].

Как рассчитать время, используя формулу скорости?

Формула скорости задается как [Скорость = Расстояние ÷ Время]. Чтобы рассчитать время, формула скорости будет иметь вид [Время = Пройденное расстояние ÷ Скорость].

Как использовать формулу скорости?

Формула скорости может использоваться в нашей повседневной жизни для определения скорости объектов. Чтобы понять, как использовать формулу скорости, рассмотрим пример.
Пример. Какова ваша скорость, если вы проедете 4000 м за 40 минут?
Решение: использование формулы скорости,
. Скорость = расстояние ÷ время
Скорость = 4000 ÷ (40 × 60) = 1,67 м/с.

Ответ: Ваша скорость, если вы проедете 4000 м за 40 минут, составит 1,67 м/с.

Какой будет общая формула скорости для объекта?

Общая формула скорости для объекта задается как [Скорость = Расстояние ÷ Время]. Единицы скорости в системе СИ – м/с.

Q18 Как определить среднюю скорость тела при неравномерном движении…

Перейти к

  • Объективные вопросы
  • Вопросы с короткими/длинными ответами
  • Числа
  • Физические величины и измерения
  • Движение
  • Энергия
  • Световая энергия
  • Нагревать
  • Звук
  • Электричество и магнетизм

Главная >

Селина Солюшнс Класс 7 Физика > Глава 2 — Движение > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 18

Вопрос 18 Вопросы с короткими/длинными ответами

В18) Как определить среднюю скорость тела при неравномерном движении?

Ответ:

Решение:

Средняя скорость = общее расстояние, пройденное телом/общее время в пути

Расшифровка видео

как определить среднюю скорость мертвых тел при равномерном движении средняя скорость средняя компьютерная скорость какая средняя скорость значит вы под каждой главой есть ремни это значит что общее расстояние пройдено до карьера общее расстояние пройденное тело Направления Общее время поездки это определение мистера. Хорошая форма ракеты была поставлена ​​под сомнение общее расстояние от тела к общему времени стула. Таким образом, общее расстояние до всех означает, какое расстояние полностью преодолевается и время, затраченное на соревнование, является критическим. Надеюсь вы поняли это видео подпишитесь на канал для регулярных обновлений и спасибо за просмотр этого видео.

Связанные вопросы

Q1) Объясните значение терминов покой и движение.

Q2) Прокомментируйте утверждение «покой и движение — относительные термины».