Взаимное расположение прямой и окружности 8 класс онлайн-подготовка на Ростелеком Лицей
Основные определения
Напомним важное определение – определение окружности]
Определение:
Окружностью с центром в точке О и радиусом R называют множество всех точек плоскости, удаленных от точки О на расстояние R.
Обратим внимание на то, что окружностью называют именно множество всех точек, удовлетворяющих описанному условию. Рассмотрим пример:
Точки A, B, C, D квадрата равноудалены от точки Е, но они не являются окружностью (рис. 1).
Рис. 1. Иллюстрация к примеру
В данном случае фигура является окружностью, так как это все множество точек, равноудаленных от центра.
Если соединить любые две точки окружности – получаем хорду. Хорда, проходящая через центр, называется диаметром.
MB – хорда; АВ – диаметр; MnB – дуга, она стягивается хордой МВ;
Угол называется центральным.
Точка О – центр окружности.
Рис. 2. Иллюстрация к примеру
Таким образом, мы вспомнили, что такое окружность и основные ее элементы. Теперь перейдем к рассмотрению взаимного расположения окружности и прямой.
Задана окружность с центром О и радиусом r. Прямая Р, расстояние от центра до прямой, то есть перпендикуляр ОМ, равна d.
Считаем, что точка О не лежит на прямой Р.
Взаимное расположение прямой и окружности, случай с двумя общими точками
По заданным окружности и прямой нам необходимо найти число общих точек.
Случай 1 – расстояние от центра окружности до прямой меньше радиуса окружности:
В первом случае, когда расстояние d меньше радиуса окружности r, точка М лежит внутри окружности. От этой точки мы отложим два отрезка – МА и МВ, длинна которых будет . Значения r и d нам известны, d меньше r, значит, выражение существует и точки А и В существуют. Эти две точки лежат на прямой по построению. Проверим, лежат ли они на окружности.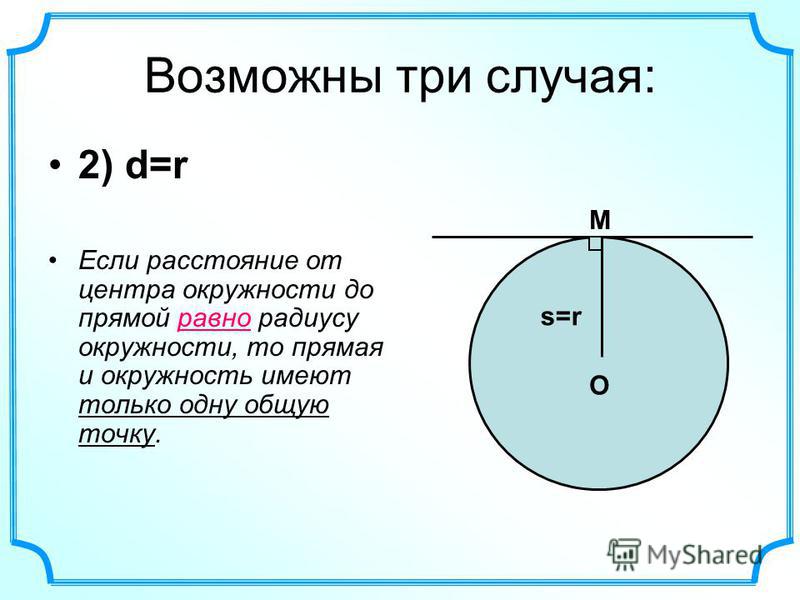 Вычислим по теореме Пифагора расстояние ОА и ОВ:
Вычислим по теореме Пифагора расстояние ОА и ОВ:
Рис. 3. Иллюстрация к случаю 1
Расстояние от центра до двух точек равно радиусу окружности, таким образом, мы доказали, что точки А и В принадлежат окружности.
Итак, точки А и В принадлежат прямой по построению, принадлежат окружности по доказанному – окружность и прямая имеют две общих точки. Докажем, что других точек нет (рис. 4).
Рис. 4. Иллюстрация к доказательству
Для этого возьмем на прямой произвольную точку С и предположим, что она лежит на окружности – расстояние ОС=r. В таком случае треугольник равнобедренный и его медиана ON, которая не совпадает с отрезком ОМ, является высотой. Мы получили противоречие: из точки О опущено два перпендикуляра на прямую.
Таким образом, на прямой Р нет других общих точек с окружностью. Мы доказали, что в случае, когда расстояние d меньше радиуса окружности r, прямая и окружность имеют только две общие точки.
Взаимное расположение прямой и окружности, случай с одной общей точкой
Случай второй – расстояние от центра окружности до прямой равно радиусу окружности (рис.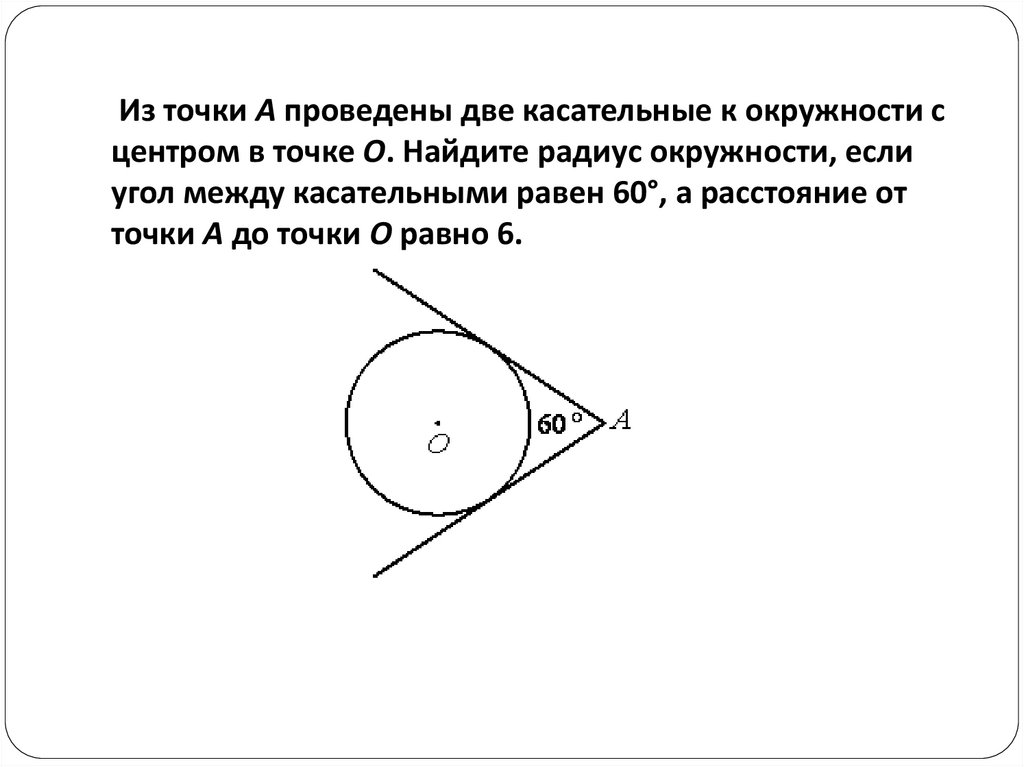 5):
5):
Рис. 5. Иллюстрация к случаю 2
Напомним, что расстояние от точки до прямой – это длина перпендикуляра, в данном случае ОН – перпендикуляр. Так как, по условию, длина ОН равна радиусу окружности, то точка Н принадлежит окружности, таким образом, точка Н общая для прямой и окружности.
Докажем что других общих точек нет. От противного: предположим, что точка С на прямой принадлежит окружности. В таком случае, расстояние ОС равно r, и тогда ОС равно ОН. Но в прямоугольном треугольнике гипотенуза ОС больше катета ОН. Получили противоречие. Таким образом, предположение неверно и нет никакой точки кроме Н, общей для прямой и окружности. Мы доказали, что в данном случае общая точка единственная.
Взаимное расположение прямой и окружности, случай, когда нет общих точек
Случай 3 – расстояние от центра окружности до прямой больше радиуса окружности:
Расстояние от точки до прямой – длина перпендикуляра.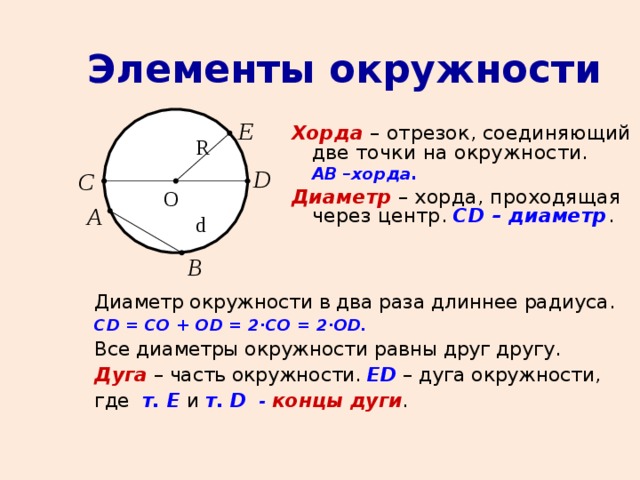 Проводим из точки О перпендикуляр к прямой Р, получаем точку Н, которая не лежит на окружности, так как ОН по условию больше радиуса окружности. Докажем, что любая другая точка прямой не лежит на окружности. Это хорошо видно из прямоугольного треугольника , гипотенуза ОМ которого больше катета ОН, а значит, больше радиуса окружности, таким образом, точка М не принадлежит окружности, как и любая другая точка на прямой. Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 6).
Проводим из точки О перпендикуляр к прямой Р, получаем точку Н, которая не лежит на окружности, так как ОН по условию больше радиуса окружности. Докажем, что любая другая точка прямой не лежит на окружности. Это хорошо видно из прямоугольного треугольника , гипотенуза ОМ которого больше катета ОН, а значит, больше радиуса окружности, таким образом, точка М не принадлежит окружности, как и любая другая точка на прямой. Мы доказали, что в данном случае окружность и прямая не имеют общих точек (рис. 6).
Рис. 6. Иллюстрация к случаю 3
Теоремы о диаметре и хорде
Рассмотрим теорему. Предположим, что прямая АВ имеет две общих точки с окружностью (рис. 7).
Рис. 7. Иллюстрация к теореме
Имеем хорду АВ. Точка Н, по условию, – середина хорды АВ и лежит на диаметре СD.
Требуется доказать, что в таком случае диметр перпендикулярен хорде.
Доказательство:
Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как .
Точка Н, по условию, – середина хорды, значит середина медианы АВ равнобедренного треугольника. Мы знаем, что медиана равнобедренного треугольника перпендикулярна его основанию, значит, является высотой: , отсюда , таким образом, доказано, что диаметр, проходящий через середину хорды, перпендикулярен ей.
Справедлива и обратная теорема: если диаметр перпендикулярен хорде, то он проходит через ее середину.
Задана окружность с центром О, ее диаметр СD и хорда АВ. Известно, что диаметр перпендикулярен хорде, нужно доказать, что он проходит через ее середину (рис. 8).
Рис. 8. Иллюстрация к теореме
Доказательство:
Рассмотрим равнобедренный треугольник ОАВ, он равнобедренный, так как . ОН, по условию, – высота треугольника, так как диаметр перпендикулярен хорде. Высота в равнобедренном треугольнике одновременно является медианой, таким образом, АН=НВ, значит, точка Н является серединой хорды АВ, значит, доказано, что диаметр, перпендикулярный хорде, проходит через ее середину.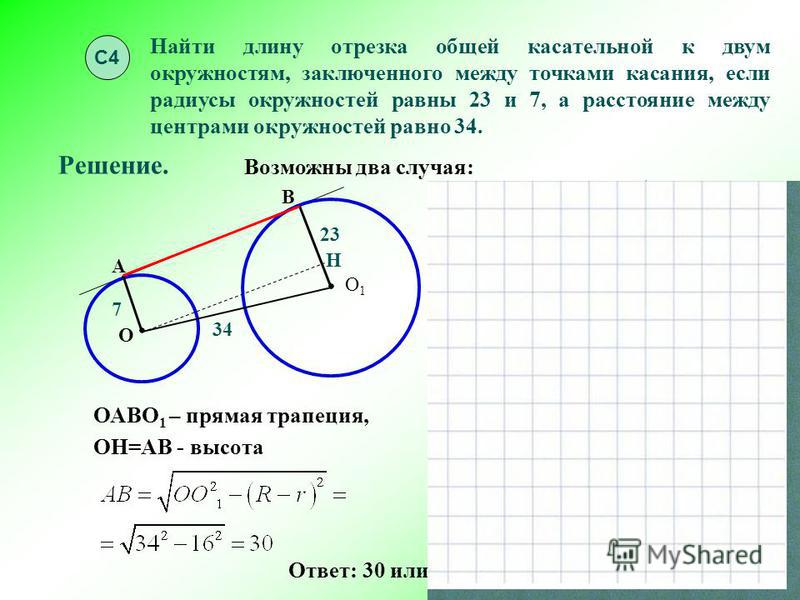
Прямую и обратную теорему можно обобщить следующим образом.
Теорема:
Диаметр перпендикулярен хорде тогда и только тогда, когда он проходит через ее середину.
Выводы по уроку
Итак, мы рассмотрели все случаи взаимного расположения прямой и окружности. На следующем уроке мы рассмотрим касательную к окружности.
Список литературы
- Александров А.Д. и др. Геометрия 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия 8. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Edu.glavsprav.ru (Источник).
- Webmath.exponenta.ru (Источник).
- Fmclass.ru (Источник).
Домашнее задание
Задание 1.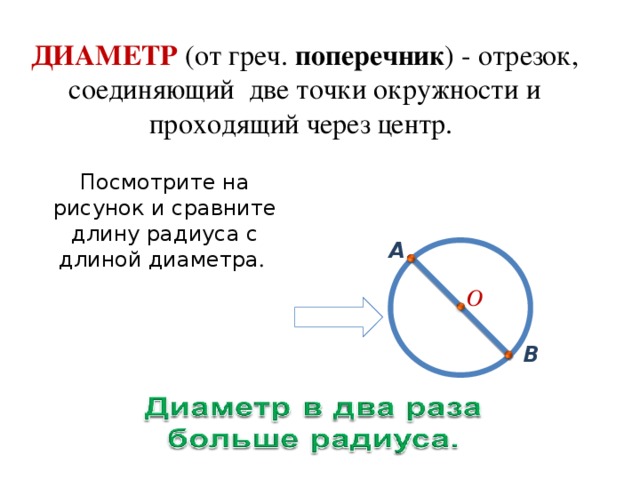 Найти длины двух отрезков хорды, на которые разделяет ее диаметр окружности, если длина хорды – 16 см, а диаметр ей перпендикулярен.
Найти длины двух отрезков хорды, на которые разделяет ее диаметр окружности, если длина хорды – 16 см, а диаметр ей перпендикулярен.
Задание 2. Указать количество общих точек прямой и окружности, если:
а) расстояние от прямой до центра окружности – 6 см, а радиус окружности – 6,05 см;
б) расстояние от прямой до центра окружности – 6,05 см, а радиус окружности – 6 см;
в) расстояние от прямой до центра окружности – 8 см, а радиус окружности – 16 см.
Задание 3. Найти длину хорды, если диаметр ей перпендикулярен, а один из отрезков, отсекаемых диаметром от нее, равен 2 см.
Взаимное расположение прямой и окружности. 8 класс
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
8 класс
Геометрия
2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
3. Как вы думаете, сколько общих точек могут иметь прямая и окружность?
О4. Сначала вспомним как задаётся окружность
BD
Окружность (О, r)
О
A
r
r – радиус
С
АВ – хорда
CD — диаметр
5. Исследуем взаимное расположение прямой и окружности в первом случае:
Первый случай:А
Н
В
d
d<r
r
О
две общие точки
АВ – секущая
d – расстояние от центра окружности до прямой
6. Второй случай:
d=rодна общая точка
АВ – касательная
А
Н
В
d
r
О
d – расстояние от центра окружности до прямой
7.
 Третий случай:H
Третий случай:Hd>r
d
r
О
не имеют общих точек
d – расстояние от центра окружности до прямой
8. Сколько общих точек могут иметь прямая и окружность?
HА
Н
В
d
d
r
О
d<r
две общие
точки
Если расстояние от
центра окружности
до прямой меньше
радиуса
окружности, то
прямая и
окружность имеют
две общие точки.
d
r
О
d=r
одна общая
точка
Если расстояние
от центра
окружности до
прямой равно
радиусу
окружности, то
прямая и
окружность
имеют только одну
общую точку.
r
О
d>r
не имеют
общих точек
Если расстояние от
центра окружности до
прямой больше радиуса
окружности, то прямая
и окружность не имеют
общих точек.
9. Касательная к окружности
Определение:Прямая, имеющая с
окружностью
только одну общую
точку, называется
касательной к
окружности, а их
общая точка
называется точкой
касания прямой и
окружности.

M
m
s=r
O
10. Выясните взаимное расположение прямой и окружности, если:
r = 15 см, s =11см
r = 6 см, s = 5,2
см
r = 3,2 м, s = 4,7 м
r = 7 см, s = 0,5
дм
r = 4 см, s = 40 мм
прямая – секущая
прямая – секущая
общих точек нет
прямая – секущая
прямая касательная
11. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная кокружности с
центром О
М – точка касания
OM — радиус
m OM
M
m
O
12. Свойство касательных, проходящих через одну точку:
▼ По свойствукасательной o
1 90 , 2 90o.
Отрезки касательных к
окружности, проведенные
из одной точки, равны и
∆АВО, ∆АСО–
составляют равные углы
прямоугольные
с прямой, проходящей через
эту точку и центр окружности. ∆АВО=∆АСО–по гипотенузе
В
1
О
3
4
2
С
А
и катету:
ОА – общая,
ОВ=ОС – радиусы
АВ=АС и
3 4
▲
13.
 Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она окружность с центром О
Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она окружность с центром Орадиуса OM
m – прямая, которая
проходит через точку М
m OM
m – касательная
M
m
O
Решение задач
Дано:Окр. О, r , АВ касательная
ОА 2см, r 1,5см
Найти: АВ
№ 1.
B
?
1,5
О
2
А
1.
2.
Рассмотрим АОВ- прямоугольный(?)
AB 2 OA 2 OB 2
AB 4 2,25 1,75
B
?
1,5
О
2
А
№ 2.
Дано: Окр. О, r
Найти:
АB, АС- касательные
ВАС
B
4,5
?
О
К
С
А
1. Рассмотрим
-ки АОВ и АОС — равны(?)
2. BАО= САО
3. BАО и BАО — прямоугольные (?)
4. ОВ =4,5 ОА=9 → (?)
5. BАС= 60
→
B
4,5
?
О
К
С
А
№ 3.
Дано:
Найти:
АВ
Окружность
АВ касательная
?
12
600
О
А
АВ 2 ОА 2 ОВ 2
АВ
24 2 12 2 12 3
tg A
OB
AB
1
12
AB
3
B
?
12
600
AB 12 3
О
А
Домашнее задание
Дано:
Найти:
Окружность
АВ касательная, АО 4см
ОВ
А
B
С
О
Дано:
Найти:
Окружность
АВ касательная
радиус
B
А
О
Окружность, R 6
АВ касательная, ОА ОВ
ОА
Дано:
Найти:
А
16
О
B
English Русский Правила
Радиус круга — Формула | Что такое Радиус?
Радиус окружности определяется как отрезок, соединяющий центр с границей окружности.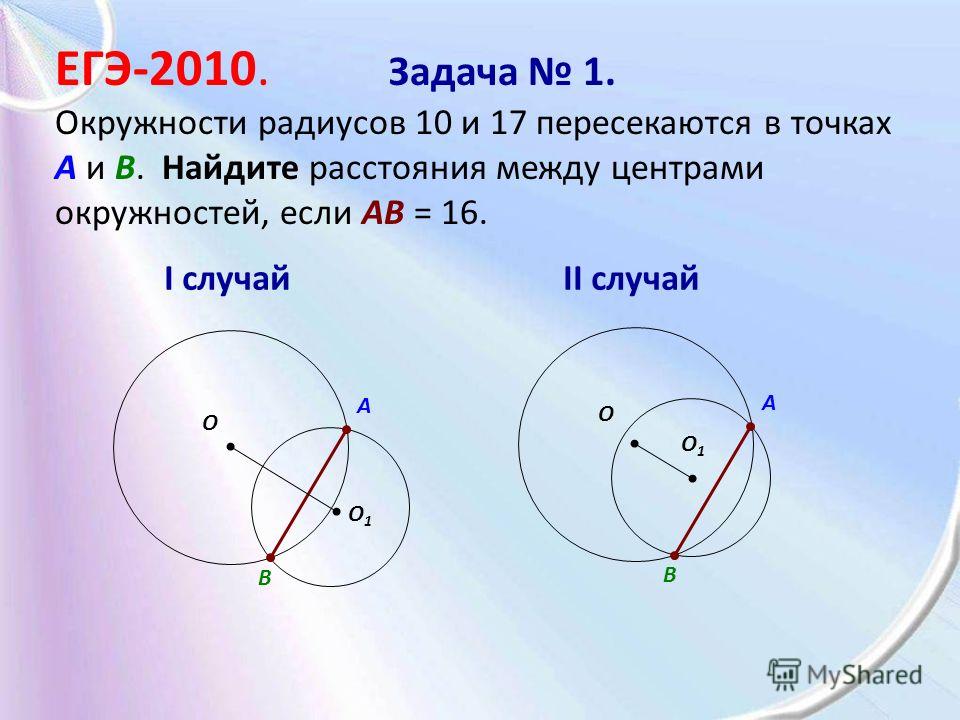
| 1. | Что такое Радиус? |
| 2. | Формулы радиуса окружности |
| 3. | Радиус окружности |
| 4. | Как найти радиус окружности? |
| 5. | Уравнение радиуса окружности |
| 6. | Радиус сферы |
| 7. | Часто задаваемые вопросы о Radius |
Что такое радиус?
Радиус определяется как отрезок, соединяющий центр круга или сферы с его окружностью или границей. Это важная часть кругов и сфер и обычно обозначается аббревиатурой «r». Множественное число от радиуса — это «радиус», который используется, когда мы говорим о более чем одном радиусе одновременно.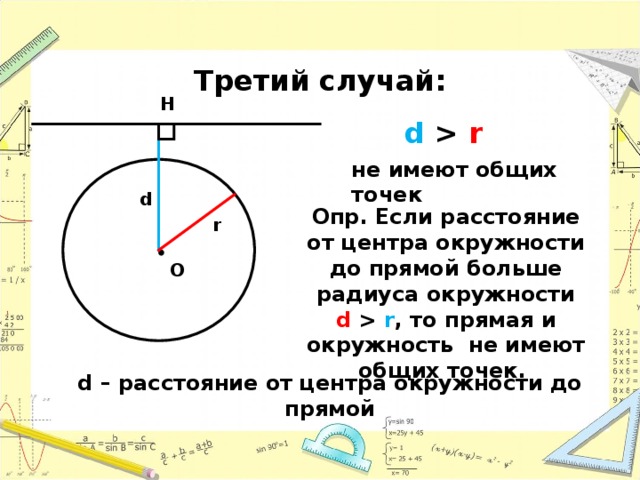
Значение радиуса
Радиус окружности — это расстояние от центра до любой точки на границе окружности. Следует отметить, что длина радиуса составляет половину длины диаметра. Его можно выразить как d/2, где d — диаметр круга или сферы. Обратите внимание на фигуру окружности, приведенную ниже, которая показывает соотношение между радиусом и диаметром.
Теперь давайте узнаем о формулах радиуса, которые используются, когда заданы другие параметры.
Формулы радиуса окружности
Радиус окружности можно рассчитать по некоторым специальным формулам, зависящим от известных величин и параметров.
Формула радиуса с диаметром
Диаметр представляет собой прямую линию, проходящую через центр и соединяющую точку на одном конце с точкой на другом конце окружности. Диаметр в два раза больше длины радиуса. Математически это записывается как диаметр = 2 × радиус. Это также самая длинная хорда окружности. Когда дан диаметр круга, формула радиуса выражается как:
Радиус = диаметр ÷ 2
Формула радиуса из длины окружности
Периметр круга называется его окружностью.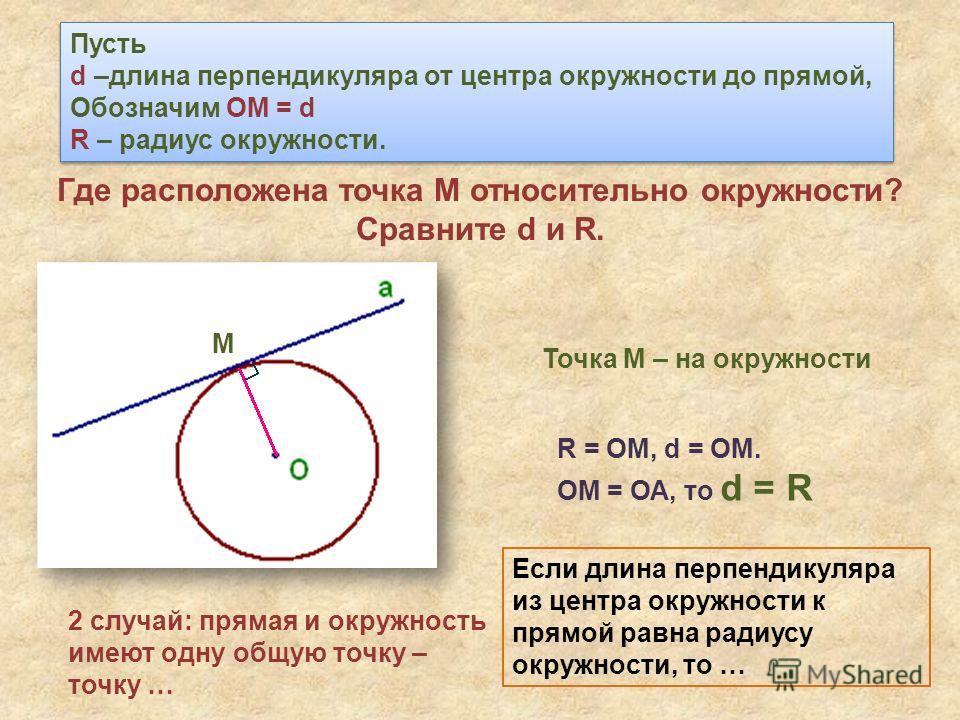 Это граница круга и может быть выражена формулой: C = 2πr. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:
Это граница круга и может быть выражена формулой: C = 2πr. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:
Радиус = Длина окружности/2π
Формула радиуса с использованием площади
Площадь круга — это пространство, занимаемое кругом. Связь между радиусом и площадью определяется формулой Площадь круга = πr 2 . Здесь r — радиус, а π — константа, равная 3,14159. Формула радиуса с использованием площади круга выражается как:
Радиус = √(Площадь/π)
Радиус окружности
Радиус является важной частью окружности. Это длина от центра круга до любой точки на его границе. Другими словами, когда мы соединяем центр круга с любой точкой его окружности с помощью прямой линии, этот отрезок линии является радиусом этого конкретного круга. Окружность может иметь несколько радиусов, потому что на окружности бесконечное количество точек.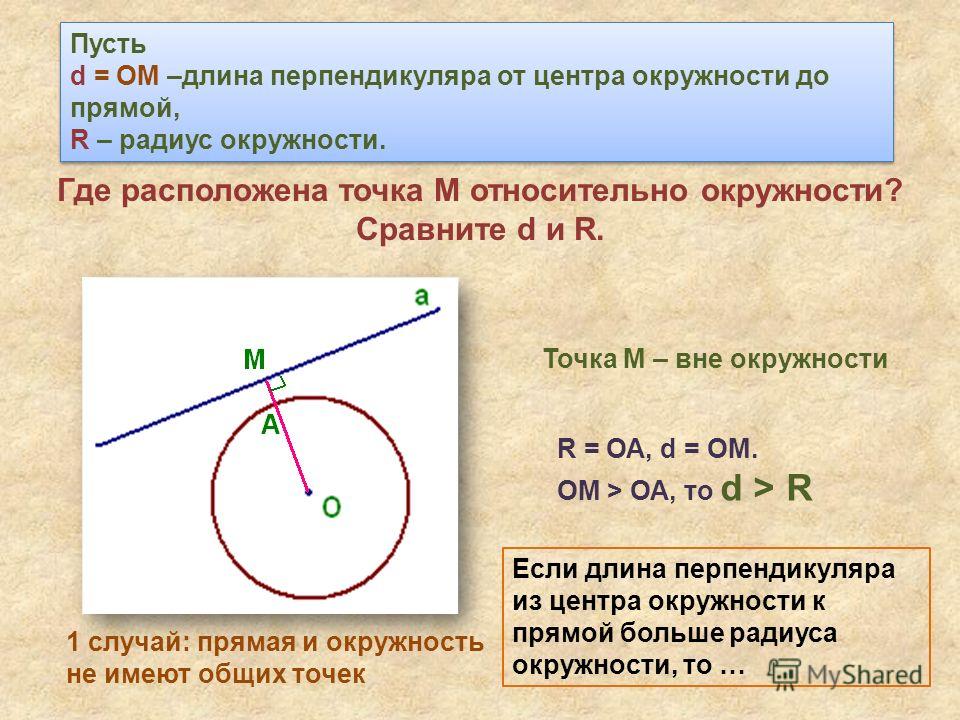
На приведенном ниже рисунке точки A, B, M, N, P, Q, X и Y лежат на границе окружности. Заметим, что эти точки равноудалены от центра O. Итак, все отрезки OA, OB, OM, ON, OY, OX, OP и OQ называются радиусами окружности. Следует отметить, что OA = OB = OM = ON = OP = OQ = OX = OY.
Как найти радиус окружности?
Радиус окружности можно найти с помощью трех основных формул радиуса. Эти формулы формируются с использованием диаметра, площади и длины окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.
- Когда диаметр круга известен, формула такова: Радиус = Диаметр/2. Например, если диаметр равен 24 единицам, то радиус равен 24/2 = 12 единицам.
- Когда длина окружности известна, формула такова: Радиус = Длина окружности/2π. Если длина окружности равна 44 единицам, то ее радиус можно рассчитать как 44/2π.

- Когда известна площадь круга, формула для радиуса: Радиус = ⎷(Площадь круга/π). если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.
Уравнение радиуса окружности
Радиус уравнения окружности на декартовой плоскости с центром (h, k) определяется как (x − h) 2 + (y − k) 2 = r 2 . Это известно как уравнение окружности, когда известен радиус. Здесь (x, y) — точки на окружности окружности, находящиеся на расстоянии «r» (радиус) от центра (h, k). Когда центр окружности находится в начале координат (0,0), уравнение окружности сводится к x  Уравнение для нахождения радиуса этой окружности: (x − 0) 2 + (y − b) 2 = r 2 ⇒ x 2 + (y − b) 2 = r
Уравнение для нахождения радиуса этой окружности: (x − 0) 2 + (y − b) 2 = r 2 ⇒ x 2 + (y − b) 2 = r
Радиус сферы
Сфера — трехмерная объемная фигура. Радиус сферы — это отрезок от центра до любой точки на границе сферы. Это определяющий фактор при рисовании сферы, так как ее размер зависит от ее радиуса. Как и в случае с кругом, внутри сферы могут быть нарисованы бесконечные радиусы, и все эти радиусы будут равны по длине. Чтобы вычислить объем и площадь поверхности сферы, нам нужно знать ее радиус. И мы можем легко вычислить радиус сферы по формулам ее объема и площади поверхности.
Радиус сферы по объему = 3 ⎷(3V/4π), где V представляет объем, а значение π приблизительно равно 3,14
Радиус сферы по площади поверхности = ⎷(A/4π), где A представляет площадь поверхности.
Используйте наш бесплатный онлайн-калькулятор радиуса сферы, чтобы рассчитать радиус с заданным объемом, площадью поверхности или диаметром сферы.
☛ Статьи по теме
Проверьте эти интересные статьи, связанные с радиусом и его формулами.
- Формула радиуса кривизны
- Сегмент круга
- Сектор круга
Часто задаваемые вопросы о радиусе окружности
Что такое радиус круга в геометрии?
Радиус окружности — это длина отрезка от центра до точки на окружности окружности. Обычно обозначается аббревиатурой «р». В круге может быть бесконечное количество радиусов, и длина всех этих радиусов будет одинаковой. Это половина диаметра круга.
Как диаметр связан с радиусом окружности?
Диаметр круга в два раза больше радиуса. Можно также сказать, что длина радиуса равна половине диаметра. Связь между радиусом и диаметром можно выразить формулой: Диаметр = 2 × радиус. Используйте бесплатный онлайн-калькулятор радиуса, чтобы рассчитать радиус с заданным диаметром.
Как найти радиус окружности?
Длина окружности и радиус связаны друг с другом, и их отношение можно выразить как Длина окружности = 2πr, где ‘r’ — радиус. Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.
Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.
Что такое формула радиуса?
Радиус круга можно рассчитать с помощью различных формул. Для расчета радиуса используйте следующие формулы:
- Когда диаметр известен, формула выглядит так: Радиус = Диаметр / 2
- Когда длина окружности известна, формула выглядит так: Радиус = Длина окружности / 2π
- Когда площадь известна, формула выглядит так: Радиус = ⎷(Площадь круга / π)
Как рассчитать радиус окружности с помощью калькулятора?
Длина радиуса равна половине длины диаметра, который можно рассчитать с помощью онлайн-калькулятора радиуса Cuemath, просто введя любое заданное значение, такое как диаметр, длина окружности или площадь круга.
Как найти радиус круга с площадью?
Если площадь круга дана, то формула для нахождения радиуса дается как Радиус = ⎷(A/π), где A – заданная площадь.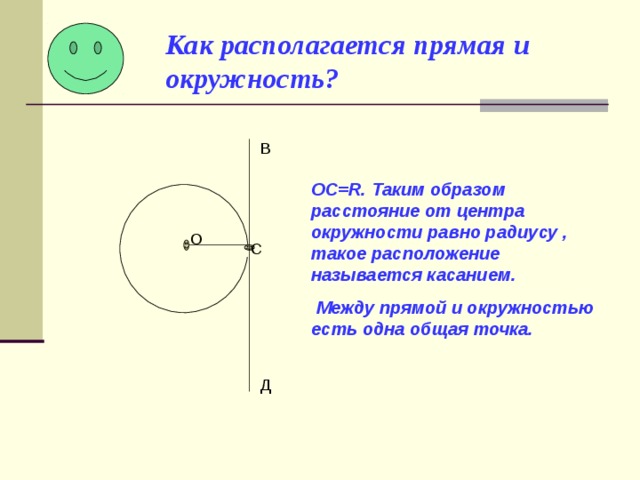
Как рассчитать радиус по диаметру?
Радиус круга можно рассчитать, если известен диаметр. Связь между радиусом и диаметром круга выражается как Радиус = Диаметр ÷ 2. Итак, если диаметр круга равен 6 единицам, то радиус будет равен 6 ÷ 2 = 3 единицам.
Что такое круг? Определение, формулы, свойства, примеры
Что такое круг?
Круг — это круглая фигура, не имеющая углов и краев.
В геометрии круг можно определить как замкнутую форму, двумерную форму, изогнутую форму.
Вокруг нас есть несколько круглых вещей: автомобильная шина, настенные часы, которые показывают время, и леденец на палочке.
Родственные игры
Центр окружности
Центром окружности называется центральная точка окружности, от которой все расстояния до точек окружности равны. Это расстояние называется радиусом окружности.
Здесь точка P является центром окружности.
Связанные рабочие листы
Внутренняя и внешняя часть круга
Рассмотрим круг с центром P и радиусом r. Круг имеет внутреннюю и внешнюю области.
Круг имеет внутреннюю и внешнюю области.
Все точки, расстояние до которых меньше радиуса окружности, лежат внутри окружности. Например, точки P, Q и R лежат внутри круга.
Все точки, для которых расстояние больше радиуса окружности, лежат вне окружности. Например, точки S и T лежат снаружи круга.
Все точки, для которых расстояние равно радиусу окружности, лежат на окружности. Например, точки U и V лежат на окружности.
Полукруг:
Полу означает половину, поэтому полукруг — это половина круга. Он образуется путем разрезания целого круга по отрезку, проходящему через центр круга. Этот отрезок называется диаметром окружности.
Четверть круга:
Четверть означает одну четверть. Итак, четверть круга – это четверть круга, образованная путем разбиения круга на 4 равные части или полукруга на 2 равные части.
Четверть круга также называется квадрантом.
Части круга
Радиус круга:
Радиус — это отрезок с одной конечной точкой в центре круга и другим концом на окружности.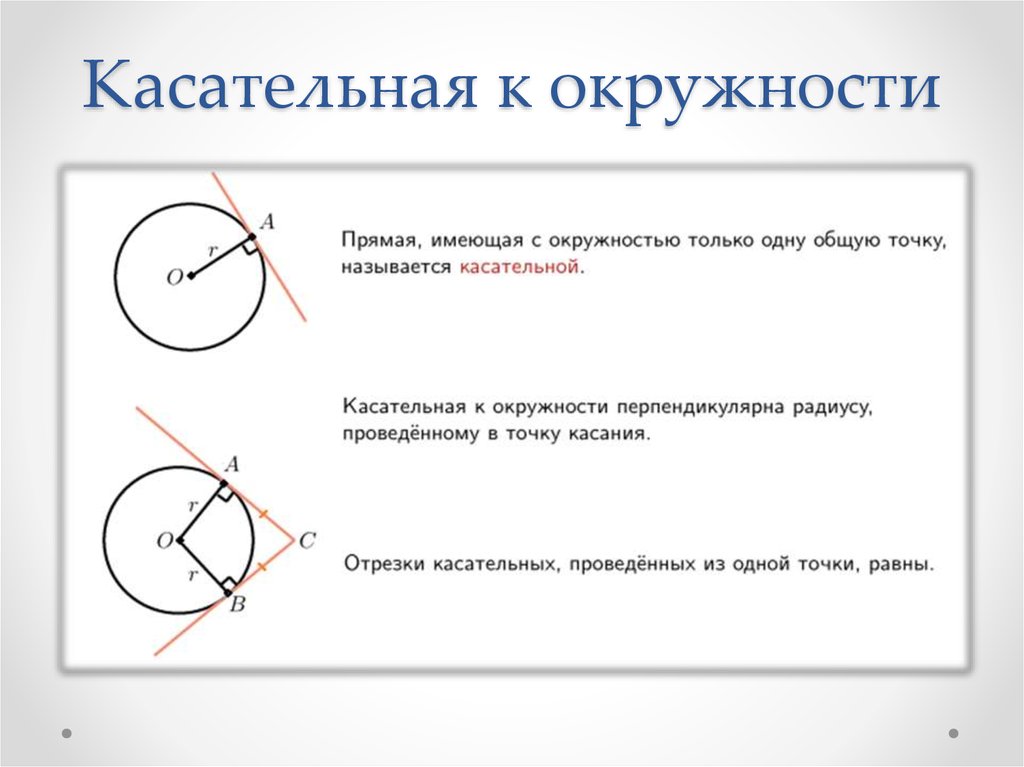
Радиус = $\frac{Diameter}{2}$
Диаметр окружности:
Отрезок, проходящий через центр окружности и имеющий концы на окружности, называется диаметром круга.
Диаметр = 2 × радиус
Окружность:
Длина окружности — это расстояние по окружности. Он такой же, как периметр других фигур.
Хорды окружностей:
Отрезок, концы которого лежат на окружности, называется хордой окружности.
Диаметром окружности является ее наибольшая хорда.
Дуга окружности:
Дуга — это часть окружности, все точки которой лежат на окружности. Это кривая, которая является частью его окружности.
Дуга, соединяющая концы диаметра, имеет размер 180° и называется полуокружностью.
Дуга делит окружность на две части. Меньшая часть называется малой дугой, а большая часть называется большой дугой.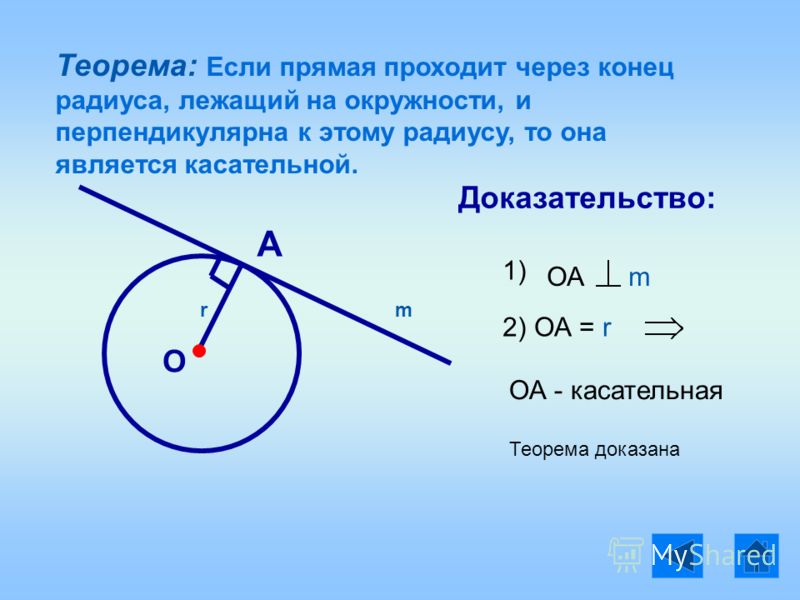
Секущая окружности:
Секущей называется прямая, пересекающая окружность ровно в двух точках.
Касательная окружности:
Касательная — это линия, пересекающая окружность ровно в одной точке.
Сегменты круга:
Хорда круга делит область круга на две части. Каждая часть называется сегментом окружности.
Сегмент, содержащий малую дугу, называется малым сегментом, а сегмент, содержащий большую дугу, называется большим сегментом.
Сектор круга:
Сектор круга – это часть круга, заключенная двумя радиусами и дугой круга как частью его границы.
Когда два радиуса встречаются в центре круга, образуя сектор, он фактически образует два сектора. Сектор окружности называется малым сектором, если малая дуга окружности является частью его границы. Сектор называется большим сектором, если большая дуга окружности является частью его границы.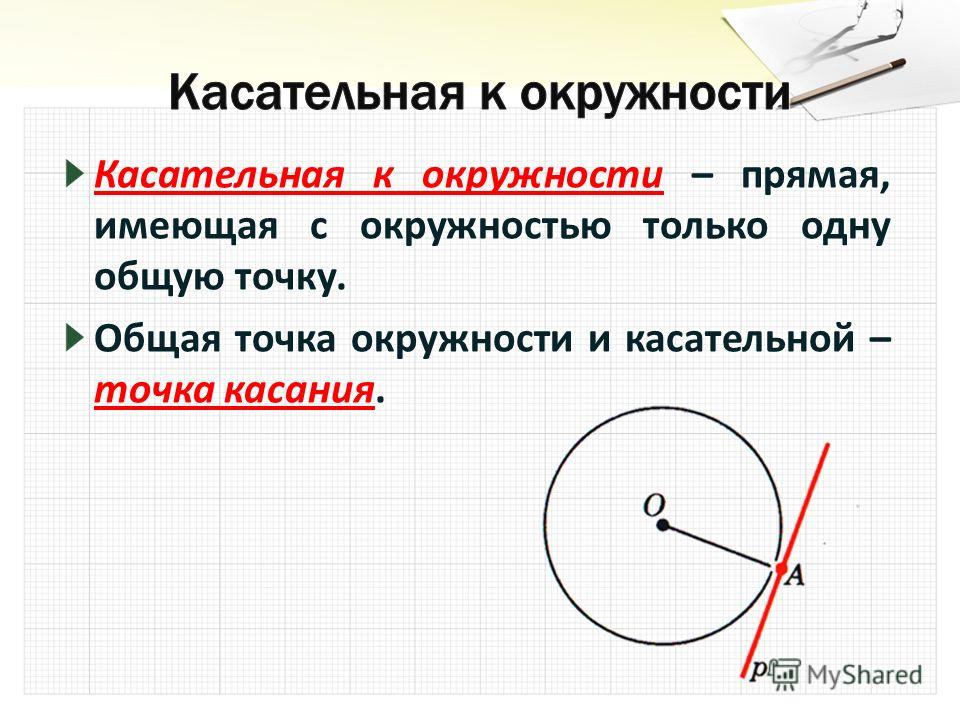
Формулы круга
Площадь круга:
Площадь круга – это область, заключенная внутри круга.
Площадь круга зависит от длины его радиуса. 9{2}$
Окружность:
Расстояние по окружности равно длине окружности.
Окружность = 2$\pi$r
Значение $\pi$ = 3,14 или $\frac{22}{7}$
Решенные примеры на окружностиПример 1. Сопоставьте каждому термину правильное определение.
Решение:
1 – b
2 – d
3 – a
4 – c
Пример 2: Используйте рисунок, чтобы ответить на вопросы.
- Какой термин лучше всего описывает OE?
- Назовите 3 отрезка линии одинаковой длины.
- Назовите секанс.
- Какие два термина можно использовать для описания AB?
Решение:
- Радиус
- OA, OB и OE
- ПК
- Диаметр и хорда
Пример 3: Если окружность имеет радиус 3 см, какова длина ее самой длинной хорды?
Решение:
Самая длинная хорда — это диаметр окружности.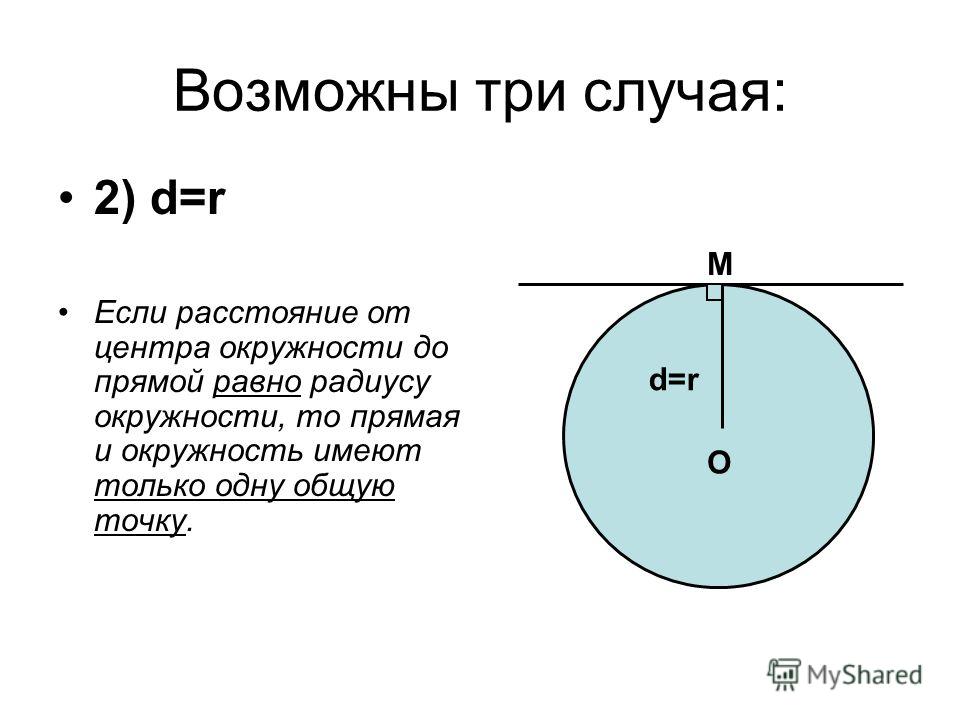
Диаметр = 2 × радиус = 2 × 3 = 6 см
Пример 4: Минутная стрелка круглых часов имеет длину 21 см. Какое расстояние проходит наконечник за 1 час?
Решение:
Расстояние, пройденное за 1 час, равно длине окружности часов, то есть окружности.
Окружность = 2$\pi$r = 2 × $\frac{22}{7}$ × 21 = 132 см
Практические задачи на круг
1
Окружность с центром O имеет радиус 5 см и OQ = 7 см, тогда где находится точка Q?
На круге.
Внутри круга.
Снаружи круга.
Правильный ответ: снаружи круга.
Длина OQ больше радиуса окружности. Значит, точка Q лежит снаружи окружности.
2
Общее количество диаметров окружности:
1
2
3
Бесконечный (неисчисляемый)
Правильный ответ: Бесконечный (неисчисляемый)
Диаметр — это отрезок, проходящий через центр окружности и имеющий концы на окружности.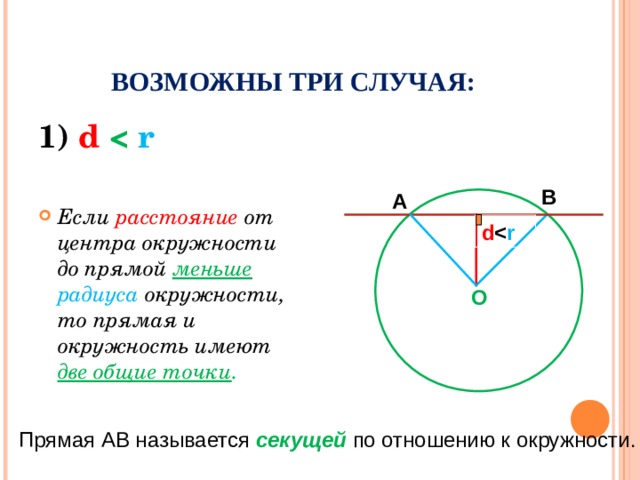 Через точку может проходить бесконечное количество прямых, поэтому существует бесконечное число диаметров окружности.
Через точку может проходить бесконечное количество прямых, поэтому существует бесконечное число диаметров окружности.
3
Две окружности с центрами P и Q радиусами 4 см и 5,5 см касаются снаружи, каково расстояние между их центрами?
4 см
5,5 см
9,5
1,5
Правильный ответ: 9,5
Расстояние между центрами = 4 см + 5,5 см = 9,5 см
4
Если длина окружности равна 176 см. Какова будет его площадь?
56 см 2
2 464 см 2
232 см 2
1232 см 2
Правильный ответ: 2,464 CM 2
. frac{22}{7}$ × r
r = 28 см
Площадь = πr 2 = $\frac{22}{7}$ × 28 × 28 = 2464 см 2
Часто задаваемые вопросы по кругу пройти через две заданные точки?
Можно провести только одну окружность, проходящую через две заданные точки.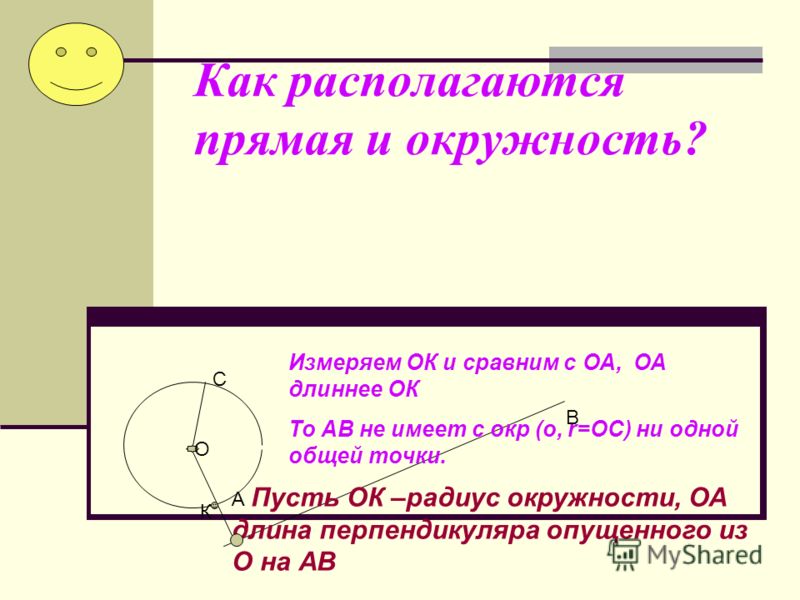

Leave A Comment