Как работают блоки?

Блок состоит из одного или нескольких колес (роликов), огибаемых цепью, ремнем или тросом. Так же, как и рычаг, блок уменьшает усилие, необходимое для подъема груза, но плюс к этому может изменять направление прикладываемой силы.
За выигрыш в силе приходится расплачиваться расстоянием: чем меньшее усилие требуется для подъема груза, тем больше путь, который должна пройти точка приложения этого усилия. Система блоков увеличивает выигрыш в силе за счет использования большего количества грузонесущих цепей. Подобные силосберегающие устройства имеют очень широкий диапазон применения — от перемещения на высоту массивных стальных балок на строительных площадках до подъема флагов.
Как и в случае других простых механизмов, изобретатели блока неизвестны. Хотя, возможно, блоки существовали и раньше, первое упоминание о них в литературе относится к пятому веку до нашей эры и связано с использованием блоков древними греками на кораблях и в театрах.
Установленные на подвесном рельсе подвижные системы блоков (рисунок сверху) широко распространены на сборочных линиях, поскольку существенно облегчают перемещение тяжелых деталей. Прикладываемая сила (F) равна частному от деления веса груза (W) на используемое количество поддерживающих его цепей (n).
Одинарные неподвижные блоки
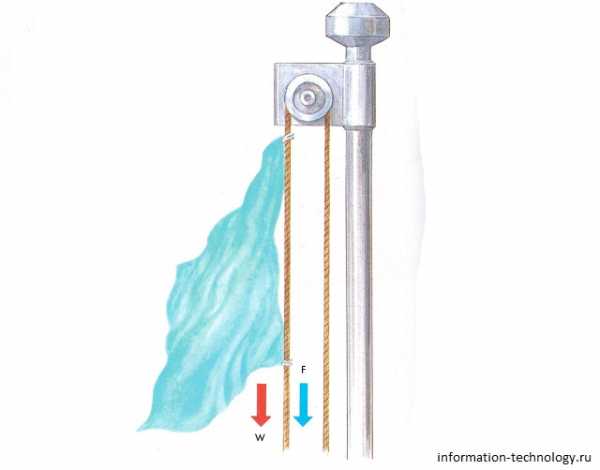
Этот простейший тип блока не уменьшает усилие, необходимое для подъема груза, но зато изменяет направление прикладываемой силы, как это показано на рисунках сверху и справа вверху.
Одинарные подвижные блоки
Одинарный блок, имеющий возможность перемещения, уменьшает наполовину усилие, требующееся для подъема груза. Однако уменьшение вдвое прикладываемой силы означает, что точка ее приложения должна пройти в два раза больший путь. В данном случае сила равна половине веса (F=1/2W).
Системы блоков
При использовании комбинации неподвижного блока с подвижным прикладываемая сила кратна общему количеству грузонесущих цепей. В данном случае сила равна половине веса (F=1/2W).
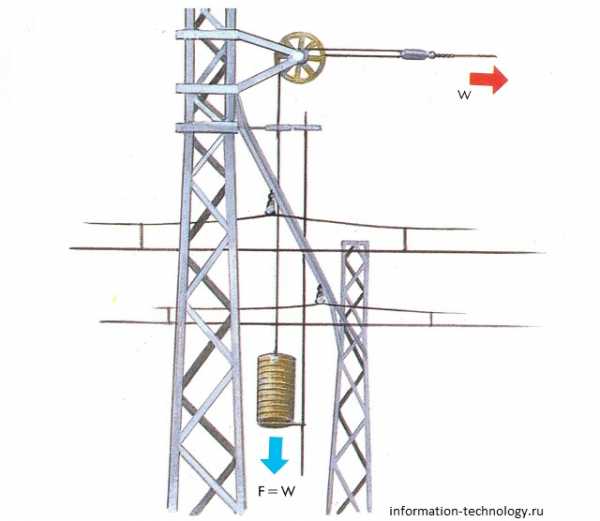
Груз, подвешенный через блок вертикально, позволяет туго натягивать горизонтальные электрические провода.

Подвесной подъемник (рисунок сверху) состоит из цепи, обвитой вокруг одного подвижного и двух неподвижных блоков. Подъем груза требует прикладывания силы, составляющей всего лишь половину от его веса.
Полиспаст, обычно используемый в больших подъемных кранах (рисунок справа), состоит из комплекта подвижных блоков, к которому подвешивается груз, и комплекта неподвижных, прикрепленного к стреле крана. Получая выигрыш в силе от столь большого количества блоков, кран может поднимать очень тяжелые грузы, например, стальные балки. В данном случае сила (F) равна частному от деления веса груза (W) на количество поддерживающих тросов (n).

information-technology.ru
Подвижный и неподвижный блок, с примерами задач
Блоки относят к простым механизмам. В группу этих устройств, которые служат для преобразования силы, помимо блоков относят рычаг, наклонную плоскость.
Изготавливаются блоки в виде дисков (колес, низких цилиндров и т. п.), имеющих желоб, через который пропускают веревку (торс, канат, цепь).
Неподвижный блок
Неподвижным называется блок, с закрепленной осью (рис.1). Он не перемещается при подъеме груза. Неподвижный блок можно рассматривать как рычаг, который имеет равные плечи.
Условием равновесия блока является условие равновесия моментов сил, приложенных к нему:
Блок на рис.1 будет находиться в равновесии, если силы натяжения нитей равны:
так как плечи этих сил одинаковы (ОА=ОВ). Неподвижный блок не дает выигрыша в силе, но он позволяет изменить направление действия силы. Тянуть за веревку, которая идет сверху часто удобнее, чем за веревку, которая идет снизу.
Если масса груза, привязанного к одному из концов веревки, перекинутой через неподвижный блок равна m, то для того, чтобы его поднимать, к другому концу веревки следует прикладывать силу F, равную:
при условии, что силу трения в блоке мы не учитываем. Если необходимо учесть трение в блоке, то вводят коэффициент сопротивления (k), тогда:
Заменой блока может служить гладкая неподвижная опора. Через такую опору перекидывают веревку (канат), которая скользит по опоре, но при этом растет сила трения.
Неподвижный блок выигрыша в работе не дает. Пути, которые проходят точки приложения сил, одинаковы, равны силы, следовательно, равны работы.
Комбинация неподвижных блоков
Для того чтобы получить выигрыш в силе, применяя неподвижные блоки применяют комбинацию блоков, например, двойной блок. При блоки должны иметь разные диаметры. Их соединяют неподвижно между собой и насаживают на единую ось. К каждому блоку прикрепляется веревка, что она может наматываться на блок или сматываться с него без скольжения. Плечи сил в таком случае будут неравными. Двойной блок действует как рычаг с плечами разной длины. На рис.2 изображена схема двойного блока.
Условие равновесия для рычага на рис.2 станет формула:
Двойной блок может преобразовывать силу. Прикладывая меньшую силу к веревке, намотанной на блок большого радиуса, получают силу, которая действует со стороны веревки, навитой на блок меньшего радиуса.
Подвижный блок
Подвижным блоком называют блок, ось которого перемещается совместно с грузом. На рис. 2 подвижный блок можно рассматривать как рычаг с плечами разной величины. В этом случае точка О является точкой опоры рычага. OA – плечо силы ; OB – плечо силы . Рассмотрим рис. 3. Плечо силы в два раза больше, чем плечо силы , следовательно, для равновесия необходимо, чтобы величина силы F была в два раза меньше, чем модуль силы P:
Можно сделать вывод о том, что при помощи подвижного блока мы получаем выигрыш в силе в два раза. Условие равновесия подвижного блока без учета силы трения запишем как:
Если попытаться учесть силу трения в блоке, то вводят коэффициент сопротивления блока (k) и получают:
Иногда применяют сочетание подвижного и неподвижного блока. В таком сочетании неподвижный блок используют для удобства. Он не дает выигрыша в силе, но позволяет изменять направление действия силы. Подвижный блок применяют для изменения величины прилагаемого усилия. Если концы веревки, охватывающей блок, составляют с горизонтом одинаковые углы, то отношение силы, оказывающей воздействие на груз к весу тела, равна отношению радиуса блока к хорде дуги, которую охватывает веревка. В случае параллельности веревок, сила необходимая для подъема груза потребуется в два раза меньше, чем вес поднимаемого груза.
Золотое правило механики
Простые механизмы выигрыша в работе не дают. Во сколько мы получаем выигрыш в силе, во столько же раз проигрываем в расстоянии. Так как работа равна скалярному произведению сила на перемещение, следовательно, она не изменится при использовании подвижного (как и неподвижного) блоков.
В виде формулы «золотое правило№ можно записать так:
где – путь, который проходит точка приложения силы – путь проходимый точкой приложения силы .
Золотое правило является самой простой формулировкой закона сохранения энергии. Это правило распространяется на случаи, равномерного или почти равномерного движения механизмов. Расстояния поступательного движения концов веревок связаны с радиусами блоков ( и ) как:
Получим, что для выполнения «золотого правила» для двойного блока необходимо, чтобы:
Если силы и уравновешены, то блок покоится или движется равномерно.
Примеры решения задач
ru.solverbook.com
Неподвижный и подвижный блоки — Справочник химика 21
I — подвижный блок. 2 — неподвижный блок, 3 — отводные блоки, Q — грузоподъемность полиспаста, Р — тяговое усилие [c.34] Примечание, Для блока БМ-630 в числителе указаны параметры неподвижного, а в знаменателе — подвижного блоков.
Определим усилие в любой ветви полиспаста (рис. 2.6), имеющего а рабочих ветвей и нагруженного силой (Эп- Номер рабочей ветви = 0, 1, 2,…, а—1 (закрепленная ветвь считается нулевой). Чтобы определить число рабочих ветвей (ниток) в полиспасте, надо мысленно перерезать все ветви троса, отбросить неподвижный блок полиспаста и подсчитать число ветвей, на которых остался висеть подвижный блок с грузом. При сбега-нии ходового конца троса с неподвижного блока полиспаста (см. рис. 2.6, а) [c.32]
Для установки в блоке пакета, состоящего из стационарной части I и съемной части II (см. рис. 2.124, в и 2.121), прихваты д неподвижной части блока располагают опорными поверхностями Г на плите 9, прихваты 3 подвижной части блока — поверхностями Е на опорной плите 2 при этом выступы г прихватов входят в пазы в.
Количество роликов п соответствует количеству рабочих нитей т, если сбегающий конец полиспаста сходит с неподвижного блока если сбегающий конец сходит с подвижного блока, количество роликов принимают на один меньше, по сравнению с количеством рабочих нитей. [c.171]
I — мачта 2 — неподвижный блок 3 — подвижный блок 4 — тонкий трос в полиспасте б — рабочий трос Я — барабан с рабочим тросом 7 — электролебедка 8 — отводные блоки. [c.442]
Система подвижных блоков в комбинации с неподвижными называется полиспастом. На рис. 68 показана схема одной из таких систем, состоящая из двух неподвижных блоков, вращающихся в верхней обойме, и двух подвижных блоков, вращающихся в нижней обойме. Канат, прикрепленный одним концом к ушку неподвижной обоймы, обходит последовательно все блоки, оканчиваясь свободным кон- [c.154]
Система подвижных блоков в комбинации с неподвижными называется полиспастом. [c.178]
На рис. 61 показана схема одной из таких систем, состоящей из двух неподвижных блоков, вращающихся в верхней обойме, и такого же количества подвижных блоков, вращающихся в нижней обойме. Канат, прикрепленный одним концом к ушку неподвижной обоймы, обходит последовательно все блоки, оканчиваясь свободным концом Н, сбегающим на лебедку. В данном случае вес груза Г распределяется на четыре ветви каната и поэтому, теоретически, на каждую ветвь приходится нагрузка в четыре раза меньшая. Таким образом, применение полиспаста дает выигрыш в силе, равный количеству ветвей каната. [c.178]
Полиспаст состоит из двух многорольных блоков верхнего неподвижного и нижнего подвижного. Блоки соединяются между собой тросом, последовательно огибающим ролики неподвижного н подвижного блоков. [c.152]
При оснастке грузовых полиспастов подъемных мачт следует иметь в виду грузоподъемность верхнего неподвижного блока полиспаста должна быть больше грузоподъемности нижнего подвижного блока на величину усилия в сбегающей ветви полиспаста грузоподъемность нижнего отводного блока должна быть примерно в 1,5 раза больше усилия в обегающей нитке полиспаста, идущей яа лебедку. [c.161]
Запасовку выполняют по предварительно составленной схеме, учитывающей выбранный вариант подъема или перемещения груза. Как правило, запасовку производят при горизонтально расположенных блоках. Для этого их кладут плашмя на деревянный или металлический настил, закрепляют на расстоянии 5— 10 м друг от друга, после чего конец троса, сматываемого с бухты или катушки, последовательно пропускают через все ролики подвижного и неподвижного блоков. Неподвижный конец троса, сходящего с последнего ролика, крепят к одному из блоков. Далее полиспаст растягивают тракторами так, чтобы при подъеме неподвижного блока к оголовку мачты или стрелы подъемного крана подвижный блок остался на земле. Чаще всего неподвижный блок прикрепляют к мачте тогда, когда она еще не поднята. В этих случаях блоки временно крепят к корпусу мачты, чтобы они не раскачивались при подъеме. [c.135]
Система подвижных и неподвижных роликов, соединенных между собой тросом или цепью, называется полиспастом. Простейший полиспаст состоит из неподвижного блока 1, который подвешивается к несу-ш,ей конструкции, подвижного блока 2, к которому крепится груз (рис. 44). На монтажных работах применяют полиспасты, в которых свободная ветвь троса сбегает с неподвижного блока. [c.65]
I — неподвижный блок г — подвижный блок 3—трос. [c.66]
Магнитный пускатель состоит из контактора и теплового реле. Контактор имеет неподвижный магнитопровод с катушкой, подвижный магнитопровод с подвижными контактами, неподвижные контакты, блок-контакты и основание, на котором монтируются все узлы контактора. [c.200]
Полиспасты (рис. 66) служат для уменьшения усилий в канате при подъеме грузов и снижения необходимой грузоподъемности лебедок. Полиспасты состоят из системы подвижных I и неподвижных 2 блоков, соединенных канатом. Канат последовав тельно огибает ролики обоих блоков, свободный конец каната подводится к лебедке, а другой конец неподвижно крепится на одном из блоков. В конструкцию полиспаста входят отводные блоки, служащие для направления нити полиспаста на лебедку. [c.97]
НЕПОДВИЖНЫЙ И подвижный БЛОКИ 31 [c.31]
НЕПОДВИЖНЫЙ И ПОДВИЖНЫЙ БЛОКИ [c.31]
| Фиг. 10. Схемы полиспастов а — полиспаст со свободным концом гибкого органа, сбегающим с неподвижного бло.ча б — полиспаст со свободным концом гибкого органа, сбегающим с подвижного блока. |
www.chem21.info
Подвижный и неподвижный блоки » Народна Освіта
Первый блок был изобретен, когда через колесо, вращающееся вокруг своей оси, неизвестный механик древности перебросил веревку и с помощью этого устройства стал поднимать грузы. По легенде, Архимед с помощью нескольких блоков смог спустить на воду тяжелое судно, которое не могли сдвинуть с места десятки лошадей. сейчас блоки используют во многих машинах и механизмах. Чем объясняется их широкое применение?
Выясняем связь неподвижного блока и рычага
На рис. 35.1, аизображено колесо (1) с желобом (2). Колесо может вращаться вокруг своей оси (3), неподвижно закрепленнной в обойме (4). Через желоб переброшен шнур (5). Перед вами простой механизм — неподвижный блок.
Блок — это простой механизм, имеющий форму колеса с желобом по ободу, через который переброшен шнур (канат, веревка).
На первый взгляд, рычаг и неподвижный блок — абсолютно разные механизмы. На самом деле неподвижный блок — это рычаг с одинаковыми плечами. Действительно, приложим к концам шнура, переброшенного через блок, силы F1 и F2 и проведем перпендикуляры из точки опоры к линиям действия сил (рис. 35.1, б,в). Видим, что плечо каждой силы равно радиусу Вблока:
Из условия равновесия рычага
следует, что
или:
Таким образом, неподвижный блок не дает выигрыша в силе, однако позволяет изменять направление действия силы(см., например, рис. 35.1-35.3).
Рассмотрите рис. 35.1, б, в. Если свободный конец шнура тянуть вниз, куда будет двигаться груз? куда будет двигаться тележка?
Исследуем подвижный блок
С помощью обоймы прикрепим груз к оси блока. Сам блок подвесим на шнуре, один конец которого закреплен (рис. 35.4). Если поднимать свободный конец шнура, то за шнуром будет подниматься и блок с грузом. Полученный простой механизм — это подвижный блок.
Подвижный блок можно рассматривать как рычаг, который вращается вокруг оси, проходящей через точку опоры O(см. рис. 35.4). Из рисунка видно, что плечо силы Е2 равно радиусу блока (отрезок OA), а плечо силы Е1 — диаметру блока (отрезок ОВ), то есть двум его радиусам.
Таким образом, использование подвижного блока позволяет получить выигрыш в силе в два раза.
Понятно, что выигрыш в силе будет сопровождаться таким же проигрышем в расстоянии: если свободный конец шнура поднять на высоту h, то блок вместе с грузом поднимется
лишь на высоту
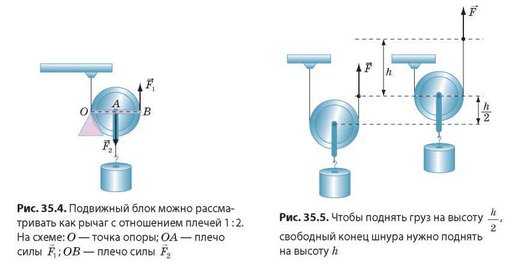
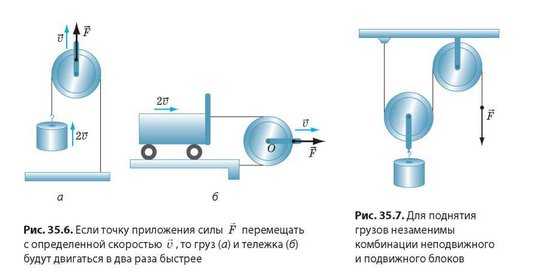
Как и рычаг, подвижный блок можно также использовать для получения выигрыша в расстоянии (либо выигрыша в скорости движения). Для этого груз прикрепляют к свободному концу шнура, а тянут за обойму, к которой прикреплена ось блока (рис. 35.6).
Неподвижные и подвижные блоки, как правило, используются одновременно — в виде системы блоков (рис. 35.7).
Как вы считаете, позволяет ли система блоков на рис. 35.7 изменить направление действия силы? получить выигрыш в силе?
Учимся решать задачи
Задача. На рис. 35.8 представлена система блоков. Определите силы натяжения шнуров a и Ь, если масса груза равна 20 кг. Какой выигрыш в силе дает данная система блоков? На какое расстояние hA опустится точка Л, если груз поднимется на высоту 10 см? Массой блоков и силой трения пренебречь.
Анализ физической проблемы. Система блоков состоит из двух подвижных блоков (1 и 2) и одного неподвижного блока (3). По условию массой блоков следует пренебречь, значит, натяжение шнура вызвано только весом груза. Для определения выигрыша в силе сравним вес Р груза и силу F, которая приложена к с
narodna-osvita.com.ua
Современный взгляд на простой механизм «блок», изучаемый по учебникам физики для 7 класса
Учебники физики для 7 класса при изучении простого механизма блок по-разному трактуют получение выигрыша в силе при подъёме груза с помощью этого механизма, например: в учебнике Пёрышкина А. В. выигрыш в силе достигается с помощью колеса блока, на который действуют силы рычага, а в учебнике Генденштейна Л. Э. тот же выигрыш получают с помощью троса, на который действует сила натяжения троса. Разные учебники, разные предметы и разные силы — для получения выигрыша в силе, при подъёме груза. Поэтому целью данной статьи служит поиск предметов и сил, с помощью которых получается выигрыш в силе, при подъёме груза простым механизмом блок.
Ключевые слова: блок, двойной блок, неподвижный блок, подвижный блок, полиспаст.
Сначала ознакомимся и сравним как получают выигрыш в силе, при подъёме груза простым механизмом блок, в учебниках физики для 7 класса, для этого выдержки из текстов учебников, с одинаковыми понятиями, для наглядности разместим в таблице.
|
Пёрышкин А. В. Физика. 7 класс. § 61. Применение правила равновесия рычага к блоку, стр.180–183. |
Генденштейн Л. Э. Физика. 7 класс. § 24. Простые механизмы, стр.188–196. |
|
«Блок представляет собой колесо с жёлобом, укреплённое в обойме. По жёлобу блока пропускают верёвку, трос или цепь. «Неподвижным блоком называют такой блок ось которого закреплена и при подъёме грузов не поднимается и не опускается (рис.177).
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис.178): ОА=ОВ=r. Такой блок не даёт выигрыша в силе (F1 = F2), но позволяет изменять направление действия силы» [1, с.181, 182]. |
«Даёт ли неподвижный блок выигрыш в силе? …на рис.24.1а трос натянут силой, приложенной рыбаком к свободному концу троса. Сила натяжения троса остаётся постоянной вдоль троса, поэтому со стороны троса на груз (рыбу) действует такая же по модулю сила. Следовательно, неподвижный блок не даёт выигрыша в силе. 6.Как с помощью неподвижного блока получить выигрыш в силе? Если человек поднимает самого себя, как показано на рис.24.6, то при этом вес человека распределяется поровну на две части троса (по разные стороны блока). Поэтому человек поднимает себя прикладывая силу, которая вдвое меньше его веса», [2, с.190, 193]. |
|
«Подвижный блок — это блок, ось которого поднимается и опускается вместе с грузом (рис.179).
На рисунке 180 показан соответствующий ему рычаг: О — точка опоры рычага, АО — плечо силы Р и ОВ — плечо силы F. Так как плечо ОВ в 2 раза больше плеча ОА, то сила F в 2 раза меньше силы Р: F=Р/2. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза» [1, с.182]. |
«5. Почему подвижный блок даёт выигрыш в силе в два раза?
Рис. 24.5 При равномерном подъёме груза подвижный блок тоже движется равномерно. Значит равнодействующая всех приложенных к нему сил равна нулю. Если массой блока и трением в нём можно пренебречь, то можно считать, что к блоку приложены три силы: вес груза Р, направленный вниз, и две одинаковые силы натяжения троса F, направленные вверх. Поскольку равнодействующая этих сил равна нулю, то Р=2F, то есть вес груза в 2 раза больше силы натяжения троса. Но сила натяжения троса — это как раз и есть сила, которую прикладывают поднимая груз с помощью подвижного блока. Таким образом мы доказали, что подвижный блок даёт выигрыш в силе в 2 раза» [2, с.192]. |
|
«Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.181). Неподвижный блок применяется только для удобства. Он не даёт выигрыша в силе, но изменяет направление действия силы, например позволяет поднимать груз, стоя на земле.
Рис.181. Комбинация подвижных и неподвижных блоков — полиспаст» [1, с.182]. |
«12.На рис 24.7 изображена система блоков. Сколько в ней подвижных блоков и сколько неподвижных? Какой выигрыш в силе даёт такая система блоков, если трением и массой блоков можно пренебречь?» [2, с.195].
Рис.24.7. Ответ на стр.240: «12.Три подвижных блока и один неподвижный; в 8 раз» [2, с.240]. |
Подведём итог ознакомления и сравнения текстов и рисунков в учебниках:
Доказательства получения выигрыша в силе в учебнике Пёрышкина А. В. проводятся на колесе блока и действующая сила — сила рычага; при подъёме груза неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе в 2 раза. О тросе, на котором висит груз на неподвижном блоке и подвижный блок с грузом, нет упоминания.
С другой стороны, в учебнике Генденштейна Л. Э. доказательства выигрыша в силе проводятся на тросу, на котором висит груз или подвижный блок с грузом и действующая сила — сила натяжения троса; при подъёме груза неподвижный блок может давать выигрыш в силе в 2 раза, а о рычаге, на колесе блока, в тексте нет упоминания.
Поиск литературы с описанием получения выигрыша в силе блоком и тросом привели к «Элементарному учебнику физики» под редакцией академика Г. С. Ландсберга, в §84. Простые машины на стр.168–175 даны описания: «простого блока, двойного блока, ворота, полиспаста и дифференциального блока». Действительно, по своей конструкции, «двойной блок даёт выигрыш в силе, при подъёме груза, за счёт разницы в длине радиусов блоков», с помощью которых происходит подъём груза, а «полиспаст — даёт выигрыш в силе, при подъёме груза, за счет верёвки, на нескольких частях которой, висит груз» [3, с.168–175]. Таким образом удалось узнать почему дают выигрыш в силе, при подъёме груза, по отдельности блок и трос (верёвка), но не удалось узнать, как блок и трос взаимодействуют между собой и передают вес груза друг другу, так как груз может быть подвешен на тросу, а трос перекинут через блок или груз может висеть на блоке, а блок висит на тросу. Выяснилось, что сила натяжения троса постоянна и действует по всей длине троса, поэтому передача веса груза тросом блоку будет в каждой точке соприкосновения троса и блока, а также передача веса груза подвешенного на блоке — тросу. Для уточнения взаимодействия блока с тросом проведём опыты по получению выигрыша в силе подвижным блоком, при подъёме груза, с использованием оборудования школьного кабинета физики: динамометры, лабораторные блоки и набор грузов в 1Н (102 г). Опыты начнём с подвижного блока, потому что имеем три разные версии получения выигрыша в силе этим блоком. Первая версия — это «Рис.180. Подвижный блок как рычаг с неравными плечами» — учебник Пёрышкина А. В., вторая «Рис.24.5… две одинаковые силы натяжения троса F», — по учебнику Генденштейна Л. Э. и наконец третья «Рис.145.Полиспаст». Подъём груза подвижной обоймой полиспаста на нескольких частях одной верёвки — согласно учебника Ландсберга Г. С.
Опыт №1. «Рис.183» [1, с.184]
Для проведения опыта № 1, получение выигрыша в силе на подвижном блоке «рычагом с неравными плечами ОАВ рис.180» по учебнику Пёрышкина А. В., на подвижном блоке «рис.183» положение 1, нарисуем рычаг с неравными плечами ОАВ, как на «рис.180», и начнём подъём груза из положения 1 в положение 2. В это же мгновение блок начинает вращение, против часовой стрелки, вокруг своей оси в точке А, а точка В — конец рычага, за который происходит подъём, выходит за пределы полуокружности, по которой трос снизу огибает подвижный блок. Точка О — точка опоры рычага, которая должна быть неподвижной, уходит вниз см. «рис.183» — положение 2, т. е. рычаг с неравными плечами ОАВ изменяется как рычаг с равными плечами (одинаковые пути проходят точки О и В).
На основе полученных данных в опыте № 1 об изменений положения рычага ОАВ на подвижном блоке при подъёме груза из положения 1 в положение 2, можно сделать вывод о том, что представление подвижного блока как рычага с неравными плечами на «рис.180», при подъёме груза, с вращением блока вокруг своей оси, соответствует рычагу с равными плечами, который не даёт выигрыша в силе, при подъёме груза [1, с.182].
Опыт № 2 начнём с крепления динамометров на концы троса, на который повесим подвижный блок с грузом весом 102 г, что соответствует силе тяжести 1 Н. Один из концов троса закрепим на подвесе, а за второй конец троса будем производить подъём груза на подвижном блоке. Перед подъёмом показания обоих динамометров по 0,5 Н, вначале подъёма показания динамометра, за который происходит подъём, изменилось до 0,6 Н, и оставалось таким во время подъёма, по окончании подъёма показания вернулись к 0,5 Н. Показания динамометра, закреплённого за неподвижный подвес не менялось во время подъёма и оставалось равным 0,5 Н. Проведём анализ результатов опыта:
- Перед подъёмом, когда груз в 1 Н (102 г) висит на подвижном блоке, вес груза распределяется на всё колесо и передаётся тросу, который снизу огибает блок, всей полуокружностью колеса.
- Перед подъёмом показания обоих динамометров по 0,5 Н, что свидетельствует о распределении веса груза в 1 Н (102 г) на две части троса (до и после блока) или о том, что сила натяжения троса равна 0,5 Н, и одинакова по всей длине троса (какая в начале, такая же и в конце троса) — оба эти утверждения верны.
Проведём сравнение анализа опыта № 2 с версиями учебников о получении выигрыша в силе в 2 раза подвижным блоком. Начнём с утверждения в учебнике Генденштейна Л. Э. «… что к блоку приложены три силы: вес груза Р, направленный вниз, и две одинаковые силы натяжения троса, направленные вверх (рис.24.5)». Точнее будет утверждение, что вес груза на «рис. 14.5» распределился на две части троса, до и после блока, так как сила натяжения троса — одна [2, с.192]. Осталось проанализировать подпись под «рис.181» из учебника Пёрышкина А. В. «Комбинация подвижных и неподвижных блоков — полиспаст». Описание устройства и получения выигрыша в силе, при подъёме груза, полиспастом дано в Элементарном учебнике физики под ред. Лансберга Г. С. где сказано: «Каждый кусок верёвки между блоками будет действовать на движущийся груз с силой Т, а все куски верёвки будут действовать с силой nT, где n — число отдельных участков верёвки, соединяющих обе части блока». Получается, что если к «рис.181» [1, с.182] применить получение выигрыша в силе «верёвкой, соединяющей обе части» полиспаста из Элементарного учебника физики Ландсберга Г. С., то описание получение выигрыша в силе подвижным блоком на «рис.179 и соответственно рис.180» будет ошибкой [1, с.182].
Проанализировав четыре учебника физики можно сделать вывод, что существующее описание получения выигрыша в силе простым механизмом блок не отвечает реальному положению дела и поэтому требует нового описания работы простого механизма блок.
Простой грузоподъёмный механизм состоит из блока и троса (верёвки или цепи).
Блоки этого грузоподъёмного механизма подразделяются:
по конструкции на простые и сложные;
по способу подъёма груза на подвижные и неподвижные.
Знакомство с конструкцией блоков начнём с простого блока, который представляет собой колесо, вращающееся вокруг своей оси, с жёлобом по окружности для троса (верёвки, цепи) рис.1 и его можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса: ОА=ОВ=r. Такой блок не даёт выигрыша в силе, но позволяет изменять направление движение троса (верёвки, цепи).
Двойной блок состоит из двух блоков разных радиусов, жестко скреплённых между собой и насаженных на общую ось рис.2. Радиусы блоков r1 и r2 различны и при подъёме груза действуют как рычаг с неравными плечами, а выигрыш в силе будет равен отношению длин радиусов блока большего диаметра к блоку меньшего диаметра F =Р·r1/r2.
Ворот состоит из цилиндра (барабана) и прикреплённой к нему рукоятки, которая выполняет роль блока большого диаметра, Выигрыш в силе, даваемый воротом, определяется отношением радиуса окружности R, описываемой рукояткой, к радиусу цилиндра r, на который намотана верёвка F = Р·r/R.
Перейдём к способу подъёма груза блоками. Из описания конструкции все блока имеют ось, вокруг которой они вращаются. Если ось блока закреплена и при подъёме грузов не поднимается и не опускается, то такой блок называется неподвижным блоком, простой блок, двойной блок, ворот.
У подвижного блока ось поднимается и опускается вместе с грузом рис.10 и он предназначен в основном для устранения перегиба троса в месте подвеса груза.
Ознакомимся к устройством и способом подъёма груза второй частью простого грузоподъёмного механизма — это трос, верёвка или цепь. Трос свит из стальных проволочек, верёвка свита из нитей или прядей, а цепь состоит из звеньев, соединённых между собой.
Способы подвеса груза и получение выигрыша в силе, при подъёме груза, тросом:
На рис. 4 груз закреплён на одном конце троса и если поднимать груз за другой конец троса, то для подъёма этого груза потребуется сила чуть больше веса груза, так как простой блок выигрыша в силе не даёт F = Р.
На рис.5 груз рабочий поднимает самого себя за трос, который сверху огибает простой блок, на одном конце первой части троса закреплено сидение, на котором сидит рабочий, а за вторую часть троса рабочий поднимает самого себя с силой в 2 раза меньшей своего веса, потому что вес рабочего распределился на две части троса, первая — от сидения до блока, а вторая — от блока до рук рабочего F = Р/2.
На рис.6 груз поднимают двое рабочих за два троса и вес груза распределятся поровну между тросами и поэтому каждый рабочий будет поднимать груз с силой половины веса груза F = Р/2.
На рис.7 рабочие поднимают груз, который висит на двух частях одного троса и вес груза распределятся поровну между частями этого троса (как между двумя тросами) и каждый рабочий будет поднимать груз с силой равной половине веса груза F = Р/2.
На рис.8 конец троса, за который поднимал груз один из рабочих, закрепили на неподвижном подвесе, а вес груза распределился на две части троса и при подъёме груза рабочим за второй конец троса, сила, с которой рабочий будет поднимать груз, в два раза меньше веса груза F = Р/2 и подъём груза будет в 2 раза медленнее.
На рис.9 груз висит на 3 частях одного троса, один конец которого закреплён и выигрыш в силе, при подъёме груза, будет равен 3, так как вес груза распределится на три части троса F = Р/3.
Для устранения перегиба и уменьшения силы трения в месте подвеса груза устанавливается простой блок и сила необходимая для подъёма груза не изменилась, так как простой блок не даёт выигрыша в силе рис.10 и рис.11, а сам блок будет называться подвижным блоком, так как ось этого блока поднимается и опускается вместе с грузом.
Теоретически груз можно подвесить на неограниченное число частей одного троса, но практически ограничиваются шестью частями и такой грузоподъёмный механизм называется полиспаст, который состоит из неподвижной и подвижной обойм с простыми блоками, которые поочерёдно огибаются тросом, одним концом закреплённый на неподвижной обойме, а подъём груза производят за второй конец троса. Выигрыш в силе зависит от количества частей троса между неподвижной и подвижной обоймами, как правило это 6 частей троса и выигрыш в силе 6 раз.
Выводы.
В статье рассмотрены реально существующие взаимодействия между блоками и тросом при подъёме груза. Существующая практика в определении что «неподвижный блок не даёт выигрыша в силе, а подвижный блок даёт выигрыш в силе в 2 раза» ошибочно трактовала взаимодействие троса и блока в подъёмном механизме и не отражала всего многообразия конструкции блоков, что вело к развитию односторонних ошибочных представлений о блоке. По сравнению с существующими объёмами материала для изучения простого механизма блок, объём статьи увеличился в 2 раза, но это позволило наглядно и доходчиво объяснить процессы, протекающие в простом грузоподъёмном механизме не только ученикам, но и учителям.
Литература:
- Пёрышкин, А. В. Физика, 7 кл.: учебник/ А. В. Пёрышкин.- 3-е изд., доп.- М.: Дрофа, 2014, — 224 c,: ил. ISBN 978–5-358–14436–1. § 61. Применение правила равновесия рычага к блоку, стр.181–183.
- Генденштейн, Л. Э. Физика. 7 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений/ Л. Э. Генденштен, А. Б. Кайдалов, В. Б. Кожевников; под ред. В. А. Орлова, И, И. Ройзена.- 2-е изд., испр. — М.: Мнемозина, 2010.-254 с.: ил. ISBN 978–5-346–01453–9. § 24. Простые механизмы, стр.188–196.
- Элементарный учебник физики, под редакцией академика Г. С. Ландсберга Том 1. Механика. Теплота. Молекулярная физика.- 10 изд.- М.: Наука, 1985. § 84. Простые машины, стр. 168–175.
- Громов, С. В. Физика: Учеб. для 7 кл. общеобразоват. учреждений/ С. В. Громов, Н. А. Родина.- 3-е изд. — М.: Просвещение, 2001.-158 с,:ил. ISBN-5–09–010349–6. §22. Блок, стр.55 -57.
yun.moluch.ru
Вопрос: Решите, кто действительно разбирается в этом, пожалуйста) 1)Система,состоящая из подвижного и неподвижного блоков и двух грузов находится в равновесии. Масса левого груза m1= 3кг, масса каждого из блоков равна m=1кг, массой нитей можно принебречь. Найдите массу m2, правого груза. Трения нет. 2)У гидравлического пресса большой поршень имеет площадь S1=80см^2, а малый поршень S2=25мм^2. На малый поршень пресса действуют направленной вертикально вниз силой F=0,1Н. При этом большой поршень давит вертикально установленный металлический цилиндр, площадь горизонтального основания которого S(ноль) =0,6см^2 (верхнее основание цилиндра упирается в потолок). Какое давление оказывает большой поршень на нижнее основание цилиндра? Силой тяжести можно принебречь.
Решите, кто действительно разбирается в этом, пожалуйста) 1)Система,состоящая из подвижного и неподвижного блоков и двух грузов находится в равновесии. Масса левого груза m1= 3кг, масса каждого из блоков равна m=1кг, массой нитей можно принебречь. Найдите массу m2, правого груза. Трения нет. 2)У гидравлического пресса большой поршень имеет площадь S1=80см^2, а малый поршень S2=25мм^2. На малый поршень пресса действуют направленной вертикально вниз силой F=0,1Н. При этом большой поршень давит вертикально установленный металлический цилиндр, площадь горизонтального основания которого S(ноль) =0,6см^2 (верхнее основание цилиндра упирается в потолок). Какое давление оказывает большой поршень на нижнее основание цилиндра? Силой тяжести можно принебречь.
Ответы:
№ 1 m₁ = 3 кг m = 1 кг m₂ — ? m₁g = N N = m₂g/2 + mg m₂g = 2N — 2mg m₂g = 2m₁g — 2mg m₂ = 2(m₁ — m) = 2(3 кг — 1 кг) = 4 кг № 2 s₁ = 80 см² = 8*10⁻³ м² s₂ = 25 мм² = 2,5*10⁻⁵ м² F₂ = 0,1 Н s₀ = 0,6 см² = 6*10⁻⁵ м² p₀ — ? p = F₂ / s₂ = 0,1 Н / 2,5*10⁻⁵ м² = 2,5*10⁶ Па — давление масла в прессе F₁ = p * s₁ = 2,5*10⁶ Па * 8*10⁻³ м² = 2*10⁴ Н p₀ = F / s₀ = 2*10⁴ Н / 6*10⁻⁵ м² = 3,3*10⁸ Па = 0,33 ГПа
cwetochki.ru

Leave A Comment