Синус внешнего угла равен синусу внутреннего: Внешний угол треугольника. Синус и косинус внешнего угла

Внешний угол треугольника

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-02-01

Внешний угол треугольника. Продолжаем рассматривать задачи на решение прямоугольного треугольника. Такие типы заданий имеются в прототипах открытого банка заданий по математике. Некоторые примеры мы уже рассмотрели в статьях «Прямоугольный треугольник. Часть 1» и «Прямоугольный треугольник. Часть 2». В этой статье разберём задачи, в которых необходимо определить значения тригонометрических функций внешнего угла треугольника (или внутреннего, когда дано значение внешнего).

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине

Угол DAB является внешним.

Стоит повторить определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике, также основные тригонометрические формулы для решения прямоугольного треугольника.  Вспомним основные из них:

А также формулы приведения (не все). Отмечу одну типичную ошибку, которую допускают (из-за невнимательности). При решении подобных задач часто используется формула основного тригонометрического тождества:

Из  неё мы получаем:

*Запись с ошибкой (её часто допускают — теряют квадрат):

Будьте внимательны!

Рассмотрим задачи:

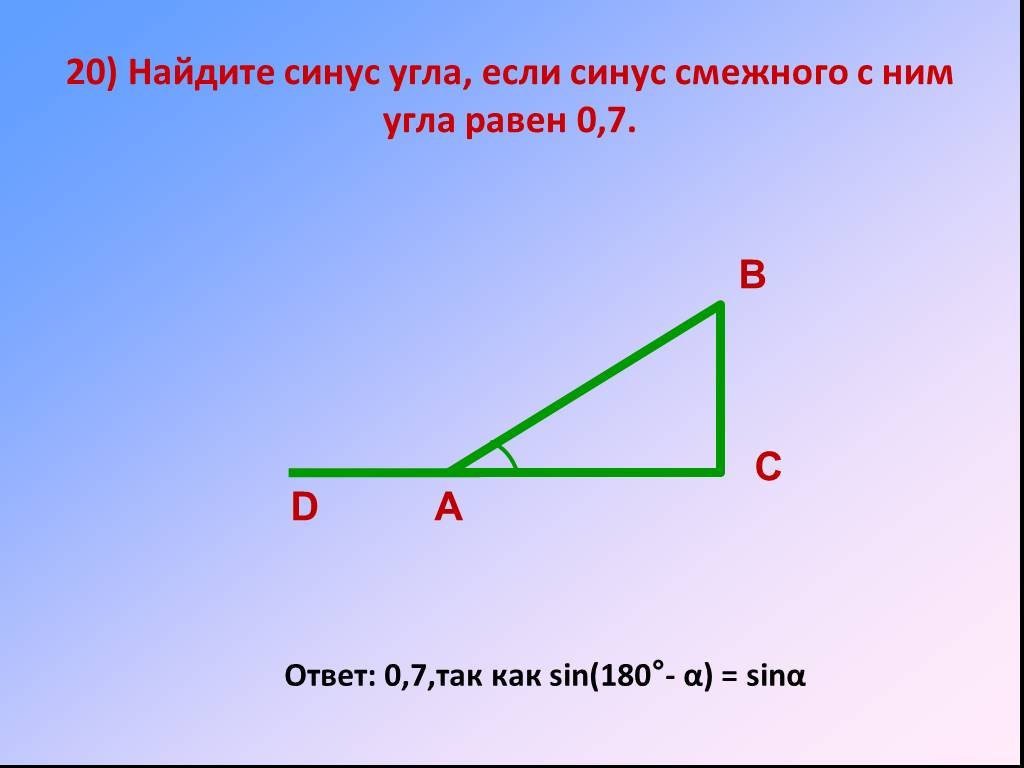
В треугольнике ABC угол C равен 90⁰, sin A = 0,27. Найдите синус внешнего угла при вершине А.

Углы ВАС и BAD смежные, значит:

По свойству синуса:

А лучше раз и навсегда запомнить сам факт того, что синусы смежных углов равны, и вам даже не будет необходимости что-то записывать при решении такой задачи, ответ вы озвучите сразу.

Ответ: 0,27

Решите самостоятельно:

Посмотреть решение 

 

В треугольнике ABC угол C равен 90⁰, . Найдите тангенс внешнего угла при вершине A.

Углы ВАС и BAD смежные, значит:

Значит по свойству тангенса (используем формулу приведения):

То есть необходимо найти тангенс угла ВАС.  Известно, что:

Синус угла ВАС нам известен. Найдём его косинус.

Из основного тригонометрического тождества:

Вычисляем тангенс:

Таким образом  tg BAD = – tg BAC = – 0,3

Ответ: – 0,3

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC угол C равен 90⁰, АВ = 6, .  Найдите косинус внешнего угла при вершине A.

 

Углы ВАС и BAD смежные, значит:

По свойству косинуса:

Найдём cos BAC   Для этого необходимо найти сторону АС. По теореме Пифагора:

Значит АС = 3.

По определению косинуса:

Таким образом, cos DAB = – cos BAC = – 0,5.    

Ответ: – 0,5

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A равен  . Найдите sin A.

Углы ВАС и BAD смежные, значит:

В данной задаче можем найти косинус угла ВАС, а затем используя основное тригонометрическое тождество синус этого угла.

По свойству косинуса (используем формулу приведения):

Значит

Найдём sin BAC.  Из основного тригонометрического тождества получим:

Ответ: 0,9

В треугольнике ABC угол C равен 90⁰, тангенс внешнего угла при вершине A равен  –2/9.  Найдите tg = B.

Из свойств прямоугольного треугольника мы знаем, что tg ABC = ctg BAC.

Найдём ctg BAC. Известно, что tg BAC ∙ ctg BAC = 1, значит

Тангенс угла ВАС найти не сложно. Углы BAC и BAD смежные. Это  значит, что

По свойству тангенса:   

Значит

Таким образом:

Ответ: 4,5

В треугольнике ABC угол C равен 90⁰, косинус внешнего угла при вершине A  равен  – 0,7; АВ = 20. Найдите AC.

Найти АС мы сможем, если нам будет известен косинус угла ВАС. Так как по определению косинуса в прямоугольном треугольнике:

Найдём косинус. По его свойству:

*Использовали формулу приведения.

Значит

Таким образом:

Ответ: 14

Решите самостоятельно:

Посмотреть решение 

Посмотреть решение 

Посмотреть решение 

Посмотреть решение 

В треугольнике ABC АС = ВС, АВ = 12, тангенс внешнего угла при вершине A равен  . Найдите AC.

Построим  высоту CH.

Найдём  тангенс внутреннего угла.  По свойству тангенса:

Сторона АС является гипотенузой в прямоугольном треугольнике АСН. В этом треугольнике зная тангенс острого угла и один катет мы без труда можем найти второй катет.

Высота проведённая к основанию равнобедренного треугольника является медианой, то есть АН = ВН, a АВ = 2АН:

Рассмотрим прямоугольный треугольник ACH: по определению тангенса в прямоугольном треугольнике:

Следовательно:

В прямоугольном треугольнике  нам известны катеты АН и СН.

По теореме Пифагора мы можем найти гипотенузу АС:

Таким образом, АС = 9.

Ответ: 9

Решите самостоятельно:

Посмотреть решение

В будущем будем рассматривать другие задачи, не пропустите! Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Решение треугольников | ЕГЭ-№1

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Внешний угол треугольника. Синус и косинус внешнего угла

В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?

Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .

Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине  — это угол, смежный с углом . Если угол  острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:

Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.

Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

1. В треугольнике угол  равен , . Найдите тангенс внешнего угла при вершине .

Пусть — внешний угол при вершине . Имеем:

Зная , найдем  по формуле

Получим:

2. В треугольнике угол  равен , . Найдите синус внешнего угла при вершине .

Задача решается за четыре секунды. Поскольку сумма углов  и  равна  , . Тогда и синус внешнего угла при вершине  также равен .

Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.

В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.

Один из типов экзаменационных задач В6 в банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:

Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и  . Смотрим внимательно на рисунок и находим на нем

равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.

Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол .

Иными словами, каждый из трех углов треугольника равен одному из углов треугольника и треугольника . Треугольники , и  называются подобными. Давайте нарисуем их рядом друг с другом.

Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?

Возьмем треугольники и  . Стороны треугольника длиннее, чем стороны треугольника , в  некоторое число  раз:

При решении задач нам пригодится равенство углов треугольников , и  , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.

1. В треугольнике угол  равен ,  — высота, , . Найдите .

Рассмотрим треугольник . В нем известны косинус угла  и противолежащий катет . Зная синус угла  , мы могли бы найти гипотенузу . Так давайте найдем :

(поскольку значение синуса острого угла положительно). Тогда:

Рассмотрим прямоугольный треугольник , . Имеем:

Отсюда, поскольку :

и тогда

Ответ: .

2. В треугольнике угол  равен , , . Найдите высоту .

Сделайте чертеж и рассмотрите прямоугольный треугольник .

Ответ: .

3. В треугольнике угол  равен , , . К гипотенузе проведена высота . Найдите .

Это чуть более сложная задача. Ведь вам неизвестны катеты  и  .

Зато можно записать теорему Пифагора:

Нам известно также, что

Решая эту систему из двух уравнений, найдем:

Запишем площадь треугольника двумя способами:

и найдем .

Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.

Unit Circle: Функции синуса и косинуса

Результаты обучения

• Найдите значения функции для синуса и косинуса особых углов.
• Определение области определения и диапазона функций синуса и косинуса.
• Используйте опорные углы для оценки тригонометрических функций.
• Вычислите значения синуса и косинуса с помощью калькулятора.

Чтобы определить наши тригонометрические функции, мы начнем с рисования единичной окружности с центром в начале координат и радиусом 1, как показано на рисунке 2. Угол (в радианах), который пересекает [латекс]t[/латекс], образует дуга длиной [латекс]s[/латекс]. Используя формулу [latex]s=rt[/latex] и зная, что [latex]r=1[/latex], мы видим, что для

единичный круг , [латекс]s=t[/латекс].

Напомним, что оси x- и y- делят координатную плоскость на четыре четверти, называемые квадрантами. Мы помечаем эти квадранты, чтобы имитировать направление положительного угла. Четыре квадранта обозначены I, II, III и IV.

Для любого угла [латекс]t[/латекс] пересечение конечной стороны и единичной окружности можно обозначить его координатами [латекс]\влево(х,у\вправо)[/латекс]. Координаты [латекс]х[/латекс] и [латекс]у[/латекс] будут выходами тригонометрических функций [латекс]f\left(t\right)=\cos t[/латекс] и [латекс] f\left(t\right)=\sin t[/latex] соответственно.

Это означает [латекс]x=\cos t[/латекс] и [латекс]у=\sin t[/латекс].

Рис. 2. Единичная окружность, центральный угол которой равен [латекс]t[/латекс] радианам

A Общее примечание: Единичная окружность

0\right)[/latex] и радиус [latex]1[/latex] . В единичном круге длина пересекаемой дуги равна радианной мере центрального угла [латекс]1[/латекс].

Пусть [латекс]\влево(х,у\вправо)[/латекс] будет концом единичной окружности дуги с длиной дуги [латекс]s[/латекс]. Координаты [латекс]\влево(х,у\вправо)[/латекс] этой точки можно описать как функции угла.

Определение функций синуса и косинуса

Теперь, когда мы пометили нашу единичную окружность, мы можем узнать, как координаты [латекс]\влево(х,у\вправо)[/латекс] соотносятся с длиной дуги и углом . Функция синуса связывает действительное число [latex]t[/latex] с y -координатой точки, где соответствующий угол пересекает единичную окружность.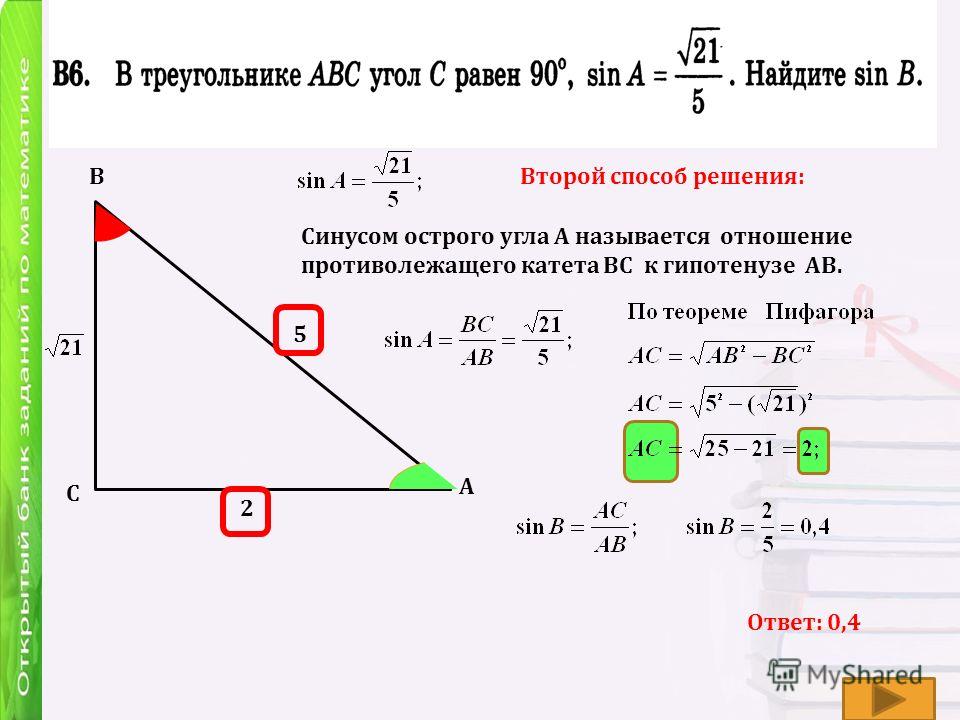 {2} [ /латекс]. Имейте в виду, что многие калькуляторы и компьютеры не распознают стенографию. Если вы сомневаетесь, используйте дополнительные скобки при вводе вычислений в калькулятор или компьютер.

Общее примечание: функции синуса и косинуса

Если [latex]t[/latex] является действительным числом и точка [latex]\left(x,y\right)[/latex] на единичной окружности соответствует угол [латекс]t[/латекс], затем

[латекс]\cos t=x[/латекс]

[латекс]\sin t=y[/латекс]

Как: Дана точка

P [латекс]\влево(х,у\вправо)[/латекс] на единичной окружности, соответствующей углу [латекс]t[/латекс], найдите синус и косинус.

1. Синус [latex]t[/latex] равен y -координата точки [latex]P:\sin t=y[/latex].
2. Косинус [latex]t[/latex] равен x -координате точки [latex]P: \text{cos}t=x[/latex].

Пример 1. Нахождение значений функции для синуса и косинуса

Точка [latex]P[/latex] — это точка на единичной окружности, соответствующая углу [latex]t[/latex], как показано на рисунке 4.

Найдите [латекс]\cos\left(t\right)[/latex] и [латекс]\text{sin}\left(t\right)[/latex].

Рисунок 4

Показать решение

Попробуйте

Некоторый угол [латекс]t[/латекс] соответствует точке на единичной окружности в точке [латекс]\левый(-\frac{\sqrt{2}}{2},\frac{\ sqrt{2}}{2}\right)[/latex], как показано на рисунке 5. Найдите [latex]\cos t[/latex] и [latex]\sin t[/latex].

Рисунок 5

Показать решение

Нахождение синусов и косинусов углов на оси

Для четырехугольных углов соответствующая точка на единичной окружности приходится на 9{2}t=1[/latex], известный как Пифагорейская идентичность .

Мы можем использовать тождество Пифагора, чтобы найти косинус угла, если мы знаем синус, или наоборот. Однако, поскольку уравнение дает два решения, нам нужно дополнительное знание угла, чтобы выбрать решение с правильным знаком. Если мы знаем квадрант, в котором находится угол, мы можем легко выбрать правильное решение.

Общее примечание: Пифагорейская идентичность

Пифагорейская идентичность 9{2}t=1[/latex]

Как сделать: Зная синус некоторого угла [latex]t[/latex] и его положение в квадранте, найдите косинус [latex]t[/latex].

1. Подставить известное значение [латекс]\sin\left(t\right)[/латекс] в тождество Пифагора.
2. Найдите [латекс]\cos\left(t\right)[/latex].
3. Выберите решение с соответствующим знаком для значений x в квадранте, где находится [латекс]t[/латекс].

Пример 3. Нахождение косинуса по синусу или синуса по косинусу

Если [латекс]\sin \left(t\right)=\frac{3}{7}[/latex] и [latex]t[/latex] находится во втором квадранте, найти [latex]\cos \ влево(т\вправо)[/латекс].

Показать раствор

Попробуйте

Если [латекс]\cos \left(t\right)=\frac{24}{25}[/latex] и [латекс]t[/латекс] находится в четвертом квадранте, найдите [латекс ]\sin\left(t\right)[/латекс].

Показать решение

Попробуйте

Нахождение синусов и косинусов специальных углов

Мы уже изучили некоторые свойства специальных углов, например преобразование радианов в градусы. Мы также можем вычислить синусы и косинусы специальных углов, используя 9\circ [/latex] треугольник является равнобедренным треугольником, поэтому координаты x- и y соответствующей точки на окружности совпадают. Поскольку значения x- и y одинаковы, значения синуса и косинуса также будут равны. Рис. 9 Это означает, что радиус лежит вдоль линии [латекс]у=х[/латекс]. Радиус единичной окружности равен 1. Итак, прямоугольный треугольник, образованный под линией [latex]y=x[/latex], имеет стороны [latex]x[/latex] и [latex]y\text{ }\left (y=x\right)[/latex], а радиус = 1,9{2}=\frac{1}{2}\\ x=\pm \frac{1}{\sqrt{2}}\end{gathered}[/latex]

В квадранте I [latex]x= \frac{1}{\sqrt{2}}[/latex].

В [латекс]t=\frac{\pi }{4}[/латекс] или 45 градусов,

[латекс]\начало{собрано}\влево(х,у\вправо)=\влево(х, x\right)=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right) \\ x=\frac{1}{\sqrt{2 }},y=\frac{1}{\sqrt{2}}\\ \cos t=\frac{1}{\sqrt{2}},\sin t=\frac{1}{\sqrt{2 }} \end{gathered}[/latex]

Если мы затем рационализируем знаменатели, то получим

9\circ [/latex], как показано на рисунке 12.

Рисунок 11

 

Рисунок 12

Поскольку все углы равны, стороны также равны. Вертикальная линия имеет длину [latex]2y[/latex], и поскольку все стороны равны, мы также можем заключить, что [latex]r=2y[/latex] или [latex]y=\frac{1}{2 }р[/латекс]. Поскольку [латекс]\sin t=y[/латекс] ,

[латекс]\sin \left(\frac{\pi }{6}\right)=\frac{1}{2}r[/latex]

А так как [latex]r=1[/latex] в нашем 9\circ [/латекс]. Теперь у нас есть равносторонний треугольник. Поскольку каждая сторона равностороннего треугольника [латекс]ABC[/латекс] имеет одинаковую длину, и мы знаем, что одна сторона является радиусом единичной окружности, все стороны должны иметь длину 1.

Рисунок 13

Угол [латекс]ABD[/латекс] равен 30°. Итак, если число двойное, угол [латекс]АВС[/латекс] равен 60°. [latex]BD[/latex] является серединным перпендикуляром к [latex]AC[/latex], поэтому он делит [latex]AC[/latex] пополам. Это означает, что [latex]AD[/latex] — это [latex]\frac{1}{2}[/latex] радиус, или [latex]\frac{1}{2}[/latex]. Обратите внимание, что [latex]AD[/latex] — это 9\circ [/latex] равны [латекс]\left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\[/latex], поэтому мы можем найти синус и косинус.

[латекс] \ begin {собраны} \ влево (x, y \ вправо) = \ влево (\ frac {1} {2}, \ frac {\ sqrt {3}} {2} \ right) \\ x =\ frac {1} {2}, y = \ frac {\ sqrt {3}} {2} \\ \ cos t = \ frac {1} {2}, \ sin t = \ frac {\ sqrt {3 }}{2} \end{gathered}[/latex]

Теперь мы нашли значения косинуса и синуса для всех наиболее часто встречающихся углов в первом квадранте единичной окружности. В таблице ниже приведены эти значения.

Уголок	0	[латекс]\frac{\pi }{6}[/латекс], или 30°	[латекс]\frac{\pi }{4}[/латекс], или 45°	[латекс]\frac{\pi }{3}[/латекс], или 60°	[латекс]\frac{\pi }{2}[/латекс], или 90°
Косинус	1	[латекс]\frac{\sqrt{3}}{2}[/латекс]	[латекс]\frac{\sqrt{2}}{2}[/латекс]	[латекс]\фракция{1}{2}[/латекс]	0
Синус	0	[латекс]\фракция{1}{2}[/латекс]	[латекс]\frac{\sqrt{2}}{2}[/латекс]	[латекс]\frac{\sqrt{3}}{2}[/латекс]	1

На рисунке 14 показаны общие углы в первом квадранте единичной окружности.

Рисунок 14

 

Использование калькулятора для нахождения синуса и косинуса0015 специальные углы

, обратимся к компьютеру или калькулятору. Имейте в виду : Большинство калькуляторов можно установить в режим «градусы» или «радианы», которые сообщают калькулятору единицы измерения для входного значения. Когда мы оцениваем [латекс]\cos \left(30\right)[/латекс] на нашем калькуляторе, он будет оценивать его как косинус 30 градусов, если калькулятор находится в режиме градусов, или как косинус 30 радиан, если калькулятор находится в радианном режиме.

Как: Зная угол в радианах, используйте графический калькулятор, чтобы найти косинус.

1. Если в калькуляторе есть режимы в градусах и в радианах, установите его в режим в радианах.
2. Нажмите клавишу COS.
3. Введите значение угла в радианах и нажмите клавишу закрытия скобок «)».
4. Нажмите ВВОД.

Пример 4.

Использование графического калькулятора для нахождения синуса и косинуса

Вычислите значение [latex]\cos \left(\frac{5\pi }{3}\right)[/latex] с помощью графического калькулятора или компьютера.

Показать решение

Попробуйте

Вычислить [латекс]\sin\left(\frac{\pi }{3}\right)[/latex].

Показать решение

Определение области определения и диапазона функций синуса и косинуса

Теперь, когда мы можем найти синус и косинус угла, нам нужно обсудить их области определения и диапазоны. Каковы области определения функций синуса и косинуса? То есть, каковы наименьшее и наибольшее числа, которые могут быть входными данными функций? Поскольку углы меньше 0 и углы больше [латекс]2\пи [/латекс] все еще могут быть изображены на единичном круге и имеют реальные значения [латекс]x,y[/латекс] и [латекс]r[/ латекс], нет нижнего или верхнего предела углов, которые могут быть входными данными для функций синуса и косинуса. Входными данными для функций синуса и косинуса является вращение от положительной x -ось, и это может быть любое действительное число.

Каковы диапазоны функций синуса и косинуса? Каковы наименьшее и максимальное возможные значения их выхода? Мы можем увидеть ответы, изучив единичный круг размером , как показано на рисунке 15. Границы координаты x равны [латекс]\лево[-1,1\право][/латекс]. Границы координаты y также равны [латекс]\влево[-1,1\вправо][/латекс]. Таким образом, диапазон функций синуса и косинуса составляет [латекс]\влево[-1,1\вправо][/латекс].

Рисунок 15

Мы обсудили нахождение синуса и косинуса для углов в первом квадранте, но что, если наш угол находится в другом квадранте? Для любого заданного угла в первом квадранте существует угол во втором квадранте с таким же значением синуса. Поскольку значением синуса является координата y на единичной окружности, другой угол с таким же синусом будет иметь такое же значение y , но противоположное значение x . Следовательно, его значение косинуса будет противоположно значению косинуса первого угла.

Аналогично, в четвертом квадранте будет угол с тем же косинусом, что и исходный угол. Угол с тем же косинусом будет иметь такое же значение x , но будет иметь противоположное значение y . Следовательно, его значение синуса будет противоположно значению синуса исходного угла.

Как показано на рисунке 16, угол [латекс]\альфа [/латекс] имеет то же значение синуса, что и угол [латекс]t[/латекс]; значения косинуса противоположны. Угол [латекс]\бета [/латекс] имеет то же значение косинуса, что и угол [латекс]t[/латекс]; значения синуса противоположны.

[латекс]\begin{array}{ccc}\sin\left(t\right)=\sin\left(\alpha\right)\hfill & \text{and}\hfill & \cos\left(t \right)=-\cos \left(\alpha \right)\hfill \\ \sin \left(t\right)=-\sin \left(\beta \right)\hfill & \text{and}\hfill & \cos \left(t\right)=\cos \left(\beta \right)\hfill \end{array}[/latex]

Рисунок 16

острый угол, [латекс]t[/латекс], образованный конечной стороной угла [латекс]t[/латекс] и горизонтальной осью. \circ \mathrm{-t}|[/латекс]. 9\circ [/latex], как показано на рис. 18.

рис. 18

Показать решение

Попробуйте

Найдите исходный угол [латекс]\фракция{5\пи }{3}[/латекс].

Показать решение

Использование опорных углов

Теперь давайте еще раз рассмотрим колесо обозрения, представленное в начале этого раздела. Предположим, всадник делает снимок, остановившись в двадцати футах над уровнем земли. Затем всадник вращается на три четверти круга. Какова новая высота всадника? Чтобы ответить на такие вопросы, как этот, нам нужно оценить функции синуса или косинуса при углах, превышающих 90 градусов или под отрицательным углом . Опорные углы позволяют вычислять тригонометрические функции для углов вне первого квадранта. Их также можно использовать для нахождения [латексных]\левых(х,у\правых)[/латексных] координат для этих углов. Мы будем использовать опорный угол угла поворота в сочетании с квадрантом, в котором лежит конечная сторона угла.

Использование опорных углов для вычисления тригонометрических функций

Мы можем найти косинус и синус любого угла в любом квадранте, если знаем косинус или синус его опорного угла. Абсолютные значения косинуса и синуса угла такие же, как у опорного угла. Знак зависит от квадранта исходного угла. Косинус будет положительным или отрицательным в зависимости от знака числа 9.0019 x — значения в этом квадранте. Синус будет положительным или отрицательным в зависимости от знака значений и в этом квадранте.

A Общее примечание. Использование опорных углов для нахождения косинуса и синуса

Углы имеют косинусы и синусы с тем же абсолютным значением, что и их опорные углы. Знак (положительный или отрицательный) можно определить по квадранту угла.

Как сделать: по заданному углу в стандартном положении найдите опорный угол, а также косинус и синус исходного угла.

1. Измерьте угол между конечной стороной заданного угла и горизонтальной осью. Это опорный угол.
2. Определить значения косинуса и синуса опорного угла.
3. Присвойте косинусу тот же знак, что и значениям x в квадранте исходного угла.
4. Присвойте синусу тот же знак, что и y -значения в квадранте исходного угла.

Пример 6. Использование опорных углов для нахождения синуса и косинуса 9\circ \right)[/латекс].

б. Используйте опорный угол [латекс]-\frac{\pi }{6}[/латекс], чтобы найти [латекс]\cos\left(-\frac{\pi }{6}\right)[/латекс] и [латекс]\sin\left(-\frac{\pi}{6}\right)[/латекс].

Показать решение

Попробуйте

Использование опорных углов для поиска координат

Теперь, когда мы научились находить значения косинуса и синуса для специальных углов в первом квадранте, мы можем использовать симметрию и опорные углы для заполнения значений косинуса и синуса для остальные специальные углы на единичной окружности. Они показаны на рисунке 19. . Потратьте время, чтобы узнать [латексные]\левые(х,у\правые)[/латексные] координаты всех главных углов в первом квадранте.

Помимо изучения значений специальных углов, мы можем использовать эталонные углы для нахождения [латексных]\левых(х,у\правых)[/латексных] координат любой точки на единичной окружности, используя то, что мы знаем об эталонных углы вместе с тождествами

[латекс]\begin{gathered}x=\cos t \\ y=\sin t \end{gathered}[/latex]

Сначала находим опорный угол, соответствующий заданному угол. Затем мы берем значения синуса и косинуса опорный угол , и присвойте им знаки, соответствующие y — и x -значениям квадранта.

Как сделать: Зная угол точки на окружности и радиус окружности, найдите [латекс]\влево(х,у\вправо)[/латекс] координаты точки.

1. Найдите опорный угол, измерив наименьший угол относительно оси x .
2. Найдите косинус и синус опорного угла.
3. Определите соответствующие знаки для [latex]x[/latex] и [latex]y[/latex]
   в данном квадранте.

Пример 7. Использование единичной окружности для поиска координат

Найдите координаты точки на единичной окружности под углом [latex]\frac{7\pi }{6}[/latex].

Показать решение

Попробуйте

Найдите координаты точки на единичной окружности под углом [latex]\frac{5\pi }{3}[/latex].

Показать решение

Ключевые уравнения

Косинус

[латекс]\cos t=x[/латекс] 9{2}t=1[/латекс]

Ключевые понятия

• Нахождение значений функции для синуса и косинуса начинается с рисования единичной окружности с центром в начале координат и радиусом в 1 единицу.
• Используя единичную окружность, синус угла [latex]t[/latex] равен y -значению конечной точки единичной окружности дуги длины [latex]t[/latex], тогда как косинус угла угол [latex]t[/latex] равен x -значению конечной точки.
• Значения синуса и косинуса наиболее непосредственно определяются, когда соответствующая точка на единичной окружности попадает на ось.
• Когда известен синус или косинус, мы можем использовать тождество Пифагора, чтобы найти другой. Тождество Пифагора также полезно для определения синусов и косинусов специальных углов.
• Калькуляторы и программы для построения графиков полезны для нахождения синусов и косинусов, если известна правильная процедура ввода информации.
• Областью определения функций синуса и косинуса являются все действительные числа.
• Диапазон функций синуса и косинуса: [латекс]\влево[-1,1\вправо][/латекс].
• Синус и косинус угла имеют то же абсолютное значение, что и синус и косинус исходного угла.
• Знаки синуса и косинуса определяются из значений x – и y в квадранте исходного угла.
• Опорный угол угла — это угол размера, [latex]t[/latex],
  образованный конечной стороной угла [latex]t[/latex] и горизонтальной осью.
• Опорные углы можно использовать для нахождения синуса и косинуса исходного угла.
• Справочные углы также можно использовать для определения координат точки на окружности.

Глоссарий

Функция косинуса

x -значение точки на единичной окружности, соответствующей заданному углу

Пифагорейская идентичность

следствие теоремы Пифагора, утверждающее, что квадрат косинуса данного угла плюс квадрат синуса этого угла равен 1

функция синуса

y -значение точки на единичной окружности, соответствующей заданному углу

единичный круг

круг с центром в [латекс]\влево(0,0\вправо)[/латекс]
и радиусом

Углы в многоугольниках: внутренние и внешние

Вы, наверное, много раз слышали, что сумма углов треугольника составляет 180 градусов, а сумма углов четырехугольника составляет 360 градусов. Если нет, то это напоминание о том, что сумма углов треугольника составляет 180 градусов, а сумма углов четырехугольника — 360 градусов. Однако задумывались ли вы когда-нибудь, чему равна сумма углов в пяти-, шести- или даже семигранной фигуре? Что, если бы у нас была 24-сторонняя фигура? Ладно, наверное, нет. Несмотря на это, в этой статье мы будем исследовать углы в многоугольниках. Однако сначала мы должны обрисовать в общих чертах, что мы подразумеваем под « полигон ’.

Термин ‘ поли ‘ означает много , поэтому многоугольник — это просто форма с много сторон . Когда мы говорим « много », мы имеем в виду три или больше . Таким образом, многоугольник может быть любой 2D формой не кругом . Многоугольник является правильным многоугольником, если все сторон и углов равны тот же .

Внутренние углы в многоугольниках

Когда мы говорим о сумме углов многоугольника, мы имеем в виду сумму внутренних углов . С этого момента мы будем часто использовать этот термин, поэтому важно его знать.

Углы в многоугольниках — многоугольник с маркировкой внутренних углов, Jordan Madge — StudySmarter Originals

Для многоугольника внутренний угол — это угол внутри многоугольника (см. схему выше). сумма из интерьер углы это то, что все углы внутри многоугольника складываются до до . Итак, формально мы уже знаем, что сумма внутренних углов в треугольнике равна 180°, а в четырехугольнике — 360°.

Формула суммы внутренних углов

Ранее мы просто должны были знать, что сумма внутренних углов треугольника равна 180°, а сумма внутренних углов четырехугольника равна 360°. Мы просто приняли это как факт и никогда не подвергали его сомнению. Однако сейчас вы можете подумать, почему так ли это? А может и нет.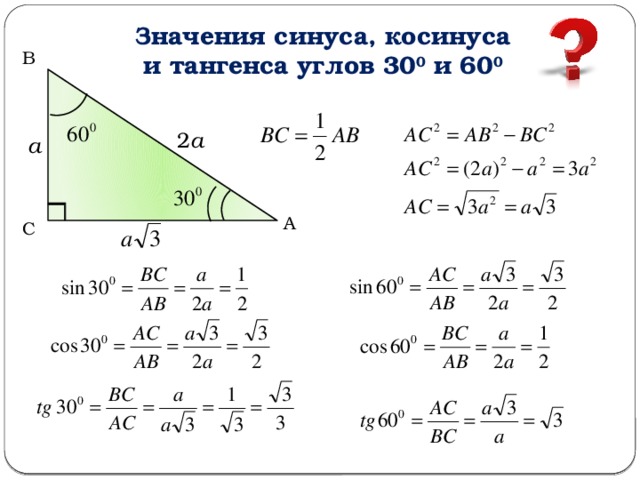 .. Однако удобная формула говорит нам сумму внутренних углов любого многоугольника. Это выглядит следующим образом…

Для любого заданного многоугольника с n сторонами

SumofInteriorAngles=(n-2)×180°

Итак, когда у нас есть треугольник, n=3, и поэтому сумма внутренних углов равна (3-2)×180=180°.

Точно так же, когда у нас есть четырехугольник, n=4 и поэтому сумма внутренних углов равна (4-2)×180=360°

Мы уже знали эти два результата. Однако теперь мы можем применить эту формулу к фигурам с более чем четырьмя сторонами.

Вычислите сумму внутренних углов пятиугольника.

Решение:

Пятиугольник имеет пять сторон, поэтому по формуле сумма внутренних углов равна (5-2)×180=540°

Вычислите сумму внутренних углов пятиугольника.

Решение:

У девятиугольника девять сторон, поэтому по формуле сумма внутренних углов равна (9-2)×180=1260°

Вычислите сумму внутренних углов для фигуры ниже.

Углы в многоугольниках — 14-сторонний многоугольник, Jordan Madge — StudySmarter Originals

Решение:

Вышеприведенная фигура имеет 14 сторон, поэтому сумма внутренних углов равна (14-2)×180=2160°

Вычислите сумму внутренних углов 24-гранной фигуры.

Решение:

Когда role=»math» n=24, сумма внутренних углов равна (24-2)×180=3960°

Вычислите величину угла x на изображении ниже.

Углы в многоугольниках – пример четырехугольника, Jordan Madge – StudySmarter Originals прямые углы в фигуре равны 90°, поэтому мы можем вычислить недостающий угол, вычитая все заданные углы из 540. Таким образом, x=540-90-90-90-130=140°

Таблица общего внутреннего пространства Углы

В таблице ниже показана сумма внутренних углов для первых восьми полигонов. Однако вы можете подтвердить эти результаты для себя, используя формулу.

Shape	# sides	Sum of Interior Angles (°)
Triangle	3	180
Quadrilateral	4	360
Pentagon	5	540
Hexagon	6	720
Heptagon	7	900
Octagon	8	1080
Nonagon	9	1260
Decagon	10	1440

Calculating Each Interior Angle

Earlier, we defined regular polygons as polygons with equal стороны и углы . Поэтому мы можем захотеть вычислить для каждого внутреннего угла правильного многоугольника. Сначала вычисляем сумма из внутренних углов и разделить это число на количество сторон .

Вычислите каждый внутренний угол правильного шестиугольника.

Решение:

Из таблицы 1 видно, что сумма внутренних углов шестиугольника равна 720°. Поскольку этот шестиугольник правильный, все углы одинаковы, и поэтому мы можем определить каждый внутренний угол, разделив 720 на 6. Следовательно, каждый внутренний угол равен 120°.

Ниже представлена ​​часть мозаики, состоящей из трех правильных пятиугольников. Вычислите угол, обозначенный х.

Углы в многоугольниках — пример пятиугольника, Jordan Madge — StudySmarter Originals

Решение:

Сумма внутренних углов каждого правильного шестиугольника равна 720° (используя таблицу общих внутренних углов).

Таким образом, каждый внутренний угол в каждом шестиугольнике равен 120°.

Углы в многоугольниках — Пример пятиугольника, Джордан Мэдж — StudySmarter Originals

Напомним, что сумма углов вокруг точки равна 360 градусам. Следовательно, x можно найти, вычитая другие известные углы из 360. Таким образом, x=360-108-108=144°

Внешние углы в многоугольниках

Для каждого внутреннего угла в многоугольнике также существует внешний угол. Внешний угол образован между любой стороной формы и прямой линией , продолженной за пределы формы. Это может показаться не очень ясным, но это легче увидеть на иллюстрации.

Углы в многоугольниках — пятиугольник с маркировкой внутренних и внешних углов, Jordan Madge — StudySmarter Originals

На приведенной выше диаграмме внутренние углы помечены оранжевым цветом, а внешние углы — зеленым . Поскольку внешний угол лежит на той же прямой прямой , что и внутренний угол, сумма внутреннего и внешнего углов равна 180°. Следовательно, внешний угол можно вычислить путем вычитания внутреннего угла из 180°.

На изображении ниже углы x и y являются внешними углами. Вычислите х и у.

Углы в многоугольниках — Пятиугольник с внутренними и внешними углами, Jordan Madge — StudySmarter Originals

Решение:

Для внешнего угла x внутренний угол равен 109°. Таким образом, поскольку сумма углов на прямой составляет 180°, x=180-109=71°. Угол y — это еще один внешний угол, и, поскольку сумма углов на прямой равна 180, y = 180-81 = 9.9°.

Вычислите каждый внешний угол правильного семиугольника. Решение: Семиугольник имеет семь сторон, поэтому сумма внутренних углов равна 900°.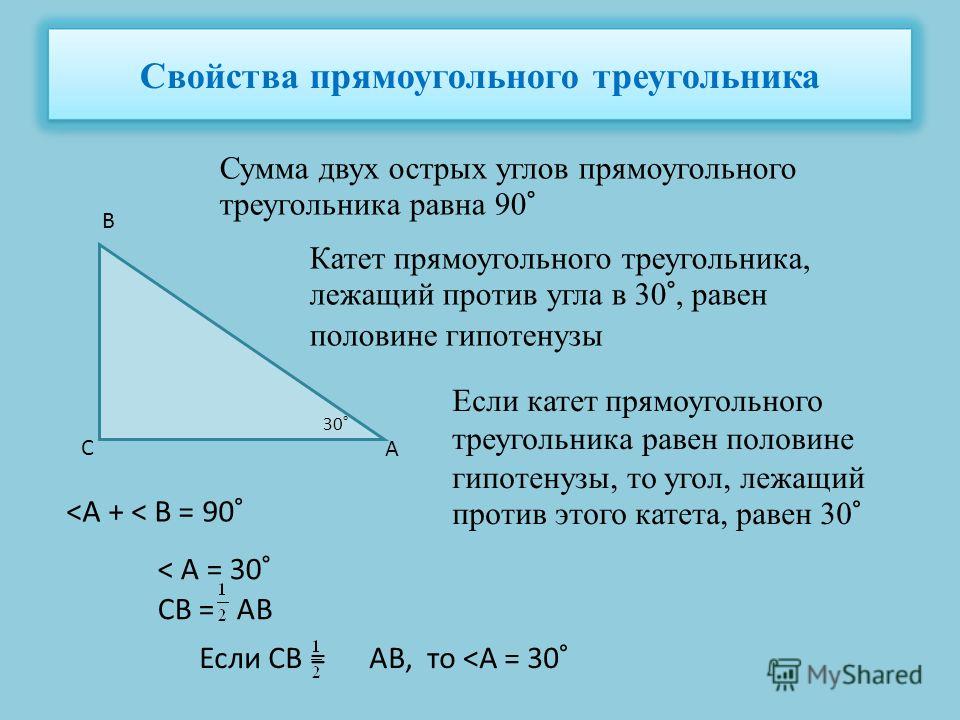 Поскольку этот семиугольник правильный, мы можем вычислить каждый внутренний угол, разделив 900 на 7, чтобы получить 128,6°. Следовательно, мы можем вычислить каждый внешний угол, вычитая его из 180. Таким образом, каждый внешний угол равен 180-128,6=51,4°.

Семиугольник также иногда называют септагоном.

Сумма внешних углов

Сумма внешних углов для любого многоугольника предельно проста. Это 360°. В отличие от внутренних углов, нам не нужно запоминать какие-то замысловатые формулы, чтобы вычислить сумму внешних углов; нам просто нужно запомнить сумму внешних углов для любого многоугольника 360°. Используя это, мы можем начать отвечать еще на несколько вопросов.

Каждый внешний угол правильного многоугольника равен 10. Определите количество сторон многоугольника.

Решение:

Так как сумма внешних углов равна 360°, а каждый внешний угол равен 10°, мы можем вычислить количество сторон как 360÷10=36.