Синус меньше a
Рассмотрим решение тригонометрических неравенств вида синус меньше a (sinx<a) на единичной окружности.
Синус — это ордината точки. Соответственно, sinx=a в точках пересечения единичной окружности и прямой y=a. Часть окружности, расположенная выше прямой y=a, соответствует значениям синуса, большим a. Поскольку мы решаем неравенство sinx<a, его решениям будет соответствовать часть окружности, расположенная ниже прямой y=a. Рассмотрим несколько вариантов взаимного расположения прямой y=a и единичной окружности.
1) sinx<a при 0<a<1
Основная задача здесь — правильно определить точки пересечения прямой и окружности. Первая точка находится легко — это arcsina. Для определения второй точки рассуждаем так: так как sin<a, нам нужна часть окружности под прямой y=a. Значит, из первой точки во вторую идем нижним путем, то есть по часовой стрелке. Но при движении по часовой стрелке угол уменьшается. От arcsina мы дошли до 0, а дальше пошли отрицательные углы (точнее, сам угол положительный, а минус — всего лишь знак обхода от нуля по часовой стрелке).
Мы нашли только один интервал, на котором sinx<a. Чтобы учесть все решения (а таких интервалов — бесконечное множество), с учетом периодичности синуса к каждому из концов интервала прибавляем 2пn, где n — целое число (то есть n принадлежит Z).
Если неравенство нестрогое, точки пересечения окружности и прямой закрашиваем, а затем включаем в решение (круглую скобку заменяем на квадратную).
2) sinx<-a при 0<a<1
Первая точка arcsin(-a)=-arcsina. Чтобы попасть во вторую, идем нижним путем, то есть по часовой стрелке. До п, точнее до -п, не доходим на arcsina. Поэтому вторая точка — (п-arcsina). Мы не дошли до угла п arcsina, а поскольку движение происходит по часовой стрелке, то перед разностью ставим знак минус. Чтобы учесть все решения, к обоим концам промежутка прибавляем 2пn, где n — целое число.
Для нестрого неравенства точки закрашиваем и включаем в ответ (с квадратной скобкой вместо круглой).
В этом случае удобнее решение записывать не от нуля до -п, а от п до 2п. Для нестрогого неравенства- квадратные скобки, закрашенные точки.
4) sinx<1
И в этом случае тоже удобнее выбирать положительные точки. Решением данного неравенства являются все x, кроме п/2+2пn. Чтобы записать это в виде промежутка, надо определить его концы. Если первую точку взять п/2, то во вторую мы попадем через полный оборот окружности, то есть п/2+2п=5п/2. К обоим концам прибавляем 2пn.
В этом случае никакие точки не исключаются, а значит, x — любое число:(-∞;+∞).
В этом случае единственной точкой на окружности, удовлетворяющей данному условию, является точка -п/2. С учетом периодичности синуса решение данного неравенства — множество точек вида x=-п/2+2пn, где n — целое число.
7) sinx<a при a>1
Окружность в этом случае целиком лежит ниже прямой y=a, а значит, решением данного неравенства является любое значение x: (-∞;+∞).
8) sinx< -a при a>1
Окружность целиком лежит выше прямой y=a, а значит, нет ни одного x, удовлетворяющего условию неравенства. Значит, решений нет.
И в заключении, рассмотрим пример.
Решить неравенство sinx<-1/2
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| Найти точное значение | sin(pi/3) | ||
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | cos(150) | ||
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | ||
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Показать sin(x) меньше или равно x
Интеграция Дифференциация
Клэр Х.
спросил 09.04.16Показать, что sin(x)≤x для всех x≥0 (подсказка посмотреть на производную от x-sin(x))
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Арнольд Ф.
ответил 09.04.16
Репетитор
5 (53)
Профессор колледжа и репетитор-эксперт по статистике и исчислению
См. таких репетиторов
Смотрите таких репетиторов
, если y = x – sin(x), то y’ = 1 – cos(x).
Это говорит о том, что y’>=0, поэтому y — неубывающая функция.
Поскольку y=0, когда x=0, это говорит о том, что, поскольку y не уменьшается, он не опускается ниже нуля.
По всем вопросам обращайтесь в комментарии.
Голосовать за 1 голос против
Подробнее
Отчет
Рено О. Б. ответил 09.04.16
Репетитор
4,8 (102)
Репетитор по химии и математике
Об этом репетиторе ›
Об этом репетиторе ›
sin(x) всегда будет находиться в диапазоне от -1 до 1.
Он расходится. Он никогда не сойдется к одному предельному значению, когда x стремится к бесконечности.
Пусть sin(x)=c, где c — некоторое значение от -1 до 1
Тогда предел sin(x)/x, когда x становится больше 0, равен c/x
Для значения x = 1,
c = x, когда c = 1,
c , когда x> 1 c всегда будет меньше x. -1 и 1 меньше 2, 3, 4 и так далее. предел c/x, когда x становится больше нуля, составляет c/∞, что в конечном итоге будет равно 0. Если отношение c/x становится равным нулю, то sin(x) меньше или равно к x для значений x больше 0, Голосовать за 0 голос против Подробнее Отчет Все еще ищете помощи? Получите правильный ответ, быстро.
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Исчисление— Как доказать, что $\lim\limits_{x\to0}\frac{\sin x}x=1$?
Это новый пост о старой пиле, потому что это одна из тех вещей, где я вижу, как это, к сожалению, то, как мы структурировали текущий учебный план по математике, на самом деле не позволяет делайте такие вещи по справедливости, которых они заслуживают, и я думаю, что в конечном итоге это оказывает медвежью услугу многим ученикам.
Правда в том, что этому пределу нельзя дать честное доказательство, во-первых, без честного определения функции синуса. И это , а не так просто, как кажется. Даже если мы рассмотрим простое понятие из многих тригонометрических трактовок о том, что синус равен «длине противоположной стороны прямоугольного треугольника, деленной на длину его гипотенузы», это на самом деле не решает проблему, потому что на самом деле существует тонкий недостающий элемент, а именно то, что синус не является функцией «прямоугольного треугольника» (хотя вы могли бы определить это, если хотите, и это было бы легко!), а угловая мера .
И на самом деле выясняется, что означает «угловая мера», оказывается, по сути, эквивалентно определению функции синуса в первую очередь, так что этот подход круговой! (каламбур, замеченный после написания, несмотря на то, что это изначально не предполагалось!)
Итак, как мы определяем синус или угловую меру? К сожалению, любой подход к этому таков, что он должен включать исчисление. Это связано с тем, что используемая нами угловая мера является «гладкой и устойчивой», а это означает, что, по сути, если у нас есть какой-то угол, мы хотели бы дробить эту угловую меру, чтобы дробить угол таким же образом, как разрезая куски пирога: если у меня есть угол с заданной угловой мерой $\theta$, то для работы системы мер я должен иметь возможность получить угол с мерой $\frac{\theta}{n}$, должен быть угол, который геометрически представляет собой $n$-сечение угла на $n$ равных меньших углов, которые в сумме составляют полный угол.
Но уже сейчас мы видим, что это не тривиально: рассмотрим $n = 3$.
Затем у нас есть знаменитая «невозможная» задача о «трисекции угла», которая досаждала даже древним грекам и над которой люди продолжали биться, пока Пьер Ванцель, наконец, не доказал ее неразрешимость более чем через два тысячи лет спустя. Мы просим математический виджет, который может не только треугольно, но и 5-секционно, 629-секционно и т.д. углы и в систематический способ загрузки!
В самом деле, не только функция синуса , а не функция тривиальна, мы можем утверждать, что даже экспоненциальную функцию обрабатывать значительно легче, чем синус, хотя я не буду приводить здесь такую трактовку.
Итак, как мы это делаем? Что ж, ключевое наблюдение заключается в том, что наша «устойчивая» мера угла — это мера, которая фактически определяется длиной 90 144 дуги 90 145 сегмента круга, пересекаемого углом, когда он проведен в центре круга и спроецирован наружу. В частности, это должно быть «очевидно» из геометрической формулы (введенной циклически)
$$\mbox{Длина дуги окружности} = r\theta$$
Поскольку это всего лишь тривиальное умножение, вся нетривиальность должна заключаться либо в определении $\theta$ через геометрические углы, образованные линиями, либо с точки зрения определения «длины дуги окружности» и, кроме того, эти две задачи должны быть одинаково трудными.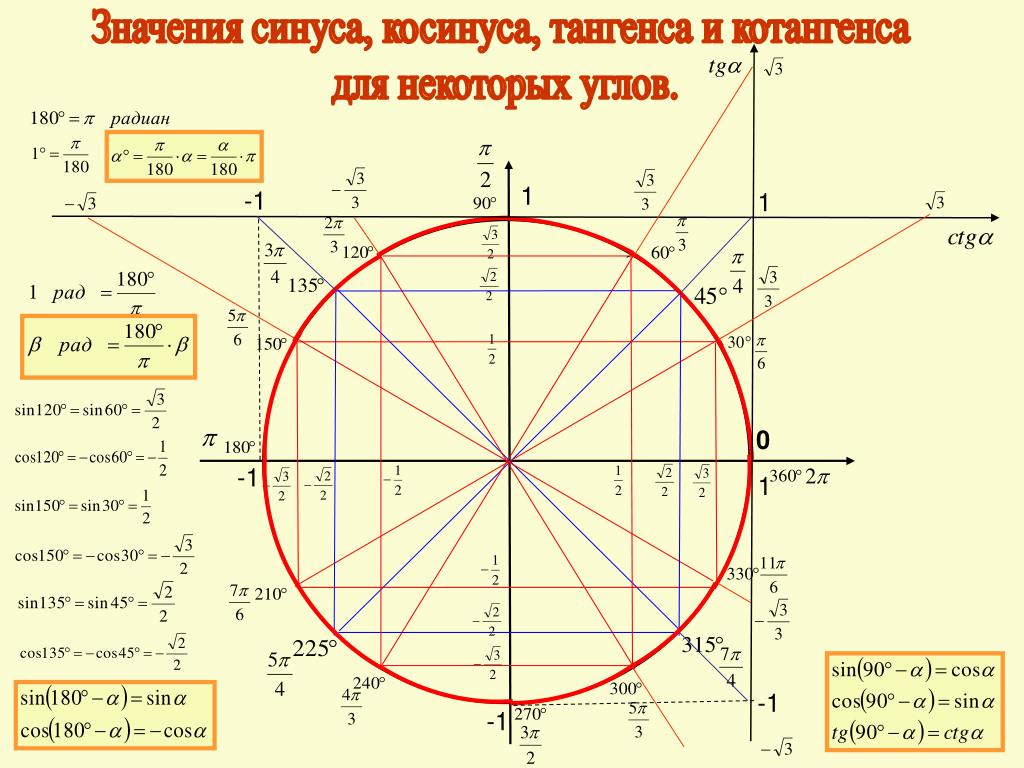
Следовательно, мы начнем сначала с дугового вопроса, и вы увидите, что этот ответ в конечном итоге будет использовать изрядное количество материала Исчисления II, чтобы ответить на этот вопрос уровня Исчисления I о предположительно предварительный расчет математический объект. На самом деле, это то, чем является вся «радианная мера»: это мера углов с точки зрения длины дуги куска, который они вырезают из единичного круга (т.е. $r = 1$). Тогда «градусы» представляют собой просто странные кратные единицы фактической длины, равные $\frac{2\pi}{360}$ (или лучше, $\frac{\tau}{360}$) какой-либо другой единицы длины. .
Если вы возьмете несколько более честную книгу по тригонометрии, вы увидите кое-что о том, что синус и косинус определяются как координаты на единичной окружности, когда мера угла $\theta$ была помещена из $ x$-ось:
$$C(\theta) := (\cos(\theta), \sin(\theta))$$
Теперь, как сказано выше, $\theta$ составляет длины дуги. Таким образом, то, что у нас есть выше, называется параметризацией длины дуги окружности, и это говорит нам, как нам нужно действовать.
Во-первых, нам нужно отдельное определение длины дуги окружности.
Как нам это получить? Ну, во-первых, нам, очевидно, понадобится более элементарное уравнение окружности, чем то, которое мы только что дали, а это означает переход к простому 9{-1}(\тета)$$
.
Наконец, теперь, когда у нас есть полное, надежное определение $\sin(x)$, мы готовы оценить предел:
$$\lim_{x \rightarrow 0} \frac{\ sin(x)}{x}$$
Поскольку «действительная» или базовая функция здесь на самом деле является обратной функцией, т. е. $\arcsin$, мы сначала произведем замену переменных: вместо этого рассмотрим предел в терминах $y$, где $y(x) := \arcsin(x)$. Обратите внимание, что тривиально $\arcsin(0) = 0$ из определения интеграла, таким образом, мы получаем 9{y} 1\ d\xi$$
, когда $y \ приблизительно 0$, и тогда правый интеграл приблизительно равен $y$, следовательно, $\arcsin(y) \ приблизительно y$, когда $y \ приблизительно 0 $ и
$$\lim_{y \rightarrow 0} \frac{y}{\arcsin(y)} = \lim_{y \rightarrow 0} \frac{y}{y} = \lim_{y \rightarrow 0} 1 = 1$$
, следовательно,
$$\lim_{x \rightarrow 0} \frac{\sin(x)}{x} = 1$$
КЭД.
Тем не менее, как я упоминал ранее, это не решает требований вопроса, который, хотя я уверен, что его первоначальный задавший уже давно перешел, тем не менее, по-прежнему актуален для студентов, изучающих математику, после студентов математики до сегодняшнего дня: доказать ограничение с использованием только методов исчисления I / предварительного исчисления. Я хочу сказать, что на самом деле это не совсем возможно и показывает слабость учебного плана в том, что он на самом деле не следует надлежащему логическому построению математической системы.
На самом деле следует сделать оставить триггер на потом , то есть пропустить триггер и сначала перейти к исчислению. Когда я изучал математику самостоятельно, я делал именно это. На самом деле, я бы сказал, как предположили многие преподаватели, что большинству людей не нужно ни то, ни другое, а вместо этого действительно нужно больше статистики. Затем для тех, кто делает высшую математику, если мы изучили алгебру и статистику, у нас уже есть много интересного материала, на котором мы можем основываться для исчисления, включая показательную функцию.
2}$, что является очень хорошим примером интегрирования по площади. отношения, и это может, если сделать более сильный акцент, потенциально вызвать более тонкое размышление об интегралах, помимо простого «подключения и пыхтения правил интеграции». В частности, с более ограниченным набором функций мы можем подумать о других способах, которыми мы могли бы подойти к ним именно так, и/или о различных способах интерпретации интеграла, которые, я думаю, могут быть только хорошими, чтобы развить более творческий подход. размышления о проблемах и меньшее углубление в методы с небольшим реальным пониманием (и механическое перемалывание интегралов еще менее актуально сейчас с программным обеспечением компьютерной алгебры; более важно действительно уметь понять проблему и то, как ее части сочетаются друг с другом и приводят к решению. Тем не менее, механическое перемалывание — это не то, что я предлагаю запретить , но я предлагаю, чтобы идеи, концепции и творчество были на первом месте, затем вы осваиваете эти техники, потому что очень часто они все еще полезны в анализе и свободном владении ими.
Leave A Comment