 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | ||
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Предварительное вычисление алгебры — Решение тригонометрического уравнения $\sin(2x) = \frac{1}{2}$ 9\circ = \arcsin \frac 12$.
 Они оба должны сказать следующее: если $\sin W=k$, то $W=\arcsin k$ является одним из возможных решений. А $W = 180-\arcsin k$ — это еще одно возможное значение. И $W= \arcsin k \pm 360m$ или $W=180 -\arcsin k \pm 360n$ для любых целых чисел $m,n$ — бесконечное число возможных решений.
Они оба должны сказать следующее: если $\sin W=k$, то $W=\arcsin k$ является одним из возможных решений. А $W = 180-\arcsin k$ — это еще одно возможное значение. И $W= \arcsin k \pm 360m$ или $W=180 -\arcsin k \pm 360n$ для любых целых чисел $m,n$ — бесконечное число возможных решений.$\arcsin k$ — это всего лишь одно значение , и это всегда значение между $-90$ и $90$. Это не два или более значений одновременно, и это никогда не все решения $\sin W=k$. это , а не , что $\arcsin\frac 12 = 30, 150$. Дело в том, что $\arcsin\frac 12 = 30$ только . И что решение s , поэтому $\sin W = \frac 12$ включает $W= \arcsin \frac 12 =30$ как одно решение и $W =180- \arcsin \frac 12=180 -30 = 150$ в качестве другого решения.
Затем после они сделали эту ошибку и заявили, что $W=\arcsin k = M$, они пытаются исправить ошибку, делая заявление
Если $W = M$, то $W = 180-M$.
Само по себе это просто чушь. Ведь только $27 = 27$, но $27\ne 180-27 = 153$.
Но попытка состоит в том, чтобы учесть два возможных решения и исправить ошибку, описанную выше.
Компенсируя $W= 30$ (т.е. $W= \arcsin \frac 12 = 30$), они учитывают $W= 180 -30$ (т.е. $W=180 -\arcsin \frac 12 = 30$) в качестве другого решения, и поэтому, хотя он и неверен, первый метод дает правильные ответы.
Метод 1 говорит, что если $W = 2x = 30$ или $W= 2x = 150$, то $x = 15$ или 75$.
Метод 2 всегда брал одно решение $2x=30$ и делил на $2$, чтобы получить $x = 15$. В этой точке $x = \frac W2$ равен , а не углу, который был введен в выражение $\sin$. Но метод 2 пытается сказать, что если $x = 15$, то $x =180-15$ все еще в порядке.
Это не так. Единственная причина, по которой метод 1 дал неверный ответ, утверждая, что $2x = W = 30$, поэтому $2x = W = 180-30$ дал правильный ответ, заключалась в том, что $2x = W = \arcsin \frac 12;2x = W = 180 -\arcsin \frac 12$ — два действительных возможных решений.

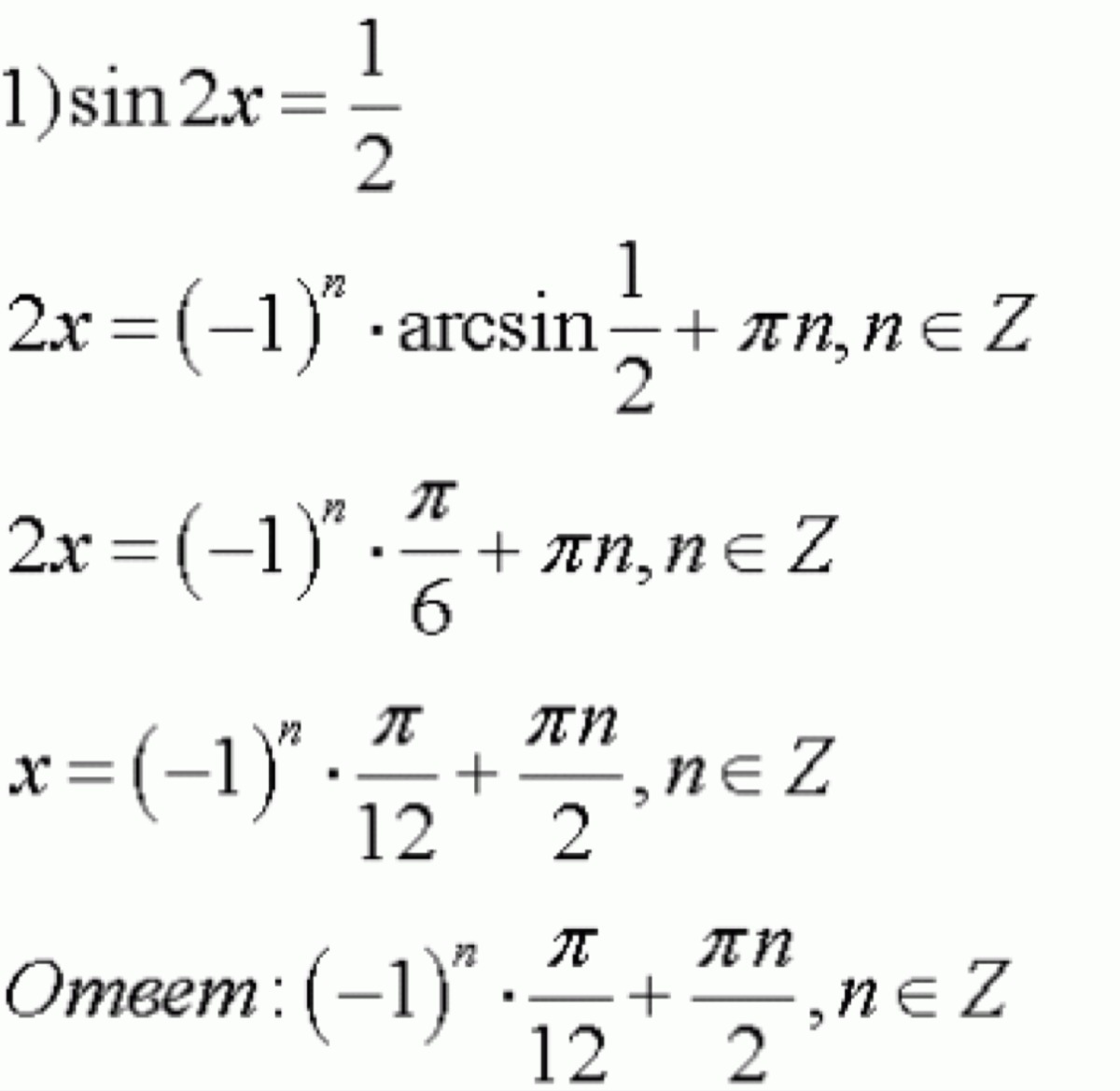 10.17
10.17
Leave A Comment