| 1 | Найти точное значение | sin(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найти точное значение | sin(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти точное значение | sin(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найти точное значение | sin(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти точное значение | tan(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найти точное значение | arcsin(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти точное значение | sin(pi/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | cos(pi/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найти точное значение | sin(45 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти точное значение | sin(pi/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти точное значение | arctan(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найти точное значение | cos(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | cos(30 град. ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найти точное значение | tan(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найти точное значение | csc(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | tan(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найти точное значение | sec(30 град. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найти точное значение | cos(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найти точное значение | cos(150) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найти точное значение | sin(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти точное значение | tan(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найти точное значение | csc(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найти точное значение | sec(45 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найти точное значение | csc(30 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найти точное значение | sin(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найти точное значение | sin(120) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найти точное значение | cos(90) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Преобразовать из радианов в градусы | pi/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найти точное значение | tan(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Преобразовать из градусов в радианы | 45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Найти точное значение | cos(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Преобразовать из радианов в градусы | pi/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найти точное значение | cot(30 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найти точное значение | arccos(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | arctan(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найти точное значение | cot(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразовать из градусов в радианы | 30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найти точное значение | sin((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найти точное значение | sin((3pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найти точное значение | tan(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найти точное значение | sin(300) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найти точное значение | cos(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найти точное значение | cos(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | Найти точное значение | cos(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | Найти точное значение | cos(135) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | Найти точное значение | cos((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найти точное значение | cos(210) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | Найти точное значение | sec(60 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | Найти точное значение | sin(300 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | Преобразовать из градусов в радианы | 135 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | Преобразовать из градусов в радианы | 150 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Преобразовать из градусов в радианы | 89 град. | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Преобразовать из градусов в радианы | 60 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найти точное значение | sin(135 град. ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найти точное значение | sin(150) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Найти точное значение | sin(240 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Найти точное значение | cot(45 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Найти точное значение | sin(225) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найти точное значение | sin(240) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Найти точное значение | cos(150 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Найти точное значение | tan(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Вычислить | sin(30 град.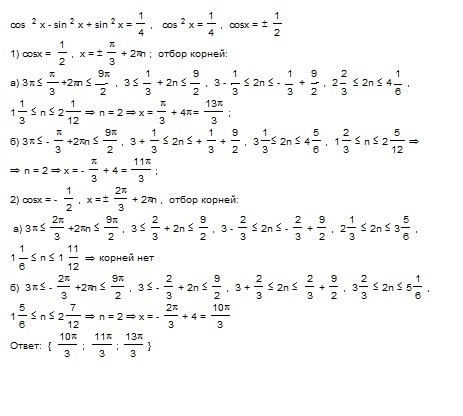 ) ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найти точное значение | sec(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найти точное значение | cos((5pi)/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Найти точное значение | csc(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | Найти точное значение | tan((5pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Найти точное значение | tan(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Вычислить | sin(60 град. ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | Найти точное значение | sin((7pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Найти точное значение | arcsin(-1/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | Найти точное значение | sin((4pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | Найти точное значение | csc(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | Упростить | arctan( квадратный корень из 3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | Найти точное значение | sin(135) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найти точное значение | sin(105) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | sin(150 град. ) ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | sin((2pi)/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Найти точное значение | tan((2pi)/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | Преобразовать из радианов в градусы | pi/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | Найти точное значение | sin(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | Найти точное значение | sec(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | Найти точное значение | cos((5pi)/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Найти точное значение | cos((7pi)/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | Найти точное значение | arcsin(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найти точное значение | sin(120 град. 2((3п/2)-x))=cosx — вопрос №1568841 — Учеба и наука 2((3п/2)-x))=cosx — вопрос №1568841 — Учеба и наука | ||||||||||||||||||||||||||||||||||||||||||||||||||||
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
()+()+()-=30 Заполните пустые места используя данные числа (1,3,5,7,9,11,13,15) Одно и тоже число можно использовать несколько раз.
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз
как решить задачу *+*+*=30 использовать цифры 1,3,5,7,9,11,13,15. одну цифру можно использовать несколько раз
?+?+?=30 как решит? использовать 1,3,5,7,9,11,13,15 одно и то же число можно использовать несколько раз
Пользуйтесь нашим приложением
Sin 3pi/2 — Найдите значение Sin 3pi/2
LearnPracticeDownload
Значение sin 3pi/2 равно -1 . Sin 3pi/2 радиан в градусах записывается как sin ((3π/2) × 180°/π), т. е. sin (270°). В этой статье мы обсудим методы нахождения значения sin 3pi/2 на примерах.
- Sin 3pi/2: -1
- Sin (-3pi/2): 1
- Sin 3pi/2 в градусах: sin (270°)
Каково значение Sin 3pi/2?
Значение sin 3pi/2 равно -1. Sin 3pi/2 также можно выразить с помощью эквивалента заданного угла (3pi/2) в градусах (270°).
Мы знаем, используя преобразование радиан в градусы, θ в градусах = θ в радианах × (180°/pi)
⇒ 3pi/2 радиана = 3pi/2 × (180°/pi) = 270° или 270 градусов
∴ sin 3pi/2 = sin 3π/2 = sin(270°) = -1
Объяснение:
Для sin 3pi/2 угол 3pi/2 лежит на отрицательной оси y. Таким образом, значение sin 3pi/2 = -1
Поскольку функция синуса является периодической функцией, мы можем представить sin 3pi/2 как sin 3pi/2 = sin(3pi/2 + n × 2pi), n ∈ Z.
⇒ sin 3pi/2 = sin 7pi/2 = sin 11pi/2 и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-3pi/2) = -sin(3pi/2).
Методы определения значения Sin 3pi/2
Значение sin 3pi/2 задается как -1. Мы можем найти значение sin 3pi/2 по:
- Используя Unit Circle
- Использование тригонометрических функций
Sin 3pi/2 с помощью единичной окружности
Чтобы найти значение sin 3π/2 с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 3pi/2 с положительной осью x.
- Синус 3pi/2 равен координате y(-1) точки пересечения (0,-1) единичной окружности и r.
Следовательно, значение sin 3pi/2 = y = -1
Sin 3pi/2 в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 3pi/2 как:
- ± √(1-cos²(3pi/2))
- ± тангенс(3pi/2)/√(1 + тангенс²(3pi/2))
- ± 1/√(1 + раскладушка²(3pi/2))
- ± √(сек²(3pi/2) — 1)/сек(3pi/2)
- 1/косек(3pi/2)
Примечание: Поскольку 3pi/2 лежит на отрицательной оси Y, конечное значение sin 3pi/2 равно -1.
Мы можем использовать тригонометрические тождества для представления sin 3pi/2 как
- sin(pi — 3pi/2) = sin(-pi/2)
- -sin(pi + 3pi/2) = -sin 5pi/2
- cos(pi/2 — 3pi/2) = cos(-pi)
- -cos(pi/2 + 3pi/2) = -cos 2pi
☛ Также проверьте:
- tan 3pi/8
- кроватка 15pi/4
- детская кроватка pi/4
- рыжевато-коричневый 5pi/3
- cos пи/3
- грех 4pi/3
Примеры использования Sin 3pi/2
Пример 1. Найдите значение 2 × (sin(3pi/4) cos(3pi/4)). [Подсказка: используйте sin 3pi/2 = -1]
Решение:
Используя формулу sin 2a,
2 sin(3pi/4) cos(3pi/4) = sin(2 × 3pi/4) = sin 3pi/2
∵ sin 3pi/2 = -1
⇒ 2 × (sin(3pi/4) cos(3pi/4)) = -1Пример 2: Упростить: 2 (sin(3pi/2)/sin(7pi/2))
Решение:
Мы знаем sin 3pi/2 = sin 7pi/2
⇒ 2 sin(3pi/2)/sin(7pi/2) = 2(sin(3pi/2)/sin(3pi/2))
= 2(1) = 2Пример 3.
 Используя значение sin 3pi/2, найдите: (1-cos²(3pi/2)).
Используя значение sin 3pi/2, найдите: (1-cos²(3pi/2)). Решение:
Мы знаем, (1-cos²(3pi/2)) = (sin²(3pi/2)) = 1
⇒ (1-cos²(3pi/2)) = 1
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 3pi/2
Что такое Sin 3pi/2?
Sin 3pi/2 — значение тригонометрической функции синуса для угла, равного 3pi/2 радианам. Значение sin 3pi/2 равно -1.
Каково значение Sin 3pi/2 в пересчете на Cos 3pi/2?
Используя тригонометрические тождества, мы можем записать sin 3pi/2 через cos 3pi/2 как sin(3pi/2) = -√(1-cos²(3pi/2)). Здесь значение cos 3pi/2 равно 0,9. 0003
0003
Каково значение Sin 3pi/2 в пересчете на Cosec 3pi/2?
Поскольку функция косеканса является обратной функцией синуса, мы можем записать sin 3pi/2 как 1/cosec(3pi/2). Значение cosec 3pi/2 равно -1.
Как найти значение Sin 3pi/2?
Значение sin 3pi/2 можно вычислить, построив угол 3π/2 радиана с осью x, а затем найдя координаты соответствующей точки (0, -1) на единичной окружности. Значение sin 3pi/2 равно координате y (-1). ∴ sin 3pi/2 = -1.
Как найти Sin 3pi/2 с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение sin 3π/2 можно выразить через другие тригонометрические функции следующим образом:
- ± √(1-cos²(3pi/2))
- ± тангенс(3pi/2)/√(1 + тангенс²(3pi/2))
- ± 1/√(1 + раскладушка²(3pi/2))
- ± √(сек²(3pi/2) — 1)/сек(3pi/2)
- 1/косек(3pi/2)
☛ Также проверьте: тригонометрическую таблицу
Загрузить БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
Наставник Карла по исчислению — Trig Identities
© 1997 Карл Хан Здесь снова рисунок 7-3, так что вы можете посмотреть на графики
sin(x) и cos(x), пока мы их обсуждаем. А вот таблица значений sin(x) и cos(x)
для некоторых общих значений x. Все эти результаты могут быть
производные от базовой геометрии.
А вот таблица значений sin(x) и cos(x)
для некоторых общих значений x. Все эти результаты могут быть
производные от базовой геометрии.
х градусов sin(x) cos(x)
|
Я бы хотел, чтобы вы на мгновение задумались о поезде на кольцевом пути. |
cos(-x) = cos(x) ур. 7.1б-1
На математическом жаргоне мы говорим, что косинус — это функция даже . Любой f(x), который подчиняется свойству f(-x) = f(x) называется четной функцией. Обратите внимание, например, что x, возведенный в любую четную степень, является четным числом. функция. Это, кстати, и есть причина вызова таких функций даже.
Точно так же, что происходит по-другому с положением поезда север-юг
в зависимости от того, идет ли он на 50 метров назад или вперед на 50 метров?
Что ж, на этот раз есть разница. Но здесь тоже есть симметрия.
также. Поезд доедет до севернее Мейн-стрит по
пройти 50 метров вперед, так как это закончится южнее Мейн-стрит по
пройдя 50 метров назад. И снова вы можете заменить любой другой
количество на 50 метров, и то же самое было бы еще верно. Теперь вспомните, что
как далеко к северу или югу от главной улицы находится поезд, так мы ввели синус. Так
с синусом связь
Но здесь тоже есть симметрия.
также. Поезд доедет до севернее Мейн-стрит по
пройти 50 метров вперед, так как это закончится южнее Мейн-стрит по
пройдя 50 метров назад. И снова вы можете заменить любой другой
количество на 50 метров, и то же самое было бы еще верно. Теперь вспомните, что
как далеко к северу или югу от главной улицы находится поезд, так мы ввели синус. Так
с синусом связь
sin(-x) = -sin(x) ур. 7.1б-2Как вы могли догадаться, на математическом жаргоне мы говорим, что синус — это нечетных . функция. Любая f(x), которая подчиняется f(-x) = -f(x) называется нечетной функцией. И, как и следовало ожидать, мы получили эту терминологию, потому что x поднял в любой нечетной степени является нечетной функцией.
( Пища для размышлений: Можете ли вы показать, что единственная функция, которая одновременно является четной
функция, а нечетная функция f(x) = 0?
Можете ли вы также показать, что всякая действительная функция вещественной переменной является
сумма четной функции и нечетной функции? Подумайте о сумме
и разность f(x) и f(-x). )
)
Вот еще одно свойство синуса и косинуса, которое должно быть очевидно из модель кругового пути и график, показанный на рисунке 7-3. Оба синуса и косинус имеют период 2p. То есть везде, где вы находятся на трассе, если вы проедете на 2p километров дальше, вы оказаться в одном и том же месте. Почему? Потому что ты уйдешь полный круг. А если снова пройти 2р, то же самое. Действительно если вы проедете любое расстояние, кратное 2p километрам вы окажетесь именно там, где ты начал. И это означает, что как можно дальше к северу или югу от Мейн-стрит, и так же далеко к востоку или западу от Мейн-авеню, как вы начали. И что в терминах синуса и косинуса это означает, что для любого целого числа n это всегда так
sin(x) = sin(x + 2np) ур. 7.1б-3а cos(x) = cos(x + 2np) ур. 7.1б-3б
Теперь мы готовы рассмотреть целый ряд полезных взаимосвязей между триггерами.
функции.
Если вы не можете их запомнить, вам следует научиться быстро их выводить. Они
скоро станут инструментами, которые вам понадобятся для выполнения домашних заданий и экзаменационных задач.
Они
скоро станут инструментами, которые вам понадобятся для выполнения домашних заданий и экзаменационных задач.
Вот еще два, которые мы развили в основном тексте:
sin 2 (x) + cos 2 (x) = 1 экв. 7.1-1и
cos(a+b) = cos(a)cos(b) - sin(a)sin(b) ур. 7.1-6Из уравнения 7.1-1 сразу видно, что
___________
|кос(х)| = Ö1 - sin 2 (x) ур. 7.1-1а
___________
| грех (х) | = Ö1 - cos 2 (x) экв. 7.1-1б
Теперь посмотрите на таблицу 7-1. Заметить, что sin(p/2) = 1 и потому что (р / 2) = 0. По нечетным и четным свойствам синуса и косинуса мы также знаем что sin(-p/2) = -1 и потому что (-p/2) = 0. Предположим, вы положили b = -p/2 и вставили его в уравнение 7.1-6.
cos(a - p/2) = cos(a)cos(-p/2) - sin(a)sin(-p/2) ур. 7.1б-3а cos(a - p/2) = cos(a)×0 - sin(a)×(-1) ур. 7.1б-3б cos(a - p/2) = sin(a) ур.А поскольку косинус — четная функция, отсюда также следует, что7.1б-3с
cos(p/2 - a) = sin(a) ур. 7.1b-3dОба они верны для любого действительного числа, а. Теперь подставьте u = p/2 — a в уравнение 7.1b-3d и у вас есть
cos(u) = sin(p/2 - u) ур. 7.1б-3дЧто верно для любого действительного числа, u. Но предположим, что вместо этого вы подставил u = a — p/2 в уравнение 7.1b-3c. Вы получите
cos(u) = sin(u + p/2) ур. 7.1b-3fчто опять-таки верно для любого действительного числа u.
Теперь давайте возьмем уравнение 7.1-6 и везде, где вы видите a, замени на п/2 — а и везде увидишь a b, замените его на -b
cos(p/2 - a - b) = cos(p/2 - a)cos(-b) - sin(p/2 - a)sin(-b)
экв. 7.1б-4а
Теперь просто примените тождества, которые у нас есть до сих пор:sin(a + b) = sin(a)cos(b) + cos(a)sin(b) ур.и у нас есть способ найти синус суммы двух углов. А сейчас у нас есть формулы как для синуса, так и для косинуса суммы углов, но а как же разница углов? Вы можете использовать формулы суммы вместе с четными и нечетными свойствами to, заменив -b на b, получить:7.1б-4б
cos(a - b) = cos(a)cos(b) + sin(a)sin(b) ур. 7.1б-5а sin(a - b) = sin(a)cos(b) - cos(a)sin(b) ур. 7.1б-5бВы также можете использовать формулы суммы для получения выражений для синуса и косинус двойного угла. Просто заметьте, что 2x = x + x и подставить в выражения суммы.
cos(2x) = cos(x + x) = cos 2 (x) - sin 2 (x) ур. 7.1б-6а sin(2x) = sin(x + x) = 2sin(x)cos(x) ур. 7.1б-6бВы можете проделать хитрый трюк с уравнением 7.1b-6a, чтобы получить половинный угол подставив x/2 и объединив его с экв. 7.1-1.
cos(x) + 1 = cos(x/2 + x/2) + 1 = cos 2 (x/2) - sin 2 (x/2) + 1 =
cos 2 (x/2) - sin 2 (x/2) + sin 2 (x/2) + cos 2 (x/2) ур. 7.1б-7а
7.1б-7а
Когда вы отмените и упростите, вы получите
cos(x) + 1 = 2cos 2 (x/2) экв. 7.1б-7б
______________
Öcos(x)/2 + 1/2 = |cos(x/2)| экв. 7.1б-7в
Точно так же вы можете изменить знаки и получить
1 - cos(x) = 1 - cos(x/2 + x/2) = 1 - cos 2 (x/2) + sin 2 (x/2) =
sin 2 (x/2) + cos 2 (x/2) - cos 2 (x/2) + sin 2 (x/2) ур. 7.1б-8а
Когда вы отмените и упростите, вы получите
1 - cos(x) = 2sin 2 (x/2) ур. 7.1б-8б
______________
…1/2 - cos(x)/2 = |sin(x/2)| экв. 7.1б-8в
Вставив x вместо x/2, вы можете использовать приведенное выше для
получить формулы квадрата синуса и квадрата косинуса:sin 2 (x) = 1/2 - cos(2x)/2 ур. 7.1б-9а cos 2 (x) = 1/2 + cos(2x)/2 ур. 7.1б-9б(Посмотрите, что получится, если сложить правые части этих двух уравнений.
 )
)Комбинируя уравнения 7.1-6 и 7.1b-5a, вы получаете
cos(a+b) + cos(a-b) = cos(a)cos(b) - sin(a)sin(b) +
cos(a)cos(b) + sin(a)sin(b) =
2cos(a)cos(b) экв. 7.1б-10а
Если вы разделите 2, вы увидите, что произведение
Косинусы двух чисел равны половинному косинусу их
сумма плюс половина косинуса их разности. Так же
cos(a+b) - cos(a-b) = cos(a)cos(b) - sin(a)sin(b) +
-cos(a)cos(b) - sin(a)sin(b) =
-2sin(a)sin(b) экв. 7.1-10б
Опять же, если вы разделите -2, вы увидите, что произведение
синусов двух чисел то же самое, что взять половину косинуса их
разница минус половина косинуса их суммы. Точно так же вы можете
объедините уравнения 7.1b-4b и 7.1b-5b, чтобы получить
грех (а+б) + грех (а-б) = грех (а) потому что (б) + потому что (а) грех (б) +
грех (а) соз (б) - соз (а) грех (б) =
2sin(a)cos(b) ур. 7.1б-11а
грех (а+б) - грех (а-б) = грех (а) потому что (б) + потому что (а) грех (б) +
-sin(a)cos(b) + cos(a)sin(b) =
2cos(a)sin(b) ур. 7.1б-11б
7.1б-11а
грех (а+б) - грех (а-б) = грех (а) потому что (б) + потому что (а) грех (б) +
-sin(a)cos(b) + cos(a)sin(b) =
2cos(a)sin(b) ур. 7.1б-11б
Вот вам симпатичный.
_ _ _
sin(x) + cos(x) = …2 (…2/2)sin(x) + (…2/2)cos(x) ) =
_
…2 ( cos(p/4)sin(x) + sin(p/4)cos(x) ) =
_
…2 sin(x + p/4) ур. 7.1б-12
Это также равно
_
Ö2 cos(p/4 - x)
но я
уверен, что вы можете доказать это, используя тождества, которые у нас есть до сих пор.Тангенс, котангенс, секанс и косеканс
Наверняка вы помните из триггера, что синус и косинус были не единственными триггерами. функции, которые вы изучали. Они также познакомили вас с
грех (х)
tan(x) = экв. 7.1б-13а
потому что (х)
потому что (х)
кроватка(х) = экв. 7.1б-13б
грех (х)
1
сек (х) =
7.1б-13б
грех (х)
1
сек (х) = экв. 7.1б-13в
потому что (х)
1
csc(x) = экв. 7.1б-13г
грех (х)
На рис. 7-4 показана геометрическая интерпретация этих функций. Один раз опять же, радиус окружности равен 1. Угол x равен еще в радианах. Обратите внимание, что точка L , есть координаты (cos(x), sin(x) ). У нас есть
- длина NK равна tan(x).
- длина MJ равна кроватке(х).
- длина OK равна сек(х).
- длина OJ равна csc(x).
В отличие от синуса и косинуса эти новые функции не везде непрерывны.
Например, согласно
экв. 7.1b-13a, tan(x) имеет
cos(x) в знаменателе. Итак, везде, где cos(x) равно
ноль, tan(x) разрывен и не определен. Это происходит в
нечетные кратные p/2. Посмотрите на синюю кривую на рис. 7-5, чтобы
посмотрите, что здесь происходит.
Это происходит в
нечетные кратные p/2. Посмотрите на синюю кривую на рис. 7-5, чтобы
посмотрите, что здесь происходит.
Сходным образом, уравнение 7.1b-13b показывает, что кроватка(х) имеет sin(x) в знаменателе, поэтому везде, где sin(x) равно ноль, cot(x) не определен и разрывен. Бывает кратно p. Посмотрите на зеленую кривую на рис. 7-5, чтобы посмотреть, что происходит в этом случае. Мы будем обсуждать больше о непрерывности триггерных функций позже. раздел. | |
Функции sec(x) и csc(x) следуют аналогичному шаблону. Обратите внимание на рис. 7-6, что sec(x) (синяя кривая) является прерывистой. при нечетных кратных p/2 и csc(x) (зеленая кривая) разрывен в точках, кратных p. И разрывы происходят по тем же причинам, что и в tan(x) и детская кроватка(х). Есть только несколько тождеств, которые мы рассмотрим в отношении этих
функции.
1
сек (х) = поэтому также должно быть верно, что
1
сек 2 (х) = |
Но все мы знаем из ур. 7.1-1 что 1 в числителе выше то же самое, что и sin 2 (х) + cos 2 (х). Итак, заменив на него числитель, получим
sin 2 (х) + cos 2 (х)
сек 2 (x) = экв. 7.1б-14а
потому что 2 (х)
Немного алгебры и оглядываясь назад на
экв. 7.1b-13a, вы можете видеть
чтосек 2 (x) = tan 2 (x) + 1 экв. 7.1б-14би, используя идентичный подход, вы можете показать, что
csc 2 (x) = детская кроватка 2 (x) + 1 экв.7.1б-14в
Разработка формулы для загара (a+b) не составляет труда, если вы используете уже имеющиеся у нас формулы для sin(a+b) и потому что (а+б).
грех(а+б)
tan(a+b) = экв. 7.1б-15а
потому что (а+б)
грех (а) потому что (б) + грех (б) потому что (а)
tan(a+b) = экв. 7.1б-15б
cos(a)cos(b) - sin(a)sin(b)
Если разделить числитель и знаменатель уравнения. 7.1б-15б по
cos(a)cos(b), вы получаете отмену.
грех (а) грех (б)
+
потому что (а) потому что (б)
tan(a+b) = экв. 7.1б-15в
грех (а) грех (б)
1 -
потому что (а) потому что (б)
Наконец, применяя
экв. 7.1b-13a, вы получаете личность
загар (а) + загар (б)
загар (а+б) = экв. 7.1б-15г
1 - загар (а) загар (б)
Используя очень похожий метод, вы можете найти его для котангенса.

 07.15
07.15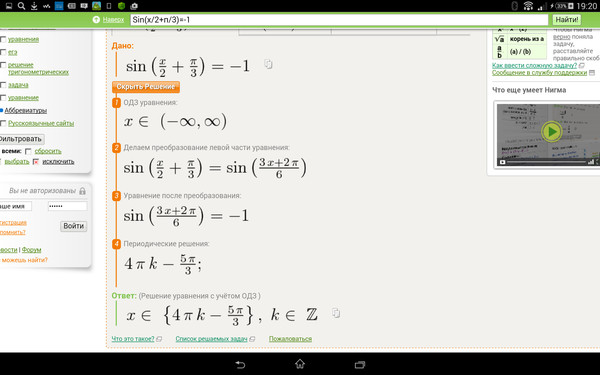 Используя значение sin 3pi/2, найдите: (1-cos²(3pi/2)).
Используя значение sin 3pi/2, найдите: (1-cos²(3pi/2)).  снова. Предположим, что поезд находится на станции на Мейн-стрит и 10-й авеню.
Восток. Чем отличается движение назад от движения вперед?
Если он отступит назад на 50 метров, не окажется ли он так же далеко к востоку от Мейн-авеню?
как это происходит на 50 метров вперед? Разве это не
то же верно, если он резервирует любую сумму, а не продвигается вперед на ту же сумму.
количество? Теперь вспомните
что, как далеко к востоку или западу от Главной авеню находится поезд, так мы представили
косинус. Это иллюстрирует симметрию функций косинуса:
снова. Предположим, что поезд находится на станции на Мейн-стрит и 10-й авеню.
Восток. Чем отличается движение назад от движения вперед?
Если он отступит назад на 50 метров, не окажется ли он так же далеко к востоку от Мейн-авеню?
как это происходит на 50 метров вперед? Разве это не
то же верно, если он резервирует любую сумму, а не продвигается вперед на ту же сумму.
количество? Теперь вспомните
что, как далеко к востоку или западу от Главной авеню находится поезд, так мы представили
косинус. Это иллюстрирует симметрию функций косинуса: 7.1б-3с
7.1б-3с
 7.1б-4б
7.1б-4б
 7.1б-7а
7.1б-7а
 7.1б-11а
грех (а+б) - грех (а-б) = грех (а) потому что (б) + потому что (а) грех (б) +
-sin(a)cos(b) + cos(a)sin(b) =
2cos(a)sin(b) ур. 7.1б-11б
7.1б-11а
грех (а+б) - грех (а-б) = грех (а) потому что (б) + потому что (а) грех (б) +
-sin(a)cos(b) + cos(a)sin(b) =
2cos(a)sin(b) ур. 7.1б-11б
 7.1б-13б
грех (х)
1
сек (х) =
7.1б-13б
грех (х)
1
сек (х) =  Во-первых, вы помните из
экв. 7.1b-13c, что
Во-первых, вы помните из
экв. 7.1b-13c, что 7.1б-14в
7.1б-14в
Leave A Comment