Сила действующая со стороны магнитного поля на проводник с током формула: Сила Ампера. Сила Лоренца. | Объединение учителей Санкт-Петербурга

Действие магнитного поля на проводник с током кратко

4.2

Средняя оценка: 4.2

Всего получено оценок: 292.

4.2

Средняя оценка: 4.2

Всего получено оценок: 292.

На проводник с током, помещенный в магнитное поле, действует сила, величина которой зависит от абсолютной величины тока, длины проводника и величины магнитной индукции. Чему равна величина этой силы и как определить направление силы, действующей на проводник, если известны направления тока и магнитной индукции? Попробуем найти ответы на эти вопросы.

Магнитное взаимодействие

Французский физик Андре-Мари Ампер в 1820 г. обнаружил, что два проводника, по которым пропущен электрический ток, расположенные параллельно друг другу, притягиваются, если направления токов совпадают, и отталкиваются, если токи направлены в разные стороны. Ампер назвал этот эффект электродинамическим взаимодействием.

Рис. 1. Опыт Ампера по взаимодействию токов в параллельных проводниках.

Для объяснения этого явления Ампер ввел понятие магнитного поля, которое возникает вокруг любого движущегося электрического заряда. Магнитное поле непрерывно в пространстве и проявляет себя, оказывая силовое воздействие на другие движущиеся электрические заряды.

Предшественники Ампера пытались построить теорию магнитного поля по аналогии с электрическим полем с помощью магнитных зарядов с разными знаками (северным N и южным S). Однако, эксперименты показали, что отдельных магнитных зарядов в природе не существует. Магнитное поле возникает только в результате движения электрических зарядов.

Сила магнитного взаимодействия

Сила, действующая на проводник с током со стороны магнитного поля, была названа в честь первооткрывателя — силой Ампера. Эксперименты показали, что модуль силы Ампера

F пропорционален длине проводника L и зависит от пространственного положения проводника в магнитном поле.

Для количественного описания действия магнитного поля на проводник с током была введена величина, названная магнитной индукцией B. Тогда сила Ампера будет равна:

$F = B*I*L$ (1),

где I — сила тока. Эта формула справедлива при вычислении модуля максимального значения силы Ампера, действующей на прямолинейный проводник в магнитном поле, вектор магнитного поля B направлен под 90⁰ к вектору тока I

. Если проводник расположен под углом α к вектору магнитной индукции B, то вместо формулы (1) следует применять следующую формулу:

$F = B*I*L*sinα$ (2).

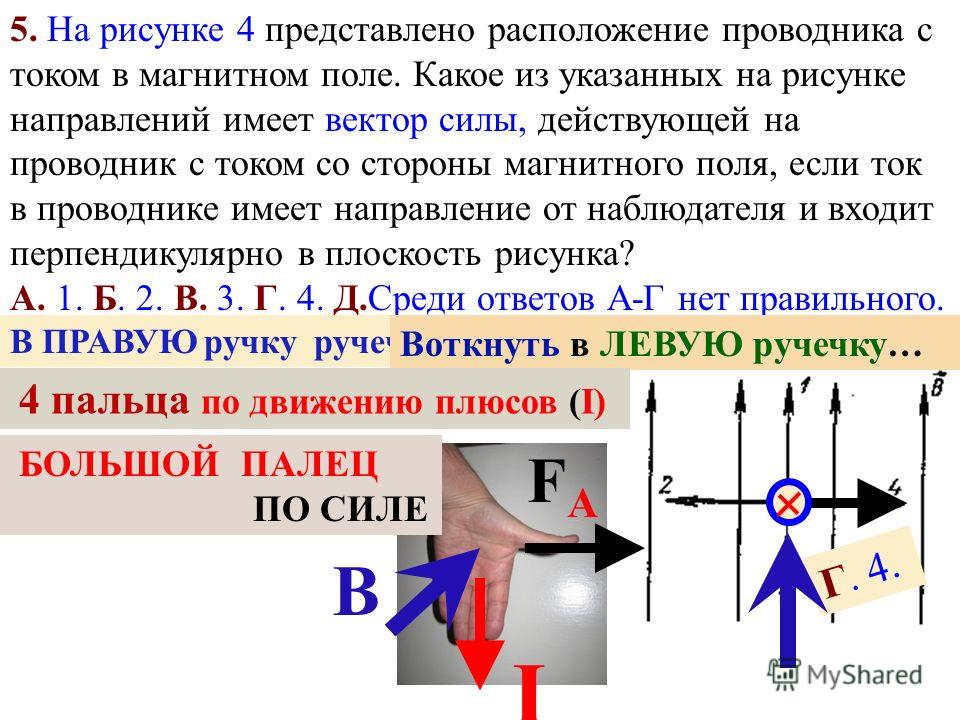
Правило левой руки

Для определения направления вектора силы Ампера применяется “правило левой руки”.

Рис. 2. Правило левой руки для определения направления силы Ампера.

Левая рука располагается так, чтобы пальцы ладони (все кроме большого) указывали направление тока в проводнике. Затем плоскость ладони устанавливается перпендикулярно плоскости, в которой находятся проводник с током и вектор магнитной индукции B. Вектор B должен входить в ладонь.

Тогда большой палец левой руки, развернутый под прямым углом, укажет направление силы Ампера.

Единица измерения индукции

Единица индукции в системе СИ определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока действует сила Ампера величиной 1 Н. Единица называется тесла (Тл).

$1 Тл = {1 Н\over {1 A*1 м}}$ (3).

Единица индукции названа в честь выдающегося сербского инженера, физика Николы Тесла (1856-1943 г.г.). Тесла изобрел электромеханические генераторы, высокочастотный трансформатор. Исследовал свойства токов высокой частоты, изобрел многофазный электродвигатель и системы передачи электроэнергии с помощью переменного тока. Тесла сформулировал основные принципы радиосвязи, изобрел мачтовую антенну для приемки и передачи радиосигналов.

Рис. 3. Портрет Никола Тесла.

Что мы узнали?

Итак, мы узнали что на проводник с током, помещенный в магнитное поле, действует сила Ампера. В статье рассказано кратко о действии магнитного поля на проводник с током. Дано определение понятия магнитной индукции. Приведены формулы для вычисления силы Ампера. Для определения направления силы Ампера дано описание “правила левой руки”.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Давид Мартиросов

  9/10

Оценка доклада

4.2

Средняя оценка: 4.2

Всего получено оценок: 292.

---

А какая ваша оценка?

Высшее образование БГПУ

Сила Ампера. Сила взаимодействия параллельных токов. Контур с то-ком в магнитном поле. Магнитный момент тока. Действие электриче-ского и магнитного полей на движущиеся заряды. Сила Лоренца. Опре-деление удельного заряда электрона. Эффект Холла и его применение. Принцип работы магнитогидродинамических генераторов.

20.1. Сила Ампера. Взаимодействие параллельных токов

При исследовании действия магнитного поля на расположенный в нем прямолинейный проводник с током французский физик А. Ампер пришел к выводу, что модуль этой силы можно рассчитать по формуле

                                                      .                                            (20.1)

Позднее эта сила была названа силой Ампера, а формула – законом Ампера. Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы нормальная к проводнику составляющая B_┴ вектора индукции магнитного поля B входила в ладонь, четыре вытянутых пальца были направлены по току, то отогнутый на 90° большой палец покажет направление силы Ампера, которая действует на проводник с током (рис.20.1).

 

Рис. 20.1

На основе закона Ампера можно объяснить взаимодействие параллельных проводников с током (рис.20.2).

 

Рис. 20.2

 

Ток I₁ создает в месте расположения проводника с током I₂ магнитное поле B₁, которое действует на ток I₂ с силой F₁₂=B₁I₂l.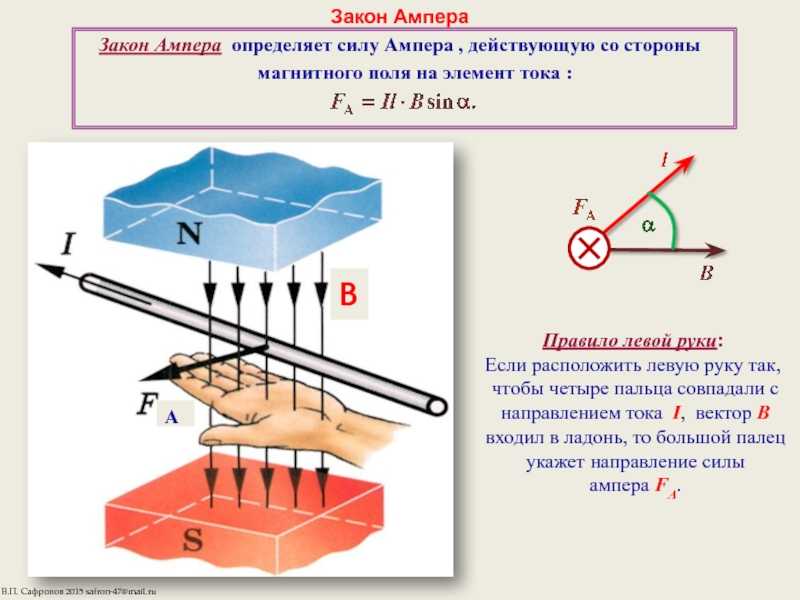 Ток I₂ в свою очередь также создает магнитное поле, индукция которого в месте расположения проводника с током I₁ равна B₂. Это поле действует на ток I₁ с силой F₂₁=B₂I₁l. Силы F₁₂ и F₂₁ находятся в одной плоскости с проводниками и являются силами притяжения, если токи направлены в одну сторону, и силами отталкивания, если токи направлены в противоположные стороны (рис.20.2).

Если расстояние между проводниками равно d, то индукция магнитного поля, созданного током I₁ в тех точках пространства, где находится второй проводник,

                                                          .                                               (20. 2)

Соответственно индукция магнитного поля, созданного током I₂ в тех точках пространства, где расположен первый проводник,

                                                         .                                               (20.3)

Таким образом, для проводников длиной l:

                                                    .                                         (20.4)

Если проводники находятся в вакууме (μ=1) на расстоянии d=1 м м и токи в них одинаковые и равны единице, то сила взаимодействия между участками проводников длиной по 1 м F₀=μ₀/2π=2·10^–7 Н. Эта формула используется для определения единицы силы тока – ампера – в СИ.

20.2. Контур с током в магнитном поле

Поместим замкнутый контур с током в однородное магнитное поле. Пусть плоскость контура перпендикулярна линиям индукции поля. Если разделить контур на элементы dl, то на каждый из них действует сила dF=IBdl, которая лежит в плоскости контура и направлена к его центру (рис. 20.3).

 

Рис. 20.3

Если изменить направление тока на противоположное, то сила dF будет направлена в противоположную сторону (рис.20.4).

 

Рис. 20.4

Значит, силы, которые действуют на замкнутый контур с током в однородном перпендикулярном магнитном поле, могут только деформировать его (растянуть или сжать). Перемещение контура при этом не происходит.

Если расположить контур параллельно направлению линий магнитной индукции (рис.20.5), то на контур будет действовать вращательный момент сил M. Под действием этого момента контур поворачивается так, чтобы его плоскость стала перпендикулярной линиям магнитной индукции.

 

Рис. 20.5

Определим величину вращательного момента. Для этого разделим контур на малые элементы Δl. Выделим два элемента Δl₁ и Δl₂, заключенные между двумя параллельными линиями магнитной индукции, отстоящими друг от друга на расстоянии Δh. На эти элементы со стороны поля действуют силы ΔF₁ и ΔF₂, направленные соответственно перпендикулярно плоскости контура «от нас» и «к нам». Модули этих сил равны: ΔF₁=IBΔl₁sinα₁ и ΔF₂=IBΔl₂sinα₂. Если учесть, что Δl₁sinα₁=Δh, а Δl₂sinα₂=Δh, то очевидно, что эти силы равны по модулю и направлены в противоположные стороны. Они образуют пару сил, момент которой ΔM=ΔF_x=IBΔhx=IBΔS, где x – среднее расстояние между элементами Δl₁ и Δl₂, ΔS=Δhx – площадь, ограниченная линиями магнитной индукции и элементами контура Δl₁ и Δl₂. Очевидно, что весь контур состоит из суммы всех пар элементов. Поэтому суммарный момент действующий на контур, равен

.

Если контур расположен в магнитном поле так, что угол между его нормалью n и вектором магнитной индукции B поля равен β, то под действием проекции вектора B на нормаль к контуру равную B_┴=Bcosβ контур будет растягиваться (сжиматься), а под действием проекции B на плоскость контура Bsinβ – поворачиваться.

Поэтому в общем случае формула расчета вращательного момента имеет вид:

                                                     .                                           (20.5)

Как уже отмечалось, величину p_m=IS называют магнитным моментом контура с током. Это величина векторная, и она совпадает по направлению с еди­ничным вектором нормали n: p_m=ISn. Тогда формулу (20.5) можно записать в векторном виде:

                                                      .                                           (20.6)

Если контур с током поместить в неоднородное магнитное поле, то кроме ориентирующего действия вращательного момента на контур будет действовать сила f в направлении возрастания магнитного поля (рис.20.6).

g

Рис. 20.6

Эта сила является равнодействующей всех сил dF_┴ на каждый элемент тока со стороны составляющей поля B_║. Расчет показывает, что модуль силы, которая действует на весь контур, равен:

                                     ,                          (20.7)

где α – угол между векторами p_m и B;  – градиент индукции магнитного поля.

20.3. Сила Лоренца

Как уже отмечалось, на проводник с током, который находится в магнитном поле, действует сила Ампера F_A=IBlsinα. Поскольку ток представляет упорядоченное движение свободных электрических зарядов, то это означает, что магнитное поле действует на каждый из этих зарядов. Сила, действующая на заряд, который движется в магнитном поле, называется силой Лоренца. Х.Лоренц (1853–1928), нидерландский физик, создатель классической электронной теории.

Если учесть, что сила тока в проводнике

,

где q – заряд носителей тока; n – концентрация носителей тока; υ – скорость их упорядоченного движения; S – площадь поперечного сечения проводника, то формула (20.1) примет вид:

.

Силу Лоренца можно выразить, как

,

где N – общее количество носителей тока в проводнике (N=nV=nSl). С учетом того, что Sl=V (V – объем проводника):

                                                      ,                                           (20.8)

где α – угол между направлением вектора индукции магнитного поля и направлением вектора скорости движения положительного заряда. Направление силы Лоренца, как и силы Ампера, также определяется по правилу левой руки.

20.4. Определение удельного заряда электрона

Под действием силы Лоренца частицы, обладающие электрическим зарядом, движутся в магнитном поле по криволинейным траекториям. Причем если скорость частицы υ _┴ B, то траектория ее движения в магнитном поле представляет окружность (рис.20.7).

 

Рис. 20.7

Определив радиус этой окружности, скорость частицы и величину индукции магнитного поля, можно рассчитать удельный заряд этой частицы. Этот метод используется для определения удельного заряда электрона.

Так, ввиду малости величины силы тяжести, действующей на электрон, движущийся в перпендикулярном магнитном поле, можно записать в соответствии со вторым законом Ньютона:

 или ,

откуда радиус окружности равен

,

а удельный заряд электрона:

                                                          .                                                (20.9)

Для определения скорости необходимо знать ускоряющую разность потенциалов электрического поля. Известно, что на заряженную частицу со стороны электрического поля действует сила

,

где q – заряд частицы, E – напряженность электрического поля. Если скорость частицы υ<<c и электрическое поле является однородным, то она будет двигаться в поле с постоянным ускорением.

Если скорость частицы в момент включения электрического поля равна нулю, то изменение ее кинетической энергии происходит за счет работы сил поля, т.е.

,

где U – напряжение между точками входа и выхода частицы из электрического поля. Поэтому скорость частицы при выходе из электрического поля

                                                         .                                            (20.10)

С учетом (20.10)выражение (20.9) примет вид:

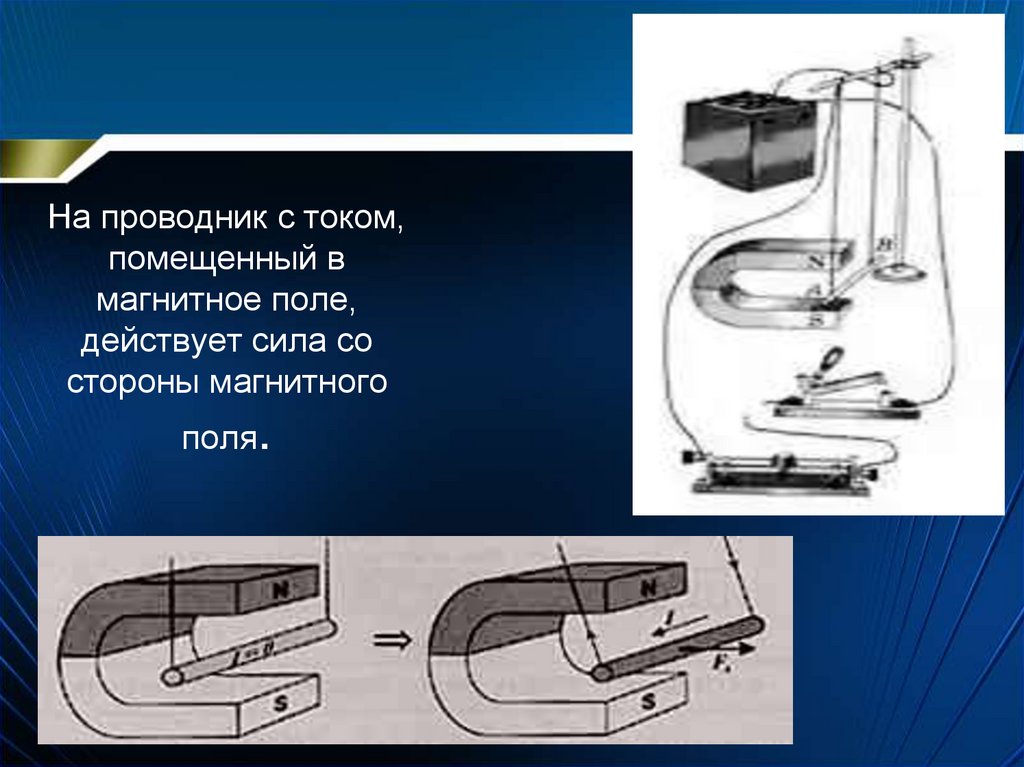                                                          .                                              (20.11)

Опыты, проведенные таким образом, позволили рассчитать отношение

Если заряженная частица влетает в магнитное поле так, что направление ее скорости υ образует с вектором индукции магнитного поля B угол α (причем α≠0, α≠π), то траектория движения частицы представляет винтовую линию (рис.20.8).

 

Рис. 20.8

На частицу, которая движется вдоль линий индукции магнитного поля со скоростью υ_y, сила Лоренца не действует.

Перпендикулярная составляющая скорости υ_x обеспечивает движение частицы по окружности радиуса R. Таким образом, под действием двух составляющих скорости υ_y и υ_x частица движется по винтовой линии.

Радиус винтовой траектории согласно формуле (20.9) будет равен:

                                                       ,                                          (20. 12)

а шаг винта

                                                      ,                                         (20.13)

где  – период обращения по окружности радиуса R.

Как уже отмечалось ранее, электрическое и магнитное поля являются частями единого электромагнитного поля. Поэтому в произвольной системе отсчета полная сила, с которой электромагнитное поле действует на заряженную частицу, равна векторной сумме электрической F_э и магнитной F_м составляющих, т.е.

.

 

20.5. Эффект Холла

Если пластинку, вдоль которой течет постоянный ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлению тока и поля, возникает разность потенциалов. Это явление впервые исследовал американский физик Е.Холл (1811–1890) в 1879 г., и оно впоследствии было названо эффектом Холла (рис.20.9).

 

Рис.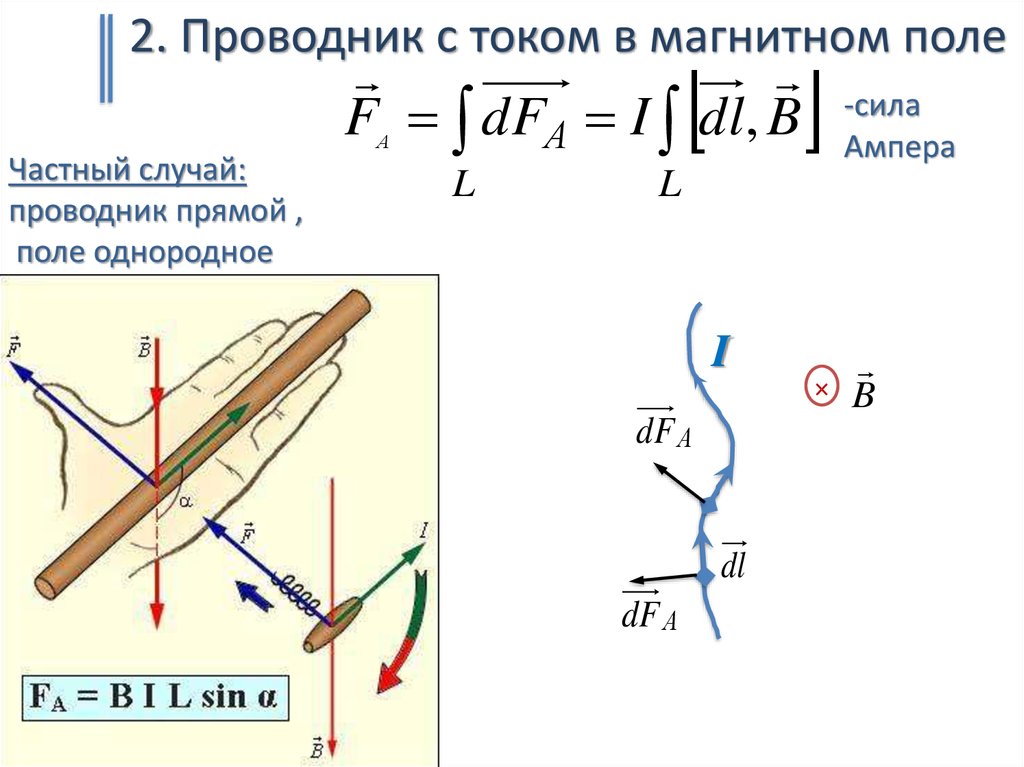 20.9

Экспериментально определено, что разность потенциалов Холла определяется по формуле:

                              ,                  (20.14)

где b – ширина пластинки, j – плотность тока, B – магнитная индукция поля, R – коэффициент пропорциональности, который называется постоянной Холла.

Эффект Холла можно объяснить согласно электронной теории. Если магнитное поле отсутствует, ток в пластинке обусловлен электрическим полем E₀ (рис.20.10).

 

Рис. 20.10

Потенциал во всех точках поверхности одинаков, в том числе и в точках 1 и 2. Электроны как носители отрицательного заряда двигаются со скоростью υ против вектора плотности тока j. При включении магнитного поля на каждый электрон действует сила Лоренца, направленная вдоль стороны b и численно равная F_л=eυB.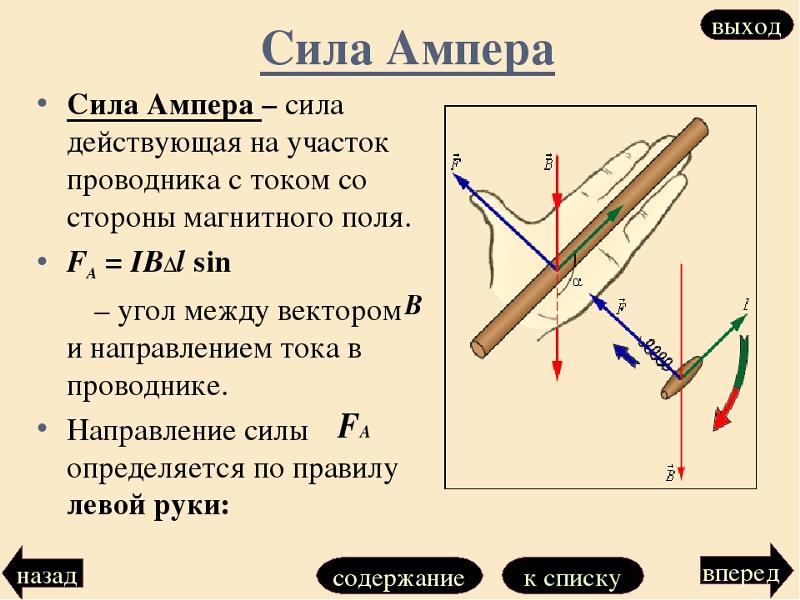 Поэтому электроны приобретают составляющую скорости, которая направлена к верхней грани пластинки. Значит, на этой грани накапливается отрицательный заряд, на нижней – положительный. Таким образом, возникает поперечное электрическое поле E_B. Если сила F_B=eE_B уравновесит силу Лоренца F_л=eυB, то установится стационарное равновесие: eE_B=eυB. Откуда E_B=υB. Результирующее поле E равно векторной сумме полей E₀ и E_B. Так как эквипотенциальные линии перпендикулярны вектору напряженности поля E, то точки 1 и 2, которые ранее лежали на одной эквипотенциальной поверхности, уже имеют разный потенциал.

Значит, разность потенциалов между этими точками равна:

                                               .                                   (20.15)

Сравнивая выражения (20.14) и (20.15), определим постоянную Холла:

                                                           .                                              (20.16)

Из формулы (20.14) следует, что величина постоянной Холла, как и разности потенциалов Холла, зависит от концентрации носителей заряда в проводящей пластинке. Так как концентрация носителей тока в полупроводниках значительно меньше, чем в металлах, то и эффект Холла в полупроводниках наблюдать легче.

Эффект Холла используется в датчиках Холла, которые используют для измерения напряженности постоянных и переменных магнитных полей, силы и мощности электрического тока, превращения постоянного ток в переменный, модулирования и детектирования сигналов, анализа спектра частот, «чтения» магнитных записей и во многих элементах автоматики и вычислительной техники.

20.6. Принцип работымагнитогидродинамических генераторов

Магнитогидродинамический (МГД) генератор – энергетическая установка, в которой тепловая энергия рабочего тела (плазмы) превращается в электрическую. Принцип работы МГД-генератора основан на взаимодействии магнитного поля с заряженными частицами, которые движутся в нем (рис.20.11).

 

Рис. 20.11

Если создать поток плазмы в магнитном поле, линии индукции B которого перпендикулярны скорости зарядов υ, то под действием силы Лоренца произойдет их разделение. Это значит, положительные заряды магнитным полем будут отклоняться в одну сторону, а отрицательные – в другую. В результате один электрод заряжается положительно, а второй – отрицательно. Между ними возникает разность потенциалов. Если электроды соединить проводником, то в нем возникнет электрический ток.

Использование МГД-генераторов является перспективным направлением развития тепловой энергетики, так как позволяет получать КПД 60 %, в то время как КПД тепловых станций достигает 40 %. Органическое топливо, которое используется в МГД-генераторах, вместе с нагретым воздухом поступает в камеру сгорания с температурой 3000°C.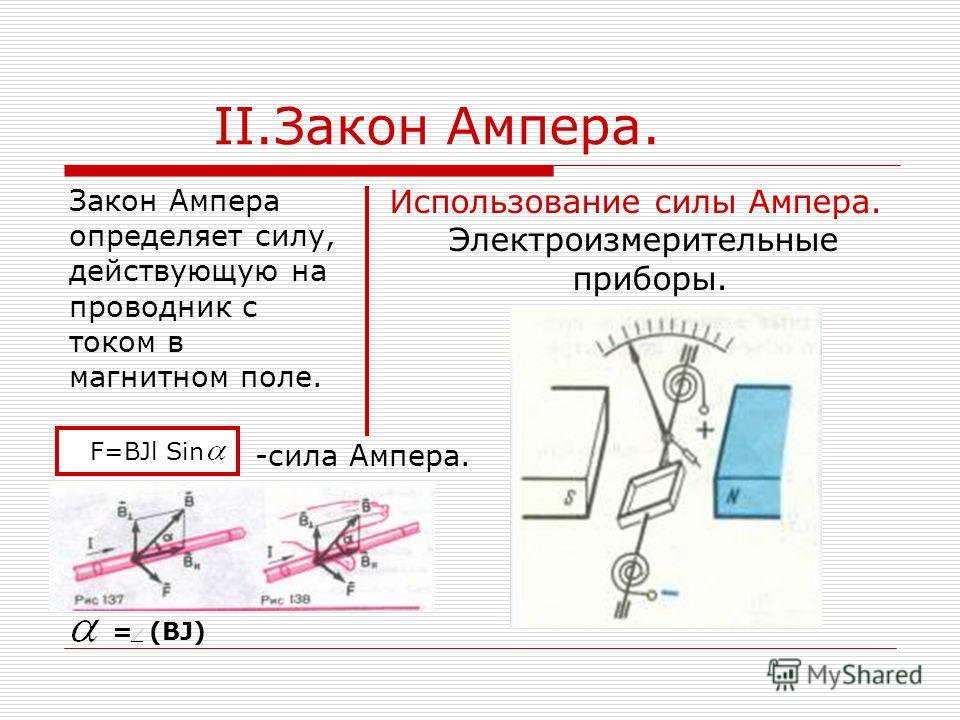 Там они превращаются в плазму. С целью увеличения электропроводности плазмы в нее могут добавлять специальные присадки – соли калия или цезия, уменьшающие выброс серы в атмосферу, тем самым решая часть экологических проблем.

 

22.7 Магнитное воздействие на проводник с током – Колледж физики, главы 1-17

22 Магнетизм

Магнитное воздействие на проводник с током

• Описать действие магнитной силы на проводник с током.
• Рассчитайте магнитную силу, действующую на проводник с током.

Поскольку обычно заряды не могут выйти из проводника, магнитная сила зарядов, движущихся в проводнике, передается самому проводнику.

Магнитное поле действует на проводник с током в направлении, определяемом правилом правой руки 1 (то же направление, что и на отдельные движущиеся заряды). Эта сила легко может быть достаточно большой, чтобы сдвинуть провод, поскольку типичные токи состоят из очень большого количества движущихся зарядов.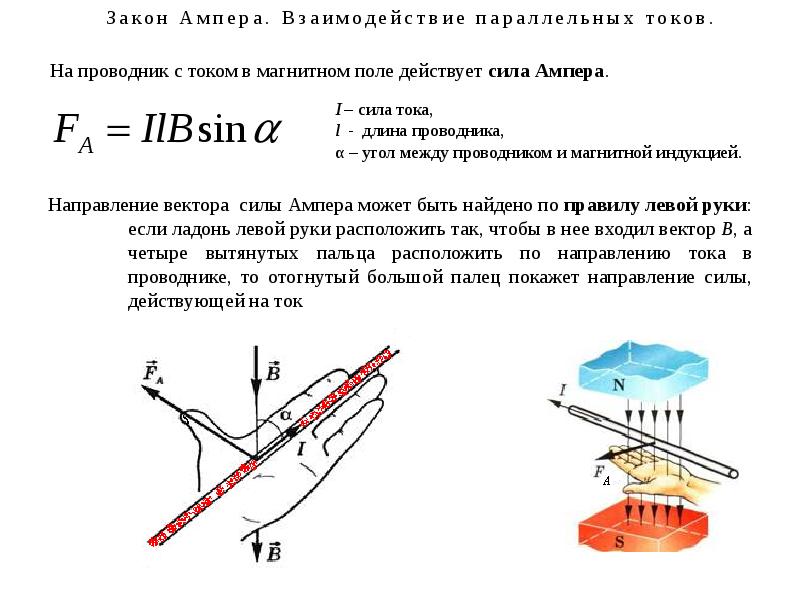

Мы можем получить выражение для магнитной силы, действующей на ток, взяв сумму магнитных сил, действующих на отдельные заряды. (Силы складываются, поскольку они действуют в одном направлении.) Сила, действующая на отдельный заряд, движущийся со скоростью дрейфа vdvd, определяется выражением F=qvdBsinθF=qvdBsinθ. Приняв размер BB 12{B} {} равным по длине провода ll и равным нулю в других местах, общая магнитная сила, действующая на провод, равна F=(qvdBsinθ)(N)F=(qvdBsinθ)(N) размера 12{ F= ( ital «qv» rSub { size 8{d} } B»sin»θ ) ( N ) } {}, где NN size 12{N} {}

— количество носителей заряда на отрезке провода длиной ll размера 12{l} {} . Теперь N=nVN=nV size 12{N= ital «nV»} {}, где nn size 12{n} {} — число носителей заряда в единице объема, а VV size 12{V} {} — объем провода в поле. Учитывая, что V=AlV=Al размер 12{V= ital «Al»} {}, где AA размер 12{A} {} — площадь поперечного сечения провода, тогда сила на проводе равна F=(qvdBsinθ )(nAl)F=(qvdBsinθ)(nAl). Условия сбора,

F=(nqAvd)lBsinθ.

F=(nqAvd)lBsinθ. size 12{F= ( ital «nqAv» rSub { size 8{d} } ) ital «lB»»sin»θ} {}

Поскольку nqAvd=InqAvd=I size 12{ ital «nqAv» rSub { size 8{d} } =I} {} (см. Current),

F=IlBsinθF=IlBsinθ размер 12{F= итал. “IlB””sin”θ} {}

— это уравнение для магнитной силы на длине ll провода, несущего ток II в однородном магнитном поле BB , как показано в [ссылка]. Если мы разделим обе части этого выражения на ll, то найдем, что магнитная сила на единицу длины провода в однородном поле равна Fl=IBsinθFl=IBsinθ size 12{ { {F} over {l} } = ital «IB» грех”θ} {}. Направление этой силы задается RHR-1, большим пальцем в направлении тока II размера 12{I}{}. Затем, с пальцами в направлении BB размера 12 {B} {}, перпендикуляр к ладони указывает в направлении FF размера 12 {F} {}, как в [ссылка].

Сила, действующая на проводник с током в магнитном поле, равна F=IlBsinθF=IlBsinθ size 12{F= ital «IlB»”sin”θ} {}. Его направление задает RHR-1.

Расчет силы магнитного поля на проводе с током: сильное магнитное поле

Рассчитайте силу на проводе, показанном в [ссылка], учитывая B=1,50 TB=1,50 T, размер 12{B=1 «. » «50» «T»} {}, l=5,00 смl=5,00 см размер 12{l=5 «.» «00»» см»} {} и I=20.0AI=20.0A размер 12{I=»20″ «.» 0 А} {}.

Стратегия

Силу можно найти с данной информацией, используя F=IlBsinθF=IlBsinθ размер 12{F= ital «IlB»”sin”θ} {} и отметив, что угол θθ размер 12{θ} {} между размером II 12{I} {} и размером BB 12{B} {} равно 90º90º, так что sinθ=1sinθ=1.

Решение

Ввод данных значений в F=IlBsinθF=IlBsinθ size 12{F= ital “IlB””sin”θ} {} дает

F=IlBsinθ=20,0 A0,0500 м1,50 T1. =IlBsinθ=20,0 A0,0500 м1,50 T1 . размер 12{F= ital «IlB»»sin»θ= левый («20» «. 0″ A» правый) левый (0 «.» «0500» «м» правый) левый (1 «.» «50 ””T” справа ) слева (1 справа )} {}

Единицы для тесла: 1 T=NA⋅m1 T=NA⋅m size 12{“1 T”= {{N} over {A cdot m} } } {}; таким образом,

F=1,50 N.F=1,50 N. размер 12{F=1 «.» «50» «Н»} {}

Обсуждение

Это большое магнитное поле создает значительную силу на проводе небольшой длины.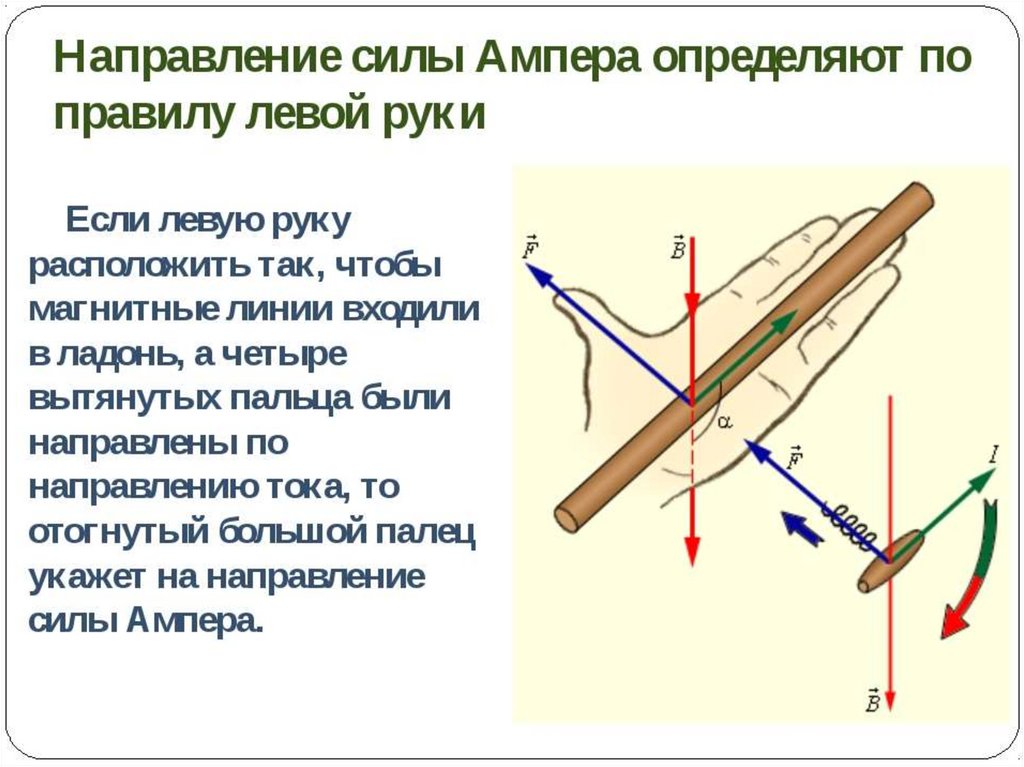

Магнитная сила на проводниках с током используется для преобразования электрической энергии в работу. (Ярким примером являются двигатели — в них используются петли из проволоки, и они рассматриваются в следующем разделе.) Магнитогидродинамика (МГД) — это техническое название, данное умному приложению, в котором магнитная сила перекачивает жидкости без движущихся механических частей. (См. [ссылка].)

Магнитогидродинамика. Магнитная сила тока, проходящего через эту жидкость, может быть использована в качестве немеханического насоса.

Сильное магнитное поле прикладывается к трубке, и ток проходит через жидкость под прямым углом к ​​полю, в результате чего на жидкость действует сила, параллельная оси трубки, как показано на рисунке. Отсутствие движущихся частей делает его привлекательным для перемещения горячего химически активного вещества, такого как жидкий натрий, используемый в некоторых ядерных реакторах. Экспериментальные искусственные сердца тестируются с использованием этой техники для перекачивания крови, возможно, для обхода неблагоприятных последствий механических насосов. (Однако на клеточные мембраны влияют большие поля, необходимые для МГД, что задерживает его практическое применение у людей.) Был предложен двигатель МГД для атомных подводных лодок, потому что он может быть значительно тише, чем обычные гребные двигатели. Сдерживающая ценность атомных подводных лодок основана на их способности скрыться и пережить первый или второй ядерный удар. По мере того, как мы медленно разбираем наши арсеналы ядерного оружия, подводные лодки будут выведены из эксплуатации последними из-за этой способности (см. [ссылка]). Существующие МГД-приводы тяжелые и неэффективные — требуется много доработок.

Двигательная установка МГД на атомной подводной лодке может создавать значительно меньшую турбулентность, чем гребные винты, и обеспечивать более тихую работу. Разработка бесшумной подводной лодки была драматизирована в книге и фильме «Охота на Красный Октябрь ».

• Магнитная сила, действующая на проводники с током, определяется выражением

  F=IlBsinθ,F=IlBsinθ, размер 12{F= ital «IlB»”sin”θ} {}

  где II размер 12{I} {} — ток, ll размер 12{l} {} — длина прямого проводника в однородном магнитном поле BB размера 12{B} {} и θθ размера 12{θ} {} — это угол между II размером 12{I} {} и BB размера 12{B} {} . Сила следует за RHR-1 большим пальцем в направлении II размера 12{I} {} .

Нарисуйте схему ситуации в [ссылка], показывающую направление электронов, несущих ток, и используйте RHR-1, чтобы проверить направление силы, действующей на провод.

Убедитесь, что направление силы в МГД-приводе, таком как в [ссылка], не зависит от знака зарядов, переносящих ток через жидкость.

Почему магнитогидродинамический привод лучше работает в морской воде, чем в пресной? Кроме того, зачем нужны сверхпроводящие магниты?

Что больше мешает показаниям компаса, переменный ток в вашем холодильнике или постоянный ток, когда вы заводите машину? Объяснять.

Каково направление магнитной силы на ток в каждом из шести случаев в [ссылка]?

(а) запад (слева)

(б) на страницу

(в) север (вверх)

(г) без сил

(д) восток (справа)

(е) юг (вниз)

Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев в [ссылка], если предположить, что ток течет перпендикулярно BB размера 12{B} {}?

Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев в [ссылка], при условии, что размер BB 12{B} {} перпендикулярен размеру II 12{I} {}?

(a) на стр.

(b) запад (слева)

(c) вне стр.

(a) Какова сила на метр на молнию на экваторе, которая несет 20 000 А перпендикулярно Земле 3,00×10-5-T3,00×10-5-T размером 12{3 «.» «00» умножить на «10» rSup {размер 8{ – 5} } «-T»} {} поле? б) Каково направление силы, если течение направлено прямо вверх, а направление поля Земли строго на север, параллельно земле?

(a) Линия электропередачи постоянного тока для системы легкорельсового транспорта передает 1000 А под углом 30,0º30,0º к размеру Земли 5,00×10−5-T5,00×10−5-T 12{5″. «00» умножить на «10» rSup {размер 8{ – 5} } «-T»} {} поле. Какая сила действует на отрезке этой линии длиной 100 м? (b) Обсудите практические проблемы, которые это вызывает, если таковые имеются.

(а) 2,50 Н

(б) Это примерно полфунта силы на 100 м проволоки, что намного меньше веса самой проволоки. Поэтому особых опасений не вызывает.

Какая сила действует на воду в МГД-приводе с трубкой диаметром 25,0 см, если через трубку, перпендикулярную магнитному полю напряженностью 2,00 Тл, пропускают ток силой 100 А? (Относительно небольшой размер этой силы указывает на необходимость очень больших токов и магнитных полей для создания практических МГД-приводов. )

Проводник с током 30,0 А проходит между полюсами сильного магнита, перпендикулярного его полю, и испытывает силу 2,16 Н на 4,00 см провода в поле. Какова средняя напряженность поля?

1,80 т

(a) Участок кабеля длиной 0,750 м, по которому подается ток к стартеру автомобиля, образует угол 60º60º с полем Земли 5,50×10-5 Т5,50×10-5 Тл. Какова сила тока, когда на провод действует сила 7,00×10-3Н7,00×10-3Н? б) Если пропустить провод между полюсами сильного подковообразного магнита и подвергнуть его 5,00 см воздействию поля силой 1,75 Тл, какая сила будет действовать на этот отрезок провода?

а) Чему равен угол между проводом, по которому течет ток 8,00 А, и полем 1,20 Тл, в котором он находится, если на 50 см провода действует магнитная сила 2,40 Н? (b) Какова сила, действующая на проволоку, если ее повернуть на угол 90º90º размером 12{«90″°} {} с полем?

(a) 30º30º размер 12{“30″°} {}

(b) 4,80 Н

Сила, действующая на прямоугольную проволочную петлю в магнитном поле в [ссылка], может использоваться для измерения напряженности поля. Поле однородно, и плоскость петли перпендикулярна полю. а) Как направлена ​​магнитная сила, действующая на петлю? Обоснуйте утверждение, что силы на сторонах петли равны и противоположны, независимо от того, какая часть петли находится в поле, и не влияют на результирующую силу, действующую на петлю. (b) Если используется ток 5,00 А, какова сила на тесла на петле шириной 20,0 см?

Прямоугольная проволочная петля, по которой течет ток, перпендикулярна магнитному полю. Поле однородно в показанной области и равно нулю вне этой области.

11.4 Магнитное воздействие на проводник с током – University Physics Volume 2

Глава 11. Магнитные силы и поля

Цели обучения

К концу этого раздела вы сможете:

• Определять направление, в котором на проводник с током действует сила во внешнем магнитном поле
• Расчет силы, действующей на проводник с током во внешнем магнитном поле

На движущиеся заряды действует сила магнитного поля. Если эти движущиеся заряды находятся в проводе, то есть если по проводу течет ток, на провод также должна действовать сила. Однако, прежде чем мы обсудим силу, действующую на ток со стороны магнитного поля, мы сначала исследуем магнитное поле, создаваемое электрическим током. Здесь мы изучаем два отдельных эффекта, которые тесно взаимодействуют друг с другом: проводник с током создает магнитное поле, и магнитное поле воздействует на проводник с током.

Магнитные поля, создаваемые электрическими токами

Обсуждая исторические открытия в области магнетизма, мы упомянули открытие Эрстеда о том, что провод, по которому течет электрический ток, заставляет ближайший компас отклоняться. Была установлена ​​связь, что электрические токи создают магнитные поля. (Эта связь между электричеством и магнетизмом обсуждается более подробно в разделе «Источники магнитных полей».)

На стрелку компаса, расположенную рядом с проводом, действует сила, которая выравнивает стрелку по касательной к окружности вокруг провода. Следовательно, провод с током создает круговые петли магнитного поля. Чтобы определить направление магнитного поля, создаваемого проводом, мы используем второе правило правой руки. В RHR-2 большой палец указывает в направлении тока, а пальцы обхватывают провод, указывая направление создаваемого магнитного поля (рис. 11.11). Если магнитное поле исходило от вас или исходило от страницы, мы обозначаем это точкой. Если бы магнитное поле попадало на страницу, мы представили бы это с помощью [латекс]×.[/латекс]. Эти символы возникли при рассмотрении векторной стрелки: стрелка, направленная к вам, с вашей точки зрения выглядела бы как точка или наконечник стрелы. Стрелка, направленная от вас, с вашей точки зрения выглядела бы как крест или [латекс]×.[/латекс] Составной эскиз магнитных кругов показан на рис. 11.11, где показано, что напряженность поля уменьшается по мере того, как вы отойдите от проволоки на петли, которые находятся дальше друг от друга.

Рисунок 11.11  (a) Когда провод находится в плоскости бумаги, поле перпендикулярно бумаге. Обратите внимание на символы, используемые для поля, указывающего внутрь (например, хвост стрелы), и поля, указывающего наружу (например, кончик стрелки). (b) Длинный и прямой провод создает поле с силовыми линиями магнитного поля, образующими круглые петли.

Расчет магнитной силы

Электрический ток представляет собой упорядоченное движение заряда. Следовательно, проводник с током в магнитном поле должен испытывать силу, обусловленную полем. Чтобы исследовать эту силу, давайте рассмотрим бесконечно малый отрезок провода, как показано на рис. 11.12. Длина и площадь поперечного сечения секции дл и А соответственно, поэтому его объем равен [латекс]V=A·дл.[/латекс] Проволока изготовлена ​​из материала, который содержит n носителей заряда в единице объема, поэтому количество носителей заряда в сечении [латекс]нА·дл.[/латекс] Если носители заряда движутся с дрейфовой скоростью [латекс]{\stackrel{\to }{\textbf{v}}}_{\text{d}}, [/latex] ток I в проводе равен (от тока и сопротивления)

[latex]I=neA{v}_{d}.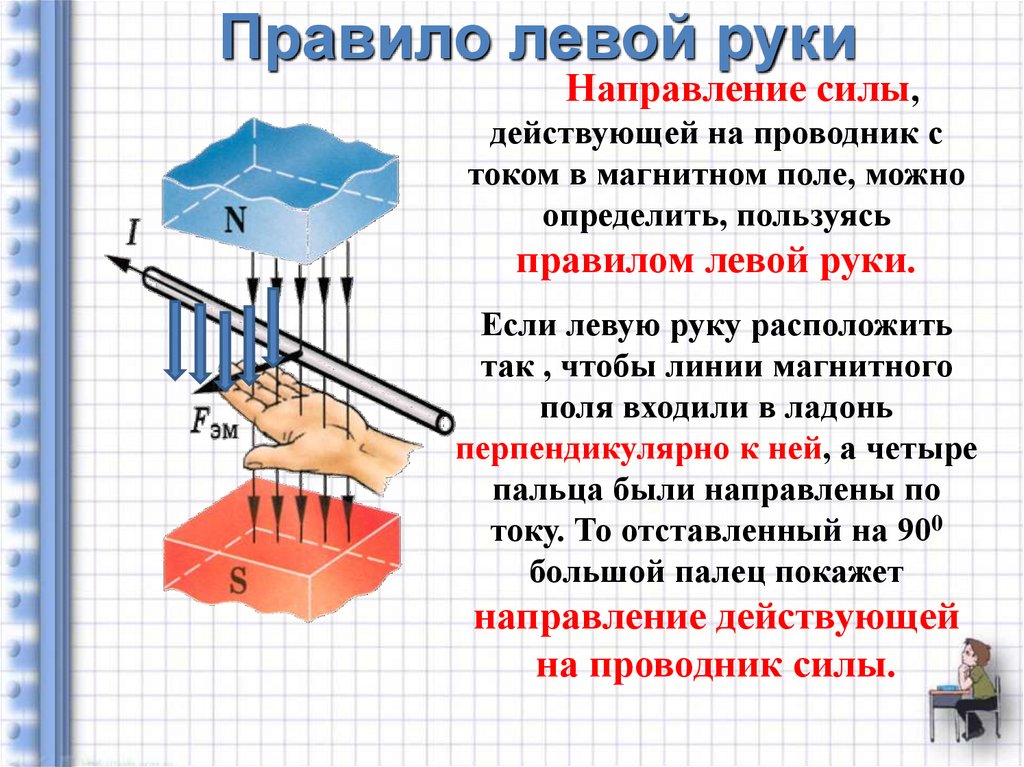 [/latex]

Магнитная сила на любом отдельном носителе заряда равна [латекс] e {\ stackrel {\ to } {\ textbf {v}}} _ {\ text {d}} \ phantom {\ rule {0.2em} {0ex}} × \ phantom {\ rule {0.2em} {0ex}}\stackrel{\to }{\textbf{B}},[/latex], поэтому общая магнитная сила [латекс]d\stackrel{\to }{\textbf{F}}[/latex] на [латекс]нА·дл[/латекс] носители заряда в сечении провода

[латекс] d \ stackrel {\ to }{\ textbf {F}} = \ left (nA · dl \ right) e {\ stackrel {\ to } {\ textbf {v}}} _ {\ text { d}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}.[/latex]

Мы можем определить dl как вектор длины dl , указывающий вдоль [latex]{\stackrel{\to }{\textbf{v}}}_{\text{d}},[/latex], что позволяет нам переписать это уравнение в виде }\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}},[/latex]

или

[латекс] d\stackrel{\to }{\textbf{F}}=I\stackrel{\to }{\textbf{dl}}\phantom{\rule{0.2em}{0ex}} ×\phantom{\rule{0. 2em}{0ex}}\stackrel{\to }{\textbf{B}}.[/latex]

Это магнитная сила, действующая на сечение провода. Обратите внимание, что на самом деле это чистая сила, действующая со стороны поля на сами носители заряда. Направление этой силы задается RHR-1, где вы указываете пальцами в направлении тока и скручиваете их в сторону поля. Затем ваш большой палец указывает направление силы.

Рис. 11.12  Бесконечно малый отрезок провода с током в магнитном поле.

Чтобы определить магнитную силу [латекс]\stackrel{\to }{\textbf{F}}[/латекс] на проводе произвольной длины и формы, мы должны проинтегрировать уравнение 11.12 по всему проводу. Если сечение провода прямое, а B однородное, дифференциалы уравнения становятся абсолютными величинами, что дает нам

[латекс]\stackrel{\to }{\textbf{F}}=I\stackrel{\to} {\textbf{l}}\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}.[/ латекс]

Это сила, действующая на прямой провод с током в однородном магнитном поле.

Пример

Уравновешивание гравитационной и магнитной сил на проводе с током

Провод длиной 50 см и массой 10 г подвешен в горизонтальной плоскости на паре гибких проводов (рис. 11.13). Затем провод подвергается воздействию постоянного магнитного поля величиной 0,50 Тл, которое направлено, как показано на рисунке. Каковы величина и направление тока в проводе, необходимые для снятия напряжения в опорных выводах?

Рис. 11.13  (a) Провод, подвешенный в магнитном поле. (b) Диаграмма свободного тела для проволоки.

Стратегия

Судя по диаграмме свободного тела на рисунке, натяжение в опорных проводах становится равным нулю, когда гравитационные и магнитные силы уравновешивают друг друга. Используя RHR-1, мы обнаруживаем, что магнитная сила направлена ​​вверх. Затем мы можем определить ток I , приравняв две силы.

Решение

Показать Ответ

Приравняйте две силы веса и силы магнитного поля, действующие на провод: 9{2}\right)}{\left(0. 50\phantom{\rule{0.2em}{0ex}}\text{m}\right)\left(0.50\phantom{\rule{0.2em}{0ex}} \text{T}\right)}=0,39\phantom{\rule{0.2em}{0ex}}\text{A.}[/latex]

Значение

Это сильное магнитное поле создает значительную силу на длине провода, противодействующую весу провода.

Пример

Расчет силы магнитного поля на проводе с током

Длинный жесткий провод, лежащий вдоль оси y , несет ток силой 5,0 А, протекающий в положительной у -направление. а) Если постоянное магнитное поле величиной 0,30 Тл направлено вдоль положительной оси х , какова магнитная сила, действующая на единицу длины провода? (б) Если постоянное магнитное поле 0,30 Тл направлено под углом 30 градусов от оси + x к оси + y , какова магнитная сила на единицу длины провода?

Стратегия

Магнитная сила, действующая на провод с током в магнитном поле, определяется выражением [латекс]\stackrel{\to }{\textbf{F}}=I\stackrel{\to }{\textbf{l }}\phantom{\rule{0. 2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}.[/latex] Для части a , поскольку в этой задаче ток и магнитное поле перпендикулярны, мы можем упростить формулу, чтобы получить величину и найти направление через RHR-1. Угол θ равно 90 градусам, что означает [латекс]\текст{грех}\фантом{\правило{0.1em}{0ex}}\тета =1.[/латекс] Кроме того, длину можно разделить влево — стороны, чтобы найти силу на единицу длины. Для части b текущая длина записывается в виде единичного вектора, а также магнитное поле. После взятия перекрестного произведения направленность очевидна по результирующему единичному вектору.

Решение

Показать Ответ

1. Начнем с общей формулы для магнитной силы, действующей на провод. Мы ищем силу на единицу длины, поэтому мы делим на длину, чтобы вывести ее в левую часть. Мы также устанавливаем [latex]\text{sin}\phantom{\rule{0.1em}{0ex}}\theta =1.[/latex] Таким образом, решение равно 9.0002 [латекс]\begin{array}{ccc}\hfill F& =\hfill & IlB\phantom{\rule{0. 2em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex} }\theta \hfill \\ \hfill \frac{F}{l}& =\hfill & \left(5.0\phantom{\rule{0.2em}{0ex}}\text{A}\right)\left( \text{0.30 T}\right)\hfill \\ \hfill \frac{F}{l}& =\hfill & 1.5\phantom{\rule{0.2em}{0ex}}\text{N/m.} \hfill \end{массив}[/латекс]

   
   Направленность: Направьте пальцы в положительном направлении y и согните пальцы в положительном направлении x — направление. Ваш большой палец будет указывать в направлении [латекс]\текст{−}\stackrel{\to }{\textbf{k}}[/латекс]. Следовательно, с направленностью решение
   

   [латекс] \ frac {\ stackrel {\ to } {\ textbf {F}}} {l} = -1,5 \ stackrel {\ to } {\ textbf {k}} \ phantom {\ rule {0.2em} 0ex}}\text{Н/м.}[/латекс]

2. Текущая длина и магнитное поле записываются в виде единичного вектора. Затем мы используем перекрестное произведение, чтобы найти силу:

   [латекс]\begin{array}{ccc}\hfill \stackrel{\to }{\textbf{F}}& =\hfill & I\stackrel{\to }{\textbf{l}}\phantom{\rule{0. 2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}=\ влево (5,0 А \ вправо) л \ шляпа {\ textbf {j}} \ фантом {\ правило {0,2em} {0ex}} × \ фантом {\ правило {0,2em} {0ex}} \ влево (0,30T \ text{cos}\left(30\text{°}\right)\hat{\textbf{i}}+0.30T\phantom{\rule{0.1em}{0ex}}\text{sin}\left(30 \text{°}\right)\hat{\textbf{j}}\right)\hfill \\ \hfill \stackrel{\to }{\textbf{F}}\text{/}l& =\hfill & — 1.30\шляпа{\textbf{k}}\phantom{\rule{0.2em}{0ex}}\text{N/m.}\hfill \end{массив}[/latex]

Значение

Это большое магнитное поле создает значительную силу на проводе небольшой длины. По мере того, как угол магнитного поля становится ближе к току в проводе, на него действует меньшая сила, как видно из сравнения частей а и б.

Проверьте свое понимание

Прямая гибкая медная проволока погружена в магнитное поле, направленное на страницу. (a) Если ток в проводе течет в пределах + x -направление, в какую сторону будет изгибаться провод? б) В какую сторону изгибается провод, если ток течет в направлении – x ?

Показать раствор

а. наклоняется вверх; б. наклоняется вниз

Пример

Сила на круглом проводе

Круговая петля с током радиуса R , по которой течет ток I , расположена в плоскости xy . Постоянное однородное магнитное поле прорезает контур параллельно оси y (рис. 11.14). Найдите магнитную силу, действующую на верхнюю половину петли, нижнюю половину петли и полную силу, действующую на петлю.

Рис. 11.14  Петля из проволоки, по которой течет ток в магнитном поле.

Стратегия

Магнитная сила, действующая на верхнюю петлю, должна быть выражена в терминах дифференциальной силы, действующей на каждый сегмент петли. Если мы проинтегрируем по каждой дифференциальной части, мы найдем общую силу на этом участке петли. Аналогично находится сила на нижней петле, а полная сила есть сложение этих двух сил.

Решение

Показать ответ

Дифференциальная сила на произвольном отрезке проволоки, расположенном на верхнем кольце:

[латекс] dF = IB\phantom{\rule{0. 1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta \phantom{\rule{0.1em}{ 0ex}}дл.[/латекс]

, где [латекс]\тета[/латекс] — угол между направлением магнитного поля (+ y ) и отрезком провода. Дифференциальный сегмент расположен на том же радиусе, поэтому, используя формулу длины дуги, мы имеем:

[латекс]\begin{array}{ccc}\hfill dl& =\hfill & R\phantom{\rule{0.1em}{0ex}}d\theta \hfill \\ \hfill dF& =\hfill & IBR\phantom {\rule{0.1em}{0ex}}\text{sin}\phantom{\rule{0.1em}{0ex}}\theta \phantom{\rule{0.1em}{0ex}}d\theta.\hfill \end{массив}[/латекс] 9{}=-2IBR.[/латекс]

Чистая сила равна сумме этих сил, которая равна нулю.

Значение

Суммарная сила, действующая на любой замкнутый контур в однородном магнитном поле, равна нулю. Несмотря на то, что на каждую часть петли действует сила, результирующая сила, действующая на систему, равна нулю. (Обратите внимание, что в петле есть чистый крутящий момент, который мы рассмотрим в следующем разделе. )

Резюме

• Электрический ток создает вокруг провода магнитное поле.
• Направленность создаваемого магнитного поля определяется правилом правой руки-2, где большой палец указывает в направлении тока, а пальцы обхватывают провод в направлении магнитного поля.
• Магнитная сила, действующая на проводники с током, определяется как [латекс]\stackrel{\to }{\textbf{F}}=I\stackrel{\to }{\textbf{l}}\phantom{\rule{0,2 em}{0ex}}×\phantom{\rule{0.2em}{0ex}}\stackrel{\to }{\textbf{B}}[/latex], где I  – текущий, а l — длина провода в однородном магнитном поле B .

Концептуальные вопросы

Опишите ошибку, возникающую в результате случайного использования левой, а не правой руки при определении направления магнитной силы.

Принимая во внимание закон магнитной силы, всегда ли скорость и магнитное поле перпендикулярны? Всегда ли сила и скорость перпендикулярны? А как насчет силы и магнитного поля?

Показать раствор

Скорость и магнитное поле можно установить вместе в любом направлении. Если есть сила, то скорость перпендикулярна ей. Магнитное поле также перпендикулярно силе, если она существует.

Почему соседний магнит может искажать телевизионную картинку с электронно-лучевой трубкой?

Магнитное поле воздействует на движущиеся электроны в проводнике с током. Какая сила действует на провод?

Показать решение

На провод действует внешнее магнитное поле, создаваемое проводом или другим магнитом.

Есть регионы, где магнитное поле Земли почти перпендикулярно поверхности Земли. Какие трудности это вызывает при использовании компаса?

Задачи

Каково направление магнитной силы на ток в каждом из шести случаев?

Показать решение

а. левый; б. на страницу; в. вверх; д. нет силы; е. верно; ф. вниз

Каково направление тока, на который действует магнитная сила, показанная в каждом из трех случаев, если предположить, что ток течет перпендикулярно [латексу]\stackrel{\to }{\textbf{B}}[/латексу]?

Каково направление магнитного поля, которое создает магнитную силу, показанную на токах в каждом из трех случаев, при условии, что [латекс]\stackrel{\to }{\textbf{B}}[/латекс] перпендикулярно I ?

Показать решение

а.