Страница не найдена
Согласие на обработку персональных данныхНастоящим в соответствии с Федеральным законом № 152-ФЗ «О персональных данных» от 27.07.2006 года свободно, своей волей и в своем интересе выражаю свое безусловное согласие на обработку моих персональных данных АНО ДПО «ИНСТИТУТ СОВРЕМЕННОГО ОБРАЗОВАНИЯ» (ОГРН 1143600000290, ИНН 3666999768), зарегистрированным в соответствии с законодательством РФ по адресу:
УЛ. КАРЛА МАРКСА, ДОМ 67, 394036 ВОРОНЕЖ ВОРОНЕЖСКАЯ ОБЛАСТЬ, Россия (далее по тексту — Оператор).
Персональные данные — любая информация, относящаяся к определенному или определяемому на основании такой информации физическому лицу.
Настоящее Согласие выдано мною на обработку следующих персональных данных:
— Телефон.
Согласие дано Оператору для совершения следующих действий с моими персональными данными с использованием средств автоматизации и/или без использования таких средств: сбор, систематизация, накопление, хранение, уточнение (обновление, изменение), использование, обезличивание, а также осуществление любых иных действий, предусмотренных действующим законодательством РФ как неавтоматизированными, так и автоматизированными способами.
Данное согласие дается Оператору для обработки моих персональных данных в следующих целях:
— предоставление мне услуг/работ;
— направление в мой адрес уведомлений, касающихся предоставляемых услуг/работ;
— подготовка и направление ответов на мои запросы;
— направление в мой адрес информации, в том числе рекламной, о мероприятиях/товарах/услугах/работах Оператора.
Настоящее согласие действует до момента его отзыва путем направления соответствующего уведомления на электронный адрес [email protected]. В случае отзыва мною согласия на обработку персональных данных Оператор вправе продолжить обработку персональных данных без моего согласия при наличии оснований, указанных в пунктах 2 – 11 части 1 статьи 6, части 2 статьи 10 и части 2 статьи 11 Федерального закона №152-ФЗ «О персональных данных» от 27.06.2006 г.
«Научное направление было и будет в приоритете»: в НГАСУ (Сибстрин) отметили День российской науки 8 февраля 2021 года в Новосибирском государственном архитектурно-строительном университете (Сибстрин) прошло торжественное собрание, посвященное Дню российской науки. |
НГАСУ (Сибстрин) приглашает к участию во Всероссийской конференции преподавателей и научных работников технических вузов, посвященной 75-летию со дня рождения Р.М. Гусейнова Новосибирский государственный архитектурно-строительный университет (Сибстрин) объявляет о проведении Всероссийской конференции преподавателей и научных работников технических вузов «Экономические системы: целевые ориентиры в условиях четвертой промышленной революции». Конференция состоится 14-15 апреля 2021 года по адресу: 630008 г. Новосибирск, ул. Ленинградская 113.
Конференция посвящается 75-летию со дня рождения известного специалиста в области истории экономики и истории экономических учений Рифата Мир-Ахмедовича Гусейнова (1946 – 2012 гг.).
Р.М. Гусейнов – доктор экономических наук, профессор, заслуженный экономист РФ, почетный работник высшей школы.
Р.М. Гусейнов закончил Азербайджанский государственный университет, аспирантуру МГУ им. Ломоносова, докторантуру Академии общественных наук. С 1999 года до конца жизни (8 мая 2012г.)…
Конференция состоится 14-15 апреля 2021 года по адресу: 630008 г. Новосибирск, ул. Ленинградская 113.
Конференция посвящается 75-летию со дня рождения известного специалиста в области истории экономики и истории экономических учений Рифата Мир-Ахмедовича Гусейнова (1946 – 2012 гг.).
Р.М. Гусейнов – доктор экономических наук, профессор, заслуженный экономист РФ, почетный работник высшей школы.
Р.М. Гусейнов закончил Азербайджанский государственный университет, аспирантуру МГУ им. Ломоносова, докторантуру Академии общественных наук. С 1999 года до конца жизни (8 мая 2012г.)… |
С 8 февраля для студентов и преподавателей университета открыт тестовый доступ к ЭБС «Айбукс»  д.
Полный объем контента в ЭБС – более 30 000 книг и изданий от 150 ведущих издательств нашей страны. Более 3000 изданий в ЭБС «Айбукс» – абсолютный эксклюзив. Только в электронно-библиотечной системе «Айбукс» представлены книги издательств Питер и БХВ-Петербург, которых нет в других ЭБС (в том числе переводные издания от: O’Reilly Media, Manning Publication, Peachpit Press, Packt Publishing, Pearson EducationInc., Artima Press, Dan Bader и т.д.). д.
Полный объем контента в ЭБС – более 30 000 книг и изданий от 150 ведущих издательств нашей страны. Более 3000 изданий в ЭБС «Айбукс» – абсолютный эксклюзив. Только в электронно-библиотечной системе «Айбукс» представлены книги издательств Питер и БХВ-Петербург, которых нет в других ЭБС (в том числе переводные издания от: O’Reilly Media, Manning Publication, Peachpit Press, Packt Publishing, Pearson EducationInc., Artima Press, Dan Bader и т.д.). |
13 февраля приглашаем студентов и сотрудников принять участие в «Лыжне России-2021» в Новосибирске! 13 февраля 2021 года (суббота) в Новосибирске пройдут Всероссийские соревнования по массовой лыжной гонке «Лыжня России». Старт в Академгородке (ул. Ионосферная, 3) Приглашаем студентов, преподавателей, сотрудников университета принять участие в оздоровительном мероприятии! По вопросам организационного выезда на соревнование и проката лыжного снаряжения обращаться на кафедру Физического воспитания НГАСУ (Сибстрин) к инструктору по спорту Олегу Сергеевичу Амелину или заведующей кафедрой Марине Александровне Калитовой. |
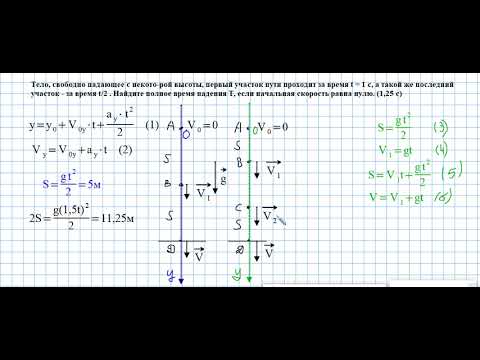
Методические материалы по теме «Механические явления»- 9 класс. Часть 1

2 4) 0,8 см/с 2 5. Два одинаковых бруска поставлены друг на друга разными способами (см. рисунок). Сравните давления р и силы давления F брусков на стол. 1) р 1 = р 2 ; F 1 = F 2 2) р 1 > р 2 ; F 1 < F 2 3) р 1 > р 2 ; F 1 = F 2 4) р 1 = р 1 ; F 1 < F 2 6. На рисунке изображены четыре пары сфери чески симметричных тел, расположенных друг относительно друга на разных расстояниях между центрами этих тел. Сила взаимодействия двух тел одинаковых масс M, находящихся на расстоянии R друг от друга, равна F 0. Для какой пары тел сила гравитационного взаимодействия равна 4F 0? 1) для пары А 2) для пары Б 3) для пары В 4) для пары Г 7.
3 9. По гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях движутся две шайбы массами m 1 = 2 кг и m 2 = 1 кг со скоростями v 1 = 1 м/с и v 2 = 2 м/с соответственно, как показано на рисунке. Общая величина кинетической энергии этих двух шайб равна 1) 1 Дж 2) Дж 3) 3 Дж 4) 6 Дж 10. Два шара разной массы подняты на разную высоту относительно поверхности стола (см.
4 2) 2 3) 3 4) 1 и Математический маятник совершает свободные незатухающие колебания между положениями 1 и 3 (см. рисунок). В процессе перемещения маятника из положения 1 в положение 2 1) кинетическая энергия маятника увеличивается, полная механическая энергия маятника уменьшается 2) кинетическая энергия маятника увеличивается, потенциальная энергия маятника уменьшается 3) кинетическая энергия и полная механическая энергия маятника уменьшаются 4) кинетическая энергия и потенциальная энергия маятника уменьшаются 14. На рисунке представлен график гармонических колебаний математического маятника. Амплитуда и частота колебаний маятника равны соответственно 1) 4 см и 0,25 Гц 2) 4 см и 5 Гц 3) 8 см и 0,25 Гц 4) 8 см и 5 Гц 15. На концах коромысла равноплечих весов подвешены два однородных шарика. Один шарик сделан из железа, а другой из меди. Весы находятся в равновесии. Что произойдёт с равновесием весов, если оба шарика полностью погрузить в воду? 1) весы останутся в равновесии, так как массы шариков одинаковы 2) весы останутся в равновесии, так как шарики имеют одинаковые объёмы 3) равновесие весов нарушится — опустится шарик, сделанный из железа 4) равновесие весов нарушится — опустится шарик, сделанный из меди 16. На рисунке показана система, состоящая из очень лёгкого рычага и невесомого подвижного блока. К правому концу рычага подвешена гиря массой m = 1 кг. Гирю какой массой M нужно подвесить к оси блока, чтобы система находилась в равновесии? 1) 0,5 кг 2) 1 кг 3) 2 кг 4) 4 кг
На рисунке представлен график гармонических колебаний математического маятника. Амплитуда и частота колебаний маятника равны соответственно 1) 4 см и 0,25 Гц 2) 4 см и 5 Гц 3) 8 см и 0,25 Гц 4) 8 см и 5 Гц 15. На концах коромысла равноплечих весов подвешены два однородных шарика. Один шарик сделан из железа, а другой из меди. Весы находятся в равновесии. Что произойдёт с равновесием весов, если оба шарика полностью погрузить в воду? 1) весы останутся в равновесии, так как массы шариков одинаковы 2) весы останутся в равновесии, так как шарики имеют одинаковые объёмы 3) равновесие весов нарушится — опустится шарик, сделанный из железа 4) равновесие весов нарушится — опустится шарик, сделанный из меди 16. На рисунке показана система, состоящая из очень лёгкого рычага и невесомого подвижного блока. К правому концу рычага подвешена гиря массой m = 1 кг. Гирю какой массой M нужно подвесить к оси блока, чтобы система находилась в равновесии? 1) 0,5 кг 2) 1 кг 3) 2 кг 4) 4 кг
5 17. Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость ее координаты от времени. Выберите два утверждения, которые можно сделать на основании графика. 1) Скорость бусинки на участке 1 постоянна, а на участке 2 равна нулю. 2) Проекция ускорения бусинки на участке 1 положительна, а на участке 2 отрицательна. 3) Участок 1 соответствует равномерному движению бусинки, а на участке 2 бусинка неподвижна. 4) Участок 1 соответствует равноускоренному движению бусинки, а на участке 2 равномерному. 5) Проекция ускорения бусинки на участке 1 отрицательна, а на участке 2 положительна. Ответ: 18. Шарик катится по желобу. Изменение координаты шарика с течением времени в инерциальной системе отсчета показано на графике. Выберете два утверждения, которые соответствуют результатам опыта. 1) Проекция скорости шарика постоянно увеличивалась и оставалась отрицательной на всем пути. 2) Первые 2 с скорость шарика возрастала, а затем оставалась постоянной. 3) Первые 2 с шарик двигался с уменьшающейся скоростью, а затем покоился.
Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость ее координаты от времени. Выберите два утверждения, которые можно сделать на основании графика. 1) Скорость бусинки на участке 1 постоянна, а на участке 2 равна нулю. 2) Проекция ускорения бусинки на участке 1 положительна, а на участке 2 отрицательна. 3) Участок 1 соответствует равномерному движению бусинки, а на участке 2 бусинка неподвижна. 4) Участок 1 соответствует равноускоренному движению бусинки, а на участке 2 равномерному. 5) Проекция ускорения бусинки на участке 1 отрицательна, а на участке 2 положительна. Ответ: 18. Шарик катится по желобу. Изменение координаты шарика с течением времени в инерциальной системе отсчета показано на графике. Выберете два утверждения, которые соответствуют результатам опыта. 1) Проекция скорости шарика постоянно увеличивалась и оставалась отрицательной на всем пути. 2) Первые 2 с скорость шарика возрастала, а затем оставалась постоянной. 3) Первые 2 с шарик двигался с уменьшающейся скоростью, а затем покоился. 4) На шарик действовала все увеличивающаяся сила. 5) Первые 2 с проекция ускорения шарика не изменялась, а затем стала равной нулю. 19. Тело массой 2 кг движется вдоль оси Ox. На рисунке представлен график зависимости проекции скорости v x этого тела от времени t. Используя график, выберите из предложенного перечня два верных утверждения. Укажите их номера. 1) На участках OA и БВ на тело действовала одинаковая по модулю и по направлению равнодействующая сила. 2) На участке АБ тело двигалось со скоростью, равной по модулю 1 м/с. 3) На участке ВГ ускорение тела равно по модулю 10 м/с 2. 4) Модуль равнодействующей силы на участке ВГ равен 40 Н. 5) На участке БВ тело двигалось с ускорением, равным по модулю 2 м/с 2.
4) На шарик действовала все увеличивающаяся сила. 5) Первые 2 с проекция ускорения шарика не изменялась, а затем стала равной нулю. 19. Тело массой 2 кг движется вдоль оси Ox. На рисунке представлен график зависимости проекции скорости v x этого тела от времени t. Используя график, выберите из предложенного перечня два верных утверждения. Укажите их номера. 1) На участках OA и БВ на тело действовала одинаковая по модулю и по направлению равнодействующая сила. 2) На участке АБ тело двигалось со скоростью, равной по модулю 1 м/с. 3) На участке ВГ ускорение тела равно по модулю 10 м/с 2. 4) Модуль равнодействующей силы на участке ВГ равен 40 Н. 5) На участке БВ тело двигалось с ускорением, равным по модулю 2 м/с 2.
6 Ответ: 20. На рисунке представлен график зависимости модуля скорости и от времени t для тела, движущегося прямолинейно в инерциальной системе отсчёта. Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера. 1) На участке DE тело двигалось равномерно. 2) Наибольшее ускорение тело имело на участке АВ. 3) В интервале времени от 6 до 8 с тело прошло путь 6 м. 4) На участке CD кинетическая энергия тела уменьшалась. 5) В интервале времени от 0 до 2 с тело прошло путь 6 м. Ответ: 21. Под действием тормозящей силы в 150 кн тормозной путь поезда массой 150 т составил 50 м. До начала торможения поезд имел скорость Ответ: м/с. 22. На коротком плече рычага укреплён груз массой 100 кг. Для того чтобы поднять груз на высоту 8 см, к длинному плечу рычага приложили силу, равную 200 Н. При этом точка приложения этой силы опустилась на 50 см. Определите КПД рычага. Ответ: % 23. Тело массой 2 кг брошено с поверхности земли вертикально вверх со скоростью 25 м/с. Чему будет равна кинетическая энергия тела через 1 с подъёма, если сопротивлением движению можно пренебречь? Ответ: Дж 24. Брусок массой 100 г, подвешенный на лёгкой нити, движется вверх с таким ускорением, что его вес увеличивается в три раза по сравнению с состоянием покоя.
Укажите их номера. 1) На участке DE тело двигалось равномерно. 2) Наибольшее ускорение тело имело на участке АВ. 3) В интервале времени от 6 до 8 с тело прошло путь 6 м. 4) На участке CD кинетическая энергия тела уменьшалась. 5) В интервале времени от 0 до 2 с тело прошло путь 6 м. Ответ: 21. Под действием тормозящей силы в 150 кн тормозной путь поезда массой 150 т составил 50 м. До начала торможения поезд имел скорость Ответ: м/с. 22. На коротком плече рычага укреплён груз массой 100 кг. Для того чтобы поднять груз на высоту 8 см, к длинному плечу рычага приложили силу, равную 200 Н. При этом точка приложения этой силы опустилась на 50 см. Определите КПД рычага. Ответ: % 23. Тело массой 2 кг брошено с поверхности земли вертикально вверх со скоростью 25 м/с. Чему будет равна кинетическая энергия тела через 1 с подъёма, если сопротивлением движению можно пренебречь? Ответ: Дж 24. Брусок массой 100 г, подвешенный на лёгкой нити, движется вверх с таким ускорением, что его вес увеличивается в три раза по сравнению с состоянием покоя. Чему равен модуль ускорения бруска, если ускорения свободного падения g=10 м/с 2? Ответ: м/с Под действием силы 40 Н груз массой 4 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости 50%. Чему равна длина наклонной плоскости, если её высота 1 м? Ответ: м
Чему равен модуль ускорения бруска, если ускорения свободного падения g=10 м/с 2? Ответ: м/с Под действием силы 40 Н груз массой 4 кг перемещается вверх по наклонной плоскости. Коэффициент полезного действия наклонной плоскости 50%. Чему равна длина наклонной плоскости, если её высота 1 м? Ответ: м
7 Часть 2 1. Два одинаковых латунных шарика падают с одной и той же высоты. Первый шарик упал в песок и остановился, а второй, ударившись о камень, отскочил и был пойман рукой на некоторой вы
2.7 Падающие объекты — Физика колледжа: OpenStax
Пример 1: Расчет положения и скорости падающего объекта: камень, брошенный вверх
Человек, стоящий на краю высокого обрыва, бросает камень вверх с начальной скоростью 13,0 м / с . Камень не задевает край обрыва, когда падает на землю. Рассчитайте положение и скорость камня через 1,00 с, 2,00 с и 3,00 с после того, как он был брошен, пренебрегая влиянием сопротивления воздуха.
Стратегия
Нарисуйте эскиз.
Рисунок 2.Нас просят определить положение [latex] \ boldsymbol {y} [/ latex] в разное время. Разумно принять начальную позицию [latex] \ boldsymbol {y_0} [/ latex] равной нулю. Эта задача связана с одномерным движением в вертикальном направлении. Мы используем знаки «плюс» и «минус» для обозначения направления, при этом «вверх» является положительным, а «вниз» — отрицательным. Поскольку верх положительный, и камень отбрасывается вверх, начальная скорость также должна быть положительной. Ускорение силы тяжести направлено вниз, поэтому [latex] \ boldsymbol {a} [/ latex] отрицательно.Очень важно, чтобы начальная скорость и ускорение свободного падения имели противоположные знаки. Противоположные знаки указывают на то, что ускорение свободного падения противостоит начальному движению и замедлит его, а затем обратит его вспять.
Поскольку нас запрашивают значения положения и скорости трижды, мы будем называть их [латекс] \ boldsymbol {y_1} [/ latex] и [latex] \ boldsymbol {v_1} [/ latex]; [latex] \ boldsymbol {y_2} [/ latex] и [латекс] \ boldsymbol {v_2} [/ latex]; и [латекс] \ boldsymbol {y_3} [/ latex] и [латекс] \ boldsymbol {v_3} [/ latex]. 2 = 8,10 \ textbf {m}} [/ latex]
2 = 8,10 \ textbf {m}} [/ latex]
Обсуждение
Камень находится на 8,10 м выше своей начальной точки в [латексе] \ boldsymbol {t = 1.00} [/ latex] s, поскольку [latex] \ boldsymbol {y_1> y_0} [/ latex]. Это может быть , перемещающее вверх или вниз; единственный способ узнать — это вычислить [латекс] \ boldsymbol {v_1} [/ latex] и выяснить, положительное оно или отрицательное.
Решение для Velocity [латекс] \ boldsymbol {v_1} [/ latex]
1. Определите известные. Мы знаем, что [латекс] \ boldsymbol {y_0 = 0} [/ latex]; [латекс] \ boldsymbol {v_0 = 13.2} [/ латекс]; и [латекс] \ boldsymbol {t = 1.00 \ textbf {s}} [/ latex]. Мы также знаем из решения выше, что [latex] \ boldsymbol {y_1 = 8.10 \ textbf {m}} [/ latex].
2. Определите лучшее уравнение для использования. Самый простой — [латекс] \ boldsymbol {v = v_0-gt} [/ latex] (от [latex] \ boldsymbol {v = v_0 + at} [/ latex], где [latex] \ boldsymbol {a = \ textbf {ускорение свободного падения} = — g} [/ латекс]). 2) (1.00 \ textbf {s}) = 3.20 \ textbf {m / s}} [/ latex]
2) (1.00 \ textbf {s}) = 3.20 \ textbf {m / s}} [/ latex]
Обсуждение
Положительное значение для [latex] \ boldsymbol {v_1} [/ latex] означает, что камень все еще движется вверх на [latex] \ boldsymbol {t = 1.00 \ textbf {s}} [/ latex]. Однако, как и ожидалось, он замедлился с исходных 13,0 м / с.
Решение оставшегося времени
Процедуры для вычисления положения и скорости в [latex] \ boldsymbol {t = 2.00 \ textbf {s}} [/ latex] и [latex] \ boldsymbol {3.00 \ textbf {s}} [/ latex] такие же, как указано выше. Результаты сведены в Таблицу 1 и показаны на Рисунке 3.
| Время, т | Позиция, л | Скорость, в | Разгон, а |
|---|---|---|---|
| 1,00 с | 8,10 м | 3,20 м / с | −9. 80 м / с2 80 м / с2 |
| 2,00 с | 6.40 м | −6.60 м / с | −9.80 м / с2 |
| 3,00 с | −5,10 м | −16,4 м / с | −9.80 м / с2 |
| Таблица 1. Результаты . | |||
Графическое представление данных помогает нам лучше понять их.
Рисунок 3. Зависимость вертикального положения, вертикальной скорости и вертикального ускорения от времени для камня, подброшенного вертикально вверх на краю обрыва. Обратите внимание, что скорость изменяется линейно со временем, а ускорение постоянно. Предупреждение о заблуждении! Обратите внимание, что график зависимости положения от времени показывает только вертикальное положение. Легко создать впечатление, что график показывает какое-то горизонтальное движение — форма графика похожа на траекторию снаряда. Но это не так; горизонтальная ось — время, а не пространство. Фактический путь камня в космосе — прямо вверх и прямо вниз.
Фактический путь камня в космосе — прямо вверх и прямо вниз.Обсуждение
Важна интерпретация этих результатов. На 1,00 с камень находится выше своей начальной точки и движется вверх, поскольку [latex] \ boldsymbol {y_1} [/ latex] и [latex] \ boldsymbol {v_1} [/ latex] оба положительны.2} [/ latex] на всю поездку — пока он движется вверх и пока движется вниз. Обратите внимание, что значения для [latex] \ boldsymbol {y} [/ latex] — это положения (или смещения) породы, а не общее пройденное расстояние. Наконец, обратите внимание, что свободное падение относится как к движению вверх, так и вниз. У обоих одинаковое ускорение — ускорение свободного падения, которое остается постоянным все время. Например, космонавты, тренирующиеся в знаменитой рвоте-комете, испытывают свободное падение, как вверх, так и вниз по дуге, о чем мы поговорим более подробно позже.
Модель падающего объекта
Объект называется свободно падающим телом, если его бросают или бросают вертикально с начальной скоростью, и тогда на его движение влияет только сила тяжести.
Положение любого свободно падающего тела определяется начальной скоростью и начальной высотой.
Если час высота, измеренная в футах, т это количество секунд, в течение которых объект упал с начальной высоты час 0 с начальной скоростью или скоростью v 0 (дюйм / сек), тогда модель высоты падающего объекта: час ( т ) знак равно — 16 т 2 + v 0 т + час 0
Значок « — 16 т 2 Термин происходит от ускорения из-за силы тяжести, притягивающей объект к земле.Скорость объекта в определенное время т дан кем-то: v ( т ) знак равно — 32 т + v 0
Когда объект подбрасывается вверх с земли с определенной начальной скоростью, начальная высота равна нулю, а когда объект падает с начальной высоты, начальная скорость равна нулю. Если значение
час
находится в метрах и
s
в метрах / сек, ускорение свободного падения в метрах / сек равно
4.9
, уравнение принимает следующий вид:
час
(
т
)
знак равно
—
4.9
т
2
+
v
0
т
+
час
0
а затем скорость объекта в конкретное время
т
дан кем-то:
v
(
т
)
знак равно
—
9.8
т
+
v
0
Если значение
час
находится в метрах и
s
в метрах / сек, ускорение свободного падения в метрах / сек равно
4.9
, уравнение принимает следующий вид:
час
(
т
)
знак равно
—
4.9
т
2
+
v
0
т
+
час
0
а затем скорость объекта в конкретное время
т
дан кем-то:
v
(
т
)
знак равно
—
9.8
т
+
v
0
Пример 1:
Мяч подбрасывается вертикально вверх с начальной скоростью
80
фут / сек. Как высоко будет мяч после
3
секунды?
Как высоко будет мяч после
3
секунды?
т знак равно 3 и v 0 знак равно 80 фут / сек
Так:
час знак равно — 16 ( 3 ) 2 + 80 ( 3 )
знак равно — 144 + 240
знак равно 96 футов
Пример 2:
Объект падает с высоты
120
ноги. Если предположить, что сопротивления воздуха нет, сколько времени нужно, чтобы достичь земли?
Если предположить, что сопротивления воздуха нет, сколько времени нужно, чтобы достичь земли?
Если час измеряется в футах, т — количество секунд, в течение которых объект упал, и час 0 — начальная высота, с которой объект был сброшен, тогда модель высоты падающего объекта:
час знак равно — 16 т 2 + час 0
Обратите внимание, что начальная скорость здесь равна нулю.
Замена 0 для час и 120 для час 0 в модели. 0 знак равно — 16 т 2 + 120
Решите уравнение для
т
.
0 — 120 знак равно — 16 т 2 + 120 — 120
— 120 знак равно — 16 т 2
— 120 — 16 знак равно — 16 т 2 — 16
7.5 знак равно т 2
Извлекаем квадратный корень:
т знак равно 7,5
≈ ± 2,74
поскольку
т
представляет время, оно не может быть отрицательным.
Следовательно, объект достигнет земли примерно за 2.74 секунд.
Эти уравнения упрощены. Они игнорируют сопротивление воздуха, а гравитационная постоянная является приблизительной. Кроме того, эта модель работает только для поверхности Земли (на уровне моря). Модель на других планетах будет другой, потому что у них другая сила тяжести. Например, на поверхности Луны с час в метрах и v 0 в м / сек модель падающего объекта час знак равно — 0.8 т 2 + v 0 т + час 0 .
4.3 Движение снаряда — Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.

- Рассчитайте дальность, время полета и максимальную высоту снаряда, который выпущен и попадает в плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитайте траекторию полета снаряда.
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, с ускорением только под действием силы тяжести. Применение движения снаряда в физике и технике многочисленно.Некоторые примеры включают метеоры при входе в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядов , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Самый важный факт, о котором следует помнить, это то, что движений вдоль перпендикулярных осей являются независимыми и, следовательно, могут быть проанализированы отдельно. Мы обсуждали этот факт в книге «Векторы смещения» и «Векторы скорости», где мы увидели, что вертикальные и горизонтальные движения независимы. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения: одно по горизонтальной оси, а другое по вертикали. (Этот выбор осей является наиболее разумным, поскольку ускорение силы тяжести является вертикальным; таким образом, нет ускорения по горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x осью, а вертикальную ось y осью. Необязательно использовать этот выбор осей; это просто удобно в случае ускорения свободного падения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение смещения, где мы определяем
— полное смещение, а
и
— его составляющие векторы по горизонтальной и вертикальной осям соответственно. Величины этих векторов равны s , x и y .
Величины этих векторов равны s , x и y .
имеет компоненты
и
по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.
Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также смещение.Мы должны найти их компоненты по осям x и y . Предположим, что все силы, кроме силы тяжести (например, сопротивление воздуха и трение), незначительны. Определив положительное направление как восходящее, компоненты ускорения будут очень простыми:
Поскольку сила тяжести вертикальная,
Если
, это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или
. С этими условиями для ускорения и скорости мы можем записать кинематику (Уравнение) через (Уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из Движение с постоянным ускорением. Кинематические уравнения движения в однородном гравитационном поле становятся кинематическими уравнениями с
Кинематические уравнения движения в однородном гравитационном поле становятся кинематическими уравнениями с
Горизонтальное перемещение
Вертикальное перемещение
Используя этот набор уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем: движение снаряда
- Разложите движение на горизонтальные и вертикальные компоненты по осям x и y .Величины компонентов смещения
по этим осям равны x и y. Величины компонент скорости
—
, где v — величина скорости, а θ — ее направление относительно горизонтали, как показано на (Рисунок).
- Рассматривайте движение как два независимых одномерных движения: одно горизонтальное, а другое вертикальное.Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.

- Найдите неизвестные в двух отдельных движениях: одном горизонтальном и одном вертикальном. Обратите внимание, что единственная общая переменная между движениями — это время t . Процедуры решения проблем здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
- Перекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное смещение
и скорость
Найдите величину и направление смещения и скорости, используя
, где θ — направление смещения
и
— постоянная величина. (c) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости.(d) Движения по осям x и y объединяются для получения полной скорости в любой заданной точке траектории.
В самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости.(d) Движения по осям x и y объединяются для получения полной скорости в любой заданной точке траектории.
Пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка в воздух с начальной скоростью 70,0 м / с под углом
выстреливается снаряд.выше горизонтали, как показано на (Рисунок). Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда.б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
Рис. 4.13 Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальное и вертикальное, в котором
и
Затем мы можем определить
и
равняться нулю и найти требуемые количества.
Решение
(a) Под «высотой» мы понимаем высоту или вертикальное положение y над начальной точкой. Наивысшая точка любой траектории, называемая апексом , достигается, когда
Поскольку нам известны начальная и конечная скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
Потому что
и
равны нулю, уравнение упрощается до
Решение и дает
Теперь мы должны найти
составляющая начальной скорости в направлении y .Выдается
где
— начальная скорость 70,0 м / с,
— начальный угол. Таким образом,
Таким образом,
и и равно
Таким образом, имеем
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательное.Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха). Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других задачах физики, существует более одного способа решения, пока снаряд достигает своей наивысшей точки. В этом случае самый простой способ — использовать
.
Потому что
на вершине, это уравнение сводится к просто
или
Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что до взрыва снаряда проходит несколько секунд.Другой способ узнать время — использовать
.Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивление воздуха незначительно,
, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение — это горизонтальная скорость, умноженная на время согласно
.где
равно нулю. Таким образом,
где
— это составляющая x скорости, равная
.Время t для обоих движений одинаково, поэтому x равно
Горизонтальное движение — это постоянная скорость при отсутствии сопротивления воздуха.Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, сопротивление воздуха оказывает большое влияние, и многие фрагменты падают прямо под ним.
Когда снаряд взрывается, сопротивление воздуха оказывает большое влияние, и многие фрагменты падают прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, это найти величину и направление смещения в наивысшей точке:
Обратите внимание, что угол для вектора смещения меньше, чем начальный угол запуска.Чтобы понять, почему это так, просмотрите (рисунок), на котором показана кривизна траектории к уровню земли.
При решении (рисунок) (а), выражение, которое мы нашли для и , справедливо для любого движения снаряда, когда сопротивление воздуха незначительно. Назовем максимальную высоту y = h . Затем
Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание
Камень сброшен со скалы горизонтально
со скоростью 15,0 м / с.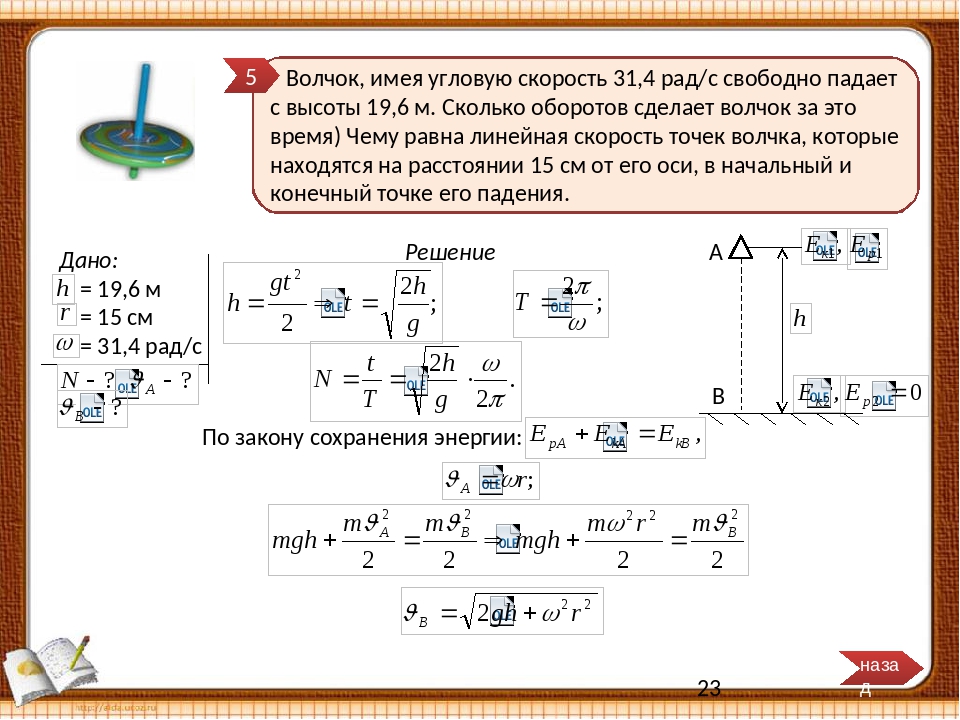 (а) Определите начало системы координат. (б) Какое уравнение описывает горизонтальное движение? (c) Какие уравнения описывают вертикальное движение? (d) Какова скорость породы в точке удара?
(а) Определите начало системы координат. (б) Какое уравнение описывает горизонтальное движение? (c) Какие уравнения описывают вертикальное движение? (d) Какова скорость породы в точке удара?
[show-answer q = ”fs-id1165168031779 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168031779 ″]
(a) Выберите вершину утеса, куда бросается камень из начала системы координат.Хотя это произвольно, мы обычно выбираем время t = 0, чтобы соответствовать началу координат. (b) Уравнение, описывающее горизонтальное движение:
с
это уравнение становится
(c) (рисунок) — (рисунок) и (рисунок) описывают вертикальное движение, но с
эти уравнения значительно упрощаются и становятся
и
(d) Мы используем кинематические уравнения, чтобы найти составляющие x и y скорости в точке удара.Используя
и учитывая, что точка удара равна -100,0 м, мы находим, что составляющая скорости при ударе y равна
Нам дается компонент x ,
, поэтому мы можем рассчитать общую скорость при ударе: v = 46,8 м / с и
ниже горизонтали.
[/ hidden-answer]
Пример
Расчет движения снаряда: теннисист
Теннисист выигрывает матч на стадионе Артура Эша и забивает мяч в трибуны со скоростью 30 м / с и под углом
над горизонтом ((рисунок)).Спускаясь вниз, зритель ловит мяч на 10 м выше точки удара. (а) Подсчитайте время, за которое теннисный мяч достигает зрителя. (б) Каковы величина и направление скорости мяча при ударе?
Рисунок 4.14 Траектория удара теннисного мяча о трибуны.Стратегия
Опять же, разделение этого двумерного движения на два независимых одномерных движения позволяет нам найти желаемые величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением.Таким образом, сначала мы решаем т . Пока мяч поднимается и опускается вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается окончательная скорость. Таким образом, мы рекомбинируем вертикальные и горизонтальные результаты, чтобы получить
в конечный момент времени т , определенный в первой части примера.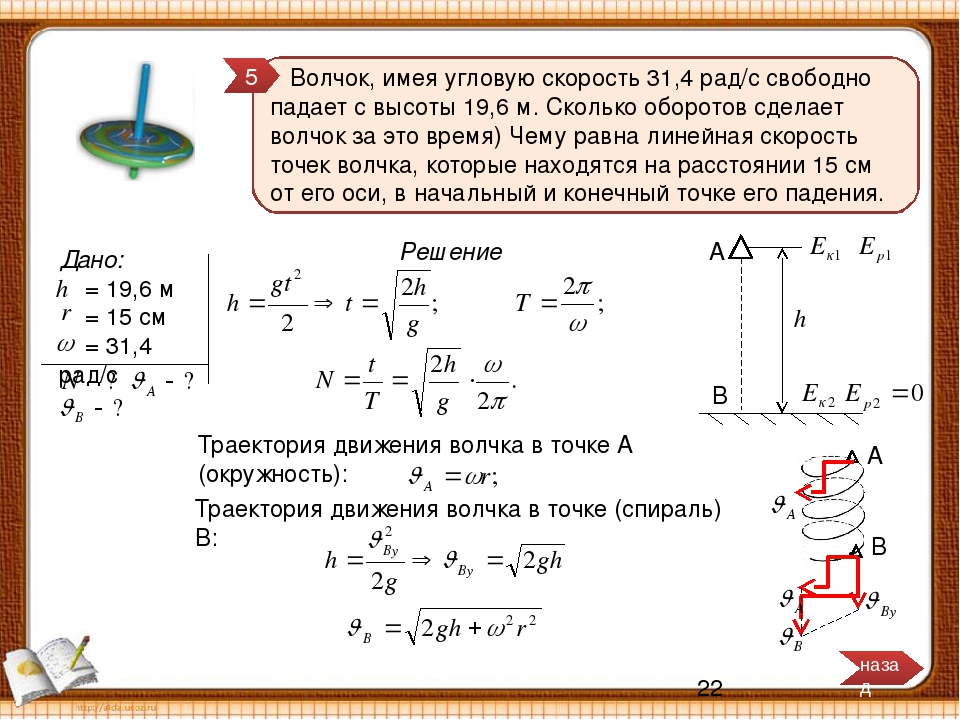
Решение
(a) Пока мяч находится в воздухе, он поднимается, а затем опускается в конечное положение на 10,0 м выше его начальной высоты.Время для этого можно найти, используя (Рисунок):
Если взять начальную позицию
равняется нулю, тогда конечная позиция будет y = 10 м. Начальная вертикальная скорость — это вертикальная составляющая начальной скорости:
Подставив в (рисунок) и , мы получим
Перестановка членов дает квадратное уравнение в t :
Использование формулы корней квадратного уравнения дает т = 3.79 с и т = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз, — мы берем более длительное решение для времени, которое требуется мячу, чтобы достичь зрителя:
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже начальной высоты, проводит в воздухе 3,79 с.
Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже начальной высоты, проводит в воздухе 3,79 с.
(б) Мы можем найти окончательные горизонтальную и вертикальную скорости
и
с использованием результата из (а).Затем мы можем объединить их, чтобы найти величину вектора полной скорости
и угол
делает с горизонтальным. С
является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем как начальную скорость, так и начальный угол. Следовательно,
Окончательная вертикальная скорость определяется как (рисунок):
с
оказался в части (а) как 21.2 м / с, имеем
Величина конечной скорости
это
Направление
находится через арктангенс:
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м / с, попадает на 10.0 м ниже начальной высоты проводит в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость равна
Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м / с, попадает на 10.0 м ниже начальной высоты проводит в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость равна
ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется о точку с другой стороны от вершины траектории и, следовательно, имеет отрицательную составляющую скорости y . Величина скорости меньше, чем величина ожидаемой начальной скорости, поскольку он падает на 10,0 м над точкой старта.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, выпущенного по плоской горизонтальной поверхности и ударяющегося по этой же поверхности. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем вычислить время полета снаряда, который запускается и падает на плоскую горизонтальную поверхность, выполнив некоторые манипуляции с кинематическими уравнениями. Мы отмечаем, что положение и смещение в y должны быть нулевыми при запуске и при ударе о ровную поверхность. Таким образом, мы устанавливаем смещение в y равным нулю и находим
Мы отмечаем, что положение и смещение в y должны быть нулевыми при запуске и при ударе о ровную поверхность. Таким образом, мы устанавливаем смещение в y равным нулю и находим
Факторинг, у нас
Решение для т дает нам
Это время полета для снаряда, выпущенного и попавшего в плоскую горизонтальную поверхность. (Рисунок) неприменимо, когда снаряд приземляется на высоте, отличной от того, на каком он был запущен, как мы видели на (Рисунок), когда теннисист отбивает мяч в трибуны.Другое решение, t = 0, соответствует времени запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g . Таким образом, на Луне, где сила тяжести в шесть раз меньше земной, снаряд, запущенный с той же скоростью, что и на Земле, будет лететь в шесть раз дольше.
Траектория
Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольных t и решения для y ( x ). Берем
Берем
, поэтому снаряд запускается из исходной точки. Кинематическое уравнение для x дает
Подставляя выражение для t в уравнение для положения
дает
Переставляя сроки, получаем
Это уравнение траектории имеет вид
, которое представляет собой уравнение параболы с коэффициентами
Диапазон
Из уравнения траектории мы также можем найти дальность , или горизонтальное расстояние, пройденное снарядом.Факторинг (рисунок), имеем
Положение y равно нулю как для точки запуска, так и для точки удара, поскольку мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решения x = 0, соответствующие точке запуска, и
соответствует точке удара. Использование тригонометрического тождества
и установив x = R для диапазона, находим
Обратите особое внимание на то, что (рисунок) действительно только для запуска и удара о горизонтальную поверхность. Мы видим, что диапазон прямо пропорционален квадрату начальной скорости
Мы видим, что диапазон прямо пропорционален квадрату начальной скорости
и
, и это обратно пропорционально ускорению свободного падения. Таким образом, на Луне диапазон будет в шесть раз больше, чем на Земле при той же начальной скорости. Кроме того, из множителя
видно, что диапазон максимален на
Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше диапазон.В (б) мы видим, что диапазон максимален на
Это верно только для условий, не учитывающих сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что одинаковый диапазон найден для двух начальных углов пуска, которые в сумме составляют
.Снаряд, выпущенный с меньшим углом, имеет меньшую вершину, чем больший угол, но оба имеют одинаковую дальность.
Рис. 4.15. Траектории полета снарядов на ровной поверхности. (а) Чем больше начальная скорость
(а) Чем больше начальная скорость, тем больше диапазон для данного начального угла. (б) Влияние начального угла
на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон такой же для начальных углов
.и
, хотя максимальная высота этих путей отличается.
Пример
Сравнение снимков в гольф
Гольфист оказывается в двух разных ситуациях на разных лунках.На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и позволить ему вылететь на грин. Он направляет выстрел низко к земле, на
.в горизонтальное положение, чтобы мяч катился после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным перекатом после удара. Здесь он смотрит на
.в горизонтальное положение, чтобы минимизировать перекатывание после удара. Оба выстрела попадают и попадают на ровную поверхность.
(а) Какова начальная скорость мяча во второй лунке?
(b) Какова начальная скорость мяча на четвертой лунке?
(c) Напишите уравнение траектории для обоих случаев.
(d) Постройте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Решение
(а)
(б)
(в)
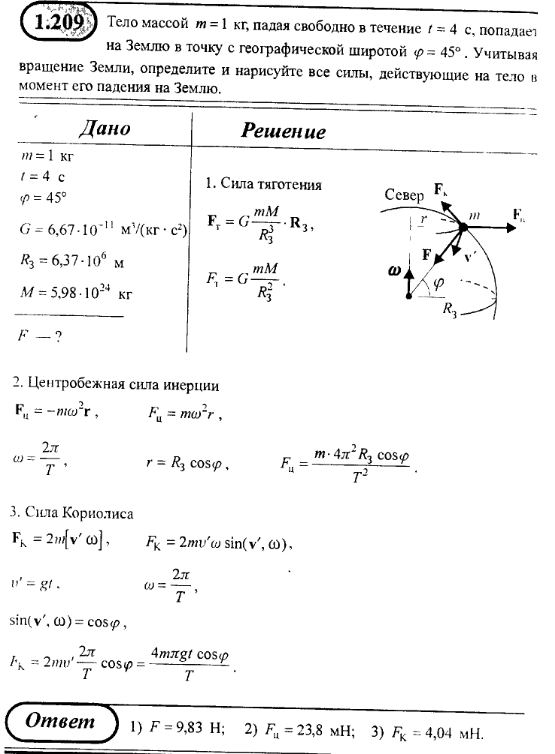
(d) Используя графическую утилиту, мы можем сравнить две траектории, которые показаны на (Рисунок).
Рисунок 4.16 Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка взлета.Значение
Начальная скорость для выстрела на
больше начальной скорости выстрела на
Примечание из (Рисунок), что два снаряда, выпущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска складываются с
.Углы запуска в этом примере складываются, чтобы получить число больше
.
Таким образом, выстрел на
должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он приземлится на меньшем расстоянии.
Проверьте свое понимание
Если бы два удара в гольф на (Рис.) Были запущены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
[show-answer q = ”fs-id1165166636799 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166636799 ″]
Удар для гольфа на
[/ hidden-answer]
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мало по сравнению с окружностью Земли.Если, однако, дальность полета велика, Земля изгибается под ударом снаряда, и ускорение силы тяжести меняет направление на траектории. Диапазон больше, чем предсказывалось уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на чертеже Ньютона Principia. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с объект падает на 5 м без сопротивления воздуха.Таким образом, если объекту задана горизонтальная скорость
Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с объект падает на 5 м без сопротивления воздуха.Таким образом, если объекту задана горизонтальная скорость
(или
у поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно падает от объекта. Это примерно скорость космического челнока на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в книге «Гравитация».
Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости дальность полета увеличивается и становится больше, чем на ровной поверхности, потому что Земля изгибается под своим путем. Со скоростью 8000 м / с достигается орбита.
Сводка
- Движение снаряда — это движение объекта, подверженного только ускорению силы тяжести, причем ускорение постоянно, как у поверхности Земли.
- Для решения задач о движении снаряда мы анализируем движение снаряда в горизонтальном и вертикальном направлениях с использованием одномерных кинематических уравнений для x и y .
- Время полета снаряда, выпущенного с начальной вертикальной скоростью.
на ровной поверхности дает
Это уравнение действительно только тогда, когда снаряд приземляется на той же высоте, с которой был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью. Опять же, уравнение для диапазона действительно только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
Концептуальные вопросы
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, при начальном угле
или
(a) Скорость когда-нибудь равна нулю? (б) Когда скорость минимальна? Максимум? (c) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0? (d) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0?
[show-answer q = ”fs-id1165167780957 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167780957 ″]
а. нет; б. минимум на вершине траектории и максимум при старте и ударе; c. нет, скорость — вектор; d. да, где приземляется
нет; б. минимум на вершине траектории и максимум при старте и ударе; c. нет, скорость — вектор; d. да, где приземляется
[/ hidden-answer]
Ответьте на следующие вопросы относительно движения снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, при начальном угле
или
(a) Ускорение всегда равно нулю? (б) Направлено ли ускорение в том же направлении, что и компонент скорости? (c) Ускорение когда-либо противоположно направлению компонента скорости?
Монета кладется на край стола так, чтобы она немного свешивалась.Четверть скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о десятицентовик. Какая монета первой падает на землю?
[show-answer q = ”fs-id1165166623383 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166623383 ″]
Они оба упали на землю одновременно.
[/ hidden-answer]
Проблемы
Пуля выпускается горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м / с. а) Сколько времени проходит до того, как пуля упадет на землю? б) Как далеко пуля летит по горизонтали?
а) Сколько времени проходит до того, как пуля упадет на землю? б) Как далеко пуля летит по горизонтали?
[show-answer q = ”fs-id1165168072758 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168072758 ″]
а.
, корп.
[/ hidden-answer]
Мрамор скатывается со столешницы высотой 1,0 м и ударяется об пол на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Как долго мрамор витает в воздухе? б) С какой скоростью шарик отрывается от края стола? (c) С какой скоростью он падает на пол?
Дротик летит горизонтально со скоростью 10 м / с в мишень мишени для дротика 2.На расстоянии 4 м, как показано на следующем рисунке. (а) Насколько далеко ниже намеченной цели попадает дротик? (б) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?
[show-answer q = ”fs-id1165168078466 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168078466 ″]
а.
, корп. Они стремятся высоко.
[/ hidden-answer]
Самолет, летящий горизонтально со скоростью 500 км / ч на высоте 800 м, сбрасывает ящик с припасами (см. Следующий рисунок).Если парашют не открывается, как далеко от точки сброса ящик ударяется о землю?
Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально в своем направлении движения со скоростью 300 м / с относительно самолета. (а) На каком расстоянии от точки срабатывания снаряд падает на землю? б) С какой скоростью он ударяется о землю?
[show-answer q = ”fs-id1165167989106 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167989106 ″]
а.,
г.
[/ hidden-answer]
Питчер для фастбола может бросать бейсбольный мяч со скоростью 40 м / с (90 миль / ч). (a) Предполагая, что питчер может выпустить мяч на расстоянии 16,7 м от пластины дома, поэтому мяч движется горизонтально, сколько времени требуется, чтобы мяч достиг пластины дома? (b) Как далеко падает мяч между рукой питчера и тарелкой хозяина?
Снаряд запускается под углом
и приземляется через 20 с на той же высоте, на которой был запущен. а) Какова начальная скорость снаряда? б) Какая максимальная высота? (c) Каков диапазон? (d) Рассчитайте смещение от точки запуска до положения на траектории за 15 с.
а) Какова начальная скорость снаряда? б) Какая максимальная высота? (c) Каков диапазон? (d) Рассчитайте смещение от точки запуска до положения на траектории за 15 с.
[show-answer q = ”fs-id1165166793284 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166793284 ″]
а.
, корп.
г.
г.
[/ hidden-answer]
Баскетболист делает бросок в корзину 6.1 м и 3,0 м над уровнем пола. Если мяч выпущен на высоте 1,8 м от пола под углом
выше горизонтали, какой должна быть начальная скорость, если он пройдет через корзину?
В определенный момент воздушный шар находится на высоте 100 м и снижается с постоянной скоростью 2,0 м / с. Именно в этот момент девушка бросает мяч горизонтально относительно себя с начальной скоростью 20 м / с. Когда она приземлится, где она найдет мяч? Игнорируйте сопротивление воздуха.
[show-answer q = ”fs-id11651665
″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11651665
″][/ hidden-answer]
Человек на мотоцикле, едущем с постоянной скоростью 10 м / с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м / с. Найдите уравнение траектории, которую видит полицейский на обочине дороги. Предположим, что исходное положение банки — это точка, в которую она брошена.Игнорируйте сопротивление воздуха.
Найдите уравнение траектории, которую видит полицейский на обочине дороги. Предположим, что исходное положение банки — это точка, в которую она брошена.Игнорируйте сопротивление воздуха.
В прыжке в длину спортсмен может прыгнуть на расстояние 8,0 м. На какое максимальное расстояние спортсмен может прыгнуть на Луне, где ускорение свободного падения в шесть раз меньше земного?
[Показать-ответ q = ”fs-id1165167996165 ″] Показать решение [/ Показать-ответ]
[скрытый-ответ a = ”fs-id1165167996165 ″]
[/ hidden-answer]
Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 м. Предположим, он может бросать с одинаковой начальной скоростью под любым углом.Насколько высоко он подбрасывает мяч, когда бросает его прямо вверх?
Камень сброшен со скалы под углом
по горизонтали. Высота обрыва 100 м. Начальная скорость камня 30 м / с. а) Насколько высоко над краем утеса возвышается скала? б) Как далеко он переместился по горизонтали, когда находится на максимальной высоте? (c) Через какое время после выброса он падает на землю? г) Каков радиус действия скалы? (e) Каковы горизонтальное и вертикальное положение породы относительно края обрыва при t = 2. 0 с, т = 4,0 с и т = 6,0 с?
0 с, т = 4,0 с и т = 6,0 с?
[show-answer q = ”fs-id1165167746378 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167746378 ″]
а.
,
б.
,
г.
,
г.
,
e.
[/ hidden-answer]
Пытаясь убежать от преследователей, секретный агент спускается на лыжах со склона
. ниже горизонтали на скорости 60 км / ч. Чтобы выжить и приземлиться на снегу на 100 м ниже, он должен преодолеть ущелье шириной 60 м. Он это делает? Игнорируйте сопротивление воздуха.
Игрок в гольф на фервее находится в 70 м от грина, который находится ниже уровня фервея на 20 м.Если гольфист отбивает мяч под углом
с начальной скоростью 20 м / с, насколько близко она к грин?
[show-answer q = ”fs-id1165168065281 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168065281 ″]
Таким образом, удар гольфиста попадает на расстояние 13,3 м от грина.
[/ hidden-answer]
Снаряд выпущен по холму, основание которого находится на расстоянии 300 м.Снаряд выпущен на
над горизонтом с начальной скоростью 75 м / с. Холм можно представить как плоскость с уклоном
.к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой линии равно
. Куда на холме приземляется снаряд?
Астронавт на Марсе бьет футбольный мяч под углом
с начальной скоростью 15 м / с.Если ускорение свободного падения на Марсе составляет 3,7 м / с, (а) каков радиус действия футбольного удара по плоской поверхности? б) Какова будет дальность такого же удара на Луне, где сила тяжести в шесть раз меньше земной?
[show-answer q = ”fs-id1165166572087 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166572087 ″]
а.
,
б.
[/ hidden-answer]
Майк Пауэлл является рекордсменом по прыжкам в длину из 8. 95 м, установлен в 1991 году. Если он оторвался от земли под углом
95 м, установлен в 1991 году. Если он оторвался от земли под углом
какова была его начальная скорость?
Робот-гепардMIT может перепрыгивать через препятствия высотой 46 см и развивает скорость 12,0 км / ч. (а) Если робот запускается под углом
на этой скорости, какова его максимальная высота? (б) Какой должен быть угол запуска, чтобы достичь высоты 46 см?
[show-answer q = ”fs-id1165167842253 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167842253 ″]
а.
[/ hidden-answer]
Mt. Асама в Японии — действующий вулкан. В 2009 году в результате извержения были выброшены твердые вулканические породы, которые упали на 1 км по горизонтали от кратера. Если бы вулканические породы были запущены под углом
°.относительно горизонтали и приземлились на 900 м ниже кратера, (а) какова будет их начальная скорость и (б) каково время их полета?
Дрю Брис из Нового Орлеана Сэйнтс умеет бросать футбольный мяч 23. 0 м / с (50 миль / ч). Если он направит бросок под углом
0 м / с (50 миль / ч). Если он направит бросок под углом
от горизонтали, на какое расстояние он пролетит, если должен быть пойман на той же высоте, что и брошенный?
[show-answer q = ”fs-id1165168098591 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165168098591 ″]
[/ hidden-answer]
Лунный движущийся аппарат, использовавшийся в последних миссиях НАСА Apollo , достиг неофициальной наземной скорости Луны 5.0 м / с — астронавт Юджин Сернан. Если бы марсоход двигался с этой скоростью по плоской лунной поверхности и ударился о небольшую неровность, которая выступала за поверхность под углом
°.как долго он будет «летать» на Луне?
Высота футбольных ворот 2,44 м. Игрок отбивает мяч ногой на расстоянии 10 м от ворот под углом
Какова начальная скорость футбольного мяча?
[show-answer q = ”fs-id1165167854326 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165167854326 ″]
[/ hidden-answer]
Олимп-Монс на Марсе — крупнейший вулкан Солнечной системы, высотой 25 км и радиусом 312 км. Если вы стоите на вершине, с какой начальной скоростью вам нужно было бы запустить снаряд из пушки по горизонтали, чтобы очистить вулкан и приземлиться на поверхности Марса? Обратите внимание, что у Марса ускорение свободного падения
Если вы стоите на вершине, с какой начальной скоростью вам нужно было бы запустить снаряд из пушки по горизонтали, чтобы очистить вулкан и приземлиться на поверхности Марса? Обратите внимание, что у Марса ускорение свободного падения
В 1999 году Робби Книвель первым прыгнул через Гранд-Каньон на мотоцикле. В узкой части каньона (ширина 69,0 м), двигаясь со взлетной рампы 35,8 м / с, он достиг другой стороны. Какой у него был угол запуска?
[Показать-ответ q = ”fs-id1165168009639 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a = ”fs-id1165168009639 ″]
[/ hidden-answer]
Вы бросаете бейсбольный мяч с начальной скоростью 15.0 м / с под углом
по горизонтали. Какой должна быть начальная скорость мяча при
на планете, которая имеет вдвое большее ускорение свободного падения, чем Земля, чтобы достичь той же дальности? Рассмотрим запуск и удар о горизонтальную поверхность.
Аарон Роджерс бросает мяч со скоростью 20,0 м / с в свой широкий ресивер, который бежит прямо по полю со скоростью 9,4 м / с на 20,0 м. Если Аарон бросает мяч, когда дальний приемник достигает 10.0 м, под каким углом должен быть Аарон, чтобы запустить мяч, чтобы получатель поймал его на отметке 20,0 м?
[show-answer q = ”fs-id1165166777489 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1165166777489 ″]
Широкому ресиверу требуется 1,1 с, чтобы покрыть последние 10 м своего бега.
[/ hidden-answer]
Глоссарий
- движение снаряда
- движение объекта, подверженного только ускорению свободного падения
- диапазон
- максимальное горизонтальное расстояние, которое проходит снаряд
- время вылета
- Время нахождения снаряда в воздухе
- траектория
- путь снаряда в воздухе
Как рассчитать скорость падающего объекта на основе высоты
Ускорение под действием силы тяжести заставляет падающий объект набирать скорость во время движения. Поскольку скорость падающего объекта постоянно меняется, вы не сможете точно измерить ее. Однако вы можете рассчитать скорость, исходя из высоты падения; принцип сохранения энергии или основные уравнения для высоты и скорости обеспечивают необходимую взаимосвязь. Чтобы использовать закон сохранения энергии, вы должны сбалансировать потенциальную энергию объекта до его падения с его кинетической энергией при приземлении. Чтобы использовать основные уравнения физики для высоты и скорости, решите уравнение высоты для времени, а затем решите уравнение скорости.2), или 9,9 м / с.
Поскольку скорость падающего объекта постоянно меняется, вы не сможете точно измерить ее. Однако вы можете рассчитать скорость, исходя из высоты падения; принцип сохранения энергии или основные уравнения для высоты и скорости обеспечивают необходимую взаимосвязь. Чтобы использовать закон сохранения энергии, вы должны сбалансировать потенциальную энергию объекта до его падения с его кинетической энергией при приземлении. Чтобы использовать основные уравнения физики для высоты и скорости, решите уравнение высоты для времени, а затем решите уравнение скорости.2), или 9,9 м / с.
Если вы можете рассчитать время, за которое объект падает, просто умножьте это время на ускорение свободного падения, чтобы найти конечную скорость.
Если вы хотите узнать скорость объекта в некоторой точке, прежде чем он упадет на землю, используйте расстояние, на которое объект упал в этой точке, вместо расстояния до земли в любом уравнении.
Умножьте футы в секунду на 0,68, чтобы найти скорость объекта в милях в час.

Свободное падение — Практика — Физический гипертекст
Следующие отрывки представляют собой отрывки из «Длинного, одинокого прыжка» капитана ВВС США Джозефа Киттингера в том виде, в каком они были опубликованы в журнале National Geographic . Это история его рекордного прыжка с парашютом на большой высоте с гелиевого шара над Нью-Мексико 16 августа 1960 года.Проверьте заявление автора о скорости. (На этой высоте g = 9,72 м / с 2 .)Через час и тридцать одну минуту после запуска мой высотомер останавливается на отметке 103 300 футов. При наземном контроле радиолокационные высотомеры также остановились на показаниях 102800 футов — цифра, которую мы позже сочли более надежной.Сейчас 7 часов утра, я вышел на плавучую высоту.
При нулевом счете я выхожу в космос. Ветер не свистит и не развевает мою одежду. Я совершенно не ощущаю увеличения скорости падения.
Хотя мой стабилизирующий парашют открывается на высоте 96 000 футов, я ускоряюсь еще на 6 000 футов, прежде чем достигнуть пика в 614 миль в час, что составляет девять десятых скорости звука на моей высоте.
Камера ВВС на гондоле сделала этот снимок, когда хлопковые облака все еще лежали на глубине 80 000 футов.На высоте 21000 футов они устремились вверх так пугающе, что мне пришлось напомнить себе, что они были паром, а не твердым телом.
Джозеф Киттингер, 1960
У большинства парашютистов ускорение при падении непостоянно. По мере того как скорость парашютиста увеличивается, увеличивается и аэродинамическое сопротивление, пока его скорость не выровняется до типичной для конечной скорости 55 м / с (120 миль / ч).В таких обстоятельствах сопротивление воздуха не является незначительным. Однако история капитана Киттингера исключительна. На той высоте, на которой началось его погружение, плотность атмосферы Земли на уровне моря составляет лишь 1,5% от ее плотности. По сути, это вакуум, который не оказывает сопротивления падающему человеку.
Ускорение свободного падения часто считается постоянным и составляет 9,8 м / с 2 . Для всей поверхности Земли до высоты 18 км это значение с точностью до двух значащих цифр.На самом деле эта «постоянная» изменяется от 9,81 м / с 2 на уровне моря до 9,75 м / с 2 на 18 км. На высоте пикирования капитана Киттингера ускорение свободного падения было ближе к 9,72 м / с 2 .
По этим данным можно рассчитать максимальную скорость капитана Киттингера во время его спуска. Сначала нам нужно будет преобразовать измерения высоты. Чтобы сэкономить время расчета, мы будем преобразовывать только изменение высоты, а не каждую высоту. Учитывая, что он вышел из гондолы на высоте 102 800 футов, свободно упал до высоты 96 000 футов, а затем продолжил ускоряться еще на 6 000 футов; расстояние, на котором он равномерно ускорялся, составляло…
| 102,800 — 96,00 + 6,000 | = 12 800 футов | |||||
| = 3900 м |
Теперь остается только выбрать правильную формулу и ввести числа.
| v 0 = | 0 м / с |
| a = | 9,72 м / с 2 |
| ∆ с = | 3900 м |
| v = | ? |
| v 2 = | v 0 2 + 2 a ∆ s |
| v = | √ (2 a ∆ s ) |
| v = | √ (2 (9.72 м / с 2 ) (3900 м)) |
| v = | 275 м / с |
Этот результат удивительно близок к значению, зафиксированному в отчете Киттингера.
| 614 миль | 1609 кв.м | 1 час | = 274 м / с | ||
| 1 час | 1 миля | 3600 с |
Как и следовало ожидать, фактическое значение немного меньше теоретического.Это согласуется с понятием небольшого, но все же ненулевого сопротивления.
- как раз перед тем, как упасть на пол при спуске
- сразу после того, как он оторвался от пола на пути вверх
- на спуске
- при контакте с полом
- на подъеме
3. 3.
Projectile Motion
3.
Projectile Motion
Самый большой азарт в бейсболе — это хоумран. Движение мяча по изогнутой траектории к трибунам — это распространенный тип двумерного движения, называемого «движением снаряда». Хорошее описание такого движения часто можно получить, если предположить, что сопротивление воздуха отсутствует.
ОБЗОР КОНЦЕПЦИИ Следуя подходу, описанному на рисунке 3.6, мы рассматриваем горизонтальную и вертикальную части движения отдельно. В горизонтальном направлении или по оси x движущийся объект (снаряд) не замедляется при отсутствии сопротивления воздуха.Таким образом, компонент x скорости остается постоянным на своем начальном значении или v x = v 0x , а компонент x ускорения равен x = 0 м / с 2 . Однако в вертикальном направлении или в направлении y снаряд испытывает действие силы тяжести. В результате y-составляющая скорости v y не постоянна, а изменяется. Компонент y ускорения a y — это ускорение силы тяжести вниз. Если путь или траектория снаряда близка к поверхности земли, y имеет звездную величину 9.80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равняются ускорению свободного падения, как показано в краткой концепции на рисунке 3.8 подводит итог. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
Если путь или траектория снаряда близка к поверхности земли, y имеет звездную величину 9.80 м / с 2 . Таким образом, в этом тексте фраза «движение снаряда» означает, что x = 0 м / с 2 и y равняются ускорению свободного падения, как показано в краткой концепции на рисунке 3.8 подводит итог. Пример 2 и другие примеры в этом разделе иллюстрируют, как уравнения кинематики применяются к движению снаряда.
|
| Пример 2 Пакет помощи при падении |
На рис. 3.9 показан самолет, движущийся горизонтально с постоянной скоростью +115 м / с на высоте 1050 м. Направления вправо и вверх были выбраны как положительные.Самолет выпускает «посылку», которая падает на землю по кривой траектории. Не обращая внимания на сопротивление воздуха, определите время, необходимое для того, чтобы пакет упал на землю.
Рассуждения
Время, необходимое для того, чтобы пакет ударился о землю, — это время, за которое пакет упал с высоты 1050 м по вертикали.
С этими данными уравнение 3.
Решение Поскольку v 0y = 0 м / с, из уравнения 3.5b следует, что и | ||||||||||||||||||||||
Свободно падающий пакет в Примере 2 набирает вертикальную скорость при спуске.Однако горизонтальная составляющая скорости сохраняет свое начальное значение v 0x = + 115 м / с на протяжении всего спуска. Поскольку самолет также движется с постоянной горизонтальной скоростью +115 м / с, он остается прямо над падающим пакетом. Пилот всегда видит пакет прямо под самолетом, как показывают пунктирные вертикальные линии на рис. 3.9. Этот результат является прямым следствием того факта, что упаковка не имеет ускорения в горизонтальном направлении. В действительности сопротивление воздуха могло бы замедлить пакет, и он не оставался бы непосредственно под самолетом во время снижения.Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке. Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета ударились о землю одновременно.
Поскольку самолет также движется с постоянной горизонтальной скоростью +115 м / с, он остается прямо над падающим пакетом. Пилот всегда видит пакет прямо под самолетом, как показывают пунктирные вертикальные линии на рис. 3.9. Этот результат является прямым следствием того факта, что упаковка не имеет ускорения в горизонтальном направлении. В действительности сопротивление воздуха могло бы замедлить пакет, и он не оставался бы непосредственно под самолетом во время снижения.Рисунок 3.10 дополнительно поясняет этот момент, показывая, что происходит с двумя пакетами, выпущенными одновременно с одной и той же высоты. Пакет B получает начальную составляющую скорости v 0x = + 115 м / с в горизонтальном направлении, как в Примере 2, и пакет следует по пути, показанному на рисунке. Пакет A, с другой стороны, сбрасывается с неподвижного аэростата и падает прямо на землю, поскольку v 0x = 0 м / с. Оба пакета ударились о землю одновременно.
|
Пакеты на рис. 3.10 не только достигают земли одновременно, но и компоненты y их скоростей также равны во всех точках на пути вниз. Однако пакет B ударяется о землю с большей скоростью, чем пакет A.Помните, что скорость — это величина вектора скорости, и скорость B имеет компонент x, а скорость A — нет. Величина и направление вектора скорости для пакета B в момент непосредственно перед тем, как пакет упадет на землю, вычислены в Примере 3.
| Пример 3 Скорость пакета для ухода |
Важной особенностью движения снаряда является что нет ускорения в горизонтальном направлении или в направлении оси x. В концептуальном примере 4 обсуждается интересное значение этой функции.
| Концептуальный пример 4 Я выстрелил пулей в воздух… |
| ./art/common/example_line.gif» colspan=»2″> | |||
Предположим, вы едете в кабриолете с опущенным верхом. Автомобиль движется вправо с постоянной скоростью. Как показано на рис. 3.11, вы наводите винтовку прямо вверх и стреляете из нее. Где бы пуля приземлилась при отсутствии сопротивления воздуха — позади вас, впереди вас или в стволе винтовки?
Обсуждение и решение Если бы сопротивление воздуха присутствовало, пуля замедлилась бы и она приземлилась бы позади вас, к задней части автомобиля. Однако сопротивления воздуха нет, поэтому нужно более внимательно относиться к движению пули. Родственное домашнее задание: Концептуальный вопрос 12, проблема 34 | |||
| ./art/common/example_line.gif» colspan=»2″> |
| Концептуальное моделирование 3.1 |
| |
Часто снаряды, такие как футбольные и бейсбольные мячи, запускаются в воздух под углом по отношению к земле.Зная начальную скорость снаряда, можно получить большой объем информации о движении. Например, в примере 5 показано, как рассчитать максимальную высоту, достигаемую снарядом.
Например, в примере 5 показано, как рассчитать максимальную высоту, достигаемую снарядом.
| Пример 5 Высота начальной точки |
Также можно найти общее время или «время зависания», в течение которого футбольный мяч на рис. 3.12 находится в воздухе. Пример 6 показывает, как определить это время.
| Пример 6 Время полета стартового снаряда |
Еще одна важная особенность движения снаряда называется «дальность полета».«Дальность, как показано на рисунке 3.12, — это горизонтальное расстояние, пройденное между пуском и приземлением, при условии, что снаряд возвращается на тот же вертикальный уровень, на котором он был выпущен. Пример 7 показывает, как получить диапазон.
| Концептуальное моделирование 3.2 |
| |
| Пример 7 Диапазон начального удара |
Диапазон в предыдущем примере зависит от угла q , по которому выстреливается снаряд выше горизонтали. Когда сопротивление воздуха отсутствует, максимальный диапазон достигается при.
| Проверьте свое понимание 3 |
| ||
В примерах, рассмотренных до сих пор, использовалась информация о начальном местоположении и скорости снаряда для определения конечного местоположения и скорости. В примере 8 рассматривается противоположная ситуация и показано, как конечные параметры могут использоваться с уравнениями кинематики для определения начальных параметров.
Бейсболист выполняет хоумран, и мяч приземляется на сиденье слева, на 7,5 м выше точки, в которую он был нанесен. Он приземляется со скоростью 36 м / с под углом 28 ° от горизонтали (см. Рисунок 3.13). Не обращая внимания на сопротивление воздуха, найдите начальную скорость, с которой мяч покидает биту.
Рассуждения Чтобы найти начальную скорость, мы должны определить ее величину (начальная скорость v 0 ) и ее направление (угол q на чертеже). Эти величины связаны с горизонтальной и вертикальной составляющими начальной скорости (v 0x и v 0y ) соотношениями 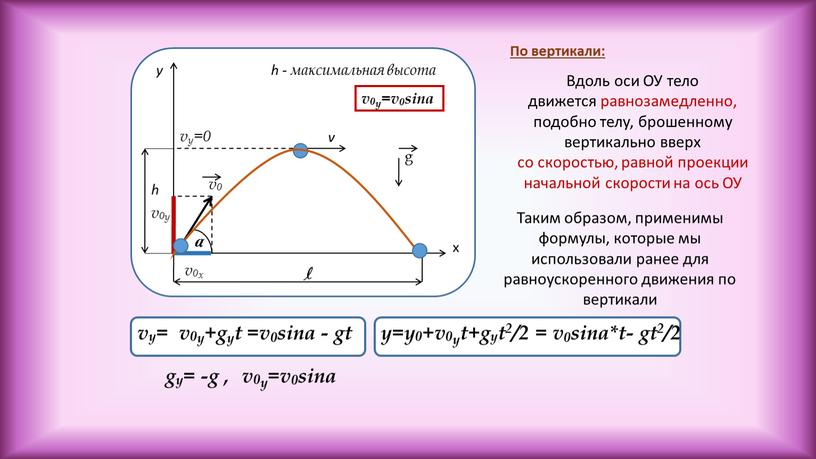 Решение Поскольку сопротивление воздуха игнорируется, горизонтальная составляющая скорости v x остается постоянной на протяжении всего движения. Таким образом,
При определении v 0y мы выбираем знак плюса для квадратного корня, потому что вертикальный компонент начальной скорости указывает вверх на рис. 3.13, что является положительным направлением. Начальная скорость v 0 и угол q бейсбольного мяча равны | ||||||||||||||||||||||||||
| ||
При движении снаряда величина ускорения силы тяжести существенно влияет на траекторию. Например, бейсбольный мяч или мяч для гольфа на Луне полетел бы намного дальше и выше, чем на Земле, если бы был запущен с той же начальной скоростью. Причина в том, что гравитация Луны лишь примерно в шесть раз меньше земной.
В разделе 2.6 указывается, что определенные типы симметрии относительно времени и скорости присутствуют для свободно падающих тел. Эти симметрии также обнаруживаются в движении снарядов, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, рисунок 3.14 показывает, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
Эти симметрии также обнаруживаются в движении снарядов, поскольку снаряды свободно падают в вертикальном направлении. В частности, время, необходимое снаряду для достижения максимальной высоты H, равно времени, затраченному на возвращение на землю. Кроме того, рисунок 3.14 показывает, что скорость v объекта на любой высоте над землей на восходящей части траектории равна скорости v на той же высоте на нисходящей части.Хотя две скорости одинаковы, скорости разные, потому что они указывают в разных направлениях. Концептуальный пример 9 показывает, как использовать этот тип симметрии в своих рассуждениях.
|
| Концептуальный пример 9 Два способа бросить камень |
| ./art/common/example_line.gif» colspan=»2″> | |||
С вершины утеса над озером человек бросает два камня.Камни имеют одинаковую начальную скорость v 0 , но камень 1 бросается вниз под углом q ниже горизонтали, а камень 2 бросается вверх под тем же углом над горизонтом, как показано на рисунке 3.15. Не обращайте внимания на сопротивление воздуха и решите, какой камень ударяет в воду с большей скоростью.
Обсуждение и решение Мы можем предположить, что камень 1, брошенный вниз, ударится по воде с большей скоростью. Родственное домашнее задание: Задачи 37, 65 | |||
Во всех примерах этого раздела снаряды движутся по криволинейной траектории.В общем, если единственное ускорение вызвано действием силы тяжести, форму траектории можно представить как параболу.
| Тест самооценки 3,1 |
| |
| Авторские права © 2000-2003 John Wiley & Sons, Inc. или связанных компаний. Все права защищены. |
4.3 Движение снаряда | Университетская физика, том 1,
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.

- Рассчитайте дальность, время полета и максимальную высоту снаряда, который выпущен и попадает в плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитайте траекторию полета снаряда.
Движение снаряда — это движение объекта, брошенного или выброшенного в воздух, с ускорением только под действием силы тяжести. Применение движения снаряда в физике и технике многочисленно.Некоторые примеры включают метеоры при входе в атмосферу Земли, фейерверки и движение любого мяча в спорте. Такие объекты называются снарядов , а их путь называется траекторией . Движение падающих объектов, описанное в разделе «Движение по прямой», представляет собой простой одномерный тип движения снаряда, в котором нет горизонтального движения. В этом разделе мы рассматриваем двумерное движение снаряда и не учитываем влияние сопротивления воздуха.
Самый важный факт, о котором следует помнить, это то, что движений вдоль перпендикулярных осей являются независимыми и, следовательно, могут быть проанализированы отдельно. Мы обсуждали этот факт в книге «Векторы смещения» и «Векторы скорости», где мы увидели, что вертикальные и горизонтальные движения независимы. Ключ к анализу двумерного движения снаряда состоит в том, чтобы разбить его на два движения: одно по горизонтальной оси, а другое по вертикали. (Этот выбор осей является наиболее разумным, поскольку ускорение силы тяжести является вертикальным; таким образом, нет ускорения по горизонтальной оси, когда сопротивление воздуха незначительно.) Как обычно, мы называем горизонтальную ось x осью, а вертикальную ось y осью. Необязательно использовать этот выбор осей; это просто удобно в случае ускорения свободного падения. В других случаях мы можем выбрать другой набор осей. (Рисунок) иллюстрирует обозначение для смещения, где мы определяем [latex] \ overset {\ to} {s} [/ latex] как полное смещение, а [latex] \ overset {\ to} {x} [/ latex ] и [latex] \ overset {\ to} {y} [/ latex] — его составляющие векторы по горизонтальной и вертикальной осям соответственно.Величины этих векторов равны s , x и y .
Рисунок 4.11 Общее смещение s футбольного мяча в точке на его пути. Вектор [латекс] \ overset {\ to} {s} [/ latex] имеет компоненты [latex] \ overset {\ to} {x} [/ latex] и [latex] \ overset {\ to} {y} [ / латекс] по горизонтальной и вертикальной осям. Его величина равна s, и он составляет угол θ с горизонтом.
Чтобы полностью описать движение снаряда , мы должны включить скорость и ускорение, а также смещение.{2}). [/ латекс]
Поскольку сила тяжести вертикальная, [латекс] {a} _ {x} = 0. [/ latex] Если [latex] {a} _ {x} = 0, [/ latex] это означает, что начальная скорость в направлении x равна конечной скорости в направлении x , или [латекс] {v} _ {x} = {v} _ {0x}. [/ latex] С этими условиями на ускорение и скорость, мы можем записать кинематическое (Уравнение) через (Уравнение) для движения в однородном гравитационном поле, включая остальные кинематические уравнения для постоянного ускорения из Движения с постоянным ускорением.{2} -2 г (г- {у} _ {0}) [/ латекс]
Используя этот набор уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем: движение снаряда
- Разложите движение на горизонтальные и вертикальные компоненты по осям x и y . Величины компонентов смещения [latex] \ overset {\ to} {s} [/ latex] по этим осям равны x и y. Величины компонентов скорости [latex] \ overset {\ to} {v} [/ latex] равны [latex] {v} _ {x} = v \ text {cos} \, \ theta \, \ text {and} \, {v} _ {y} = v \ text {sin} \, \ theta, [/ latex], где v — величина скорости, а θ — ее направление относительно горизонтали, как показано на (Рисунок).
- Рассматривайте движение как два независимых одномерных движения: одно горизонтальное, а другое вертикальное. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: одном горизонтальном и одном вертикальном. Обратите внимание, что единственная общая переменная между движениями — это время t . Процедуры решения проблем здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.{2}}, [/ латекс]
, где θ — направление смещения [латекс] \ overset {\ to} {s}. [/ латекс]
Рисунок 4.12 (a) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения по вертикальной и горизонтальной осям. (б) Горизонтальное движение простое, потому что [латекс] {a} _ {x} = 0 [/ latex] и [latex] {v} _ {x} [/ latex] является константой. (c) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта.В самой высокой точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает в направлении, противоположном начальной вертикальной скорости. (d) Движения по осям x и y объединяются для получения полной скорости в любой заданной точке траектории.
Пример
Снаряд фейерверка взрывается высоко и далеко
Во время фейерверка в воздух запускается снаряд с начальной скоростью 70 единиц.0 м / с под углом [латекс] 75,0 \ text {°} [/ latex] над горизонтом, как показано на (Рисунок). Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей наивысшей точки над землей. (а) Рассчитайте высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? (c) Каково горизонтальное смещение снаряда при взрыве? (d) Каково полное смещение от точки запуска до самой высокой точки?
Рисунок 4.13 Траектория выстрела фейерверка. Взрыватель настроен так, чтобы взорвать снаряд в наивысшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальные и вертикальные движения, в которых [latex] {a} _ {x} = 0 [/ latex] и [latex] {a} _ {y} = \ text {-} g. [/ latex] Затем мы можем определить [latex] {x} _ {0} [/ latex] и [latex] {y} _ {0} [/ latex] равными нулю и найти желаемые количества.{2}} {2g}. [/ латекс]
Теперь мы должны найти [latex] {v} _ {0y}, [/ latex] компонент начальной скорости в направлении y . Он задается как [латекс] {v} _ {0y} = {v} _ {0} \ text {sin} {\ theta} _ {0}, [/ latex] где [латекс] {v} _ {0 } [/ latex] — начальная скорость 70,0 м / с, а [latex] {\ theta} _ {0} = 75 \ text {°} [/ latex] — начальный угол. Таким образом,
[латекс] {v} _ {0y} = {v} _ {0} \ text {sin} \, \ theta = (70.0 \, \ text {m} \ text {/} \ text {s}) \ текст {sin} \, 75 \ text {°} = 67.6 \, \ text {m} \ text {/} \ text {s} [/ latex]
и и равно
[латекс] y = \ frac {{(67.{2})}. [/ латекс]
Таким образом, имеем
[латекс] y = 233 \, \ text {m} \ text {.} [/ Latex]
Обратите внимание, что поскольку верх положительный, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение свободного падения отрицательное. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м / с достигает максимальной высоты 233 м (без учета сопротивления воздуха).Цифры в этом примере приемлемы для больших фейерверков, снаряды которых достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя пренебречь, поэтому начальная скорость должна быть несколько больше, чем заданная для достижения той же высоты.
(b) Как и во многих других задачах физики, существует более одного способа решения, пока снаряд достигает своей наивысшей точки. В этом случае самый простой способ — использовать [latex] {v} _ {y} = {v} _ {0y} -gt.{2}} = 6.90 \ text {s} \ text {.} [/ Latex]
Это время также подходит для больших фейерверков. Если вы видите запуск фейерверка, обратите внимание, что до взрыва снаряда проходит несколько секунд. Другой способ узнать время — использовать [latex] y \, \ text {=} \, {y} _ {0} + \ frac {1} {2} ({v} _ {0y} + {v} _ {y}) t. [/ latex] Это оставлено вам в качестве упражнения.
(c) Поскольку сопротивление воздуха незначительно, [латекс] {a} _ {x} = 0 [/ latex] и горизонтальная скорость постоянна, как обсуждалось ранее.Горизонтальное смещение — это горизонтальная скорость, умноженная на время по формуле [latex] x = {x} _ {0} + {v} _ {x} t, [/ latex] где [latex] {x} _ {0} [/ latex] равен нулю. Таким образом,
[латекс] x = {v} _ {x} t, [/ латекс]
, где [latex] {v} _ {x} [/ latex] — это составляющая x скорости, которая определяется как
.[латекс] {v} _ {x} = {v} _ {0} \ text {cos} \, \ theta = (70.0 \, \ text {m} \ text {/} \ text {s}) \ текст {cos} 75 \ text {°} = 18,1 \, \ text {m} \ text {/} \ text {s}. [/ латекс]
Время t для обоих движений одинаково, поэтому x равно
[латекс] x = (18.1 \, \ text {m} \ text {/} \ text {s}) 6.90 \, \ text {s} = 125 \, \ text {m} \ text {.} [/ Latex]
Горизонтальное движение — это постоянная скорость при отсутствии сопротивления воздуха. Обнаруженное здесь горизонтальное смещение могло быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, сопротивление воздуха оказывает большое влияние, и многие фрагменты падают прямо под ним. {- 1} (\ frac {233} {125}) = 61.{2}} {2g}. [/ латекс]
Это уравнение определяет максимальную высоту снаряда над его стартовой позицией и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание
Камень падает горизонтально со скалы [латекс] 100,0 \, \ text {m} [/ latex] высотой со скоростью 15,0 м / с. (а) Определите начало системы координат. (б) Какое уравнение описывает горизонтальное движение? (c) Какие уравнения описывают вертикальное движение? (d) Какова скорость породы в точке удара?
Показать решение(a) Выберите вершину утеса, куда бросается камень из начала системы координат.Хотя это произвольно, мы обычно выбираем время t = 0, чтобы соответствовать началу координат. (б) Уравнение, описывающее горизонтальное движение: [латекс] x = {x} _ {0} + {v} _ {x} t. [/ latex] Если [латекс] {x} _ {0} = 0, [/ latex] это уравнение становится [латексом] x = {v} _ {x} t. [/ latex] (c) (рисунок) — (рисунок) и (рисунок) описывают вертикальное движение, но поскольку [latex] {y} _ {0} = 0 \, \ text {и} \, {v} _ {0y} = 0, [/ latex] эти уравнения значительно упрощаются и превращаются в [latex] y = \ frac {1} {2} ({v} _ {0y} + {v} _ {y}) t = \ frac {1} {2} {v} _ {y} t, \ enspace [/ latex] [латекс] {v} _ {y} = \ text {-} gt, \ enspace [/ latex] [латекс] y = — \ frac {1} {2} g {t} ^ {2}, \ enspace [/ latex] и [latex] {v} _ {y} ^ {2} = — 2gy.{2} = — 2gy [/ latex] и, учитывая, что точка удара составляет -100,0 м, мы находим, что составляющая y скорости при ударе равна [latex] {v} _ {y} = 44,3 \, \ text {м} \ текст {/} \ текст {s}. [/ latex] Нам дается компонент x , [latex] {v} _ {x} = 15.0 \, \ text {m} \ text {/} \ text {s}, [/ latex], чтобы мы могли рассчитайте общую скорость при ударе: v = 46,8 м / с и [латекс] \ theta = 71,3 \ text {°} [/ latex] ниже горизонтали.
Пример
Расчет движения снаряда: теннисист
Теннисист выигрывает матч на стадионе Артура Эша и ударяет мячом о трибуны со скоростью 30 м / с и под углом [латекс] 45 \ text {°} [/ latex] над горизонталью ((Рисунок)).Спускаясь вниз, зритель ловит мяч на 10 м выше точки удара. (а) Подсчитайте время, за которое теннисный мяч достигает зрителя. (б) Каковы величина и направление скорости мяча при ударе?
Рисунок 4.14 Траектория удара теннисного мяча о трибуны.
Стратегия
Опять же, разделение этого двумерного движения на два независимых одномерных движения позволяет нам найти желаемые величины.Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, сначала мы решаем т . Пока мяч поднимается и опускается вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается окончательная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить [латекс] \ overset {\ to} {v} [/ latex] в конечный момент времени t , определенный в первой части примера.
Решение
(a) Пока мяч находится в воздухе, он поднимается, а затем опускается в конечное положение 10.{2}. [/ латекс]
Если мы возьмем начальное положение [latex] {y} _ {0} [/ latex] равным нулю, то конечное положение будет y = 10 м. Начальная вертикальная скорость — это вертикальная составляющая начальной скорости:
[латекс] {v} _ {0y} = {v} _ {0} \ text {sin} \, {\ theta} _ {0} = (30.0 \, \ text {m} \ text {/} \ текст {s}) \ text {sin} \, 45 \ text {°} = 21,2 \, \ text {m} \ text {/} \ text {s}. [/ латекс]
Подставив в (рисунок) и , мы получим
[латекс] 10.0 \, \ text {m} = (21.{2} — (21,2 \, \ text {m / s}) t + 10,0 \, \ text {m} = 0. [/ латекс]
Использование квадратичной формулы дает т = 3,79 с и т = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз, — мы берем более длительное решение для времени, которое требуется мячу, чтобы достичь зрителя:
[латекс] t = 3,79 \, \ text {s} \ text {.} [/ Латекс]
Время движения снаряда полностью определяется вертикальным движением.Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже начальной высоты, проводит в воздухе 3,79 с.
(b) Мы можем найти окончательную горизонтальную и вертикальную скорости [латекс] {v} _ {x} [/ latex] и [latex] {v} _ {y} [/ latex] с использованием результата из ( а). Затем мы можем объединить их, чтобы найти величину вектора полной скорости [latex] \ overset {\ to} {v} [/ latex] и угол [latex] \ theta [/ latex] относительно горизонтали. Поскольку [latex] {v} _ {x} [/ latex] является постоянным, мы можем найти его в любом горизонтальном положении.Мы выбираем начальную точку, потому что знаем как начальную скорость, так и начальный угол. Следовательно,
[латекс] {v} _ {x} = {v} _ {0} \ text {cos} {\ theta} _ {0} = (30 \, \ text {m} \ text {/} \ text { s}) \ text {cos} \, 45 \ text {°} = 21,2 \, \ text {m} \ text {/} \ text {s}. [/ латекс]
Окончательная вертикальная скорость определяется как (рисунок):
[латекс] {v} _ {y} = {v} _ {0y} -gt. [/ латекс]
Поскольку [латекс] {v} _ {0y} [/ latex], как было обнаружено в части (а), составлял 21,2 м / с, мы имеем
[латекс] {v} _ {y} = 21.{-1} (\ frac {21.2} {- 15.9}) = — 53,1 \ text {°}. [/ латекс]
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, который имеет начальную вертикальную скорость 21,2 м / с и приземляется на 10,0 м ниже начальной высоты, проводит в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость [latex] 53,1 \ text {°} [/ latex] ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется о точку с другой стороны от вершины траектории и, следовательно, имеет отрицательную составляющую скорости y .Величина скорости меньше, чем величина ожидаемой начальной скорости, поскольку он падает на 10,0 м над точкой старта.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, выпущенного по плоской горизонтальной поверхности и ударяющегося по этой же поверхности. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем вычислить время полета снаряда, который запускается и падает на плоскую горизонтальную поверхность, выполнив некоторые манипуляции с кинематическими уравнениями.{2} = 0. [/ латекс]
Факторинг, у нас
[латекс] t ({v} _ {0} \ text {sin} {\ theta} _ {0} — \ frac {gt} {2}) = 0. [/ латекс]
Решение для т дает нам
[латекс] {T} _ {\ text {tof}} = \ frac {2 ({v} _ {0} \ text {sin} {\ theta} _ {0})} {g}. [/ латекс]
Это время полета для снаряда, выпущенного и попавшего в плоскую горизонтальную поверхность. (Рисунок) неприменимо, когда снаряд приземляется на высоте, отличной от того, на каком он был запущен, как мы видели на (Рисунок), когда теннисист отбивает мяч в трибуны.Другое решение, t = 0, соответствует времени запуска. Время полета линейно пропорционально начальной скорости в направлении y и обратно пропорционально g . Таким образом, на Луне, где сила тяжести в шесть раз меньше земной, снаряд, запущенный с той же скоростью, что и на Земле, будет лететь в шесть раз дольше.
Траектория
Траектория снаряда может быть найдена путем исключения временной переменной t из кинематических уравнений для произвольных t и решения для y ( x ).{2} \ text {sin} 2 {\ theta} _ {0}} {g}. [/ латекс]
Обратите особое внимание на то, что (рисунок) действительно только для запуска и удара о горизонтальную поверхность. Мы видим, что диапазон прямо пропорционален квадрату начальной скорости [latex] {v} _ {0} [/ latex] и [latex] \ text {sin} 2 {\ theta} _ {0} [/ latex] , и он обратно пропорционален ускорению свободного падения. Таким образом, на Луне диапазон будет в шесть раз больше, чем на Земле при той же начальной скорости. Кроме того, из фактора [латекс] \ text {sin} 2 {\ theta} _ {0} [/ latex] мы видим, что диапазон максимален при [latex] 45 \ text {°}.[/ latex] Эти результаты показаны на (Рисунок). В (а) мы видим, что чем больше начальная скорость, тем больше диапазон. В (b) мы видим, что диапазон максимален при [latex] 45 \ text {°}. [/ latex] Это верно только для условий, не учитывающих сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон обнаружен для двух начальных углов запуска, которые в сумме составляют [латекс] 90 \ text {°}. [/ latex] Снаряд, выпущенный с меньшим углом, имеет меньшую вершину, чем больший угол, но они оба имеют одинаковую дальность.
Рисунок 4.15 Траектории полета снарядов на ровной поверхности. (а) Чем больше начальная скорость [латекс] {v} _ {0}, [/ латекс], тем больше диапазон для данного начального угла. (b) Влияние начального угла [латекс] {\ theta} _ {0} [/ latex] на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаков для начальных углов [latex] 15 \ text {°} [/ latex] и [latex] 75 \ text {°}, [/ latex], хотя максимальные высоты этих путей различаются.
Пример
Сравнение снимков в гольф
Гольфист оказывается в двух разных ситуациях на разных лунках.На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и позволить ему вылететь на грин. Он направляет удар низко к земле [латекс] 30 \ text {°} [/ latex] к горизонтали, чтобы мяч катился после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным перекатом после удара. Здесь он поворачивает выстрел [латекс] 70 \ text {°} [/ latex] к горизонтали, чтобы минимизировать перекатывание после удара. Оба выстрела попадают и попадают на ровную поверхность.
(а) Какова начальная скорость мяча во второй лунке?
(b) Какова начальная скорость мяча на четвертой лунке?
(c) Напишите уравнение траектории для обоих случаев.
(d) Постройте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (a), так и для (b). Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.{2} \ hfill \ end {array} [/ latex]
(d) Используя графическую утилиту, мы можем сравнить две траектории, которые показаны на (Рисунок).
Рисунок 4.16 Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка взлета.
Значение
Начальная скорость выстрела в [латекс] 70 \ text {°} [/ latex] больше начальной скорости выстрела в [латекс] 30 \ text {°}. [/ latex] Примечание из (Рисунок), что два снаряда, выпущенные с одинаковой скоростью, но под разными углами, имеют одинаковую дальность, если углы запуска прибавляются к [latex] 90 \ text {°}.[/ latex] Углы запуска в этом примере складываются, чтобы получить число больше [latex] 90 \ text {°}. [/ latex] Таким образом, выстрел в [латекс] 70 \ text {°} [/ latex] должен иметь большую скорость запуска, чтобы достичь 90 м, иначе он приземлится на меньшем расстоянии.
Проверьте свое понимание
Если бы два удара в гольф на (Рис.) Были запущены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
Показать решениеУдар в гольф [латекс] 30 \ text {°}. [/ латекс]
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мало по сравнению с окружностью Земли.Если, однако, дальность полета велика, Земля изгибается под ударом снаряда, и ускорение силы тяжести меняет направление на траектории. Диапазон больше, чем предсказывалось уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на (Рисунок), который основан на чертеже Ньютона Principia. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с объект падает на 5 м без сопротивления воздуха.Таким образом, если объекту задана горизонтальная скорость [latex] 8000 \, \ text {m} \ text {/} \ text {s} [/ latex] (или [latex] 18000 \ text {mi} \ text { /} \ text {hr}) [/ latex] у поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность постоянно падает от объекта. Это примерно скорость космического челнока на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в книге «Гравитация».
Рисунок 4.17 Снаряд в спутник. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости дальность полета увеличивается и становится больше, чем на ровной поверхности, потому что Земля изгибается под своим путем. Со скоростью 8000 м / с достигается орбита.
Сводка
- Движение снаряда — это движение объекта, подверженного только ускорению силы тяжести, причем ускорение постоянно, как у поверхности Земли.
- Для решения задач о движении снаряда мы анализируем движение снаряда в горизонтальном и вертикальном направлениях с использованием одномерных кинематических уравнений для x и y .
- Время полета снаряда, выпущенного с начальной вертикальной скоростью [латекс] {v} _ {0y} [/ латекс] по ровной поверхности, определяется выражением
[латекс] {T} _ {tof} = \ frac {2 ({v} _ {0} \ text {sin} \, \ theta)} {g}. [/ латекс]
Это уравнение действительно только тогда, когда снаряд приземляется на той же высоте, с которой был запущен.
- Максимальное горизонтальное расстояние, пройденное снарядом, называется дальностью. Опять же, уравнение для диапазона действительно только тогда, когда снаряд приземляется на той же высоте, с которой он был запущен.
Концептуальные вопросы
Ответьте на следующие вопросы о движении снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом не [латекс] 0 \ text {°} [/ latex] и [латекс] 90 \ text {°}: [/ latex] (а) Скорость когда-нибудь равна нулю? (б) Когда скорость минимальна? Максимум? (c) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0? (d) Может ли скорость когда-либо быть такой же, как начальная скорость в любой момент времени, кроме t = 0?
Показать решениеа.нет; б. минимум на вершине траектории и максимум при старте и ударе; c. нет, скорость — вектор; d. да, где приземляется
Ответьте на следующие вопросы о движении снаряда по ровной поверхности, предполагая незначительное сопротивление воздуха, с начальным углом не [латекс] 0 \ text {°} [/ latex] и [латекс] 90 \ text {°}: [/ latex] (а) Ускорение когда-либо равно нулю? (б) Направлено ли ускорение в том же направлении, что и компонент скорости? (c) Ускорение когда-либо противоположно направлению компонента скорости?
Монета кладется на край стола так, чтобы она немного свешивалась.Четверть скользит горизонтально по поверхности стола перпендикулярно краю и ударяется о десятицентовик. Какая монета первой падает на землю?
Показать решениеОни оба упали на землю одновременно.
Проблемы
Пуля выпускается горизонтально с высоты плеча (1,5 м) с начальной скоростью 200 м / с. а) Сколько времени проходит до того, как пуля упадет на землю? б) Как далеко пуля летит по горизонтали?
Показать решениеа. [латекс] t = 0.55 \, \ text {s} [/ latex], б. [латекс] x = 110 \, \ text {m} [/ latex]
Мрамор скатывается со столешницы высотой 1,0 м и ударяется об пол на расстоянии 3,0 м от края стола в горизонтальном направлении. а) Как долго мрамор витает в воздухе? б) С какой скоростью шарик отрывается от края стола? (c) С какой скоростью он падает на пол?
Дротик метается горизонтально со скоростью 10 м / с в мишень мишени для мишени на расстоянии 2,4 м, как показано на следующем рисунке.(а) Насколько далеко ниже намеченной цели попадает дротик? (б) Что ваш ответ говорит вам о том, как опытные игроки в дартс бросают свои дротики?
Показать решениеа. [латекс] t = 0,24 \ text {s,} \ enspaced = 0,28 \, \ text {m} [/ latex], b. Они стремятся высоко.
Самолет, летящий горизонтально со скоростью 500 км / ч на высоте 800 м, сбрасывает ящик с припасами (см. Следующий рисунок). Если парашют не открывается, как далеко от точки сброса ящик ударяется о землю?
Предположим, что самолет в предыдущей задаче выпускает снаряд горизонтально в своем направлении движения со скоростью 300 м / с относительно самолета.(а) На каком расстоянии от точки срабатывания снаряд падает на землю? б) С какой скоростью он ударяется о землю?
Показать решениеa., [Латекс] t = 12,8 \, \ text {s,} \ enspacex = 5619 \, \ text {m} [/ latex] b. [латекс] {v} _ {y} = 125.0 \, \ text {m} \ text {/} \ text {s,} \ enspace {v} _ {x} = 439.0 \, \ text {m} \ text {/} \ text {s,} \ enspace | \ overset {\ to} {v} | = 456.0 \, \ text {m} \ text {/} \ text {s} [/ latex]
Питчер для фастбола может бросать бейсбольный мяч со скоростью 40 м / с (90 миль / ч). (a) Предполагая, что питчер может выпустить мяч 16.7 м от пластины дома, чтобы мяч двигался горизонтально, сколько времени требуется мячу, чтобы добраться до пластины дома? (b) Как далеко падает мяч между рукой питчера и тарелкой хозяина?
Снаряд запускается под углом [латекс] 30 \ text {°} [/ latex] и падает через 20 секунд на той же высоте, на которой был запущен. а) Какова начальная скорость снаряда? б) Какая максимальная высота? (c) Каков диапазон? (d) Рассчитайте смещение от точки запуска до положения на траектории за 15 с.
Показать решениеа. [латекс] {v} _ {y} = {v} _ {0y} -gt, \ enspacet = 10 \ text {s,} \ enspace {v} _ {y} = 0, \ enspace {v} _ { 0y} = 98.0 \, \ text {m} \ text {/} \ text {s}, \ enspace {v} _ {0} = 196.0 \, \ text {m} \ text {/} \ text {s} [/ латекс], б. [латекс] h = 490,0 \, \ text {m}, [/ latex]
г. [латекс] {v} _ {0x} = 169.7 \, \ text {m} \ text {/} \ text {s,} \ enspacex = 3394.0 \, \ text {m,} [/ latex]
г. [латекс] \ begin {array} {cc} x = 2545,5 \, \ text {m} \ hfill \\ y = 465,5 \, \ text {m} \ hfill \\ \ overset {\ to} {s} = 2545,5 \, \ text {m} \ hat {i} +465.5 \, \ text {m} \ hat {j} \ hfill \ end {array} [/ latex]
Баскетболист делает бросок в корзину 6.1 м и 3,0 м над уровнем пола. Если мяч выпущен на высоте 1,8 м над полом под углом [латекс] 60 \ text {°} [/ latex] над горизонтом, какой должна быть начальная скорость, если он пройдет через корзину?
В определенный момент воздушный шар находится на высоте 100 м и снижается с постоянной скоростью 2,0 м / с. Именно в этот момент девушка бросает мяч горизонтально относительно себя с начальной скоростью 20 м / с. Когда она приземлится, где она найдет мяч? Игнорируйте сопротивление воздуха.{2}, [/ latex] [латекс] t = 4.3 \, \ text {s,} [/ latex] [latex] x = 86.0 \, \ text {m} [/ latex]
Человек на мотоцикле, едущем с постоянной скоростью 10 м / с, бросает пустую банку прямо вверх относительно себя с начальной скоростью 3,0 м / с. Найдите уравнение траектории, которую видит полицейский на обочине дороги. Предположим, что исходное положение банки — это точка, в которую она брошена. Игнорируйте сопротивление воздуха.
В прыжке в длину спортсмен может прыгнуть на расстояние 8,0 м.На какое максимальное расстояние спортсмен может прыгнуть на Луне, где ускорение свободного падения в шесть раз меньше земного?
Показать решение[латекс] {R} _ {Moon} = 48 \, \ text {m} [/ latex]
Максимальное горизонтальное расстояние, на которое мальчик может бросить мяч, составляет 50 м. Предположим, он может бросать с одинаковой начальной скоростью под любым углом. Насколько высоко он подбрасывает мяч, когда бросает его прямо вверх?
Камень сброшен со скалы под углом [латекс] 53 \ text {°} [/ latex] по отношению к горизонтали.Высота обрыва 100 м. Начальная скорость камня 30 м / с. а) Насколько высоко над краем утеса возвышается скала? б) Как далеко он переместился по горизонтали, когда находится на максимальной высоте? (c) Через какое время после выброса он падает на землю? г) Каков радиус действия скалы? (e) Каковы горизонтальное и вертикальное положение породы относительно края обрыва при t = 2,0 с, t = 4,0 с и t = 6,0 с?
Показать решениеа. {2} -2gy⇒h = 23.{2} [/ latex] [латекс] ⇒t = 7,58 \, \ text {s} [/ latex],
г. [латекс] x = 136,44 \, \ text {m} [/ latex],
e. [латекс] t = 2.0 \, \ text {s} \ enspacey = 28.4 \, \ text {m} \ enspacex = 36 \, \ text {m} [/ latex]
[латекс] t = 4.0 \, \ text {s} \ enspacey = 17.6 \, \ text {m} \ enspacex = 22.4 \, \ text {m} [/ latex]
[латекс] t = 6.0 \, \ text {s} \ enspacey = -32.4 \, \ text {m} \ enspacex = 108 \, \ text {m} [/ latex]
Пытаясь убежать от преследователей, секретный агент съезжает со склона, наклоненного [латекс] на 30 \ text {°} [/ latex] ниже горизонтали, на скорости 60 км / ч.Чтобы выжить и приземлиться на снегу на 100 м ниже, он должен преодолеть ущелье шириной 60 м. Он это делает? Игнорируйте сопротивление воздуха.
Игрок в гольф на фервее находится в 70 м от грина, который находится ниже уровня фервея на 20 м. Если игрок в гольф ударяет по мячу под углом [латекс] 40 \ text {°} [/ latex] с начальной скоростью 20 м / с, насколько близко он подойдет к грину?
Показать решение[латекс] {v} _ {0y} = 12. {2} \ enspace-20.{2} [/ латекс]
[латекс] t = 3,7 \, \ text {s} \ enspace {v} _ {0x} = 15.3 \, \ text {m} \ text {/} \ text {s} ⇒x = 56.7 \, \ text {m} [/ латекс]
Таким образом, удар гольфиста попадает на расстояние 13,3 м от грина.
Снаряд выпущен по холму, основание которого находится на расстоянии 300 м. Снаряд выстреливается на [латекс] 60 \ text {°} [/ latex] над горизонтом с начальной скоростью 75 м / с. Холм можно представить как плоскость с уклоном [латекс] 20 \ text {°} [/ latex] к горизонтали. Относительно системы координат, показанной на следующем рисунке, уравнение этой прямой линии имеет вид [latex] y = (\ text {tan} 20 \ text {°}) x-109.[/ latex] Где на холме приземляется снаряд?
Астронавт на Марсе пинает футбольный мяч под углом [латекс] 45 \ text {°} [/ latex] с начальной скоростью 15 м / с. Если ускорение свободного падения на Марсе составляет 3,7 м / с, (а) каков радиус действия футбольного удара по плоской поверхности? б) Какова будет дальность такого же удара на Луне, где сила тяжести в шесть раз меньше земной?
Показать решениеа. [латекс] R = 60,8 \, \ text {m} [/ latex],
г.[латекс] R = 137,8 \, \ text {m} [/ латекс]
Майк Пауэлл является рекордсменом по прыжкам в длину 8,95 м, установленным в 1991 году. Если он оторвался от земли под углом [латекс] 15 \ text {°}, [/ latex], какой была его начальная скорость?
Робот-гепардMIT может перепрыгивать через препятствия высотой 46 см и развивает скорость 12,0 км / ч. (a) Если робот запускается под углом [латекс] 60 \ text {°} [/ latex] с этой скоростью, какова его максимальная высота? (б) Какой должен быть угол запуска, чтобы достичь высоты 46 см?
Показать решениеа.{2}} {2g} ⇒ \ text {sin} \, \ theta = 0.91⇒ \ theta = 65.5 \ text {°} [/ latex]
Mt. Асама в Японии — действующий вулкан. В 2009 году в результате извержения были выброшены твердые вулканические породы, которые упали на 1 км по горизонтали от кратера. Если вулканические породы были запущены под углом [латекс] 40 \ text {°} [/ latex] по отношению к горизонтали и приземлились на 900 м ниже кратера, (а) какова была бы их начальная скорость и (б) какая время их полета?
Дрю Брис из Нового Орлеана Сэйнтс умеет бросать футбольный мяч 23.0 м / с (50 миль / ч). Если он направит бросок под углом [latex] 10 \ text {°} [/ latex] от горизонтали, на какое расстояние он пролетит, если должен быть пойман на той же высоте, что и был брошен?
Показать решение[латекс] R = 18,5 \, \ text {m} [/ латекс]
Лунный движущийся аппарат, использовавшийся в последней миссии NASA Apollo , достиг неофициальной скорости движения Луны 5,0 м / с астронавтом Юджином Сернаном. Если бы марсоход двигался с этой скоростью по плоской лунной поверхности и ударился о небольшую неровность, которая отбрасывала его на поверхность под углом [латекс] 20 \ text {°}, [/ latex], как долго он был бы «в воздухе» на Луне?
Футбольный гол — 2.{2} \ text {sin} \, 2 {\ theta} _ {0}} {g} ⇒ {\ theta} _ {0} = 15.0 \ text {°} [/ latex]
Вы бросаете бейсбольный мяч с начальной скоростью 15,0 м / с под углом [latex] 30 \ text {°} [/ latex] по отношению к горизонтали. Какой должна быть начальная скорость мяча при [latex] 30 \ text {°} [/ latex] на планете, которая имеет вдвое большее ускорение силы тяжести, чем Земля, чтобы достичь такой же дальности? Рассмотрим запуск и удар о горизонтальную поверхность.
Аарон Роджерс бросает мяч со скоростью 20,0 м / с в свой ресивер, который бежит прямо по полю на скорости 9.4 м / с для 20,0 м. Если Аарон бросает мяч, когда принимающий достигает 10,0 м, под каким углом должен быть Аарон, чтобы запустить мяч, чтобы принимающий поймал его на отметке 20,0 м?
Показать решениеШирокому ресиверу требуется 1,1 с, чтобы покрыть последние 10 м своего бега.
[латекс] {T} _ {\ text {tof}} = \ frac {2 ({v} _ {0} \ text {sin} \, \ theta)} {g} ⇒ \ text {sin} \, \ theta = 0,27⇒ \ theta = 15.6 \ text {°} [/ latex]
Глоссарий
- движение снаряда
- движение объекта, подверженного только ускорению свободного падения
- диапазон
- максимальное горизонтальное расстояние, которое проходит снаряд
- время вылета
- Время нахождения снаряда в воздухе
- траектория
- путь снаряда в воздухе




 Камера ВВС на гондоле сделала этот снимок, когда хлопковые облака все еще лежали на глубине 80 000 футов.На высоте 21000 футов они устремились вверх так пугающе, что мне пришлось напомнить себе, что они были паром, а не твердым телом.
Камера ВВС на гондоле сделала этот снимок, когда хлопковые облака все еще лежали на глубине 80 000 футов.На высоте 21000 футов они устремились вверх так пугающе, что мне пришлось напомнить себе, что они были паром, а не твердым телом. м
м (© Стивен Далтон / Фотоисследователи).
(© Стивен Далтон / Фотоисследователи). При падении он движется как вправо, так и вниз, но эти две части движения происходят независимо. Поэтому мы можем сосредоточиться исключительно на вертикальной части. Отметим, что первоначально пакет движется в горизонтальном направлении или по оси x, а не по оси y, так что v 0y = 0 м / с. Кроме того, когда пакет ударяется о землю, компонент y его смещения составляет y = –1050 м, как показано на рисунке. Это ускорение свободного падения, поэтому y = –9,80 м / с 2 .Эти данные резюмируются следующим образом:
При падении он движется как вправо, так и вниз, но эти две части движения происходят независимо. Поэтому мы можем сосредоточиться исключительно на вертикальной части. Отметим, что первоначально пакет движется в горизонтальном направлении или по оси x, а не по оси y, так что v 0y = 0 м / с. Кроме того, когда пакет ударяется о землю, компонент y его смещения составляет y = –1050 м, как показано на рисунке. Это ускорение свободного падения, поэтому y = –9,80 м / с 2 .Эти данные резюмируются следующим образом: 5b () можно использовать для определения времени спада.
5b () можно использовать для определения времени спада.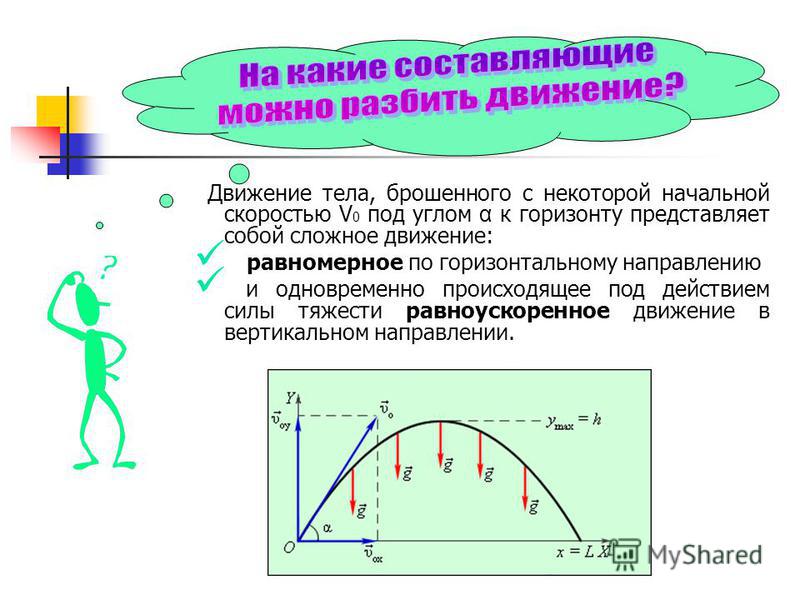 10 Пакет A и пакет B выпускаются одновременно на одной высоте и одновременно ударяются о землю, потому что их переменные y (y, a y и v 0y ) одинаковы.
10 Пакет A и пакет B выпускаются одновременно на одной высоте и одновременно ударяются о землю, потому что их переменные y (y, a y и v 0y ) одинаковы. Перед выстрелом из винтовки пуля, винтовка и автомобиль движутся вместе, поэтому пуля и винтовка имеют такую же горизонтальную скорость, что и автомобиль. При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость машины в качестве начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не изменяется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается непосредственно под плоскостью.
Перед выстрелом из винтовки пуля, винтовка и автомобиль движутся вместе, поэтому пуля и винтовка имеют такую же горизонтальную скорость, что и автомобиль. При выстреле из винтовки пуле придается дополнительная составляющая скорости в вертикальном направлении; пуля сохраняет скорость машины в качестве начальной горизонтальной составляющей скорости, поскольку винтовка направлена прямо вверх. Поскольку для замедления нет сопротивления воздуха, пуля не испытывает горизонтального ускорения. Таким образом, горизонтальная составляющая скорости пули не изменяется.Он сохраняет свою первоначальную ценность и остается такой же, как у винтовки и автомобиля. В результате пуля все время остается прямо над винтовкой и упадет прямо обратно в ствол винтовки , как показано на рисунке. Эта ситуация аналогична ситуации на рис. 3.9, где посылка при падении остается непосредственно под плоскостью. Вы можете контролировать начальную скорость и угол шара, а затем видеть, как компоненты его скорости меняются со временем, когда он движется по изогнутой траектории.Моделирование также отображает графики положения и скорости как функции времени.
Вы можете контролировать начальную скорость и угол шара, а затем видеть, как компоненты его скорости меняются со временем, когда он движется по изогнутой траектории.Моделирование также отображает графики положения и скорости как функции времени. Сопротивления воздуха нет. В любой момент снаряд имеет скорость v и ускорение a. Какой из рисунков или несколько не могут представлять направления для v и a в любой точке траектории?
Сопротивления воздуха нет. В любой момент снаряд имеет скорость v и ускорение a. Какой из рисунков или несколько не могут представлять направления для v и a в любой точке траектории? 5 м
5 м  Однако траектория полета отличалась от той, которая была бы на Земле, потому что ускорение свободного падения на Луне примерно в шесть раз меньше, чем на Земле. Рассмотрим тот же шар на земле, запущенный под тем же углом и с одинаковой скоростью. Найдите отношение (а) максимальной высоты лунного шара к максимальной высоте земного шара и (б) расстояния между лунным шаром и земным шаром.
Однако траектория полета отличалась от той, которая была бы на Земле, потому что ускорение свободного падения на Луне примерно в шесть раз меньше, чем на Земле. Рассмотрим тот же шар на земле, запущенный под тем же углом и с одинаковой скоростью. Найдите отношение (а) максимальной высоты лунного шара к максимальной высоте земного шара и (б) расстояния между лунным шаром и земным шаром. Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается к своей исходной высоте; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью.
Чтобы показать, что это не так, давайте проследим путь камня 2, когда он поднимается на максимальную высоту и падает обратно на землю. Обратите внимание на точку P на рисунке, где камень 2 возвращается к своей исходной высоте; здесь скорость камня 2 равна v 0 , но его скорость направлена под углом q ниже горизонтали.Это именно тот тип симметрии снаряда, который показан на рис. 3.14. Таким образом, в этот момент камень 2 имеет скорость, идентичную скорости, с которой камень 1 бросается вниз с вершины утеса. С этого момента скорость камня 2 изменяется точно так же, как и скорость камня 1, поэтому оба камня ударяются о воду с одинаковой скоростью. 
Leave A Comment