Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Основные действия со степенями
В первую очередь степень — это повторяющееся умножение. Число 134 — это 13 × 13 × 13 × 13, где перемножаются четыре одинаковых сомножителя. Если умножить 134 на 132, то мы получим (13 × 13 × 13 × 13) × (13 × 13), что логично превращается в 136. Это и есть первое правило возведения в степень, которое гласит: при умножении чисел, возведенных в степень, их показатели суммируются. Математически это записывается как:
am × an = a(m+n).
Если разделить 134 на 132, то нам потребуется вычислить дробь вида:
(13 × 13 × 13 × 13) / (13 × 13).
Мы можем просто сократить числа в числителе и знаменателе, и в результате останется 13 × 13 = 13
am / an = a(m – n).
Теперь давайте возведем 114 в куб, то есть в третью степень. Для этого нам потребуется вычислить выражение (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11) × (11 × 11 × 11 × 11). Получилось 12 сомножителей, следовательно, при возведении в n-ную степень числа в степени m, показатели перемножаются. Третье правило записывается так:
(am)n = a(m × n).
Это основные правила работы со степенными выражениями. Однако число можно возвести в отрицательную степень, дробную и нулевую. Какой результат даст выражение 15
154 / 154.
Очевидно, что в числителе и знаменателе стоят одни и те же числа, а когда число делится само на себя, оно превращается в единицу. Но согласно правилу действий со степенными числами это будет эквивалентно 150. Следовательно:
154 / 154 = 150 = 1.
Таким образом, четвертое правило гласит, что любое положительное число в нулевой степени равняется единице. Выглядит это правило так:
При помощи второго правила легко объяснить и работу с отрицательными степенями. К примеру, давайте разделим 82 на 84 и запишем выражение в виде дроби.
(8 × 8) / (8 × 8 × 8 × 8).
Мы можем сократить две восьмерки в числителе и знаменателе и преобразовать дробь в 1 / (8 × 8). Но согласно правилу в ответе мы должны получить 8-2. В знаменателе у нас как раз стоит восьмерка в квадрате. Таким образом:
a-m = 1 / am
При этом для значения -1 правило трансформируется в элегантную формулу:
a-1 = 1 / a.
И последнее правило, которое пригодится вам при работе со степенными функциями, гласит о дробных степенях. Что мы можем сделать с выражением 7
a(m/n) есть корень n-ной степени из am.
Теперь вы знаете, как проводить любые арифметические операции со степенными выражениями.
Вы можете использовать наш калькулятор для вычисления степенных функций. Программа позволяет определить основание, показатель и результат операции. Кроме того, калькулятор сопровождается иллюстрацией графика функций: параболы, кубической параболы и параболы в n-ной степени. Рассмотрим пару примеров.
Примеры из реальной жизни
Депозит в банке
Если мы положим на банковский депозит $1 000 под годовую ставку в размере 9% годовых, то сколько денег на счету будет через 20 лет? Рост с течением времени рассчитываются по экспоненциальной формуле вида:
Рост = a × e(kt),
где a – начальное значение, e – константа, равная 2,718; k – коэффициент роста; t – время.
Для решения банковской задачи нам потребуется возвести 2,718 в степень, равную 20 × 0,09 = 1,8. Воспользуемся нашим калькулятором и введем в ячейку «Число, x =» значение 2,718, а в ячейку «Степень, n =» значение 1,8. Мы получим ответ, равный 6,049. Теперь, для подсчета суммы на банковском счету нам необходимо умножить начальное значение $1 000 на прирост в размере 6,049. В итоге, через 20 лет на депозите будет $6 049.
Школьная задача
Пусть в школьной задаче требуется построить график функции y = x2,5. Это алгебраическая задача, для решения которой требуется задаться тремя значениями «x» и вычислить соответствующие ему значения «y». После чего по найденным точкам построить график функции. Введите в ячейку «Степень, n =» значение 2,5. После этого последовательно рассчитайте значения «y», вводя в «Число, x =» аргументы 1, 2, 3. Вы получите соответствующие значения функции 1; 5,657; 15,588. Вам останется только нарисовать кривую по найденным точкам.
Заключение
Возведение в степень — арифметическая операция последовательного умножения. Степени имеют больше значение в прикладных науках, так как большинство реальных процессов описываются при помощи степенных функций. Используйте наш калькулятор для расчетов любых практических или школьных задач.
Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.
Только корректные расчеты по всем правилам математики!
В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.
Всё для вашего удобства:
- быстрые вычисления и загрузка,
- верные расчеты по всем правилам,
- полный функционал,
- понятный интерфейс,
- адаптация под любой размер устройства
- бесплатно
- не надо ничего устанавливать,
- никакой всплывающей назойливой рекламы,
- подробная инструкция с примерами
Содержание справки:
1. Комплекс операций инженерного калькулятора
2. Инструкция по функциям инженерного калькулятора
3. Как пользоваться инженерным калькулятором – на примерах
4. Тригонометрический калькулятор онлайн — примеры
Комплекс операций инженерного калькулятора
Встроенный
Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.
Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.
Ввод цифр производится в двух вариантах:
- с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
- с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами
Инструкция по функциям инженерного калькулятора
Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в

- [Inv] – обратная функция для sin, cos, tan, переключает интерфейс на другие функции
- [Ln] – натуральный логарифм по основанию «e»
- [ ( ] и
- [Int] – отображает целую часть десятичного числа
- [Sinh] — гиперболический синус
- [Sin] – синус заданного угла
- [X2] – возведение в квадрат (формула x^2)
- [n!] — вычисляет факториал введенного значения — произведение n последовательных чисел, начиная с единицы до самого введенного числа, например 4!=1*2*3*4, то есть 24
- [Dms] – переводит из десятичного вида в формат в градусы, минуты, секунды.
- [Cosh] — гиперболический косинус
- [Cos] – косинус угла
- [xy] – возведение икса в степ. игрик (формула x^y)
- [y√x] – извлечение корня в степени y из икс
- [Pi] – число Пи, выдает значение Pi для расчетов
- [tanh] — гиперболический тангенс
- [tan] – тангенс угла онлайн, tg
- [X3] — помогает возвести в степень 3, в куб (формула x^3)
- [3√x] — извлечь корень кубический
- [F – E] — переключает ввод чисел в экспоненциальном представлении и обратно
- [Exp] — позволяет вводить данные в экспоненциальном представлении.
- [Mod] — позволяет нам вычислить остаток от деления одного числа на другое
- [Log] – рассчитывает десятичный логарифм
- [10^x] – возведение десяти в произвольную степень
- [1/X] — подсчитывает обратную величину
- [e^x] – Возведение числа Эйлера в степень
- [Frac] – отсекает целую часть, оставляет дробную
- [sinh-1] – обратный гиперболический синус
- [sin-1] – арксинус или обратный синус, arcsin или 1/sin
- [deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее
- [cosh-1] — обратный гиперболический косинус
- [cos-1] – аркосинус или обрат. косинус arccos или 1/cos
- [2*Pi] – рассчитывает число Пи, помноженное на два
- [tanh-1] – обрат. гиперболический тангенс
- [tan-1] – арктангенс или обратный тангенс, arctg
Как пользоваться MR MC M+ M- MS
Как пользоваться инженерным калькулятором – на примерах
Как возвести в степень
Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:
12 [xy] 3 [=]
12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]
Ответ: 1728
Как найти корень кубический
Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:
729 [3√x] [=]
729, [3√x] «кубический корень из икс», равенства [=]
Как найти корень на калькуляторе
Задача: Найти квадратный корень 36.
Решение: всё просто, нажимаем так:
36 [y√x] 2 [=]
36, [y√x] «корень из икса, в степени игрик», нужную нам степень 2, равно [=]
Ответ: 6
При помощи этой функции вы можете найти корень в любой степени, не только квадратный.
Как возвести в квадрат
Для возведения в квадрат онлайн вычислительная программа содержит две функции:
[xy] «икс в степени игрик», [X2] «икс в квадрате»
Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».
Например: 45 [xy] 6 [=]
Ответ: сорок пять в шестой степ. равно 8303765625
Тригонометрический калькулятор онлайн — примеры
Как произвести онлайн расчет синусов и косинусов, тангенсов
Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.
1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.
Для включения того или иного режима измерения нажмите нужную кнопку:
где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.
В качестве самого простого примера найдем синус 90 градусов. Нажмите:
90 [sin] [=]
Ответ: единица
Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:
60 [cos] [=]
Решение: 0,5
Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.
Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.
Преобразование с кнопкой Dms и Deg на калькуляторе
[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».
Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:
35,140453 [Deg] [=] 35,23459166666666666666
Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453
Десятичный логарифм онлайн
Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:
1 [log] [=]
Получается 0 в итоге. Для подсчета lg100 нажмем так:
100 [log] [=]
Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.
Так же вычисляется натуральный логарифм, но кнопкой [ln].
Как пользоваться памятью на калькуляторе
Существующие кнопки памяти: M+, M-, MR, MS, MC.
Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.
MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.
Пример. Внесем сто сорок пять в память программы:
145 [MR]
После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:
[MR]
На экране отобразится снова 145.
Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.
Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.
Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!
Инженерный калькулятор онлайн
Современный уклад жизни требует постоянной динамики. Производя расчеты на калькуляторе, мы заметно экономим свое время, не рискуем в чем-то ошибиться и получаем точный результат. Благодаря изобретению данного устройства, многие люди забыли что такое недостачи и погрешности в расчетах. Однако калькулятор калькулятору рознь, и если примитивные вычислительные функции можно сделать на математической модели, то сложнейшие расчеты возможно совершить только при помощи инженерной. Отныне приобретать данное чудо современной техники не нужно – достаточно обратиться за помощью к нашему инженерному калькулятору онлайн! Программа работает без дополнительной установки – достаточно зайти на электронную страницу и начать действовать.
Функции инженерного калькулятора онлайн
Калькулятор математического типа поможет вам совершить только примитивные расчеты. С его помощью можно сделать то, чему нас учили в начальных классах средней школы:
- сложение;
- вычитание;
- деление;
- умножение;
- вычитание процентов;
- возведение числа в степень;
- нахождение корня квадратного.
Инженерный калькулятор онлайн включает в себя все эти и дополнительные функции, которые необходимы для проведения сложных расчетов. Теперь вам не придется тратить дополнительные деньги на покупку этого устройства, ведь сделать вычисления можно на нашем сайте.
Помимо вышеперечисленных, наш универсальный калькулятор поможет вам выполнить такие расчеты:
Нахождение:
- синуса угла;
- тангенса;
- косинуса;
- котангенса;
- арксинуса;
- арктангенса;
- арккосинуса;
- арккотангенса.
Интерфейс инженерного калькулятора онлайн
Выполнить все вышеперечисленные расчеты достаточно просто. Наш инженерный калькулятор онлайн обладает понятным интерфейсом, а потому работать с ним весьма удобно. По своему виду он полностью имитирует настоящий калькулятор, поэтому долгого изучения функций вам не потребуется. Несмотря на это мы прилагаем подробную инструкцию и описание каждой клавиши.
Пользоваться нашей программой выгодно еще и потому, что расчеты производятся моментально – вам не нужно обновлять страницу сайта, ведь калькулятор работает во флеш-режиме. Ежедневно нашей программой пользуется огромное количество людей. Среди них ученики высших заведений, преподаватели, архитекторы-проектировщики, ученые и другие люди, заинтересованные в точности расчетов. Инженерный калькулятор онлайн не требует скачивания и установки дополнительных плагинов, а потому вы можете начать пользоваться им прямо сейчас!
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
- Сложение, вычитание, деление и умножение дробей.
- Расчет дробей с подробнейшим решением.
- Расчет дробей со степенями, скобками и буквами.
- Сокращение дробей.
- Поддержка до трех дробей онлайн.
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:
- Вносить целую часть дроби в числитель для смешанных дробей.
- Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
- Расчет дробей со степенями — степенью может быть только число.
- Расчет дробей с буквами — любые анг. буквы или символы.
- Сокращение дробей — только для дробей без букв.
Основные символы:
- * символ звездочки интерпретируется как умножение.
- / слеш интерпретируется как деление.
- + и — интерпретируются как сложение и вычитание.
- ^ символ интерпретируется как степень.
- ( ) символы интерпретируются как открывающаяся и закрывающаяся скобки.
Подробности:
- Между двумя буквами необязательно ставить знак умножения (если они умножаются). Пример вместо x*x можно написать xx.
- После знака степени ^ должно стоять число степени. Если оно отрицательно необходимо заключить его в скобки. Пример x^2+1 или x^(-2) +1.
- При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.
- При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
Калькулятор степеней
Онлайн калькулятор помогает возвести число в любую степень и найти корень любой степени из числа (квадратные, кубические корни, а также корни других степеней). Основанием степени могут быть любые числа, показателем степени также может быть любые числа, в том числе и отрицательные.
Возведение в степень — это арифметическая операция повторяющегося умножения. Если требуется перемножить число n-ное количество раз, то достаточно возвести его в n-ную степень.
Как возвести число в степень?
Чтобы возвести число X в степень n, достаточно всего лишь умножить число X его само на себя n раз.
Что такое отрицательная степень числа?
Отрицательная степень числа — это единица, поделённая на число в степени n, то есть a-n = 1/ an.
Основные действия со степенями
- Число 34— это 3×3×3×3, где перемножаются четыре одинаковых множителя. Если умножить 34 на 32, то мы получим (3×3×3×3)×(3×3), то есть 36. Отсюда первое правило возведения в степень: при умножении чисел, возведенных в степень, их показатели суммируются. Математически: xm * xn = x(m+n).
- Число 35разделить на 32, это означает следующее: (3×3×3×3×3)/(3×3), то есть останется (3×3×3) или 33.Отсюда второе правило действий со степенями: при делении чисел, возведенных в степень, их показатели вычитаются. Математически: xm / xn = x(m-n).
- Число 54возвести в куб, то есть в третью степень. Для этого нужно вычислить выражение (5×5×5×5)×(5×5×5×5)×(5×5×5×5). Получилось 12 сомножителей. Отсюда третье правило: при возведении в n-ную степень числа в степени m, показатели перемножаются. Математически: (xm)n = x(m×n).
- Любое положительное число в степени 0 всегда равно единице. Математически: x0= 1. Например можно представить 70 как 74 разделить на 74 или 74/74=1.
- При возведении числа в отрицательную степень необходимо единицу разделить на число в положительной степени. Например, если разделить 82на 84, то получим 8-2 или (8×8)/(8×8×8×8). Если сократить восьмерки в числителе и знаменателе, то получим 1/(8×8). Математически: x-m = 1 / xm.
- Если в качестве степени выступает дробное число, то знаменатель дробного показателя означает извлечение корня, а числитель — возведение в степень. Математически: x(m/n)есть корень n-ной степени из xm. Например, 4(2/3) означает, что нужно найти корень третьей степени от числа 42.
Навигация по записям
Калькулятор онлайн
Этот удобный калькулятор производит элементарные арифметичиеские операции (сложение, вычитание, умножение, деление) с положительными и отрицательными целыми числами и дробями. Доступны действия с процентами, возведение в степень, вычисление корня из числа, а также логарифм.
Для всех возможных действий приведены примеры. Если вам нужны дополнительные функции, то откройте инженерный калькулятор.
Арифметические операции
Сложение
Сложение объединяет два числа (слагаемые) в одно (сумму чисел).
2 + 3 =
Вычитание
Вычитание является обратной операцией к сложению. Вычитание находит разность между двумя числами (уменьшаемое число минус вычитаемое).
3 − 2 =
Умножение
Умножение объединяет два числа в одно число – произведение чисел. Два исходных числа называются множимым и множителем.
2 × 3 =
Деление
Деление является обратной операцией к умножению. Деление находит частное от двух чисел (делимого, поделенного на делитель). Деление любого числа на 0 не определено.
4 ÷ 2 =
Действия с дробями
Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.
1 ÷ 2 + 1 ÷ 4 =
Десятичные дроби
Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.
. 2 + . 0 3 =
Нахождение обратного числа
Обратное число к x, обозначаемое 1/x или x-1, представляет собой число, которое при умножении на x дает единицу.
2 1/x =
Действия с процентами
Процент — сотая часть (обозначается знаком %), используется для обозначения доли чего-либо по отношению к целому.
Нахождение процента от числа
40 × 5 % =
Увеличение (уменьшение) числа на процент
40 + 5 % =
Возведение в степень
Возведение в степень — математическая операция, записанная как xy, включающая два числа: основание x и показатель степени (или степень) y. Когда y — положительное целое число, возведение в степень соответствует многократному умножению основания на себя: то есть, xy — произведение умножения y оснований.
2 xy 4 =
Возведение числа в квадрат
Выражение x2 называется «квадратом x» или «x в квадрате», потому что площадь квадрата с длиной стороны x равна x×x или x2.
2 x2 =
Возведение числа в куб
Выражение x3 называется «кубом x» или «x в кубе», потому что объем куба с длиной стороны x равен x×x×x или x3.
2 x3 =
Возведение в степень числа 10
Возведение в степень с основанием 10 используется для обозначения больших или малых чисел. Например, 299792458 м/с (скорость света в вакууме в метрах в секунду) можно записать как 2,99792458 × 108 м/с, а затем округлить до 2,998 × 108 м/с.
4 10x =
Мнимая единица
Мнимая единица i определяется только тем свойством, что её квадрат равен −1.
i x2 =
Корень из числа
В математике y-ый корень числа x, где y обычно является положительным целым числом, представляет собой число z, которое при возведении в степень y дает x, где y — степень корня.
16 y√x 4 =
Квадратный корень
Квадратный корень числа x — это число z, которое в квадрате становится x.
9 √x =
Кубический корень
Кубический корень числа x — это число z, куб которого является x.
8 3√x =
Вычисление логарифма
Логарифм заданного числа x является показателем степени, в которую должно быть возведено другое фиксированное число (основание) y, чтобы получить это число x.
log 8 , 2 =
Десятичный логарифм
Десятичным логарифмом является логарифм с основанием 10.
log 100 =
Натуральный логарифм
Натуральный логарифм числа — это его логарифм по основанию число е.
log 3 , e =
Обычный инженерный калькулятор онлайн. ¼ + ½ = ¾.
Обычный калькулятор
Обычный калькулятор позволяет выполнять простые операции на калькуляторе, такие как сложение, вычитание, умножение и деление.
Вы можете воспользоваться быстрым математическим калькулятором
Инженерный калькулятор позволяет выполнять более сложные операции на калькуляторе, такие как синус, косинус, арксинус, арккосинус, тангенс, арктангенс, возведение в степень, экспонента, логарифм, проценты, также есть операции в памяти калькулятора онлайн. Можно набирать прямо с клавиатуры, для этого предварительно кликните на область с калькулятором.
Выполняет простые операции с числами, а также более сложные как
математический калькулятор онлайн.
¼ + ½ = ¾.
Здесь представлены два калькулятора:
- Первый вычисляет как обычный
- Второй вычисляет как инженерный
Правила относятся к калькулятору, который вычисляет на сервере
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- e
- e число, которое примерно равно 2.7
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - pi
- Число — «Пи», которое примерно равно 3.14
- sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- Действительные числа
- вводить в виде 7.5, не 7,5
- 2*x
- — умножение
- 3/x
- — деление
- x^3
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
Зачем нужен этот он-лайн калькулятор?
 Калькулятор онлайн — чем отличается от обычного калькулятора? Во-первых, обычный калькулятор не удобно носить с собой, во-вторых — уже сейчас интернет есть практически везде, по-этому не составить проблем зайти на наш сайт и воспользоваться онлайн калькулятором.
Калькулятор онлайн — чем отличается от обычного калькулятора? Во-первых, обычный калькулятор не удобно носить с собой, во-вторых — уже сейчас интернет есть практически везде, по-этому не составить проблем зайти на наш сайт и воспользоваться онлайн калькулятором.
Калькулятор он-лайн — чем он отличается от java-калькулятора, а также от других калькуляторов для операционных систем? — опять же — мобильность. Если Вы находитесь за другим компьютером, то не надо снова устанавливать
Итак, пользуйтесь этим онлайн!
: Wolfram | Alpha
О решении уравнений
Говорят, что значение является корнем многочлена if.
Самый большой показатель появления в называется степенью. Если есть степень, то хорошо известно, что есть корни, если учесть множественность. Чтобы понять, что подразумевается под множественностью, возьмем, к примеру,. Считается, что этот многочлен имеет два корня, оба равны 3.
Каждый узнает о «факторной теореме», обычно во втором курсе по алгебре, как способ найти все корни, являющиеся рациональными числами.Также изучается, как найти корни всех квадратичных полиномов, используя квадратные корни (возникающие из дискриминанта), когда это необходимо. Существуют более продвинутые формулы для выражения корней кубических и квартичных многочленов, а также ряд численных методов для аппроксимации корней произвольных многочленов. Они используют методы из сложного анализа, а также сложные численные алгоритмы, и, действительно, это область постоянных исследований и разработок.
Системы линейных уравнений часто решаются с использованием исключения Гаусса или связанных методов.Это также обычно встречается в средних или математических программах колледжа. Более сложные методы необходимы, чтобы найти корни одновременных систем нелинейных уравнений. Аналогичные замечания справедливы для работы с системами неравенств: линейный случай может быть обработан с использованием методов, описанных в курсах по линейной алгебре, тогда как для полиномиальных систем более высокой степени обычно требуются более сложные вычислительные инструменты.
Как Wolfram | Alpha решает уравнения
Для решения уравнений Wolfram | Alpha называет функции Wolfram Language Solve и Reduce, которые содержат широкий спектр методов для всех видов алгебры, от базовых линейных и квадратных уравнений до многомерных нелинейных систем.В некоторых случаях используются методы линейной алгебры, такие как исключение Гаусса, с оптимизацией для увеличения скорости и надежности. Другие операции основаны на теоремах и алгоритмах из теории чисел, абстрактной алгебры и других расширенных областей для вычисления результатов. Эти методы тщательно разработаны и выбраны, чтобы позволить Wolfram | Alpha решать самые разнообразные задачи, а также минимизировать время вычислений.
Хотя такие методы полезны для прямых решений, для системы также важно понять, как человек решит ту же проблему.В результате, Wolfram | Alpha также имеет отдельные алгоритмы, чтобы шаг за шагом показывать алгебраические операции, используя классические методы, которые людям легко распознать и следовать. Это включает исключение, замену, квадратную формулу, правило Крамера и многое другое.
Введите полиномиальное неравенство вместе с переменной, для которой нужно найти решение, и нажмите кнопку «Решить».
В главе 2 мы установили правила для решения уравнений с использованием чисел арифметики. Теперь, когда мы изучили операции со знаковыми числами, мы будем использовать те же правила для решения уравнений с отрицательными числами. Мы также изучим методы решения и построения графиков неравенств, имеющих одно неизвестное.
РЕШЕНИЕ УРАВНЕНИЙ С УЧЕТОМ НОМЕРОВ
ЦЕЛЕЙ
По завершении этого раздела вы сможете решать уравнения, включающие числа со знаком.
Пример 1 Решите для х и проверьте: х + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 с каждой стороны уравнения, получая
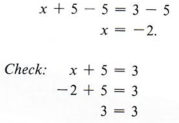
Пример 2 Решите для х и проверьте: — 3х = 12
Решение
Разделив каждую сторону на -3, получим
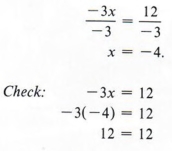
| Всегда проверяйте в исходном уравнении. |

| Другой способ решения уравнения 3x — 4 = 7x + 8 — сначала вычесть 3x с обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x , Теперь разделите обе стороны на 4, получив — 3 = x или x = — 3. |

| Сначала удалите скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЦЕЛЕЙ
По завершении этого раздела вы сможете:
- Определите буквальное уравнение.
- Применение ранее изученных правил для решения буквальных уравнений.
Уравнение, имеющее более одной буквы, иногда называется буквальным уравнением . Иногда необходимо решить такое уравнение для одной буквы с точки зрения других. Пошаговая процедура, обсуждаемая и используемая в главе 2, остается в силе даже после удаления любых символов группировки.
Пример 1 Решить для c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите скобки.
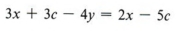
В этот момент мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения. Таким образом, мы получаем
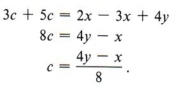

| Помните, что abx — это то же самое, что и 1abx. Разделим на коэффициент х, который в данном случае равен ab. |

| Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2.V с обеих сторон. Сравните решение с полученным в примере. |
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значение ответа) и получить
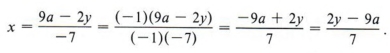
Преимущество этого последнего выражения перед первым состоит в том, что в ответе не так много отрицательных признаков.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
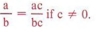
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и так далее.
Пример 4 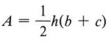 — формула для площади трапеции. Решить для ц.
— формула для площади трапеции. Решить для ц.
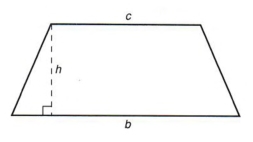

| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает просто стереть их. Мы должны умножить каждый член в скобках на коэффициент, предшествующий скобкам. Изменение формы ответа не является необходимым, но вы должны быть в состоянии распознать, когда у вас есть правильный ответ, даже если форма не совпадает. |
Пример 5 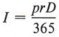 — это формула, дающая проценты (I), заработанные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда сумма процентов, основная сумма и количество дней все известны.
— это формула, дающая проценты (I), заработанные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда сумма процентов, основная сумма и количество дней все известны.
Решение
Задача требует решения 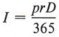 по р.
по р.
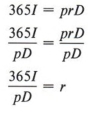
Обратите внимание, что в этом примере r было оставлено справа и, таким образом, вычисление было проще. Мы можем переписать ответ другим способом, если пожелаем.
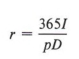
графическое неравенство
ЦЕЛЕЙ
По завершении этого раздела вы сможете:
- Используйте символ неравенства для представления взаимных позиций двух чисел в числовой строке.
- График неравенства на числовой линии.
Мы уже обсуждали набор из рациональных чисел как те, которые могут быть выражены как отношение двух целых чисел. Существует также набор чисел, называемых иррациональных чисел, , которые не могут быть выражены как отношение целых чисел. В этот набор входят такие номера, как 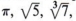 и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительными числами .
и так далее. Множество, состоящее из рациональных и иррациональных чисел, называется действительными числами .
Учитывая любые два действительных числа a и b, всегда можно утверждать, что 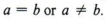 Много раз нас интересует только, равны ли два числа, но существуют ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Много раз нас интересует только, равны ли два числа, но существуют ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Символы представляют собой символов неравенства или отношения порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание, что мы заявили, что мы обычно читаем
а

| Какое положительное число можно добавить к 2, чтобы получить 5? |

Проще говоря, это определение гласит, что a меньше b, если мы должны добавить что-то к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой строке, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой строке. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3

| Мы могли бы также написать 6> 3. |
Пример 2 — 4

| Мы могли бы также написать 0> — 4. |
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.

Пример 4 — 6

Математическое утверждение х
| Видите ли вы, почему найти наибольшее число меньше 3 невозможно? |
На самом деле, назвать число х, которое является наибольшим числом меньше 3, является невыполнимой задачей. Однако это может быть указано в числовой строке.Чтобы сделать это, нам нужен символ для обозначения значения утверждения, такой как х
Символы (и), используемые в числовой строке, указывают, что конечная точка не включена в набор.
Пример 5 График х
Решение

Обратите внимание, что на графике есть стрелка, указывающая, что линия продолжается без конца влево.
| Этот график представляет каждое действительное число меньше 3. |
Пример 6 График x> 4 на числовой линии.
Решение

| Этот график представляет каждое действительное число больше 4. |
Пример 7 График x> -5 на числовой линии.
Решение

| Этот график представляет каждое действительное число больше -5. |
Пример 8 Построить числовой линейный график, показывающий, что x> — 1 и x
Решение

Утверждение х> — 1 и х
| Этот график представляет все действительные числа в диапазоне от — 1 до 5. |
Пример 9 График — 3
Решение

Если мы хотим включить конечную точку в набор, мы используем другой символ, 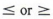 :. Мы читаем эти символы как «равно или меньше» и «равно или больше чем».
:. Мы читаем эти символы как «равно или меньше» и «равно или больше чем».
Пример 10 х>; 4 обозначает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и], используемые в числовой строке, указывают, что конечная точка включена в набор.
| Вы найдете, что использование скобок и скобок соответствует их использованию в будущих курсах математики. |

| Этот график представляет число 1 и все действительные числа больше 1. |
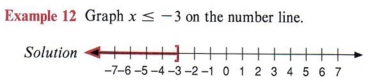
| Этот график представляет число 1 и все действительные числа, меньшие или равные — 3. |
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.
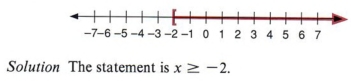
Пример 14 Напишите алгебраическое утверждение для следующего графика.
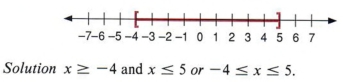
| Этот график представляет все действительные числа от -4 до 5 , включая -4 и 5. |
Пример 15 Напишите алгебраическое утверждение для следующего графика.
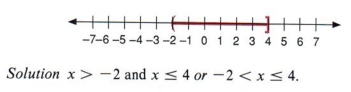
| Этот график включает 4, но , а не -2. |
Пример 16 График 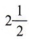 на числовой линии.
на числовой линии.
Решение
Этот пример представляет небольшую проблему. Как мы можем указать 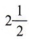 в числовой строке? Если мы оценим суть, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка
в числовой строке? Если мы оценим суть, то другой человек может неправильно понять утверждение. Не могли бы вы сказать, представляет ли точка 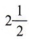 или
или 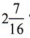 ? Поскольку целью графика является уточнение, всегда обозначает конечную точку.
? Поскольку целью графика является уточнение, всегда обозначает конечную точку.
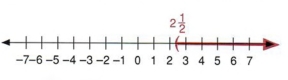
| График используется для передачи заявления. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, чтобы быть точными. |
РЕШЕНИЕ НЕРАВЕНСТВ
ЦЕЛЕЙ
По завершении этого раздела вы сможете решить неравенства, связанные с одним неизвестным.
Решения для неравенств обычно включают те же основные правила, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Первое правило, однако, аналогично тому, которое используется при решении уравнений.
Если к каждой стороне неравенства добавлено одинаковое количество, результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств.
Пример 3 Решить для х: х + 6
Решение
Если мы добавим -6 к каждой стороне, мы получим
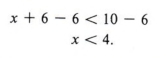
Графики этого решения на числовой линии, у нас есть


| Обратите внимание, что процедура такая же, как при решении уравнений. |
Теперь мы будем использовать правило сложения, чтобы проиллюстрировать важную концепцию, касающуюся умножения или деления неравенств.
Предположим, что x> a.
Теперь добавьте -x в обе стороны по правилу сложения.
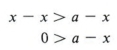
| Помните, что добавление одинакового количества к обеим сторонам неравенства не меняет его направление. |
Теперь добавьте -a в обе стороны.
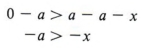
Последнее утверждение, — a> -x, может быть переписано как — x <-a.Поэтому мы можем сказать: «Если х> а, то — х
Если неравенство умножается или делится на отрицательное число , равное , результаты будут в неравном порядке в , противоположном порядку .
| Например: если 5> 3, то -5 |
Пример 5 Решите для х и построите график решения: -2x> 6
Решение
Чтобы получить x с левой стороны, мы должны разделить каждый член на — 2. Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
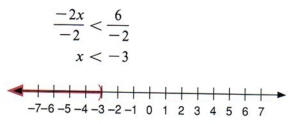
| Обратите внимание, что как только мы делим на отрицательную величину, мы должны изменить направление неравенства. |
Обратите особое внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменить направление символа неравенства. Это единственная разница между решением уравнений и решением неравенств.
| Когда мы умножаем или делим на положительное число, без изменений.Когда мы умножаем или делим на отрицательное число, направление неравенства меняется. Будьте осторожны — это источник многих ошибок. |
После того как мы удалили скобки и в выражении есть только отдельные термины, процедура поиска решения почти такая же, как в главе 2.
Давайте теперь рассмотрим пошаговый метод из главы 2 и отметим разницу при решении неравенств.
Первые Исключить дроби, умножив все члены на наименьший общий знаменатель из всех дробей.(Без изменений, когда мы умножаем на положительное число.)
Секунда Упростим, скомбинировав одинаковые термины на каждой стороне неравенства. (Без изменений)
Третий Сложите или вычтите количества, чтобы получить неизвестное на одной стороне и числа на другой. (Без изменений)
Четвертый Разделите каждый член неравенства на коэффициент неизвестного. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным.(Это важное различие между уравнениями и неравенствами.)
| Единственная возможная разница заключается в последнем шаге. |

| Что нужно сделать при делении на отрицательное число? |

| Не забудьте обозначить конечную точку. |
РЕЗЮМЕ
Ключевые слова
- Буквальное уравнение — это уравнение, включающее более одной буквы.
- Символы представляют собой символов неравенства или отношений порядка .
- a a находится слева от b на линии вещественных чисел.
- Двойные символы
 : указывают, что конечные точки включены в набор решений .
: указывают, что конечные точки включены в набор решений .
процедур
- Чтобы решить буквальное уравнение для одной буквы в терминах других, выполните те же шаги, что и в главе 2.
- Для решения неравенства используйте следующие шаги:
Шаг 1 Удалите дроби, умножив все члены на наименьший общий знаменатель из всех дробей.
Шаг 2 Упростите, объединив одинаковые термины с каждой стороны неравенства.
Шаг 3 Сложите или вычтите количества, чтобы получить неизвестное на одной стороне и числа на другой.
Шаг 4 Разделите каждый член неравенства на коэффициент неизвестного. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет обратным.
Шаг 5 Проверьте свой ответ.
Решение полиномов
Полином выглядит так:| пример полинома |
Решение
«Решение» означает поиск «корней» …
… «корень» (или «ноль») — это когда функция равна нулю :
Между корнями функция либо полностью вверху,
, либо полностью внизу, ось х
Пример: -2 и 2 — корни функции x 2 — 4
Давайте проверим:
- , когда х = -2, то х 2 — 4 = (-2) 2 — 4 = 4 — 4 = 0
- , когда х = 2, то х 2 — 4 = 2 2 — 4 = 4 — 4 = 0
Как мы решаем полиномы? Это зависит от Степень !
Степень
Первый шаг в решении полинома — найти его степень.
Степень полинома с одной переменной …
… самый большой показатель этой переменной.
Когда мы знаем степень, мы также можем дать многочлену имя:
| Степень | Имя | Пример | График выглядит как |
|---|---|---|---|
| 0 | Константа | 7 | |
| 1 | Линейный | 4x + 3 | |
| 2 | Quadratic | x 2 −3x + 2 | |
| 3 | куб. | 2x 3 −5x 2 | |
| 4 | Quartic | x 4 + 3x − 2 | .. |
| и т. Д. | … | … | … |
Как решить
Итак, теперь мы знаем степень, как решить?
- Узнайте, как решать линейные полиномы (степень 1), используя простую алгебру.
- Прочитайте, как решить квадратичные полиномы (степень 2) с небольшой работой,
- Может быть трудно решить кубические (степень 3) и квартические (степень 4) уравнения,
- И, кроме того, может быть невозможным , чтобы решать полиномы напрямую.
Так что же нам делать с теми, кого мы не можем решить? Попробуйте решить их по частям!
Если мы найдем один корень, мы можем затем уменьшить многочлен на один градус (пример позже), и этого может быть достаточно, чтобы решить весь многочлен.
Вот несколько основных способов найти корни.
1. Базовая алгебра
Мы можем решить с помощью базовой алгебры:
Пример: 2x + 1
2x + 1 является линейным полиномом:
График у = 2х + 1 — прямая линия
Это линейно, поэтому есть один корень.
Используйте алгебру для решения:
«Корень» — это когда у равен нулю: 2x + 1 = 0
Вычтите 1 с обеих сторон: 2x = −1
Разделите обе стороны на 2: x = −1/2
И это решение:
x = -1/2
(Вы также можете увидеть это на графике)
Мы также можем решать квадратичные полиномы, используя базовую алгебру (см. Эту страницу для объяснения).
2. По опыту или просто догадкам.
Всегда полезно посмотреть, сможем ли мы сделать простой факторинг:
Пример: x 3 + 2x 2 −x
Это кубический … но подождите … мы можем выделить «х»:
x 3 + 2x 2 −x = x (x 2 + 2x − 1)
Теперь у нас есть один корень (x = 0), и то, что осталось, является квадратичным, что мы можем точно решить.
Или мы можем заметить знакомую картину:Пример: х 3 −8
Опять это куб… но это также «разница двух кубов»:
x 3 −8 = x 3 -2 3
И так мы можем превратить это в это:
x 3 −8 = (x − 2) (x 2 + 2x + 4)
Существует корень при х = 2, потому что:
(2−2) (2 2 + 2 × 2 + 4) = (0) (2 2 + 2 × 2 + 4)
И тогда мы можем решить квадратичный х 2 + 2х + 4, и мы сделали
3.Графически.
Постройте график полинома и посмотрите, где он пересекает ось X.
| Мы можем ввести многочлен в График функций, а затем увеличить масштаб, чтобы найти, где он пересекает ось X. |
Графики — это хороший способ найти приблизительные ответы, и нам также может повезти и найти точный ответ.
Осторожно: прежде чем прыгать и составлять график, вы должны действительно знать, как ведут себя полиномы, чтобы найти все возможные ответы!
Факторы
Полезно знать: Когда множитель вычисляется так:
f (x) = (x-a) (x-b) (x-c)…
Тогда a, b, c и т. Д. — корней !
Итак, линейные факторы и корни связаны, знайте одно, а мы можем найти другое.
(подробнее см. В «Теореме фактора»).
Пример: f (x) = (x 3 + 2x 2 ) (x − 3)
Мы видим «(x − 3)», и это означает, что 3 является корнем (или «нулем») функции.
Конечно?
Хорошо, давайте поместим «3» вместо x:
f (x) = (3 3 + 2 · 3 2 ) (3–3)
f (3) = (3 3 + 2 · 3 2 ) (0)
Да! f (3) = 0, поэтому 3 является корнем.
Как проверить
Нашли рут? Проверьте это!
Просто поставьте корень вместо «х»: многочлен должен быть равен нулю.
Пример: 2x 3 −x 2 −7x + 2
Полином 3-й степени, и его может быть трудно решить. Итак, давайте подготовим это сначала:
Кривая пересекает ось X в трех точках, и одна из них может быть в 2 .Мы можем легко проверить, просто поставив «2» вместо «x»:
f (2) = 2 (2) 3 — (2) 2 −7 (2) +2
= 16−4−14 + 2
= 0
Да! f (2) = 0 , поэтому мы нашли корень!
Как насчет того, где он пересекает около -1,8 :
f (-1,8) = 2 (-1,8) 3 — (- 1,8) 2 −7 (-1,8) +2
= −11,664-3,24 + 12,6 + 2
= −0,304
Нет, он не равен нулю, поэтому -1.8 не будет рутом (но может быть близко!)
Но мы сделали , открыли один корень, и мы можем использовать его для упрощения полинома, например
Пример (продолжение): 2x 3 −x 2 −7x + 2
Итак, f (2) = 0 — это корень … это означает, что мы также знаем фактор:
(x − 2) должно быть в 2 раза больше 3 −x 2 −7x + 2
Затем разделите 2x 3 −x 2 −7x + 2 на (x − 2), используя полиномиальное длинное деление, чтобы найти:
2x 3 −x 2 −7x + 2 = (x − 2) (2x 2 + 3x − 1)
Итак, теперь мы можем решить 2x 2 + 3x − 1 как квадратное уравнение, и мы будем знать все корни.
Этот последний пример показал, насколько полезно найти только один корень. Помните:
Если мы найдем один корень, мы можем затем уменьшить многочлен на один градус , и этого может быть достаточно, чтобы решить весь многочлен.
Как далеко влево или вправо
При попытке найти корни, , как далеко и налево должны пройти от нуля?
Можно сказать, , и есть несколько вычислений, но все это простая арифметика.Читайте Bounds on Zeros для всех деталей.
Мы все получили корни?
Существует простой способ узнать , сколько существует корней . Фундаментальная теорема алгебры гласит:
Многочлен степени n …
…
имеет n корней (нулей)
, но нам может понадобиться использовать комплексные числа
Итак: число корней = степень полинома .
Пример: 2x 3 + 3x — 6
Степень 3 (потому что самый большой показатель степени 3), и так:
Есть 3 корней.
Но некоторые корни могут быть сложными
Да, действительно, некоторые корни могут быть комплексными числами (то есть иметь мнимую часть) и поэтому не будут отображаться как простое «пересечение оси X» на графике.
Но есть интересный факт:
Сложные корни всегда идут парами !
Итак, мы получаем , а не сложных корней, или , 2 сложных корней, или , 4 и т. Д … Никогда нечетное число.
Что означает, что мы автоматически знаем это:
| Степень | корни | Возможные комбинации |
|---|---|---|
| 1 | 1 | 1 Real Root |
| 2 | 2 | 2 настоящих корня, или 2 сложных корня |
| 3 | 3 | 3 реальных корня, или 1 реальных и 2 сложных корня |
| 4 | 4 | 4 реальных корня, или 2 реальных и 2 сложных корня, или 4 сложных корня |
| и т. Д. | и т. Д.! |
положительных или отрицательных корней?
Существует также особый способ узнать, сколько корней составляет отрицательных или положительных , называемых Правилами Знаков, о которых вы можете прочитать.
Кратность корня
Иногда фактор появляется более одного раза. Мы называем это Кратность :
Кратность — это то, как часто определенный корень является частью факторинга.
Пример: f (x) = (x − 5) 3 (x + 7) (x − 1) 2
Это можно записать более длинным способом, например:
f (x) = (x − 5) (x − 5) (x − 5) (x + 7) (x − 1) (x − 1)
(x − 5) используется 3 раза, поэтому корень «5» имеет кратность 3 , аналогично (x + 7) появляется один раз, а (x − 1) появляется дважды.Итак:
- корень +5 имеет кратность 3
- корень −7 имеет кратность 1 («простой» корень)
- корень +1 имеет кратность 2
В: Почему это полезно?
A: Это заставляет график вести себя особым образом!
Когда мы видим такой фактор, как (x-r) n , «n» — это кратность, а
- четная кратность просто касается оси в точке «r» (и в остальном остается на одной стороне оси X)
- с нечетной кратностью пересекает ось в точке «r» (изменяется с одной стороны оси X на другую)
Мы можем видеть это на этом графике:
Пример: f (x) = (x − 2) 2 (x − 4) 3
(x − 2) имеет четной кратности , поэтому он просто касается оси в x = 2
(x − 4) имеет нечетную кратность , поэтому она пересекает ось при x = 4
Как это:
Резюме
- Мы можем напрямую решать полиномы степени 1 (линейный) и 2 (квадратичный)
- Для степени 3 и выше, графики могут быть полезны
- Также полезно:
- Знать, как далеко могут быть левые или правые корни
- Знать, сколько корней (столько же, сколько его степень)
- Оцените, сколько может быть сложным, положительным или отрицательным
- Кратность — это то, как часто определенный корень является частью факторинга.
Purplemath
При решении тригонометрических уравнений используются запоминаемые углы отсчета и тригонометрические тождества, а также многие изученные вами алгебры. Будьте готовы к , подумайте , чтобы решить эти уравнения.
В дальнейшем предполагается, что у вас есть хорошее представление о значениях отношения триггеров в первом квадранте, о том, как работает единичная окружность, взаимосвязи между радианами и градусами и как выглядят кривые различных функций триггера, в минимум на первый период.Если вы не уверены в себе, вернитесь и сначала просмотрите эти темы.
MathHelp.com

Решить грех ( x ) + 2 = 3 за интервал 0 ° & leq; x <360 °
Как и в случае с линейными уравнениями, я сначала выделю член, содержащий переменную:
грех ( x ) + 2 = 3
грех ( х ) = 1
Теперь я буду использовать опорные углы, которые я запомнил, чтобы получить мой окончательный ответ.
Примечание: инструкции дали мне интервал в градусах, что означает, что я должен дать свой ответ в градусах. Да, синус в первом периоде принимает значение 1 при π / 2 радианах, но это не тот тип угловой меры, который они хотят, и использование этого в качестве моего ответа, вероятно, приведет к тому, что я по крайней мере потеряю несколько моментов по этому вопросу.
Итак, в градусах мой ответ:
Solve tan 2 (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 °
Есть соблазн быстро вспомнить, что тангенс 60 ° включает в себя квадратный корень из 3 и дать ответ, но это уравнение фактически не имеет решения.Я вижу это, когда замедляюсь и делаю шаги. Мой первый шаг:
Может ли любой квадрат (касательной или любой другой функции триггера) быть отрицательным ? Нет! Итак, мой ответ:
Решить на интервале 0 ° & leq; x <360 °
Левая часть этого уравнения учитывает.Я привык делать простой факторинг, как это:
2 y 2 + 3 y = 0
у (2 у + 3) = 0
… а потом решаем каждый из факторов. То же самое работает здесь. Чтобы решить уравнение, которое они мне дали, я начну с факторинга:
Я сделал алгебру; то есть я выполнил факторинг, а затем решил каждое из двух уравнений, связанных с факторами.Это создало два уравнения триггера. Так что теперь я могу сделать триггер; а именно, решение этих двух полученных тригонометрических уравнений, используя то, что я запомнил о косинусной волне. Из первого уравнения я получаю:
Из второго уравнения я получаю:
Соединяя эти два набора решений, я получаю решение для исходного уравнения как:
x = 30 °, 90 °, 270 ° и 330 °
Решить грех 2 (θ) — грех (θ) = 2 на интервале 0 & leq; θ <2π
Во-первых, я перейду все на одну сторону знака «равно»:
грех 2 (θ) — грех (θ) — 2 = 0
Это уравнение является «квадратичным по синусу»; то есть форма уравнения является форматом квадратного уравнения:
В случае уравнения, которое они хотят, чтобы я решил, X = sin (θ), a = 1, b = –1 и c = –2.
Поскольку это квадратичная форма, я могу применить некоторые методы квадратного уравнения. В случае этого уравнения я могу вычислить квадратичную величину:
грех 2 (θ) — грех (θ) — 2 = 0
(sin (θ) — 2) (sin (θ) + 1) = 0
Первый фактор дает мне соответствующее уравнение триггера:
Но синус никогда не больше 1, поэтому это уравнение не разрешимо; у него нет решения.
Другой фактор дает мне второе связанное уравнение триггера:
грех (θ) + 1 = 0
sin (θ) = –1
θ = (3/2) π
Тогда мой ответ:
(Если вы используете решения только для степеней в своем классе, приведенное выше значение решения равно «270 °».)
Решить cos 2 (α) + cos (α) = sin 2 (α) на интервале 0 ° & leq; x <360 °
Я могу использовать тождество триггера для получения квадратичного в косинусе:
cos 2 (α) + cos (α) = sin 2 (α)
cos 2 (α) + cos (α) = 1 — cos 2 (α)
2cos 2 (α) + cos (α) — 1 = 0
(2cos (α) — 1) (cos (α) + 1) = 0
cos (α) = 1/2, cos (α) = –1
Первое уравнение триггера, cos (α) = 1/2, дает мне α = 60 ° и α = 300 °.Второе уравнение дает мне α = 180 °. Итак, мое полное решение:
Решить sin (β) = sin (2β) на интервале 0 ° & leq; β <360 °
Я могу использовать двойное угловое тождество с правой стороны, переставить и упростить; тогда я буду фактор:
sin (β) = 2sin (β) cos (β)
sin (β) — 2sin (β) cos (β) = 0
sin (β) (1 — 2cos (β)) = 0
sin (β) = 0, cos (β) = 1/2
Синусоида (из первого уравнения триггера) равна нулю при 0 °, 180 ° и 360 °.Но в исходном упражнении 360 ° не включено, поэтому это последнее значение решения не учитывается, в данном конкретном случае.
Косинус (из второго уравнения триггера) равен 1/2 при 60 °, и, следовательно, также при 360 ° — 60 ° = 300 °. Итак, полное решение:
β = 0 °, 60 °, 180 °, 300 °
Решить грех ( x ) + cos ( x ) = 1 на интервале 0 ° & leq; x <360 °
Хм… Я действительно ничего не вижу здесь. Было бы неплохо, если бы одно из этих триггеров было в квадрате …
Ну, почему бы мне не выровнять обе стороны и посмотреть, что получится?
(грех ( x ) + cos ( x )) 2 = (1) 2
sin 2 ( x ) + 2sin ( x ) cos ( x ) + cos 2 ( x ) = 1
[sin 2 ( x + cos 2 ( x )] + 2sin ( x ) cos ( x ) = 1
1 + 2sin ( x ) cos ( x ) = 1
2sin ( x ) cos ( x ) = 0
sin ( x ) cos ( x ) = 0
Ха; пойди разберись: я в квадрате и получил то, с чем я мог бы работать .Ницца!
Из последней строки выше, либо синус равен нулю, либо косинус равен нулю, поэтому мое решение выглядит так:
x = 0 °, 90 °, 180 °, 270 °
Однако (и это важно!) Я пришел в квадрат, чтобы получить это решение, а возведение в квадрат — это «необратимый» процесс.
(Почему? Если вы что-то возводите в квадрат, вы не можете просто получить квадратный корень, чтобы вернуться к тому, с чего начали, потому что квадрат мог где-то изменить знак.)
Итак, чтобы быть уверенным в моих результатах, мне нужно проверить свои ответы в исходном уравнении , чтобы убедиться, что я случайно не создал решения, которые на самом деле не учитываются. Подключаю обратно, вижу:
sin (0 °) + cos (0 °) = 0 + 1 = 1
… так что решение « x = 0 °» работает
sin (90 °) + cos (90 °) = 1 + 0 = 1
..так что решение « x = 90 °» тоже работает
sin (180 °) + cos (180 °) = 0 + (–1) = –1
… о, хорошо, поэтому « x = 180 °» НЕ работает
sin (270 °) + cos (270 °) = (–1) + 0 = –1
… так что « x = 270 °» не работает, либо
Хорошо, что я проверил свои решения, потому что два из них на самом деле не работают.Они были созданы в процессе возведения в квадрат.
Мое фактическое решение :
Примечание. Выше я мог остановиться на этой строке:
… и использовал тождество двойного угла для синуса, наоборот, вместо деления на 2 в строке, следующей за последней, в моих вычислениях. Ответ был бы таким же, но мне нужно было бы учесть интервал решения:
2sin ( x ) cos ( x ) = sin (2 x ) = 0
Тогда 2 x = 0 °, 180 °, 360 °, 540 ° и т. Д., И деление 2 на x даст мне x = 0 °, 90 °, 180 °, 270 °, это почти то же решение, что и раньше.После выполнения необходимой проверки (из-за возведения в квадрат) и отбрасывания посторонних решений мой окончательный ответ был бы таким же, как и ранее.
Квадратный трюк в последнем примере не часто встречается, но если ничего не работает, возможно, стоит попробовать. Имейте это в виду для следующего теста.
URL: https: // www.purplemath.com/modules/solvtrig.htm
,
Leave A Comment