Равнозамедленное движение формула – Равнозамедленное движение Википедия

Равнозамедленное движение Википедия

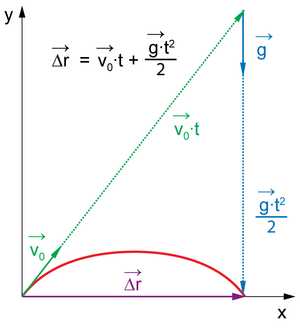Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение a→{\displaystyle {\vec {a}}} постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

v→(t)=v→0+a→t{\displaystyle {\vec {v}}(t)={\vec {v}}_{0}+{\vec {a}}t},

где v→0{\displaystyle {\vec {v}}_{0}} — начальная скорость тела, t{\displaystyle t} — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом α{\displaystyle \alpha } к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением a→=g→{\displaystyle {\vec {a}}={\vec {g}}}, направленным вертикально вниз.

Частным случаем равноускоренного движения является

равнозамедленное, когда векторы v→{\displaystyle {\vec {v}}} и a→{\displaystyle {\vec {a}}} противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для α=900{\displaystyle \alpha =90^{0}} при подъёме).

Характер равноускоренного движения

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения a→{\displaystyle {\vec {a}}} и начальной скорости v→0{\displaystyle {\vec {v}}_{0}}. С учётом того, что v→=dr→/dt{\displaystyle {\vec {v}}={\rm {d}}{\vec {r}}/{\rm {d}}t} (здесь r→{\displaystyle {\vec {r}}} — радиус-вектор), траектория описывается выражением

r→(t)=r→0+v→0t+a→t22{\displaystyle {\vec {r}}(t)={\vec {r}}_{0}+{\vec {v}}_{0}t+{\frac {{\vec {a}}t^{2}}{2}}}.

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со- или противо- направленности) векторов a→{\displaystyle {\vec {a}}} и v→0{\displaystyle {\vec {v}}_{0}} превращается в отрезок прямой.

Для каждой из координат, скажем y{\displaystyle y}, могут быть записаны аналогичные по структуре выражения:

y(t)=y0+v0yt+ayt22{\displaystyle y(t)=y_{0}+v_{0y}t+{\frac {a_{y}t^{2}}{2}}},

где ay{\displaystyle a_{y}} — составляющая ускорения вдоль оси y{\displaystyle y}, а r→0=x0i→+y0j→+z0k→{\displaystyle {\vec {r}}_{0}=x_{0}{\vec {i}}+y_{0}{\vec {j}}+z_{0}{\vec {k}}} — радиус-вектор материальной точки в момент t=0{\displaystyle t=0} (i→{\displaystyle {\vec {i}}}, j→{\displaystyle {\vec {j}}}, k→{\displaystyle {\vec {k}}} — орты).

В примере с камнем x0=y0=z0=0{\displaystyle x_{0}=y_{0}=z_{0}=0}, компоненты ускорения ax=az=0{\displaystyle a_{x}=a_{z}=0}, ay=−g{\displaystyle a_{y}=-g}, начальной скорости vx0=v0cos⁡α{\displaystyle v_{x0}=v_{0}\cos \alpha }, vy0=v0sin⁡α{\displaystyle v_{y0}=v_{0}\sin \alpha }, vz0=0{\displaystyle v_{z0}=0}, при этом x(t)=v0xt{\displaystyle x(t)=v_{0x}t}, а значит, y=tg⁡α⋅x−g/2v02cos2⁡α⋅x2{\displaystyle y=\operatorname {tg} \alpha \cdot x-g/2v_{0}^{2}\cos ^{2}\alpha \cdot x^{2}}.

Перемещение и скорость

В случае равноускоренного движения любая из компонент скорости, например vx{\displaystyle v_{x}}, зависит от времени линейно:

vx=v0x+axt{\displaystyle v_{x}=v_{0x}+a_{x}t}.

При этом имеет место следующая связь между перемещением (Δx=x−x0{\displaystyle \Delta x=x-x_{0}}) вдоль координаты x{\displaystyle x} и скоростью вдоль той же координаты:

Δx=vx2−v0x22ax{\displaystyle \Delta x={\frac {v_{x}^{2}-v_{0x}^{2}}{2a_{x}}}}.

Отсюда можно получить выражение для x{\displaystyle x}-составляющей конечной скорости тела при известных x{\displaystyle x}-составляющих начальной скорости и ускорения:

vx=±v0x2+2axΔx{\displaystyle v_{x}=\pm {\sqrt {v_{0x}^{2}+2a_{x}\Delta x}}}.

Если ax=0{\displaystyle a_{x}=0}, то vx=vox{\displaystyle v_{x}=v_{ox}}, а Δx=v0xt{\displaystyle \Delta x=v_{0x}t}.

Выражения для смещений Δy{\displaystyle \Delta y}, Δz{\displaystyle \Delta z} и компонент скорости вдоль координат y{\displaystyle y} и z{\displaystyle z} принимают точно такой же вид, как для Δx{\displaystyle \Delta x} и vx{\displaystyle v_{x}}, но символ x{\displaystyle x} всюду заменяется на y{\displaystyle y} или z{\displaystyle z}.

Суммарно, по теореме Пифагора, перемещение составит

|Δr→|=(Δx)2+(Δy)2+(Δz)2{\displaystyle |\Delta {\vec {r}}|={\sqrt {(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}}}},

а модуль конечной скорости находится как

|v→|=vx2+vy2+vz2{\displaystyle |{\vec {v}}|={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}}.

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени t{\displaystyle t}, модуль скорости тела |v→|{\displaystyle |{\vec {v}}|} превысит величину скорости света в вакууме c{\displaystyle c}, что исключается теорией относительности.

Теорема о кинетической энергии точки

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

maxΔx=mvx22−mv0x22{\displaystyle ma_{x}\Delta x={\frac {mv_{x}^{2}}{2}}-{\frac {mv_{0x}^{2}}{2}}}.

Записав аналогичные соотношения для координат y{\displaystyle y} и z{\displaystyle z} и просуммировав все три равенства, получим соотношение:

F→⋅Δr→=mv22−mv022{\displaystyle {\vec {F}}\cdot \Delta {\vec {r}}={\frac {mv^{2}}{2}}-{\frac {mv_{0}^{2}}{2}}}.

Слева стоит работа постоянной равнодействующей силы F→{\displaystyle {\vec {F}}}, а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Криволинейное равноускоренное движение

Криволинейным равноускоренным (равнопеременным) называется движение по любой кривой, при котором составляющая ускорения, параллельная скорости, является постоянной. Такое движение не подпадает под определение равноускоренного, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата S{\displaystyle S}, часто называемая путём. Эта координата соответствует длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

ΔS=v2−v022aτ{\displaystyle \Delta S={\frac {v^{2}-v_{0}^{2}}{2a_{\tau }}}},

где aτ{\displaystyle a_{\tau }} — тангенциальное ускорение, которое «отвечает» за изменение модуля скорости тела. Для скорости получаем:

v=±v02+2aτΔS{\displaystyle v=\pm {\sqrt {v_{0}^{2}+2a_{\tau }\Delta S}}}.

При aτ=0{\displaystyle a_{\tau }=0} имеем движение с постоянной по модулю скоростью.

См. также

Равноускоренное движение

Примечания

wikiredia.ru

Равнопеременное прямолинейное движение | Физика для всех

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

vcp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости

на ось ОХ:

vx = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

 

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

vx = v0x ± axt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени

– это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v0
bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

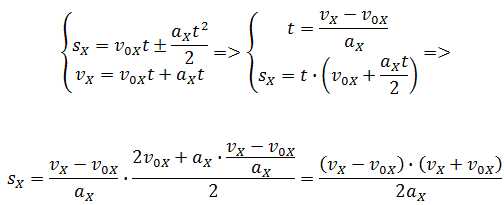
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

av-mag.ru

Типы движений | Учеба-Легко.РФ — крупнейший портал по учебе

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

vcp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

vx = v,	то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x0

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x0 - vt

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение

– это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

 

 

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

vcp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

= ‘

Проекция вектора скорости на ось ОХ:

vx = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

= ‘ = » Учитывая, что ₀ – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:

Отсюда формула скорости равнопеременного движения в любой момент времени:

= ₀ + t Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

vx = v0x ± axt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v0
bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

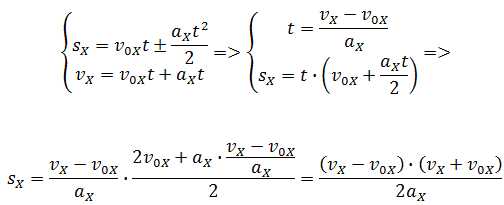
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

uclg.ru

Репетитор-онлайн — подготовка к ЦТ

Пример 2. Материальная точка движется вдоль оси Ox. Проекция ее скорости с течением времени меняется по закону v = 9,0 − 1,5t, где скорость задана в метрах в секунду, время — в секундах. Определить путь, пройденный материальной точкой за интервал времени от 4,0 с до 7,0 с.

Решение. При равнопеременном движении зависимость проекции скорости от времени имеет вид:

v_x = v_0x + a_xt,

где v_0x = 9,0 м/с — проекция начальной скорости; a_x = −1,5 м/с² — проекция ускорения на указанную координатную ось.

Запишем уравнение движения материальной точки:

x(t)=x0+v0xt+axt22=x0+9,0t−0,75t2,

где x0 — начальная координата точки.

Точка остановки, вычисленная по формуле

τост=v0a=9,01,5=6,0 c,

попадает в интервал времени, указанный в условии задачи.

В интервале времени от t1 = 4,0 c до τост = 6,0 с точка движется равнозамедленно. Следовательно, пройденный путь вычисляем по формуле

S1=|x(τост)−x(t1)|,

где

x(τост)=x0+9,0τост−0,75τост2=

=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;

x(t1)=x0+9,0t1−0,75t12=x0+9,0⋅4,0−0,75⋅(4,0)2=(x0+24) м.

Таким образом, путь S1, пройденный материальной точкой в указанном интервале времени, равен:

S1=|x(τост)−x(t1)|=|(x0+27)−(x0+24)|=3,0 м.

В интервале времени от τост = 6,0 с до t2 = 7,0 c точка движется равноускоренно. Следовательно, пройденный путь вычисляем по формуле

S1=|x(t2)−x(τост)|,

где

x(τост)=x0+9,0τост−0,75τост2=

=x0+9,0⋅6,0−0,75⋅(6,0)2=(x0+27) м;

x(t2)=x0+9,0t2−0,75t22=

=x0+9,0⋅7,0−0,75⋅(7,0)2=(x0+26,25) м.

Таким образом, путь S₂, пройденный материальной точкой в указанном интервале времени, равен:

S2=|x(t2)−x(τост)|=|(x0+26,25)−(x0+27)|=0,75 м≈0,8 м.

Суммарный путь S, пройденный материальной точкой в интервале времени от 4,0 с до 7,0 с, составляет

S=S1+S2≈3,0+0,8=3,8 м.

vedy.by

Равнопеременное движение. Ускорение. | Объединение учителей Санкт-Петербурга

Равнопеременное движение. Ускорение.
Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.
Обозначим: — вектор начальной скорости,  — изменение скорости, а Δt — промежуток времени. Пусть  Δt1= Δt2=Δt3=…, тогда по определению
Следовательно,   Т.о., это характеристика движения.
Если t0=0, то
УСКОРЕНИЕ — физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.
Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ —    м/с2.	Например, ускорение равно 5 м/с2  — это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения.
В случае не равнопеременного движения: тогда мгновенное ускорение
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.	Условие р.у.д. —.
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается.	Условие р.з.д. — .
Графики равнопеременного движения.
или  — в проекциях; или – через модули.
Линейная функция. График — прямая.
Движения, совпадающие с направлением координатной оси: равноускоренноес начальной скоростью равноускоренное без начальной скорости равнозамедленное Движения против координатной оси. равнозамедленное равноускоренное без начальной скорости равноускоренное с начальной скоростью
Перемещение при равнопеременном движении.
Площадь под графиком скорости численно равна перемещению. Следовательно, площадь трапеции численно равна перемещению.
	Решение основной задачи механики для р.у.д. :
Графики перемещения и координаты.
Функции   и   — квадратичные. График – парабола!

www.eduspb.com

Равнопеременное прямолинейное движение

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

vcp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

= ‘

Проекция вектора скорости на ось ОХ:

vx = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

 = ' = "

Учитывая, что ₀ – скорость тела в начальный момент времени (начальная скорость), – скорость тела в данный момент времени (конечная скорость), t – промежуток времени, в течение которого произошло изменение скорости, формула ускорения будет следующей:

Отсюда формула скорости равнопеременного движения в любой момент времени:

 = 0 + t

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

vx = v0x ± axt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v0
bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

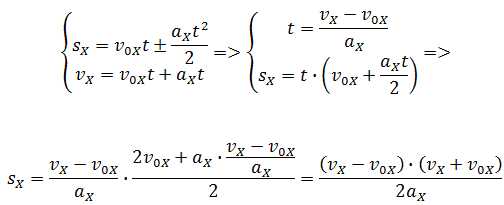
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

av-physics.narod.ru

Равнопеременное движение. Формулы. Ускорение. Конечная, начальная скорость, путь, перемещение, формулы

Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.

Траектория такого движения —  прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:

• вектор скорости тела при равнопеременном движении

 

(1)

• где
• вектор перемещения тела при равнопеременном движении

(2)

• где
  • — вектор перемещения тела

Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.

Рис. 1. Равноускоренное движение 1

Пример 1. Тело движется прямо с начальной скоростью  и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор

 направлен по оси) и ускоряется (вектор также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:

• Для уравнения (1): 
• Для уравнения (2): 

В общем случае, мы не можем предугадать направления векторов 

и , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.

www.abitur.by