Расстояние между параллельными прямыми равно 4: Расстояние между параллельными прямыми равно 4. На одной из них лежит точка C, а на другой — точки

Что ⭐ называется расстоянием между двумя параллельными прямыми

Что такое расстояние между двумя параллельными прямыми

Определение 1

Расстояние в плоскости или пространстве представляет собой величину, характеризующую удаленность объектов друг от друга.

Определение 2

Параллельными прямыми называют такие прямые в трехмерном пространстве, которые расположены в общей плоскости и не имеют точек пересечения.

Условия параллельности двух прямых:

• расположение в одной плоскости;
• отсутствие каких-либо общих точек.

Теорема о расстоянии между двумя параллельными прямыми

Теорема 

Расстояние между параллельными прямыми представляет собой перпендикулярный отрезок между этими прямыми. Данный перпендикуляр можно провести в любом месте, при этом полученные отрезки будут равны между собой.

Представим краткое доказательства записанной теоремы аналитическим способом. Для начала построим прямые, которые параллельны друг другу, но не должны скрещиваться. Назовем их l и k. Отметим произвольно пару точек на первой прямой. Пусть это будут Х и Y. Построим перпендикуляры с началом в этих точках ко второй прямой. Важно, чтобы отмеченные точки были удалены на какое-то расстояние в см или других единицах друг от друга.

 

Предположим, что перпендикуляры пересекают прямую k в точках А и В. Построим отрезок, который соединяет Х и В. Заметим, что это гипотенуза прямоугольника XYBA. Накрест друг от друга расположены углы данного четырехугольника XBA и BXY. Данные углы равны. Рассмотрим их подробнее и выявим общие элементы:

• единая сторона ХВ;
• равные длины сторон ХY и АВ;
• углы XBA и BXY равны и образованы с помощью одинаковых сторон.

В результате, можно сделать вывод о равенстве перпендикуляров АХ и BY. Это условие выполнимо при любых точках Х и Y, что можно узнать и проверить на уроках в классе или при решении самостоятельных работ. Таким образом, перпендикуляры, как на рисунке, опущенные в каком-либо месте и расположенные между двумя параллельными прямыми, обладают одинаковой величиной.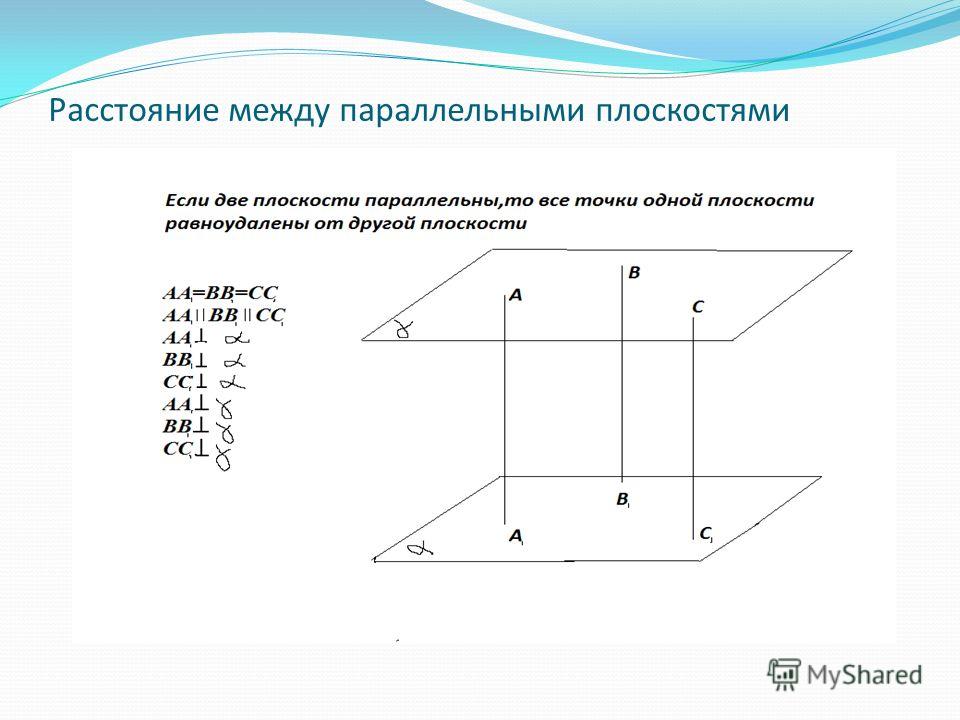 Исходя из того, что пара прямых, являющихся параллельными друг другу, образует плоскость, теорема о расстоянии между параллельными прямыми справедлива в начертательной геометрии, планиметрии и 3D-пространстве.

Формула 

Определить расстояние между параллельными прямыми, к примеру, d и k в пространстве можно таким образом:

Здесь  обозначают координаты нормального вектора прямой d. При этом l, m, n являются направляющим вектором данной прямой с координатами в виде знаменателей из канонических уравнений прямой в пространстве. Переменные  обозначают  координаты нормального вектора второй прямой.

Примеры задач с решением

Задача 1

Записаны уравнения пары прямых, которые расположены параллельно и не совпадают между собой. Уравнение для прямой d:

Уравнение для параллельной ей прямой k:

Требуется определить, чему равен перпендикуляр построенный между этими прямыми.

Решение

Запишем координаты для нормального вектора, относящегося к прямой k:

{3; -1;2}

Выполним то же самое действие в случае прямой d:

{-1;2;-4}

Запишем координаты, которыми обладает направляющий вектор для первой прямой:

{1;3;5}

Путем подстановки преобразуем формулу для поиска расстояния между параллельными прямыми. В итоге получим:

Ответ: ≈6,568.

Задача 2

Даны две параллельные прямые с условиями, аналогичными первому примеру. Запишем их. Уравнение для прямой d:

Уравнение для параллельной ей прямой k:

Нужно определить, чему равно расстояние между заданными прямыми, с помощью векторного произведения.

Решение

В данном случае пригодится формула для определения расстояния между прямыми:

Здесь  является вектором, который соединяет пару каких-то точек на рассматриваемых параллельных прямых.

Запишем, чему соответствуют нормальные вектора для первой и второй прямой:

{3; -1;2}

{-1;2;-4}

Можно заметить совпадение направляющего вектора для данных прямых. Координаты этого вектора соответствуют следующим значениям:

s = {1;3;5}

Вычислим, чему равна векторная разность между нормальными векторами, которая соответствует координатам вектора 

Далее требуется определить векторное произведение вектора  

Таким образом, можно приступить к определению длины направляющего вектора s:

Запишем окончательный ответ:

Ответ: 6,568.

Расстояние между двумя параллельными прямыми: определение и примеры нахождения

В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.

Расстояние между двумя параллельными прямыми: определение

Определение 1

Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.

Приведем иллюстрацию для наглядности:

На чертеже изображены две параллельные прямые a и b. Точка М1 принадлежит прямой a, из нее опущен перпендикуляр на прямую b. Полученный отрезок М1Н1 и есть расстояние между двумя параллельными прямыми aи b.

Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.

Теорема

Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.

Доказательство

Пусть нам заданы две параллельные прямые a и b. Зададим на прямой а

точки М1 и М2, опустим из них перпендикуляры на прямую b, обозначив их основания соответственно как Н1 и Н2. М1Н1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что |М1Н1|=|М2Н2|.

Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠M2M1h3=∠h2h3M1. Прямая М2Н2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a. Получившиеся треугольники М1Н1Н2 и М2М1Н2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М1Н2 – общая гипотенуза, ∠M2M1h3=∠h2h3M1.

Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: |М1Н1| = |М2Н2|. Теорема доказана.

Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.

Нахождение расстояния между параллельными прямыми

Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.

Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b. Необходимо определить расстояние между заданными прямыми.

Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:

— найти координаты некоторой точки М1, принадлежащей одной из заданных прямых;

— произвести вычисление расстояния от точки М1 до заданной прямой, которой эта точка не принадлежит.

Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М1 просто. При нахождении расстояния от точки М1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.

Вернемся к примеру. Пусть прямая a описывается общим уравнением Ax+By+C1=0, а прямая b – уравнением Ax+By+C2=0. Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:

M1h2=C2-C1A2+B2

Выведем эту формулу.

Используем некоторую точку М1 (x1, y1), принадлежащую прямой a. В таком случае координаты точки М1 будут удовлетворять уравнению Ax1+By1+C1=0. Таким образом, справедливым является равенство: Ax1+By1+C1=0; из него получим: Ax1+By1=-C1.

Когда С2<0, нормальное уравнение прямой b будет иметь вид:

AA2+B2x+BA2+B2y+C2A2+B2=0

При С2≥0 нормальное уравнение прямой b будет выглядеть так:

AA2+B2x+BA2+B2y-C2A2+B2=0

И тогда для случаев, когда С2<0, применима формула: M1h2=AA2+B2x1+BA2+B2y1+C2A2+B2.

А для С2≥0 искомое расстояние определяется по формуле M1h2=-AA2+B2x1-BA2+B2y1-C2A2+B2==AA2+B2x1+BA2+B2y1+C2A2+B2

Таким образом, при любом значении числа С2 длина отрезка |М1Н1| (от точки М1 до прямой b) вычисляется по формуле: M1h2=AA2+B2x1+BA2+B2y1+C2A2+B2

Выше мы получили: Ax1+By1=-C1, тогда можем преобразовать формулу: M1h2=-C1A2+B2+C2A2+B2=C2-C1A2+B2. Так мы, собственно, получили формулу, указанную  в алгоритме метода координат.

Разберем теорию на примерах.

Пример 1

Заданы две параллельные прямые y=23x-1 и x=4+3·λy=-5+2·λ. Необходимо определить расстояние между ними.

Решение

Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями.

Таким образом, получаем точку М1 (4, -5). Требуемое расстояние – это расстояние между точкой М1(4, -5) до прямой y=23x-1, произведем его вычисление.

Заданное уравнение прямой с угловым коэффициентом y=23x-1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:

y=23x-1⇔23x-y-1=0⇔2x-3y-3=0

Вычислим нормирующий множитель: 122+(-3)2=113. Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 113·2x-3y-3=113·0⇔213x-313y-313=0.

При x=4, а y=-5 вычислим искомое расстояние как модуль значения крайнего равенства:

213·4-313·-5-313=2013

Ответ: 2013.

Пример 2

В фиксированной прямоугольной системе координат Oxy заданы две параллельные прямые, определяемые уравнениями x-3=0 и x+50=y-11. Необходимо найти расстояние между заданными параллельными прямыми.

Решение

Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x+50=y-11⇔x+5=0. При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:

M1h2=C2-C1A2+B2=5-(-3)12+02=8

Ответ: 8.

Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.

Пример 3

В прямоугольной системе координат Oxyz заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x-31=y-1=z+24 и x+51=y-1-1=z-24. Необходимо найти расстояние между этими прямыми.

Решение

Из уравнения x-31=y-1=z+24 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М1(3, 0, -2). Произведем вычисление расстояния |М1Н1| от точки М1 до прямой x+51=y-1-1=z-24.

Прямая x+51=y-1-1=z-24 проходит через точку М2(-5, 1, 2). Запишем направляющий вектор прямой x+51=y-1-1=z-24 как b→ с координатами (1, -1, 4).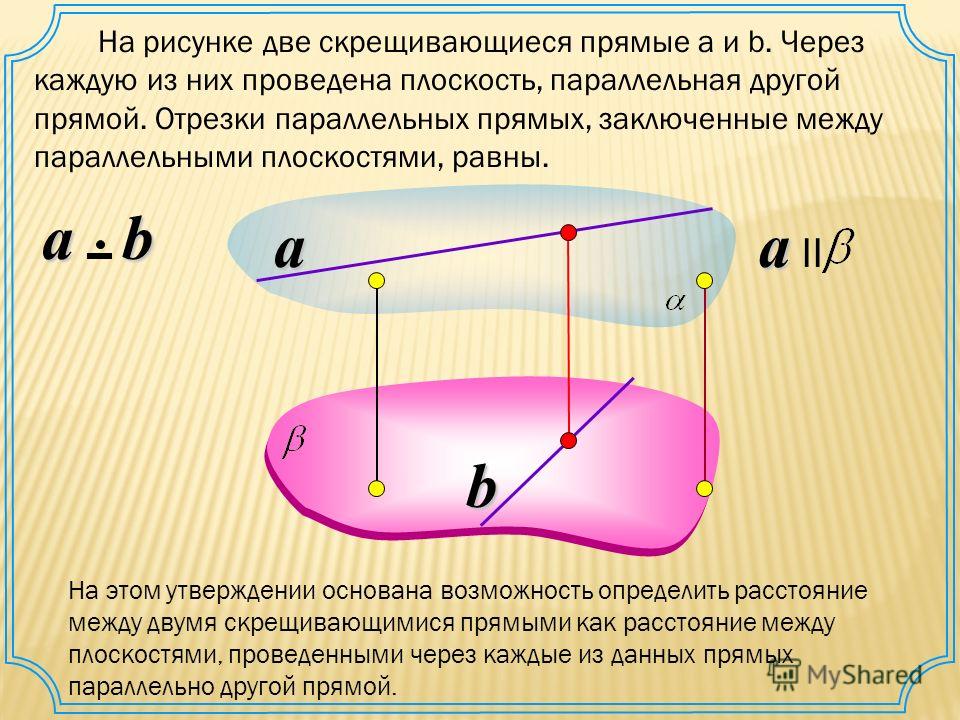 Определим координаты вектора M2M→: 

M2M1→=3-(-5, 0-1, -2-2)⇔M2M1→=8, -1, -4

Вычислим векторное произведение векторов :

b→×M2M1→=i→j→k→1-148-1-4=8·i→+36·j→+7·k→⇒b→×M2M1→=(8, 36, 7)

Применим формулу расчета расстояния от точки до прямой в пространстве:

M1h2=b→×M2M1→b→=82+362+7212+(-1)2+42=140932

Ответ: 140932.

Расстояние между двумя линиями — формула, определение, примеры

Расстояние между двумя линиями означает, насколько далеко две линии расположены друг от друга. Линия – это фигура, образованная соединением двух точек на минимальном расстоянии между ними, а оба конца линии оттянуты в бесконечность. Расстояние между двумя линиями можно рассчитать, измерив перпендикулярное расстояние между ними. Обычно мы находим расстояние между двумя параллельными прямыми.

Также для двух непересекающихся прямых, лежащих в одной плоскости, кратчайшим расстоянием между ними является расстояние, являющееся кратчайшим из всех расстояний между двумя точками, лежащими на обеих прямых.

Давайте узнаем больше о расстоянии между двумя линиями вместе с несколькими решенными примерами и практическими вопросами.

1.	Расстояние между двумя линиями
2.	шагов для расчета расстояния между двумя линиями
3.	Расстояние между двумя линиями Формула
4.	Расстояние между двумя параллельными линиями
5.	Кратчайшее расстояние между двумя наклонными линиями
6.	Часто задаваемые вопросы о расстоянии между двумя линиями

Расстояние между двумя линиями

Расстояние между двумя линиями измеряется относительно двух точек, находящихся на каждой из линий. На плоскости расстояние между двумя прямыми линиями — это минимальное расстояние между любыми двумя точками, лежащими на этих прямых. Для расстояния между двумя линиями мы часто имеем дело с разными наборами линий, такими как параллельные линии, пересекающиеся линии или наклонные линии.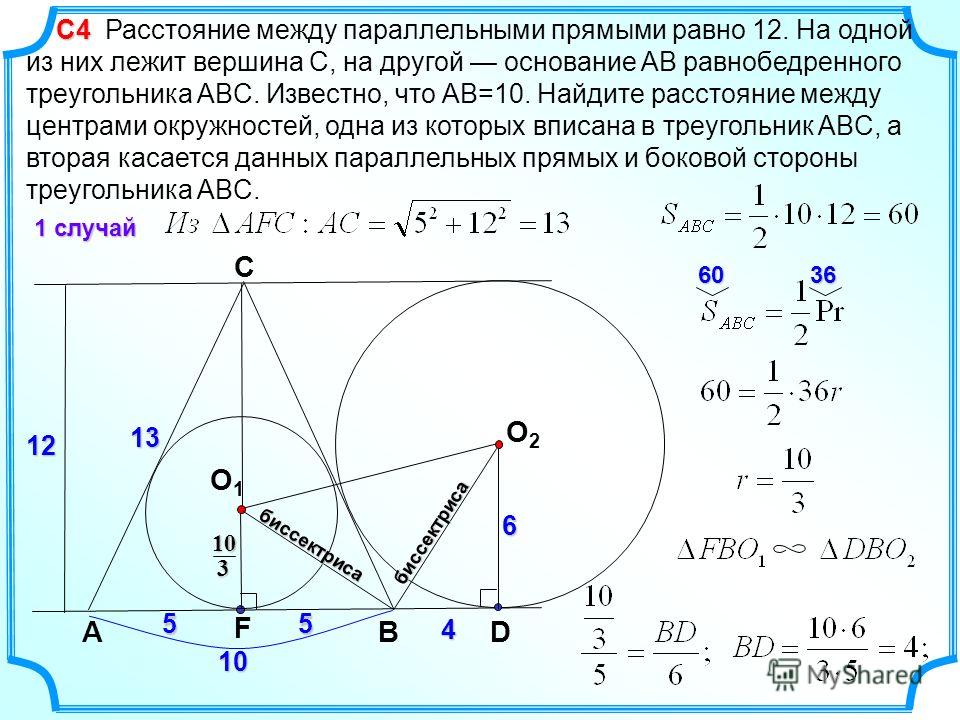 Таким образом, расстояние между двумя параллельными прямыми равно перпендикулярному расстоянию от любой точки одной прямой до другой прямой. Для двух пересекающихся прямых кратчайшее расстояние между такими прямыми в конечном итоге стремится к нулю, а расстояние между двумя скрещивающимися прямыми равно длине перпендикуляра между прямыми.

шагов для расчета расстояния между двумя линиями

• Проверить, имеют ли данные уравнения параллельных линий форму пересечения наклона (т. е. y= mx + c) или нет.
• Также, если уравнения линий заданы в форме наклон-пересечение, значение наклона должно быть общим для обеих линий.
• Теперь найдите значение точки пересечения (c ₁ и c ₂ ) и найдите значение наклона для обеих линий.
• Подставьте значения в уравнение пересечения наклона, чтобы вычислить значение y.
• В конце подставьте все значения в формулу расстояния, обсуждаемую ниже, чтобы найти расстояние между двумя линиями.

Расстояние между двумя линиями Формула

Формула для расстояния между двумя параллельными линиями приведена ниже:

Если у нас есть форма пересечения наклона двух линий как y = mx + c ₁  и y = mx + c 92}}\)

Расстояние между двумя параллельными линиями

На плоскости расстояние между двумя прямыми линиями — это минимальное расстояние между любыми двумя точками, лежащими на этих линиях. Для расстояния между двумя линиями мы часто имеем дело с разными наборами линий, такими как параллельные линии, пересекающиеся линии или наклонные линии. Таким образом, расстояние между двумя параллельными прямыми равно перпендикулярному расстоянию от любой точки одной прямой до другой прямой. Для двух пересекающихся прямых кратчайшее расстояние между такими прямыми в конечном итоге стремится к нулю, а расстояние между двумя скрещивающимися прямыми равно длине перпендикуляра между прямыми.

Давайте проверим следующие шаги, чтобы найти расстояние между двумя параллельными линиями.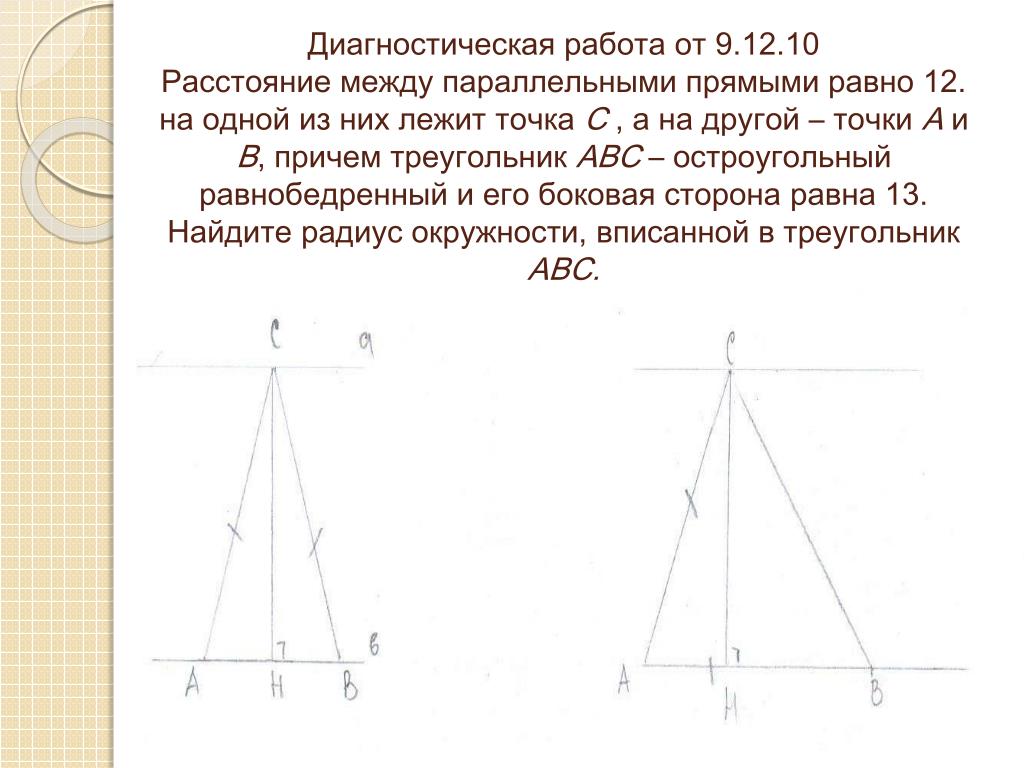

• Проверить, имеют ли данные уравнения параллельных линий форму пересечения наклона (т. е. y= mx + c) или нет.
• Кроме того, если уравнения линий заданы в форме наклон-пересечение, значение наклона должно быть одинаковым для обеих линий.
• Теперь найдите значение точки пересечения (c ₁ и c ₂ ) и значение наклона для обеих линий.
92}}\).

Кратчайшее расстояние между двумя скрещивающимися линиями

Прежде чем найти формулу для расчета кратчайшего расстояния между скрещивающимися линиями, вспомним, что такое скрещивающиеся линии. Косые линии существуют в многомерной системе, где две линии не параллельны, но никогда не пересекаются друг с другом. Это возможно только в 3-х и более измерениях.

Давайте посмотрим на формулу для расчета кратчайшего расстояния между двумя косыми линиями, уравнения которых \( \vec{r_1} = \vec{a_1} + t \vec{b_1} \) и \(\vec{r_2} = \vec{a_2} + t \vec{b_2}\), равно:

\(d = |\dfrac{ (\vec{a_2} — \vec{a_1}). {1/2}}\)

Давайте посмотрим несколько решенных примеров на расстояние между двумя линиями.

Связанные темы:

• Формула Евклидова расстояния
• Формула расстояния
• Расстояние между двумя точками
• х-перехват
• y-точка пересечения

 

Решенные примеры расстояния между двумя линиями

1. Пример 1

   Каким будет расстояние между двумя линиями 5x + 3y + 6 = 0 и 5x + 3y – 6 = 0? Найдите это, используя формулу расстояния между двумя линиями. 92}}\)

   d = 12/√34

   Ответ: Расстояние между двумя прямыми равно 12/√34.

2. Пример 2

   Определить кратчайшее расстояние между двумя скрещивающимися прямыми, если уравнения прямых имеют вид \(\vec{r}_1 = \vec{i} + \vec{j} + \lambda (2 \vec{j} {i} – \vec{j} + \vec{k} ) \) и \(\vec{r}_2 = 2 \vec{i} + \vec{j} – \vec{k}+ \mu ( 3\vec{i} – 5 \vec{j} + 2 \vec{k})\).

   Решение:

   Найти: расстояние между двумя прямыми

   Сравнение со стандартной формой уравнения прямой, т. е. \( \vec{r_1} = \vec{a_1} + t \vec{b_1} \) и \(\vec{r_2} = \vec{ a_2} + t \vec{b_2}\), получаем,

   \(a_1 = \vec{i} + \vec{j} , \ \ a_2 = 2 \vec{i} + \vec{j} – \vec{k} \\ b_1 = 2 \vec{i} — \vec{j} + \vec{k} , \ \ b_2 = 3\vec{i} — 5 \vec{j} + 2 \vec{ k} \)

   Теперь, подставив значения в формулу для расчета расстояния между двумя скрещивающимися прямыми, получим:

   \(d = | [(2 \vec{i} – \vec{j} + \ vec{k}) \times (3\vec{i} – 5 \vec{j} + 2 \vec{k} )] .(\vec{i} – \vec{k}) | / | (2 \ vec{i} – \vec{j} + \vec{k}) \times (3 \vec{i} – 5 \vec{j} + 2 \vec{k}) |\)

   При решении получаем:

   = | 3 – 0 + 7 | / (59) ^1/2

   = 10 / (59) ^1/2 = 10/7,68

   = 1,30 ед.

   Ответ: Кратчайшее расстояние между двумя линиями равно 1,30 единицы

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath. 92}}\).

Здесь

• c ₁ константа линии l ₁  
• c ₂ константа для линии l ₂

Что произойдет, если две линии параллельны?

Если две линии параллельны, расстояние между ними никогда не изменится. Для двух параллельных линий наклон обеих линий будет одинаковым, но y-пересечение каждой линии будет разным. Кратчайшее расстояние между двумя линиями можно рассчитать, если у нас есть уравнение двух линий.

Какое расстояние между двумя параллельными линиями?

Расстояние между двумя параллельными прямыми является постоянным расстоянием, которое не увеличивается и не уменьшается. Расстояние между двумя параллельными прямыми можно вычислить из заданных уравнений двух прямых.

Как найти расстояние между двумя параллельными линиями?

Расстояние между двумя параллельными линиями можно рассчитать по уравнениям прямой. Расстояние между двумя параллельными прямыми уравнениями y = mx + c 92}\). Эта формула также известна как формула расстояния.

Откуда вы знаете, что две линии параллельны?

Чтобы узнать, параллельны две линии или нет, мы можем проверить наклон двух линий. Если наклон двух прямых равен, то эти две прямые параллельны. Чтобы узнать наклон, мы преобразуем данное уравнение линии в форму пересечения наклона и сравниваем два уравнения, чтобы найти значение наклона линий.

Параллельные линии не означают решения?

Поскольку свойство параллельных прямых состоит в том, что они никогда не пересекаются друг с другом, кроме как на бесконечности, они не могут иметь никаких решений. Решений параллельных прямых не существует, поэтому известно, что параллельные прямые не имеют решений. А уравнения параллельных прямых известны как несовместимая система уравнений.

Что такое параллельные линии? Приведите 2 примера.

Параллельные линии — это линии с одинаковым наклоном. Расстояние между двумя линиями никогда не изменится. Вот несколько примеров параллельных прямых: 5x + 3y + 6 = 0 и 5x + 3y — 6 = 0 — параллельные прямые, y = 5x + 5 и y = 5x — 7 — параллельные прямые. Мы можем подтвердить, что наклон параллельных линий, приведенных здесь, одинаков. т. е. m1 = m2 = 5,

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по параллельным линиям

4.38: Расстояние между параллельными линиями

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  4973

Длина перпендикулярного отрезка между параллельными линиями.

Все вертикальные линии имеют вид \(x=a\), где \(a\) — точка пересечения \(x\). Чтобы найти расстояние между двумя вертикальными линиями, посчитайте квадраты между двумя линиями. Вы можете использовать этот метод и для горизонтальных линий. Все горизонтальные линии имеют вид \(y=b\), где \(b\) — точка пересечения \(y\).

В общем случае кратчайшее расстояние между двумя параллельными прямыми равно длине перпендикулярного отрезка между ними. Между двумя параллельными прямыми бесконечно много перпендикулярных отрезков, но все они будут одинаковой длины.

Рисунок \(\PageIndex{1}\)

Помните, что расстояния всегда положительны!

Пример \(\PageIndex{1}\)

Найти расстояние между \(x=3\) и \(x=-5\).

Рисунок \(\PageIndex{2}\)

Решение

Две строки разделены \(3 – (-5)\) единицами или 8 единицами.

Пример \(\PageIndex{2}\)

Найти расстояние между \(x=-5\) и \(x=-10\).

Решение

Две линии находятся на расстоянии \(-5 – (-10)\) единиц или 5 единиц друг от друга.

Пример \(\PageIndex{3}\)

Найти расстояние между \(y=5\) и \(y=-8\).

Рисунок \(\PageIndex{3}\)

Решение

Две строки разделены \(5 – (-8)\) единицами или 13 единицами.

Пример \(\PageIndex{4}\)

Найти расстояние между \(y=x+6\) и \(y=x−2\).

Рисунок \(\PageIndex{4}\)

Решение

Шаг 1 : Найдите перпендикулярный уклон.

\(m=1\), поэтому \(m_{\perp} =-1\).

Шаг 2 : Найдите точку пересечения по оси Y верхней строки, \(y=x+6\).

Пересечение равно \((0, 6)\).

Шаг 3 : Используйте наклон и считайте 1 вниз и 1 вправо, пока не нажмете \(y=x−2\).

Всегда подниматься/бегать на одинаковую величину для \(m=1\) или \(m=-1\) .

Рисунок \(\PageIndex{5}\)

Шаг 4 : Используйте эти две точки в формуле расстояния , чтобы определить расстояние между линиями. 92} \\ &=\sqrt{16+16} \\ &=\sqrt{32}=5,66\: единицы\конец{выравнивание*}\)

Пример \(\PageIndex{5}\)

Найти расстояние между \(y=-x−1\) и \(y=-x−3\).

Рисунок \(\PageIndex{6}\)

Решение

Шаг 1. Найдите перпендикулярный уклон.

\(m=-1\), поэтому \(m_{\perp} =1\).

Шаг 2: Найдите точку пересечения по оси Y верхней строки, \(y=-x−1\).

Пересечение равно \((0, -1)\).

Шаг 3: Используйте наклон и сосчитайте от 1 до 92} \\ &=\sqrt{1+1} \\ &=\sqrt{2}=1,41\: единицы \end{align*}\)

Обзор

Используйте каждый график ниже, чтобы определить, насколько далеко друг от друга находится каждая пара параллельных линий.

1. Рисунок \(\PageIndex{8}\)
2. Рисунок \(\PageIndex{9}\)
3. Рисунок \(\PageIndex{10}\)
4. Рисунок \(\PageIndex{11}\)

Определите кратчайшее расстояние между каждой парой параллельных прямых. Округлите ответ до сотых.

5. \(х=5\),\(х=1\)
6. \(у=-6\),\(у=4\)
7. \(у=3\),\(у=15\)
8. \(х=-10\),\(х=-1\)
9. \(х=8\),\(х=0\)
10. \(у=7\),\(у=-12\)

Найдите расстояние между заданными параллельными прямыми.

11. \(у=х-3\),\(у=х+11\)
12. \(у=-х+4\), \(у=-х\)
13. \(у=-х-5\), \(у=-х+1\)
14. \(у=х+12\), \(у=х-6\)

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 3.11. 9{\circ}\) угол. Произведение наклонов двух перпендикулярных прямых равно -1.

Дополнительные ресурсы

Интерактивный элемент

Видео: Нахождение расстояния между параллельными линиями. Принципы — основы

Задания: Расстояние между параллельными линиями Вопросы для обсуждения

Учебные пособия: Линии в Co ордината Плоскость

Практика: Расстояние между Параллельные линии

Реальный мир: переворачивание

---

Эта страница под названием 4.