Как найти радиус описанной около треугольника abc окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, описанной около произвольного (любого), прямоугольного или равностороннего треугольника. Также разберем примеры решения задач для закрепления представленного теоретического материала.
Формулы вычисления радиуса описанной окружности
Произвольный треугольник
Радиус окружности, описанной вокруг любого треугольника, рассчитывается по формуле:
где a, b, c – стороны треугольника, S – его площадь.
Прямоугольный треугольник
Радиус окружности, описанной около прямоугольного треугольника, равен половине его гипотенузы или высоте, проведенной к гипотенузе.
Равносторонний треугольник
Радиус описанной около правильного треугольника окружности вычисляется по формуле:
где a – сторона треугольника.
Примеры задач
Задание 1
Дан треугольник со сторонами 4, 6 и 9 см. Найдите радиус описанной около него окружности.
Решение
Для начала нам необходимо найти площадь треугольника. Т.к. нам известны длины всех его сторон, можно применить формулу Герона:
Теперь мы можем воспользоваться первой формулой из перечисленных выше для расчета радиуса круга:
Задание 2
Дан треугольник, у которого известны две стороны из трех: 6 и 8 см. Найдите радиус описанной вокруг него окружности.
Решение
Треугольник со сторонами 6 и 8 см может быть только прямоугольным, причем известные по условиям задачи стороны являются его катетами. Таким образом, мы можем найти гипотенузу фигуры, воспользовавшись теоремой Пифагора:
Как мы знаем, радиус круга, описанного вокруг прямоугольного треугольника, равняется половине его гипотенузы, следовательно: R = 10 : 2 = 5.
Радиус описанной окружности прямоугольного треугольника
Определение и формулы описанной окружности прямоугольного треугольника
ОПРЕДЕЛЕНИЕ Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью.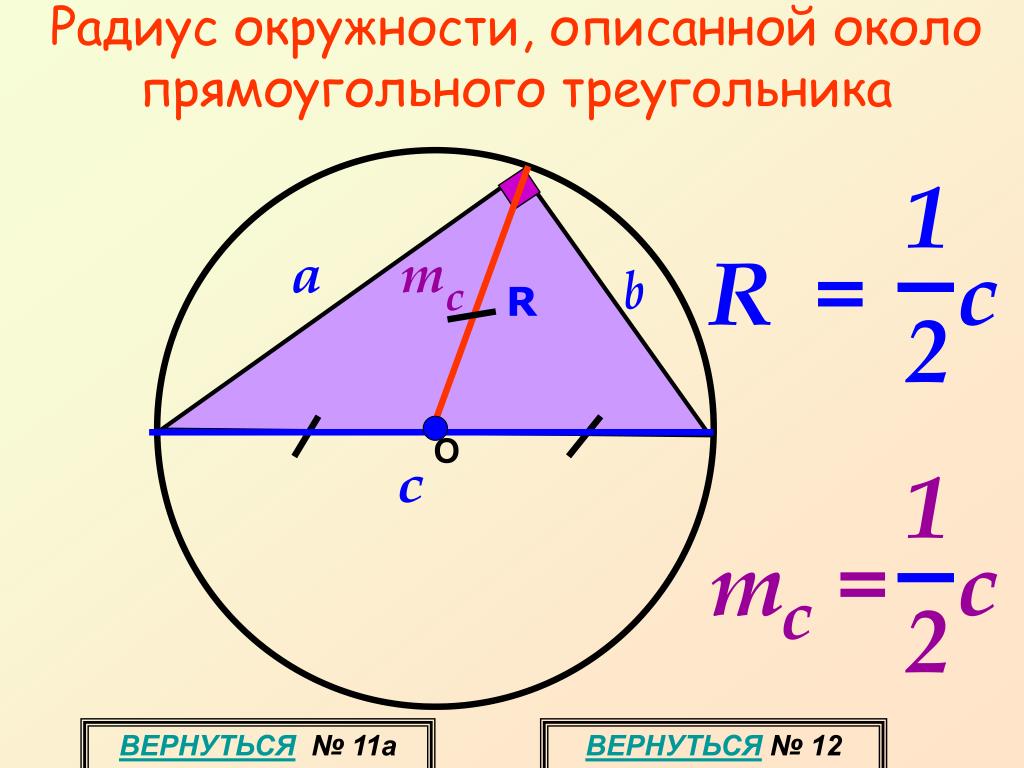
Окружность, описанная около треугольника, содержит все вершины треугольника. Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
Рассмотрим прямоугольный треугольник с гипотенузой и катетами и . Центр этой окружности лежит на середине гипотенузы, а ее радиус равен половине гипотенузы
Примеры решения задач
ПРИМЕР 1| Задание | В прямоугольном треугольнике с катетом 4 см и прилежащим острым углом найти радиус описанной окружности. |
| Решение | Рассмотрим прямоугольный треугольник (), в котором и катет см. Найдем величину угла :
В прямоугольном треугольнике катет, лежащий против угла , равен половине гипотенузы, т.е.
Теперь найдем радиус описанной окружности:
|
| Ответ | см |
| Задание | Около прямоугольного треугольника, один из катетов которого на 7 см меньше второго, описана окружность диаметра 13 см. Найти все стороны треугольника. Найти все стороны треугольника.
|
| Решение | Рассмотрим прямоугольный треугольник с (рис. 1) Пусть катет , тогда . Поскольку диаметр описанной окружности равен 13 см, а гипотенуза , то см. Запишем теорему Пифагора для рассматриваемого треугольника:
или
Решая квадратное уравнение , получаем положительный корень , т.е.
|
| Ответ | см см см |
Окружность, описанная около прямоугольного треугольника
Определение и формулы описанной окружности прямоугольного треугольника
ОПРЕДЕЛЕНИЕОкружность, описанная около треугольника, содержит все вершины треугольника.
Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
Рассмотрим прямоугольный треугольник .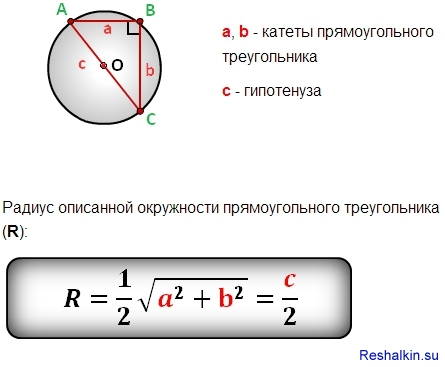
Для прямоугольного треугольника справедлива теорема синусов:
где – радиус описанной около прямоугольного треугольника окружности, – катеты этого треугольника, – его гипотенуза, – острые углы треугольника.
Примеры решения задач
ПРИМЕР 2| Задание | В прямоугольном треугольнике медиана , проведенная к гипотенузе, делит прямой угол в отношении . Найти катеты треугольника. |
| Решение | Рассмотрим прямоугольный треугольник и проведем медиану . Так как центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы, то медиана является радиусом описанной окружности и
Пусть , тогда из условия задачи следует, что и
Отсюда получаем, что . Поскольку , то – равнобедренный, а значит и
А это означает, что – равносторонний, т.е. . Тогда по теореме Пифагора
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Вписанные и описанные окружности — PDF Free Download
Вписанные и описанные окружности
Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины.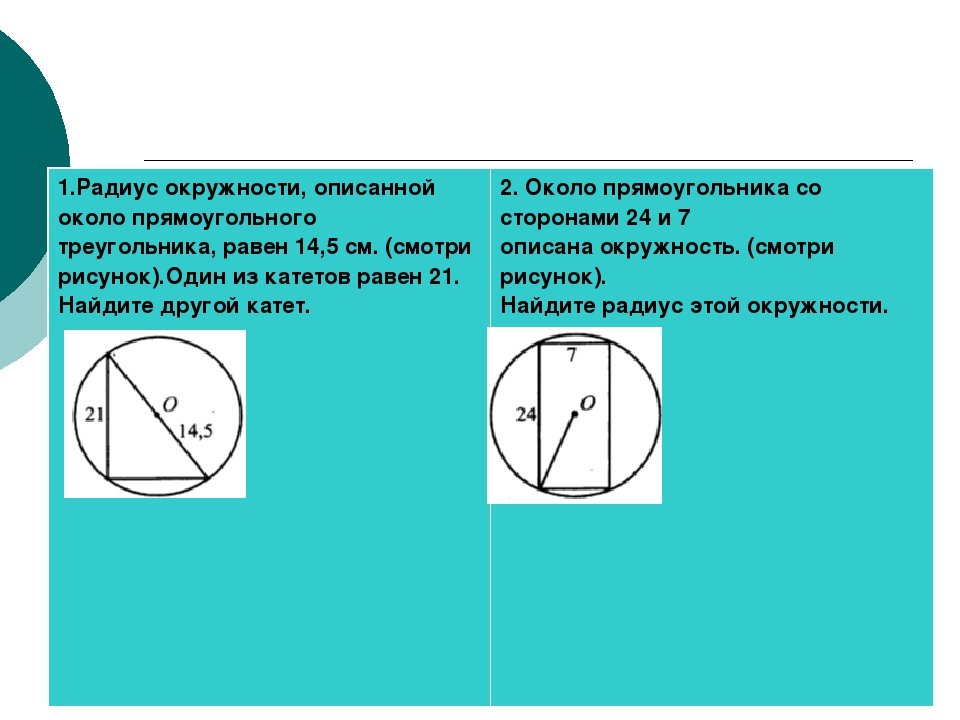 Около всякого треугольника можно описать единственную окружность.
Около всякого треугольника можно описать единственную окружность.
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
Произвольный треугольник
Произвольный треугольник В приведенных ниже формулах используются следующие обозначения: а) с длины сторон АВС лежащие против углов А В и С соответственно б) высоты медианы l l l биссектрисы в) радиус
Подробнее ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееМетод ключевых задач
Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и
ПодробнееОсновные определения, теоремы и формулы планиметрии.
Основные определения, теоремы и формулы планиметрии. Обозначения: AВС треугольник с вершинами А, B, С. а = BC, b = AС, с = АB его стороны, соответственно, медиана, биссектриса, высота, проведенные к стороне
Задание 16. Планиметрия
Задание 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ»)
ОГЭ 2015 (задание 13, модуль «ГЕОМЕТРИЯ») 169915 Какие из следующих утверждений верны? 1) Если угол равен 45, то вертикальный с ним угол равен 45. 2) Любые две прямые имеют ровно одну общую точку. 3) Через
ПодробнееПланиметрия: комбинации фигур.
А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: комбинации фигур. 27624. Периметр треугольника
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Прототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнее7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ID_7510 1/9 neznaika.pro
1 Анализ геометрических высказываний Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
ПодробнееВ 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
Задание 3, 6, 16. Планиметрия
Задание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные
ПодробнееОКРУЖНОСТИ И ЧЕТЫРЁХУГОЛЬНИКИ
ОКРУЖНОСТИ И ЧЕТЫРЁХУГОЛЬНИКИ wwwfmclssru Задача В параллелограмм можно вписать окружность Найдите ее радиус, если известно, что радиус окружности, описанной около него, равен Задача Диагонали ромба равны
ПодробнееПланиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр. 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
AC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
ПодробнееА.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
ПодробнееТема 21 «Трапеция. Многоугольники».
Тема 1 «Трапеция. Многоугольники». Трапеция четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Параллельные стороны называются основаниями трапеции. Две другие стороны называются
Параллельные стороны называются основаниями трапеции. Две другие стороны называются
tgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееВсе прототипы заданий В3
1. Прототип задания B3 ( 27543) Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 Все прототипы заданий В3 2. Прототип задания B3 ( 27544) Найдите площадь треугольника,
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Работа по геометрии для 8 класса.
Работа по геометрии для 8 класса. 1.Вид работы: промежуточная аттестация по геометрии в 8 классе Цель работы: оценка уровня достижения учащимися 8 класса планируемых результатов обучения геометрии 2.Перечень
ПодробнееЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1. На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
ПодробнееТеоретическая часть экзамена по Г-8 кл.
Теоретическая часть экзамена по Г-8 кл. Знать и понимать (сделать чертеж и показать на рисунке) следующие определения и теоремы (без доказательства) из учебника Г-8 А. Г. Мерзляка Глава 1 1. Сумма углов
Г. Мерзляка Глава 1 1. Сумма углов
Площадь треугольника через площадь описанной окружности
Треугольник называется вписанным, если все его вершины лежат на окружности. В этом случае окружность называется описанной вокруг треугольника. Расстояние от ее центра до каждой вершины треугольника будет одинаковым и равным радиусу этой окружности. Вокруг любого треугольника можно описать окружность, но только одну.
Центр описанной окружности будет лежать в точке пересечения серединных перпендикуляров, проведенных к каждой из сторон треугольника. Если окружность описана вокруг прямоугольного треугольника, то ее центр будет лежать на середине гипотенузы. Для любого треугольника, вокруг которого описана окружность действует формула площади треугольника через радиус описанной окружности:
в которой a,b,c – стороны треугольника, а R – радиус описанной окружности.
Пример расчета площади треугольника через радиус описанной окружности:Пусть дан треугольник со сторонами a = 5 см, b = 6 см, c = 4 см.
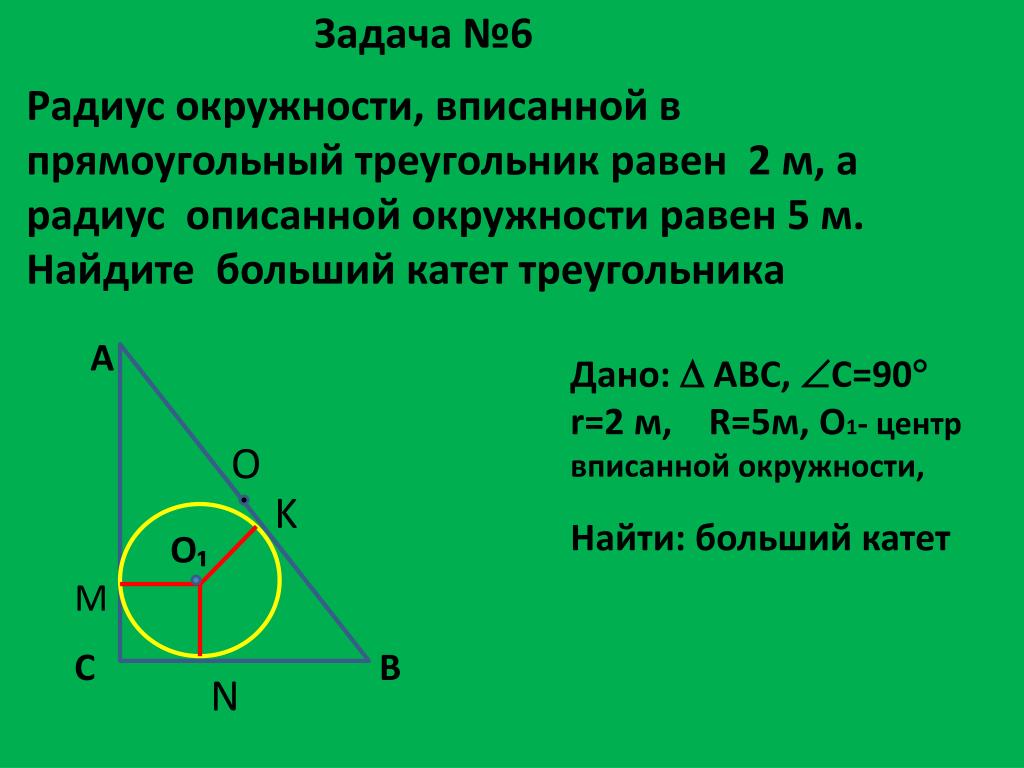 Вокруг него описана окружность с R = 3 см. найдите площадь.
Вокруг него описана окружность с R = 3 см. найдите площадь.Имея все требуемые данные, просто подставляем значения в формулу:
Площадь треугольника будет равна 10 кв. см
Довольно часто по условиям можно встретить данную площадь описанной окружности, которую необходимо использовать для нахождения площади вписанного треугольника. Формула площади треугольника через площадь описанной окружности находится после вычисления радиуса. Его можно вычислить несколькими способами. Для начала рассмотрим формулу площади окружности:
Преобразовав эту формулу, мы получим, что радиус:
Используя эту формулу, мы получаем, что зная площадь описанной окружности, можно найти площадь треугольника следующим способом:
Зная все три стороны заданного треугольника можно применить для нахождения площади формулу Герона. Из нее же можно найти и радиус описанной окружности. То есть если в условиях даны все стороны треугольника и требуется поиск площади через радиус описанной окружности, мы сначала должны вычислить его по формуле:
То есть, зная длины всех сторон треугольника, мы можем найти площадь треугольника через радиус описанной окружности.
Статьи Новости сайта
|
Как определить центр описанной окружности треугольника
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника. Что же это такое?
| Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана. |
И вот, представь себе, имеет место удивительный факт:
| Вокруг всякого треугольника можно описать окружность. |
Почему этот факт удивительный?
Но ведь треугольники – то бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта можешь найти в следующих уровнях теории, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины. Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
| Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника. |
Знаешь ли ты, что такое серединный перпендикуляр?
| Это прямая, проходящая через середину отрезка и перпендикулярная ему.Прямая – это серединный перпендикуляр к отрезку . |
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке .
Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке .
| Это и есть центр описанной около (вокруг) треугольника окружности. |
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
А вот если остроугольный, то – внутри:
Что же делать с прямоугольным треугольником?
| В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы. |
| Правда, здорово?Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов! |
Да ещё с дополнительным бонусом:
| в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы |
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
| В произвольном треугольнике: |
Так что ты теперь всегда сможешь найти и центр , и радиус окружности, описанной вокруг треугольника.То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол. Хорошая формула? По-моему, просто отличная!
ОПИСАННАЯ ОКРУЖНОСТЬ. СРЕДНИЙ УРОВЕНЬ
В этой части мы обсудим окружность, описанную вокруг (часто говорят «около») треугольника. Прежде всего дадим определение.
| Окружность , описанная около треугольника – такая окружность, что происходит через все три вершины этого треугольника. |
1. Существование и центр описанной окружности
Тут возникает вопрос: а для всякого ли треугольника существует такая окружность? Вот оказывается, что да, для всякого. И более того, мы сейчас сформулируем теорему, которая ещё и отвечает на вопрос, где же находится центр описанной окружности.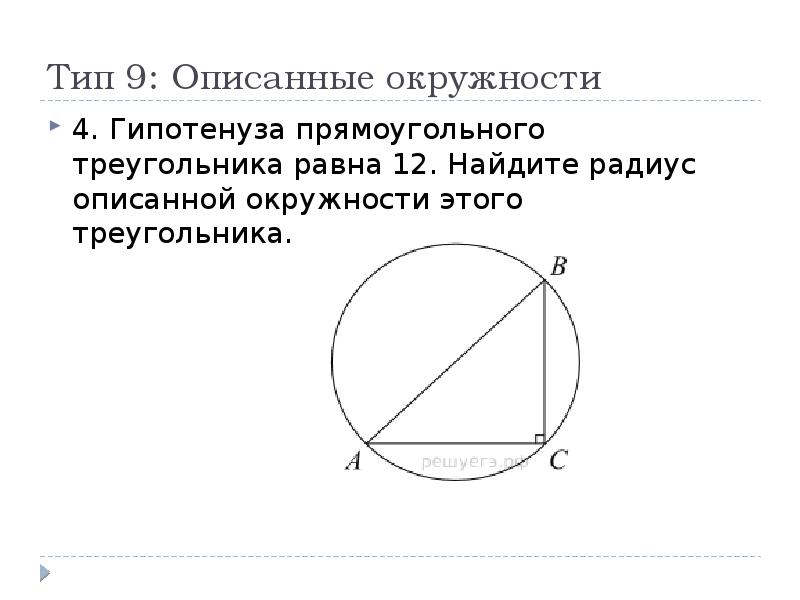
Теорема. Вокруг всякого треугольника можно описать окружность , при том единственным образом .
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Давай наберёмся мужества и докажем эту теорему. Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
| Геометрическое место точек , обладающих свойством « » – такое множество точек, что все они обладают свойством « » и никакие другие точки этим свойством не обладают. |
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы. А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют. В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
| Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка. |
Тут множество – это серединный перпендикуляр, а свойство « » – это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
- Всякая точка на серединном перпендикуляре находится на одинаковом расстоянии от концов отрезка
- Всякая точка, которая равноудалена от концов отрезка – находится на серединном перпендикуляре к ему.
| Проверим 1. Пусть точка лежит на серединном перпендикуляре к отрезку . |
Соединим с и с .Тогда линия является медианой и высотой в . Значит, – равнобедренный, – убедились, что любая точка , лежащая на серединном перпендикуляре, одинаково удалена от точек и .
| Теперь 2. Почти точно так же, но в другую сторону. Пусть точка равноудалена от точек и , то есть . |
Возьмём – середину и соединим и . Получилась медиана . Но – равнобедренный по условию не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка – точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Рассмотрим треугольник . Проведём два серединных перпендикуляра и , скажем, к отрезкам и . Они пересекутся в какой-то точке, которую мы назовем .
А теперь, внимание!
Точка лежит на серединном перпендикуляре ;
точка лежит на серединном перпендикуляре .
И значит, и .
Отсюда следует сразу несколько вещей:
Во – первых , точка обязана лежать на третьем серединном перпендикуляре, к отрезку .
То есть серединный перпендикуляр тоже обязан пройти через точку , и все три серединных перпендикуляра пересеклись в одной точке.
Во – вторых : если мы проведём окружность с центром в точке и радиусом , то эта окружность также пройдёт и через точку , и через точку , то есть будет описанной окружностью . Значит, уже есть, что пересечение трёх серединных перпендикуляров – центр описанной окружности для любого треугольника.
И последнее: о единственности. Ясно (почти), что точку можно получить единственным образом, поэтому и окружность – единственная. Ну, а «почти» – оставим на твоё размышление. Вот и доказали теорему. Можно кричать «Ура!».
2. Радиус описанной окружности.
А если в задаче стоит вопрос «найдите радиус описанной окружности»? Или наоборот, радиус дан, а требуется найти что – то другое? Есть ли формула, связывающая радиус описанной окружность с другими элементами треугольника?
Есть, конечно! И эта формула называется «Теорема синусов» (доказательство смотри именно в этой теме). |
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, тебе нужна одна сторона (любая!) и противолежащий ей угол . И всё!
3. Центр окружности – внутри или снаружи
А теперь вопрос: может ли центр описанной окружности лежать снаружи треугольника.
Ответ: ещё как может. Более того, так всегда бывает в тупоугольном треугольнике.
| В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника. |
| В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника |
| В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы , а радиус равен половине гипотенузы. |
ОПИСАННАЯ ОКРУЖНОСТЬ. КОРОТКО О ГЛАВНОМ
1. Окружность, описанная около треугольника
– это окружность, которая проходит через все три вершины этого треугольника.
|
2. Существование и центр описанной окружности
|
3. Радиус описанной окружности
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
4. Центр окружности – внутри или снаружи
|
|
|
P.S. ПОСЛЕДНИЙ БЕСЦЕННЫЙ СОВЕТ 🙂
Ну вот, тема закончена. Если ты читаешь эти строки, значит ты очень крут.
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, значит ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для успешной сдачи ОГЭ или ЕГЭ, для перехода в 10-й класс или поступления в институт на бюджет и, САМОЕ ГЛАВНОЕ, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это – не главное.
Главное то, что они БОЛЕЕ СЧАСТЛИВЫ (есть такие исследования). Возможно потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю.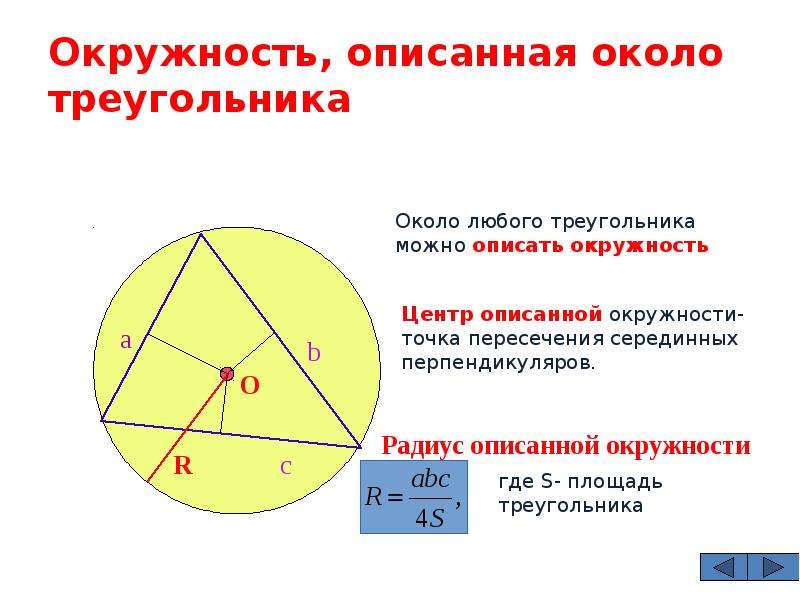
Что нужно, чтобы быть наверняка лучше других на ЕГЭ и быть в конечном итоге… более счастливым?
НАБИТЬ РУКУ, РЕШАЯ ЗАДАЧИ ПО ЭТОЙ ТЕМЕ.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время.
И, если ты не решал их (МНОГО!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь.
Это как в спорте – нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Я рекомендую использовать для этих целей наш учебник «YouClever» (который ты сейчас читаешь) и решебник и программу подготовки «100gia».
Условия их приобретения изложены здесь. Кликните по этой ссылке, приобретите доступ к YouClever и 100gia и начните готовиться прямо сейчас!
И в заключение.
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
| Серединный перпендикуляр к отрезку |
| Окружность описанная около треугольника |
| Свойства описанной около треугольника окружности. Теорема синусов |
| Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим.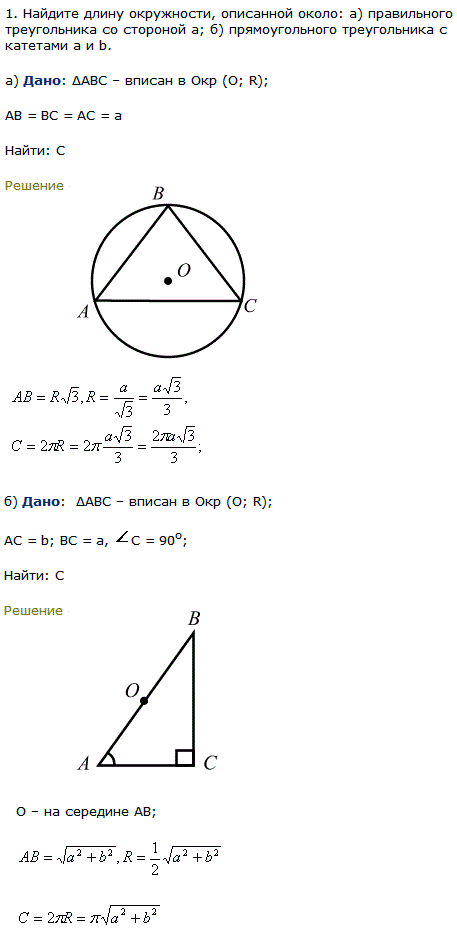 Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис. 4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | |
| Окружность, описанная около треугольника | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.Посмотреть доказательство | |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | |
| Центр описанной около тупоугольного треугольника окружности | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | |
| Теорема синусов | ||
| Площадь треугольника | ||
| Радиус описанной окружности |
| Серединные перпендикуляры к сторонам треугольника |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.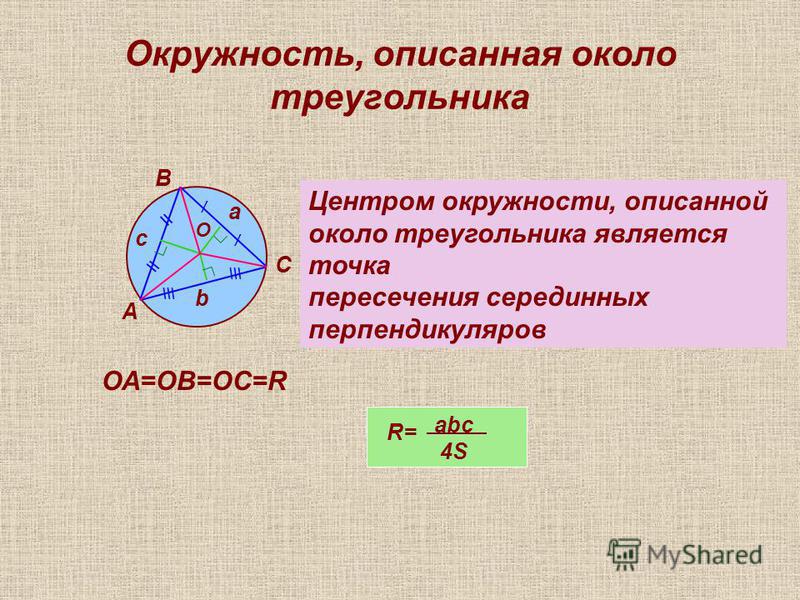
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Для любого треугольника справедливы равенства (теорема синусов):
,
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.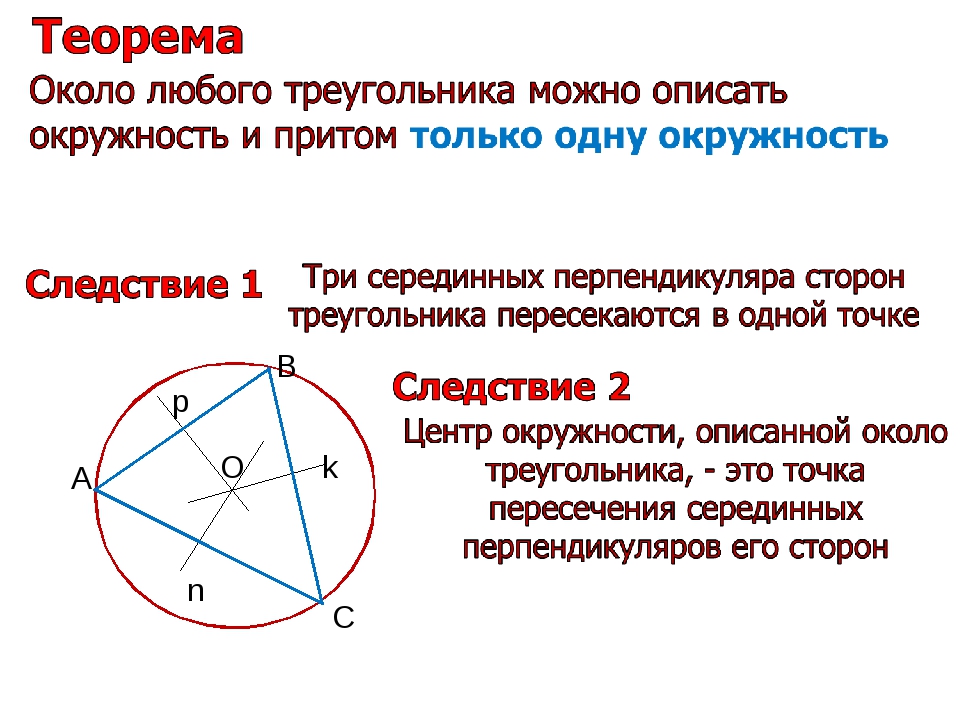
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)
.
Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис. 8).
8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Где находится центр описанной около треугольника окружности? Что можно сказать о центре окружности, описанной около многоугольника?
Центр описанной около треугольника окружности является точкой пересечения серединных перпендикуляров к сторонам треугольника.
окружность (O;R) — описанная около ∆ ABC.
O — точка пересечения серединных перпендикуляров к сторонам ∆ ABC.
Соединим отрезками точки O и A, O и C.
OA=OC (как радиусы), следовательно, треугольник AOC — равнобедренный с основанием AC (по определению).
По свойству равнобедренного треугольника, высота и медиана, проведенные к основанию AC, совпадают):
Следовательно, центр описанной окружности — точка O — лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину, то есть на серединном перпендикуляре к AC.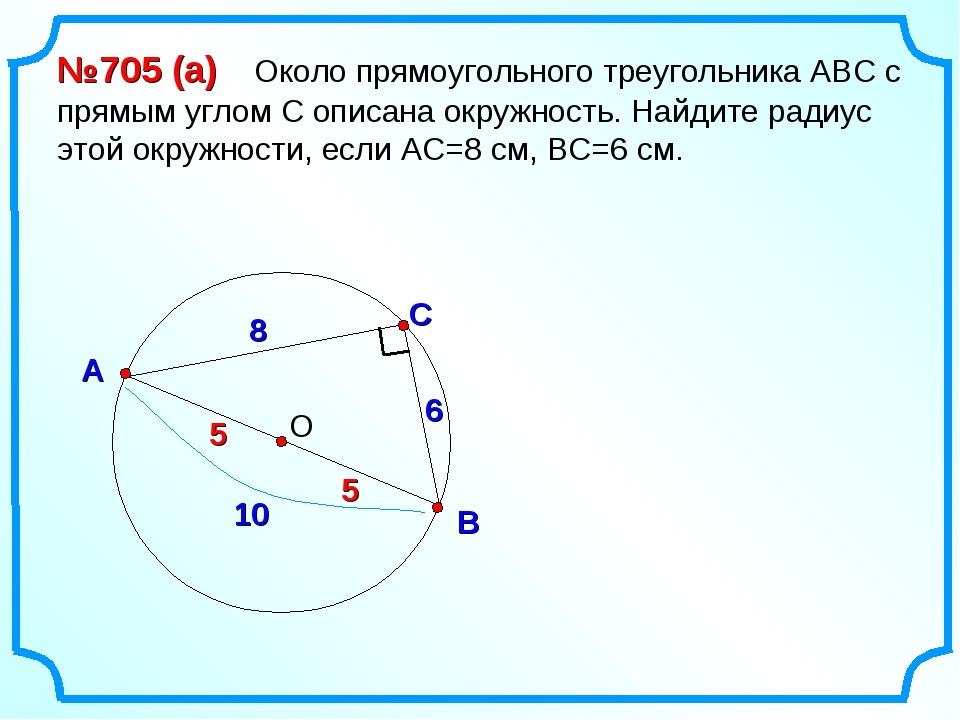
Аналогично доказывается, что точка O лежит на серединном перпендикуляре к стороне AB.
Так как серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, то точка O — центр описанной около треугольника ABC окружности.
Что и требовалось доказать.
Аналогичные рассуждения можно применить и для многоугольника, около которого можно описать окружность.
Центр описанной около многоугольника окружности является точкой пересечения серединных перпендикуляров к сторонам этого многоугольника.
на мой взгляд у вас опечатка — «Соединим отрезками точки O и A, O и C.
OA=OB( написано ОВ вместо ОС) (как радиусы), следовательно, треугольник AOB — равнобедренный с основанием AC (по определению).»
Описанный круг | Math Wiki
В геометрии описанная окружность или описанная окружность многоугольника — это круг, который проходит через все вершины многоугольника. Центр этой окружности называется , центр описанной окружности .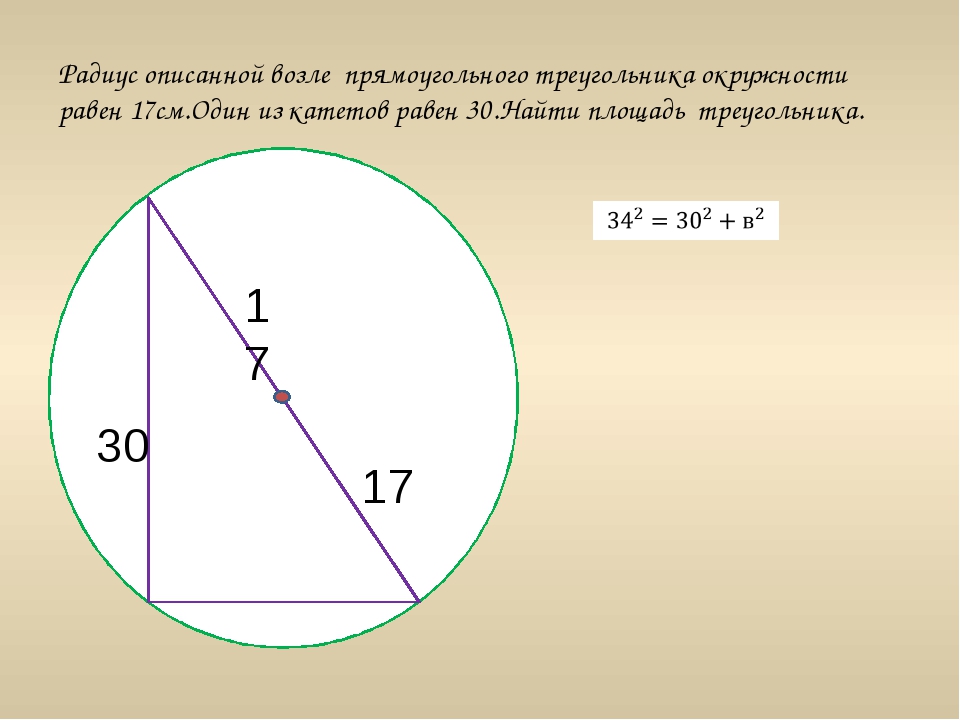
Многоугольник, имеющий описанную окружность, называется циклическим многоугольником . Все правильные простые многоугольники, все треугольники и все прямоугольники циклические.
Связанное понятие — это понятие минимальной ограничивающей окружности, которая является наименьшей окружностью, полностью содержащей внутри себя многоугольник.Не каждый многоугольник имеет описанную окружность, поскольку вершины многоугольника не обязательно должны лежать на окружности, но каждый многоугольник имеет уникальный минимальный ограничивающий круг, который может быть построен с помощью алгоритма линейного времени. Даже если многоугольник имеет описанную окружность, он может не совпадать с минимальной ограничивающей окружностью; например, для тупого треугольника минимальная ограничивающая окружность имеет самую длинную сторону в качестве диаметра и не проходит через противоположную вершину.
Все треугольники циклические, т.е.е. у каждого треугольника есть описанный круг.
Центр описанной окружности треугольника находится как пересечение трех серединных перпендикуляров. (Серединный перпендикуляр — это линия, которая образует прямой угол с одной из сторон треугольника и пересекает эту сторону в его средней точке.) Это связано с тем, что центр описанной окружности равноудален от любой пары точек треугольника, а все точки на перпендикуляре биссектрисы равноудалены от этих точек треугольника.
В прибрежной навигации, описанная окружность треугольника иногда используется как способ получения линии положения с помощью секстанта, когда компас недоступен.Горизонтальный угол между двумя ориентирами определяет описанную окружность, на которой лежит наблюдатель.
Положение центра описанной окружности зависит от типа треугольника:
- Если и только если треугольник острый (все углы меньше прямого), центр описанной окружности лежит внутри треугольника
- Если и только если она тупая (имеет угол на один угол больше прямого), центр описанной окружности лежит за пределами
- Если и только если это прямоугольный треугольник, центр описанной окружности лежит на одной из его сторон (а именно, гипотенуза).
 Это одна из форм теоремы Фалеса.
Это одна из форм теоремы Фалеса.
Диаметр
Диаметр описанной окружности можно вычислить как длину любой стороны треугольника, деленную на синус противоположного угла. (Как следствие закона синусов, не имеет значения, какая сторона выбрана: результат будет таким же.) Окружность из девяти точек треугольника имеет половину диаметра описанной окружности. Диаметр описанной окружности треугольника равен
где — длины сторон треугольника, а — полупериметр.Радикал во втором знаменателе выше — это площадь треугольника по формуле Герона.
В любом данном треугольнике центр описанной окружности всегда коллинеарен центроиду и ортоцентру. Линия, которая проходит через все они, известна как линия Эйлера.
Изогональный элемент, сопряженный с центром описанной окружности, является ортоцентром.
Полезный минимальный ограничивающий круг из трех точек определяется либо описанной окружностью (где три точки находятся на минимальном ограничивающем круге), либо двумя точками самой длинной стороны треугольника (где две точки определяют диаметр круга. .). Обычно минимальную ограничивающую окружность путают с описанной.
.). Обычно минимальную ограничивающую окружность путают с описанной.
Радиус
Описанная окружность трех коллинеарных точек — это линия, на которой лежат эти 3 точки, которую часто называют окружностью бесконечного радиуса . Почти коллинеарные точки часто приводят к численной нестабильности при вычислении описанной окружности.
Окружности треугольников тесно связаны с триангуляцией Делоне набора точек.
Радиус:
Для прямоугольного треугольника:
Площадь
Площадь:
Периметр
По периметру:
Радиус
Для прямоугольника
Для любого четырехугольника
Окружности многоугольников
Радиус описанной окружности правильного n-стороннего многоугольника равен:
Для диаметра:
Площадь и периметр
Площадь круга:
Периметр окружности:
Уравнения окружности
Следующий контент либо скопирован, либо скопирован из Википедии. Тот или иной источник должен ссылаться на исходное содержание.
Тот или иной источник должен ссылаться на исходное содержание.
В евклидовой плоскости можно явно задать уравнение описанной окружности через декартовы координаты вершин вписанного треугольника. Итак, предположим, что
— координаты точек. Описанная окружность — это геометрическое место точек на декартовой плоскости, удовлетворяющих уравнениям
, гарантирующий, что все точки находятся на одинаковом расстоянии от общего центра круга.С помощью поляризационного тождества эти уравнения сводятся к условию, что матрица
имеют ненулевое ядро. Таким образом, описанную окружность можно также описать как геометрическое место нулей определителя этой матрицы:
Расширение с помощью сомножителя, пусть
, тогда мы имеем и, предполагая, что три точки не были на одной линии (в противном случае описанная окружность — это та линия, которую также можно рассматривать как обобщенную окружность с S на бесконечности), что дает центр описанной окружности и радиус описанной окружности. Подобный подход позволяет вывести уравнение описанной сферы тетраэдра.
Подобный подход позволяет вывести уравнение описанной сферы тетраэдра.
Уравнение описанной окружности в трилинейных координатах имеет вид
Уравнение описанной окружности в барицентрических координатах имеет вид
Изогональное сопряжение описанной окружности — это линия на бесконечности, заданная в трилинейных координатах посредством и в барицентрических координатах посредством.
Координаты центра окружности
Декартовы координаты
Декартовы координаты центра описанной окружности
с
Без ограничения общности это может быть выражено в упрощенной форме после перевода вершины A в начало декартовых систем координат, т.е.э., когда. В этом случае координаты вершин и представляют собой векторы от вершины A ‘до этих вершин. Обратите внимание, что этот тривиальный перевод возможен для всех треугольников, и координаты центра описанной окружности треугольника выглядят как
с
Барицентрические координаты как функция длин сторон
Центр описанной окружности имеет трилинейные координаты (cos ( α ), cos ( β ), cos ( γ )), где α , β , γ — углы треугольника. Центр окружности имеет барицентрические координаты
Центр окружности имеет барицентрические координаты
где a , b , c — длины ребер ( BC , CA , AB соответственно) треугольника.
Барицентрические координаты из кросс- и точечных произведений
В евклидовом пространстве существует уникальный круг, проходящий через любые заданные три неколлинеарные точки P 1 , P 2 и P 3 .Используя декартовы координаты для представления этих точек как пространственных векторов, можно использовать скалярное произведение и перекрестное произведение для вычисления радиуса и центра круга. Позволять
Тогда радиус круга определяется как
Центр круга задается линейной комбинацией
где
Параметрическое уравнение
Единичный вектор, перпендикулярный плоскости, содержащей круг, задается выражением
Следовательно, учитывая радиус, r , центр, P c , точку на окружности, P 0 и единичную нормаль к плоскости, содержащей окружность, одно параметрическое уравнение окружности, начинающееся с точки P 0 и продолжающееся в положительно ориентированном (т. е.е., правша) смысл о следующем:
е.е., правша) смысл о следующем:
Углы, под которыми окружность встречается со сторонами
Углы, под которыми описанная окружность встречается со сторонами треугольника, совпадают с углами, под которыми стороны встречаются друг с другом. Сторона, противоположная углу α, пересекает окружность дважды: по одному на каждом конце; в каждом случае под углом α (аналогично для двух других углов). Теорема об альтернативном сегменте утверждает, что угол между касательной и хордой равен углу в альтернативном сегменте.
Треугольник с центром в описанной окружности треугольника ABC
В этом разделе углы при вершинах обозначены как A , B , C , и все координаты являются трехлинейными:
- Точка Штейнера = = невершинная точка пересечения описанной окружности с эллипсом Штейнера. (Эллипс Штейнера с центром = центроид ( ABC ) — это эллипс наименьшей площади, который проходит через A , B и C .
 Уравнение для этого эллипса: 1 / ( ax ) + 1 / ( на ) + 1 / ( cz ) = 0.)
Уравнение для этого эллипса: 1 / ( ax ) + 1 / ( на ) + 1 / ( cz ) = 0.)
- Tarry point = sec ( A + ω): sec. ( B + ω): sec ( C + ω) = антипод точки Штейнера
Циклические четырехугольники
Четырехугольники, которые можно описать, обладают особыми свойствами, включая тот факт, что противоположные углы являются дополнительными углами (в сумме или радианах).
См. Также
Внешние ссылки
Интерактивный
Окружность центра треугольника — математический путь
Центр описанной окружности треугольника ( O ) — это точка, где пересекаются три серединных перпендикуляра (M a , M b y M c ) сторон треугольника.Его также можно определить как одну из точек параллелизма в треугольнике.
Серединный перпендикуляр треугольника — это линия, перпендикулярная стороне, проходящей через его середину.
Центр описанной окружности ( O ) является центральной точкой, которая формирует начало описанной окружности (описанной окружности), в которой все три вершины треугольника лежат на окружности.
Можно найти радиус ( R ) описанной окружности, если мы знаем три стороны и полупериметр треугольника.
Радиус описанной окружности также называется радиусом описанной окружности треугольника .
Формула радиуса описанной окружности:
Загрузите этот калькулятор , чтобы получить результаты формул на этой странице. Выберите исходные данные и введите их в верхнем левом поле. Для получения результатов нажмите ENTER.
Triangle-total.rar или Triangle-total.exe
Примечание. Предоставлено автором: Хосе Мария Пареха Маркано .Химик. Севилья, испания.
Где находится окружность треугольника?
- Если это тупой треугольник, центр описанной окружности расположен на вне треугольника (как мы видим на рисунке выше).

- Если это острый треугольник, центр описанной окружности расположен на внутри треугольника.
- Если это прямоугольный треугольник, центр описанной окружности лежит на средней точке гипотенузы (самая длинная сторона треугольника, противоположная прямому углу (90 °).Мы можем увидеть пример на рисунке ниже.
См. Теорему Фалеса.
В любом неравностороннем треугольнике ортоцентр ( H ), центроид ( G ) и центр окружности ( O ) выровнены. Линия, содержащая эти три точки, называется линией Эйлера.
В равностороннем треугольнике все три центра находятся в одном месте.
Относительные расстояния между центрами треугольников остаются постоянными.
Расстояния между центрами :
Это правда, что расстояние от ортоцентра ( H ) до центроида ( G ) вдвое больше, чем от центроида ( G ) до центра окружности ( O ). Или, другими словами, сегмент HG в два раза больше сегмента GO :
Или, другими словами, сегмент HG в два раза больше сегмента GO :
Когда треугольник равносторонний, центроид, ортоцентр, центр описанной окружности и центр совпадают в одной и той же внутренней точке, которая находится на одинаковом расстоянии от трех вершин.
Это расстояние до трех вершин равностороннего треугольника равно
с одной стороны и, следовательно, до вершины, составляющей h ее высоты (или высоты).Упражнение 1
Найдите радиус R описанной окружности (или описанной окружности ) треугольника со сторонами a = 9 см, b = 7 см и c = 6 см.
Решение:
Получаем полупериметр с :
Применяем формулу для радиуса R описанной окружности, получая следующие значения:
Итак, радиус R равен 4.5 см.
Упражнение 2
Найдите координаты центра описанной окружности треугольника O ABC , вершины которого равны A (3, 5), B (4, -1) y C (-4, 1).
РЕШЕНИЕ:
Чтобы найти центр описанной окружности O, мы должны решить уравнения для двух перпендикулярных биссектрис M a (перпендикулярно стороне a ) и M b (перпендикулярно стороне b ) и посмотреть где находится точка пересечения (то есть центр описанной окружности O ) обоих перпендикулярных биссектрис.
ШАГ 1. Найдите уравнение для серединного перпендикуляра M a .
Сначала мы найдем уравнение прямой, которая проходит через сторону a , которая является противоположностью вершине A . Это уравнение получено с учетом того, что оно проходит через точки B (4, -1) и C (-4, 1). Общее уравнение прямой, проходящей через две известные точки:
Уравнение прямой, содержащей сторону BC и ее уклон м , будет:
Итак, уклон м для прямой а равен -1/4.
Теперь мы получаем координаты средней точки r между вершинами B и C , то есть середины стороны a .
Где г?
Итак,
Наклон линии, которая содержит серединный перпендикуляр M a , перпендикулярный стороне a , является обратным и имеет противоположный знак наклона найденной прямой, которая содержит сторону a . Итак, имеем:
Итак, наклон линии M a равен 4, потому что наклон линии a был -1/4.
Поскольку мы знаем, что срединный перпендикуляр M a проходит через среднюю точку r (расположен в (0, 0)), и мы знаем его наклон m p , который равен 4, теперь мы можем получить уравнение для линии M a :
Это уравнение для серединного перпендикуляра M a .
ШАГ 2: Найдите уравнение для серединного перпендикуляра M b .
Теперь мы действуем таким же образом, чтобы найти уравнение прямой, которая содержит серединный перпендикуляр M b , то есть ту, которая проходит через среднюю точку s и перпендикулярна стороне b между вершины A и C .
Сначала вычисляем наклон прямой b (или стороны b ):
Затем находим координаты середины s между вершинами A и C :
Уравнение прямой, содержащей серединный перпендикуляр M b , то есть прямая, начинающаяся из средней точки s , перпендикулярна стороне b .Следовательно, наклон этой прямой будет –7/4 (обратный и противоположный знак). С наклоном прямой и одной из ее точек можно найти уравнение:
У нас есть уравнения двух серединных перпендикуляров треугольника: M a и M b :
Затем мы решаем эту систему двух уравнений с двумя переменными, используя метод подстановки, наиболее подходящий, учитывая форму первого уравнения:
В итоге получаем, что x = 0,37 и y = 1,48.
Следовательно, центр описанной окружности O (0,37, 1,48).
Центр описанной окружности O — это центр описанной окружности:
Окружность треугольника Калькулятор
- Цель использования
- Найдите минимальный размер трубы для треугольного креста конструкция профиля
[1] 2021.01.14 10:33 Мужчина / Уровень 20 лет / Учитель / Исследователь / Очень /
- Цель использования
- Рассчитать диаметр окружности шага (PCD) для детали, которая будет изготовлена с Фрезерный станок с ЧПУ.
[2] 2020/05/03 00:27 Мужчина / 50 лет / Пенсионер / Очень /
- Цель использования
- Подготовка к SAT.
- Комментарий / запрос
- Спасибо.
[3] 2020/04/01 00:27 Женский / Моложе 20 лет / Старшая школа / Университет / аспирант / Очень /
- Цель использования
- Рассчитайте размеры запасной детали для 3D-печати
[4] 2020/02/22 21:44 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- домашнее задание
[5] 2020/02/01 02:39 Мужской / До 20 лет / Начальная школа / Неполный средний класс / Очень /
- Цель использования
- Learn Circumscribing.

[6] 2019/09 / 02 07:09 Мужской / До 20 лет / Начальная школа / Младший школьник / Очень /
- Цель использования
- Написание компьютерной программы BASIC для фрезерования многоугольников из стального прутка акции, я машинист-хобби
- Комментарий / запрос
- Спасибо за доступ к формулам.
[7] 2019/06/09 09:31 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цели использования
- Для расчета внутреннего диаметра для стопорного кольца 3d принтера на задней части корпуса отражателя фары.
[8] 2019/05/02 4:22 Мужчины / до 20 лет / средней школы / университета / аспирант / очень /
- Цель использования
- Проектирование гибкой стопорное кольцо для прототипа 3D печатной части.
[9] 2019/03/31 18:35 Мужчина / 50 лет / Уровень Инженер / очень /
- Цель использования
- Исключительное любопытство к треугольникам и кругам
[10] 2018/12/07 12:01 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Немного /
Как найти площадь равностороннего треугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как так как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить преподавателям Varsity Tutors найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как рассчитать радиус квадрата
Обновлено 3 ноября 2020 г.
Дэвид Сарокин
Вы, вероятно, думаете о радиусе как о свойстве круга в двух измерениях или трехмерной сферы. Однако математики также используют этот термин для обозначения определенных расстояний в правильных многоугольниках. В более повседневном использовании радиус квадрата может также относиться к радиусу круга, связанного с рассматриваемым квадратом.
Однако математики также используют этот термин для обозначения определенных расстояний в правильных многоугольниках. В более повседневном использовании радиус квадрата может также относиться к радиусу круга, связанного с рассматриваемым квадратом.
Использование термина «Радиус» для многоугольников
Радиус правильного многоугольника, такого как квадрат, пятиугольник или восьмиугольник, — это расстояние от центра многоугольника до любой из его вершин. Хотя это правильное использование слова «радиус», на практике редко можно встретить его таким образом.Чаще всего используется для более общего значения, как расстояние от центра круга до окружности.
Расчет радиуса квадрата
Расстояние от центра квадрата до любого из его четырех углов можно рассчитать, взяв половину длины одной стороны квадрата, возведя в квадрат это значение, удвоив результат, затем взяв квадратный корень из этого числа. 2 = 3 × 3 = 9 \\ \ text {Удвоение} 9 = 2 × 9 = 18 \\ \ sqrt {18} = 4.2
2 = 3 × 3 = 9 \\ \ text {Удвоение} 9 = 2 × 9 = 18 \\ \ sqrt {18} = 4.2
Радиус квадрата равен c , гипотенуза прямоугольного треугольника со сторонами a и b , которые составляют половину длины стороны квадрата. Шаги по вычислению радиуса вытекают непосредственно из этой формулы.
Расчет радиуса вписанной окружности
Для круга в квадрате, который только касается краев квадрата, радиус круга равен половине длины стороны квадрата. Для 2-дюймового квадрата радиус круга составляет один дюйм.
Расчет радиуса описанной окружности
Для окружности на внешней стороне квадрата, проходящей через все вершины, известной как описанная окружность, радиус окружности равен радиусу квадрата. Для 2-дюймового квадрата радиус круга составляет 1,414 дюйма.
описанная окружность в квадрате
INFORMATIVA ai sensi dell’articolo 13 del Regolamento (UE) 2016/679 («GDPR»)
Gentile Utente, Piaggio & C. Спа, Le dà il benvenuto sul nostro sito (il «Sito Web») и La invita a prestare attzione alla seguente informativa (l ‘»Informativa»), rilasciata ai sensi dell’articolo 13 del Regolamento (UE) 2016/679 relativo alla Protezione delle persone fisiche con riguardo al trattamento dei dati personali, nonché alla libera circolazione di tali dati («GDPR»).
Спа, Le dà il benvenuto sul nostro sito (il «Sito Web») и La invita a prestare attzione alla seguente informativa (l ‘»Informativa»), rilasciata ai sensi dell’articolo 13 del Regolamento (UE) 2016/679 relativo alla Protezione delle persone fisiche con riguardo al trattamento dei dati personali, nonché alla libera circolazione di tali dati («GDPR»).
Этот документ содержит описание всех переводов, полученных на Titolare, после перехода на сайт Sito Web.
Si Precisa, Inoltre, Che l’Informativa riguarda esclusivamente il Sito Web, si considera pertanto escluso ogni sito internet a cui Lei potrà essere reindirizzato dal Sito Web.
Inoltre, qualora Lei dovesse acquistare prodotti or fruire di servizi Piaggio non tramite il Sito Web ma tramite canali ufficiali Piaggio, al momento dell’acquisto Le verrà rilasciata una specifica informativa, ex art. 13 del GDPR, relativa ai Suoi dati personali trattati in quell’occasione.
1) Chi è il Titolare del trattamento
Il Titolare del trattamento è Piaggio & C. S.p.A., con sede legale по адресу: Viale Rinaldo Piaggio, 25, Pontedera (PI) (il «Titolare»).
S.p.A., con sede legale по адресу: Viale Rinaldo Piaggio, 25, Pontedera (PI) (il «Titolare»).
Il Titolare ha altresì nominato un Responsabile della protezione dei dati («DPO»), che Lei potrà contattare direttamente per l’esercizio dei Suoi diritti, nonché per draw qualsiasi informazione relativa al trattamento dei dei dati scrivendo a:
Responsabile della Protezione di Dati («Сотрудник по защите данных — DPO»)
Viale Piaggio 25
56025 PONTEDERA (PI)
Эл. почта: dpo @ piaggio.com
Факс: +39 0587272961
Тел: +39 0587272495
2) Персональные данные
2.1) Данные навигации
Информационные системы и программное обеспечение для процедур, подготовленное для функционирования Sito Web acquisiscono, nel corso del lizio все личные данные, передаваемые через Titolare, являются неявными протоколами связи в Интернете.
Si tratta di informazioni che non sono raccolte per essere Associate a interessati identity, ma che per loro stessa natura potrebbero, привлекательно разработанные ассоциации с данными detenuti da terzi, permettere di Identificare gli utenti.
В данной категории данных используется IP-адрес, который используется в компьютере, использующем компьютер, который используется в качестве идентификатора URI (Uniform Resource Identifier). богатый сервер, размер файла, отображаемый в системе, числовой код, указанный на сервере (buon fine, errore, ecc.), и другие параметры, относящиеся к действующей системе и всем информационным элементам.
Эти данные используют только точные статистические данные, анонимные данные о месте и для управления правильными функциями и временем отмены лабораторных работ. Я хочу, чтобы пользователи использовали ответы на вопросы, связанные с получением информации о данных сайта Sito Web.
2.2) Dati forniti volontariamente dall’utente
Il Titolare tratta i seguenti dati personali, da Lei forniti tramite la compilazione dei format (maschere) del Sito Web:
— данные anagrafici: come ad esempio nome, numero, diiriz telefono, электронная почта ed altri recapiti, nonché Sue imagini;
— относительные данные для заключения;
— Дати Банкари (I. е. il Suo IBAN).
е. il Suo IBAN).
3) Для окончательных результатов своих личных данных и квалификационных данных
личных данных из Lei forniti compilando le varie maschere presenti sul Sito Web sono trattati dal Titolare per le finalità di seguito riport.
3.1) Erogazione dei servizi e vendita di prodotti
Il Titolare intende trattare i Suoi dati personali al fine di consentirle l’accesso al Sito Web, для окончательного подтверждения того, что все поставщики услуг онлайн, все эрогазионы на сайте line, di volta in volta offerte dal sito, tra cui, в частности, per rispondere all Sue richieste di invio di materiale informativo su prodotti e servizi offerti dal Titolare, для gestione di richieste di «test ride», per consentirle di Accedere a Рекламные и рекламные предложения представлены на сайте Sito Web, для каждого участника, участвующего в сообществе, и не только для поддержки клиентов, но и для обслуживания клиентов.
Natura del conferimento: Facoltativa.
Conseguenze rifiuto conferimento dati: Il mancato conferimento dei dati comporterà l’impossibilità per il Titolare di soddisfare le Sue richieste ai sensi del priordente paragrafo.
Base giuridica del trattamento: статья 6, paragrafo 1, lettera b), GDPR. Pertanto, non è needaria l’acquisizione di un Suo preventtivoconnso al trattamento.
Periodo conservazione dati personali: Suoi dati personali per tali finalità saranno trattati per il tempo strettamente needario soddisfare la Sua richiesta e successivamente conservati per il tempo previsto dalla normativa application, dopo l’evasione della stessa.
3,2) Маркетинговая деятельность на продуктах и аналогах услуг
Il Titolare intende trattare i Suoi dati personali al fine di inviarLe comunicazioni Commerciali de prodotti e servizi analoghi an quelltiolche dall’Utente. tramite i soggetti Responsabili, all’uopo nominati ai sensi dell’art. 28 дель GDPR.
Finalità del trattamento: Invio di materiale pubblicitario, Promozione e vendita di prodotti, nonché indagini or ricerche di mercato e / o comunicazioni Commerciali.
Natura del conferimento: Facoltativa.
Conseguenze rifiuto conferimento dati: Il mancato conferimento dei dati comporterà l’impossibilità per il Titolare di inviarle comunicazioni Promozionali e di marketing
Base giuridica del trattamento: Legittimo interesse.
Periodo conservazione dati personali: I Suoi dati personali per story finalità saranno trattati fino alla sua solutione di opporsi al relativo trattamento e / o di ottenere la cessazione dello stesso in qualunque momento.
3.3) Маркетинговая деятельность
Il Titolare intende trattare i Suoi Dati personali al fine di inviarLe comunicazioni Commerciali, as all’uopodits of all’uopoll’i sensi nominati, all ’ 28 дель GDPR.
Finalità del trattamento: Invio di materiale pubblicitario, Promozione e vendita di prodotti, nonché indagini or ricerche di mercato e / o comunicazioni Commerciali.
Natura del conferimento: Facoltativa.
Conseguenze Rifiuto Conferimento Dati: Il mancato conferimento dei dati comporterà l’impossibilità per il Titolare di inviarle comunicazioni Promozionali e di marketing
Base giuridica del trattamento: Consenso
Periodo dei dati fininance datio conservazio datira Decisione di opporsi al relativo trattamento e / o di ottenere la cessazione dello stesso in qualunque momento.
4) Con quali modalità saranno trattati i Suoi dati personali
Il trattamento dei Suoi dati avverrà, nel rispetto delle disizioni previste dal GDPR, mediante comstrumenti cartacei, informatici e telematici, cone strettamente logic, con коррелирует со строгой логикой modalità idonee a garantirne la sicurezza e la riservatezza в соответствии со всеми положениями, предшествующими статье 32 GDPR.
5) A quali soggetti potranno essere comunicati i Suoi dati personali e chi può venirne a conoscenza
Per il perseguimento delle finalità descritte al Priordente punto 3, i Suoi dati personali saranno conosciuti dai dai dai dai assindenti, dai dai dai assoured person. Che opereranno in qualità di soggetti autorizzati al trattamento dei dati personali.
Inoltre, i Suoi data personali saranno comunicati e trattati da soggetti terzi appartenenti all seguenti category:
a) soggetti di cui il Titolare si avvale per la gestione del Sito Web;
b) società che gestiscono il sistema informatico del Titolare;
c) общество и потребители, занимающиеся юридической деятельностью и потреблением финансовых средств;
d) орган управления общественным обществом и контроль над общими общественными организациями или частными лицами с функциями государственного управления;
e) soggetti di cui il titolare a vario titolo si avvale per la fornitura servizio richiesto;
f) ad altre società del Gruppo Piaggio, per finalità di marketing, di vendita diretta, al fine di svolgere indagini di mercato, per разработанная статистика, качественный мониторинг качества обслуживания клиентов или клиентов, предоставляющих услуги / продукты продукции altre società del Gruppo Piaggio, nonché per la comunicazione a soggetti esterni (per esempio fornitori) qualora ciò sia needario per consentirle di beneficiare dei nostri servizi
Lei avrà in ogni momento il diritto di rewocial. Вы можете определить возможности для продолжения работы с объявлениями, используя все персональные данные для окончательного результата в отношениях всех качеств, полученных после отрицательного согласия.
Вы можете определить возможности для продолжения работы с объявлениями, используя все персональные данные для окончательного результата в отношениях всех качеств, полученных после отрицательного согласия.
У меня есть приложение для всех категорий, которые сопряжены с операциями, в alcune ipotesi, в целом autonomia приходят с отличием Titolari del trattamento, в altre ipotesi, в качестве Responsabili del trattamento appositamente nominati dal Titolare nel rispeticolto 28 GDPR.
L’elenco complete e agiornato dei soggetti a cui i Suoi dati personali posono essere comunicati può essere richiesto presso la sede legale del Titolare or contattando il DPO.
I Suoi dati personali non saranno trasferiti a soggetti terzi all’ westerno dell’Unione europea e non sono oggetto di diffusione.
6) Меньшие данные
Титульные данные, не являющиеся личными 16-ю годами, для окончательных результатов с предшествующими пунктами 3.1 и 3.2.
Qualora l’Utente abbia dichiarato di essere minore di anni 16, il campo relativo alla raccolta del consnso verrà precompilato in maniera negativa.
7) Dati di geolocalizzazione
Il sito potrà raccogliere e trattare dati di geolocalizzazione per l’erogazione dei servizi richiesti dall’Utente, solo previo connso specifico dell’Interessato, che potrà semper essere revocato.In questo caso il consnso verrà richiesto tramite un c.d. выскакивать.
8) Quali diritti Lei ha in qualità di interessato
In relazione ai trattamenti descritti nella presente Informativa, in qualità di interessato Lei potrà, all condizioni previste dal GDPR, esercitare i diritti sanciti dagli dagli Partolare, i seguenti diritti:
— diritto di accesso — статья 15 GDPR: diritto di ottenere conferma che sia o meno in corso un trattamento di dati personali che La riguardano e, in tal caso, ottenere l’accesso ai Suoi dati personali — compres una copia degli stessi — e la comunicazione, tra le altre, delle seguenti informazioni:
— finalità del trattamento
— category di personali trattati
— destinatari cui questi sono stati o saranno comunicazione, or saranno comunicazione
— periodo di conservatiazi
— период использования — diritti dell’interessato (rettifica, cancellazione dei dati personali, limitazione del trattamento e diritto di opposizione al trattamento
— diritto di proporre u n reclamo
— информация об исходной информации, полученная при помощи персонализированных данных, не зависит от качества печати
— система обработки автоматических решений, сжатая информация;
diritto di rettifica — статья 16 GDPR: diritto di ottenere, senza ingiustificato ritardo, la rettifica dei dati personali inesatti che La riguardano e / o l’integrazione dei dati personali unpleti;
diritto alla cancellazione (diritto all’oblio) — статья 17 GDPR: diritto di ottenere, senza ingiustificato ritardo, la cancellazione dei dati personali che La riguardano, quando:
— dati non sono più needari rispetto alle finalità per cui sono finalità altrimenti trattati;
— Lei ha revocato il Suo console e non sussiste alcun altro fondamento giuridico per il trattamento;
— Lei si è opposto con successo al trattamento dei dati personali;
— i dati sono stati trattati illecitamente,
— i dati devono essere cancellati per adempiere un obbligo legale;
— Персональные данные, относящиеся к статистике, относятся ко всем услугам, предоставляемым обществом по вопросам искусства, 8, параграф 1, GDPR.
Il diritto alla cancellazione non si application misura in cui il trattamento sia needario per l’adempimento di un obbligo legale o per l’esecuzione di un compito svolto nel pubblico interesse o per l’accertamento, l’esercizio un la Difesa diritto in sede giudiziaria.
— diritto di limitazione di trattamento — статья 18 GDPR: diritto di ottenere la limitazione del trattamento, quando:
— l’interessato contesta l’esattezza dei dati personali;
— il trattamento è illecito e l’interessato si oppone alla cancellazione dei dati personali e chiede invece che ne sia limitato l’utilizzo
— Benché il titolare del trattamento non ne abbia più bisogno ai fini del trattamenti sono, i datiments ‘interessato per l’accertamento, l’esercizio o la difesa di un diritto in sede giudiziaria;
— l’interessato si è opposto al trattamento, come oltre indicato, in attesa della verifica in merito all’eventuale prevalenza dei motivi legaltimi del titolare del trattamento rispetto a quelli dell’interessato;
— diritto alla portabilità dei dati — статья 20 GDPR: diritto di risvere, in un formato strutturato, di uso comune e leggibile da un dispositivo automatico, i dati personali che La riguardano forniti al Titolare e il diritto di trasmetterli a un altro titolare Impedimenti, qualora il trattamento si basi sul консенсус e sia effettuato con mezzi automatizzati. Inoltre, il diritto di ottenere che i Suoi dati personali siano trasmessi direttamente dal Titolare ad altro titolare qualora ciò sia tecnicamente fattibile;
Inoltre, il diritto di ottenere che i Suoi dati personali siano trasmessi direttamente dal Titolare ad altro titolare qualora ciò sia tecnicamente fattibile;
— diritto di opposizione — статья 21 GDPR: diritto di opporsi, in qualsiasi momento, al trattamento dei dati personali che La riguardano basati sulla condizione di legaltimità del законный интерес, compresa la profilazione, salvo che susstimistani непрерывно иль мотивации trattamento che prevalgono sugli interessi, sui diritti e sulle libertà dell’interessato oppure per l’accertamento, l’esercizio o la difesa di un diritto in sede giudiziaria.
— proporre reclamo all’Autorità Garante per la protezione dei dati personali, Piazza di Montecitorio n. 121, 00186, Рома (РМ).
I diritti di cui sopra potranno essere esercitati, nei confronti del Titolare, contattando i riferimenti indicati nel prevdente punto 1. Il Titolare provvederà a prendere carico della Sua richiesta ea fornirle, senza ingiusentro meunsecto ritard dal risvimento della stessa, ле информация об относительной all’azione intrapresa riguardo alla Sua richiesta.
L’esercizio dei Suoi diritti in qualità di interessato è gratuito ai sensi dell’articolo 12 GDPR. Tuttavia, nel caso di richieste manifestamente infondate o eccessive, anche per la loro ripetitività, il Titolare potrebbe addebitarle un contributo spese ragionevole, alla luce dei costi amministrativi sostenuti per gestired la Sua rich deoda, sua richiesta.
La informiamo, infine, che il Titolare potrà richiedere ulteriori informazioni, needarmare l’identità dell’interessato.
ПОЛИТИКА COOKIES
Если Piaggio использует технологию cookie, чтобы узнать больше о навигации для всех пользователей, посещающих этот сайт.
Файл cookie содержит размер изображений, которые можно посещать в браузере, и запоминать их, чтобы сохранять данные по ритрамам в Sito Stesso alla successiva visita del medesimo Utente.
I cookie sono usati per Difference finalità tra cui esecuzione di autenticazioni informatiche; monitoraggio di sessioni; Запомните информацию о конкретной конфигурации, которая будет использоваться для доступа к серверу.
Questi consentendo al Sito di ricordare i dati dell’Utente per la durata della visita o per le visite sequence, permettono all’Utente di navigare tra le pagine in modo efficiente, memorizzano le sue preferenze, согласие на quest’ultimo di intergire con i Социальные сети включают Facebook, Google, Instagram и сервисы Google Maps.
Файлы cookie могут быть использованы для запоминания данных входа в систему и автоматически отрисованы с помощью riconoscimento dell’Utente (что очень важно для процедуры установки имени пользователя и пароля, который может быть использован).
Il trattamento dei dati avviene con l’ausilio di Strumenti elettronici o, comunque, automatizzati, informatici o telematici, с логикой, которая соотносится со всеми finalità pi sopra espresse e, comunque, в modo da garantire la sicurezzatessa de la rize.
Cookie tecnici (che NON richiedono il Suo Consunso)
In base alla normativa vigente in Italia, per l’utilizzo dei cookie non semper è richiesto un espresso connso dell’utente. В частности, не Richiedono Tale Connso i cookie tecnici, cioè quelli utilizzati al solo fine di effettuare la trasmissione di una comunicazione su una rete di comunicazione elettronica, или nella misura strettamente, mustaria per erogare un servizio esplicit richiestolicit.Si tratta, in altre parole, di cookie indispensabili for il funzionamento del sito or required per eseguire attività richieste dall’utente.
В частности, не Richiedono Tale Connso i cookie tecnici, cioè quelli utilizzati al solo fine di effettuare la trasmissione di una comunicazione su una rete di comunicazione elettronica, или nella misura strettamente, mustaria per erogare un servizio esplicit richiestolicit.Si tratta, in altre parole, di cookie indispensabili for il funzionamento del sito or required per eseguire attività richieste dall’utente.
Tra i cookie tecnici, che non richiedono un connso espresso per il loro utilizzo, il Garante per la protezione dei dati personali italiano, ricomprende anche:
— i cookie analytics laddove utilizzati direttamente dal gestore del gestore del sito perccogl , sul numero degli utenti e su come questi visitano il sito stesso,
— i cookie di navigation or di sessione (per autenticarsi, per realizzare un acquisto, ecc.),
— файл cookie функционального назначения, который позволяет выполнять все функции навигации в серии критериев выбора (ad esempio, lingua, i prodotti selezionati per l’acquisto) в прекрасном улучшении обслуживания.
Cookie di profilazione (che richiedono il Suo CONSENSO): это место, где используется печенье и компакт-диск. профиль, который можно установить соло с предварительным соглашением.
I cookie профилированного звука создает профили релятивов, которые используются и используются прекрасными сообщениями для публикации в линии с предпочтениями, проявляют не только стессо, но и навигацию в сети.Эти файлы cookie, которые используются в настоящее время, содержат больше всего содержимого и являются собственными интересами. Вы можете использовать для публичных визуализаций мира или ограничивать количество изменяемых визуализаций, которые публикуются.
Per la medesima finalità, e Attributeverso trattamenti automatizzati di vario typeo, i dati così raccolti potranno essere arricchiti e incrociati con dati proofs da altre fonti, в частности с данными азиады навигации по альтернативным азиатским сторонам, основанным на новостях utenti, create classi omogene e dati di sintesi relativi a ciascun utente; Эти данные и информация о потенциальных клиентах с электронной формой и статистикой для атрибутов бизнес-аналитики и автоматизации маркетинга. Для получения информации о программах NESSIE и других участниках щелкните по следующему адресу: https://www.neodatagroup.com/it/security-policy/neodata-services-privacy-policy.
Для получения информации о программах NESSIE и других участниках щелкните по следующему адресу: https://www.neodatagroup.com/it/security-policy/neodata-services-privacy-policy.
In ragione della special invasività che tali dispositivi Possono avere nell’ambito della sfera privata degli utenti, la normativa europea e italiana prevede che l’utente debba essere adeguatamente informato sull’uso degli stessi ed esprimeore esprimeore. I cookie di profilazione, needitano dell’acquisizione превентивная del libero consnso informato dell’utente, che il Sito acquisisce nelle forme previste dal Provvedimento Attributeverso il banner, che compare alla prima visita nonché tramite l’informativa estesa che permette di Concedere all’utente относительный консенсус.
Cookie di prima parte e di terze parti
Эти файлы cookie должны быть прекращены для прекращения использования файлов cookie, установленных непосредственно на сайте, где вы находитесь, на сайте, где вы находитесь, при отправке файлов cookie в первую очередь. Nel corso della navigazione sul sito, l’Utente può però risvere sul suo terminale anche cookie di siti o di web server diversi (cd cookie di terze parti) sui quali Possono risiedere alcuni elementi (quali, ad esempio, imagini, mappe, suoni, конкретная ссылка на страницу других доминант) presenti sul sito che lo stesso sta visitando.В этом случае, если вы хотите, чтобы файлы cookie были представлены на сайте, вы можете найти его в Интернете.
Nel corso della navigazione sul sito, l’Utente può però risvere sul suo terminale anche cookie di siti o di web server diversi (cd cookie di terze parti) sui quali Possono risiedere alcuni elementi (quali, ad esempio, imagini, mappe, suoni, конкретная ссылка на страницу других доминант) presenti sul sito che lo stesso sta visitando.В этом случае, если вы хотите, чтобы файлы cookie были представлены на сайте, вы можете найти его в Интернете.
Blocco dei cookie
L’Utente può selezionare quali cookie autorizzare attverso l’apposita procedure di seguito prevista, nonché autorizzare, bloccare or cancellare (in tutto or in parte) i cookie anche Attributes le specifiche funzioni del proprio programma browser): tuttavia, nell’ipotesi in cui tutti o alcuni dei cookie vengano disabilitati, возможно, что это не консультируемое место или какие-либо услуги или определенные функции для сайта, не являющегося синонимом, или не функциональные, соответствующие e / cost или estete модифицируйте подробное руководство по всей информации или предпочтительнее всего, чтобы посетить сайт.
Если хотите изменить импостационы из восточных файлов cookie в сегменты, которые будут отправлены по истечении срока действия, чтобы выполнить работу в более поздних браузерах:
Microsoft Internet Explorer
Cliccare l’icona ‘Strumenti’ nell’angolo in alto destroy ‘ ‘. Nella finestra всплывающее окно выбора «Конфиденциальность». Qui potrete regolare le impstazioni dei vostri cookies.
Google Chrome
Cliccare la chiave inglese nell’angolo in alto a destra e selezionare ‘Impostazioni’.Questo punto selezionare «Mostra imstazioni avanzate» («Под капотом») и cambiare le Impostazioni della «Privacy».
Mozilla Firefox
Сделать меню «Тендина не анголо», а также альтернативный выбор «Варианты». Nella finestra di pop up selezionare «Privacy». Qui potrete regolare le impstazioni dei vostri cookies.
Safari
Это меню с добавлением тенниски без анголо в альте с выбором «Preferenze». Выберите «Sicurezza» и попробуйте приготовить печенье.
Come già disposto nel banner di немедленное сравнение с первым посещением Сито, с согласованным использованием всех файлов cookie, использующих верный предварительный выбор после полного выбора виртуального вкуса (ad esempio un OK, un check и т. Д.) la navigazione all’interno del Sito (ad esempio ignorando il banner / pop-up e effettuando ulteriori operazioni). L’Utente avrà inoltre libero accesso al link all’informativa estesa, complete di all informazioni relative ai cookies (descrizione, finalità e conservazione), nella quale l’Utente del Sito avrà la возможная категория esprimere il consnso solo per alcuneorie .
Д.) la navigazione all’interno del Sito (ad esempio ignorando il banner / pop-up e effettuando ulteriori operazioni). L’Utente avrà inoltre libero accesso al link all’informativa estesa, complete di all informazioni relative ai cookies (descrizione, finalità e conservazione), nella quale l’Utente del Sito avrà la возможная категория esprimere il consnso solo per alcuneorie .
Tipologia di cookie
Al fine di giungere a una corretta regolamentazione dei cookies, nonché ad una consapevole manifestazione del Connso all’utilizzo o meno degli stessi, di seguito viene riportata una breve informativa delle различные категории в различных категориях.
1) Cookie tecnici
Di seguito vengono elencati i cookie tecnici utilizzati dal sito:
Google Analytics: https://developers.google.com/analytics/devguides/collection/analyticsjs/
cookie-usage
2) Cookie di profilazione
Il Sito non utilizza cookie di profilazione di prima parte, non ritiene opporre il Consunso esplicito dell’utente.
Di seguito vengono elencati i cookie di profilazione di terze parti utilizzati dal sito:
Amnet: https://www.amnetgroup.com/terms-and-privacy/
Adform: http://site.adform.com/privacy -policy / en
Doubleclick: https://www.google.com/intl/en/policies/technologies/ads/
Sizmek: https://www.sizmek.com/privacy-policy/optedin/
Facebook: https : //www.facebook.com/policies/cookies/
Zanox: https://www.awin.com/gb/legal
Tradedoubler: http: //www.tradedoubler.com / it / politica-sulla-privacy /
Уточнить: https://site.adform.com/privacy-policy-opt-out
Sono consapevole, который согласован и действителен в соответствии с предварительным статусом, если он находится в этой области или на Маджоре 16 лет назад. Это предложение, compilando il campo di seguito indicato, dichiaro di aver raggiunto story limit di età. Conriferimento al trattamento dei miei dati personali для finalità di marketing, di cui al punto 3.3 dell’Informativa, attverso modalità automatizzate (качественная электронная почта, sms, mms, push-уведомления и социальная сеть) и традиционные (quali posta cartacea e telefonate con operato) :
Вписанные и ограниченные круги и многоугольники в GMAT
Вписанные и ограниченные
Еще один сложный тип геометрической диаграммы включает в себя многоугольники «внутри» окружностей или окружности «внутри» многоугольников. Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на окружности:
Когда многоугольник находится «внутри» круга, каждая вершина должна лежать на окружности:
На этой диаграмме неправильный пятиугольник ABCDE — это , вписанный в окружность , а окружность — , описанная вокруг пятиугольника, . Можно также сказать: окружность ограничивает пятиугольник. Слово «вписанный» описывает внутреннюю форму, а слово «описанный» описывает внешнюю форму. Вот еще одна диаграмма с многоугольником снаружи.
Обратите внимание на то, что каждая сторона этого неправильного пятиугольника составляет касательных к окружности.Теперь пятиугольник — это , описанный на по окружности, а круг — это , вписанный в пятиугольник . В обоих случаях внешняя форма описывается, а внутренняя форма вписывается.
Треугольники
Как это часто бывает при обсуждении многоугольников, треугольники — это особый случай при обсуждении вписанного и описанного. Каждый возможный треугольник может быть вписан в один круг и описывать другой круг .Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Каждый возможный треугольник может быть вписан в один круг и описывать другой круг .Это «универсальное двойное членство» верно ни для каких других многоугольников более высокого порядка — оно верно только для треугольников. Вот небольшая галерея треугольников, каждый из которых вписан в один круг и описывает другой.
Обратите внимание, что когда один угол особенно тупой, близкий к 180 °, разница в размерах между описанной окружностью и вписанной окружностью становится довольно большой. Также обратите внимание: в случае прямоугольного треугольника, второго изображения, гипотенуза треугольника — это диаметр описанной окружности.Мы вернемся к этому моменту.
Четырехугольники
Многие четырехугольники нельзя ни вписать в круг, ни описать кругом: то есть невозможно построить круг, проходящий через все четыре вершины, а также невозможно построить круг, к которому все четыре стороны обращены. касательная.
Некоторые четырехугольники, например продолговатый прямоугольник, можно вписать в круг, но нельзя описать круг. Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в него.
Другие четырехугольники, такие как наклонный ромб, описывают круг, но не могут быть вписаны в него.
Несколько элитных четырехугольников могут описывать один круг и вписываться в другой круг. Конечно, квадрат (внизу слева), самый элитный из четырехугольников, обладает этим свойством. Другой пример — «правый змей» (внизу справа), змей с парой противоположных прямых углов:
Хотя это «двойное членство» верно для всех треугольников, оно ограничено некоторыми частными случаями с четырехугольниками.
Высшие полигоны
То, что было верно для четырехугольников, верно и для всех высших многоугольников.
а. Большинство, подавляющее большинство, не могут ни описать круг, ни вписать круг.
г. Некоторые можно вписать в круг, но нельзя описать круг.
г. Некоторые могут описать круг, но не могут быть вписаны в круг.
г. Некоторые избранные могут как описать круг, так и вписаться в него.
Последняя категория, элитные члены, всегда включает правильный многоугольник.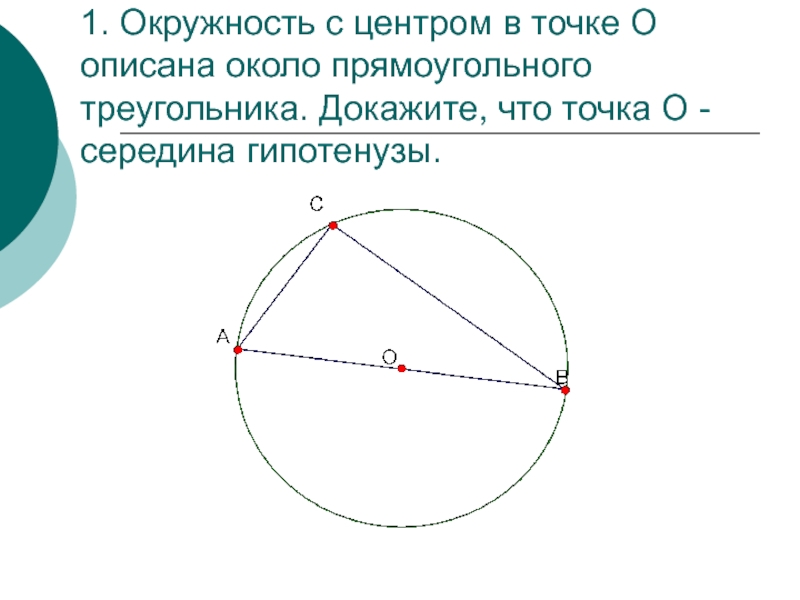 Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.Вот галерея правильных многоугольников, как с вписанными, так и с описанными кругами.
Подобно тому, как все треугольники имеют это «двойное членство», так и все правильные многоугольники.Вот галерея правильных многоугольников, как с вписанными, так и с описанными кругами.
Очевидно, что по мере увеличения количества сторон размеры двух окружностей становятся все ближе и ближе.
ВопросыGMAT о вписанных и описанных многоугольниках встречаются редко и могут проверить ваше понимание терминологии и навыки визуализации, описывая геометрическую ситуацию (например, «прямоугольник JKLM вписан в круг») и , а не , дающий вам диаграмму .
Особый случай: треугольник, вписанный в полукруг
Это особый случай, который нравится GMAT. Он появляется в OG13 (DS # 118) и может легко появиться где-нибудь в разделе Quant вашего настоящего GMAT.
Если все, что вам известно, это то, что KL — это диаметр окружности, этого достаточно, чтобы установить, что ∠J = 90 ° и что треугольник JKL — это прямоугольный треугольник с KL в качестве гипотенузы. С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром.Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
С другой стороны, если все, что вам известно, это то, что треугольник JKL является прямоугольным с KL в качестве гипотенузы, этого достаточно, чтобы установить, что дуга KJL является полукругом, а KL — диаметром.Это мощный набор идей, потому что выводы работают в обоих направлениях и потому, что он неразрывно связывает две, казалось бы, несопоставимые идеи.
Кстати, этот пост — четвертый в серии из пяти статей. Вот вся серия.
1) Введение в круги на GMAT
2) GMAT Geometry: круги и углы
3) Круговые и линейные диаграммы по GMAT
4) Вписанные и ограниченные круги и многоугольники в GMAT
5) Нарезка кругов GMAT: длины арок, секторы и числа Пи
Практический вопрос
1) На диаграмме выше S — центр круга.Если QS = 5 и QR = 6, что такое PQ?
А. 7
Б. 8
C. 9
Д. 10
E. 11
Разъяснение практических вопросов
1) Прежде всего, QS — это радиус, поэтому, если QS = 5, это означает PS = SR = 5 и диаметр PR = 10.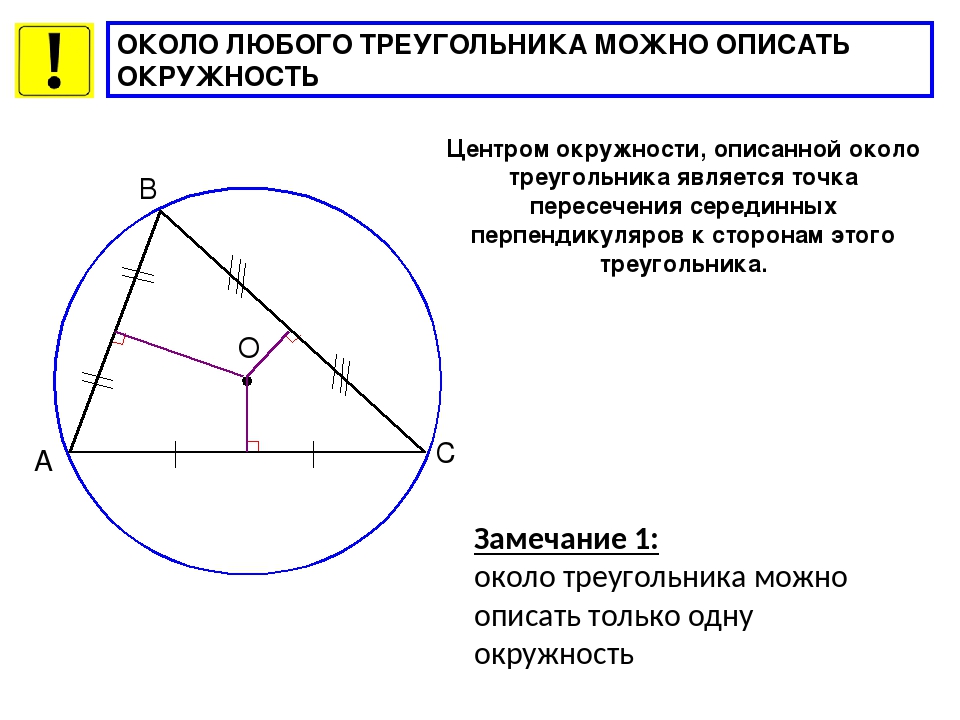 Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным треугольником с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
Кроме того, поскольку PR — это диаметр, это означает, что треугольник PQR является прямоугольным треугольником с ∠PQR = 90 °. Нам известны две стороны этого прямоугольного треугольника: QR = 6 и PR = 10, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону.2 = 100 — 36 = 64
PQ = sqrt {64} = 8
Ответ = B
Готовы получить отличный результат GMAT? Начните здесь.
Самые популярные ресурсы
О Майке MᶜGarry
Майк создает уроки для экспертов и практические вопросы, чтобы помочь студентам GMAT добиться успеха. У него есть степень бакалавра физики и магистра религии в Гарварде, а также более 20 лет опыта преподавания, специализирующегося на математике, естественных науках и стандартизированных экзаменах.Майк любит разбивать футбольные мячи на орбите, и, несмотря на отсутствие очевидных черепных дефектов, он настаивает на том, чтобы поддержать Нью-Йорк Метс. .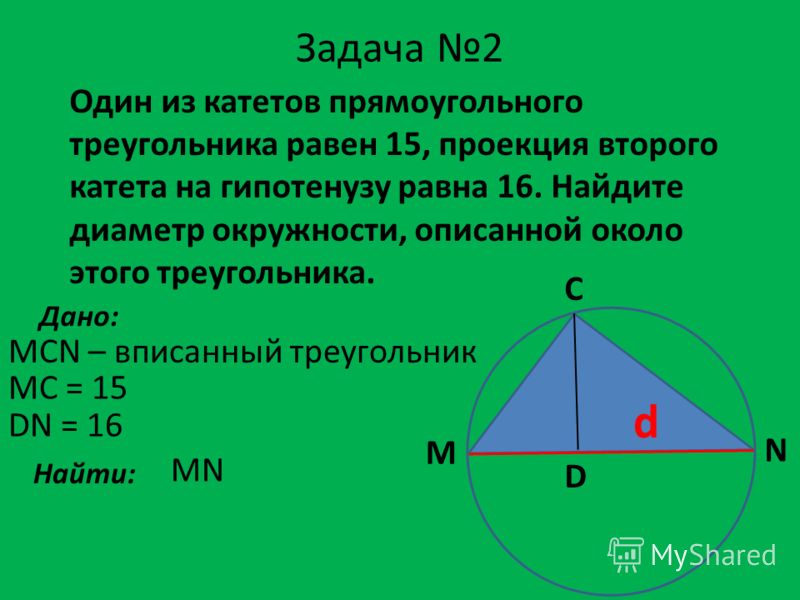



 В перечень консалтинговых услуг также входят разработка миссии, внедрение системы сбалансированных показателей (BSC), реорганизация системы управления компанией, создание системы стратегического управления, системы планирования и контроля, а также другие услуги консалтинга.
В перечень консалтинговых услуг также входят разработка миссии, внедрение системы сбалансированных показателей (BSC), реорганизация системы управления компанией, создание системы стратегического управления, системы планирования и контроля, а также другие услуги консалтинга.
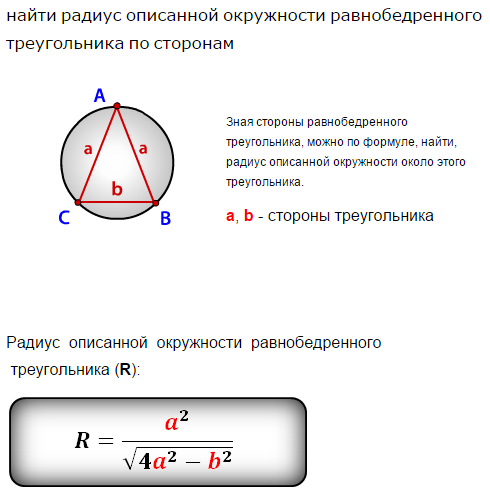
 Если никто из пользователей не подскажет, тогда помочь попытается администрация сайта. Если Вы не нашли в онлайн курсах задачу, похожую на Вашу, напишите об этом на форуме и администрация сайта или его посетители попробуют помочь. За решение задач можно получить небольшое материальное вознаграждение. Многие учебные материалы формируются именно на основе изучения администрацией сайта содержания форума
Если никто из пользователей не подскажет, тогда помочь попытается администрация сайта. Если Вы не нашли в онлайн курсах задачу, похожую на Вашу, напишите об этом на форуме и администрация сайта или его посетители попробуют помочь. За решение задач можно получить небольшое материальное вознаграждение. Многие учебные материалы формируются именно на основе изучения администрацией сайта содержания форума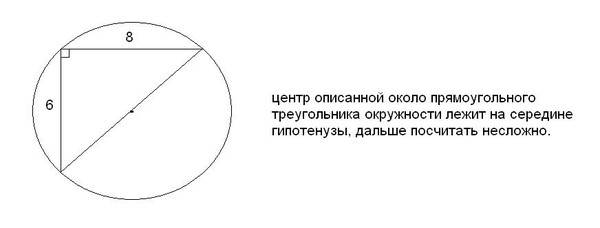 Как оформить выплаты по беременности и родам (декретные)?
Как оформить выплаты по беременности и родам (декретные)? 09.16 вступив в силу новий Закон України «Про судоустрій та статус суддів» за яким визначаються як зміни у структурі суду, так і зміни в управлінській діяльності суду та фінансовому забезпеченні. На це також, безсумнівно, вплинули зміни до Конституції України, а саме…
09.16 вступив в силу новий Закон України «Про судоустрій та статус суддів» за яким визначаються як зміни у структурі суду, так і зміни в управлінській діяльності суду та фінансовому забезпеченні. На це також, безсумнівно, вплинули зміни до Конституції України, а саме… 
 В общем, смеемся вместе
В общем, смеемся вместе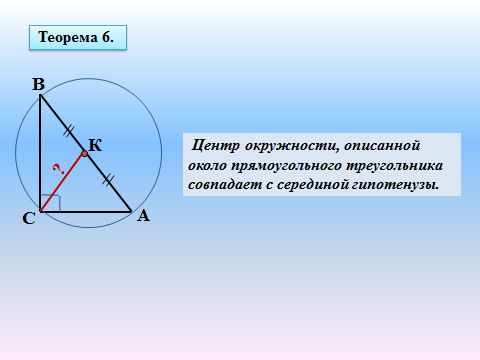 д.
д.
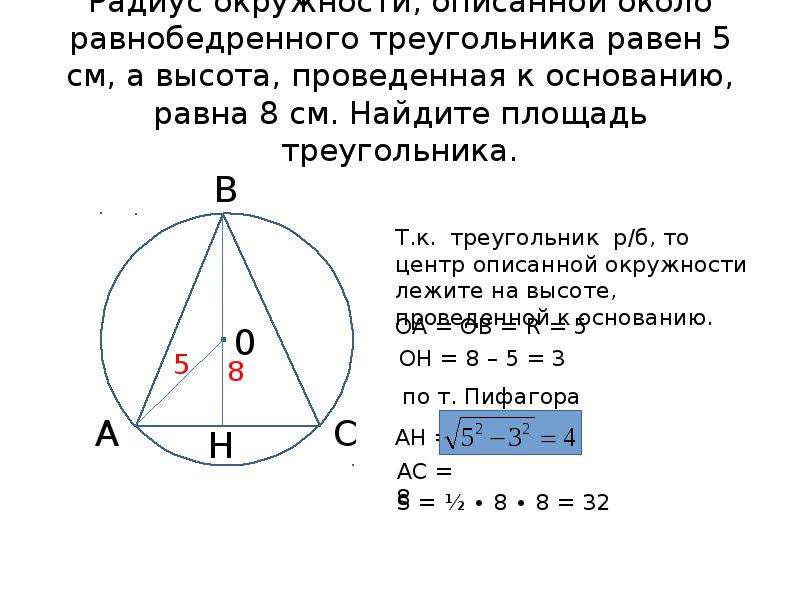
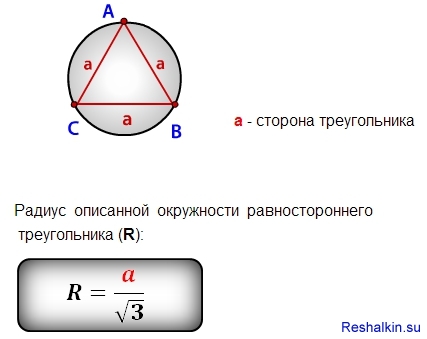
 Это одна из форм теоремы Фалеса.
Это одна из форм теоремы Фалеса.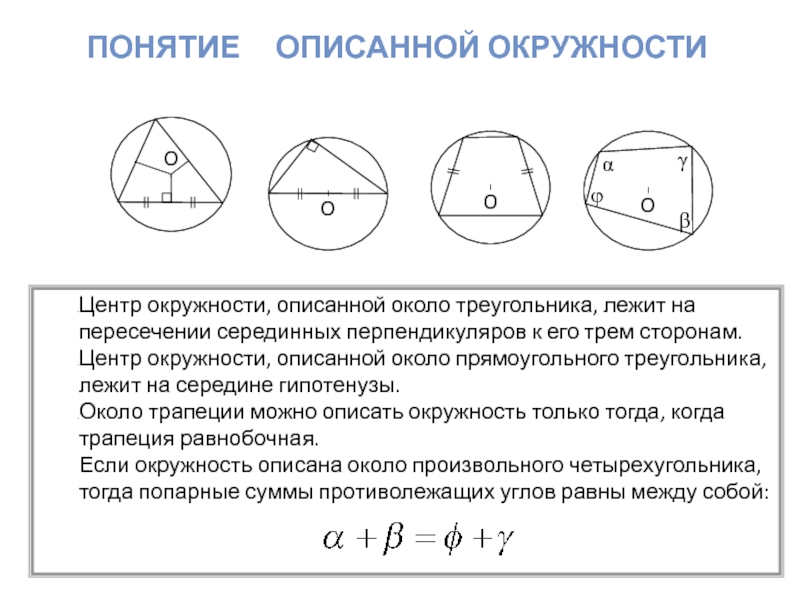 Уравнение для этого эллипса: 1 / ( ax ) + 1 / ( на ) + 1 / ( cz ) = 0.)
Уравнение для этого эллипса: 1 / ( ax ) + 1 / ( на ) + 1 / ( cz ) = 0.)
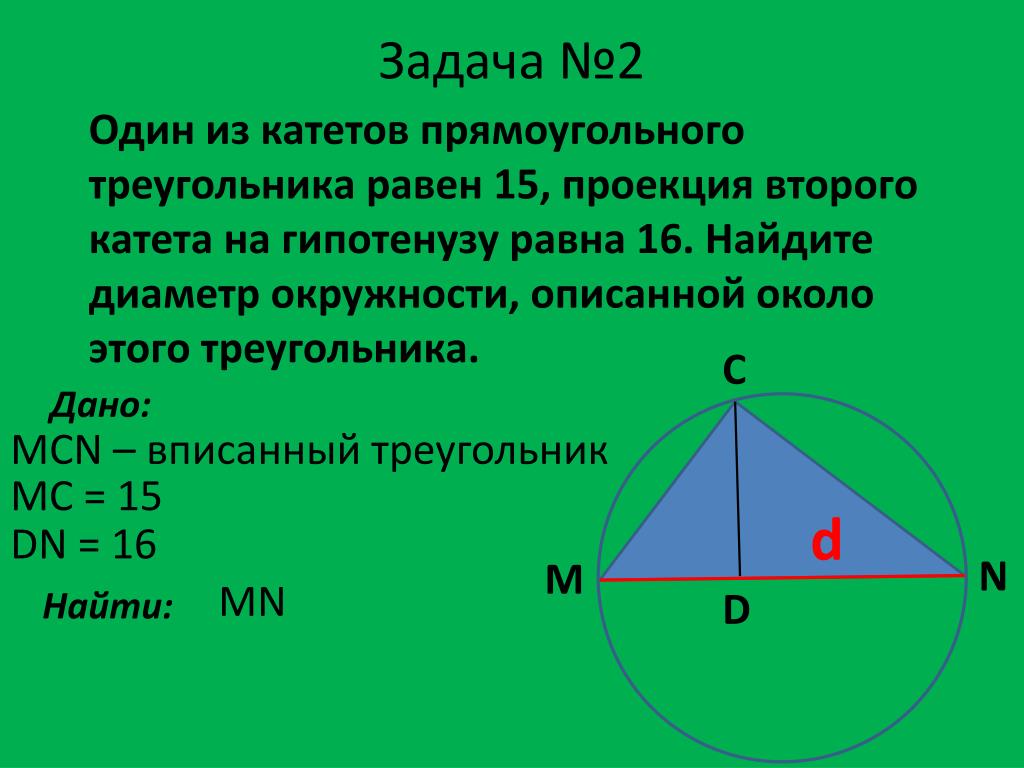
Leave A Comment