Касательная к окружности — свойства, теорема, правила
Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку. |
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой. |
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Найдите величину дуги АВ.
Решение:
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника
∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
Ответ: АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
 Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши
Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Ответ: ∠BDA = 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла
Требуется определить величину угла
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°
Ответ: ∠NМК = 65°.
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
AB2 = AD × AC
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ — ВС = 16 — 12 = 4 (см)
МА2 = МВ × МС = 16 х 4 = 64
МА = √ 64= 8 (см)
Ответ: MA = 8 см.
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА2 = МВ × МС.
Значит:
(у + R)2 : 4 = (у + R) × (у — R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
(у + R) : 4 = (у — R)
у = 5R : 3
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
∠АВС = ½ АВ
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Ответ: АВ = 64°.
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠КОМ = КМ = 168°
∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°
Ответ: ∠ОМК = 6°.
Вписанный и описанный четырехугольники: свойства, признаки, диагонали
Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.
Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.
Рассмотрим теоремы о вписанных и описанных четырехугольниках и их свойствах.
Теорема 1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны
Теорема 2. Четырёхугольник можно описать вокруг окружности тогда и только тогда, когда суммы его противоположных сторон равны.
Теорема 3. Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.
Теорема 4. (Птолемея). Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Теорема 5. Площадь описанного четырехугольника равна произведению полупериметра четырёхугольника на радиус вписанной в него окружности.
Теорема 6. Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Теорема 7. Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Теорема 8. Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.
Теорема 9. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 10. В любой ромб можно вписать окружность.
Теорема 11. В любой квадрат можно вписать окружность.
Теорема 12. В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом.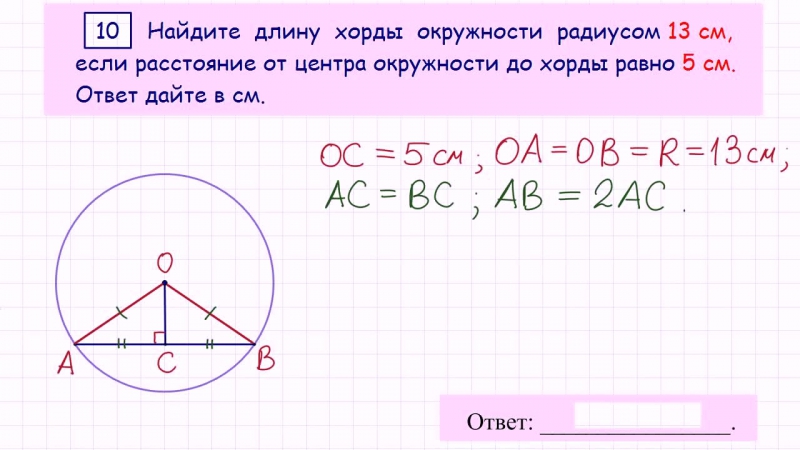
Теорема 13. В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Теорема 14. В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований.
Посмотрим, как эти свойства применяются в решении задач ЕГЭ.
Задача 1. Два угла вписанного в окружность четырехугольника равны и . Найдите больший из оставшихся углов. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна . Пусть угол равен . Тогда напротив него лежит угол в градусов. Если угол равен , то угол равен .
Ответ: 122.
Задача 2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен .
Решение:
Пусть сторона равна , равна , а . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,
Получается, что равна . Тогда периметр четырехугольника равен . Мы получаем, что , а большая сторона равна .
Ответ: 12.
Задача 3. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.
Решение:
Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны и , а боковые стороны — и . По свойству описанного четырехугольника,
, и значит, периметр равен .
Получаем, что , а средняя линия равна .
Ответ: 10.
Задача 4. Угол A четырехугольника , вписанного в окружность, равен . Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Четырехугольник вписан в окружность. Значит, сумма его противоположных углов равна
Поэтому
Ответ: 148.
Задача 5. Углы четырехугольника относятся как . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Решение:
Пусть
Сумма всех углов четырехугольника равна
А сумма каждой пары противоположных углов равна (т.к. четырехугольник вписан в окружность).
Запишем эти два условия в виде двух уравнений с двумя неизвестными:
Подставляем второе уравнение в первое и получаем
Ответ: 90.
Задача 6. Стороны четырехугольника и стягивают дуги описанной окружности, градусные величины которых равны соответственно и . Найдите угол C этого четырехугольника. Ответ дайте в градусах.
Решение:
Сумма противоположных углов вписанного четырехугольника равна .
Поэтому
Угол А – вписанный, опирается на дугу , равную сумме дуг и , т.е.
Тогда вписанный угол А равен половине дуги , т.е.
Ответ: 107.
Задача 7. Точки расположенные на окружности, делят эту окружность на четыре дуги и градусные величины которых относятся соответственно как Найдите угол A четырехугольника Ответ дайте в градусах.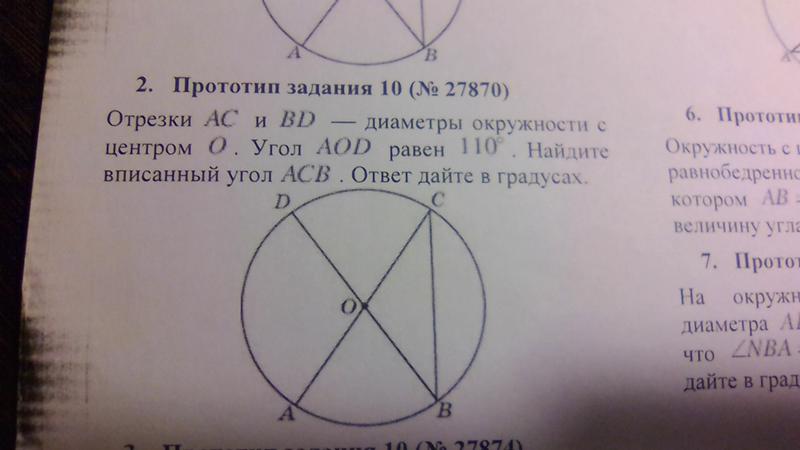
Решение:
Угол А – вписанный, опирается на дугу равную сумме дуг и Найдем дуги и
Обозначим градусные величины дуг и как согласно заданному соотношению между дугами.
Тогда или
Сумма дуг и составляет
Вписанный угол А равен половине дуги т.е.
Ответ: 15.
Задача 8. Радиус окружности, описанной около квадрата, равен Найдите длину стороны этого квадрата.
Решение:
Радиус окружности, описанной около квадрата, равен половине диагонали квадрата. Тогда диагональ квадрата равна
Выразим сторону квадрата через его диагональ:
Ответ: 32.
Задача 9. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Решение:
Если правильный шестиугольник вписан в окружность, то радиус окружности равен стороне шестиугольника. Поэтому сторона равна 6.
Ответ: 6.
Задача 10. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Найдите радиус описанной окружности этой трапеции.
Решение:
Поскольку трапеция вписана в окружность, она равнобедренная.
Рассмотрим равнобедренную трапецию с основаниями
Тогда боковые стороны
Проведем параллельно Тогда треугольник – равнобедренный, т.к. и равносторонний, т.к. Поэтому
– параллелограмм по построению, но , поэтому – ромб, и
Получаем, что О – центр описанной окружности с радиусом, равным меньшему основанию –
Ответ: 6.
Задача 11. Найти диагональ параллелограмма, вписанного в окружность радиусом 6 см.
Решение:
Согласно одной из теорем, окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру, см.
Ответ: 12.
Задача 12. Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.
Найдите боковую сторону трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Поэтому сумма оснований
Сумму боковых сторон найдем как разность между периметром и суммой оснований:
Трапеция вписана в окружность, следовательно, трапеция равнобедренная, боковые стороны равны:
Ответ: 5.
Задача 13. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и
Решение:
Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру окружности.
В то же время по теореме Пифагора диагональ найдем как
Радиус окружности равен половине диаметра:
Ответ: 9.
Задача 14. Найдите радиус окружности, вписанной в квадрат со стороной 16.
Решение:
Радиус окружности, вписанной в квадрат, равен половине его стороны. Поэтому
Ответ: 8.
Задача 15. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Найдите радиус окружности.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна 11 (половине периметра).
Боковая сторона тогда боковая сторона
Радиус вписанной окружности равен половине т.е. 2.
Ответ: 2.
Задача 16. Найдите высоту трапеции, в которую вписана окружность радиуса 14.
Решение:
Высота трапеции, в которую вписана окружность, равна диаметру этой окружности:
Ответ: 28.
Задача 17. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.
Решение:
Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна
Средняя линия трапеции равна полусумме оснований
Ответ: 16.
Задача 18. Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 16. Найдите его площадь.
Решение:
Площадь описанного многоугольника можно найти как произведение полупериметра на радиус вписанной окружности:
Ответ: 16.
Задача 19. В равнобедренной трапеции, вписанной в окружность, диагонали взаимно перпендикулярны. Средняя линия трапеции равна 12. Найти радиус вписанной окружности.
Решение:
Радиус окружности, вписанной в трапецию, равен половине ее высоты.
Рассмотрим равнобедренную трапецию
Проведем Треугольник – прямоугольный (с прямым углом С) и равнобедренный. Его гипотенуза равна сумме оснований трапеции (т.к. – параллелограмм, и ),
Высота трапеции является также высотой и медианой, проведенной из прямого угла равнобедренного прямоугольного треугольника .
Радиус вписанной окружности
Ответ: 6.
Задача 20. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.
Решение:
Пусть О – центр описанной окружности. Проведем высоту проходящую через точку О. Тогда (радиусы окружности),
Треугольники и – прямоугольные. Применяя теорему Пифагора, найдем:
Ответ: 7.
Это были задачи по теме «Вписанные и описанные четырехугольники» из первой части ОГЭ и ЕГЭ. Покажем более сложную задачу, из второй части ОГЭ по математике.
Задача 21. В четырёхугольник можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника перпендикулярны. Найдите его площадь, если радиус описанной окружности равен 5, а
Решение:
Обозначим Тогда
Обозначим также
Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны.
Значит, Отсюда
Пусть О – точка пересечения диагоналей четырёхугольника
При пересечении и образуется четыре прямоугольных треугольника. Это
Пусть
Запишем для каждого из этих треугольников теорему Пифагора:
Из
Из
Из
Из
Мы получили систему уравнений.
Сложив первое и третье из них и выразив как получим:
Кроме того, Это мы нашли в самом начале.
Из системы уравнений
находим:
Значит,
Перестроим чертеж. Это надо сделать обязательно. Появились новые данные – рисуем новый чертеж. По условию, четырехугольник вписан в окружность.
Треугольники и равны по трем сторонам. Значит, углы и равны.
Четырехугольник вписан в окружность, поэтому сумма углов и равна 180 градусов. Мы получили, что углы и – прямые. Тогда – диаметр окружности.
По условию, , тогда
опирается на диаметр.
– прямоугольный, – его гипотенуза.
По теореме Пифагора для :
Отсюда
Ответ: 40.
Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Вписанные и описанные четырехугольники» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.02.2023
Свойства круга из circle.center:(0,7).radius:16
☰
Этот сайт лучше всего просматривать с помощью Javascript. Если вы не можете включить Javascript, нажмите здесь.
Введите уравнение или задачу
Помощь в форматировании
Вход с камеры не распознается!
Мы думаем, что вы писали:
circle.center:(0,7).radius:16
Это решение имеет дело со свойствами кругов.
92-14y-207=0См. шаги
1. Найдите диаметр
Диаметр окружности () в два раза больше ее радиуса (). Чтобы найти диаметр, подставьте в формулу:
2.
 Найдите длину окружности
Найдите длину окружностиДлина окружности () равна удвоенной длине ее радиуса (), умноженной на π. Чтобы найти длину окружности, подставьте r в формулу:
3. Найдите площадь
Площадь круга () равна его радиусу () в квадрате, умноженному на π. Чтобы найти площадь, подставьте в формулу:
4. Найдите уравнение окружности в стандартной форме
Стандартная форма уравнения окружности: центр круга, представляет радиус круга и представляют координаты любой точки по периметру круга.
Чтобы найти уравнение окружности в стандартной форме, подставьте и в уравнение:
5. Найдите уравнение окружности в развернутом виде
Расширенное уравнение окружности имеет вид . Чтобы найти уравнение окружности в развернутом виде, разверните стандартную форму уравнения окружности:
2 дополнительных шага
изобретение колеса считается одним из величайших подвигов человечества и нововведением, которое, наконец, привело к тому, что все стало.
 .. ну, катиться. На протяжении всей истории человечество восхищалось кругами, часто считая их совершенными формами, символизирующими симметрию и равновесие в природе. Несмотря на то, что существует мало доказательств того, что в природе существуют идеальные круги, существует, казалось бы, бесконечное количество созданных человеком примеров и множество в природе, которые приближаются к ним. От контура Стоунхенджа до пиццы, сечения апельсина, ствола дерева, монет и так далее. Поскольку мы окружены кругами и взаимодействуем с ними на регулярной основе, понимание их свойств может помочь нам понять мир вокруг нас.
.. ну, катиться. На протяжении всей истории человечество восхищалось кругами, часто считая их совершенными формами, символизирующими симметрию и равновесие в природе. Несмотря на то, что существует мало доказательств того, что в природе существуют идеальные круги, существует, казалось бы, бесконечное количество созданных человеком примеров и множество в природе, которые приближаются к ним. От контура Стоунхенджа до пиццы, сечения апельсина, ствола дерева, монет и так далее. Поскольку мы окружены кругами и взаимодействуем с ними на регулярной основе, понимание их свойств может помочь нам понять мир вокруг нас.Термины и темы
Ссылки по теме
Вернуться к началуКак найти уравнение окружности
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
ACT Math Help » Алгебра » Координатная плоскость » Круги » Как найти уравнение окружности
Каковы радиус и центр круга в стандартной координатной плоскости?
Возможные ответы:
Правильный ответ:
Объяснение:
При нахождении центра и радиуса круга центр равен , а радиус равен . Обратите внимание, что они не отрицательны, хотя в уравнении перед ними стоят отрицательные знаки. Это становится важным при работе с действительными числами. Также обратите внимание на квадрат .
Обратите внимание, что они не отрицательны, хотя в уравнении перед ними стоят отрицательные знаки. Это становится важным при работе с действительными числами. Также обратите внимание на квадрат .
В нашем круге применяются те же принципы, что и в предыдущем, поэтому он является нашим центром. Обратите внимание, как поменялись местами знаки чисел. Это относится ко всем кругам из-за отрицательного значения в основном уравнении выше.
Чтобы найти радиус окружности, нужно взять число, которому равно уравнение, и извлечь из него квадратный корень. Это связано с упомянутым выше квадратом. . Используйте наименьшее общее кратное 27, чтобы найти, что три тройки составляют 27. Вычтите две тройки, так как квадратный корень из числа, умноженного на самого себя, равен самому себе. Это оставляет один 3 под радикалом. Поэтому наш радиус равен .
Центр: Радиус:
Сообщить об ошибке
Какова площадь круга в стандартной координатной плоскости?
Возможные ответы:
Правильный ответ:
Объяснение:
Общее уравнение окружности .
Согласно вопросу, . Таким образом, .
Общее уравнение площади круга.
Когда мы подставляем 13 вместо , наша площадь становится равной .
Сообщить об ошибке
Окружность в стандартной координатной плоскости касается оси X в точке (3,0) и оси Y в точке (0,3). Что такое уравнение окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула уравнения окружности: (x – h) 2 + (y – k) 2 = r 2 , где (h, k) представляет собой координаты центра круг, а r представляет радиус круга.
Если окружность касается оси x в точке (3,0), это означает, что она касается оси x в этой точке. Если окружность касается оси y в точке (0,3), это означает, что она касается оси y в этой точке. Зная эти две точки, мы можем определить центр и радиус окружности.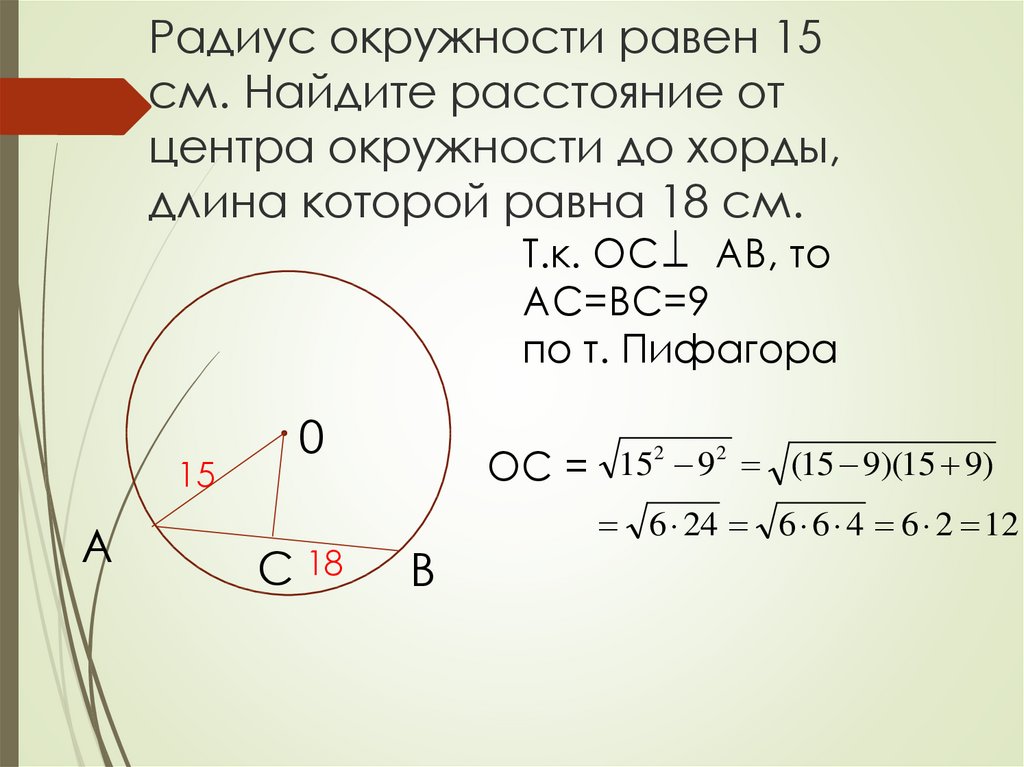 Центр круга должен быть равноудален от любой из точек на окружности. Это означает, что и (0,3), и (3,0) находятся на одинаковом расстоянии от центра. Если мы нарисуем эти точки на координатной плоскости, станет очевидным, что центр окружности должен быть (3,3). Эта точка находится ровно в трех единицах от каждой из заданных точек, что указывает на то, что радиус окружности равен 3,9.0003
Центр круга должен быть равноудален от любой из точек на окружности. Это означает, что и (0,3), и (3,0) находятся на одинаковом расстоянии от центра. Если мы нарисуем эти точки на координатной плоскости, станет очевидным, что центр окружности должен быть (3,3). Эта точка находится ровно в трех единицах от каждой из заданных точек, что указывает на то, что радиус окружности равен 3,9.0003
Когда мы вводим эту информацию в формулу для окружности, мы получаем (x – 3) 2 + (y – 3) 2 = 9.
Сообщить об ошибке
Найти уравнение окружности с координаты центра и радиус .
Возможные ответы:
Правильный ответ:
Объяснение:
Уравнение окружности
Центр равен или, записанному по-другому . Заменив для и для , наша формула становится
Наконец, формула круга
Сообщить об ошибке
На плоскости xy, какова площадь круга со следующим уравнением:
Возможные ответы: 5 5 ответ:
Объяснение:
Уравнение стандартной формы окружности , где – центр окружности, – радиус. Таким образом, поскольку у нас уже есть стандартное уравнение формы окружности, мы можем игнорировать и , поскольку все, что нам нужно, это .
Таким образом, поскольку у нас уже есть стандартное уравнение формы окружности, мы можем игнорировать и , поскольку все, что нам нужно, это .
Площадь круга равна , что равно .
Сообщить об ошибке
Окружность имеет центр в точке (5,5) и радиус 2. Если формат уравнения для окружности (x-A) 2 + (y-B) 2 =C, что такое С?
Возможные ответы:
Правильный ответ:
4
Пояснение:
Центр окружности находится в точке (5,5) и имеет радиус 2. Следовательно, уравнение (x-5) 2 +(y-5) 2 =2 2 , или (x-5) 2 +(y-5) 2 =4.
Сообщить об ошибке
Если центр окружности находится в точке (0,4), а диаметр окружности равен 6, каково уравнение этой окружности?
Возможные ответы:
(x-4) 2 + Y 2 =
(x-4) 2 + y 2 = 36
x 2 + y
2 = 9х 2 + (у-4) 2 = 36
x 2 + (Y-4) 2 = 9
Правильный ответ:
x 2 + (Y-4) 2 =
+ (Y-4) 2 =
. Пояснение:
Пояснение:
Формула уравнения окружности:
(x-h) 2 + (y-k) 2 = r 2
Где (h,k) — центр окружности.
h = 0 и k = 4
и диаметр = 6, поэтому радиус = 3
(x-0) 2 + (y-4) 2 = 3 2
x 2 + (y-4) 2 = 9
Сообщить об ошибке
9000 – 4) 2 + (y + 3) 2 = 29. Окружность A сдвинута вверх на пять единиц и влево на шесть единиц. Затем его радиус удваивается. Какое новое уравнение для окружности A?Возможные ответы:
(x + 2) 2 + (y – 2) 2 = 116
(x + 2) 2 + (у – 2) 2 = 58
(х – 10) 2 + (у + 8) 2 = 116
(х + 5 (2) 2 2 2 = 58
(x — 10) 2 + (Y + 8) 2 = 58
Правильный ответ:
(x + 2) 2 + (Y — 2) 2 = 116
Пояснение:
Общее уравнение окружности: (x – h) 2 + (y – k) 2 = r 2 , где (h, k) представляет собой положение центра круга, а r представляет собой длину его радиуса.
Окружность A сначала имеет уравнение (x – 4) 2 + (y + 3) 2 = 29. Это означает, что ее центр должен находиться в точке (4, –3), а ее радиус равен √ 29.
Затем нам сообщают, что круг А сдвинут вверх на пять единиц, а затем влево на шесть единиц. Это означает, что координата y центра увеличится на пять, а координата x центра уменьшится на 6. Таким образом, новый центр будет расположен в точке (4 – 6, –3 + 5), или ( –2, 2).
Затем нам сообщают, что радиус круга A удвоился, что означает, что его новый радиус равен 2√29.
Теперь, когда у нас есть новый центр и радиус окружности A, мы можем написать ее общее уравнение, используя (x – h) 2 + (y – k) 2 = r 2 . 11
(x + 2) 2 + (y – 2) 2 = 116.
Ответ: (x + 2) 2 + (y – 2) 2 = 116.
Сообщить об ошибке
Какое из следующих уравнений описывает все точки (x, y) на координатной плоскости, которые находятся на расстоянии пяти единиц от точки (– 3, 6)?
Возможные ответы:
у + 6 = 5 – (х – 3) 2
(х – 3) 2 + (у + 6) 3 х 5 0 = 3 0 8 5 0 = 0 = 0 0 = 0 ) 2 – (у + 6) 2 = 25
(х + 3) 2 + (у – 6) 2 = 25
(x — 3) 2 + (y + 6) 2 = 25
Правильный ответ:
(x + 3) 2 + (Y — 6) 2 = 25
Объяснение:
Мы пытаемся найти уравнение для всех точек, находящихся на одинаковом расстоянии (5 единиц) от (–3, 6). Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5.
Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5.
Стандартная форма окружности приведена ниже:
(x – h) 2 + (y – k) 2 = r 2 , где центр расположен в точках (h, k) и r это длина радиуса.
В этом случае h будет равно –3, k будет равно 6, а r будет равно 5.
(x + 3) 2 + (y – 6) 2 = 25
Ответ: (x + 3) 2 + (y – 6) 2 = 25.
Сообщить об ошибке
Уравнение для окружности радиусом 12 с центром на пересечении двух прямых:
y 1 = 4 x + 3
8
у 2 = 5 х + 44?
Возможные ответы:
Ни один из других ответов
(x + 41) 2 + (Y + 161) 2 = 144
(x — 22) 2 + (Y — 3
(x — 22) 2 + (Y — 3. ) 2 = 12
) 2 = 12
(x — 41) 2 + (Y — 161) 2 = 144
(x — 3) 2 + (Y — 44) 2 = 144
Правильный ответ:
(x + 41) 2 + (y + 161) 2 = 144
Объяснение:
Для начала определим точку пересечения этих двух линий, установив равенства между собой:
4 x + 3 = 5 x + 44; 3 = х + 44; –41 = x
Чтобы найти координату y , подставьте в одно из уравнений. Возьмем y 1 :
y = 4 * –41 + 3 = –164 + 3 = –161
Таким образом, центр нашей окружности: (–41, –161).
Теперь вспомним, что общая форма круга с центром в ( x 0 , y 0 ) такова:
( x — x 7 70572) 2 + ( Y — Y 0 ) 2 = R 2
Для наших данных, это означает, что наше равное:
8888 (8 ( (888 (8888 (8888 (8 (888888 (8888 (
8.

Leave A Comment