Радиусы описанной и вписанной окружностей в квадрат
Окружность вписанная в квадрат
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.
Если предположить, что сторона квадрата равна
Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.
Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Находим из этого уравнения неизвестное значение: .
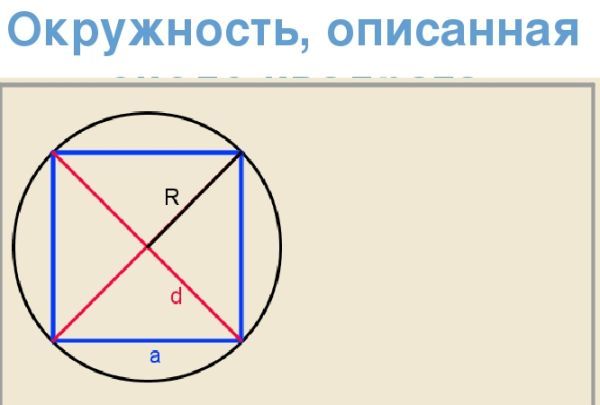
Окружность описанная около квадрата
Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):
Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:
- угол CDA=90°;
- стороны AD=CD. Признак равнобедренного треугольника;
- угол DAC равен ACD. Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности.
Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
Рассмотрим пример
Задача: радиус окружности вписанной в квадрат равен . Найти радиус окружности описанной около этого квадрата.
Дано:
- треугольник ОСЕ – равнобедренный и прямоугольный;
- ОЕ=ЕС=;
- ОЕС=90°;
- ЕОС=ОСЕ=45°;
Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R.
формула. Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапецию? Как найти площадь круга
Словари. Энциклопедии. История. Литература. Русский язык » Энциклопедия » Площадь круга: формула. Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапецию? Как найти площадь круга
Кругом называется часть плоскости, ограниченная окружностью. Основным показателем и для окружности, и для круга является радиус. Если он задан, площадь круга можно вычислить по основной формуле S=πR2, где S – площадь круга, R – радиус окружности, ограничивающей круг, а π – константа, равная 3,14. В условиях задачи может быть дана длина окружности. Она равна L=2πR. В этом случае сначала необходимо вычислить радиус, разделив заданную величину L на 2π, то есть воспользоваться формулой R=L/2π.
По сторонам вписанного четырехугольника
В окружность, ограничивающую круг, может быть вписан четырехугольник, сумма противолежащих углов которого составляет 180°, то есть это квадрат или прямоугольник. В этом случае диаметр описанной вокруг четырехугольника окружности является одновременно диагональю. Если в условиях заданы размеры сторон четырехугольника, найти эту диагональ не составит особого труда, воспользовавшись теоремой Пифагора. Диагональ делит квадрат или прямоугольник на два прямоугольных треугольника, то есть является гипотенузой каждого из этих треугольников. Соответственно, найти ее можно, сложив квадраты сторон четырехугольника, то есть по формуле d2=a2+b2. Чтобы найти площадь круга, даже не нужно из полученного результата извлекать квадратный корень, поскольку R=d/2. Чтобы найти квадрат радиуса, достаточно квадрат диаметра разделить на 4.
По параметрам вписанного в окружность треугольника
Способ решения этого варианта задачи зависит от того, какой треугольник вписан и какие его параметры заданы.
Если треугольник прямоугольны, алгоритм решения будет таким же, как для квадрата или , поскольку сторона, противолежащая прямому углу, всегда является диаметром описанной окружности. Если даны размеры катетов, возведите каждый из них в квадрат и найдите сумму, а затем полученный результат разделите на 4 и умножьте на число π. Если треугольник равносторонний, придется выполнить несколько дополнительных построений, чтобы в итоге получились прямоугольные треугольники, параметры которых вам известны. Например, в окружность с центром О вписан равносторонний треугольник АВС, сторона которого вам задана. Проведите высоты AN, ВM и СQ. Рассмотрите, например, прямоугольный треугольник AQO. Вам известна его гипотенуза AQ, которая равна половине стороны исходного треугольника, а также все углы, так что найти длину отрезка AQ, который одновременно является радиусом круга, площадь которого вам надо найти, можно по теореме синусов или косинусов.
Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура.
У квадрата:
- все углы прямые, то есть, равны 90°;
- все стороны, как и углы, равны;
- диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.
При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат
Если предположить, что сторона квадрата равна у , то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:
Объяснение : в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол
В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.Для наглядности приведем численный пример нахождения величины радиуса вписанной окружности в квадрат со стороной равной 13 см. В данном случае значение вписанного радиуса будет равно:
Легко решить и обратную задачу. Предположим, что известен радиус вписанной окружности – 9 см, тогда анализируя пример нахождения величины радиуса вписанной окружности в квадрат, можно найти сторону квадрата:
Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):
Объяснение : после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA .
- угол CDA=90°;
- стороны AD =CD . Признак равнобедренного треугольника;
- угол DAC равен ACD . Они равны по 45°.
Чтобы найти в этом прямоугольном треугольнике гипотенузу АС , необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:
Поскольку AD =CD , а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:
Численный пример нахождения величины радиуса описанной окружности около квадрата будет таким.
Предположим, что диагональ квадрата равна , тогда:
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.
Величины, участвующие в расчете площади круга
Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. Длины всех радиусов одного круга одинаковы. Отрезок между 2 любыми точками окружности, который проходит через центральную точку, называется диаметром. Длина диаметра равна длине радиуса, умноженной на 2.
Для подсчета площади круга применяется значение числа π. Эта величина равна отношению длины окружности к длине диаметра круга и имеет неизменное значение. Π = 3,1415926. Длина окружности высчитывается по формуле L=2πR.
Найти площадь круга через радиус
Следовательно, площадь круга равна произведению числа π на радиус окружности, возведенный во 2 степень.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
Читайте статью, чтобы знать, как находить площадь квадрата разными способами.
Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами.
Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.
Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b . Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени . Как узнать величину стороны квадрата, зная его площадь?
- Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
- К примеру, площадь угольника равна 49, то чему равняется сторона?
- 49=(а) во второй степени . Решение: а=корень из 49=7. Ответ: 7 .
Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.
В этом примере будем использовать теорему Пифагора.
У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а . Теперь находим диагональ квадрата, если известна его площадь:
- Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата.
- Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
- Получается d=8√2 . Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2 . Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084 .
Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2 .
Формула нахождения площади квадрата через диагональ простая:
Теперь напишем решение по нахождению площади квадрата через диагональ:
- Диагональ d=8.
- 8 в квадрате равняется 64.
- 64 разделить на 2 равно 32.
- Площадь квадрата равна 32.
Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.
Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:
- Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.
- Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36 .
- Ответ: 36
Как видите, зная периметр квадрата, просто найти его площадь.
Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R . Далее находим площадь квадрата вписанного в окружность с заданным радиусом:
- Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10 .
- Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
- Ответ — 50 .
Например радиус равен 5, тогда диагональ равна 2*5=10 .Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.
На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r . Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате . Решение:
- Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
- S=14 в квадрате=196 .
Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.
Примеры решения задач на тему «Площадь квадрата»
Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата».
Начинаем с простой задачи и движемся к решению более сложных: Примеры решения сложных задач на тему «Площадь квадрата»
Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!
Видео: Вычисление площади квадрата
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку.
Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус.
Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
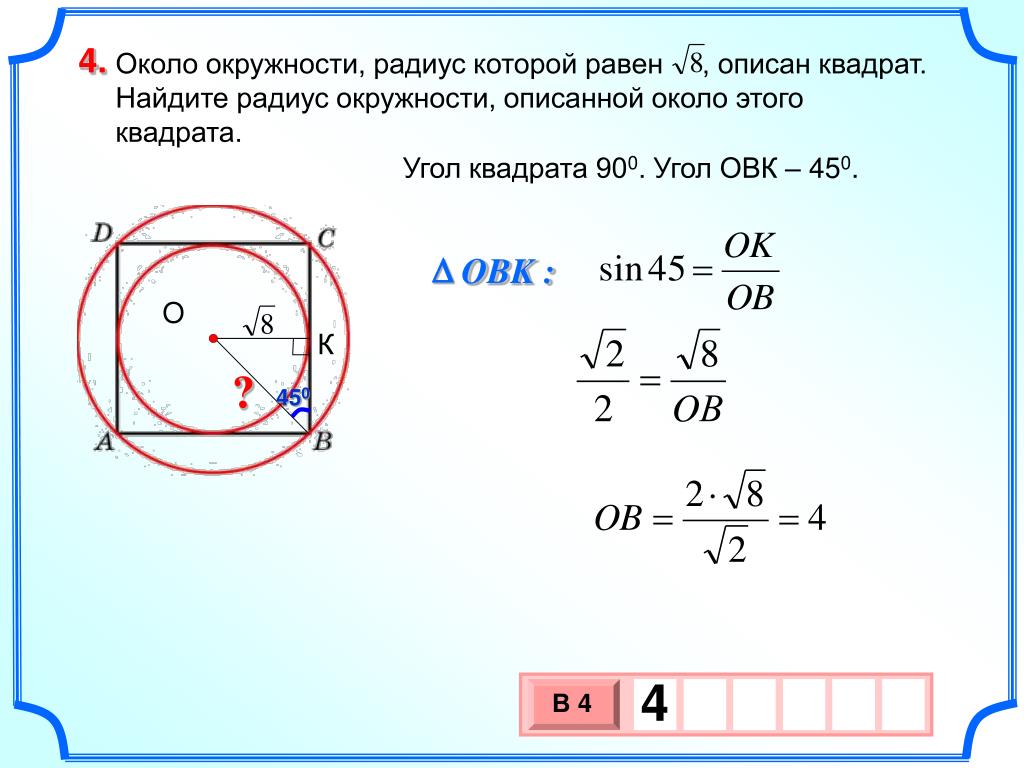
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один.
Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение.
Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи.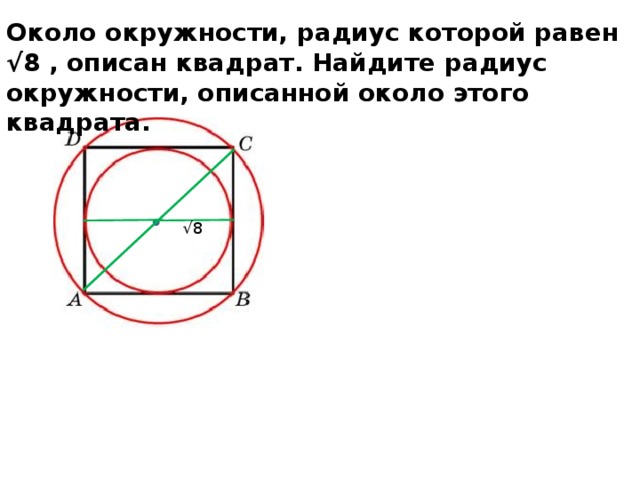
Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
геометрия — Радиус окружности, касающейся прямоугольника, оба из которых находятся внутри квадрата
спросил
Изменено 4 года, 7 месяцев назад
Просмотрено 20 тысяч раз
$\begingroup$
Учитывая эту конфигурацию:
Нам дано, что прямоугольник имеет размеры 20 см на 10 см, и мы должны найти радиус окружности.
Если мы каким-то образом знаем расстояние между окружностью и углом квадрата, то мы можем легко найти радиус. (равно $ \sqrt{2}\times R-R$)
Я действительно не понимаю, как это решить.
Любая помощь приветствуется.
- геометрия
- круги
- прямоугольники
$\endgroup$
92-60r+500=0$
$r=50$ $cm$
$r=10$ $cm$
Приемлемым ответом является $r=50$ $cm$.
$\endgroup$
7
$\begingroup$
Поместите центр криклы в $O.$
Пусть радиус будет $R$
Угол квадрата $(R,R)$ Я сделал небольшое изменение в изображении, чтобы создать меньше негатива числа.
Смещение по прямоугольнику, сердцевина прямоугольника $(R-20, R-10)$ 92,$$, которая имеет решения $$R_{1,2} = a+b\pm\sqrt{2ab}.$$
Одно решение соответствует большему прямоугольнику (по сравнению с окружностью), касаясь окружности на с другой стороны, чего здесь нет. Меньший прямоугольник по сравнению с кругом означает, что круг больше, если прямоугольник остается фиксированным, поэтому правильный радиус равен $$R = a+b+\sqrt{2ab}.
$$
Подстановка $a=10$ и $ b=20$ дает $R=50$.
$\endgroup$
$\begingroup$ 92 — 60R + 500 = 0$
$(R — 50)(R-10) = 0$
$R = 50$ — единственный разумный вариант.
$\endgroup$
6
$\begingroup$
Вы можете использовать триггер, чтобы получить тот же ответ, что и выше.
Нарисуйте три линии: одну от центра круга до угла, общего между квадратом и прямоугольником. Затем проведите линию от центра круга к углу, ближайшему к центру круга. Нарисуйте последнюю линию, которая будет диагональю, соединяющей ранее упомянутые углы.
Длину третьей линии мы знаем по теореме Пифагора. Если мы назовем длину стороны квадрата L, длина более короткой из двух оставшихся линий будет L/2. Длина более длинной, л/кв.
м.(2).
Найдите угол, который образует диагональ с более длинной из нарисованных линий, чтобы применить правило косинуса.
Более длинная линия пересекает угол квадрата под углом 45 градусов к обеим сторонам. Тогда угол, который образует диагональ с левой стороной квадрата, имеет тангенс 2,9.0005
Примените правило косинусов, затем решите полученное квадратное уравнение, и вы получите два возможных ответа, только один из которых правдоподобен.
$\endgroup$
Квадрат, вписанный в круг
Главная » Круги » Вписанные фигуры » Квадрат, вписанный в круг
Последнее обновление: Идо Сариг · Этот веб-сайт получает доход от рекламы и использует файлы cookie · Условия использования · Политика конфиденциальности
Когда квадрат вписан в круг, мы можем вывести формулы для всех его свойств- длина сторон, периметр, площадь и длина диагоналей, используя только радиус круга.
И наоборот, мы можем найти радиус, диаметр, длину окружности и площадь круга, используя только сторону квадрата.
Задача 1
Квадрат вписан в окружность радиуса r. Найдите формулы для длины стороны, длины диагонали, периметра и площади квадрата через r.
Стратегия
Ключевым моментом для решения этой задачи является то, что диагональ квадрата равна диаметру круга. Мы можем показать это, используя аргумент симметрии — квадрат симметричен относительно своей диагонали, поэтому диагональ должна проходить через центр круга.
Кроме того, мы знаем, что все внутренние углы квадрата прямые, равные 90°. Поскольку эти углы вписаны в окружность, они измеряют половину центрального угла на той же дуге. Таким образом, центральный угол равен 180°, что означает диаметр.
Вооружившись этим знанием, длина диагонали квадрата равна просто 2r, каждая сторона измеряет r·√2 (теорема Пифагора, примененная к треугольнику 45-45-90), тогда площадь равна 2r 2 , а периметр равно 4·r·√2.
Теперь сделаем обратное, найдем свойства окружности по длине стороны вписанного квадрата.
Задача 2
Квадрат со стороной а вписан в окружность. Найдите формулы для радиуса, диаметра, длины окружности и площади круга через а.
Стратегия
У нас уже есть ключевое понимание сверху — диаметр — это диагональ квадрата. Мы уже видели, как найти длину диагонали квадрата, считая от его стороны: это ·√2. Радиус равен половине диаметра, поэтому r=a·√2/2 или r=a/√2. Длина окружности равна 2·r·π, значит, это a·√2·π. А площадь π·r 2 , значит, это π·a 2 /2.
Теперь, когда мы сделали это, мы можем применить наши знания для решения различных задач «найти площадь заштрихованной фигуры», связанных с квадратом, вписанным в круг, например:
Задача 3
A квадрат со стороной а вписан в окружность. Найдите площадь заштрихованной фигуры.
Стратегия
Стратегия поиска области неправильной формы обычно заключается в том, чтобы посмотреть, можем ли мы выразить эту площадь как разницу между областями, образованными двумя или более правильными фигурами.
Leave A Comment