\circ\), \(B_2=\frac{1}{2}B_1\), \(\frac{\nu_2}{\nu_1}-?\)

Решение задачи:

Под действием силы Лоренца протон в магнитном поле будет совершать равномерное движение по окружности. Очевидно, что если протон движется по окружности радиуса \(R\) со скоростью \(\upsilon\), то период обращения \(T\), то есть время, за которое протон сделает один оборот (или пройдет одну длину окружности, равную \(2\pi R\)), можно найти так:

\[T = \frac{{2\pi R}}{\upsilon }\]

Частоту вращения протона \(\nu\) можно найти как величину, обратную периоду обращения \(T\):

\[\nu = \frac{1}{T}\]

\[\nu = \frac{\upsilon }{{2\pi R}}\;\;\;\;(1)\]

Силу Лоренца \(F_Л\) определяют по следующей формуле:

\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(2)\]

Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость протона, \(e\) – модуль заряда протона, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. 2}}}{R}\]

Имеем:

\[Be\sin \alpha = \frac{{{m_p}\upsilon }}{R}\]

Откуда отношение \(\frac{\upsilon}{R}\), которое нам будет нужно в ходе дальнейшего решения, равно:

\[\frac{\upsilon }{R} = \frac{{Be\sin \alpha }}{{m_p}}\]

Полученное выражение подставим в (1):

\[\nu = \frac{{Be\sin \alpha }}{{2\pi {m_p}}}\]

Запишем полученную формулу дважды для двух случаев, описанных в условии задачи:

\[\left\{ \begin{gathered}
{\nu _1} = \frac{{{B_1}e\sin \alpha }}{{2\pi {m_p}}} \hfill \\
{\nu _2} = \frac{{{B_2}e\sin \alpha }}{{2\pi {m_p}}} \hfill \\
\end{gathered} \right.\]

Поделим нижнее равенство на верхнее, тогда искомое отношение \(\frac{\nu_2}{\nu_1}\) равно:

\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{{{B_2}}}{{{B_1}}}\]

По условию величину индукции магнитного поля уменьшают в два раза, то есть \(B_2=\frac{1}{2}B_1\), поэтому:

\[\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{B_1}{2B_1} = \frac{1}{2}\]

Ответ: \(\frac{{{\nu _2}}}{{{\nu _1}}} = \frac{1}{2}\).

\circ\), \(t=1\) с, \(N-?\)

Решение задачи:

На протон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:

\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(1)\]

Здесь \(B\) – индукция магнитного поля, \(\upsilon\) – скорость протона, \(e\) – модуль заряда протона, \(\alpha\) – угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.

Сила Лоренца \(F_Л\) сообщает протону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:

\[{F_Л} = {m_p}{a_ц}\;\;\;\;(2)\]

Центростремительное ускорение \(a_ц\) можно определить через скорость протона \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\;\;\;\;(3)\]

Подставим (3) в (2), тогда:

\[{F_Л} = \frac{{{m_p}{\upsilon ^2}}}{R}\;\;\;\;(4)\]

Приравняем правые части (1) и (4):

\[B\upsilon e\sin \alpha = \frac{{{m_p}{\upsilon ^2}}}{R}\]

Имеем:

\[Be\sin \alpha = \frac{{{m_p}\upsilon }}{R}\]

Откуда отношение \(\frac{\upsilon}{R}\), которое понадобится в ходе дальнейшего решения, равно:

\[\frac{\upsilon }{R} = \frac{{Be\sin \alpha }}{{{m_p}}}\;\;\;\;(5)\]

Протон совершает в магнитном поле равномерное движение по окружности со скоростью \(\upsilon\), поэтому пройдет за время \(t\) путь, равный \(\upsilon t\). { – 27}}}} = 304,8\]

Ответ: 304,8.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.3 Электрон и протон, двигаясь с одинаковыми скоростями, влетают в однородное магнитное
8.2.5 Два электрона ускоряются из состояния покоя электрическим полем с разностью потенциалов
8.2.6 Электрон влетает в однородное магнитное поле с индукцией 0,004 Тл так, что направление

(-27) кг)

CENGAGE ФИЗИКА-МАГНИТНОЕ ПОЛЕ И МАГНИТНЫЕ СИЛЫ-Решенный пример

20 видео

РЕКЛАМА

Ab Padhai каро бина адс ке

Khareedo DN Pro и дехо сари видео бина киси ад ке!

Обновлено: 27-06-2022

Текст Решение

Решение

В первую очередь ускоряется протон в электрическом поле.
Затем он входит в магнитное поле и описывает круговой путь. После этого он покидает магнитное поле и описывает круговой путь.
После этого он покидает магнитное поле в отрицательном направлении. Его движение тормозится в электрическом поле. Наконец, он достигает оси Y в точке
на том же расстоянии 0,167 м.

Сначала рассчитаем скорость протона, когда он входит в
магнитное поле после прохождения в электрическом поле.
Сила, действующая на протон в электрическом поле =eE
∴ Ускорение протона a=(eEm)
Используя формулу v2+u2=2as, имеем
v2=2(eEm)s=2(eEm)(0,167).. ..(и)
Теперь рассмотрим движение в магнитном поле. Протон описывает

круговых траекторий радиусом (AC/2).
Следовательно, mv2r=evBorB=mver….(ii)
∴B=me(0,1667/2)×√[2eEm(0,167)]
=2√(2me×E0,167)=2 ⎷[2(2,67×10−27)(100)1,6×10−19(0,167)]
=10−2√2=7,07×10−3T

Ответ

Пошаговое решение от экспертов, которые помогут вам сомневаюсь в допуске и получении отличных оценок на экзаменах.

Похожие видео

В области существует однородное электрическое поле, направленное в прямом направлении x.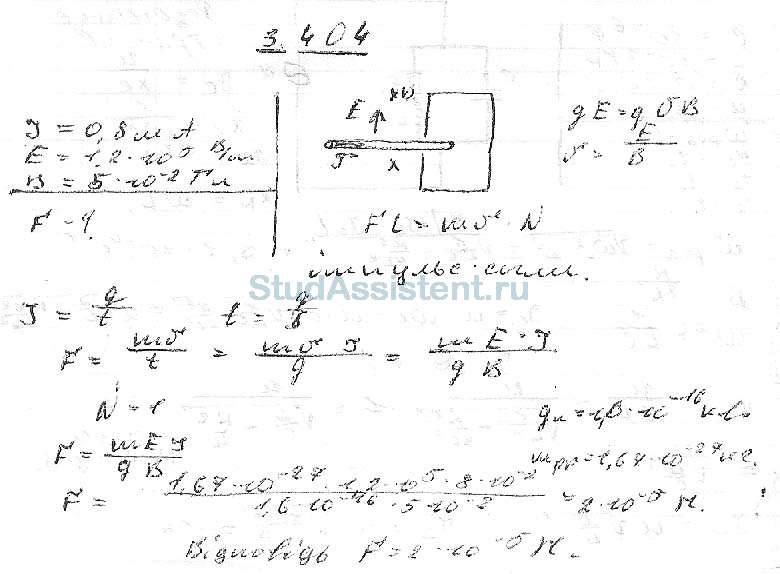 Пусть A будет началом координат, B будет точкой на оси x при x=+1cm и C будет точкой на оси y при y=+1cm . Тогда потенциалы в точках A, B и C удовлетворяют

10059570

Положительно заряженная частица, имеющая заряд q, ускоряется разностью потенциалов V. Эта частица, двигаясь вдоль оси x, попадает в область, где существует электрическое поле E. Направление электрического поля вдоль положительной оси у. Электрическое поле существует в области, ограниченной линиями x=0 и x=a. За линией x=a (т. е. в области xgta) существует магнитное поле напряженностью B, направленное вдоль положительной оси y. Найди. в какой точке частица пересекает линию x=a . б. шаг спирали, образующейся после попадания частицы в область xgea. (Масса частицы m.)

11313890

В некоторой области пространства существует однородное и постоянное электрическое поле напряженностью E по оси x и однородное постоянное магнитное поле индукции B по оси z. Заряженная частица с зарядом q и массой m выбрасывается со скоростью v параллельно оси x из точки (a, b, 0).

Когда частица достигает точки 2а, b//2, 0, ее скорость становится равной 2v. Найдите значение напряженности электрического поля m, v и координаты.

11314956

Электрон, движущийся со скоростью 106 м/с в направлении X, входит в область однородного магнитного поля напряженностью 0,2 Тл в направлении Y. Тогда его длина волны де Бробли (в области магнитного поля по сравнению с внешней) —

14939577

Электрическое поле E = – bx + a существует в области, параллельной направлению X (a и b – положительные константы). Заряженная частица с зарядом q и массой m вылетает из начала координат X = 0. Найти ускорение частицы в момент, когда ее скорость впервые после вылета становится равной нулю.

15159805

Протон X летит в область однородного электрического поля E со скоростью u. Одновременно с той же скоростью u выбрасывается другой протон Y в отдельную область с однородным магнитным полем «B». Было обнаружено, что и X, и Y имеют одинаковую длину волны де Бройля через время T.

Удельный заряд протона составляет σ (Кл / кг).
а) Найдите угол а, под которым протон X был спроецирован по отношению к направлению электрического поля.
(б) Найдите смещение протона X за время T.

15160242

Протон движется в отрицательном направлении оси X в магнитном поле, направленном вдоль положительного направления оси Y. Протон будет отклонен вдоль негативного направления

18249579

यदि समरूप विद्युतीय-क्षेत्र x- अक्ष की दिश में हो तो तल तल होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग होग अक Вибра अक अक्ष की की दिश तो समविभवीय तल होग o6 М/с Проецируется под углом 60° от направления оси x. Если в направлении оси наложено однородное магнитное поле величиной 0,104 Тесла, то вычислить радиус спирали и периодичность протона.

642662465

Положительно заряженная частица, имеющая заряд q, ускоряется разностью потенциалов V.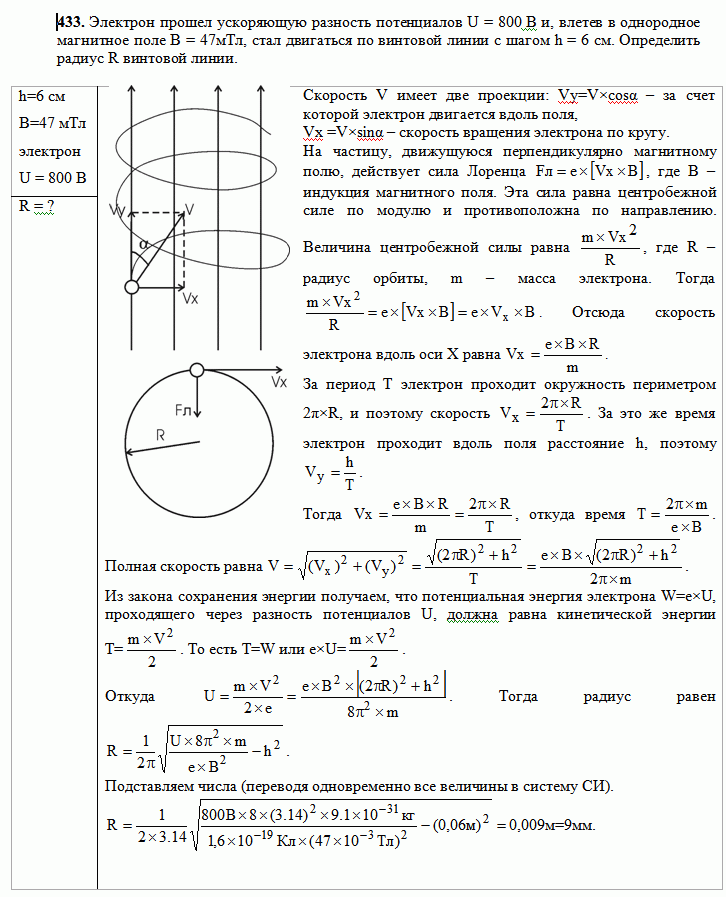 Эта частица, двигаясь вдоль оси x, попадает в область, где существует электрическое поле E. Направление электрического поля вдоль положительной оси у. Электрическое поле существует в области, ограниченной линиями x=0 и x=a. За линией x=a (т.е. в области x>a) существует магнитное поле напряженностью B, направленное вдоль положительной оси y. Найти


а. в какой точке частица пересекает линию x=a.
б. шаг спирали, образующейся после попадания частицы в область x≥a. (Масса частицы m.)

643184864

В некоторой области пространства существует однородное и постоянное электрическое поле напряженностью E вдоль оси x и однородное постоянное магнитное поле индукции B вдоль оси z. Заряженная частица с зарядом q и массой m выбрасывается со скоростью v параллельно оси x из точки (a, b, 0). Когда частица достигает точки (2a, b//2, 0), ее скорость становится равной 2v. Найти значение напряженности электрического поля через m, v и координаты.

643188421

Протон движется в отрицательном направлении оси X в магнитном поле, направленном в положительном направлении оси Y. Протон будет отклоняться в отрицательном направлении

643191597

В области x=0andx=0,167m, направленной в направлении x, существует постоянное однородное электрическое поле напряженностью 100Vm−1. Существует постоянное однородное магнитное поле B в области x=0,167man и x=0,334 м, направленное в направлении z. Протон, покоящийся в начале координат, высвобождается в положительном направлении x. Найдите минимальную напряженность магнитного поля B, чтобы протон был обнаружен обратно в точке x=0,y=0,167 м. (масса протона =1,67×10-27 кг) 9(-27) кг)

Ответить

Пошаговое решение от экспертов, которое поможет вам получить отличные оценки на экзаменах.

Стенограмма

Привет всем, поэтому мы задали мне вопрос, в котором говорится, что существует постоянное однородное электрическое поле величиной сто вольт на метр в области x = 20 2x = 2 1,67 м, направленное в направлении X, делает константу как сильное магнитное поле внутри области актер равно нулю 1672 0,334 точки в направлении Z протон, покоящийся в начале координат, высвобождается в положительном направлении X найдите минимальную напряженность магнитного поля, чтобы протон был обнаружен обратно в точке x = 20 и белые кавычки 20,16 дается масса протона 1,67 10 увеличьте до минус 27 кг, поэтому нам дается ситуация с чем-то вроде этого, как мы можем видеть, для электрического поля находится в районе с 2020,16

, а затем от 0,16 до 0,3 мм магнитное поле внутри One Direction, поскольку направление Эдварда не упоминалось, то есть оно либо положительное, либо отрицательное, мы взяли его, оно отрицательное, потому что другая причина в вопросе, это говорит, что этот протон, который я показал его красным цветом, он начинает свое путешествие от начала координат в правильном направлении, а затем, когда он входит в магнитное поле, испытывает силу, и он движется по круговой траектории, и снова обнаруживается велосипед на y = 2 0,167 м как показано на рисунке, чтобы достичь этой точки, должно быть задействовано электромагнитное поле, потому что, как мы видим, направление силы, действующей на протон, когда он действует, когда он входит в магнитное поле, задается ладонью правой руки.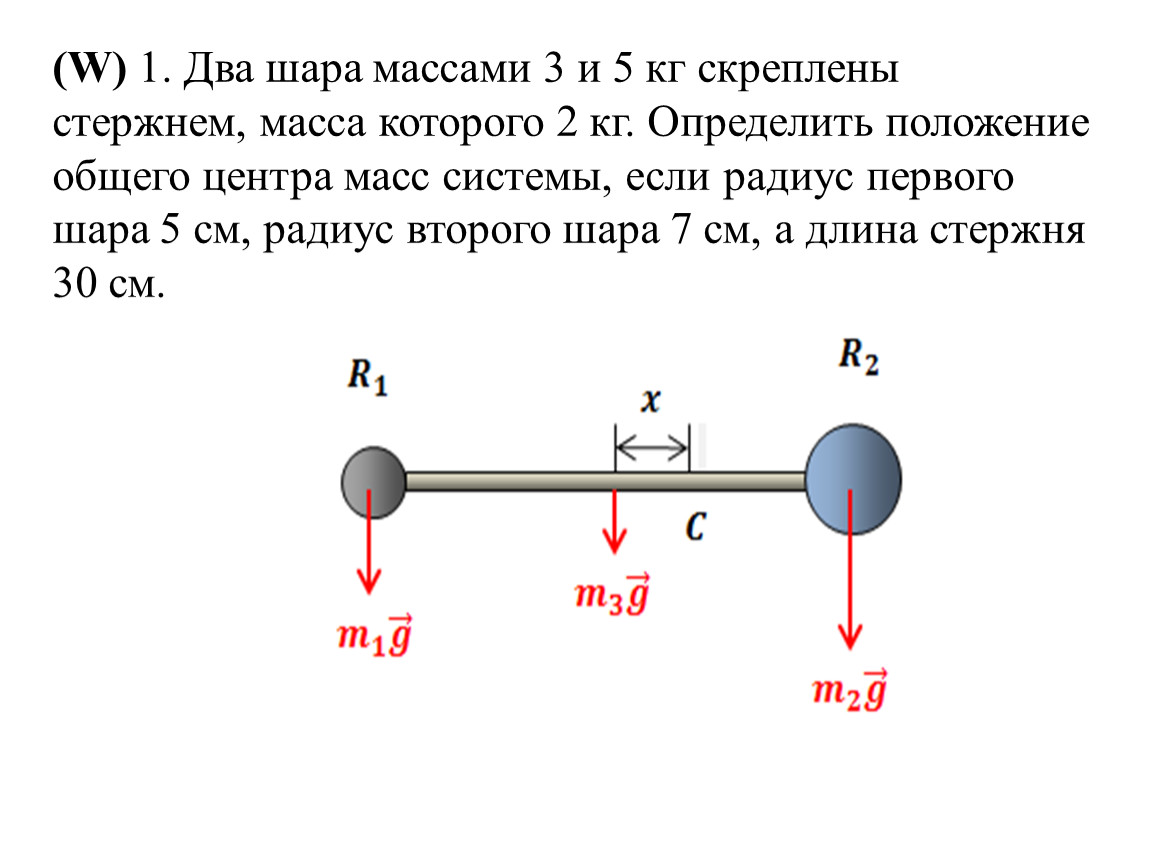

правило

мы можем рассчитать его направление, указывающее член в направлении движения, то есть вправо, и я дам направление силы, сила будет действовать в противоположном направлении, как показано на рисунке, это займет этот путь, и он покажет, так что мы можем сказать, что магнитное поле должно быть задействовано, или прямо к нему будет отрицательное направление Z. Это ось Y, это наши налоги, а это наш zx2. Надеюсь, вы поняли данный сценарий. и диаграмма, которую мы сделали, так что теперь мы можем начать, как электрон начинает двигаться, как протон начинает двигаться, поскольку он положительно заряжен, и в направлении электрического поля он ускоряется через мы можем написать от путешествия к Протон ускоряется мы можем написать ускорение будет не что иное как мы

, поскольку электрическая сила, которая будет действовать на протон, обеспечивает его, и мы получим ускорение, поэтому заряд на протоне составляет 1,6 — 2 — 19 в значениях электрического поля, заданных как сто а / масса.