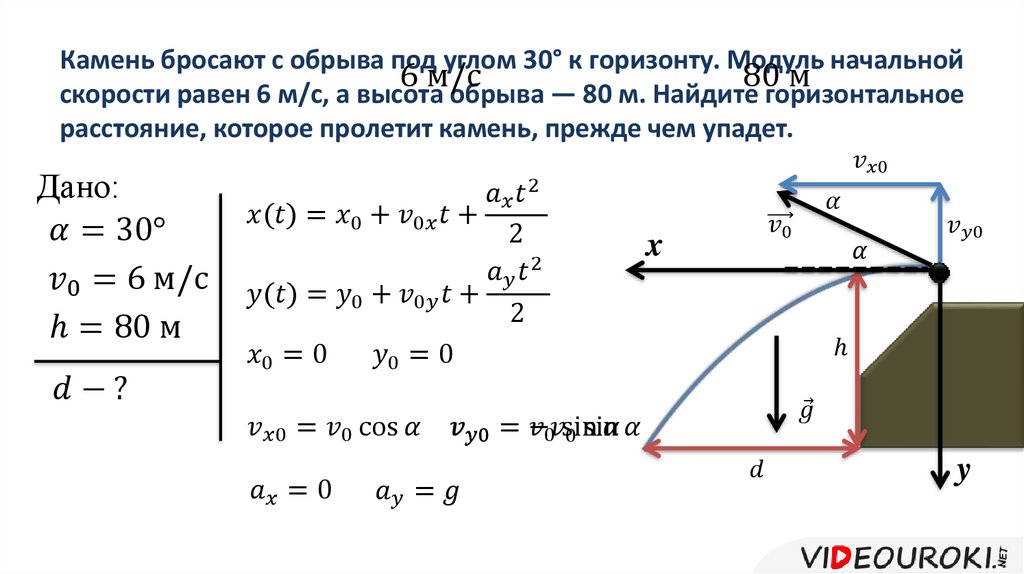
Глава 2. Ускорение. Равноускоренное движение
Характеристикой изменения скорости является ускорение. Эта величина определяется как отношение изменения скорости тела к тому интервалу времени, за который это изменение произошло
(2.1) |
где и — скорости тела в конце и начале интервала времени .
Из определения (2.1) следует, что вектор ускорения тела отличен от нуля только в том в случае, когда изменяется вектор скорости.
При этом направление вектора определяется направлением разности , и может не совпадать с направлениями векторов и .
Поэтому в задаче 2.1.1 ситуации, перечисленные в ответах 1, 3 и 4, возможны в следующих случаях. В 1 — когда тело, поворачивая на восток, в некоторый момент времени имеет вектор скорости, направленный на север. В 3 — при равноускоренном движении. В 4 — например, в такой ситуации:
тело бросили вертикально вверх и в верхней точке траектории оно имеет нулевую скорость и ускорение, равное ускорению свободного падения.
В задаче 2.1.2 вектор скорости в конце любого интервала времени меньше вектора скорости в начале этого интервала. Поэтому при направлении вектора скорости на юг вектор изменения скорости, а, следовательно, и вектор ускорения направлены на север (ответ 3).
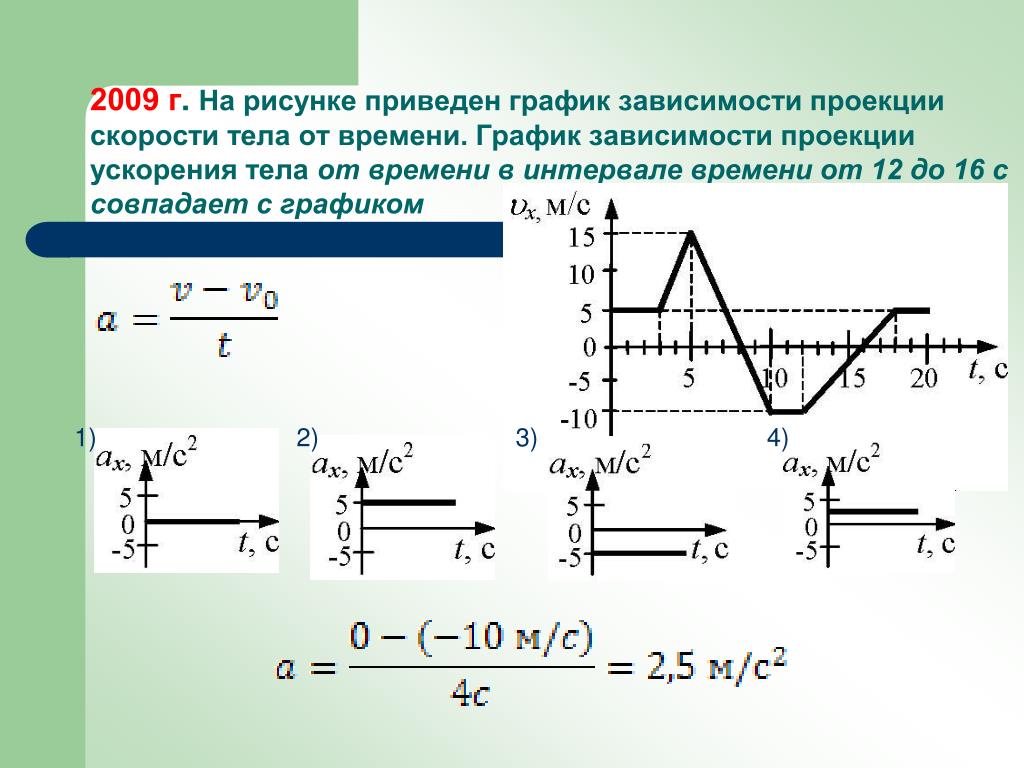
Если тело движется с постоянной скоростью, координата линейно зависит от времени, причем наклон графика определяется скоростью. Поэтому скорость тела уменьшается, если уменьшается угол наклона графика зависимости координаты от времени к оси времени (задача
Движение тела, при котором его ускорение (как величина, так и направление) не изменяется, называется равноускоренным (задача 2.1.4 — ответ 4). Из определения ускорения (2.1) следует, что при равноускоренном движении зависимость скорости от времени является линейной.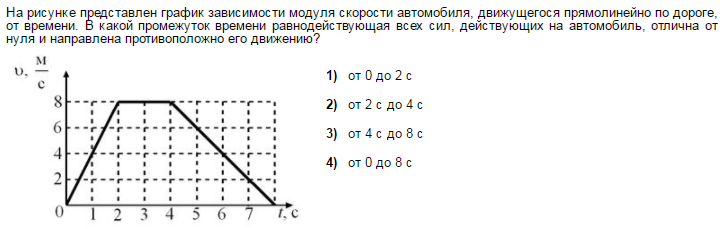 Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
Поэтому равноускоренному движению в задаче 2.1.5 отвечает график 1 (несмотря на то, что скорость тела убывает). В этой связи отметим, что равноускоренность означает не то, что тело постоянно разгоняется, а то, что оно имеет «равное ускорение».
При равноускоренном движении зависимости радиус-вектора тела по отношению к произвольной системе координат и скорости тела от времени даются соотношениями
(2.2) |
(2.3) |
где и — радиус-вектор и скорость тела в момент времени , — ускорение тела. После проецирования на оси координат зависимости (2.2) и (2.3) позволяют находить координаты тела и проекции его скорости на оси в любые моменты времени.
В задаче 2.1.6 зависимость (2.2) в проекциях на ось , которая направлена параллельно ускорению и начало которой находится в точке начала движения, дает
Поскольку тело движется из начала координат и только в одну сторону, то, очевидно, координата тела совпадает с пройденным путем. Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ
Поэтому при ускорении через 20 с после начала движения пройденный путь будет равен 100 м (ответ 2). Из этого результата следует, что задача 2.1.7 является обратной по отношению к задаче 2.1.6, поэтому правильный ответ для времени, за которое тело пройдет путь 100 м — 20 с (ответ
В задаче 2.1.8 необходимо использовать зависимость (2.3) для скорости. Так как по условию автомобиль движется из состояния покоя, проекция зависимости (2.3) на ось , направленную вдоль вектора ускорения, имеет вид
где – проекция вектора скорости тела на ось . Так как в момент времени , находим (правильный ответ – 2).
Сравнивая данную в задаче 2.1.9 зависимость координаты от времени с законом (2.2), заключаем, что начальная скорость тела , проекция ускорения тела на ось – . Поэтому из (2.3) получаем зависимость скорости тела от времени .
 Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ
Можно было также найти скорость как производную координаты по времени. Дифференцируя данную в условии функцию, получим тот же ответ
Зависимость проекции скорости от времени на ось, направленную вертикально вверх, для тела из задачи 2.1.10 имеет вид
где — начальная скорость тела. Подставляя в эту формулу время , находим скорость тела через 0,5 с после броска (ответ 3). Знак «плюс» для проекции скорости на рассматриваемую ось показывает, что через 0,5 c после броска вектор скорости тела все еще направлен вверх.
Чтобы найти время подъема тела, брошенного вертикально вверх, на максимальную высоту (задача 2.2.1) используем то обстоятельство, что в верхней точке траектории скорость тела равна нулю. Поэтому подстановка времени подъема в зависимость скорости от времени дает
где — начальная скорость тела. Отсюда получаем для времени подъема (ответ 4). А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
А самую максимальную высоту подъема (задача 2.2.2) можно найти, подставляя найденное время подъема в зависимость координаты тела по вертикальной оси от времени
Подстановка в эту формулу числовых значений дает (ответ 1).
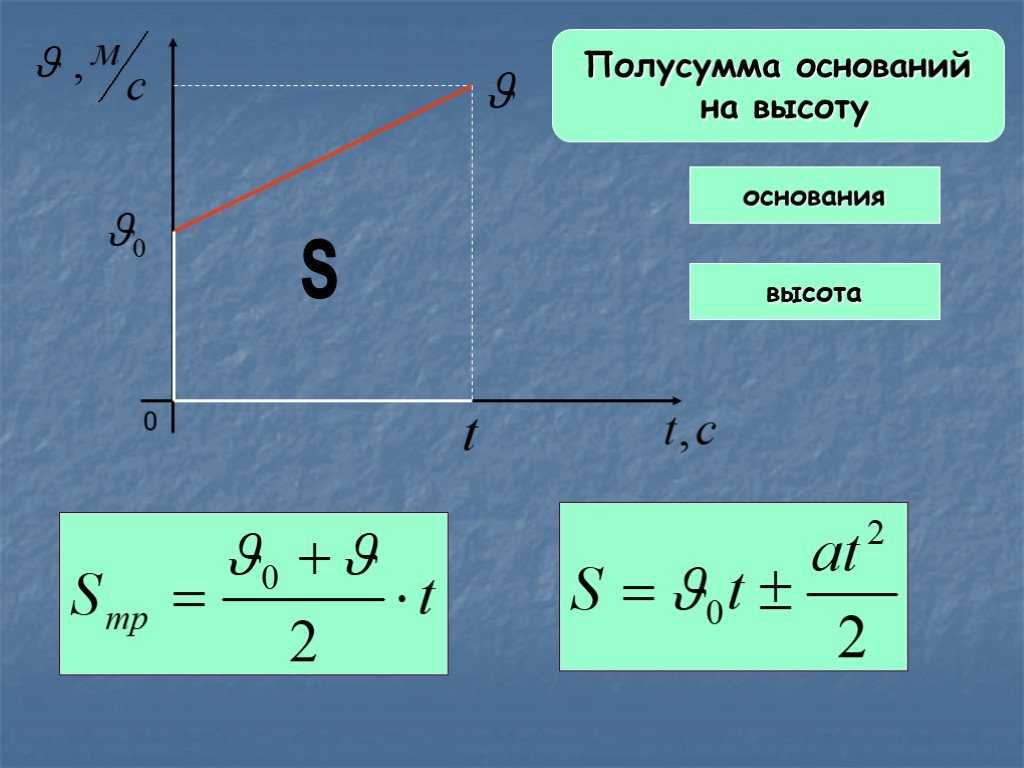
Пусть время, затраченное телом на прохождение участка пути длиной , отсчитанного от начальной точки, равно , а время, затраченное телом на прохождение участка пути длиной , отсчитанного от этой же точки, равно (задача 2.2.3). Тогда из уравнения движения (2.2) в проекции на ось, направленную вдоль вектора ускорения тела, имеем
404 Cтраница не найдена
- Сведения об образовательной организации
- Основные сведения
- Структура и органы управления образовательной организацией
- Документы
- Образование
- Образовательные стандарты
- Руководство.
 Педагогический (научно-педагогический состав)
Педагогический (научно-педагогический состав) - Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендии и иные виды материальной поддержки
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Энергосбережение и повышение энергетической эффективности
- Доступная среда
- Наш техникум
- Теоретическое и производственное обучение
- Воспитательная работа
- Доступная среда
- Противодействие коррупции
- Абитуриенту
- Приёмная комиссия
- Профессии
- Фото-экскурсия
- Видеогалерея
- Студенту
- Полезные ссылки
- Расписание
- Библиотека
- ЕГЭ
- ГИА
- Центр содействия трудоустройству выпускников
- Учебно-методические материалы
- Контакты
- WorldSkills Russia
- О нас
- Чемпионат
- Обращения граждан
- Новости
- Наши профессии
- Преподавателю
- Moodle
- Организация питания в образовательной организации
- Меню (в том числе информация о наличии диетического меню в образовательной организации)
- Организация питания, документы и иная информация
- Родительский контроль
- Обратная связь для родителей (законных представителей), обучающихся
- Международное сотрудничество
- Наставничество
- Нормативные документы
- Формы наставничества
- Новости
- Наши наставники
векторов и снарядов — с ответами №1
Перейдите к:
Обзорная сессия Главная — Список тем
Векторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || #1-9 || #10-45 || # 46-55 || # 56-72
[#1 | #2 | №3 | №4 | №5 | #6 | #7 | #8 | #9]
Часть A: Множественный выбор
1. Какие из следующих утверждений верны для скаляров и векторов? Перечислите все, что ВЕРНО.
Какие из следующих утверждений верны для скаляров и векторов? Перечислите все, что ВЕРНО.
- Векторная величина всегда имеет связанное с ней направление.
- Скалярная величина может иметь связанное с ней направление.
- Вектора можно суммировать; скалярные величины не могут.
- Векторы могут быть представлены стрелкой на масштабной диаграмме; длина стрелки представляет величину вектора, а направление, на которое она указывает, представляет направление вектора.
Ответ: AD
а. TRUE — Векторы определяются как величины, полностью описываемые как по величине, так и по направлению. По определению, вектор имеет связанное с ним направление. Если бы это было не так, то это НЕ был бы вектор.
б. ЛОЖЬ — Скаляры определяются как величины, которые полностью описываются только их величиной. Скаляры не обращают внимания на направление, и бессмысленно связывать направление с такой величиной. Если бы с величиной было связано направление, то эта величина не была бы вектором.
Если бы с величиной было связано направление, то эта величина не была бы вектором.
в. FALSE — Можно складывать как векторы, так и скаляры. Правила сложения векторов уникальны для векторов и не могут использоваться при сложении скаляров. При сложении двух векторов необходимо учитывать направление вектора. Направление не имеет значения при добавлении скаляров.
д. TRUE — Это именно так и именно так и делается во всем блоке.
2. Какие из следующих величин являются векторами? Включите все, что применимо.
- пройденное расстояние
- объем
- средняя скорость
- средняя скорость
- мгновенная скорость
- ускорение
Ответ: BDEF
Из пяти перечисленных здесь кинематических величин (расстояние, перемещение, скорость, скорость и ускорение) три являются векторами. Перемещение, скорость (как средняя, так и мгновенная) и ускорение требуют упоминания направления, чтобы полностью описать величину.
3. Для различных величин указаны числовые значения и направления. Какие из этих утверждений представляют векторное описание? Включите все, что применимо.
- 20 метров, запад
- 9,8 м/с/с
- 35 миль/ч, юг
- 16 лет
- 60 минут
- 3,5 м/с/с, юг
- -3,5 м/с/с
- +20 градусов С
Ответ: ACFG
Выражения векторных величин включают величину (число, значение и т. д.) и направление. Направление можно описать как север, юг, восток, запад или влево, вправо, вверх, вниз. Иногда для описания направления используется «+» или «-». Так как математические вычисления на калькуляторах плохо справляются с вводом «юг», для заданного направления часто заменяется знак -. В случае г , единицы указывают величину ускорения. Знак «-» указывает направление. Следует быть осторожным, предполагая, что знак «+» или «-» является верным признаком величины, являющейся направлением, поскольку другие не векторные величины также могут использовать такие знаки (как в случае h ).
4. Какие из следующих утверждений верны для диаграмм сложения векторов, вычитания векторов и диаграмм сложения векторов? Перечислите все, что применимо.
- Векторы A, B и C складываются вместе как A + B + C. Если порядок, в котором они складываются, изменить на C + B + A, то результат будет другим.
- Векторы A, B и C складываются как A + B + C. Если порядок их сложения изменить на C + B + A, то результатом будет вектор с той же величиной, но в противоположном направлении. .
- При построении векторной диаграммы для A + B + C нет абсолютной необходимости, чтобы векторы B и C использовали тот же масштаб, что и вектор A.
- Результирующая в диаграмме сложения векторов всегда простирается от начала последнего вектора до хвоста первого вектора.
- Если векторы A и B складываются под прямым углом друг к другу, то можно быть уверенным, что результирующий будет иметь величину, превышающую величины любого из отдельных векторов A и B.

- Если векторы А и В сложить под прямым углом друг к другу, то можно быть уверенным, что результирующая будет иметь величину, меньшую арифметической суммы величин А и В.
- Диаграммы сложения векторов нельзя использовать для определения результата при выполнении операции вычитания векторов.
Ответ: EF
а. FALSE — Изменение порядка добавления трех векторов не влияет на результат процесса добавления. A + B + C = C + B + A. Каждый порядок операций дает результирующую с той же величиной и направлением.
б. FALSE — Как упоминалось выше в a, изменение порядка добавления трех векторов не влияет на результат процесса добавления. Обратный порядок дает результирующую с той же величиной и тем же направлением.
в. ЛОЖЬ — При построении диаграммы сложения векторов необходимо выбрать масштаб и придерживаться его. Масштаб, использованный для рисования вектора А, должен быть использован и для векторов В и С. Нельзя менять лошадей посреди потока .
Нельзя менять лошадей посреди потока .
д. ЛОЖЬ — Результирующее значение на диаграмме сложения векторов рисуется от конца первого вектора (начальная точка ) до начала последнего вектора (конечная точка ).
е. ИСТИНА — Предположим, что A = 3 единицы и B = 4 единицы и что два вектора направлены под прямым углом друг к другу. Сумма векторов или результат A + B составляет 5 единиц, что явно больше, чем любой из добавляемых векторов. В общем случае равнодействующая в таком случае будет представлена на диаграмме сложения векторов как гипотенуза прямоугольного треугольника. Гипотенуза всегда больше двух других катетов треугольника. Так что это утверждение всегда верно.
ф. ИСТИНА — Предположим, что A = 3 единицы и B = 4 единицы и что два вектора направлены под прямым углом друг к другу. Векторная сумма или результат A + B составляет 5 единиц, тогда как арифметическая сумма составляет 7 единиц. В этом случае и во всех случаях векторная сумма двух прямоугольных векторов всегда будет меньше арифметической суммы. То есть Sqrt(a 2 + b 2 ) всегда будет меньше, чем a + b.
То есть Sqrt(a 2 + b 2 ) всегда будет меньше, чем a + b.
г. FALSE — Когда выполняется операция вычитания вектора, обычно рекомендуется просто преобразовать ее в операцию сложения векторов. Это достигается добавлением отрицательного значения вектора, который вычитается. Таким образом, A — B будет эквивалентно A + (-B). Таким образом, диаграмма сложения векторов может быть использована для определения результата.
5. Какие из следующих описаний движущихся объектов точно изображают снаряд? Перечислите все, что применимо.
- объект, движущийся по воздуху и не касающийся какой-либо поверхности
- падающий парашютист с раскрытым парашютом
- любой предмет, сопротивление воздуха которому можно пренебречь
- свободно падающий объект
- объект, на который действует только сила тяжести
- падающее перо
- Падающее перо в вакуумной камере
- Падающее перо в падающей вакуумной камере.

Ответ: DEGH
Снаряд — это объект, на который действует только сила тяжести. Сопротивление воздуха должно быть незначительным или отсутствовать. Другие силы, возникающие в результате того, что люди или предметы тянут или толкают, прикрепленных веревок или контакта с поверхностями, не должны присутствовать.
а. НЕТ — Самолет движется по воздуху и не касается какой-либо поверхности. Но самолет явно не снаряд.
б. NO — Падающий парашютист обычно испытывает значительное сопротивление воздуха. Популярно описывать таких парашютистов как находящихся в свободном падении . Это ошибочное использование термина.
в. НЕТ — Когда вы сидите в кресле, сопротивление воздуха незначительно. Вы точно не снаряд (по крайней мере, мы на это надеемся).
д. ДА — Снаряд — это объект в свободном падении.
эл. ДА — Объект, на который действует только сила тяжести, подпадает под определение снаряда (при условии, что «значительный» означает «имеющий влияние»).
ф. NO — Падающие перья сталкиваются с сопротивлением воздуха, которое препятствует нисходящему ускорению и заставляет перо падать почти с постоянной скоростью.
г. ДА — Когда перо падает в вакууме, сопротивление воздуха устраняется, и перо может свободно падать.
час. ДА — Когда перо падает в вакууме, а вакуум также свободно падает, сопротивление воздуха устраняется, и наблюдатель заметит, что и вакуумная камера, и перо находятся в свободном падении.
6. Какие из следующих утверждений верны для снарядов? Перечислите все, что применимо.
- Снаряд — свободно падающий объект.
- Снаряд испытывает незначительное сопротивление воздуха или не испытывает его вообще.
- Снаряд должен двигаться вниз.
- Снаряд должен двигаться с ускорением в направлении вниз.
- Снаряд не обязан двигаться горизонтально.

- Снаряд может начать движение с нисходящей скоростью.
- Снаряд не обязательно должен «падать».
Ответ: ABDEF и, возможно, G
a. ВЕРНО — Свободно падающие объекты, такие как снаряды, являются объектами, на которые действует только гравитация.
б. ВЕРНО — Единственная сила, действующая на снаряд, — это гравитация; сопротивления воздуха не должно быть или оно не должно влиять на движение снаряда.
в. ЛОЖЬ — Снаряды могут двигаться либо вверх, либо вниз, либо под углом к вертикали. Однако они должны двигаться вниз с ускорением в соответствии с действием гравитации на объект.
д. ВЕРНО — Сила тяжести действует прямо вниз на объект, вызывая нисходящее ускорение. Любой снаряд должен ускоряться вниз независимо от других особенностей его движения.
эл. TRUE — Снаряд мог двигаться строго в вертикальном направлении без горизонтального движения. Мяч, брошенный прямо в воздух, был бы таким случаем.
ф. ИСТИНА — Нет правила о том, в каком направлении должен двигаться снаряд в момент его выброса. Он мог бы начать свое движение с начальной нисходящей скоростью.
г. ПРАВДА — Слово «падение» может означать разные вещи для разных людей. Если «падение» предполагает движение вниз во все моменты времени, то снаряду не обязательно «падать». Для многих «падение» означает падение под действием силы тяжести. При этом снаряд должен «падать».
7. Какие из следующих утверждений верны для горизонтального движения снарядов? Перечислите все, что применимо.
- Снаряд не имеет горизонтальной скорости.
- Снаряд с направленной вправо составляющей движения будет иметь правонаправленную составляющую ускорения.
- Горизонтальная скорость снаряда изменяется на 9,8 м/с каждую секунду.
- Снаряд с горизонтальной составляющей движения будет иметь постоянную горизонтальную скорость.

- Горизонтальная скорость снаряда равна 0 м/с на пике его траектории.
- Горизонтальная скорость снаряда не зависит от вертикальной скорости; эти две составляющие движения независимы друг от друга.
- Горизонтальное смещение снаряда зависит от времени полета и начальной горизонтальной скорости.
- Конечная горизонтальная скорость снаряда всегда равна начальной горизонтальной скорости.
- По мере того, как снаряд поднимается к вершине своей траектории, горизонтальная скорость уменьшается; когда он падает с пика своей траектории, его горизонтальная скорость будет уменьшаться.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземлившийся на уровне земли. Горизонтальное смещение (т.е. диапазон ) снаряда всегда будет увеличиваться по мере увеличения угла пуска от 0 до 90 градусов.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированным углом запуска и переменной скоростью запуска, и приземлившийся на уровне земли.
 Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
Ответ: DFGHK
а. ЛОЖЬ — Многие снаряды движутся слева направо и справа налево, одновременно свободно падая. Такие снаряды имеют горизонтальное движение. Хотя снаряд может совершать горизонтальное движение, он не может иметь горизонтальное ускорение. Какое бы движение оно ни совершало в горизонтальном измерении, оно должно быть движением с постоянной скоростью.
б. ЛОЖЬ — Снаряд с движением вправо (в дополнение к вертикальному движению) будет иметь постоянную скорость в направлении вправо. Это означает, что он не имеет горизонтального ускорения.
в. ЛОЖЬ — Снаряд имеет постоянную горизонтальную скорость. Каждую секунду вертикальная скорость будет изменяться на 9,8 м/с.
д. ПРАВДА — Совершенно верно! Снаряды — это объекты, на которые действует только сила тяжести. Таким образом, есть вертикальное ускорение, но нет горизонтального ускорения. Горизонтальная скорость снаряда либо равна нулю, либо является постоянной величиной, отличной от нуля.
Горизонтальная скорость снаряда либо равна нулю, либо является постоянной величиной, отличной от нуля.
эл. ЛОЖЬ — Вертикальная скорость снаряда равна 0 м/с на пике его траектории; но горизонтальная составляющая скорости на пике равна тому значению, которое было при первом запуске .
ф. ВЕРНО — Для любого двумерного движения (будь то движение снаряда или проблемы с речным судном или …), перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикальной составляющей не повлияет на горизонтальные составляющие движения.
г. ИСТИНА — Горизонтальное смещение (x) можно рассчитать по формуле x = v ox • t, где v ox — начальная горизонтальная скорость, а t — время. Это две переменные, влияющие на горизонтальное смещение снаряда.
час. TRUE — Поскольку у снаряда нет горизонтального ускорения, начальная горизонтальная скорость равна конечной горизонтальной скорости.
я. ЛОЖЬ — Это верное описание вертикальной составляющей скорости. Горизонтальная скорость не меняется на протяжении всей траектории снаряда.
ЛОЖЬ — Это верное описание вертикальной составляющей скорости. Горизонтальная скорость не меняется на протяжении всей траектории снаряда.
л. FALSE — Диапазон (или горизонтальное смещение) будет увеличиваться при увеличении угла с 0 до 45 градусов. Максимальная дальность приходится на 45 градусов. При дальнейшем увеличении угла до значений, превышающих 45 градусов, горизонтальное смещение уменьшается.
к. TRUE — При увеличении скорости запуска компоненты начальной скорости (как горизонтальной, так и вертикальной) также увеличиваются. Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и двигаться быстрее в горизонтальном направлении. В результате увеличение скорости пуска всегда приводит к увеличению горизонтального смещения.
8. Какие из следующих утверждений верны для вертикального движения снарядов? Перечислите все, что применимо.
- Вертикальная составляющая скорости снаряда является постоянной величиной 9,8 м/с.
- Вертикальная составляющая скорости снаряда постоянна.
- Изменяется вертикальная составляющая скорости снаряда.
- Вертикальная составляющая скорости снаряда изменяется с постоянной скоростью.
- Снаряд с направленной вверх составляющей движения будет иметь направленную вверх составляющую ускорения.
- Снаряд с нисходящей составляющей движения будет иметь нисходящую составляющую ускорения.
- Величина вертикальной скорости снаряда изменяется на 9,8 м/с каждую секунду.
- Вертикальная скорость снаряда равна 0 м/с на пике его траектории.
- Горизонтальная скорость не влияет на вертикальную скорость снаряда; эти две составляющие движения независимы друг от друга.
- Конечная вертикальная скорость снаряда всегда равна начальной вертикальной скорости.
- Вертикальное ускорение снаряда равно 0 м/с/с, когда он находится на пике своей траектории.

- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение уменьшается; когда он падает с пика своей траектории, его вертикальное ускорение будет уменьшаться.
- Когда снаряд поднимается к пику своей траектории, вертикальное ускорение направлено вверх; когда он падает с пика своей траектории, его вертикальное ускорение направлено вниз.
- Пиковая высота, на которую снаряд поднимается над местом запуска, зависит от начальной вертикальной скорости.
- Когда снаряд поднимается к пику своей траектории, вертикальная скорость уменьшается; когда он падает с пика своей траектории, его вертикальная скорость будет уменьшаться.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированной скоростью пуска и переменным углом и приземлившийся на уровне земли. Вертикальное смещение снаряда в течение первой половины его траектории (т. е. высота пика ) всегда будет увеличиваться по мере увеличения угла запуска с 0 до 90 градусов.
- Рассмотрим снаряд, запущенный с уровня земли с фиксированным углом запуска и переменной скоростью запуска, и приземлившийся на уровне земли.
 Вертикальное смещение снаряда на первой половине его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения скорости пуска.
Вертикальное смещение снаряда на первой половине его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения скорости пуска.
Ответ: CDFGHINPQ
а. ЛОЖЬ — Вертикальная составляющая скорости снаряда постоянно меняется. Это ускорение, которое имеет значение 9,8 м/с/с.
б. ЛОЖЬ — Снаряды — это объекты, на которые действует только сила тяжести. Таким образом, существует вертикальное ускорение; вертикальная скорость не постоянна, а изменяется.
в. ИСТИНА — См. часть b выше.
д. ВЕРНО — Снаряд имеет вертикальное ускорение 9,8 м/с/с на протяжении всей траектории. Это значение ускорения является постоянным. Это означает, что вертикальная скорость изменяется на ту же величину — 9.8 м/с — в течение каждой секунды его движения. Вертикальная скорость изменяется на постоянную величину.
эл. ЛОЖЬ — Все снаряды испытывают нисходящее ускорение независимо от того, движутся ли они вверх или вниз. Снаряды, движущиеся вверх, имеют восходящую скорость, но реальные значения скорости становятся меньше; то есть снаряд замедляется на пути к своей вершине.
Снаряды, движущиеся вверх, имеют восходящую скорость, но реальные значения скорости становятся меньше; то есть снаряд замедляется на пути к своей вершине.
ф. ИСТИНА — Это верное утверждение. Можно также сказать, что снаряд с восходящей составляющей движения также имеет нисходящее ускорение. Все снаряды ускоряются в направлении вниз. Период.
г. ПРАВДА — Это абсолютно верно.
час. ИСТИНА — На пике своей траектории снаряд находится в процессе смены направления. Вертикальная скорость должна измениться с положительного значения (+ вверх) на отрицательное значение (- вниз). Этот переход означает, что значение вертикальной скорости должно когда-то находиться между + и — числом. Промежуточное число равно 0 м/с, и это происходит на пике.
я. ИСТИНА — Для любого двумерного движения (будь то движение снаряда или проблемы с речным судном или …), перпендикулярные компоненты движения не зависят друг от друга. Любое изменение вертикальной составляющей не повлияет на горизонтальные составляющие движения.
ж. ЛОЖЬ — Снаряд, запущенный под углом, формирует параболическую траекторию. Предположим, что нужно проследить движение снаряда вперед во времени от пика и назад во времени от пика. Если бы это было сделано, можно было бы обнаружить, что значение вертикальной скорости имеет одинаковую величину для равного количества раз, прослеживаемых вперед и назад от пика. Таким образом, за одно и то же время до и после пика снаряд имеет одинаковую скорость. Однако некоторые снаряды запускаются не с той высоты, на которой они приземляются. Конечная высота не совпадает с начальной высотой, и поэтому время подъема на пик не равно времени падения с пика. В таких случаях начальная вертикальная скорость не равна конечной вертикальной скорости.
к. ЛОЖЬ — Нет! Нет! Нет! Вертикальная скорость равна 0 м/с в пике, а вертикальное ускорение равно -9,8 м/с/с на протяжении всей траектории.
л. ЛОЖЬ — Это верное описание вертикальной скорости. Но вертикальное ускорение является постоянной величиной 9,8 м/с/с на протяжении всей траектории.
м. ЛОЖЬ — Мало того, что величина вертикального ускорения является постоянной величиной на протяжении всей траектории снаряда, направление также является постоянным. Снаряд все время, независимо от любой другой переменной, будет ускоряться вниз на 90,8 м/с/с. Это, пожалуй, самая важная истина о снарядах, которую нужно усвоить.
н. TRUE — Начальная вертикальная скорость влияет на время, необходимое снаряду, чтобы подняться к своей вершине. Это также влияет на среднюю скорость снаряда, когда он поднимается к своему пику. В результате любое изменение вертикальной скорости изменит пиковую высоту снаряда.
о. ЛОЖЬ — Взлетающие вверх снаряды имеют нисходящее ускорение; это означает, что они замедляются по мере роста. Величина их скорости уменьшается. Снаряды, движущиеся вниз, также имеют нисходящее ускорение; это означает, что они ускоряются. Величина их скорости увеличивается.
стр. TRUE — Увеличение угла запуска (от 0 до 90 градусов) всегда будет увеличивать вертикальную составляющую начальной скорости (v iy ). Это увеличение v iy приведет к увеличению времени подъема снаряда к своей вершине. А увеличенный угол заставляет снаряд двигаться с большей средней скоростью на пути к своей вершине. Оба этих эффекта приводят к тому, что пиковая высота снаряда будет увеличиваться по мере увеличения угла пуска от 0 до 9°.0 градусов.
Это увеличение v iy приведет к увеличению времени подъема снаряда к своей вершине. А увеличенный угол заставляет снаряд двигаться с большей средней скоростью на пути к своей вершине. Оба этих эффекта приводят к тому, что пиковая высота снаряда будет увеличиваться по мере увеличения угла пуска от 0 до 9°.0 градусов.
кв. TRUE — При увеличении скорости запуска компоненты начальной скорости (как горизонтальной, так и вертикальной) также увеличиваются. Это заставляет снаряд оставаться в воздухе в течение более длительного периода времени и двигаться быстрее в вертикальном направлении. В результате увеличение скорости пуска всегда приводит к увеличению высоты полета снарядов.
9. Какие из следующих утверждений о времени полета снаряда верны? Перечислите все, что применимо.
- Время, в течение которого снаряд находится в воздухе, зависит от горизонтальной составляющей начальной скорости.

- Время, в течение которого снаряд находится в воздухе, зависит от вертикальной составляющей начальной скорости.
- Для снаряда, который приземляется на той же высоте, с которой он был выпущен, время подъема до пика равно времени падения с пика до исходной высоты.
- При одинаковых углах пуска вверх снаряды будут оставаться в воздухе дольше, если увеличить начальную скорость.
- Предположим, что удар по мячу в футболе является снарядом. Если мячу требуется 3 секунды, чтобы подняться до вершины своей траектории, то ему потребуется 6 секунд, чтобы упасть с вершины своей траектории на землю.
Ответ: BCD
а. ЛОЖЬ — Время вертикального подъема снаряда до пика (и последующего падения на землю) зависит от начальной вертикальной скорости. Изменение горизонтальной скорости вызовет только большее горизонтальное смещение снаряда (x).
б. ПРАВДА — Совершенно верно. Снаряды с большей вертикальной составляющей начальной скорости будут находиться в воздухе большее количество раз (при условии, что направление v iy вверх). Изменение значения v iy изменит время полета снаряда независимо от направления v iy .
Изменение значения v iy изменит время полета снаряда независимо от направления v iy .
в. TRUE — Для снарядов, запущенных под углом вверх и приземлившихся на исходной высоте, время до подъема на пик равно времени падения с пика. Если требуется 3 секунды, чтобы подняться вверх, потребуется 3 секунды, чтобы упасть.
д. TRUE — Для постоянного угла запуска увеличение начальной скорости (v i ) увеличит вертикальную скорость (v iy ). Это приводит к увеличению времени замедления снаряда до 0 м/с по мере его подъема к своему пику. Таким образом, снаряду требуется больше времени, чтобы добраться до вершины, больше времени, чтобы упасть с вершины, и в целом более длительное время находится в воздухе.
эл. ЛОЖЬ — Близко, но очень ложно. Если подъем на вершину занимает 3 секунды, то и падение с вершины занимает 3 секунды; 6 секунд — это общее время полета снаряда.
Перейдите к:
Обзорная сессия Главная — Список тем
Векторы и снаряды — Главная || Версия для печати || Вопросы и ссылки
Ответы на вопросы: Все || #1-9 || #10-45 || # 46-55 || # 56-72
Вам также может понравиться.
 ..
.. Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, включая встроенную обратную связь и инструкции. Если это то, что вы ищете, вам также может понравиться следующее:
- Блокнот-Калькулятор
Блокнот-Калькулятор включает задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и звуковым файлом, в котором подробно объясняется, как подходить и решать проблему. Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.
Посещение: Калькулятор Главная | Блокнот калькулятора — векторы и снаряды
- Серия приложений Minds On Physics
Приложение Minds On Physics («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно относятся к улучшению своего концептуального понимания физики. Каждый модуль серии охватывает отдельную тему и далее разбит на подтемы.
 «Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh. Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.
«Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh. Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.Посещение: MOP Главная страница приложения || швабра приложение — часть 1
4.2 Вектор ускорения | University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Вычислять вектор ускорения по заданной функции скорости в представлении единичного вектора.
- Опишите движение частицы с постоянным ускорением в трех измерениях.
- Используйте уравнения одномерного движения вдоль перпендикулярных осей для решения задачи в двух или трех измерениях с постоянным ускорением.
- Выразите ускорение в виде единичного вектора.
Мгновенное ускорение
Помимо получения векторов смещения и скорости движущегося объекта, мы часто хотим знать его вектор ускорения в любой момент времени на его траектории.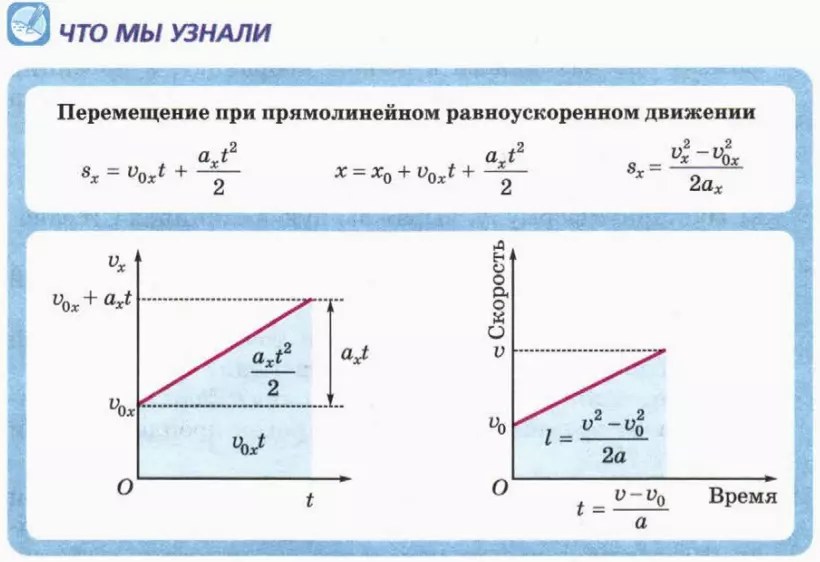 Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе. Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени [latex] \overset{\to }{v}(t), [/latex] находим
Этот вектор ускорения представляет собой мгновенное ускорение, и его можно получить из производной по времени функции скорости, как мы видели в предыдущей главе. Единственная разница в двух или трех измерениях состоит в том, что теперь это векторные величины. Взяв производную по времени [latex] \overset{\to }{v}(t), [/latex] находим
[латекс] \ overset {\ to {a} (t) = \ underset {t \ to 0} {\ text {lim}} \ frac {\ overset {\ to {v} (t + \ text { Δ} t) — \ overset {\ to {v} (t)} {\ text {Δ} t} = \ frac {d \ overset {\ to {v} (t)} {dt}. [/latex]
Ускорение по компонентам равно
[латекс] \overset{\to }{a}(t)=\text{}\frac{d{v}_{x}(t) }{dt}\hat{i}+\frac{d{v}_{y}(t)}{dt}\hat{j}+\frac{d{v}_{z}(t)}{ дт}\шляпа{к}. [/latex]
Кроме того, поскольку скорость является производной функции положения, мы можем записать ускорение через вторую производную функции положения: 9{3}\шляпа{к}\текст{м/с}. [/latex] (а) Что такое функция ускорения? б) Чему равен вектор ускорения при т = 2,0 с? Найдите его величину и направление. {2})\hat{i}+ 5t\шляпа{j}+5t\текст{}\шляпа{k}\текст{m}. [/latex] (а) Какова скорость? б) Чему равно ускорение? (c) Опишите движение из т = 0 с.
{2})\hat{i}+ 5t\шляпа{j}+5t\текст{}\шляпа{k}\текст{m}. [/latex] (а) Какова скорость? б) Чему равно ускорение? (c) Опишите движение из т = 0 с.
Стратегия
Мы можем получить некоторое представление о проблеме, взглянув на функцию позиции. Это линейно в y и z , поэтому мы знаем, что ускорение в этих направлениях равно нулю, когда мы берем вторую производную. Также обратите внимание, что позиция в направлении x равна нулю для t = 0 с и t = 10 с.
Решение
(a)
Показать ответ
(б)
Показать ответ 9{2}, [/latex], где a, b, и c — константы. Что можно сказать о функциональном виде функции скорости?
Показать решение
Постоянное ускорение
Многомерное движение с постоянным ускорением можно рассматривать так же, как показано в предыдущей главе для одномерного движения. Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое вдоль оси, перпендикулярной другим. Для построения соответствующих уравнений в каждом направлении рассмотрим двумерную задачу о движении частицы в xy плоскость с постоянным ускорением, игнорируя z -компоненту на данный момент. Вектор ускорения равен
Ранее мы показали, что трехмерное движение эквивалентно трем одномерным движениям, каждое вдоль оси, перпендикулярной другим. Для построения соответствующих уравнений в каждом направлении рассмотрим двумерную задачу о движении частицы в xy плоскость с постоянным ускорением, игнорируя z -компоненту на данный момент. Вектор ускорения равен
[латекс] \overset{\to }{a}={a}_{0x}\hat{i}+{a}_{0y}\hat{j}. [/latex]
Каждая составляющая движения имеет отдельный набор уравнений, подобных (Рисунок)–(Рисунок) из предыдущей главы об одномерном движении. Мы показываем только уравнения для положения и скорости в направлениях x и y . Аналогичная система кинематических уравнений может быть записана для движения в 9{2}+2{a}_{y}(y-{y}_{0}). [/latex]
Здесь индекс 0 обозначает начальное положение или скорость. (Рисунок) на (Рисунок) можно заменить на (Рисунок) и (Рисунок) без компонента z , чтобы получить вектор положения и вектор скорости как функцию времени в двух измерениях:
[латекс] \overset{ \ к {r} (t) = x (t) \ hat {i} + y (t) \ hat {j} \, \ text {and} \, \ overset {\ to {v} (t) = {v}_{x}(t)\шляпа{i}+{v}_{y}(t)\шляпа{j}. [/latex]
[/latex]
Следующий пример иллюстрирует практическое использование кинематических уравнений в двух измерениях. 9{2} [/latex] вниз по склону [latex] 15\text{°} [/latex] на t = 0. С началом системы координат в передней части домика, ее начальное положение и скорость являются
[латекс] \overset{\to}}{r}(0)=(75,0\шляпа{i}-50,0\шляпа{j})\,\text{m} [/латекс]
и
[латекс] \overset{\to}}{v}(0)=(4.1\шляпа{i}-1.1\шляпа{j})\,\текст{м/с}. [/latex]
(a) Каковы x- и y -компоненты положения и скорости лыжника как функции времени? б) Каковы ее положение и скорость в точке 9?{2} [/latex] вниз по склону [latex] 15\text{°}. [/latex] Начало системы координат находится в лыжной базе.
Стратегия
Поскольку мы оцениваем компоненты уравнений движения в направлениях x и y , нам необходимо найти компоненты ускорения и подставить их в кинематические уравнения. Компоненты ускорения находятся в системе координат на (рис. ). Затем, подставляя компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время т .
). Затем, подставляя компоненты начального положения и скорости в уравнения движения, мы можем найти ее положение и скорость в более позднее время т .
Решение
(a)
Показать ответ
Значение
Полезно знать, что, зная начальные условия положения, скорости и ускорения объекта, мы можем найти положение, скорость и ускорение в любое время позже.
С (Рисунок) по (Рисунок) мы завершили набор выражений для положения, скорости и ускорения объекта, движущегося в двух или трех измерениях. Если траектории объектов выглядят примерно как «красные стрелки» на заставке к главе, то выражения для положения, скорости и ускорения могут быть довольно сложными. В следующих разделах мы рассмотрим два частных случая движения в двух и трех измерениях, рассматривая движение снаряда и круговое движение.
На этом веб-сайте Университета Колорадо в Боулдере вы можете изучить позиционную скорость и ускорение божьей коровки с помощью интерактивного моделирования, позволяющего изменять эти параметры.
Резюме
- В двух- и трехмерном пространстве вектор ускорения может иметь произвольное направление и не обязательно указывает на заданную составляющую скорости.
- Мгновенное ускорение создается изменением скорости за очень короткий (бесконечно малый) период времени. Мгновенное ускорение представляет собой вектор в двух или трех измерениях. Его находят, взяв производную функции скорости по времени.
- В трех измерениях ускорение [латекс] \overset{\to }{a}(t) [/latex] может быть записано как векторная сумма одномерных ускорений [латекс] {a}_{x}(t ),{a}_{y}(t),\text{and}\,{a}_{z}(t) [/latex] вдоль x- , y — и z- осей.
- Кинематические уравнения для постоянного ускорения можно записать в виде векторной суммы уравнений постоянного ускорения в направлениях x , y и z .
Концептуальные вопросы
Если функция положения частицы является линейной функцией времени, что можно сказать о ее ускорении?
Если объект имеет постоянную составляющую скорости x и внезапно испытывает ускорение в направлении y , изменится ли составляющая его скорости x —?
Показать решение
Если объект имеет постоянную составляющую скорости x- и внезапно испытывает ускорение под углом [латекс] 70\текст{°} [/латекс] в 9{2}\шляпа{я}. {-2}\шляпа{k})\,\text{m}. [/latex] (а) Какова скорость как функция времени? б) Чему равно ускорение в зависимости от времени? в) Какова скорость частицы в точке 9?0640 т = 2,0 с? г) Какова его скорость при t = 1,0 с и t = 3,0 с? д) Какова средняя скорость между t = 1,0 с и t = 2,0 с?
{-2}\шляпа{k})\,\text{m}. [/latex] (а) Какова скорость как функция времени? б) Чему равно ускорение в зависимости от времени? в) Какова скорость частицы в точке 9?0640 т = 2,0 с? г) Какова его скорость при t = 1,0 с и t = 3,0 с? д) Какова средняя скорость между t = 1,0 с и t = 2,0 с?
Показать решение
Ускорение частицы является константой. При t = 0 скорость частицы равна [латекс] (10\шляпа{i}+20\шляпа{j})\текст{м/с}. [/latex] При t = 4 с скорость равна [латекс] 10\hat{j}\text{м/с}. [/latex] (а) Каково ускорение частицы? б) Как изменяются со временем положение и скорость? Предположим, что частица изначально находится в начале координат.
Частица имеет функцию положения [латекс] \overset{\to }{r}(t)=\text{cos}(1.0t)\hat{i}+\text{sin}(1.0t)\hat {j}+t\hat{k}, [/latex], где аргументы функций косинуса и синуса выражены в радианах. а) Чему равен вектор скорости? б) Чему равен вектор ускорения?
Показать решение
Самолет Lockheed Martin F-35 II Lighting взлетает с авианосца с взлетно-посадочной полосой длиной 90 м и скоростью взлета 70 м/с в конце взлетно-посадочной полосы.

 Например, в задаче 2.2.4 зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид
Например, в задаче 2.2.4 зависимости координаты тела по вертикальной оси и проекции скорости на эту ось имеют вид
 2.7 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. Правильный ответ — 1.
2.7 следует из зависимости скорости от времени найти время падения, а затем подставить его в зависимость координаты от времени. Правильный ответ — 1. По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось
По условию задачи 2.2.9 проекции векторов начальной скорости тел на горизонтальную ось одинаковы (это подчеркнуто на рисунке в условии с помощью вертикальной пунктирной прямой).
Поэтому дальше улетит то из них, у которого больше время движения. А оно, в свою очередь, определяется проекцией уравнения (2.2) на вертикальную ось В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение
В нашем же случае тело движется сначала вверх, потом вниз.
Действительно, время подъема для тела, брошенного вертикально вверх со скоростью 20 м/с, равно 2 с. А пройденный путь нужно найти за 3 с после броска.
Поэтому пройденный путь складывается из максимальной высоты подъема (для тела, брошенного со скоростью 20 м/с, она равна 20 м) и длины участка пути от верхней точки траектории до точки, в которой тело окажется через 3 с после броска.
Координату этой точки в системе координат, начало которой расположено на земле, а ось направлена вертикально вверх, можно найти, подставляя это значение времени в уравнение Педагогический (научно-педагогический состав)
Педагогический (научно-педагогический состав)



 Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
Горизонтальное смещение (т. е. дальность ) снаряда всегда будет увеличиваться по мере увеличения скорости пуска.
 Вертикальное смещение снаряда на первой половине его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения скорости пуска.
Вертикальное смещение снаряда на первой половине его траектории (т. е. пиковая высота ) всегда будет увеличиваться по мере увеличения скорости пуска.
 «Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh. Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.
«Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh. Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает Векторы и Снаряды.
Leave A Comment