Центростремительное ускорение. Равнопеременное движение по окружности.
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Центростремительное ускорение. Равнопеременное…
| Центростремительное ускорение. | ||
Вычислим величину ускорения при равномерном движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости . Рассмотрим треугольники АА1О и А1СВ. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. АО┴СВ и А1О┴А1С (углы со взаимно перпендикулярными сторонами). Из подобия треугольников следует пропорция: или, переходя к физическим обозначениям . Разделим правую и левую части равенства на промежуток времени, за которое совершено перемещение, и учтем, что и . Тогда: . | Примеры: — Земля при вращении вокруг оси ацс=0,03 м/с2, — Земля при вращении вокруг Солнца ацс=0,006 м/с2, — Солнечная система при вращении вокруг центра Галактики ацс=3.10-10 м/с2.
| |
Теперь определим направление ускорения. Т.к. мы должны для определения ускорения брать предел при Δt→0, то из рисунка видно, что угол Это значит, что прямая А1В (вектор ) будет стремиться наложиться на АО. Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение наз. центростремительным ускорением. | ||
Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: . | ||
Равнопеременное движение по окружности. Все уравнения для этого движения получим по аналогии с равнопеременным прямолинейным движением. | ||
Равнопеременное прямолинейноедвижение. | Равнопеременное движение по окружности. — угловое ускорение (рад/с2) | |
Следовательно, эти треугольники подобны.
Но вектор ускорения сонаправлен с вектором изменения скорости.
Движение по окружности
Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением
При малых углах поворота Δl ≈ Δs.
Рисунок 1.6.1. Линейное и угловое Δφ перемещения при движении тела по окружности |
Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt→0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:
Угловая скорость измеряется в рад/с.
Связь между модулем линейной скорости υ и угловой скоростью ω:
При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора
Равномерное движение тела по окружности является движением с ускорением. Ускорение
направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:
Для доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt. По определению ускорения
Рисунок 1.6.2. Центростремительное ускорение тела при равномерном движении по окружности |
Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках.
Модули скоростей одинаковы υA =υB = υ.
Из подобия треугольников OAB и BCD (рис. 1.6.2) следует:
При малых значениях угла Δφ = ωΔt расстояние |AB| =Δs ≈ υΔt. Так как |OA| = R и |CD| = Δυ, из подобия треугольников на рис. 1.6.2 получаем:
При малых углах Δφ направление вектора приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt→0, получаем:
При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.
В векторной форме центростремительное ускорение может быть записано в виде
где – радиус-вектор точки на окружности, начало которого находится в ее центре.
Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см 1.1):
В этой формуле Δυτ = υ2 – υ1 – изменение модуля скорости за промежуток времени Δt.
Направление вектора полного ускорения определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).
Рисунок 1.6.3. Составляющие ускорения и при неравномерном движении тела по окружности |
Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υx и υy (рис. 1.6.4).
При равномерном вращении тела величины x, y, υx, υy будут периодически изменяться во времени по гармоническому закону с периодом
Рисунок 1. Разложение вектора скорости по координатным осям |
6.4.Равномерное круговое движение
Центростремительное ускорение
Движение объекта по круговой траектории с постоянной скоростью известно как равномерное круговое движение (UCM). Объект в UCM постоянно меняет направление, а поскольку скорость является вектором и имеет направление, можно сказать, что объект, подвергающийся UCM, имеет постоянно изменяющуюся скорость, даже если его скорость остается постоянной. И если скорость объекта меняется, он должен ускоряться. Следовательно, объект, подвергающийся UCM, постоянно ускоряется. Этот тип ускорения известен как
Вопрос : Если автомобиль ускоряется, увеличивается ли его скорость?
Ответ : Это зависит.
Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедляясь). Или его скорость может оставаться постоянной, но при этом увеличиваться, если он движется равномерно по окружности.
Его скорость может увеличиваться, или он может ускоряться в направлении, противоположном его скорости (замедляясь). Или его скорость может оставаться постоянной, но при этом увеличиваться, если он движется равномерно по окружности.Не менее важно определить направление ускорения объекта, поскольку ускорение является вектором. Для этого нарисуем объект, движущийся против часовой стрелки по круговой траектории, и покажем вектор его скорости в два разных момента времени. Поскольку мы знаем, что ускорение — это скорость изменения скорости объекта во времени, мы можем определить направление ускорения объекта, найдя направление изменения его скорости, Δv.
Чтобы найти изменение скорости Δv, мы должны вспомнить, что .
Следовательно, нам нужно найти разность векторов v f и v i графически, что можно переписать в виде .
Вспомните, что для графического сложения векторов мы выстраиваем их в линию, кончик к хвосту, а затем рисуем результирующий вектор от начальной точки (хвоста) нашего первого вектора до конечной точки (конца) нашего последнего вектора.
Таким образом, вектор ускорения должен быть направлен в указанном выше направлении. Если я покажу этот вектор обратно на нашу исходную окружность, выстроив ее прямо между начальным и конечным векторами скорости, легко увидеть, что вектор ускорения указывает на центр окружности.
Вы можете повторить эту процедуру из любой точки круга… куда бы вы ни пошли, вектор ускорения всегда указывает на центр круга. На самом деле слово
Итак, теперь мы знаем направление ускорения объекта (к центру круга), но как насчет его величины? Величина центростремительного ускорения объекта находится в справочной таблице и определяется по формуле:
Круговая скорость
Так как же найти скорость объекта, движущегося по круговой траектории? Формула скорости, которую мы узнали из кинематики, по-прежнему применима.
Однако мы должны быть осторожны при использовании этого уравнения, чтобы понять, что объект, движущийся по круговой траектории, движется по окружности окружности.
Давайте рассмотрим пример задачи:
Вопрос : Миранда едет на своей машине по часовой стрелке по круговой трассе радиусом 30 м. Она проходит 10 кругов по трассе за 2 минуты. Найдите общее расстояние, пройденное Мирандой, среднюю скорость и центростремительное ускорение.
Ответ :
Центростремительная сила
Если объект, движущийся по круговой траектории, имеет внутреннее ускорение, второй закон Ньютона говорит нам, что должна существовать и результирующая сила, направленная к центру окружности.
Этот тип силы, известный как центростремительная сила, может быть силой гравитации, натяжением, приложенной силой или даже силой трения.
ПРИМЕЧАНИЕ. При решении задач с круговым движением важно понимать, что центростремительная сила на самом деле не является новой силой, центростремительная сила — это просто ярлык или группа, которую мы применяем к силе, чтобы указать, что ее направление направлено к центру. круга. Это означает, что вы никогда не захотите обозначать силу на диаграмме свободного тела как центростремительную силу, F
Мы можем объединить уравнение для центростремительного ускорения со 2-м законом Ньютона, чтобы получить 2-й закон Ньютона для кругового движения. Напомним, что второй закон Ньютона гласит:
Для объекта, движущегося по круговой траектории, должна существовать результирующая (центростремительная) сила, направленная к центру круговой траектории, чтобы вызвать (центростремительное) ускорение, направленное к центру круговой траектории.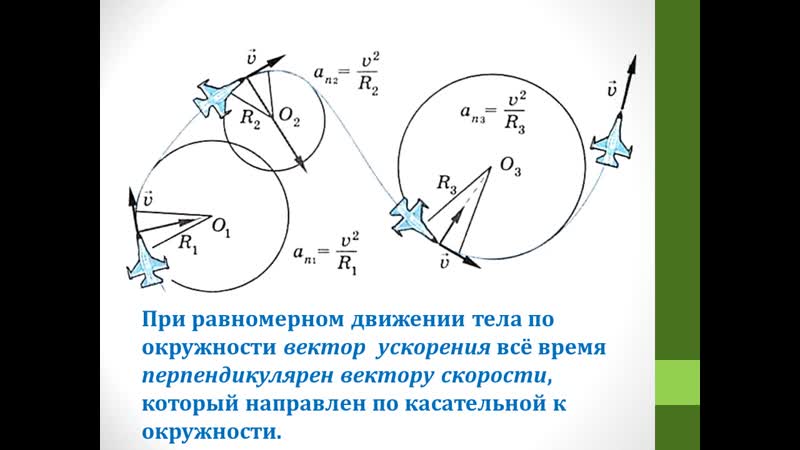
. Тогда мы можем пересмотреть второй закон Ньютона для этого конкретного случая следующим образом:0011
Затем, вспоминая нашу формулу для центростремительного ускорения как:
Мы можем сложить их вместе, заменив на в нашем уравнении, чтобы получить объединенную форму 2-го закона Ньютона для равномерного кругового движения:
Конечно, если объект движется по круговой траектории, а центростремительная сила устранена, объект будет продолжать двигаться по прямой линии в любом направлении, в котором он двигался в момент прекращения действия силы.
Вопрос : 800 Н, бегущий назад, поворачивает за угол по круговой траектории r = 1 м со скоростью 8 м/с. Найдите массу бегущего, центростремительное ускорение и центростремительную силу.
Ответ : Дано mg=800N, r=1м, v=8м/с; Найти m, ac, Fc
Давайте попробуем еще одну:
Еще одна примерная задача, на этот раз включающая только алгебраические манипуляции:
Частота и период
Для объектов, движущихся по круговым траекториям, мы можем охарактеризовать их движение по кругу, используя термины частота (f) и период (T).
Частота объекта — это количество оборотов, которое объект совершает за полную секунду. Измеряется в единицах [1/с] или Герцах (Гц). Точно так же период объекта — это время, необходимое для совершения одного полного оборота. Поскольку период представляет собой временной интервал, он измеряется в секундах. Мы можем связать период и частоту, используя уравнения:
Вопрос : Игрушечный поезд массой 500 г проходит 10 кругов по кругу за 1 мин 40 с. Найдите центростремительное ускорение поезда, если диаметр пути равен 1 м.0029 c ), центростремительная сила (F c ), период (T) и частота (f).
Ответ :
Рассмотрим другой пример:
Вертикальное круговое движение
Объекты перемещаются по кругу как вертикально, так и горизонтально.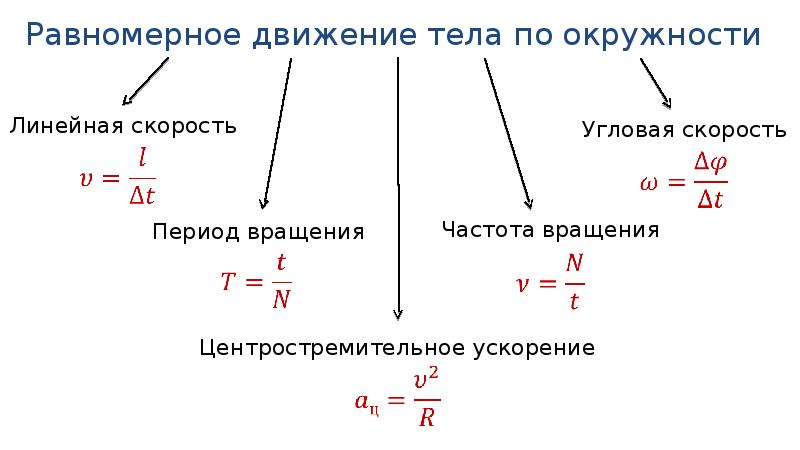
Поскольку скорость этих объектов обычно непостоянна, технически это не равномерное круговое движение , но наши навыки анализа UCM по-прежнему применимы.
Рассмотрим американские горки, движущиеся по вертикальной петле радиусом 10 м. Вы путешествуете по петле вверх ногами, но не падаете с американских горок. Как это возможно? Мы можем использовать наше понимание UCM и динамики, чтобы выяснить это!
Нижняя часть круга
Для начала давайте взглянем на каботажное судно, когда автомобиль находится в нижней части круга. На диаграмме свободного тела сила тяжести на каботажном судне, также известная как его вес, тянет его вниз, поэтому мы рисуем вектор, указывающий вниз, обозначенный «mg». Противодействующей этой силе является нормальная сила толкающих вверх поручней каботажного судна, которую мы обозначаем F 9.0029 Н .
Поскольку каботажное судно движется по круговой траектории, мы можем проанализировать его с помощью разработанных нами инструментов для равномерного кругового движения.
Второй закон Ньютона остается в силе, поэтому мы можем записать:
Обратите внимание: поскольку мы говорим о круговом движении, мы примем соглашение, что силы, направленные к центру круга, положительны, а силы, направленные от центра круга, положительны. круг отрицательный. В этот момент вспомните, что сила, которую вы «чувствуете», когда находитесь в движении, на самом деле является нормальной силой. Итак, находя нормальную силу, когда вы начинаете двигаться по кругу, мы находим, что
Поскольку мы знаем, что результирующая сила всегда равна массе, умноженной на ускорение, поэтому результирующая центростремительная сила равна массе, умноженной на центростремительное ускорение, мы можем заменить F NET c следующим образом:
Мы можем из полученного уравнения видно, что нормальная сила теперь равна весу плюс дополнительный член от центростремительной силы кругового движения. Когда мы движемся по круговой траектории в нижней части петли, мы чувствуем себя тяжелее своего веса.
Говоря простым языком, мы чувствуем дополнительные «перегрузки». Сколько g мы чувствуем, может быть получено с немного большим количеством манипуляций. Если мы перепишем наше уравнение для нормальной силы, вытянув массу, применив распределительное свойство умножения, мы получим:
Обратите внимание, что в скобках указано стандартное ускорение свободного падения, g, плюс член от центростремительного ускорения ().
Этот дополнительный термин представляет собой дополнительную перегрузку, ощущаемую человеком. Например, если c равно g (9,81 м/с 2 ), можно сказать, что человек в тележке испытывает два g (1g от центростремительного ускорения и 1g от гравитационного поля Земли). Если бы c были равны 3*g (29,4 м/с 2 ), человек будет испытывать в общей сложности четыре перегрузки.
Расширив этот анализ до аналогичной ситуации в другом контексте, попробуйте представить вместо американских горок массу, вращающуюся по вертикальному кругу на веревке.
Вы можете заменить нормальную силу натяжением струны в нашем анализе. Поскольку сила больше в нижней части круга, вероятность разрыва струны выше всего, когда масса находится в нижней части круга!
Вершина круга
В верхней части петли картина совершенно иная. Теперь нормальная сила от рельсов подставки должна давить на тележку, хотя все еще в положительном направлении, поскольку теперь вниз направлена к центру кругового пути. Однако в этом случае вес объекта также указывает на центр круга, поскольку гравитационное поле Земли всегда притягивает к центру Земли. Наша диаграмма свободного тела выглядит значительно иначе, и поэтому наше приложение ко второму закону Ньютона для кругового движения также значительно отличается.
Поскольку сила, которую вы чувствуете, на самом деле является нормальной силой, мы можем найти нормальную силу и разложить чистую центростремительную силу, как показано:
Из уравнения видно, что нормальная сила теперь равна центростремительной силе за вычетом вашего веса.
Если бы центростремительная сила была равна вашему весу, вы бы чувствовали себя невесомыми. Обратите внимание, что это также точка, где нормальная сила точно равна 0. Это означает, что рельсы дорожки больше не давит на тележку американских горок… если бы центростремительная сила была хоть немного меньше (скорость автомобиля была бы чуть меньше), нормальная сила FN была бы меньше 0. Поскольку рельсы физически не могут тянуть тележку в отрицательном направлении (от центра круга), это означает, что вагон падает с рельса. и у пассажира повозки скоро будет очень, очень плохой день. Только поддерживая высокую скорость, тележка может успешно преодолевать петлю… если двигаться слишком медленно, тележка падает.
Чтобы оставаться в безопасности, настоящие американские горки на самом деле имеют колеса с обеих сторон рельсов, чтобы предотвратить падение тележки, если она когда-либо замедляется в верхней части петли, хотя подставки спроектированы так, что на самом деле эта ситуация никогда не возникает.
.
Равномерное круговое движение (U.C.M.)
Тело совершает равномерное круговое движение (u.c.m.) , когда его траектория представляет собой окружность, а его угловая скорость постоянна. В этом разделе мы будем изучать:
- Концепция U.C.M. через его главные кинематические величины
- Основные характеристики у.к.м.
Концепция U.C.M.
Природа и ваша повседневная жизнь полны примеров равномерного кругового движения (мкм) . Сама Земля — одна из них: она совершает полный оборот вокруг своей оси каждые 24 часа. Старые проигрыватели или вентиляторы — еще один хороший пример u.c.m.
Равномерное круговое движение (u.c.m.) — движение с круговая траектория , в которой угловая скорость постоянна .
Это означает, что тело проходит равные углы за равные времена . При этом движении величина вектора скорости не меняется, но изменяется его направление (касательное к траектории в каждой точке). Это означает, что у него нет ни тангенциального, ни углового ускорения, хотя у него есть нормальное ускорение.
Размещение начала координат в центре окружности и знание ее радиуса R , мы можем выразить вектор положения следующим образом:
r→=x·i→+y·j→=R·cosφ·i→+R·sinφ·j→
остальные кинематические величины будут определяться значением угла φ в каждый момент времени.
Характеристики равномерного кругового движения (UCM)
Некоторые из основных характеристик равномерного кругового движения (UCM) следующие:
- Угловая скорость постоянна (ω = сст)
- Вектор скорости является касательной к траектории в каждой точке, и его направление совпадает с направлением движения. Это означает, что движение имеет нормальное ускорение
- Оба, угловое ускорение (α) и тангенциальное ускорение (a t ) равны нулю, поскольку скорость (модуль вектора скорости) постоянна
- Существует период (T) , то есть время, за которое тело совершает полный оборот. Это означает, что характеристики движения одинаковы каждые T секунд. Выражение для расчета периода πωT=2π/ω и справедливо только в случае равномерного кругового движения (н.ч.м.)
- Существует частота (f) , которая представляет собой число полных оборотов в секунду, совершаемых телом. Его значение обратно периоду .
Это означает, что движение имеет нормальное ускорение Экспериментируйте и учитесь
Данные
Равномерное круговое движение (u.c.m.)
На графике 900 показано равномерное круговое движение тела. Перетаскивайте значение скорости (модуль вектора скорости), чтобы наблюдать, как тело движется быстрее или медленнее.
Leave A Comment