основные ошибки и полезные лайфхаки
Вы умеете решать неравенства? Уверены?
Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя.
При решении неравенств мы можем:
1. Умножать обе части неравенства на число или выражение, не равное нулю.
При умножении обеих частей неравенства на положительное число знак неравенства сохраняется.
При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный.
2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны
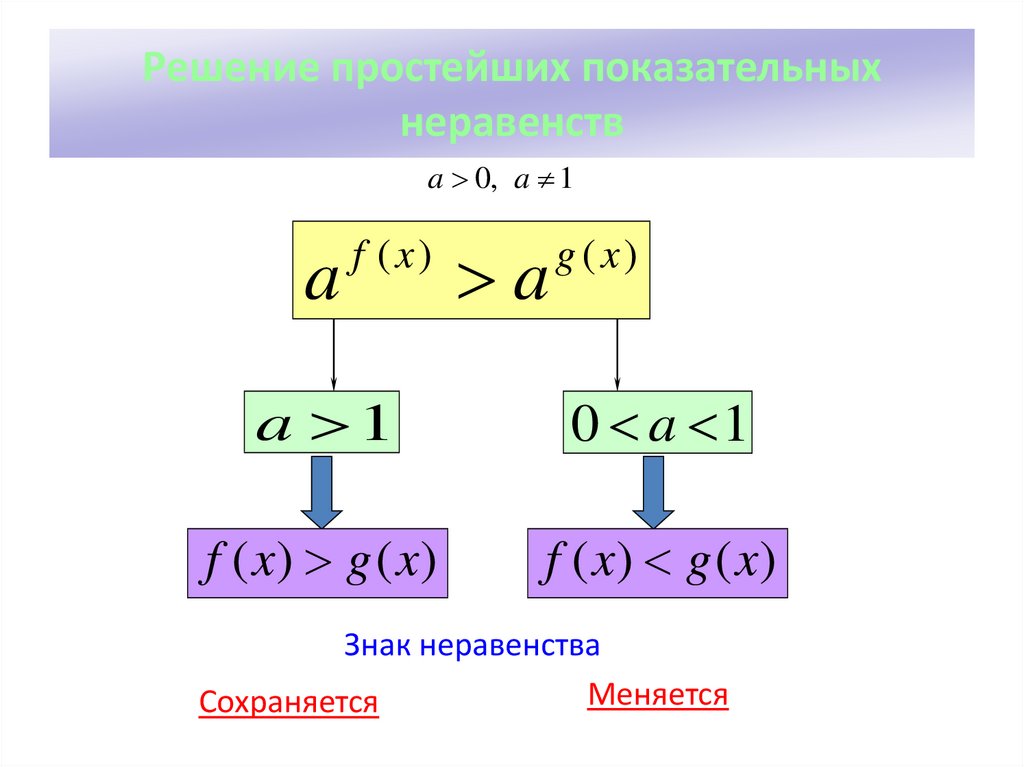
3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный.
Конечно, мы не просто «отбрасываем» основания степеней или логарифмы.
4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя).
5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени.
Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты.
1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем.
Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов.
> 0
> 0
Получаем, что < 0 или > . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
«Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет.
Как, например, решить неравенство
>
Перенесем все в левую часть неравенства, чтобы в правой остался ноль.
> 0
Разложим левую часть на множители.
> 0
Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: < или > .
Запомним: ответы типа « > » абсурдны.
Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: .
4. Возводить обе части неравенства в квадрат можно только если они неотрицательны.
5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же.
6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений.
7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать.
При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе.
Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений.
А теперь – полезный лайфхак для решения дробно-рациональных неравенств.
Решите неравенство
Запишем ОДЗ:
Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени.
Может быть, сделаем проще? Представим дробь в виде суммы дробей и .
Продолжаем упрощать левую часть:
Теперь можно и привести дроби к одному знаменателю.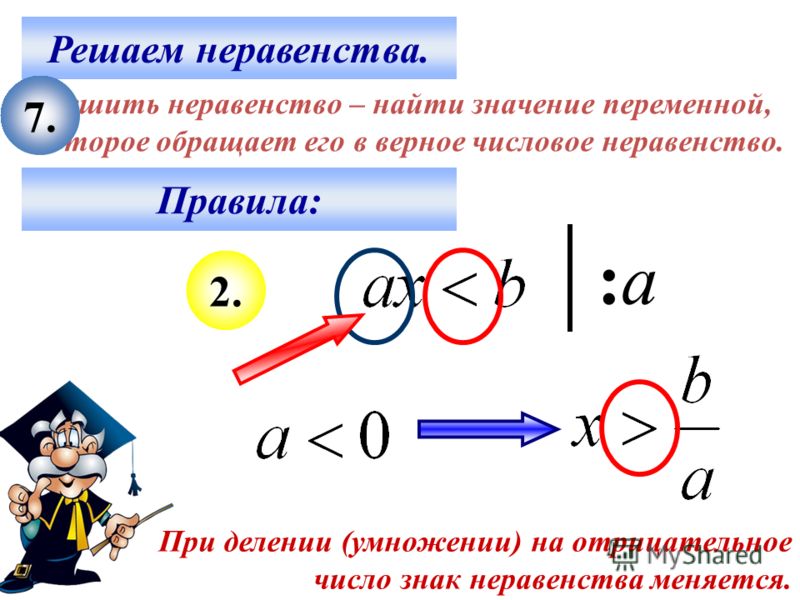
Все, больше ничего не пишем. Решаем неравенство методом интервалов.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Решение неравенств: основные ошибки и полезные лайфхаки» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена: 08.03.2023
Логарифмические неравенства. Как решать логарифмические неравенства?
Логарифмическими называют неравенства, содержащие переменную под знаком логарифма.
Если проще: это неравенства, в которых неизвестные (иксы) или выражения с ними находятся внутри логарифмов.
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
Примеры:
|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)\({(x+1)}\) \(\begin{cases}2x>4\\x > -1\end{cases}\) \(\Leftrightarrow\) \(\begin{cases}x>2\\x > -1\end{cases}\) \(\Leftrightarrow\) \(x\in(2;\infty)\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства.
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\) |
Выпишем ОДЗ. |
|
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\) |
ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами. |
|
|
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\) |
Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) |
|
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\) |
Мы привели неравенство к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем. |
|
|
\(\frac{3x-2}{2x-3}\)\(≥\) \(3\) |
Переносим \(3\) и приводим к общему знаменателю, пользуясь |
|
|
\(\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\) |
Раскрываем скобки, приводим подобные слагаемые. |
|
|
\(\frac{-3x+7}{2x-3}\)\(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
|
\(\frac{3x-7}{2x-3}\)\(≤\) \(0\) |
Далее выносим \(3\) из числителя и \(2\) из знаменателя. |
|
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\) |
Построим числовую ось и отметим на ней точки \(\frac{7}{3}\) и \(\frac{3}{2}\). Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль. |
|
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
|
Записываем окончательный ответ. |
Раскладываем левую часть неравенства на множители. |
|
\(D=1+8=9\) |
Решаем неравенство методом интервалов. |
|
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену. |
|
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
|
Запишем ответ. |
Ответ: \((0; \frac{1}{3})∪(9;∞)\)
Смотрите также:
Показательные неравенства
Когда вы переворачиваете знак неравенства?
Обновлено 14 мая 2018 г. Неравенство с большим количеством отрицаний и абсолютных значений. Помощь! Когда переворачивать знак неравенства?
Неравенство с большим количеством отрицаний и абсолютных значений. Помощь! Когда переворачивать знак неравенства?
Не бойся! Есть пара случаев, когда вы переворачиваете неравенство, и мы рассмотрим их ниже.
TL;DR (слишком длинное; не читал)
TL;DR (слишком длинное; не читал)
Переворачивать знак неравенства при умножении или делении обеих частей неравенства на отрицательное число .
Также часто приходится переворачивать знак неравенства при решении неравенств с абсолютными значениями.
Умножение и деление неравенств на отрицательные числа
Основная ситуация, когда вам нужно перевернуть знак неравенства, — это когда вы умножаете или делите обе части неравенства на отрицательное число.
Например, рассмотрим следующую задачу:
3_x_ + 6 > 6_x_ + 12
Чтобы решить, вам нужно получить все x -es на одной стороне неравенства. Вычтите 6_x_ с обеих сторон, чтобы получить только х слева.
Вычтите 6_x_ с обеих сторон, чтобы получить только х слева.
3_x_ −6_x_ + 6 > 6_x_ −6_x_ + 12
−3_x_ + 6 > 12
Теперь изолируем x в левой части, переместив константу 6 в другую часть неравенства. Для этого отнимите 6 с обеих сторон.
− 3_x_ + 6 − 6 > 12 − 6
−3_x_ > 6
Теперь разделите обе части неравенства на −3. Поскольку вы делите на отрицательное число, вам нужно перевернуть знак неравенства .
−3_x_ (÷ −3) < 6 (÷ − 3)
x < − 2.
То же правило применимо, если вы умножаете обе части на дробь. Умножение и деление являются противоположностями одного и того же процесса, вроде сложения и вычитания, поэтому к ним применяются одни и те же правила.
Проблемы с абсолютными значениями
Вам также нужно подумать об изменении знака неравенства, когда вы имеете дело с задачами с абсолютными значениями .
Возьмем следующий пример. Если у вас есть:
Если у вас есть:
| 3_x_ | + 6 < 12,
Тогда, прежде всего, вы хотите выделить выражение абсолютного значения в левой части неравенства (это облегчает жизнь). Вычтите 6 с обеих сторон, чтобы получить:
| 3_x_ | < 6.
Теперь вам нужно переписать это выражение в виде составного неравенства . | 3_x_ | < 6 можно записать двумя способами:
3_x_ < 6 («положительная» версия) или
3_x_ > −6 («отрицательная» версия).
Эти два оператора также можно записать в одну строку:
−6 < 3_x_ < 6.
Вывод выражения абсолютного значения всегда положителен, но « x » внутри знаков абсолютного значения может быть отрицательным, поэтому нам нужно рассмотреть случай, когда x равно отрицательный. По сути, мы умножаем на -1: мы умножаем x на отрицательную единицу слева (но поскольку она находится внутри знаков абсолютного значения, результат все еще положительный), а затем мы умножаем правую часть на отрицательную и переключение знака неравенства, потому что мы только что умножили на минус.
Это дает нам два наших неравенства (или наше «составное неравенство»). Мы можем легко решить обе из них.
3_x_ < 6 становится x < 2, если мы разделим обе части на 3.
3_x_ > −6 станет x > −2 после того, как мы разделим обе части на 3. 2 и x > −2 или −2 < x < 2.
Для решения подобных задач требуется некоторая практика, так что не беспокойтесь, если у вас сначала не получится! Продолжайте в том же духе, и в конечном итоге это станет вашей второй натурой.
Понимание неравенств — SAT Mathematics
Все ресурсы SAT по математике
137 Практические тесты Вопрос дня Карточки Learn by Concept
SAT Mathematics Help » Неравенства и абсолютное значение » Понимание неравенств
Какое из следующих выражений выражает полный набор значений для , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
Неравенства можно решать так же, как уравнения, с одной важной оговоркой: если вы умножаете или делите на отрицательное число, вы должны перевернуть знак неравенства. Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель:
Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель:
Затем добавьте 2 к обеим сторонам, чтобы выделить член:
Затем разделите обе части на 3, чтобы получить одно:
Сообщить об ошибке
Какое из следующих значений представляет собой полный набор значений , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
Эта задача демонстрирует важную концепцию работы с неравенствами. Если вы умножаете или делите неравенство на отрицательное число, вы должны перевернуть знак неравенства. Здесь вы можете разделить обе части исходного неравенства на , чтобы остаться в одиночестве. Однако, если вы это сделаете, вы должны перевернуть знак, чтобы получить:
Вы можете выбрать число, соответствующее вашему ответу, чтобы убедиться, что оно удовлетворяет исходному неравенству. Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что
Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что
Обратите внимание, что во многих задачах можно избежать умножения/деления на отрицательное число путем прибавления или вычитания (которые не имеют таких ограничений) членов к сторонам неравенства, где они будут положительными. Например, учитывая , если вы прибавите к обеим сторонам и вычтете 10 из обеих сторон, вы получите , и теперь вы будете делить на положительное 2, и вам не придется беспокоиться о смене знака, чтобы получить .
Сообщить об ошибке
Если , что из следующего должно быть правдой?
I.
II.
III.
Возможные ответы:
I и III только
I только
II и III только
Ни один из них не должен быть правдой
Правильный ответ:
Никто не должен быть правдой
2 Объяснение:
На первый взгляд, вы можете просто умножить обе части исходного неравенства на и поверить, что . Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован:
Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован:
Если положительный, то
Если отрицательное значение, вы должны перевернуть знак и
Данное утверждение подразумевает, что x и y либо оба отрицательны, либо оба положительны, но вы не знаете, что именно.
В результате ни одно из этих утверждений «не должно быть истинным», поэтому правильный ответ «ни одно из этих утверждений не должно быть истинным».
Сообщить об ошибке
Если , что из следующего должно быть правдой?
Возможные ответы:
Правильный ответ:
Объяснение:
Неравенства можно решать точно так же, как уравнения (с оговоркой, что если вы умножаете/делите на минус, вы должны поменять знак неравенства, но это не играет роли в этой задаче). Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете:
Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете:
1) Прибавьте 2 к обеим сторонам, чтобы получить:
2) Разделите обе части на 2, чтобы получить:
Сообщить об ошибке
Какое из следующих значений представляет собой полный набор значений , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
Неравенства можно решать так же, как и уравнения, с одной важной оговоркой, как вы увидите в этой задаче: если вы умножаете или делите на отрицательное число, вы должны изменить направление знака неравенства.
Здесь вы можете начать с умножения обеих сторон на 2, чтобы исключить знаменатель. Это приводит вас к:
Теперь у вас есть выбор, как вы перемещаете оставшиеся члены, чтобы изолировать и найти переменную. Если вы вычтете 6 из обеих сторон, вы получите:
Если вы вычтете 6 из обеих сторон, вы получите:
Здесь обратите внимание, что для решения набора решений вам придется разделить на -1, чтобы удалить отрицательный результат. Если вы это сделаете, вам нужно будет изменить направление знака, чтобы получить правильный ответ:
Теперь также признайте, что вы могли бы вообще избежать шага деления на минус. На этом этапе:
Вы могли бы прибавить к обеим сторонам, чтобы получить:
А затем, когда вы вычтете 8 из обеих сторон, вы также получите правильный ответ:
Сообщить об ошибке
2Что из следующего представляет полный набор значений , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
Неравенства можно решать точно так же, как уравнения, с той лишь оговоркой, что если вы умножаете или делите на отрицательное число, вы должны поменять знак неравенства. В этой задаче вам не нужно делать этот шаг.
В этой задаче вам не нужно делать этот шаг.
Во-первых, ваша цель состоит в том, чтобы получить все термины с одной стороны и числовые термины с другой. Для этого вы можете прибавить к обеим сторонам и вычесть из обеих сторон, чтобы получить:
Теперь вы хотите остаться наедине, так что вы можете разделить обе стороны на . Это оставляет:
или сокращенную дробь .
Обратите внимание, что вы можете читать неравенства слева направо или справа налево, поэтому здесь «две трети больше, чем» — это то же самое, что «меньше двух третей». Таким образом, вы найдете ответ, записанный как .
Обратите внимание, что вы можете проверить значение, близкое к вашему неравенству, чтобы убедиться, что оно работает. Поскольку у вас есть , вы можете попробовать . Если вы подключите это к заданному неравенству, вы увидите, что оно работает, возвращая истинное утверждение . Это поможет подтвердить ваш ответ.
Сообщить об ошибке
Что из следующего представляет собой полный набор решений для значений , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
При работе с неравенствами очень важно учитывать, что всякий раз, когда вы умножаете или делите на отрицательное число, вы должны перевернуть знак неравенства. Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить:
Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить:
Обратите внимание, что вы также можете справиться с этим, используя только сложение/вычитание, где правила точно такие же, как и в уравнениях. Для этого сложите и вычтите из обеих частей данного неравенства. затем становится:
Затем вы делите на положительное число, , чтобы изолировать . Это дает вам соответствие правильному ответу, указанному выше.
Сообщить об ошибке
Какое из следующих неравенств представляет собой полный набор решений для значений , которые удовлетворяют приведенному выше неравенству?
Возможные ответы:
Правильный ответ:
Объяснение:
Неравенства можно решать так же, как и уравнения — проделайте то же самое с обеими сторонами, пока не изолируете переменную — за одним важным исключением. Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать.
Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать.
Здесь, если вы вычтете из обеих частей, вы можете получить все члены в одной части уравнения, причем с положительным коэффициентом, поэтому вам не нужно беспокоиться о делении на отрицательное. Это дает вам:
Затем прибавьте к обеим сторонам, чтобы изолировать переменную справа:
Разделите на и вы получите ответ:
, который совпадает с
Сообщить об ошибке
900 выражает полный набор значений для , которые удовлетворяют приведенному выше неравенству?Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы ответить на этот вопрос, мы должны иметь в виду, что неравенства подчиняются тем же правилам и операциям, что и уравнения, за одним важным исключением.



 2-t-2>0\)
2-t-2>0\) 
Leave A Comment