Найдите Упражнение 7 № 3 ГДЗ Физика 9 класс Кикоин И.К. – Рамблер/класс

Найдите Упражнение 7 № 3 ГДЗ Физика 9 класс Кикоин И.К. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Пользуясь приведенными на рисунке 45 графиками проекций скоростей трех тел, выполните следующие задания: а) определите ускорения этих тел; б) составьте для каждого тела формулу зависимости скорости от времени; в) найдите, в чем сходны и в чем различаются движения, соответствующие графикам 2 и 3?

ответы

а)    Ускорение тела определяем по формуле:
Vx=V0x+axt,


б)    Формула зависимости скорости от времени:
Vx=V0x+axt.
Для первого тела:
Vx1= 1 м/с+1м/c2∙t Для второго тела:
Vx2=4м/с+0,5м/с2∙t.
Для третьего тела:
Vx3=1м/с-0,5м/с2∙t.
в)            Сходство движений, обозначенных графиками 2 и 3 в том, что они оба относятся к типу равноускоренного прямолинейного движения, но график 2 соответствует ускоренному движению, а график 3 — замедленному.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

Дополнительное задание а) б) в) г)????

(Подробнее…)

ГДЗ

Решите пожалуйста Дополнительное задание а) б) в) г)

(Подробнее…)

ГДЗЭкзамены

Можно ли § 6 № 1 ГДЗ Физика 9 класс Кикоин И.

К.

Автомобиль движется к востоку со скоростью 40 км/ч. Другой автомобиль движется к югу с той же скоростью 40 км/ч. Можно ли сказать, что (Подробнее…)

ГДЗФизика9 классКикоин И.К.

Каким движениям соответствуют § 7 № 2 ГДЗ Физика 9 класс Кикоин И.К.

Каким движениям соответствуют графики 1 и 2 на рисунке 29? (Подробнее…)

УчителяФизика9 классКикоин И.К.

Как направлен вектор § 11 № 6 ГДЗ Физика 9 класс Кикоин И.К.

Как направлен вектор ускорения при прямолинейном неравномерном движении?

ГДЗФизика9 классКикоин И.К.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

⇐ Предыдущая12345678910Следующая ⇒

1. Водитель автомобиля, движущегося со скоростью 72 км/ч, увидев красный свет светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться на 5 м/с каждую секунду. Найдите расстояния, которые автомобиль проходит в первые 2 с после начала торможения и до полной его остановки.

Решение. Координатную ось X направим по направлению движения автомобиля (рис. 42), а за начало

отсчета координаты примем то место на дороге, где началось торможение. Начало отсчета времени отнесем к моменту, когда водитель нажал на тормоз.

Начальная скорость v0 автомобиля сонаправлена с осью X, а ускорение направлено в противоположную сторону, так что проекция начальной скорости vox положительна, а проекция ускорения ах — отрицательна. Значит, vQx = vo и ах= — а. Расстояния, пройденные автомобилем,— это проекции перемещения sx, a sx=x—x0 Так как х0 = 0, то нужно найти координаты х1 и х2 автомобиля через 2 с после начала торможения и в момент

 

«тау») проекция скорости vx равна нулю. Но vx = v0x + axt Поэтому

0 = v0x + axt1, откуда ах=- v0x: t1

Все время движения равно 2т. Следовательно,

Ответ показывает, что график рисунка 43 соответствует движению тела сначала в одном направлении, а затем на такое же расстояние в противоположном направлении, в результате чего тело оказывается в исходной точке.

 

Упражнение 7

1. Постройте в координатных осях (х, t) графики скорости двух тел, движущихся равноускоренно: одно с возрастающей по модулю скоростью, другое — с убывающей. Начальные скорости и ускорения тел соответственно равны: 1 м/с и 0,5 м/с2; 9 м/с и 1,5 м/с2. Какой путь пройдет второе тело до остановки? Через какое время скорости обоих тел станут одинаковыми и какой путь пройдет за это время первое тело?

2. На рисунке 44 изображены графики проекций скоростей движения трех тел. Каков характер движения этих тел? Что можно сказать о скоростях движения тел в моменты времени, соответствующие точкам А и В графика? Определите ускорения и напишите выражения для скорости и перемещения этих тел.

3. Пользуясь приведенными на рисунке 45 графиками проекций скоростей трех тел, выполните следующие задания: а) определите ускорения этих тел; б) составьте для каждого тела формулу зависимости скорости от времени; в) найдите, в чем сходны и в чем различаются движения, соответствующие графикам 2 и 3?

4. На рисунке 46 приведены графики проекций скоростей движений трех тел. По этим графикам: а) определите, чему соответствуют отрезки OA, OB и ОС на осях координат; б) найдите ускорения тел; в) напишите выражения для скорости и перемещения каждого тела.

5. Самолет при взлете проходит взлетную полосу за 15 с и в момент отрыва от земли имеет скорость 100 м/с. С каким ускорением двигался самолет по взлетной полосе и какова ее длина?

6. Снаряд, летящий со скоростью 1000 м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200 м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.

7. Ракета движется с ускорением 45 м/с2 и к некоторому моменту времени достигает скорости 900 м/с. Какой путь она пройдет в следующие 2,5 с?

8. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался прямолинейно с ускорением 9,8 м/с2?

9. Наблюдения показали, что скаковая лошадь достигает наибольшей скорости 15 м/с после того, как она, приняв старт, «разгонится» на протяжении 30 м. Считая, что лошадь скачет с постоянным ускорением, найдите это ускорение.

10. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с

2?

11. Пассажирский поезд тормозит и движется с ускорением 0,15 м/с2. На каком расстоянии от места включения тормоза скорость поезда станет равной 3,87 м/с, если в момент начала торможения скорость была 54 км/ч?

 

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться с друзьями:

Дата добавления: 2014-01-14; Просмотров: 1802; Нарушение авторских прав?; Мы поможем в написании вашей работы!

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

параметрических уравнений: графики | Алгебра и тригонометрия

Цели обучения

В этом разделе вы будете:

  • Наносить на график плоские кривые, описываемые параметрическими уравнениями, путем построения точек.
  • Граф параметрических уравнений.

Это конец девятого иннинга, с двумя аутами и двумя игроками на базе. Хозяева проигрывают с разницей в два раунда. Тесто раскачивается и ударяет по бейсбольному мячу со скоростью 140 футов в секунду и под углом приблизительно [латекс]\,45°\,[/латекс] к горизонтали. Какое расстояние пролетит мяч? Сможет ли он очистить забор для победного хоумрана? Результат может частично зависеть от других факторов (например, ветра), но математики могут смоделировать траекторию снаряда и приблизительно предсказать, как далеко он пролетит, используя параметрические уравнения. В этом разделе мы обсудим параметрические уравнения и некоторые распространенные приложения, такие как задачи о движении снарядов.

Рисунок 1. Параметрические уравнения могут моделировать траекторию снаряда. (кредит: Пол Крехер, Flickr)

Построение графиков параметрических уравнений с помощью точек

Вместо графического калькулятора или компьютерной графической программы стандартным методом является построение точек для представления графика уравнения. Пока мы тщательно подсчитываем значения, построение точечных графиков очень надежно.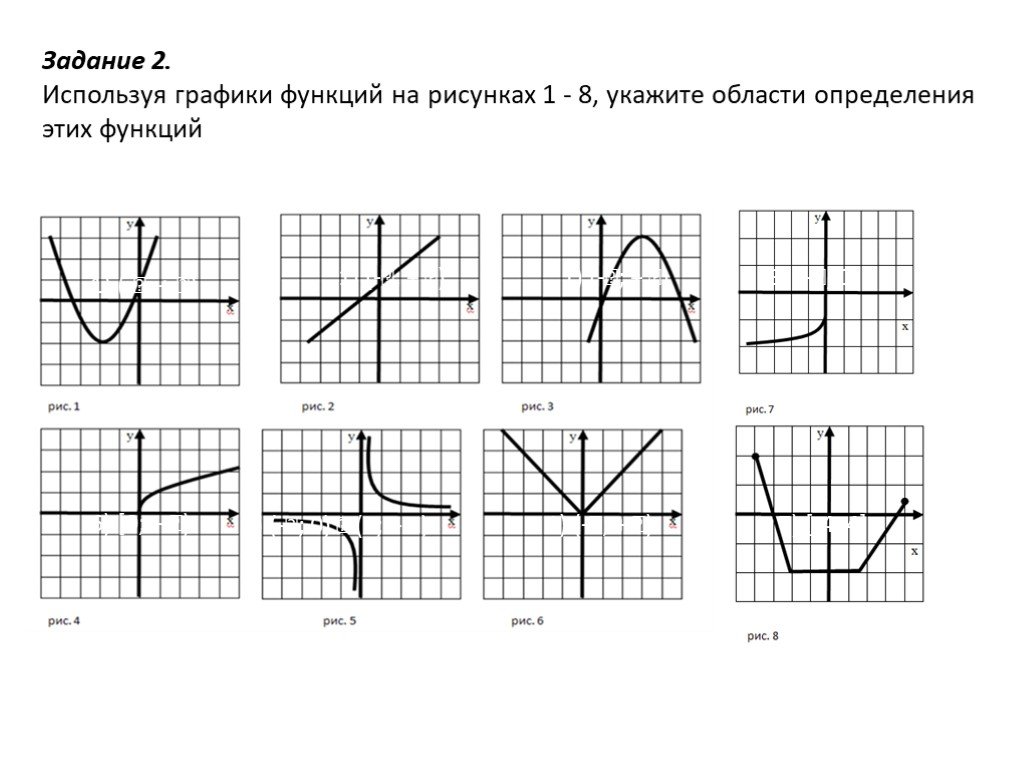 {2}+1,\,\,y \влево(т\вправо)=2+т.[/латекс]

Показать решение

Анализ

По мере того, как значения [латекс]\,t\,[/латекс] увеличиваются в положительном направлении от 0 до 5, точки на графике очерчивают верхнюю половину параболы. Когда значения [latex]\,t\,[/latex] становятся отрицательными, они очерчивают нижнюю половину параболы. Ограничений по домену нет. Стрелки указывают направление в соответствии с возрастающими значениями [latex]\,t.\,[/latex] График не представляет функцию, так как он не пройдет тест вертикальной линии. График состоит из двух частей: положительные значения для [latex]t,[/latex] и отрицательные значения для [latex]t[/latex]

Попробуйте

Нарисуйте график параметрических уравнений[латекс]\,x=\sqrt{t},\,\,y=2t+3,\,\,\,0\le t\le 3. [/latex]

Показать решение

Набросок графика тригонометрических параметрических уравнений

Построить таблицу значений заданных параметрических уравнений и начертить график:

[латекс]\begin{array}{l}\\ \begin{array}{l}x =2\mathrm{cos}\,t\hfill \\ y=4\mathrm{sin}\,t\hfill \end{массив}\end{массив}[/latex]

Показать решение

Анализ

Мы видели, что параметрические уравнения можно изобразить в виде графика, нанеся точки. Однако графический калькулятор сэкономит некоторое время и выявит нюансы на графике, которые могут быть слишком утомительными, чтобы обнаруживать их, используя только ручные вычисления.

Не забудьте изменить режим калькулятора на параметрический (PAR). Для подтверждения в окне [latex]\,Y=\,[/latex] должно отображаться

[latex]\begin{array}{c}{X}_{1T}=\\ {Y}_{1T} =\end{массив}[/latex]

вместо [latex]\,{Y}_{1}=.[/latex]

Попробуйте

График параметрических уравнений:[латекс]\,х=5\mathrm{cos}\,t,\,\,y=3\mathrm{sin}\,t.[/латекс]

Показать решение

Совместное графическое отображение параметрических уравнений и прямоугольной формы

Графическое отображение параметрических уравнений [латекс]\,x=5\mathrm{cos}\,t\,[/latex]и[латекс]\,y=2\mathrm{sin }\,t.\,[/latex]Сначала постройте график, используя точки данных, сгенерированные из параметрической формы. Затем начертите прямоугольную форму уравнения. Сравните два графика.

Показать решение

Анализ

На (рисунке) данные параметрических уравнений и прямоугольного уравнения нанесены вместе. Параметрические уравнения показаны синим цветом; график для прямоугольного уравнения нарисован поверх параметрического пунктирным красным цветом. Ясно, что обе формы дают один и тот же граф.

Рис. 5.

Графики параметрических уравнений и уравнений прямоугольной формы в системе координат sqrt{t},\,\,t\ge 0,\,[/latex] и прямоугольный эквивалент [latex]y=\sqrt{x-1}\,[/latex] в той же системе координат.

Показать решение

Анализ

С доменом [latex]\,t\,[/latex]restricted, мы наносим на график только положительные значения[latex]\,t.\,[/latex]. график прямоугольного уравнения заштрихован красным. И снова мы видим, что эти две формы пересекаются.

Попробуйте

Нарисуйте график параметрических уравнений[латекс]\,x=2\mathrm{cos}\,\theta \,\,\,\text{and}\,\,y=4\mathrm {sin}\,\theta ,\,[/latex] вместе с прямоугольным уравнением на той же сетке.

Показать решение

Применение параметрических уравнений

Многие преимущества параметрических уравнений становятся очевидными при их применении для решения реальных задач. Хотя прямоугольные уравнения в x и y дают общую картину пути объекта, они не раскрывают положение объекта в определенное время. Параметрические уравнения, однако, иллюстрируют, как значения x и y изменяются в зависимости от t , как местоположение движущегося объекта в определенное время.

Обычно параметрические уравнения применяются при решении задач, связанных с движением снаряда. В этом типе движения объект продвигается вперед в направлении вверх, образуя угол [латекс]\тета [/латекс] с горизонтом, с начальной скоростью [латекс]{v}_{0},\, [/latex]и на высоте [latex]h[/latex] над горизонталью.

Путь объекта, движущегося с наклоном [латекс]\тета[/латекс] к горизонту, с начальной скоростью [латекс]{v}_{0},\,[/латекс] и на высоте [ латекс]h[/латекс] над горизонталью равен 9{2}. \,[/latex]Уравнение для [латекс]\,x\,[/латекс] дает расстояние по горизонтали, а уравнение для [латекс]\,у\,[/латекс] дает расстояние по вертикали.

How To

Дана задача о движении снаряда. Для ее решения используйте параметрические уравнения.

  1. Горизонтальное расстояние определяется как [латекс]\,x=\left({v}_{0}\mathrm{cos}\,\theta \right)t.\,[/latex]Замените начальное скорость объекта for[latex]\,{v}_{0}.[/latex]
  2. Выражение[латекс]\,\mathrm{cos}\,\theta \,[/латекс] указывает угол, под которым перемещается объект. Подставьте этот угол в градусах вместо [латекс]\,\mathrm{cos}\,\theta .[/латекс] 9{2}.\,[/latex]Снова подставьте начальную скорость вместо [латекс]\,{v}_{0},\,[/латекс] и высоту, на которую объект был брошен вместо [латекс]\ ,ч.[/латекс]
  3. Продолжайте вычислять каждый член для решения для[latex]\,t.[/latex]

Нахождение параметрических уравнений для описания движения бейсбольного мяча

Решите задачу, представленную в начале этого раздела. Удастся ли отбивающему сделать победный хоумран? Предположим, что по мячу ударили с начальной скоростью 140 футов в секунду под углом [латекс]\,45°\,[/латекс] к горизонту, и он коснулся мяча на высоте 3 фута над землей.

  1. Найдите параметрические уравнения для моделирования траектории бейсбольного мяча.
  2. Где мяч через 2 секунды?
  3. Как долго мяч находится в воздухе?
  4. Это хоумран?

Показать решение

Доступ к следующему онлайн-ресурсу для получения дополнительных инструкций и практики с графиками параметрических уравнений.

  • Графические параметрические уравнения на TI-84

Ключевые понятия

  • Когда есть третья переменная, третий параметр, от которого зависят [латекс]\,х\,[/латекс]и[латекс]\,у\,[/латекс], параметрические уравнения могут быть использовал.
  • Чтобы построить параметрические уравнения с помощью точек, составьте таблицу с тремя столбцами, помеченными [латекс]\,t,x\left(t\right),\,[/latex] и [латекс]\,y\left(t\ right). \,[/latex]Выберите значения для[latex]\,t\,[/latex] в порядке возрастания. Постройте два последних столбца для [латекс]\,х\,[/латекс]и[латекс]\,у.\,[/латекс] См. (Рисунок) и (Рисунок).
  • При построении параметрической кривой с помощью точек обратите внимание на соответствующие значения t и покажите на графике стрелки, указывающие ориентацию кривой. См. (Рисунок) и (Рисунок). 9{2}+\left({v}_{0}\mathrm{sin}\,\theta \right)t+h.\,[/latex]Начальная скорость обозначается как[latex]\,{v}_ {0}.\,\theta [/latex] представляет собой начальный угол объекта при броске, а [latex]\,h\,[/latex] представляет высоту, на которую движется объект.

Раздел Упражнения

Вербальный

Какие два метода используются для построения графиков параметрических уравнений?

Показать решение

В чем отличие параметрических уравнений точечного построения от декартовых уравнений? 9{2}-1\hfill \end{массив}[/latex]

The first row is labeled t, the second is labeled x, and the third is labeled y. The first columns contains the numbers -3, -2, -1, 0, 1, 2, 3. The other two columns are left blank for completion.»> 9{2}\hfill \end{массив}[/latex]

 
[латекс]т[/латекс] [латекс]x[/латекс] [латекс]у[/латекс]
[латекс]-3[/латекс]
[латекс]-2[/латекс]
[латекс]-1[/латекс]
[латекс]0[/латекс]
[латекс]1[/латекс]
 
[латекс]т[/латекс] [латекс]-3[/латекс] [латекс]-2[/латекс] [латекс]-1[/латекс] [латекс]0[/латекс] [латекс]1[/латекс] [латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

Показать решение

[латекс] \{\ begin {массив} {l} x (t) = 2 + t \ hfill \\ y (t) = 3-2t \ hfill \ end {массив} [/ латекс]

The first row is labeled t, the second is labeled x, and the third is labeled y. The first row contains the numbers -2, -1, 0, 1, 2, 3. The other two columns are left blank for completion.»>
 
[латекс]т[/латекс] [латекс]-2[/латекс] [латекс]-1[/латекс] [латекс]0[/латекс] [латекс]1[/латекс] [латекс]2[/латекс] [латекс]3[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

[латекс] \{\ begin {массив} {l} x (t) = -2-2t \ hfill \\ y (t) = 3 + t \ hfill \ end {массив} [/ латекс]

«> 9{3}\hfill \\ y(t)=t+2\hfill \end{массив}[/latex]

 
[латекс]т[/латекс] [латекс]-3[/латекс] [латекс]-2[/латекс] [латекс]-1[/латекс] [латекс]0[/латекс] [латекс]1[/латекс]
9{2}\hfill \\ y(t)=t+3\hfill \end{массив}[/latex]

 
[латекс]т[/латекс] [латекс]-2[/латекс] [латекс]-1[/латекс] [латекс]0[/латекс] [латекс]1[/латекс] [латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]
The first row is labeled t, the second is labeled x, and the third is labeled y. The first row contains the numbers — -2, -1, 0, 1, 2. The other two columns are left blank for completion.»>
 
[латекс]т[/латекс] [латекс]-2[/латекс] [латекс]-1[/латекс] [латекс]0[/латекс] [латекс]1[/латекс] [латекс]2[/латекс]
[латекс]х[/латекс]
[латекс]у[/латекс]

Показать решение

Для следующих упражнений нарисуйте кривую и включите ориентацию.

[латекс] \{\ begin {массив} {l} x (t) = t \\ y (t) = \ sqrt {t} \ end {массив} [/ латекс]

[латекс] \ {\ begin{array}{l}x(t)=-\,\sqrt{t}\\ y(t)=t\end{array}[/latex]

Показать решение

[латекс]\{\begin{массив}{l}x(t)=5-|t|\\ y(t)=t+2\end{массив}[/латекс]

[латекс]\ {\begin{array}{l}x(t)=-t+2\\ y(t)=5-|t|\end{array}[/latex]

Показать решение

9{2}},\,0

[латекс]x\left(t\right)=-t,y\left(t\right)=\sqrt{t},\ ,t\ge 0[/latex]

Показать решение

[латекс]x=-2\mathrm{cos}\,t,\,y=6\,\mathrm{sin}\,t,\,0\le t\le \pi [/latex]

[латекс] x = — \ mathrm {sec} \, t, \, y = \ mathrm {tan} \, t, \, — \ frac {\, \ pi} {2}

Показать решение

В следующих упражнениях используйте параметрические уравнения для целых чисел a и b :

[латекс]\begin{array}{l}x\left(t\right)=a\mathrm{cos}\ влево (\ влево (a + b \ вправо) t \ вправо) \\ y \ влево (t \ вправо) = a \ mathrm {cos} \ влево (\ влево (a-b \ вправо) t \ вправо) \ конец {массив }[/латекс]

Граф в области [латекс]\,\слева[-\пи ,0\справа],\,[/латекс]где[латекс]\,а=2\,[/латекс]и[латекс]\, b=1,\,[/latex] и укажите ориентацию.

Граф в области [латекс]\,\слева[-\пи ,0\справа],\,[/латекс]где[латекс]\,а=3\,[/латекс]и[латекс]\, b=2[/latex] и укажите ориентацию.

Показать решение

Граф в области [латекс]\,\слева[-\pi ,0\справа],\,[/латекс],где[латекс]\,а=4\,[/латекс]и[латекс]\, b=3[/latex] и укажите ориентацию.

Граф в домене [латекс]\,\слева[-\пи ,0\справа],\,[/латекс]где[латекс]\,а=5\,[/латекс]и[латекс]\, b=4[/latex] и укажите ориентацию.

Показать решение

Если [латекс]\,а\,[/латекс] больше, чем [латекс]\,b,\,[/латекс] на 1, опишите эффект значения [латекс]\,а\,[/латекс] и [латекс]\,b\,[/латекс] имеют на графике параметрические уравнения.

Опишите график, если[латекс]\,а=100\,[/латекс]и[латекс]\,b=99.[/латекс]

Показать решение

Что произойдет, если [латекс]\,b\,[/латекс]на 1 больше, чем [латекс]\,а?\,[/латекс]Опишите график.

Если параметрические уравнения [латекс]\,х\влево(т\вправо)={т}^{2}\,[/латекс] и [латекс]\,у\влево(т\вправо)=6- 3t\,[/latex]есть график горизонтальной параболы, открывающейся вправо, что изменит направление кривой? 9{2}\,[/латекс]и[латекс]\,х\влево(т\вправо)\,[/латекс]линейно

Запишите параметрические уравнения окружности с центром[латекс]\,\влево( 0,0\right),[/latex]радиус 5 и ориентация против часовой стрелки.

Показать решение

Напишите параметрические уравнения эллипса с центром[латекс]\,\влево(0,0\вправо),[/латекс]большой осью длиной 10, малой осью длиной 6 и ориентацией против часовой стрелки.

В следующих упражнениях используйте графическую утилиту для построения графика в окне[латекс]\,\слева[-3,3\справа]\,[/латекс]по[латекс]\,\слева[-3,3 \right]\,[/latex]в домене[latex]\,\left[0,2\pi \right)\,[/latex]для следующих значений [latex]\,a\,[/latex ]and[latex]\,b[/latex] и укажите ориентацию.

[латекс] \{\ begin {array} {l} x (t) = \ mathrm {sin} (at) \\ y (t) = \ mathrm {sin} (bt) \ end {array} [/ латекс]

[латекс]a=1,b=2[/латекс]

Показать решение

[латекс]a=2,b=1[/латекс]

[латекс]a=3,b=3[/латекс]

Показать решение

[латекс]a=5,b=5[/латекс]

[латекс]a=2,b=5[/латекс]

Показать решение

[латекс]a=5,b=2[/латекс]

Технология

В следующих упражнениях посмотрите на графики, созданные с помощью параметрических уравнений вида [латекс]\,\{\begin{массив }{l}x(t)=a\text{cos}(bt)\hfill \\ y(t)=c\text{sin}(dt)\hfill \end{массив}. \,[/latex] Используйте параметрический режим графического калькулятора, чтобы найти значения [латекс]a,b,c,[/латекс] и [латекс]d[/латекс] для построения каждого графика.

Показать решение

Показать решение

В следующих упражнениях используйте графическую утилиту для построения графиков заданных параметрических уравнений.

  1. [латекс] \ {\ begin {array} {l} x (t) = \ mathrm {cos} t-1 \\ y (t) = \ mathrm {sin} t + t \ end {array} [ /латекс]
  2. [латекс] \{\ begin {array} {l} x (t) = \ mathrm {cos} t + t \\ y (t) = \ mathrm {sin} t-1 \ end {array} [/latex ]
  3. [латекс] \{\ begin {array} {l} x (t) = t- \ mathrm {sin} t \\ y (t) = \ mathrm {cos} t-1 \ end {array} [/latex ]

Постройте график всех трех наборов параметрических уравнений в области [латекс]\,\влево[0,\,2\пи \вправо].[/латекс]

Показать решение

Построить график всех трех наборов параметрических уравнений в области [латекс]\,\left[0,4\pi \right]. [/latex]

Построить график всех трех наборов параметрических уравнений в области [латекс]\, \left[-4\pi ,6\pi \right].[/latex]

Показать решение

График каждого набора параметрических уравнений «ползет» по одной из осей. Что определяет, по какой оси ползет график?

Объясните влияние на график параметрического уравнения, когда мы поменяли местами [латекс]\,\mathrm{sin}\,t\,[/latex]и [латекс]\,\mathrm{cos}\,t[/ латекс]. 9{2}+10t+5.\text{}[/latex]Напишите параметрические уравнения для положения мяча, а затем освободите время для записи высоты как функции горизонтального положения.

Для следующих упражнений используйте этот сценарий: Дротик брошен вверх с начальной скоростью 65 футов/с под углом возвышения 52°. Учитывайте положение дротика в любой момент[latex]\,t.\,[/latex]Сопротивлением воздуха пренебрегайте.

Найдите параметрические уравнения, моделирующие проблемную ситуацию.

Показать решение

Найдите все возможные значения [latex]\,x\,[/latex], представляющие ситуацию.

Когда дротик упадет на землю?

Показать решение

Найдите максимальную высоту дротика.

Когда дротик достигнет максимальной высоты?

Показать решение

В следующих упражнениях посмотрите на графики каждого из четырех параметрических уравнений. Хотя они выглядят необычно и красиво, они настолько распространены, что имеют имена, указанные в каждом упражнении. Используйте графическую утилиту, чтобы построить график каждого в указанном домене.

Эпициклоида: [латекс]\,\{\begin{array}{l}x(t)=14\mathrm{cos}\,t-\mathrm{cos}(14t)\hfill \\ y(t )=14\mathrm{sin}\,t+\mathrm{sin}(14t)\hfill \end{array}\,[/latex]в домене[latex]\,[0,2\pi ][/latex ].

Гипоциклоида: [латекс] \{\ begin {array} {l} x (t) = 6 \ mathrm {sin} \, t + 2 \ mathrm {sin} (6t) \ hfill \\ y (t) =6\mathrm{cos}\,t-2\mathrm{cos}(6t)\hfill \end{array}\,[/latex]в домене[latex]\,[0,2\pi ][/ латекс].

Показать решение

Гипотрохоид: [латекс] \{\ begin {array} {l} x (t) = 2 \ mathrm {sin} \, t + 5 \ mathrm {cos} (6t) \ hfill \\ y (t) =5\mathrm{cos}\,t-2\mathrm{sin}(6t)\hfill \end{массив}\,[/latex]в домене[latex]\,\left[0,2\pi \ справа][/латекс].

A rose: [латекс] \, \ {\ begin {array} {l} x (t) = 5 \ mathrm {sin} (2t) \ mathrm {sin} t \ hfill \\ y (t) = 5 \mathrm{sin}(2t)\mathrm{cos}t\hfill \end{array}\,[/latex]в домене[latex]\,\left[0,2\pi \right][/latex] .

Показать решение

Использование графиков и визуальных данных в науке | Научный процесс

  • Закладка
  • Глоссарий терминов

Пролистайте любой научный журнал или учебник, и вы быстро заметите, что текст перемежается графиками и рисунками. В некоторых журналах до 30% места занимают графики (Кливленд, 1984), возможно, превзойдя поговорку о том, что «картинка стоит тысячи слов». Хотя многие журналы и газеты также включают графики, визуальное изображение данных имеет фундаментальное значение для науки и представляет собой нечто совершенно отличное от фотографий и иллюстраций, опубликованных в журналах и газетах. Хотя числовые данные первоначально компилируются в таблицы или базы данных, они часто отображаются в графической форме, чтобы помочь ученым визуализировать и интерпретировать вариации, закономерности и тенденции в данных.

Данные лежат в основе любой научной деятельности. Ученые в разных областях собирают данные в самых разных формах, от магнитуды и места землетрясений до длины клюва вьюрка, концентрации углекислого газа в атмосфере и так далее. Визуальное представление научных данных использовалось на протяжении столетий — например, в 1500-х годах Коперник нарисовал схематические зарисовки планетарных орбит вокруг Солнца, — но визуальное представление числовых данных в виде графиков появилось сравнительно недавно.

Использование графиков для представления числовых данных

В 1786 году Уильям Плейфер, шотландский экономист, опубликовал Коммерческий и политический атлас , который содержал различные экономические статистические данные, представленные в виде графиков. Среди них было изображение, показанное на рисунке 1, график, сравнивающий экспорт из Англии с импортом в Англию из Дании и Норвегии с 1708 по 1780 год (Playfair, 1786). (Между прочим, Уильям Плейфер был братом Джона Плейфера, геолога, который разъяснил широкой публике фундаментальную работу Джеймса Хаттона о геологических процессах. Чтобы узнать больше, см. наш модуль «Горный цикл: униформизм и переработка».)

Рисунок 1: График Уильяма Плейфера был одним из первых примеров визуального представления числовых данных.

График Playfair очень лаконично отображал мощное сообщение. График показывает время по горизонтальной оси (x) и деньги в английских фунтах по вертикальной оси (y). Желтая линия показывает денежную стоимость импорта в Англию из Дании и Норвегии; красная линия показывает денежную стоимость экспорта в Данию и Норвегию из Англии. Хотя таблица числовых данных показала бы ту же информацию, не было бы сразу очевидно, что что-то важное произошло примерно в 1753 году: Англия начала экспортировать больше, чем импортировала, сместив «баланс в пользу Англии». Эта простая визуализация большого набора числовых данных упростила его быстрое понимание.

Графики и рисунки быстро стали стандартными компонентами науки и научной коммуникации, а использование диаграмм в научных журналах резко увеличилось в последние годы, увеличившись почти вдвое с 35 диаграмм в журнале в среднем до более чем 60 в период с 1985 по 1994 год ( Закс и др. , 2002). Это увеличение объясняется рядом причин, в том числе использованием компьютерных программ, упрощающих построение графиков, а также созданием все более крупных и сложных наборов данных, для интерпретации которых требуется визуализация.

Графики — не единственная форма визуализированных данных. Карты, спутниковые изображения, анимация и более специализированные изображения, такие как изображения атомных орбит, также состоят из данных и также стали более распространенными. Создание, использование и чтение визуальных форм данных — это всего лишь один из видов анализа и интерпретации данных (см. наш модуль «Анализ и интерпретация данных»), но он широко распространен во всех областях и методах научных исследований.

Проверка понимания

Графическое представление данных

  • а.означает фотографирование.
  • b.упрощает интерпретацию сложных наборов данных.

Интерпретация графиков

Большинство графиков, опубликованных в научных журналах, связаны с двумя переменными. Не менее 85 % графиков, опубликованных в журнале Science , фактически показывают взаимосвязь между двумя переменными, одна на оси x, а другая на оси y (Cleveland, 1984). Хотя существует много других видов графиков, знание того, как полностью интерпретировать график с двумя переменными, может не только помочь любому расшифровать подавляющее большинство графиков в научной литературе, но и стать отправной точкой для изучения более сложных графиков. В качестве примера представьте, что вы пытаетесь определить какие-либо долгосрочные тенденции в таблице данных о концентрациях углекислого газа в атмосфере, полученных за несколько лет в Мауна-Лоа (таблица 1; нажмите на отрывок ниже, чтобы увидеть полную таблицу данных).

Таблица 1: Это небольшая часть таблицы данных, содержащей концентрации углекислого газа в атмосфере, измеренные в Мауна-Лоа. Нажмите на нее, чтобы увидеть полную таблицу. Загрузите данные из CDIAC (Центр анализа информации о углекислом газе).

Переменные просты: время в месяцах в верхней строке таблицы, годы в крайнем левом столбце таблицы и концентрации углекислого газа (CO 2 ) в отдельных ячейках таблицы. Тем не менее, большинству людей сложно разобраться в таком большом количестве числовой информации. Вам придется внимательно просмотреть всю таблицу, чтобы увидеть какие-либо тенденции. Но если мы возьмем те же самые данные и нанесем их на график, то это будет выглядеть так (рис. 2):

Рисунок 2: Данные, полученные из Таблицы 1, CO 2 в атмосфере, измеренные в Мауна-Лоа (Keeling & Whorf, 2005).

Чтение графика включает следующие шаги:

Описание графика: По оси x показана переменная времени в единицах лет, а по оси Y показан диапазон переменной концентрации CO 2 в единиц частей на миллион (ppm). Точками показаны отдельные измерения концентраций – числа, указанные в таблице 1. Таким образом, график показывает нам изменение содержания CO 9 в атмосфере.0775 2 концентрации с течением времени.

Описание данных и трендов: Линия соединяет последовательные измерения, облегчая просмотр как краткосрочных, так и долгосрочных трендов в данных. На графике легко увидеть, что концентрация атмосферного CO 2 неуклонно росла с течением времени, от низкого уровня около 315 частей на миллион в 1958 году до текущего уровня около 375 частей на миллион. В рамках этой долгосрочной тенденции также легко увидеть краткосрочные годовые циклы около 5 частей на миллион.

Интерпретация: На графике ученые могут получить дополнительную информацию из числовых данных, например, насколько быстро растет концентрация CO 2 . Эту скорость можно определить, рассчитав наклон долгосрочного тренда в числовых данных, и наблюдение этой скорости на графике делает ее очевидной. В то время как внимательный наблюдатель, возможно, смог бы выделить из таблицы увеличение содержания CO 2 концентраций за пять представленных десятилетий, даже высококвалифицированному ученому было бы трудно отметить годовые циклы атмосферного CO 2 в числовых данных — особенность, элегантно продемонстрированная пилообразным рисунком линии.

Преобразование данных в визуальный формат — это один из этапов анализа и интерпретации данных, а хорошо разработанные графики могут помочь ученым интерпретировать полученные данные. Интерпретация включает в себя объяснение причин долгосрочного повышения концентрации CO 9 в атмосфере.0775 2 концентраций сверх годового колебания, таким образом выходя за рамки самого графика, чтобы поместить данные в контекст. Увидев регулярный и повторяющийся цикл около 5 ppm, ученые поняли, что это колебание должно быть связано с естественными изменениями на планете из-за сезонной активности растений. Визуальное представление этих данных также помогло ученым понять, что увеличение концентраций CO 2 за показанные пять десятилетий происходит параллельно с промышленной революцией и, таким образом, почти наверняка связано с растущим числом видов деятельности человека, которые приводят к выбросу CO 2 (МГЭИК, 2007 г.).

Важно отметить, что ни один из этих трендов (долгосрочный рост или годовая цикличность), ни интерпретация не могут быть обнаружены в одном измерении или точке данных. Это одна из причин, по которой вы почти никогда не слышите, чтобы ученые использовали слово «данные» в единственном числе — данное. Представьте себе только одну точку на графике. Вы можете провести линию тренда, проходящую через него в любом направлении. Строгая научная практика требует нескольких точек данных для четкой интерпретации, и график может иметь решающее значение не только для отображения самих данных, но и для демонстрации того, на каком количестве данных ученый основывает свою интерпретацию.

Мы только что выполнили короткий логический процесс, чтобы извлечь много информации из этого графика. Хотя в графической форме может отображаться бесконечное множество данных, та же самая процедура может применяться при чтении любого вида графика. Повторим:

  1. Опишите график: О чем говорит название? Какая переменная представлена ​​на оси x? Что находится на оси Y? Каковы единицы измерения? Что означают символы и цвета?
  2. Опишите данные: Каков числовой диапазон данных? Какие закономерности вы видите в распределении данных по мере их построения?
  3. Интерпретируйте данные: Как закономерности, которые вы видите на графике, соотносятся с другими известными вам вещами?

Одни и те же вопросы применяются независимо от того, смотрите ли вы на график двух переменных или на что-то более сложное. Поскольку создание графиков является формой анализа и интерпретации данных, важно тщательно изучать графики ученого так же, как и его или ее письменную интерпретацию.

Контрольная точка понимания

Графики важны, потому что они

  • а. может прояснить тенденции и закономерности в данных.
  • b.покажите одну часть данных ясно.

Оценка ошибок и неопределенностей в визуальных данных

Графики и другие визуальные представления научной информации также обычно содержат еще один ключевой элемент анализа научных данных — меру неопределенности или ошибки в измерениях (см. наш модуль «Неопределенность, ошибка и достоверность»). Например, на графике на Рисунке 3 представлены средние измерения выбросов ртути из почвы в разное время в течение одного дня. Столбики погрешностей на каждом вертикальном столбце показывают стандартное отклонение каждого измерения. Эти планки погрешностей включены, чтобы продемонстрировать, что изменение выбросов со временем больше, чем присущая изменчивость в каждом измерении (дополнительную информацию см. в нашем модуле «Статистика в науке»).

Рисунок 3: Столбики ошибок в этом графическом отображении данных используются для демонстрации того, что изменение значения измерения (красные столбцы) во времени больше, чем присущая изменчивость данных (показана черными столбцами ошибок). Адаптировано из Carpi et al. (2007).

Графическое отображение данных также можно использовать не только для отображения ошибки, но и для количественной оценки ошибки и неопределенности в системе. Например, на рис. 4 показан газовый хроматограф разлива мазута. Пики на хроматограмме (синяя линия) предоставляют информацию о химических веществах, обнаруженных в разливе, а размер пика может дать оценку относительной концентрации этого конкретного химического вещества в разливе. Однако, прежде чем эту информацию можно будет извлечь из графика, необходимо рассчитать погрешность и неопределенность прибора (красная линия) и вычесть их из площади пика. Как вы можете видеть на рис. 4, изменчивость прибора уменьшается по мере движения слева направо на графике, и поэтому в этом случае графическое отображение ошибки имеет решающее значение для точного анализа данных.

Рисунок 4: Графическое отображение данных можно использовать для оценки ошибки и неопределенности системы (красная линия), а также для представления этой неопределенности. изображение © Содружество Австралии 2006 г.

Контрольная точка понимания

Графическое отображение данных используется для ___________ ошибки.

  • a.отображение и количественная оценка
  • б. скрыть или спрятать

Неправильное использование научных изображений

Неправильное использование графики может выявить тенденции, которых на самом деле не существует, или может привести к исчезновению реальных тенденций. Некоторые пытались указать на ошибки в ныне широко принятом понятии изменения климата, используя вводящую в заблуждение графику. Рисунок 5 ниже — один из таких графиков, появившихся в печати. Точка зрения, сделанная создателем этого, заключается в том, что нижний график, который показывает относительно небольшое изменение температуры за последние 1000 лет, оспаривает верхний график, используемый Межправительственной группой экспертов по изменению климата, который показывает недавнее быстрое повышение температуры.

Рисунок 5: Неправильное использование графических дисплеев может привести к путанице и искажению данных.

На первый взгляд кажется, что нижний график противоречит верхнему. Однако, присмотревшись повнимательнее, вы понимаете:

  • На самом деле два графика представляют совершенно разные наборы данных. Верхний график представляет собой изменение среднегодовой глобальной температуры, нормализованное к 30-летнему периоду, 1960-1990, тогда как нижний график представляет средние температуры в Европе по сравнению со средним значением за 20-й век.
  • Кроме того, оси Y двух графиков отображаются в разных масштабах — на нижнем графике расстояние между линиями 0,5° больше.

Оба этих метода имеют тенденцию к преувеличению изменчивости на нижнем графике. Однако основная причина различий в графиках фактически не показана на графиках. Автор графика создал изображение внизу, используя различные расчеты, которые не учитывали все переменные, которые ученые-климатологи использовали для создания верхнего графика. Другими словами, графики просто не показывают одни и те же данные.

Это распространенные методы, используемые для искажения визуальной формы данных — манипулирование осями, изменение одной из переменных в сравнении, изменение вычислений без полного объяснения — которые могут исказить истинное сравнение.

Визуализация пространственных и трехмерных данных

Существуют и другие виды визуальных данных помимо графиков. Вы можете думать о топографической карте или спутниковом изображении как об изображении или наброске поверхности земли, но оба эти изображения являются способами визуализации пространственных данных. Топографическая карта показывает собранные данные о высоте и расположении географических объектов, таких как озера или горные вершины (см. рис. 6). Эти данные могли быть собраны в полевых условиях геодезистами или с помощью аэрофотоснимков, но, тем не менее, карта — это не изображение региона, а визуальное представление данных. Топографическая карта на рис. 6 на самом деле выполняет вторую задачу помимо простой визуализации данных: она берет трехмерные данные (изменения высоты земли) и отображает их в двух измерениях на плоском листе бумаги.

Рисунок 6: Часть топографической карты USGS 7,5′ Пика Уоррена. Сплошные коричневые линии — контуры высот. Это изображение берет трехмерные данные о высоте и изображает их в двух измерениях.

Точно так же спутниковые изображения обычно ошибочно принимают за фотографии Земли из космоса, но на самом деле они гораздо сложнее. Спутник записывает числовые данные для каждого пикселя, и он делает это на определенных предопределенных длинах волн в электромагнитном спектре (дополнительную информацию см. в нашем модуле Light II: Electromagnetism). Другими словами, само изображение представляет собой визуализацию данных, которые были обработаны из необработанных данных, полученных со спутника. Например, спутники Landsat записывают данные на семи различных длинах волн: три в видимом спектре и четыре в инфракрасном диапазоне. Составное изображение четырех из этих длин волн отображается на изображении части Скалистых гор Колорадо, показанном на рисунке 7. Большая красная область в нижней части изображения не является красной растительностью в горах; вместо этого это область с высокими значениями излучения инфракрасных (или тепловых) длин волн. Фактически, этот регион был местом большого лесного пожара, известного как Hayman Fire, за месяц до получения спутникового снимка в июле 2002 г.

Рисунок 7: Июль 2002 г. спутниковый снимок Landsat пожара Хейман, центральный Колорадо. изображение © Проект USGS Landsat

Контрольно-пропускной пункт понимания

Что общего у спутниковых снимков и топографических карт?

  • а. Это визуальное представление данных.
  • б. Это фотографии места.

Работа с данными на основе изображений

Появление спутниковых изображений значительно расширило один метод сбора данных: извлечение данных из изображения. Например, из серии спутниковых изображений пожара в Хеймане, полученных во время его горения, ученые и лесоустроители смогли извлечь данные о масштабах пожара (который горел глубоко на территории Национального леса, где люди не могли наблюдать за ним). на земле), скорость распространения и температура горения. Сравнивая два спутниковых снимка, они могли найти область, которая горела в течение дня, недели или месяца. Таким образом, хотя сами изображения состоят из числовых данных, из этих изображений можно извлечь дополнительную информацию в качестве формы сбора данных.

Другой пример можно взять из области атомной физики. В 1666 году сэр Исаак Ньютон обнаружил, что когда солнечный свет проходит через призму, он разделяется на характерную радугу света. Почти через 200 лет после Ньютона Джон Гершель и У. Х. Фокс Талбот продемонстрировали, что при нагревании веществ и пропускании испускаемого ими света через призму каждый элемент испускает характерный узор из ярких цветных линий, но они не поняли почему ( см. рисунок 8). В 1913, датский физик Нильс Бор использовал эти изображения, чтобы сделать поразительное предположение: он предположил, что линейчатые спектры элементов возникают из-за движения электронов между разными орбиталями, и, таким образом, эти спектры могут предоставить информацию об электронной конфигурации элементов ( см. наш модуль «Атомная теория II: ионы, изотопы и электронные оболочки» для получения дополнительной информации). На самом деле вы можете рассчитать разницу потенциальной энергии между электронными орбиталями в атомах, анализируя цвет (и, следовательно, длину волны) излучаемого света.

Рисунок 8: Линейчатые спектры гелия (вверху) и неона (внизу). Расположение и цвет линий представляют уникальную длину волны, которая определяет электронную конфигурацию атомов.

Фотографии и видео также являются визуальными данными. В 2005 году группа ученых, базирующихся частично в лаборатории орнитологии Корнелла, опубликовала свои выводы о том, что птица, считавшаяся вымершей в Северной Америке, белоклювый дятел, была замечена в Арканзасе (Fitzpatrick et al., 2005). Их основные доказательства состояли из видеозаписей и фотографий летящей птицы, которые они включили в свою статью вместе с подробным анализом особенностей изображений и видео, которые предполагали, что птица была белоклювым дятлом. (Прочитать статью и посмотреть фотографии можно здесь.)

Графики для научной коммуникации

Во многих областях науки есть более специализированные графики, используемые для определенных типов данных. Биологи-эволюционисты, например, используют эволюционные деревья или кладограммы , чтобы показать, как виды связаны друг с другом, какие у них общие характеристики и как они эволюционируют с течением времени. Геологи используют тип графика, называемый стереосетка , которая представляет собой внутреннюю часть полушария, чтобы отобразить ориентацию слоев горных пород в трехмерном пространстве. Многие поля теперь используют трехмерные графики для представления трех переменных, хотя на самом деле они могут не представлять трехмерное пространство.

Независимо от точного типа графика создание четких, понятных визуализаций данных имеет фундаментальное значение во всех отраслях науки. В знак признания критического вклада визуальных средств в науку Национальный научный фонд и Американская ассоциация содействия развитию науки спонсируют ежегодный конкурс научной и инженерной визуализации, в котором представленные работы оцениваются на основе их визуального воздействия, эффективной коммуникации и оригинальности ( НФС, 2007). Точно так же чтение и интерпретация графиков является ключевым навыком на всех уровнях, от начинающего студента до ученого-исследователя. Графики являются ключевым компонентом научно-исследовательских работ, где регулярно представляются новые данные.