Карта сайта
- Главная
- vikon
|
|
Профессионально-общественная аккредитация
Педагогический (научно-педагогический) составchast_2_zadachi — Стр 8
71
где Φ=BS=BScosα ,
(α — угол между направлением магнитного поля B и направлением вектора S, перпендикулярного к плоскости рамки).
Тогда, для ЭДС индукции получаем формулу Ei=BSsinα dα/dt. Отсюда вытекает, что Edt=BSsinα dα. Интегрируя это уравнение, находим:
T / 4 | 0 |
∫Eidt = BS ∫sinαdα .
0π /2
Сучетом полученного соотношения, для среднего значения
ЭДС индукции имеем окончательное выражение:
| 1 |
| T / 4 | 4BS | 0 | |
<Ei>= |
| ∫Eidt = | ∫sinαdα = -4nBS= -0,16 В. | |||
T / | 4 | T | ||||
| 0 | π /2 | ||||
|
|
|
|
Здесь знак минус определяет направление индукционного
тока.
Ответ: <Ei>=0.16 В.
Задача 4. С помощью реостата равномерно увеличивают силу тока в катушке на I =0,1 А в 1 с. Индуктивность L катушки равна 0,01 Гн. Найти среднее значение ЭДС самоиндукции <Esi>.
Решение Среднее значение ЭДС самоиндукции определяется выра-
жением:
<Esi> =1 ∫t Esidt .
t 0
ЭДС самоиндукции связана с током, протекающим через катушку, выражением:
Esi = — L dIdt .
Из этого выражения следует, что Esidt=-LdI. Интегрируя это соотношение, для среднего значения ЭДС самоиндукции получаем выражение:
<Esi>= — L | I | L I | = -1 мВ. | |
∫dI = − | ||||
t | ||||
t | 0 |
| ||
|
|
|
72
Ответ: <Esi>=-1 мВ.
Задача 5. Вычислить взаимную индуктивность длинного прямого провода и прямоугольной рамки со сторонами a и b. Рамка и провод лежат в одной плоскости, причем ближайшая к проводу сторона рамки длиной b параллельна проводу и отстоит от него на расстояние l.
Решение: |
|
|
|
|
|
|
|
|
Пусть рамка и провод распо- | Y |
|
|
| a | |||
ложены в плоскости x-y, как пока- |
|
|
| |||||
|
|
|
|
|
|
| ||
зано на рисунке. | I |
|
|
|
| b | ||
рамку поток магнитного поля Φ, |
|
|
|
|
|
|
| |
созданного протекающим по пря- |
|
|
|
|
|
|
| |
|
|
|
|
|
|
| ||
мому проводу током I, связан с |
|
|
|
|
|
|
| |
O |
| l |
| x | ||||
|
| |||||||
током выражением Φ=L12I, | где |
|
| |||||
|
|
|
|
|
|
| ||
L12- коэффициент взаимной | ин- |
|
|
|
|
|
|
|
Пронизывающийдуктивности рамки и прямого провода.
Следовательно, L12=Φ/I. Найдем поток Φ, пронизывающий рамку. Поток через участок рамки шириной dx по определению равен dΦ=BdS=Bbdx, где
B(x)= 4μπ0 2xI — индукция магнитного поля, созданного прямым то-
ком I, на расстоянии x от провода. После интегрирования по всей ширине рамки получаем выражение для полного потока через рамку:
| l+a | μ0 | l+a | dx = | μ0Ib ln(1 | + a ) |
|
| Φ = ∫Bbdx = | 2Ib ∫ |
| ||||
| l | 4π | l | x | 2π | l |
|
|
|
|
|
|
| ||
| Следовательно, искомый коэффициент взаимной индуктив- | ||||||
ности рамки и провода выражается формулой: | L12 | = | |||||
μ0b ln(1+ a ). |
|
|
|
|
|
| |
2π | l |
|
|
|
|
|
|
Задачи для самостоятельного решения.
Задача 6. В однородном магнитном поле с индукцией В=0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной l=10 см. Ось вращения проходит че-
73
рез один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения n=16 с-1. (Ответ: U
=201 мВ.)
Задача 7. В однородном магнитном поле с индукцией В=0,35 Тл равномерно с частотой n=480 мин-1 вращается рамка, содержащая N=500 витков площадью S=50 см2. Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную ЭДС индукции Ei max , возникающую
в рамке. (Ответ: Ei max=44 В.)
Задача 8.
Рамка площадью S=100 см2 содержит N=103 витков провода сопротивлением R1=12 Ом. К концам обмотки подключено внешнее сопротивление R2=20 Ом. Рамка равномерно вращается в однородном магнитном поле (B=0,1 Тл) с частотой n=8 c-1. Определить максимальную мощность Pmax переменного
тока в цепи. (Ответ: Pmax=79Вт)
Задача 9. Проволочный виток радиуса r=4 см с сопротивлением R=0,01 Ом находится в однородном магнитном поле с индукцией B=0,04 Тл. Плоскость рамки составляет угол α=300 с линиями индукции поля. Какое количество электричества Q протечет по витку, если магнитное поле исчезнет ? (Ответ: Q=10 мКл.)
Задача 10. В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. По цепи протекло количество электричества Q=10 мкКл. Определить магнитный поток Φ, пересеченный кольцом, если сопротивление R цепи гальванометра равно 30 Ом. (Ответ: Φ=0,3 мВб.)
Задача 11. Рамка из провода сопротивлением R=0,01 Ом равномерно вращается в однородном магнитном поле с индукцией В=0,05 Тл.
Ось вращения лежит в плоскости рамки и перпендикулярно линиям индукции. Площадь рамки S=100 см2. Найти, какое количество электричества Q протечет через рамку за время поворота ее на угол α=30° в следующих трех случаях: 1) от α0=0
до α1=30°; 2) от α1 до α2=60°; 3) от α2 до α3=90°. (Ответ: Q1=25 мКл, Q2=18,3 мКл, Q3=7 мКл.)
Задача 12. Тонкий медный провод массой m=1 г согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в одно-
74
родное магнитное поле (В=0,1 Тл) так, что его плоскость перпендикулярна линиям индукции поля. Определить количество электричества Q, которое протечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию. (Ответ:
Q=41 мКл.)
Задача 13. Индуктивность L катушки равна 2 мГн. Ток частотой ν= 50 Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю ЭДС самоиндукции <Esi>, возникающую за интервал времени t, в течение которого ток в катушке изменяется от минимального до максимального значения.
Амплитудное значение силы тока I0=10 А. (Ответ:
<Esi>=4 В.)
Задача 14. Индуктивность L соленоида длиной l=1 м, намотанного в один слой на немагнитный каркас, равна 1,6 мГн. Площадь S сечения соленоида равна 20 см2. Определить число n витков на каждом сантиметре длины соленоида. (Ответ: n=8 см-1.)
Задача 15. Две катушки расположены на небольшом расстоянии одна от другой. Когда сила тока в первой катушке изменяется с быстротой I/ t=5 А/с, во второй катушке возникает ЭДС индукции Ei=0,1 В. Определить коэффициент L12 взаимной индукции катушек. (Ответ: L12=20 мГн. )
Тема 10. Энергия магнитного поля. Электромагнитные колебания.
Примеры решения задач.
Задача 1. Конденсатор, емкость которого C=500 пФ, соединен параллельно с катушкой индуктивности длиной l=40 см и площадью сечения S, равной 5 см2. Катушка содержит N=1000 витков. Сердечник немагнитный. Найти период T колебаний.
Решение:
Период T находим, используя формулу Томсона T = 2π LC , где L — индуктивность катушки.
Индуктивность катушки (соленоида) равна L= μμ0n2lS, где n — число витков на единицу длины обмотки, то есть n=N/l. Так как по условию задачи сердечник немагнитный, то μ=1. Окончательно имеем:
75 |
|
|
|
T = 2πN | μ | 0 SC | . |
| l | ||
|
|
|
Подставляя численные значения, получаем T=5,57 мкс. Ответ: Т=5,57 мкс.
Задача 2. Изменение со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид: U=50 cos(104πt) (значения всех величин указаны в системе СИ). Емкость конденсатора равна C=0,1 мкФ. Найти период T колебаний, индуктивность L контура, и длину волны λ, соответствующую этому контуру.
Решение:
В колебательном контуре без затухания напряжение на конденсаторе и ток в цепи изменяются по гармоническому закону.
Если время отсчитывать от момента, когда напряжение на конденсаторе максимально, то можно записать U=U0cosωt, где U0 — амплитуда, ω − круговая частота. Из сравнения этого выражения с зависимостью, приведенной в условии задачи, получаем ω=104π. Так как круговая частота и период связаны соотношением T=2π /ω, то, после подстановки чисел, получаем T=2 10-4 с. Индуктивность контура L найдем, используя формулу Томсона T = 2π LC , откуда L=T2/4π2C. Длину волны, соответствующую найденному периоду, находим из выражения λ=cT, где c — ско-
рость света. Подставляя численные значения, находим L = 4 10- 8/(4π210-7)=0,01 Гн., λ=3 108 2 10-4=6,104 м.
Ответ: T=2 10- 4 с, L=0,01 Гн, λ=60 км.
Задача 3. Соленоид длиной l=50 см и площадью поперечного сечения S=2 см2 имеет индуктивность L=2 10−7 Гн. При какой силе тока объемная плотность энергии магнитного поля w внутри соленоида равна 10-3 Дж/м3?
Решение:
Полная энергия магнитного поля контура дается выражени-
ем:
W = LI2/2,
76
где L — индуктивность соленоида, I — ток, протекающий по контуру.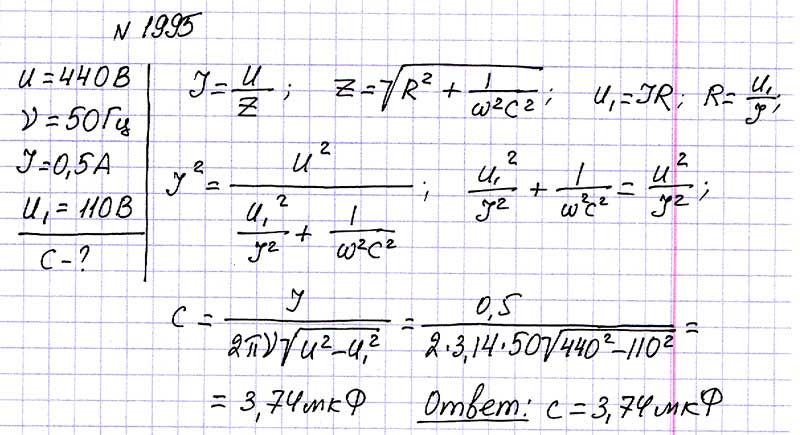
Объемная плотность энергии поля по определению равна:
w=W/V.
Здесь V — объем пространства внутри контура. Объем пространства, заключенного внутри соленоида, равен V=Sl. Следовательно, для объемной плотности энергии имеем соотношение:
w = 1 LI 2 .
2 Sl
Отсюда получаем окончательное выражение для искомой силы тока:
I = | 2Slw | = 1 А. |
| L |
|
Ответ: I=1 А.
Задача 4. Обмотка тороида с немагнитным сердечником имеет n=10 витков на каждый сантиметр длины. Определить плотность энергии w поля, если по обмотке течет ток I=16 А.
Решение:
Объемная плотность энергии однородного магнитного поля дается выражением:
w= B2 .
2μ0μ
Индукция магнитного поля тороида находится как B=μ0μnI. Тогда, для искомой плотности энергии поля получаем следующее
выражение:
w=μ0μn2I2/2 =161,3 Дж/м3.
Здесь учтено, что т. к. сердечник немагнитный, то μ=1.
Ответ: w=161,3 Дж/м3.
Задача 5. На тор из магнетика намотано N=500 витков провода. Найти энергию магнитного поля, если при токе I=2 А магнитный поток через сечение тора равен Φ=1 мВб.
Решение:
Проводник с индуктивностью L, по которому протекает ток
77
I, обладает энергией W=LI2/2, которая локализована в возбуждаемом током магнитном поле. Полный магнитный поток через контур, то есть потокосцепление, создаваемый протекающим по нему током, равен Ψ=LI, где Ψ=NΦ. Следовательно, LI=NΦ. Отсюда находим, что L=NΦ/I. Тогда, для искомой энергии магнитного поля окончательно получаем выражение:
W= 12 NΦI =0,5 дЖ
Ответ: W=0,5 дЖ.
Задачи для самостоятельного решения.
Задача 6. По обмотке соленоида индуктивностью L=0,2 Гн течет ток I=10 А. Определить энергию W магнитного поля соленоида. (Ответ: W=10 Дж.)
Задача 7. Соленоид содержит N=1000 витков. Сила тока I в его обмотке равна 1 А, магнитный поток Ф через поперечное сечение соленоида равен 0.
1 мВб. Вычислить энергию W магнитного поля соленоида. (Ответ: W=50 мДж.)
Задача 8. Катушка индуктивностью L=1 мкГн и воздушный конденсатор, состоящий из двух круглых пластин диаметром D=20 см каждая, соединены параллельно. Расстояние d между пластинами равно 1 см. Определить период T колебаний. (От-
вет: T =33,2 нс.)
Задача 9. Колебательный контур, состоящий из воздушного конденсатора с двумя пластинами площадью S=100 см2 каждая и катушки с индуктивностью L=1 мкГн, резонирует на волну длиной λ=10 м. Определить расстояние d между пластинами конденсатора. (Ответ: d=3.14 мм.)
Задача 10. Уравнение изменения со временем тока в колебательном контуре имеет вид I=-0,02sin(400πt) (значения всех величин указаны в системе СИ). Индуктивность контура равна L=1 Гн. Найти период T колебаний, емкость C контура, максимальную энергию Wм магнитного поля и максимальную энергию Wэл электрического поля. (Ответ: T=5 мс; C=0,63 мкФ; Wм=0,2
мДж; Wэл=0,2 мДж.)
78
Задача 11.
Найти отношение энергии Wм/Wэл магнитного поля колебательного контура Wм к энергии его электрического поля Wэл для момента времени t=T/8, где T — период колебаний.
(Ответ: Wм/Wэл=1.) |
| L=21 | |
Задача | 12. Через катушку, индуктивность которой | ||
мГн, течет | ток, изменяющийся | со временем по | закону |
I=I0sin(ωt), где I0=5 А, T=0,02 с. Найти зависимость от времени энергии магнитного поля W(t) катушки. (Ответ:
W(t)=0,263sin2(100πt) Дж.)
Задача 13. Колебательный контур состоит из катушки индуктивности L=0,2 Гн и конденсатора емкостью C=20 мкФ. Конденсатор зарядили до напряжения U0=4 В. Какими будут ток I, напряжение U и заряд Q в моменты времени, когда отношение энергии электрического и магнитного поля Wэл/Wм равно 1/2 ? (Ответ: I=-3,24 10-2А, U=-2,35 В, Q=4,7 10-5 Кл.
)
Задача 14. Какую индуктивность L надо включить в колебательный контур, чтобы при емкости C=2 мкФ получить часто-
ту ν=1000 Гц? (Ответ: L=12,7 мГн.)
Задача 15. Катушка с индуктивностью L=30 мкГн присоединена к плоскому конденсатору с площадью пластин S=0,01 м2 и расстоянием между ними d=0,1 мм. Найти диэлектрическую проницаемость ε среды, заполняющей пространство между пласти-
нами, если контур настроен на длину волны | λ=750 м. (Ответ: |
ε=6.) |
|
СОДЕРЖАНИЕ |
|
|
|
Введение. | 3 |
Основные формулы. | 4 |
Таблица основных физических постоянных. | 13 |
Библиографический список. | 14 |
Вопросы для подготовки к экзамену. | 14 |
Раздел III. | 16 |
Электростатика. Постоянный электрический |
|
ток |
|
79
Тема 1. Электростатическое поле в вакууме. | 16 |
Напряженность поля. Теорема Гаусса. |
|
Тема 2. Работа сил электростатического поля. | 25 |
Потенциал. |
|
Тема 3. Электроемкость. Конденсаторы. | 33 |
Тема 4. Диэлектрики в электрическом поле. | 39 |
Энергия электрического поля. |
|
Тема 5. Постоянный электрический ток. | 50 |
Раздел IY. Электромагнетизм. Электромаг- | 45 |
нитные колебания и волны. |
|
Тема 6. Магнитное поле проводников с током. | 45 |
Закон Ампера. |
|
Тема 7. Закон полного тока. Работа по пере- | 57 |
мещению проводника с током в магнитном |
|
поле. |
|
Тема 8. Движение заряженных частиц в элек- | 62 |
трическом и магнитном полях. |
|
Тема 9. Электромагнитная индукция. | 69 |
Тема 10. Энергия магнитного поля. Электро- | 74 |
магнитные колебания. |
|
80
Инна Альбертовна Анищенко Анатолий Андреевич Задерновский Михаил Митрофанович Зверев Борис Владимирович Магницкий Юрий Константинович Фетисов Андрей Юрьевич Пыркин Лидия Владимировна Соломатина.
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Учебное пособие
Калькулятор индуктивного реактивного сопротивления
Автор Purnima Singh, PhD
Отзыв Стивена Вудинга
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое индуктивное сопротивление? — Определение индуктивного сопротивления
- Формула расчета индуктивного сопротивления
- Единица измерения индуктивного сопротивления
- Как пользоваться калькулятором индуктивного сопротивления?
- Часто задаваемые вопросы
Калькулятор индуктивного сопротивления Omni (калькулятор XLX_LXL) позволяет вам определить эффективное сопротивление (импеданс) катушки индуктивности . Просто введите индуктивность катушки и частоту сигнала переменного тока, и калькулятор импеданса индуктора мгновенно рассчитает реактивное сопротивление индуктора (индуктивный импеданс)!
Продолжайте читать, чтобы узнать , что такое индуктивное сопротивление и формулу для его расчета.
Вы также найдете пример расчета индуктивного сопротивления с помощью калькулятора XLX_LXL.
Что такое индуктивное сопротивление? — Определение индуктивного реактивного сопротивления
Индуктивное реактивное сопротивление или индуктивный импеданс — это эффективное сопротивление катушки индуктивности протекающему через нее электрическому току .
Это аналогично сопротивлению резистора в том смысле, что оба сопротивления противодействуют потоку электрического заряда. Однако в случае резисторов оппозиция возникает из-за столкновения с электронов , когда они проходят через него. В катушке индуктивности именно ЭДС самоиндукции противодействует нарастанию и спаду тока .
Формула индуктивного сопротивления
Рассмотрим простую цепь, состоящую из катушки индуктивности, подключенной к источнику переменного напряжения (рис. 1).
Поскольку величина и направление переменного тока непрерывно изменяются , катушка индуктивности будет противодействовать любому изменению протекающего через нее тока, индуцируя в себе ЭДС.
Используя формулу закона Фарадея, мы можем выразить эту ЭДС самоиндукции (VVV) как:
V=−L⋅(dIdt)\scriptsize V = -L \cdot \left ( \frac{dI}{dt} \right)V=−L⋅(dtdI)
где:
- LLL — собственная индуктивность индуктора; и
- dI/dtdI/dtdI/dt — Скорость изменения тока через дроссель.
Вы можете использовать калькулятор индуктивности соленоида, чтобы найти собственную индуктивность любой катушки индуктивности.
Чтобы найти средний ток (III) через катушку индуктивности, мы можем использовать вариант закона Ома:
I=VXL\размер сценария I = \frac{V}{X_L}I=XLV
, где индуктивное сопротивление (XLX_LXL) зависит от частоты (ν\nuν) сигнала переменного тока:
XL=2πνL\scriptsize X_L = 2 \pi \nu LXL=2πνL
Мы также можем рассчитать проводимость (BLB_LBL), т.
е. насколько легко цепь пропускает через себя ток, следующим образом:
BL=1XL\scriptsize B_L = \frac{1}{X_L}BL=XL1
Единица индуктивного сопротивления
Чтобы найти единицу индуктивного сопротивления, проведем размерный анализ формулы для индуктивного сопротивления:
XL=2πνL⟹1сек⋅Генри=1сек⋅вольт(ампер/сек)=вольтампер=Ом (Ом)\scriptsize \начать{выравнивать*} X_L &= 2 \pi \nu L \\ \ подразумевает & \rm \frac{1}{sec} \cdot henry \\ & = \rm \frac{1}{sec} \cdot \frac{volt}{(amp/sec)} \\ & \rm = \frac{volt}{amp} = ohm\ (\Omega) \end{align*}XL⟹=2πνLsec1⋅henry=sec1⋅(amp/sec)volt=ampvolt=ohm (Ω)
Анализ размерностей приведенной выше формулы говорит нам, что размеры индуктивное сопротивление такое же, как сопротивление. Следовательно, индуктивное сопротивление измеряется в омах (Ом\ОмегаОм).
Для измерения проводимости мы используем ту же единицу измерения, что и проводимость, т. е. сименс (S\rm SS).
Как пользоваться калькулятором индуктивного сопротивления?
Давайте посмотрим, как использовать калькулятор индуктивного реактивного сопротивления для расчета реактивного сопротивления катушки 14 мГн , когда через нее протекает переменный ток 100 Гц .
- Введите индуктивность катушки, т. е.
14 мГн. - Подключите частоту сигнала переменного тока, т. е.
100 Гц. - Калькулятор XLX_LXL отобразит реактивное сопротивление катушки индуктивности (XLX_LXL), т. е.
8,80 Ом, и адмиттанс (BLB_LBL), т. е.0,11 S. - Вы также можете использовать этот калькулятор импеданса катушки индуктивности для расчета индуктивности катушки.
Мы также рекомендуем воспользоваться нашим калькулятором емкостного реактивного сопротивления, чтобы узнать об эффективном сопротивлении конденсатора протекающему через него току.
Часто задаваемые вопросы
Как рассчитать индуктивное сопротивление?
Для расчета индуктивного сопротивления выполните следующие действия:
- Определите частоту сигнала переменного тока.
- Умножьте частоту на 2π и индуктивность .
- Поздравляем! Вы рассчитали индуктивное сопротивление.
Что такое индуктивное сопротивление в цепи постоянного тока?
Ноль . Индуктивное сопротивление прямо пропорционально частоте сигнала. В цепях постоянного тока частота равна нулю . Следовательно, индуктивное сопротивление в цепях постоянного тока также равно нулю.
В чем разница между индуктивным реактивным сопротивлением и емкостным реактивным сопротивлением?
Основные различия между индуктивным реактивным сопротивлением и емкостным реактивным сопротивлением:
- Индуктивное реактивное сопротивление представляет собой эффективное сопротивление , обеспечиваемое дросселем . Емкостное сопротивление — это эффективное сопротивление , предлагаемое конденсатор .
- Индуктивное сопротивление прямо пропорционально частоте сигнала и индуктивности . Емкостное реактивное сопротивление обратно пропорционально частоте сигнала и емкости .
Емкостное реактивное сопротивление обратно пропорционально частоте сигнала и емкости .Как рассчитать индуктивность по реактивному сопротивлению?
Чтобы рассчитать индуктивность по реактивному сопротивлению, следуйте приведенным инструкциям:
- Умножьте на частота сигнала переменного тока с 2π .
- Разделите реактивное сопротивление на значение из шага 1 .
- Вы рассчитали индуктивность по реактивному сопротивлению!
Что такое единица измерения индуктивного сопротивления в системе СИ?
Ом . Единица СИ индуктивного реактивного сопротивления такая же, как и сопротивление, т. е. ом.
Пурнима Сингх, доктор философии
Индуктивность (л)
Частота (f)
Реактивное сопротивление (Xʟ)
Адмиттанс (Bʟ)
Посмотреть 40 похожих калькуляторов электромагнетизма 🧲
Ускорение частицы в электрическом поле Мощность переменного тока Емкость… 37 more
Какова собственная индукция катушки, индуктивность 40 мВ получается при протекании через него тока силой 2 А?
Вопрос
Обновлено: 24/05/2019
PRADEEP-ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ И ПЕРЕМЕННЫЙ ТОК-Упражнение
20 видеоРЕКЛАМА
Текст Решение
Решение
Здесь L=?,ϕ=40 милливебер =40×10−3Wb
I=2A
Из ϕ=LI,L=ϕI=40×10−32=2× 10−2Wb
Ответ
Пошаговое решение от экспертов, которое поможет вам в решении вопросов и получении отличных оценок на экзаменах.
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Похожие видео
Магнитный поток 5 мкВ связан с катушкой, когда через нее протекает ток 1 мА. Что такое собственная индуктивность катушки?
12013280
एक कुंडली का स्वप्रेरण — गुणांक गुणांक त 5 мГн त यदि इस कुंडली से 2 A की धारा प्रवाहित की जाए , तोथ क की जाए , तोथ क
95022868
Собственная индуктивность катушки составляет 5 мГн. Если по ней течет ток 2А, то магнитный поток, создаваемый в катушке, будет
127800675
Text Solution
Магнитный поток в 50 мВ создается в катушке, когда через нее протекает ток 5 А. Рассчитать собственную индуктивность катушки.
415577529
Магнитный поток 5 мкВб связан с катушкой, когда через нее протекает ток 1 мА. Чему равна собственная индуктивность катушки?
449488517
Магнитный поток 5 мкВ связан с катушкой, когда через нее протекает ток 1 мА.
Чему равна собственная индуктивность катушки?
642732556
Текст Решение
Магнитный поток в 5 микровебер связан с катушкой, когда через нее протекает ток 1 мА. Чему равна собственная индуктивность катушки?
642765298
Определите собственную индуктивность катушки из 100 витков, когда ток в 2 ампера, протекающий через катушку, создает магнитный поток в 2 мВэбера.
644164128
किसी कुण्डली से 10 माइक्रो चेबर व। लब कीय फ्लक्स सम्बद्ध होता है। यदि कुण्डली से 2 मिली ऐम्पियर धारा प्रवाहित तो, तो डली का स्व-प्रेरकत्व क्या होगा?
645775962
Магнитный поток 5 мкВб связан с катушкой, когда через нее протекает ток 1 мА. Чему равна собственная индуктивность катушки?
645998103
Текст Решение
Магнитный поток в 5 мкВ связан с катушкой, когда через нее протекает ток 1 мА. Чему равна собственная индуктивность катушки?
646936051
Текст Решение
Магнитный поток 5M omega b связан с катушкой, когда через нее протекает ток 1 MA, какова собственная индуктивность катушки.
Leave A Comment