Площадь треугольника средней линии: В треугольнике ABC DE — средняя линия. Площадь треугольника CDE равна 20. Нийдите площадь треугольника…

Как найти среднюю линию треугольника? Свойства, теорема

Поможем понять и полюбить математику

Начать учиться

149.8K

Не каждая геометрическая фигура может похвастаться таким количеством линий, как треугольник: медиана, средняя линия, биссектриса, высота, серединный перпендикуляр. В этот раз поговорим про среднюю линию и узнаем, зачем она нужна.

Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Виды треугольников:

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.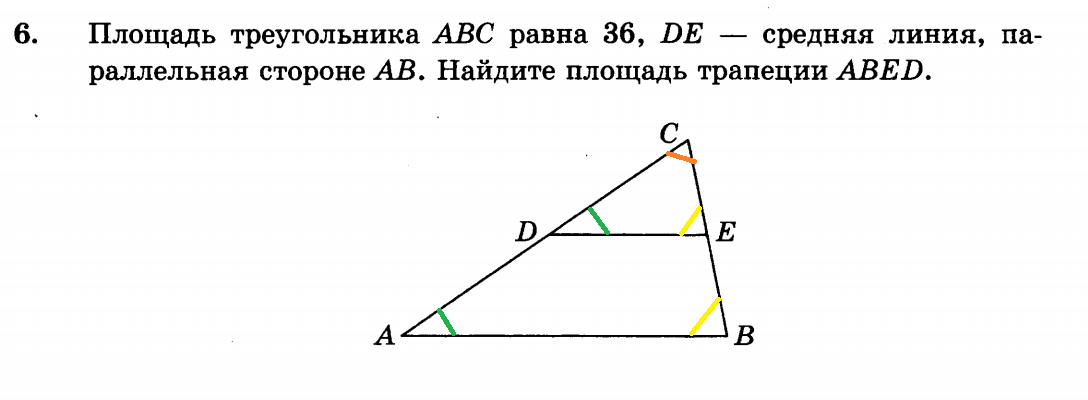

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Запоминаем

Средняя линия параллельна третьей стороне, а ее длина равна половине длины этой стороны.

Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе.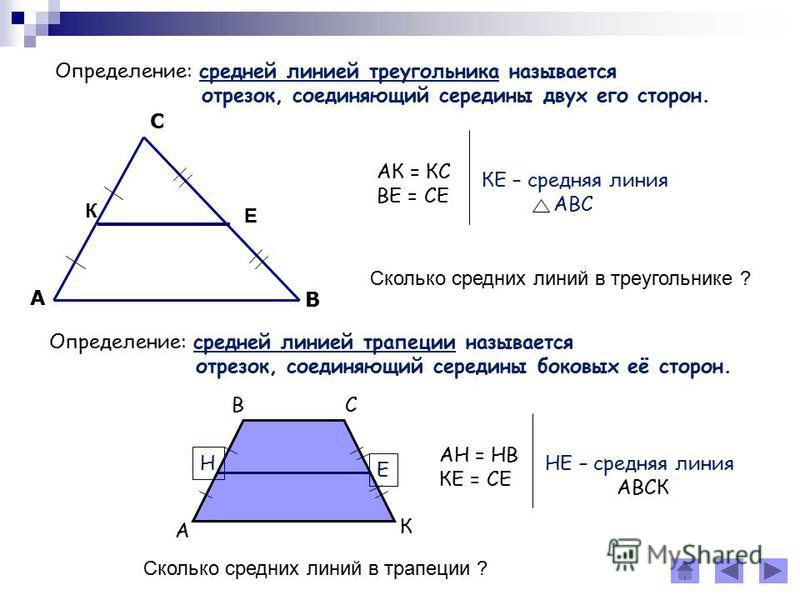

Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Важное свойство

Средняя линия прямоугольного треугольника делит его на четыре прямоугольных треугольника.

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

 

1. Средняя линия равна половине длины основания и параллельна ему.


2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.


3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.


4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Теорема о средней линии треугольника

Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

 

1. По условию нам дано, что MA = MB, NA = NC

2. Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

   (по второму признаку подобия треугольников).

3. Так как △AMN ~ △ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.

4. Так как △AMN ~ △ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

   Параллельность средней линии и соответствующего ей основания доказана.

Теорема доказана.

Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Как найти периметр треугольника:

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.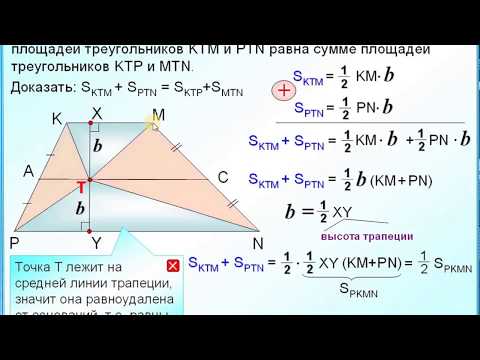

Решение:

 

1. Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

   S = ½ × AC × BC

2. Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

   MN = ½ × AC

   Значит, AC = 2MN = 2 × 3 = 6.

3. Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

   NP = ½ × BC

   Значит, BC = 2NP = 2 × 4 = 8.

4. Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

   S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

391.7K

Равнобедренный треугольник: свойства, признаки и формулы

К следующей статье

179.5K

Что такое рациональные числа?

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Средняя линия треугольника ABC: определение, свойства, признак, длина

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Геометрия Что такое средняя линия треугольника

В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.

• Определение средней линии треугольника
• Свойства средней линии треугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
• Признак средней линии треугольника
• Пример задачи

Определение средней линии треугольника

Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.

• KL – средняя линия треугольника ABC
• K – середина стороны AB: AK = KB
• L – середина стороны BC: BL = LC

Свойства средней линии треугольника

Свойство 1

Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.

На рисунке выше:

• KL параллельна AC
• KL = ¹/₂ ⋅ AC

Свойство 2

Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.

На рисунке выше:

• △KBL ∼ △ABC (подобие по пропорциональности всех сторон)
• Стороны △KBL в два раза меньше соответствующих сторон △ABC:
  AB = 2KB, BC = 2BL, AC = 2KL.
• S_△ABC = 4 ⋅ S_△KBL

Свойство 3

В любом треугольнике можно провести три средние линии.

KL, KM и ML – средние линии треугольника ABC.

• KL || AC, KL = ¹/₂ ⋅ AC
• KM || BC, KM = ¹/₂ ⋅ BC
• ML || AB, ML = ¹/₂ ⋅ AB

Свойство 4

Три средние линии треугольника делят его на 4 равных по площади треугольника.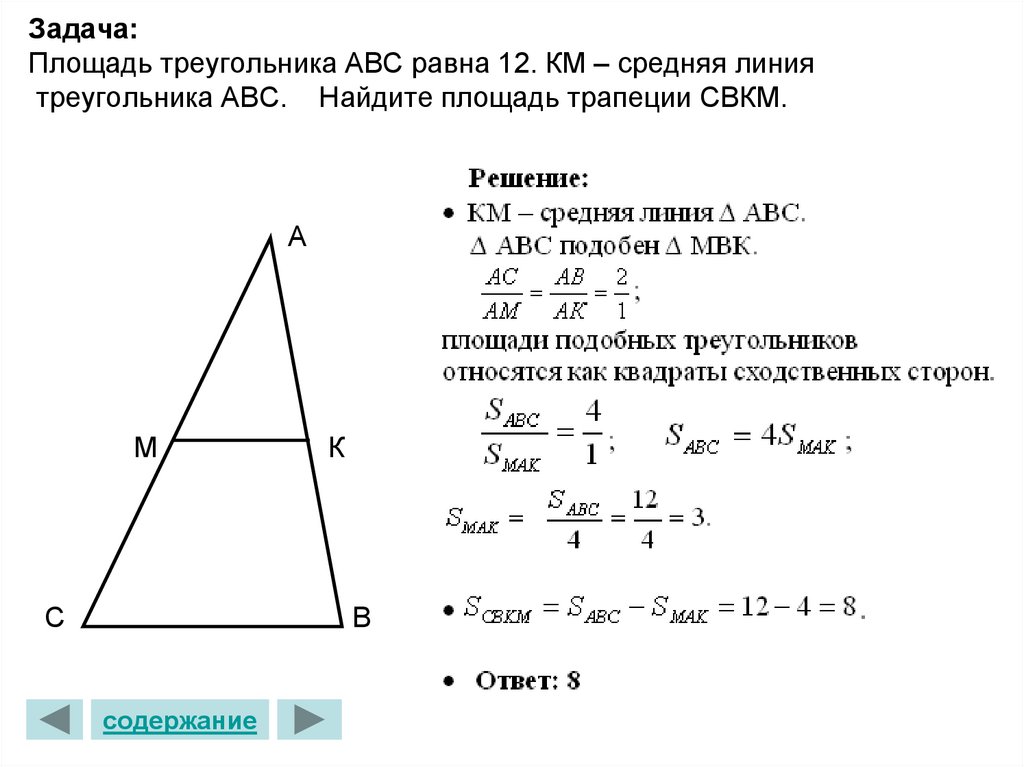

S₁ = S₂ = S₃ = S₄

Признак средней линии треугольника

Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.

Пример задачи

Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.

Решение

Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.

Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.

BC² = AB² + AC² = 6² + 8² = 100.
BC = 10.

Таким образом, средняя линия LM = ¹/₂ ⋅ BC = ¹/₂ ⋅ 10 = 5.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Середина треугольника (теорема, формула и видео)

Автор:

Малкольм МакКинси

11 января 2023 г.

Средняя линия треугольника — это линия, построенная путем соединения середины любых двух сторон треугольника. В любом прямоугольном, равнобедренном или равностороннем треугольнике все три стороны треугольника можно разделить пополам (разрезать пополам), при этом точка, равноудаленная от любой вершины, будет серединой этой стороны.

В △ASH , внизу, сбоку AS и AH 24 см и 36 см соответственно. Поскольку нам известны длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.

Середина треугольника

Соединение середины сторон, Точки C и R , on  △ASH делает что-то кроме того, чтобы сделать всю нашу фигуру CRASH . Он создает средний сегмент, CR , который имеет пять удивительных особенностей.

Пять свойств срединного отрезка

Поскольку треугольники имеют три стороны, они могут иметь три срединных отрезка. Вы можете соединить любые две стороны в их средних точках. Один средний сегмент составляет половину длины основания (третья сторона не участвует в создании среднего сегмента). Это только одна интересная особенность. Это также:

• Всегда параллелен третьей стороне треугольника; основание

• Образует меньший треугольник, аналогичный исходному треугольнику

• Меньший аналогичный треугольник имеет четверть площади исходного треугольника

• Меньший аналогичный треугольник имеет половину площади периметр исходного треугольника

Поскольку меньший треугольник, созданный средней линией, подобен исходному треугольнику, соответствующие углы двух треугольников идентичны; соответствующие внутренние углы каждого треугольника имеют одинаковые измерения.

Из пяти атрибутов срединного отрезка два самых важных заключены в теореме о срединном отрезке, утверждении, которое было доказано математически (поэтому вам не нужно доказывать его снова; вы можете воспользоваться им, чтобы сэкономить время и работа).

Теорема о средней линии треугольника

Теорема о средней линии треугольника говорит нам, что средняя линия равна половине длины третьей стороны (основания) и также параллельна основанию.

Вам не нужно доказывать теорему о средней линии, но вы можете доказать ее, используя вспомогательную прямую, конгруэнтные треугольники и свойства параллелограмма.

Средний сегмент Formula

Средний сегмент || Основание треугольников

Формула среднего сегмента треугольника

Это мощный материал; за одну лишь стоимость рисования одного отрезка линии можно создать аналогичный треугольник с площадью в четыре раза меньше исходной, периметром в два раза меньше исходной и с гарантированно параллельным исходной и только вдвое короче.

Как найти середину треугольника

Нарисуйте любой треугольник, назовите его треугольником ABC. С помощью циркуля, карандаша и линейки найдите середины любых двух сторон треугольника. Вы делаете это в четыре шага:

1. Отрегулируйте циркуль для рисования так, чтобы он двигался по дуге, превышающей половину длины любой стороны треугольника

2. Поместив стрелку компаса в каждую вершину, проведите дугу через сторону треугольника с обоих концов, создавая два противоположных , пересекающие дуги

3. Соедините точки пересечения обеих дуг с помощью линейки

4. Точка, в которой ваша линейка пересекает сторону треугольника, является серединой этой стороны)

Как найти середину треугольника

Соедините середины любых двух сторон, и вы получите середину треугольника. Независимо от того, какой средний отрезок вы создали, он будет составлять половину длины основания треугольника (сторона, которую вы не использовали), а средний отрезок и основание будут параллельными линиями!

Примеры теоремы о средней линии треугольника

Вот правильно △DOG , со стороной DO 46 дюймов и стороной DG 38,6 дюйма . Сторона 9{2}482,5 дюйма2.

Какие точки вы соедините, чтобы создать средний сегмент?

Пример теоремы о средней линии треугольника

Только соединив точек V и Y , можно создать среднюю линию треугольника. Это сделает сторону OG основой.

Вы должны быть в состоянии ответить на все эти вопросы:

1. Каков периметр исходного △СОБАКА ?

2. Какова длина среднего сегмента ВЯ ?

3. Какова длина стороны DV ?

4. Какова длина стороны DY ?

5. Каков периметр вновь созданного аналога △DVY ?

6. Какова площадь недавно созданного △DVY ?

Вот наши ответы:

1. Добавьте длины: 46 дюймов + 38,6 дюймов + 25 дюймов = 109,6 дюймов

9{2}120,625in2

Треугольник Серпинского

С помощью теоремы о среднем отрезке можно построить фигуру, используемую во фрактальной геометрии, треугольник Серпинского.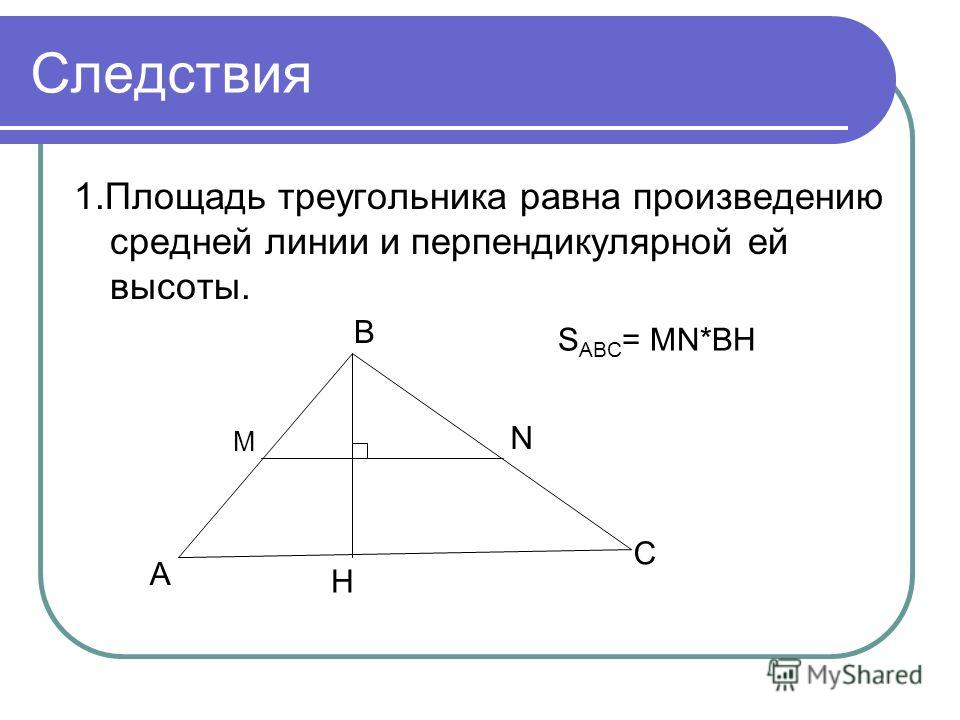 Шаги просты, а результаты визуально приятны:

1. Нарисуйте три середины любого треугольника, хотя равносторонние треугольники работают очень хорошо треугольников осталось

2. Для каждого углового треугольника соедините три новых средних сегмента

3. Снова проигнорируйте (или закрасьте) каждый из их центральных треугольников и сосредоточьтесь на угловых треугольниках

4. Для каждого из этих угловых треугольников соедините три новые средние сегменты

Эта непрерывная регрессия создаст визуально мощную фрактальную фигуру:

Треугольник Серпинского

Раздел 4.4: Средняя линия треугольника

Section_4_4

Мы начнем здесь с мощной теоремы о специальная линия в треугольнике.

• Определение: Средняя линия треугольника – это отрезок, концы которого являются серединами двух сторон треугольника.

Теорема о средней линии для треугольников полезна для установления некоторых неожиданные результаты о четырехугольниках, а также предоставление полезного теорема о трапециях.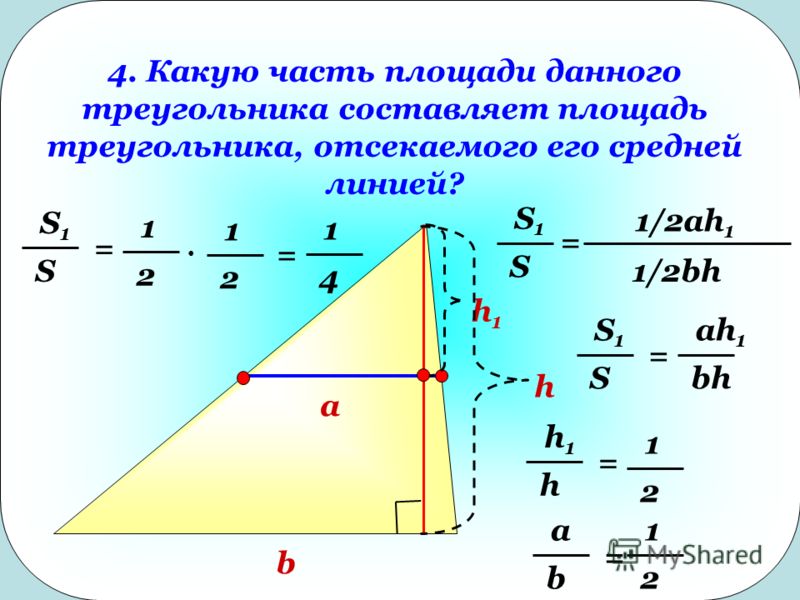

• Теорема 4.13: Теорема о средней линии
      Отрезок, соединяющий середины двух сторон треугольник параллелен третьей стороне и равен половине третьей стороны сторона.

Дано: $\треугольник ABC$ с серединами $D$ и $E$ $\overline{AB}$ и $\overline{AC}$, соответственно. Доказать: $\overline{DE}\parallel\overline{BC}$ и $DE=\dfrac{1}{2}BC$

Доказательство: Дан $\треугольник ABD$ с серединами $D$ и $E$. Продлевать $\overline{DE}$ в точку $F$ такую, что $DE=EF$. Так как $E$ середине $\overline{AC}$, мы знаем, что диагонали четырехугольники $ADCF$ делят друг друга пополам. Тогда теорема 4.8 говорит нам этот четырехугольник должен быть параллелограммом. Свойства параллелограмма говорят нам, что $\overline{ADB}\parallel\overline{CF}$ и $\overline{AD}\cong \overline{CF}$. Но $\overline{AD}\cong\overline{DB}$, так как $D$ является средней точкой $\overline{AB}$.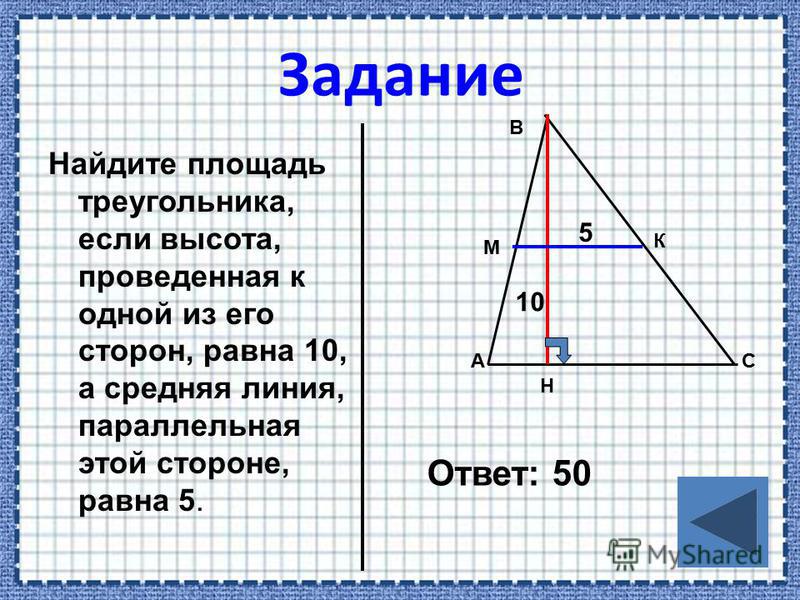 Поэтому $\overline{DB}\cong\overline{CF}$ и $\overline{DB}\parallel\overline{CF}$. Это делает $BCFD$ параллелограмм. Теперь по определению, $\overline{DEF}\parallel\overline{BC}$. Кроме того, $DF=BC$. Поскольку $E$ — это середина $\overline{DF}$, мы знаем, что $DE=\frac{1}{2}DF$ и заменой $DE=\frac{1}{2}BC$.

    В предыдущей главе при обсуждении параллельных прямые, отсекающие конгруэнтные отрезки на одной секущей, мы столкнулся со следующим следствием. Так как это частично обратная теорема о средней линии, мы повторяем ее здесь.

• Следствие: Если прямая проходит через середину одной из сторон треугольника и параллельна второй стороне, то прямая проходит через середину третья сторона треугольника.
  

Дано: $\треугольник ABC$ с $P$ серединой $\overline{AB}$ и $\overline{PQ}\parallel\overline{BC}$. Докажите: $Q$ есть середина $\overline{AC}$.

Доказательство:   Мы даны $\треугольник ABC$ с серединой стороны $P$ $\overline{AB}$ и $\overline{PQ}\parallel\overline{BC}$. Ввести прямую $\ell$ через $A$ так, чтобы $\ell\parallel\overline{BC}$. Теперь $\ell$, $\overline{PQ}$ и $\overline{BC}$ — это три параллельные прямые, пересекающие конгруэнтные сегменты на $\overline{AB}$. Затем должны отрезать конгруэнтные отрезки на любой трансверсали, в частности на $\overline{AC}$. Это делает $Q$ средней точкой $\overline{AC}$.

    Теорема о средней линии позволяет нам установить множество иногда неожиданных результатов. Одним из них является следующий факт о прямоугольные треугольники — середина гипотенузы всегда равноудалена из всех трех вершин треугольника.

• Теорема 4.14: Если $M$ — середина гипотенузы $\overline{AB}$ прямоугольного треугольника $\overline{ABC}$, затем $MA=MB=MC$.
  

Дано: Правильно $\треугольник ABC$ с $M$ серединой гипотенузы $\overline{AB}$ Доказать: $MA=MB=MC$

Доказательство:   Мы задано, что $M$ — середина гипотенузы $\overline{AB}$.