Найдите площадь треугольника изображённого

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2012-09-13

Здравствуйте! В этой статье мы разберём задачи на нахождение площади треугольника построенного на листке в клетку (масштаб клетки 1×1). Фигуры на листе в клетку с вычислением их площади — это целая группа типов задач входящая в экзамен по математике. Кроме треугольника рассматриваются следующие фигуры — трапеция, параллелограмм, ромб, квадрат.

Решение заданий с треугольником труда не представляет, относятся они к простейшим. Для решения необходимо знать формулу площади треугольника и знать один приём, о котором я вам расскажу ниже.

Вообще, способов нахождения площади любой фигуры, построенной на листе в клетку существует более пяти. Все здесь рассматривать не будем, в интернете вы без труда найдёте их описание. Уверен, что тех рекомендаций, которые представлены будет вполне достаточно для решения.  

Итак! Вам необходимо знать и понимать одну из основных формул площади треугольника, она наиболее часто используется при решении:

Длину основания и высоту считаем по клеткам. В задаче 27545 это наглядно показано. То есть, если перед вами задача, где треугольник построен именно таким образом, то считаем оговоренным способом. Например, рассмотрим треугольники:

 

У всех этих треугольников можно по клеткам установить длину основания и высоту. У первого основание равно 3, высота 5; у второго основание 6, высота 2; у третьего основание 6, высота 2; у четвертого основание равно 3, высота 8; у пятого основание равно 6, высота 2. Подставив их в формулу, остаётся только вычислить площадь (без ошибки).

Есть задачи, в которых треугольники расположены так, что по клеткам длину основания и высоту посчитать неудобно (но можно), вот примеры:

В задачах, где будут даны подобные треугольники, используйте способ, который по моему мнению универсален, его достоинство объясню в одной из следующих статей: «заключите» такой треугольник в прямоугольник, вычислите площадь прямоугольника, затем из его площади вычтите площади треугольников. Пример:

Найти площадь треугольника, изображённого на рисунке:

Заключим данный треугольник в прямоугольник:

   Теперь вычислим площадь прямоугольника. Уверен, всем известно, что она равна произведению его соседних сторон:

Далее из его площади вычитаем площади трёх треугольников:

Ответ: 26

Есть ещё подобные задачи, но в них иначе представлено условие. Также нужно найти площадь треугольника, он построен на координатной плоскости, например:

Решения аналогичны: если можем установить длину основания и высоту треугольника  по  координатам, то далее площадь вычисляем просто по формуле:

В треугольнике на рисунке 1  этого сделать  нельзя, поэтому советую построить данный треугольник по координатам на листе в клетку, и использовать уже рассмотренный нами метод, а именно описать около треугольника прямоугольник.

В будущем мы рассмотрим нахождения площадей параллелограммов, трапеций, четырёхугольников, элементов круга, а так же «сложных» фигур, не пропустите!

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.


Категория: Площади фигур | ЕГЭ-№1Треугольник

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.


Площади фигур (плоских и объемных)

Сначала мы рассмотрим площади плоских фигур.

Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?

Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!

Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)

ПЛОЩАДИ ПЛОСКИХ ФИГУР

Способы нахождения площади фигур на клетчатой бумаге:

Способ 1. Считай клетки и применяй формулы 

Удобен для стандартных фигур: треугольника, трапеции и т.д.

  • Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
  • Подставить найденные значения в уравнение площади.

Способ 2. Дострой до прямоугольника и вычти лишнее

Очень удобен для сложных фигур, но и для простых неплох

  • Достроить искомую фигуру до прямоугольника;
  • Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
  • Из площади прямоугольника вычесть сумму площадей всех лишних фигур.

Способ 3. Формула Пика

Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.

  • Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Подсчитаем, сколько узлов попадает в нашу фигуру.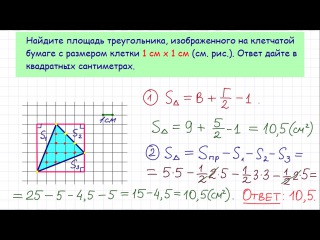 Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.

В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.

Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)

В примере на рисунке:

\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)

Способ 1. Считай клетки и применяй формулы

Удобен для стандартных фигур: треугольника, трапеции и т.д.

  • Подсчитывая клеточки и применяя простые теоремы, найти те стороны, высоту, диагонали, которые требуются для применения формулы площади;
  • Подставить найденные значения в уравнение площади.

Пусть нужно найти площадь трапеции, построенной на листе в клетку.

Просто считаем клеточки и видим, что в нашем случае \( \displaystyle a=17\), \( \displaystyle b=6\) и \( \displaystyle h=6\).

{2}}=13\).

\( \displaystyle b=\sqrt{13}\)

Подставляем в формулу:

\( \displaystyle S=\frac{1}{2}\cdot ab=\frac{1}{2}\cdot 2\sqrt{13}\cdot \sqrt{13}=13\).

Способ 2. Дострой до прямоугольника и вычти лишнее

Очень удобен для сложных фигур, но и для простых неплох

  • Достроить искомую фигуру до прямоугольника;
  • Найти площадь всех получившихся дополнительных фигур и площадь самого прямоугольника;
  • Из площади прямоугольника вычесть сумму площадей всех лишних фигур.

Давай посчитаем площадь того же треугольника вторым способом.

Нужно окружить нашу фигуру прямоугольником. Вот так:

Получился один (нужный) треугольник внутри и целых три ненужных треугольника снаружи. Но зато площади этих ненужных треугольников легко считаются на листе в клетку!

Вот мы их посчитаем, а потом просто вычтем из целого прямоугольника:

\( \displaystyle {{S}_{прямоугольника}}=6\cdot 7=42\)

\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)

\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot 7\cdot 4=14\)

\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 3\cdot 2=3\)

\( \displaystyle \Rightarrow S=42-12-14-3=13\)

Почему бы просто не считать клеточки?

Возможно, вы читаете всё это и думаете: зачем все эти сложности? Формулы запоминать. Дорисовывать. Тут ведь сразу видно, сколько клеточек в фигуре.

Вот, например, трапеция:

Посчитаем клеточки: их всего 46, верно?

Но стоп, там же некоторые из них только наполовину внутри фигуры. Отметим их – всего таких 10. Итого, 36 полных (красные точки) и 10 половинчатых, вместе \( 36+\frac{10}{2} = 41\)

Вроде бы всё верно. Но, если присмотреться, можно заметить ещё маленькие треугольнички, которые попали внутрь. А также, что «синие» клеточки слева на самом деле разрезаны не ровно пополам – какие-то чуть больше, какие-то меньше…

Как всё это учитывать?

Попробуем рассуждать так: заметно, что тот маленький розовый треугольник дополняет серый кусок клетки.

А жёлтые сколько занимают? Постарайтесь ответить сами.

Если всё сделать правильно, то увидите, что жёлтые кусочки можно сложить вместе в одну целую клетку.

Итак, 2 жёлтых куска = 1 клетка.

Розовый треугольник + серый кусок = 1 клетка. Всего у нас две таких пары (розовый+серый) – это 2 полных клетки.  

Всё остальное как было: 36 полных клеток и 6 половинок у правой стороны – это \( 36+\frac{6}{2}=39\) клетки.

Итого клеток: \( 1 + 2 + 39 = 42\).

Проверим результат по формуле площади трапеции: нижнее основание 11, верхнее основание 3, высота 6. Полусумма оснований равна 7, умножаем на высоту – получилось 42. Всё совпало.

Но! Настолько ли проще был наш способ подсчёта клеточек? Не сказал бы. А если там будет несколько косых линий, то вообще можно замучиться собирать этот паззл (искать, какие кусочки друг друга дополняют).

Способ 3. Формула Пика

Существует довольно удобная формула, которая использует клеточки для вычисления площади. А то, что мы только что проделали, – очень полезное упражнение, которое поможет эту формулу понять.

Назовём «узлами» точки пересечения линий сетки нашей клетчатой бумаги.

Теперь вместо клеточек или их частей подсчитаем, сколько узлов попадает в нашу фигуру.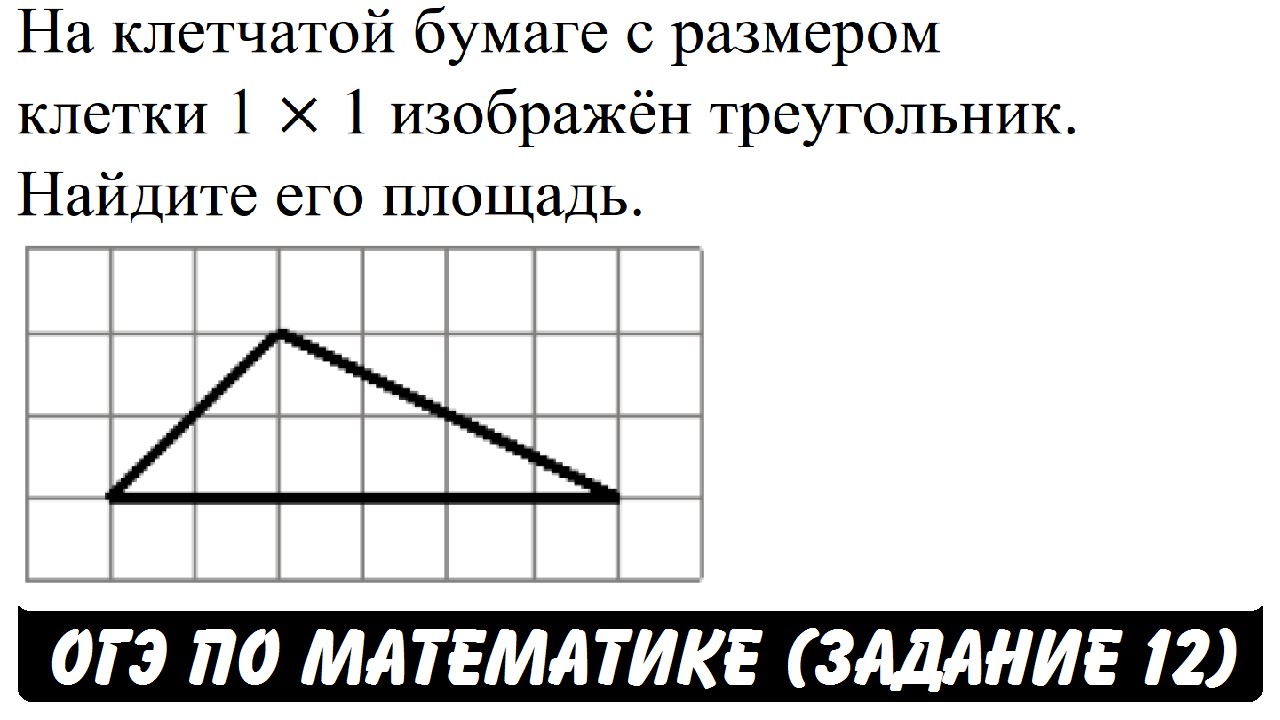 Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.

Сколько насчитали?

У меня получилось \( Г = 22\) на границе и \( В = 32\) внутри.

Ну а теперь сама формула:

Делим границу пополам, прибавляем внутренности и вычитаем 1:

\( S = Г/2 + В – 1 = 22/2 + 32 — 1 = 42.\)

Называется она формулой Пика, поскольку доказал её математик Георг Пик 120 лет назад (да, она не специально для ЕГЭ была придумана, но очень нам помогает) 🙂

Как запомнить формулу Пика

Всё, что внутри, берём целиком (клетки внутри фигуры целые).

Граница режет клетки надвое, поэтому берём половину узлов границы.

Минус 1 – это надо просто запомнить. Очень легко себя проверить на квадрате 1×1. Его площадь равна 1. Сколько там точек на границе? \( Г = 4.\) А сколько внутри? \( В = 0\) (нисколько)

Границу делим пополам, получаем 2.

Прибавляем внутренности (+0) – ничего не поменялось.

Очевидно, что осталось вычесть 1, чтобы получить 1.

Проверьте эту формулу на других простых фигурах, чтобы убедиться и закрепить.

Вычислите площадь простых фигур тремя способами

Стороны клеток равны 1. Вычислите самостоятельно площадь фигуры всеми тремя способами. Сравните результаты.

Вычислите площадь произвольных фигур по формуле Пика

Вычислите самостоятельно площади фигур с помощью формулы Пика:

Посчитайте площадь корабля и котика по формуле Пика

Посчитайте самостоятельно для тренировки и чтобы запомнить формулу Пика!

Фигуры с отверстиями — посчитайте площади двумя способами

Ну и напоследок фигуры с «дырками». Как думаешь, здесь придётся вычислять сначала площадь целой фигуры, а потом площадь дырки?

Или достаточно просто посчитать точки внутри закрашенной области и на её границах (в том числе, на границе с дыркой)?

Проверим на простом примере: это квадрат \( 4\times 4\), и в нём вырезан прямоугольник \( 1\times 2\), значит, его площадь \( 16-2=14\).

А теперь по точкам. На границах (включая внутренние) \( Г = 22\). Внутри \( В = 3\). Тогда площадь по формуле Пика

\( S = \frac{22}{2} + 3 -1 = 13.\)

Хм, близко, но не совпало. Может, я где-то ошибся? Давай ещё одну фигуру, для верности.

Сосчитай сам и проверь.

Что получилось?

У меня снова на 1 меньше.

Так может быть просто формулу немного «подкрутить»? Нет!

Очень и очень не рекомендую вам запоминать несколько похожих формул для похожих случаев, потому что придёт время, и вы обязательно перепутаете формулу.

Даже если вы уверены, что не перепутаете, оно всё равно того не стоит. В общем, наилучший вариант – это запомнить одну формулу. А если попалась фигура с дыркой, вычислить всю фигуру, а потом дырку. И вычесть.

Когда формулу Пика применять нельзя?

Естественно, эта формула не работает для окружностей и любых других фигур с «кривыми» границами.

Также она не сработает, если хотя бы одна из вершин не попадает на узел, например, вот для такой, как на рисунке.

Почему я уверен, что не сработает? Ведь можно взять и не учитывать эту вершину, раз она не в узле. То есть

\( Г = 10, В = 2, S = \frac{10}{2} + 2 – 1 = 6.\)

А очень просто: я возьму и «отрежу» эту вершину. Тогда будет не треугольник, а трапеция, и площадь, очевидно, станет меньше на тот отрезанный кусочек.

Но по формуле она останется такой же, ведь количество узлов не изменилось ни на границе, ни внутри. То есть мы получим, что площадь уменьшенного треугольника равна площади целого, чего, конечно же, не может быть.

Итак, формула Пика работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.

Какой способ лучше?

Второй и третий способы универсальные. Они помогут посчитать площадь даже самых замысловатых фигур. Вернемся еще раз ко второму способу.

Вот смотри, нужно посчитать площадь такой фигуры:

Окружаем ее прямоугольником и снова получаем одну нужную, но сложную площадь и много ненужных, но простых.

А теперь чтобы найти площадь \( \displaystyle S\) просто находим площадь прямоугольника и вычитаем из него оставшуюся площадь фигур на клетчатой бумаге \( \displaystyle {{S}_{1}}+{{S}_{2}}+{{S}_{3}}+{{S}_{4}}\).

\( \displaystyle {{S}_{прямоугольника}}=6\cdot 11=66\)

\( \displaystyle {{S}_{1}}=\frac{1}{2}\cdot 6\cdot 4=12\)

\( \displaystyle {{S}_{2}}=\frac{1}{2}\cdot a\cdot h=\frac{1}{2}\cdot 5\cdot 4=10\) (обрати внимание, \( \displaystyle {{S}_{2}}\) площадь НЕ прямоугольного треугольника, но все равно легко считается по основной формуле).

\( \displaystyle {{S}_{3}}=\frac{1}{2}\cdot 5\cdot 2=5\)

\( \displaystyle {{S}_{4}}=\frac{1}{2}\cdot 1\cdot 11=5,5\).

Значит, \( \displaystyle S={{S}_{прямоугольника}}-{{S}_{1}}-{{S}_{2}}-{{S}_{3}}-{{S}_{4}}\).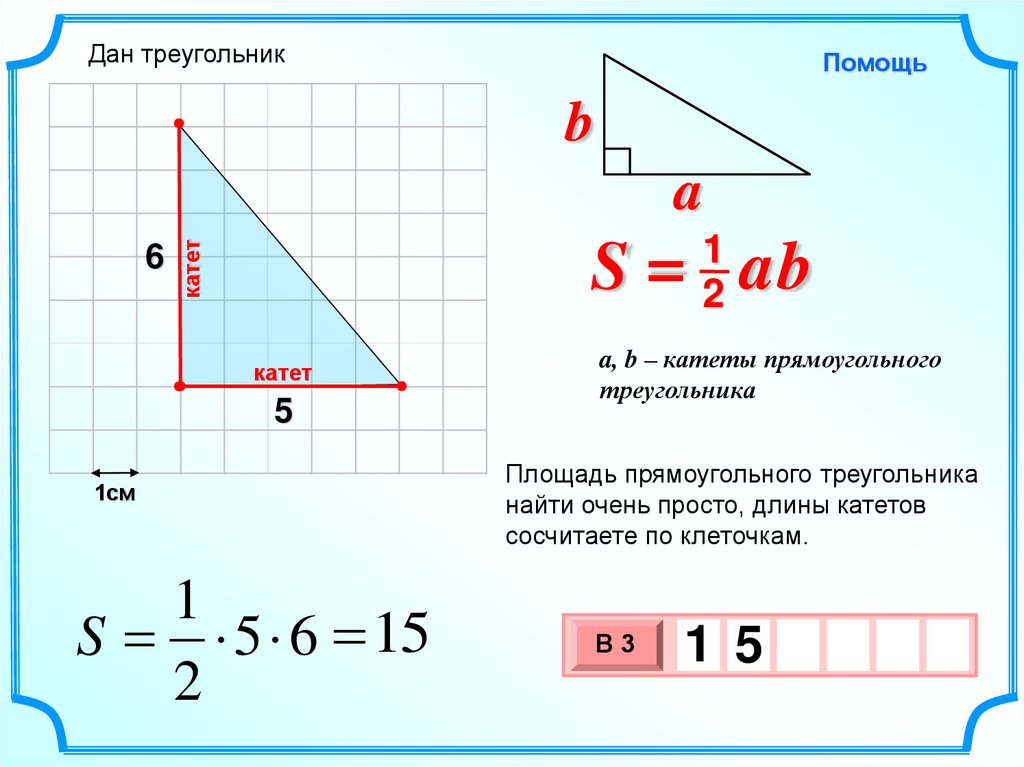

\( \displaystyle S=66-12-10-5-5,5=33,5\)

Вот и ответ: \( \displaystyle S=33,5\).Ну как тебе этот способ?


Вот смотри. С одной стороны, когда фигура занимает много клеточек, их замучаешься считать и можно ошибиться.

С другой стороны, когда мы дорисуем до прямоугольника, нужно считать много площадей.

Поэтому использование того или иного способа зависит лишь от конкретной задачи.

ПЛОЩАДИ ОБЪЕМНЫХ ФИГУР

Площадь поверхности призмы

Есть ли общая формула? Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.

Площадь полной поверхности призмы – это сумма площадей всех граней.

\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+2\cdot {{S}_{основания\ \ }}\)

Формулу можно написать для прямой призмы:

\( \displaystyle {{\text{S}}_{боков. {2}}\).

Площадь поверхности пирамиды

Для пирамиды тоже действует общее правило:

Площадь полной поверхности пирамиды – это сумма площадей всех граней.\( \displaystyle {{S}_{полн. пов.\ \ }}={{S}_{боков.пов.\ \ }}+{{S}_{основания\ \ }}\)

Теперь давай посчитаем площадь поверхности самых популярных пирамид.

Площадь поверхности правильной треугольной пирамиды

Пусть сторона основания равна \( \displaystyle a\), а боковое ребро равно \( \displaystyle b\). Нужно найти \( \displaystyle {{S}_{осн}}\) и \( \displaystyle {{S}_{ASB}}\).

И тогда

\( \displaystyle {{S}_{полн. пов.\ \ }}=3{{\text{S}}_{ASB}}+{{\text{S}}_{\text{осн}.}}\)

Вспомним теперь, что

\( \displaystyle {{S}_{осн}}\) — это площадь правильного треугольника \( \displaystyle ABC\).

И еще вспомним, как искать эту площадь.

Используем формулу площади:

\( \displaystyle S=\frac{1}{2}ab\cdot \sin \gamma \). 2}{4}}\)

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

Этот вебинар посвящен заданию №3 из ЕГЭ на нахождение площади фигур, длин отрезков и т.д на клетчатой бумаге.

И хотя эту задачу убрали из ЕГЭ в 2021 году, сам навык очень полезен для того, чтобы начать учить геометрию, для понимания планиметрии!

Ну и просто этот вебинар легкий и классный! Послушайте его и получите удовольствие!

ЕГЭ №3. Площадь фигур на клетчатой бумаге

Jenness Enterprises — Расширение сетей Surface Area

 






 

 ./images/leaves_background.jpg»>

Таким образом, это расширение вычисляет площадь поверхности, используя следующие стратегия:

mсписок изображений> msimagelist> mсписок изображений> msimagelist> mсписок изображений>

Для каждая ячейка в сетке, площадь поверхности основана на площади треугольника полученный из восьми треугольников.

каждый треугольник соединяет центральную точку центральной ячейки с центральные точки двух соседних ячеек. Эти треугольники расположены в трехмерном пространстве, так что площадь треугольник представляет истинную площадь поверхности пространства, ограниченного три точки.

площадь треугольника регулируется так, чтобы она представляла только часть треугольника, перекрывающего центральную ячейку.

площади восьми треугольников суммируются, чтобы получить общее площадь поверхности этой клетки.

коэффициент поверхности ячейки рассчитывается путем деления поверхности площадь ячейки с контурной площадью ячейки.

msimagelist>

Для Подробнее:  Это расширение является производным площади поверхности для ячейки с использованием информации из восьми ячеек рядом с центральной ячейкой. Например, учитывая примерную высоту сетка:

это расширение будет вычислять площадь поверхности для ячейки с высотой значение «183» на основе значений высоты восьми ячеек вокруг него,

и площадь поверхности для ячейки «165» на основе восьми значение высоты вокруг него:

Следующий пример расчета площади поверхности будет основан на иллюстрация выше, где мы будем вычислять площадь поверхности для ячейки со значением высоты 165, окруженным ячейками 190, 170, 155, 183, 145, 175, 160 и 122. Эта сетка значений высоты может быть на фото В трехмерном пространстве в виде набора смежных столбцов, каждый поднимаясь так высоко, как указано значение высоты.

Мы берем трехмерные центральные точки каждой из этих 9 ячеек и рассчитать длины 8 линий, соединяющих центральную ячейку centerpoint с центральными точками 8 окружающих ячеек. Мы затем рассчитайте длины линий, соединяющих каждую из 8 окружающие ячейки с той, что находится рядом с ней, так что мы получаем длины сторон восьми треугольников, пересекающихся в центре точка центральной ячейки. Используя эти длины, мы можем вычислить площади каждого из треугольников.

Эти длины легко вычислить с помощью теоремы Пифагора, которая гласит, что в прямоугольном треугольнике квадрат длины гипотенуза равна сумме квадратов двух других стороны. Таким образом, для любых двух точек А и В :

« b » легко вычислить, так как это просто разница между значениями двух ячеек. a » легко получить по ячейкам прямо на север, Восток, Юг и Запад, так как это просто значение ячейки размер. Для диагоналей снова воспользуемся теоремой Пифагора и вычислить, что « a » равно квадратному корню из ( 2 ) х ( а-квадрат ).

Однако, поскольку нас интересует только площадь поверхности внутри каждого ячейке, мы разрезаем все длины треугольников пополам. Теперь, когда мы вычислить площадь треугольника по длинам трех сторон, три стороны будут представлять часть треугольника, лежащую в границах ячеек.

Техническое примечание:  Приведенное выше описание описывает только логика, используемая для получения площади поверхности. Расширение не фактически соединяя любые линии или используя любые векторные данные вообще. Вместо этого расширение создает 16 новых сеток, где значения ячеек представляют длины одного из 16 изображенных ребер треугольника выше. Использование 3 из этих 16 сеток «Длина ребра треугольника» за раз, затем он вычисляет 8 новых сеток, представляющих площадь треугольник, который будет ограничен этими тремя длинами ребер. Окончательно, расширение складывает эти 8 сеток «Площади треугольника» для создания окончательная сетка площади поверхности.

Вычисление площади треугольника по длинам трех Стороны:   Автору известны две формулы, которые будут производить площадь треугольника по длинам трех сторон, и будет опишите их обоих здесь. Первый из них был получен автор из пары основных математических теорем, а второй был обнаружил автор после того, как разобрался с первым. Этот расширение использует первый, потому что все было отработано к тому времени автор узнал о второй формуле. У автора есть проверяется, чтобы убедиться, что эти две формулы дают идентичные результаты.

Формула 1: Выведено автором —

Формула 2:  Адаптировано из «Треугольник Калькулятор площади »(щелкните, чтобы посетить веб-сайт), авторство которого принадлежит Герону. Александрии и Архимеда (см. также Абрамовиц и Стегун [1972, с. 79]):

Вывод формулы 1:

1) Дан треугольник со сторонами a, b, и c :

и стандартная формула площади треугольника:

Основная проблема заключалась в том, чтобы выяснить, что такое h . равно, учитывая, что мы знали, что такое a, b, и c .

2) Закон косинусов полезен для определения длину третьей стороны, если известны длины двух сторон и угол между ними:

3) Поскольку мы знаем три стороны, мы можем выделить « cos C » на одной стороне уравнения:

4)  В прямоугольном треугольнике (см. выше, но посмотрите на стороны a1, h, и b ), cos C есть также равно прилежащему катету, деленному на гипотенузу:

5)  Следовательно,

6) Умножив обе части на b , мы теперь имеем изолированный a1 :

7) Мы можем использовать теорему Пифагора, чтобы изолировать ч :

Теорема Пифагора:

— или —

8) Замена a1 :

9) Наконец, снова подключите h к Area.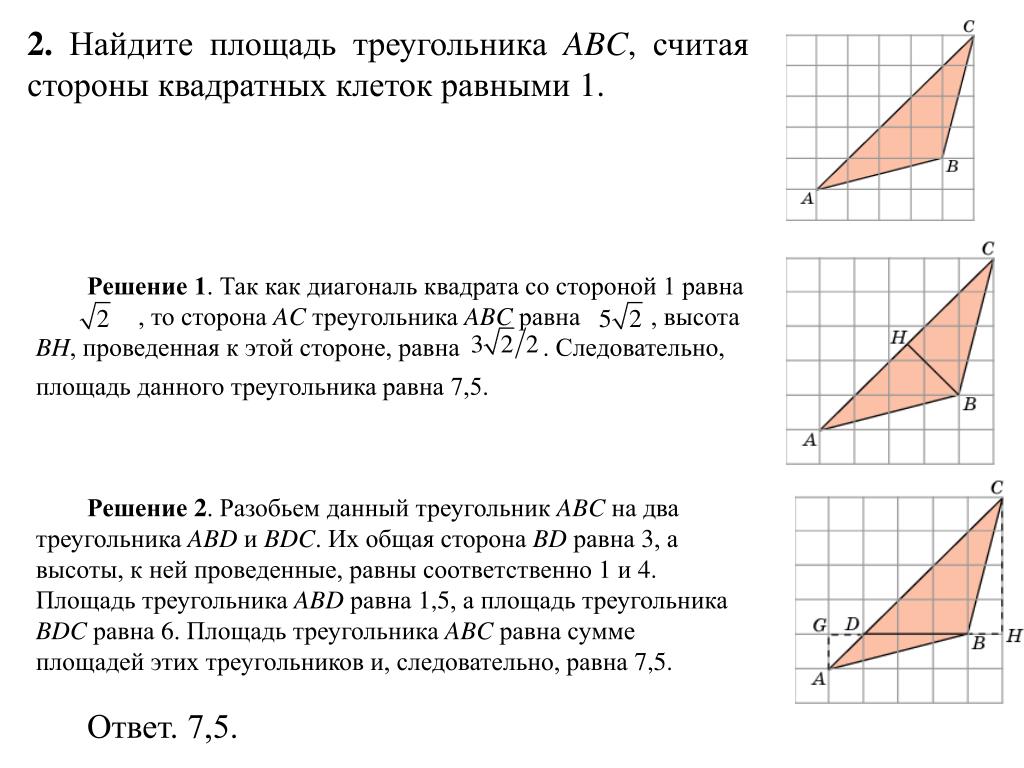 уравнение, получаем:

ССЫЛКИ:

Абрамовиц, М., и И. А. Стегун. 1972. Справочник математических функций с формулами, графики и математические таблицы. Dover Publications, Inc. Нью-Йорк, штат Нью-Йорк Йорк, США.

Наслаждайтесь! Пожалуйста, свяжитесь с автором, если у вас возникнут проблемы или вы обнаружите ошибки.

Джефф Дженнесс [email protected]

3020 бульвар Н. Схевен.

Флагстафф, Аризона, 86004

США

Дополнительная онлайн-документация для » Расширение «Площади поверхности и отношения из сетки высот»….

Up
Методы расчета площади поверхности Сравнение
TIN и площади поверхности сетки
Проблемы с запросом ‘ZonalStatsTable’. ..
Плакат Surface Area

Пожалуйста, посетите Jenness Enterprises ArcView Сайт расширений для получения дополнительных расширений ArcView и другого программного обеспечения от Автор. Мы также предлагаем индивидуальные консультации по ГИС на базе ArcView. услуги, которые помогут вам выполнить анализ ваших конкретных данных и применить их потребности развития.

Математика 7-го класса — Вычисление площади треугольника

Освойте 7 столпов школьной успеваемости

Улучшите свои оценки и снизьте стресс

Общий базовый математический стандарт: 7.G.6  7-й Класс Математика

Площадь треугольника Формула равна половине основания, умноженной на высоту (1/2 b*h). числа в области формулы треугольника. Любой катет треугольника может быть основанием, а высота отсчитывается от вершины, противоположной основанию, и перпендикулярна основанию.


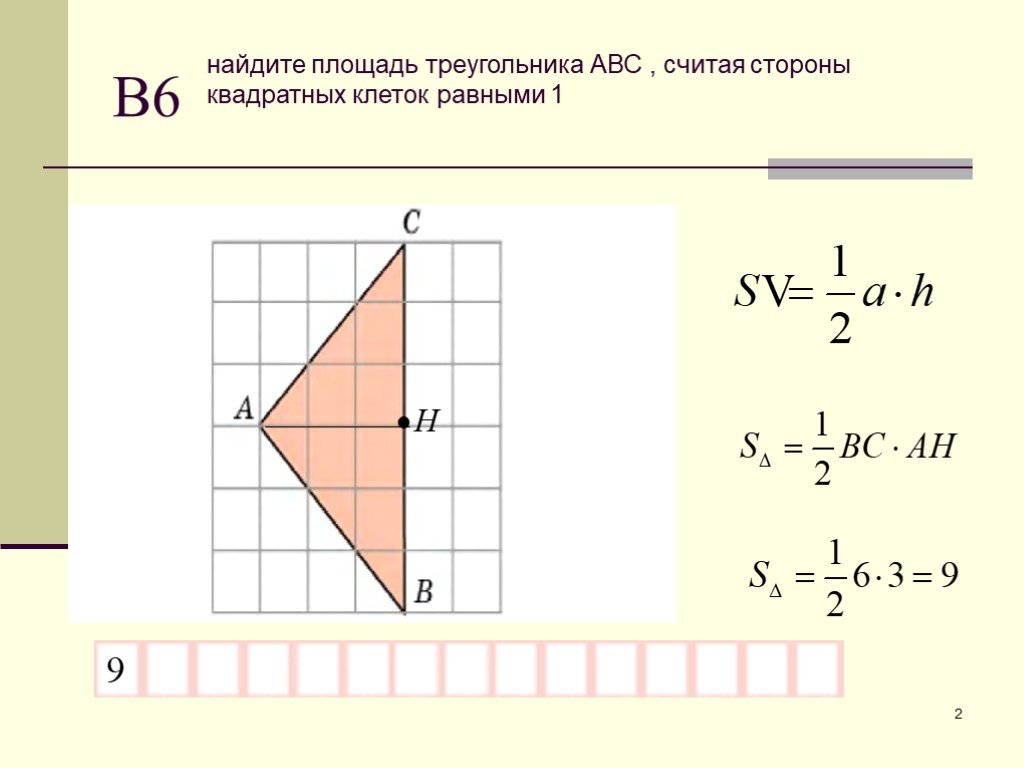
Как найти площадь треугольника?

В следующих примерах указана высота над уровнем моря. Если высота треугольника неизвестна, можно использовать формулу Герона, чтобы найти площадь.

Чем площадь треугольника отличается от периметра треугольника?

Периметр — это расстояние вокруг треугольника, а площадь — это мера пространства, покрывающего треугольник.

Формула периметра треугольника равна:

Найдите периметр треугольника со сторонами 7,9 и 11 единиц.

Решение: 7+9+11 = 27 единиц

Периметр = a+b+c, где a, b и c — стороны треугольника 003

Пример задачи 3   Треугольник  wxy  имеет площадь сколько единиц?

Пример задачи 2 Треугольник  xyz  имеет площадь сколько единиц?

9 0073 Площадь = 1/2 основания x высота   

Шаг 1.