Формулы геометрии. Площади фигур — материалы для подготовки к ЕГЭ и ОГЭ по Математике
Чтобы решать задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Начнем с квадрата.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его длины и ширины.
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне. Она также равна произведению его сторон на синус угла между ними.
Для площади треугольника есть целых 5 формул. И все они применяются в задачах ЕГЭ.
1) Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне:
2) Она также равна половине произведения его сторон на синус угла между ними:
3) По формуле Герона, где полупериметр.
4) Также площадь треугольника равна произведению его полупериметра на радис вписанной окружности, S = pr.
Есть и другие формулы для площади треугольника. Но для решения заданий ЕГЭ, и первой, и второй части, достаточно этих пяти.
Площадь прямоугольного треугольника равна половине произведения его катетов. Она также равна половине произведения гипотенузы на высоту, проведенную к этой гипотенузе:
Площадь правильного треугольника равна квадрату его стороны, умноженному на и деленному на 4:
Площадь трапеции равна произведению полусуммы оснований на высоту,
Также можно сказать, что площадь трапеции равна произведению ее средней линии на высоту,
Площадь произвольного четырехугольника равна половине произведения его диагоналей на синус угла между ними,
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. Она также равна половине произведения диагоналей:
Площадь круга равна произведению числа и квадрата радиуса круга.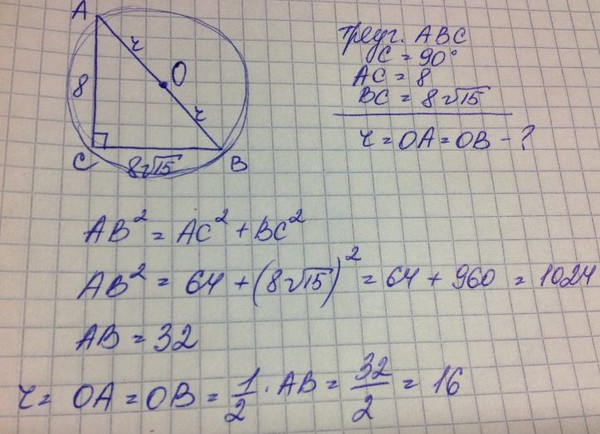
Ее также можно записать как произведение числа и квадрата диаметра круга, деленного на 4:
Вспомним важные свойства площадей фигур.
- Равные фигуры имеют равные площади.
Иногда фигуры, имеющие равные площади, еще называют равновеликими.
Пример. Найдем площадь фигуры, изображенной на клетчатой бумаге с размером клетки 1см1см.
Решение:
Найдем площадь фигуры на рисунке как сумму площадей нескольких фигур.
На рисунке это три треугольника и трапеция, указаны их площади. Тогда площадь фигуры равна 10 + 3,5 + 1,5 + 3 = 18.
Ответ: 18.
3. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Треугольники АВС и на рисунке называются подобными.
У треугольника все стороны в k раз длиннее, чем у треугольника АВС. Высота треугольника в k раз длиннее, чем высота треугольника АВС.
4. На рисунке показаны треугольники АВС и BCD, имеющие общую высоту. Отношение площадей этих треугольников равно отношению АС к CD:
5. Треугольники АВС и АЕС на рисунке имеют одинаковое основание и разные высоты.
Отношение площадей этих треугольников равно отношению их высот:
6. Медиана треугольника делит его на два равновеликих, то есть равных по площади, треугольника.
На рисунке СМ — медиана треугольника АВС. Площади треугольников АСМ и ВСМ равны.
7. Три медианы треугольника делят его на шесть равных по площади треугольников.
На рисунке все 6 треугольников, из которых состоит треугольник АВС, имеют равные лощади.
Задачи ЕГЭ и ОГЭ по теме: Площади фигур.
Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен
Решение:
Площадь треугольника равна половине произведения его сторон на синус угла между ними. Поэтому
Поэтому
Задача 2. Площадь треугольника ABC равна 4, DE — средняя линия, параллельная стороне AB. Найдите площадь треугольника CDE.
Решение:
Так как DE и АВ параллельны, треугольники CDE и САВ подобны с коэффициентом подобия Площади подобных фигур относятся как квадрат коэффициента подобия. Тогда
Ответ: 1.
Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Решение:
Выразим площадь двумя способами:
Тогда
Ответ: 6.
Задача 4. Площадь треугольника ABC равна 10, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
Решение:
Треугольник CDE подобен треугольнику CAB с коэффициентом Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Следовательно, .
Ответ: 7,5.
Задача 5. В параллелограмме ABCD AB = 3, AD = 21, . Найдите большую высоту параллелограмма.
Решение:
Большая высота — это DH, потому что проведена к меньшей стороне. Из треугольника АDН:
Ответ: 18.
Задача 6. Найдите площадь квадрата, если его диагональ равна 1.
Решение:
Квадрат — это частный случай ромба. Площадь квадрата равна половине произведения его диагоналей. Поэтому она равна 0,5.
Ответ: 0,5.
Задача 7. Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Решение:
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника равна тогда одна из сторон равна 3, а другая 6. Периметр P = 2 · 3 + 2 · 6 = 18.
Ответ: 18.
Задача 8.
Решение:
Площадь параллелограмма равна произведению его сторон на синус угла между ними. Площадь прямоугольника равна произведению длины на ширину. Пусть одна сторона параллелограмма и прямоугольника равна вторая равна а острый угол параллелограмма равен Тогда площадь параллелограмма равна а площадь прямоугольника равна
По условию площадь прямоугольника вдвое больше:
Следовательно,
Ответ: 30.
Задача 9. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Решение:
Площадь параллелограмма равна произведению его основания на высоту, проведенную к этому основанию. Пусть высоты равны соответственно a и b. Тогда S = 5 · a = 10 · b = 40. Поэтому a = 8, b = 4. Большая высота равна 8.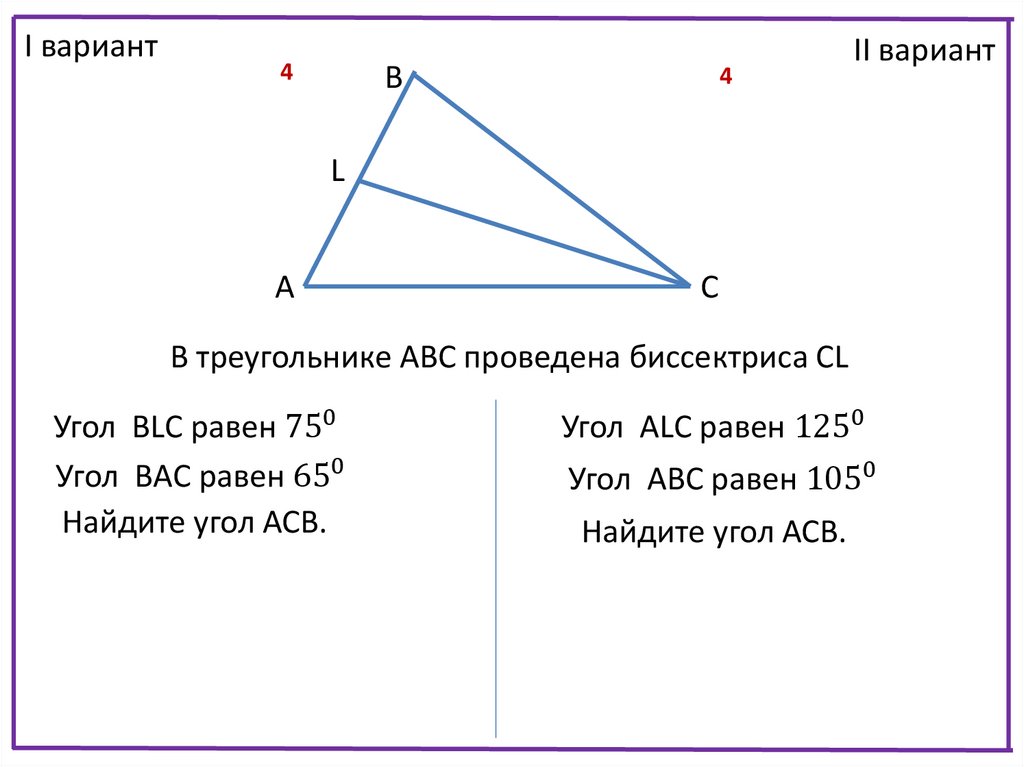
Ответ: 8.
Задача 10. Найдите площадь ромба, если его высота равна 2, а острый угол 30
Решение:
Площадь ромба равна произведению квадрата его стороны на синус угла ромба. С другой стороны, площадь ромба равна произведению его основания на высоту, проведенную к этому основанию. Пусть сторона ромба равна
Получим уравнение:
Корень уравнения a = 4, поэтому
Ответ: 8.
Задача 11. Найдите площадь ромба, если его диагонали равны 4 и 12.
Решение:
Площадь ромба равна половине произведения его диагоналей.
Ответ: 24.
Задача 12. Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Решение:
Трапеция равнобедренная, значит,
Тогда по теореме Пифагора из треугольника ADH:
Ответ: 160.
Задача 13. Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45
Решение:
Проведем высоту CH. Треугольник CHB — прямоугольный, в нем
Треугольник CHB — прямоугольный, в нем
значит, он также равнобедренный, CH = HB = 4.
Ответ: 16.
Задача 14. Высота трапеции равна 5, площадь равна 75. Найдите среднюю линию трапеции.
Решение:
Средняя линия трапеции равна полусумме оснований. Выразим её из формулы площади трапеции:
Ответ: 15.
Задача 15. Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
Решение:
Площадь трапеции равна произведению полусуммы оснований на высоту. Пусть высота равна h, тогда
Из этого уравнения получим: h = 4.
Рассмотрим прямоугольный треугольник, гипотенузой которого является боковая сторона трапеции, равная 8, а катетом — высота трапеции. Длина катета равна половине гипотенузы, следовательно, он лежит напротив угла
Ответ: 30.
Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Задача 16. Найдем площадь четырехугольника на рисунке.
Решение:
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным 5. Высоты этих треугольников равны 2 и 3. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
Ответ: 12,5.
В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Задача 17. Найдем площадь треугольника, изображенного на клетчатой бумаге.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной 5 и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
Ответ: 10,5.
Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.
Задача 18.
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
Решение:
На этом рисунке мы видим часть круга. Площадь всего круга равна так как Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R = 1), а длина дуги данного сектора равна 2, следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Ответ: 1.
Формула Пика
Покажем, как вычислять площадь фигуры, изображенной на координатной плоскости, с помощью формулы Пика.
Задача 19. Найдите площадь многоугольника АВСDE, изображенного на рисунке.
Первый способ:
Площадь многоугольника ABCDE равна сумме площадей треугольника BCD, трапеции BKDE и треугольника AKE.
Имеем:
Второй способ — применить формулу Пика.
Назовем точку координатной плоскости целочисленной, если обе ее координаты — целые числа. На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
На нашем рисунке это точки на пересечениях линий, разделяющих клетчатую бумагу на клетки.
Площадь многоугольника с целочисленными вершинами равна
.
Здесь В — количество целочисленных точек внутри многоугольника, Г — количество целочисленных точек на границе многоугольника.
Главное — аккуратно посчитать. На нашем рисунке
В = 24 (показаны зеленым),
Г = 8 (показаны красным),
S = 24 + — 1 = 27.
Ответ: 27.
Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Все формулы по геометрии. Площади фигур» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09. 03.2023
03.2023
Как найти площадь равнобедренного треугольника? Ответ на webmath.ru
Содержание:
- Формула
- Примеры вычисления площади равнобедренного треугольника
Формула
Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:
$$\mathrm{S}_{\Delta}=\frac{1}{2} a h_{a}$$
Напомним, что треугольник называется равнобедренным, если его две стороны равны. Равные стороны называются боковыми сторонами рассматриваемого треугольника, а третья сторона — основанием.
Примеры вычисления площади равнобедренного треугольника
Пример
Задание. Найти площадь равнобедренного треугольника $ABC$, если известно, что его основание равно 4 м, а высота, проведенная к этому основанию — 6 м.
Решение. Искомая площадь равна произведению высоты на основание, деленному на два:
$\mathrm{S}_{\Delta A B C}=\frac{4 \cdot 6}{2}=\frac{24}{2}=12$ (м2)
Ответ. {2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
{2}}=\sqrt{25-16}=\sqrt{9}=3$ (cм)
А тогда искомая площадь
$\mathrm{S}_{\Delta A B C}=\frac{1}{2} A C \cdot B H=\frac{8 \cdot 3}{2}=4 \cdot 3=12$ (см2)
Ответ. $\mathrm{S}_{\Delta A B C}=12$ (см2)
Остались вопросы?
Здесь вы найдете ответы.
Площадь равнобедренного треугольника с прямым углом составляет 16 см кв. Каким образом можно вычислить длину гипотенузы данной треугольной фигуры?
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.
Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:
х = 4*√2 см.
Теперь можно высчитать длину гипотенузы, которая будет равна:
х / sin45 = 8 см.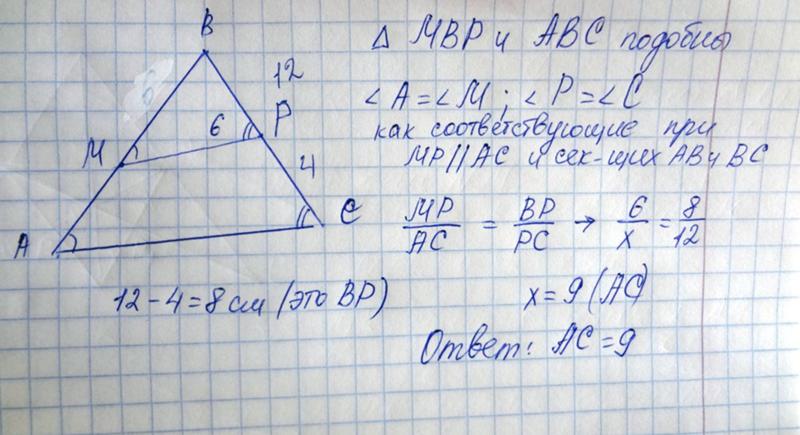
Ответ: Длина гипотенузы равна 8 см.
Имеется равнобедренный треугольник площадью 192 см кв. Его основание составляет 32 см. Как можно вычислить периметр данной треугольной фигуры?
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на высоту:
S=АС*ВН/2
Из этой формулы можно выразить ВН:
ВН=2S/АС=2*192/32=12 см.
Известно, что в равнобедренном треугольнике две стороны равны:
АВ=ВС=√(ВН²+(АС/2)²)=√(144+256)=20 см.
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:
Р=2АВ+АС=40+32=72 см.
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Длина гипотенузы равнобедренного треугольника, имеющего прямой угол, составляет 12 см. Как найти площадь данного треугольника?
Обозначим буквой х катет имеющегося треугольника.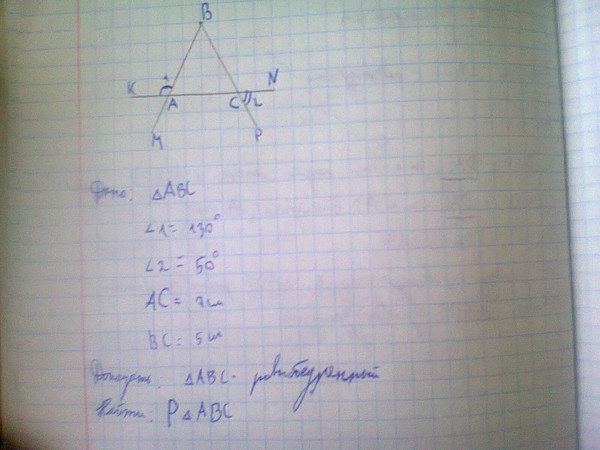 Тогда по теореме
Пифагора:
Тогда по теореме
Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
x²=72, x=√72
Зная длину катета равнобедренного треугольника, можно найти его площадь (S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Дан равнобедренный треугольник, угол в основании которого составляет 25 градусов. Площадь данной фигуры равна 16 см кв. Есть еще один равнобедренный треугольник с углом 130 градусов и площадью 4з см кв. Чему будет равно отношение оснований этих двух треугольных фигур?
Разберемся с первым из треугольников. Так как он является равнобедренным, то оба угла при его основании будут равны. Зная о том, что сумма всех углов треугольника равна 180 градусом, мы можем найти третий угол треугольника, находящийся при его вершине:
180-25-25=130 градусов.
Переходим ко второму треугольнику. Известно, что угол при его вершине
равен 230 градусом. Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
Исходя из этого можно рассчитать величины его углов,
расположенных в основании фигуры:
(180-130)/2=25 градусов.
Очевидно, что треугольники являются подобными на основании равенства углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:
49/16=kˆ2
Отсюда выражаем k:
k=7/4
Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:
С/c=k = 7/4
Ответ: Отношение оснований двух треугольников равно 7/4.
Чему равна площадь равнобедренного треугольника с прямым углом при условии, что длина его гипотенузы составляет с?
Площадь (S) треугольника с прямым углом составляет ½ часть произведения
его катетов. Принимая во внимание тот факт, что треугольник является
равнобедренным, можно утверждать, что длины его катетов равны. Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
Их можно
обозначить через х. В этом случае формулу для расчета площади треугольника
можно записать в следующем виде:
S=½x*x=½x²
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
с²=х²+х²=2x²
x²=½c²
Подставим в формулу площади получившееся равенство:
S=½*½с²=¼с² см.кв.
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Как можно рассчитать площадь равнобедренного треугольника, если длина его высоты и основания – величины известные?
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):
S = ½ c*h
Как найти площадь равнобедренного треугольника?
Площадь каждого треугольника, в том числе и равнобедренного, рассчитывается как половина, взятая от произведения длины высоты треугольника и его основания. Формула имеет следующий вид:
S=1/2 *a*h
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:
150/2=75 см.
Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):
h=√85²-75²=√7225-5625=√1600=40 см.
Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Как можно найти площадь треугольника при условии, что он является равнобедренным, и его периметр равен 100 см, а основание – 48 см?
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:
(100-48):2=26 см.
Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.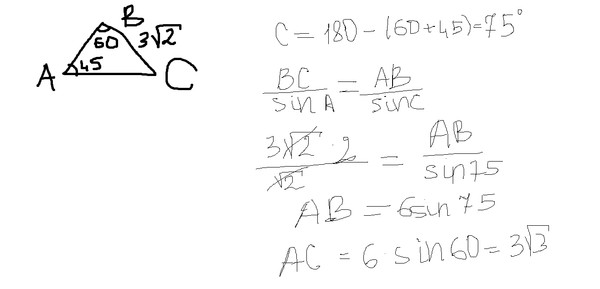
Чему равна площадь равнобедренного треугольника, длины сторон которого составляют 10 см и 12 см (сумма длин его катетов)?
К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.
В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:
h² = 10² — 6² = 64 см
Избавимся от квадратов:
h = 8 см.
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Как рассчитать площадь равнобедренного треугольника, если известно о том, что длина его гипотенузы составляет 44 см?
Введем условные обозначения, согласно которым х – это длина одного из
катетов равнобедренного треугольника. В этом случае длина второго катета
тоже будет равна х.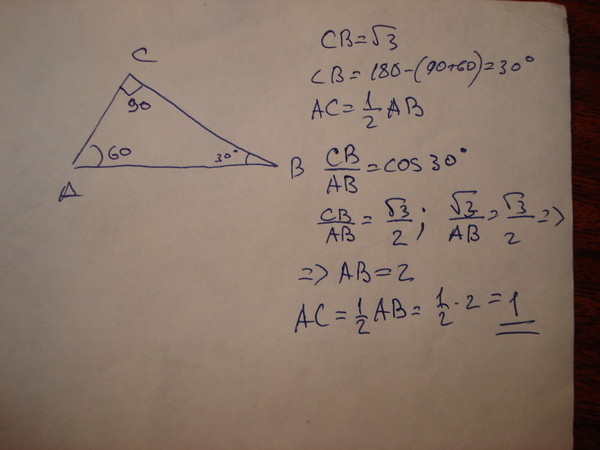 Зная длину гипотенузы, можно записать формулу теоремы
Пифагора для имеющегося треугольника:
Зная длину гипотенузы, можно записать формулу теоремы
Пифагора для имеющегося треугольника:
х²+ х² = 44²
2х² = 1936
Отсюда можем найти значение х:
x=√968
Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Каким образом возможно высчитать площадь равнобедренного треугольника через стороны и длину его основания?
Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:
S = b/4×√ 4× a²-b².
Возможно ли определить площадь равнобедренного треугольника через его боковые стороны и образованный ими угол?
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной
длины и размере угла (α), который образован этими катетами, позволит
определить площадь этой фигуры. В этом поможет следующая формула:
В этом поможет следующая формула:
S = 1/2a2 * sin(α).
Как можно высчитать площадь равнобедренного треугольника при условии, что известна длина его основания и угол?
Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:
S = ½ * a * b * sin(α)
Длина основания равнобедренного треугольника превышает длину его боковой стороны на 3 см. Периметр данной треугольной фигуры равен 30 см. Как можно высчитать длину основания данного равнобедренного треугольника?
Примем неизвестную длину основания равнобедренного треугольника за х. В данном случае длина каждой из боковых сторон, которые в равнобедренном треугольнике равны, будет составлять (х-3). Известно, что периметр (Р) треугольника равен 30 см. Тогда:
Р = 3х-6 = 30 см.
Отсюда можно вывести х:
х = (30+6)/3 = 12 см.
Ответ: Длина основания равна 12 см.
Высота, проведенная в равнобедренном треугольнике, равна 15 см. Длина основания данной фигуры превышает длину его боковой стороны на 15 см. Как найти основание равнобедренного треугольника в этом случае?
Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
225-x²-30x+225-0,25x²
0=0,75x²-30x
x(0,75x-30)=0
x¹=0 см.
x=40 см.
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см.
Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
По какой формуле можно высчитать площадь равнобедренного треугольника?
Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
В равнобедренном треугольнике к его основанию проведена высота, длина которой равна 1,2 см. Длина самого основания фигуры составляет 3,2 см. Как рассчитать длину боковой стороны этого равнобедренного треугольника?
Вычислим половину длины основания данного равнобедренного треугольника:
3,2/2 = 1,6 см.
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см
и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить,
используя теорему Пифагора:
Ее можно вычислить,
используя теорему Пифагора:
с²=а²+в²
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
с=√4=2 см.
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Один из углов равнобедренного треугольника является тупым. Одна сторона данной фигуры составляет 14 см, а другая – 8 см. Чему равно основание треугольника с двумя равными сторонами?
Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена
напротив тупого угла, имеет большую длину, чем сторона, лежащая против
острого угла треугольника. Это позволяет утверждать, что длина основания
данного треугольника больше длины его боковой стороны. По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
По причине того,
что треугольная фигура является равнобедренной, и известны длины двух ее
сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет
составлять 8 см или 14 см. Если предположить, что длина неизвестной
стороны равна 14 см, тогда длина основания будет составлять 8 см, что
невозможно, так как противоречит утверждению о расположении больших сторон
напротив тупых углов. Это означает, что длина третьей стороны треугольника
равна 8 см, а основание в данном случае составляет 14 см.
Равнобедренный треугольник имеет сторону длиной 29 см. Высота, проведенная в нем, составляет 21 см. Чему равно основание треугольника с указанными параметрами?
Для решения данной задачи следует воспользоваться теоремой Пифагора:
с²=а²+в²
Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:
29²-21² = 400.
Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:
√400*2 = 20*2 = 40 см.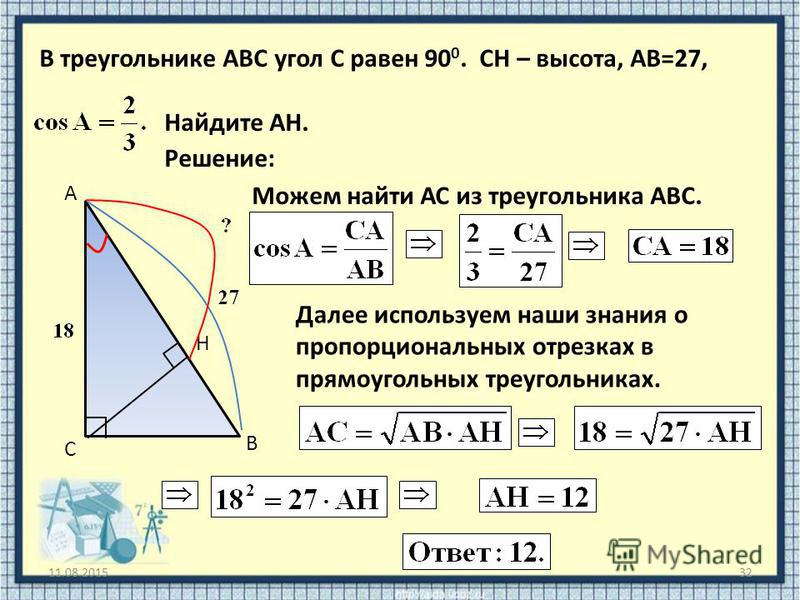
Ответ: Длина основания равнобедренного треугольника равна 40 см.
Читать дальше: как найти площадь равностороннего треугольника.
Калькулятор прямоугольного треугольника| Определение
Авторы: Альваро Диез, Матеуш Муха и Петр Малек.
Калькулятор прямоугольного треугольника поможет вам найти длины сторон прямого угла -угольный треугольник . Этот решатель треугольников также научит вас находить площадь прямоугольного треугольника, а также даст много информации о практическом использовании прямоугольного треугольника.
Что такое прямоугольный треугольник (или прямоугольный треугольник)?
Прежде всего, давайте объясним, что такое прямоугольный треугольник. Определение очень простое и может даже показаться очевидным для тех, кто его уже знает: прямоугольный треугольник — это треугольник, в котором один и только один из углов равен ровно 90° . Очевидно, что два других угла будут меньше прямого угла, потому что сумма всех углов треугольника всегда равна 180°.
В прямоугольном треугольнике стороны определяются особым образом. Сторона, противолежащая прямому углу, всегда является наибольшей в треугольнике и получает название «гипотенуза». Две другие стороны называются катетами. Связь между гипотенузой и каждым катетом прямая, как мы увидим 9.0031 когда мы говорим о теореме Пифагора .
Калькулятор гипотенузы
Если все, что вы хотите вычислить, это гипотенуза прямоугольного треугольника, эта страница и калькулятор прямоугольного треугольника отлично подойдут. Однако мы также рекомендуем использовать специальный инструмент, разработанный нами в Omni Calculators: калькулятор гипотенузы. Гипотенуза находится напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом
Однако мы также рекомендуем использовать специальный инструмент, разработанный нами в Omni Calculators: калькулятор гипотенузы. Гипотенуза находится напротив прямого угла и может быть решена с помощью теоремы Пифагора. В прямоугольном треугольнике с катетом , и b и с гипотенузой c , теорема Пифагора утверждает, что: a² + b² = c² .
Чтобы найти c , извлеките квадратный корень из обеих частей, чтобы получить c = √(b²+a²) . Мы можем рассматривать это расширение теоремы Пифагора как «формулу гипотенузы». Калькулятор теоремы Пифагора также является отличным инструментом для вычисления гипотенузы.
Давайте теперь решим практический пример того, что потребуется, чтобы вычислить гипотенузу прямоугольного треугольника без использования каких-либо калькуляторов доступен в Omni:
- Получите значения
aиb. - Квадрат
aиb.
- Суммируйте оба значения:
a² + b². - Извлеките квадратный корень из результата.
- Квадратный корень даст положительные и отрицательные результаты. Поскольку мы имеем дело с длиной, не обращайте внимания на отрицательную.
- Полученное значение является значением гипотенузы
c.
Теперь посмотрим каким будет процесс с использованием одного из калькуляторов Omni , например, калькулятор прямоугольного треугольника на этой веб-странице:
- Вставьте значение
aиbв калькулятор; и - Немедленно получить значение
c; - В качестве бонуса вы получите значение площади такого треугольника.
Как найти площадь прямоугольного треугольника
Мы уже видели, что вычислить площадь прямоугольного треугольника очень просто с калькулятором прямоугольного треугольника. В Omni Calculators у нас есть калькулятор, специально разработанный для этой цели: калькулятор площади прямоугольного треугольника. Давайте теперь более подробно рассмотрим, как вычислять площади прямоугольных треугольников.
Давайте теперь более подробно рассмотрим, как вычислять площади прямоугольных треугольников.
Способ нахождения площади прямоугольного треугольника довольно прост. Все, что вам нужно, это длины основания и высоты. В прямоугольном треугольнике основание и высота – две стороны, образующие прямой угол. Поскольку умножение этих значений на значения вместе дает площадь соответствующего прямоугольника, а площадь треугольника составляет половину этой площади, формула такова:
площадь = ½ × основание × высота .
Если вы не знаете ни основания, ни высоты, вы можете найти их по теореме Пифагора. Воспользуйтесь калькулятором прямоугольного треугольника, чтобы проверить свои расчеты или вычислить площадь треугольников, стороны которых имеют большую или десятичную длину.
Другие соображения при работе с прямоугольным треугольником
Теперь мы увидим другие вещи, которые можно вычислить из прямоугольного треугольника с помощью некоторых инструментов, доступных в Omni. Стороны треугольника имеют определенный градиент или наклон. Формула наклона
Стороны треугольника имеют определенный градиент или наклон. Формула наклона
наклон = (y₂ — y₁)/(x₂ — x₁) .
Итак, если координаты (1,-6) и (4,8) , наклон сегмента равен (8 + 6)/(4 — 1) = 14/3 . Простой способ определить, является ли треугольник правильным, и вы просто знаете координаты, — посмотреть, умножаются ли наклоны любых двух линий на равные -1 .
Существует простой способ преобразования углов из радианов в градусы и градусов в радианы с использованием преобразования углов:
- Если угол в радианах – умножить на 180/π ; и
- Если угол в градусах – умножить на π/180 .
Иногда вы можете столкнуться с проблемой отсутствия двух или даже трех длин сторон. В таких случаях калькулятор прямоугольного треугольника, калькулятор гипотенузы и метод нахождения площади прямоугольного треугольника не помогут. Вы должны использовать тригонометрические функции, чтобы найти недостающие части.
Вы должны использовать тригонометрические функции, чтобы найти недостающие части.
Особые треугольники
Прямоугольный треугольник — это лишь один из многих существующих особых треугольников. Эти треугольники обладают одной или несколькими особыми характеристиками, которые делают их уникальными. Например, как мы видели, прямоугольный треугольник имеет прямой угол и, следовательно, гипотенузу, что делает его уникальным видом треугольника. Помимо прямоугольного треугольника, есть и другие особые треугольники с интересными свойствами.
Одним из самых известных специальных треугольников является равносторонний треугольник, у которого три равные стороны и все его углы равны 60°. Это значительно упрощает вычисление различных параметров такого треугольника с помощью калькулятора решения треугольников.
Другим особым треугольником является равнобедренный треугольник, у которого две стороны одинаковой длины , а значит, два угла одинаковой величины. В отличие от равностороннего треугольника, равнобедренные треугольники бывают разных форм.
В отличие от равностороннего треугольника, равнобедренные треугольники бывают разных форм.
Есть много других специальных треугольников. Однако сейчас мы рассмотрим несколько совершенно особых прямоугольных треугольников, которые, помимо прямоугольных треугольников, обладают другими уникальными свойствами, делающими их интересными.
Особые прямоугольные треугольники
Так называемый треугольник «45 45 90», вероятно, самый особенный среди всех особых прямоугольных треугольников. Это прямоугольный треугольник, который также является равнобедренным треугольником . Оба его катета имеют одинаковую длину (равнобедренные), а также он имеет ту особенность, что непрямые углы составляют ровно половину размера прямого угла, что и дало название прямоугольному треугольнику.
Этот прямоугольный треугольник можно получить, когда вы разделить квадрат на его диагональ . Вот почему обе катеты (стороны квадрата) имеют одинаковую длину.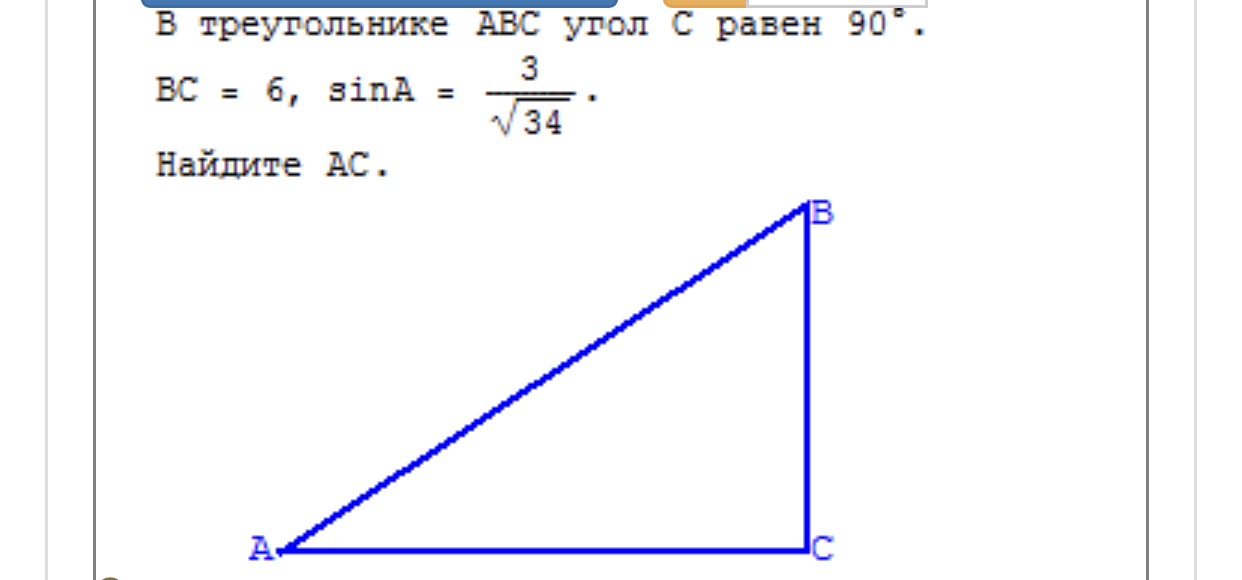 Для тех, кто хочет узнать больше о самых особенных из особых прямоугольных треугольников, мы рекомендуем проверить калькулятор треугольника 45 45 90, созданный для этой цели.
Для тех, кто хочет узнать больше о самых особенных из особых прямоугольных треугольников, мы рекомендуем проверить калькулятор треугольника 45 45 90, созданный для этой цели.
Еще один увлекательный треугольник из группы особых прямоугольных треугольников — это так называемый треугольник «30 60 90». Название происходит от наличия одного прямого угла (90°), затем одного угла 30° и другого 60°. Эти углы особенные из-за значений их тригонометрических функций (косинуса, синуса, тангенса и т. д.). Последствия этого можно увидеть и понять с помощью 30 60 90 калькулятор треугольников, но для тех, кому лень переходить по ссылке, мы приведем некоторые из них здесь . Если предположить, что длина меньшей стороны равна a , треугольник выглядит следующим образом:
- Вторая длина равна
a√3; - Гипотенуза равна
2a; - Площадь равна
a²√(3/2); и - Периметр равен
a(3 + √3).
Прямоугольные треугольники и параллелограммы
На первый взгляд может показаться, что прямоугольный треугольник и параллелограмм не имеют ничего общего. Как решатель треугольников может помочь вам понять параллелограмм? Реальность такова, что любой параллелограмм можно разложить на 2 или более прямоугольных треугольника . Давайте возьмем пример прямоугольника, который проще всего увидеть.
Представьте себе прямоугольник, любой прямоугольник. Теперь нарисуйте след на одной из диагоналей этого прямоугольника. Если разделить прямоугольник диагональю, то получится два прямоугольных треугольника . Глядя на треугольники, нет необходимости использовать калькулятор прямоугольного треугольника, чтобы убедиться, что оба треугольника равны, поэтому их площади будут одинаковыми. Это означает, что площадь прямоугольника вдвое больше площади каждого треугольника .
Если мы подумаем об уравнениях, это имеет смысл, поскольку площадь прямоугольника со сторонами a и b равна ровно площади = a × b , а для прямоугольного треугольника равна площади = основание × высота / 2 , что в данном случае будет означать площадь = a × b /2 . Это именно то, что мы уже видели, просто разрезав прямоугольник по диагонали.
Это именно то, что мы уже видели, просто разрезав прямоугольник по диагонали.
Это был простой пример прямоугольника, но то же самое относится и к площади квадрата. Для других параллелограммов процесс немного усложняется (может быть задействовано до 4-х прямоугольных треугольников разных размеров). Тем не менее, при некотором навыке, вы можете использовать ту же идею и вычислить площадь параллелограмма, используя прямоугольные треугольники. Вы можете, конечно, быть еще более эффективным и просто использовать наш калькулятор.
Пифагорейские тройки, треугольники и математика
Геометрия и многоугольники, особенно треугольники, всегда идут рука об руку. Свойства некоторых треугольников, например прямоугольных, обычно интересны и шокируют даже нематематиков. Теперь мы рассмотрим интересный набор чисел , очень тесно связанных с прямоугольными треугольниками, которые любят математики, и, возможно, вы тоже.
Эти наборы чисел называются пифагорейскими тройками и представляют собой наборы из 3 целых чисел (назовем их a , b и c ) и удовлетворяют теореме Пифагора: a² + b² = c² .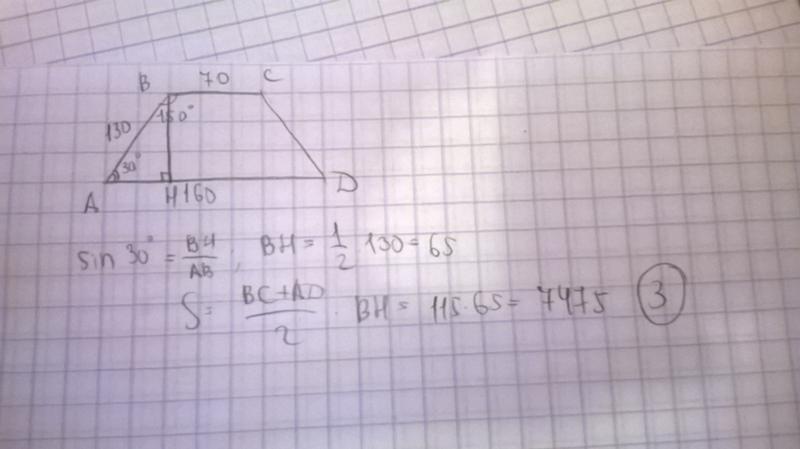 То есть они могли бы образовать прямоугольный треугольник со сторонами длиной
То есть они могли бы образовать прямоугольный треугольник со сторонами длиной a , b и c . Количество чисел, удовлетворяющих этому соотношению, ограничено, но математики находят удовольствие в поиске новых.
Помимо фактора любопытства в этих отношениях, в них есть несколько интересных свойства, которые используются в криптографии . Учитывая приложения, которые можно найти для таких наборов чисел, математики исследовали даже больше, используя 4, 5… и больше наборов чисел, которые удовлетворяют аналогичному соотношению, в котором сумма квадратов всех чисел, кроме одного, дает квадрат оставшегося числа.
С этими пифагорейскими тройками тесно связана также печально известная Последняя теорема Ферма , в которой почти легендарный загадочный математик Пьер Ферма заявил, что не может быть набора из трех целых чисел, которые удовлетворяли бы соотношению: aⁿ + bⁿ = cⁿ для n больше 2. Эта гипотеза не доказана математически, и она считается единицей. из важнейших математических задач века.
Эта гипотеза не доказана математически, и она считается единицей. из важнейших математических задач века.
Тени и прямоугольные треугольники (радиус Земли)
Мы много говорили о треугольниках, особенно прямоугольных, и их применении в математике и геометрии. О чем мы еще не говорили, так это о полезность прямоугольных треугольников для расчетов в реальной жизни . Может показаться, что возможности применения вне геометрии ограничены, но давайте взглянем на тени.
Да, тени. Темный оттенок, отбрасываемый объектом при его освещении. Если бы вы посмотрели на форму, созданную тенью, объектом и землей, вы бы заметили, что на самом деле это прямоугольный треугольник! По крайней мере, когда объект совершенно вертикальный, а земля горизонтальная. В большинстве случаев это так или, по крайней мере, достаточно близко. Это означает, что мы можем использовать калькулятор прямоугольного треугольника, чтобы найти различную информацию об объектах под солнцем. Посмотрим, как.
Посмотрим, как.
Представьте, что у вас есть здание, для которого мы хотим узнать высоту , но вы не можете измерить его напрямую, потому что оно слишком высокое, чтобы сбросить рулетку сверху. Что вы можете сделать, так это измерить длину тени на улице. Затем с помощью любого углового инструмента и листа бумаги можно узнать угол между тенью и землей. Зная, что угол между зданием и землей равен 90°, можно получить значение высоты здания.
Используя эту технику, вы можете измерить высоту многих объектов , если у вас есть яркий солнечный день или другие источники света для освещения объекта. Фактически, это был очень распространенный метод измерения в старые времена. Вероятно, самое интересное и умопомрачительное использование прямоугольных треугольников принадлежит Эратосфену, которому удалось использовать прямоугольные треугольники и тени для измерения радиуса Земли , и теперь мы объясним, как он это сделал.
Эратосфен заметил, что в день летнего солнцестояния на Земле было место, где колодцы не имели тени в полдень, т. е. солнце светило прямо на них. Заметив это, он поставил столб известной высоты на известном расстоянии от этого колодца и измерил величину тени в одно и то же время дня и в один и тот же день года в обоих местах. Затем, используя прямоугольные треугольники и тригонометрию, он смог измерить угол между двумя городами, а также радиус Земли так как знал расстояние между городами.
Это был поразительный подвиг, который теперь можно сделать гораздо проще, просто используя калькуляторы Omni, которые мы создали для вас .
Часто задаваемые вопросы
Длины каких сторон образуют прямоугольный треугольник?
Длины сторон a , b , c образуют прямоугольный треугольник тогда и только тогда, когда они удовлетворяют a² + b² = c² . Мы говорим, что эти числа образуют Тройка Пифагора .
2, 3 и 4 образуют прямоугольный треугольник?
У нас есть 4² = 16 и 2² + 3² = 4 + 9 = 13 , поэтому сумма квадратов двух меньших чисел НЕ равна квадрату наибольшего числа. То есть 2, 3 и 4 не образуют пифагорейскую тройку; другими словами, не существует прямоугольного треугольника со сторонами 2, 3 и 4.
Как найти центр описанной окружности прямоугольного треугольника?
Для прямоугольного треугольника центр описанной окружности, т. е. центр описанной на треугольнике окружности, совпадает с серединой самой длинной стороны треугольника (ее гипотенуза ).
Как найти ортоцентр прямоугольного треугольника?
Ортоцентр прямоугольного треугольника, т. е. точка пересечения высот треугольника, совпадает с вершиной прямоугольного треугольника.
Альваро Диес, Матеуш Муха и Петр Малек
c (гипотенуза)
Посмотреть 18 подобных калькуляторов треугольников0003
Калькулятор прямоугольного треугольника | PI Day
C (Hypotenuse)
Периметр
Угол 1
Угол 2
Угол 3
Вернитесь к калькуляторам. прямоугольный треугольник в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.
прямоугольный треугольник в верхние поля. Затем калькулятор определит длину оставшейся стороны, площадь и периметр треугольника, а также все углы треугольника.
Если мы знаем только две стороны прямоугольного треугольника, мы можем использовать эту информацию, чтобы найти третью сторону, площадь и периметр треугольника и все углы треугольника. Удивительно, правда? Давайте рассмотрим, как мы найдем каждую из этих частей.
Как найти недостающую сторону прямоугольного треугольникаЧтобы найти недостающую сторону прямоугольного треугольника, мы используем знаменитую теорему Пифагора.
Нам нужно быть немного осторожными, чтобы знать, какую сторону мы находим. Прямоугольные треугольники имеют два катета и гипотенузу, которая является самой длинной стороной и всегда находится напротив прямого угла. Когда мы пытаемся найти гипотенузу, мы заменяем две наши известные стороны на и b на . Неважно, какая ножка а , а какая b . Затем мы находим c , складывая квадраты значений a и b и извлечение квадратного корня из обеих частей.
Прямоугольные треугольники имеют два катета и гипотенузу, которая является самой длинной стороной и всегда находится напротив прямого угла. Когда мы пытаемся найти гипотенузу, мы заменяем две наши известные стороны на и b на . Неважно, какая ножка а , а какая b . Затем мы находим c , складывая квадраты значений a и b и извлечение квадратного корня из обеих частей.
Когда мы пытаемся найти один из катетов, мы вводим известный катет для a и известную гипотенузу для c . Затем мы находим b , используя простую алгебру (вычтем значение a в квадрате с обеих сторон, затем возьмем квадратный корень из обеих сторон).
Как найти площадь прямоугольного треугольника Чтобы найти площадь прямоугольного треугольника, нам нужно знать только длину двух катетов. Нам вообще не нужна гипотенуза. Это потому, что катеты определяют основание и высоту треугольника в каждом прямоугольном треугольнике. Поэтому мы используем общую формулу площади треугольника (A = основание • высота/2) и подставляем a и b для основание и высота . Итак, наша новая формула для площади прямоугольного треугольника: A = ab/2.
Поэтому мы используем общую формулу площади треугольника (A = основание • высота/2) и подставляем a и b для основание и высота . Итак, наша новая формула для площади прямоугольного треугольника: A = ab/2.
Чтобы найти периметр или расстояние вокруг нашего треугольника, нам просто нужно сложить все три стороны вместе. Если мы знаем только две стороны, нам нужно сначала использовать теорему Пифагора, чтобы найти третью сторону.
Как найти углы прямоугольного треугольникаЧтобы найти углов прямоугольного треугольника, мы используем тригонометрию. Это не так сложно, как кажется. Нам просто нужно найти одну специальную кнопку на наших карманных калькуляторах. Для начала нам нужно знать все длины сторон, поэтому, если мы их еще не знаем, мы сначала воспользуемся теоремой Пифагора, чтобы найти их.
Когда у нас есть все стороны, мы определяем, какой угол мы собираемся найти. Затем мы берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне 9.0374 с . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто помечается как SIN -1 . Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой режим, а не на радианный.
Затем мы берем сторону, противоположную этому углу, и делим ее на длину гипотенузы, которая равна стороне 9.0374 с . Это даст нам значение от 0 до 1. Теперь нам просто нужно найти кнопку ARCSIN на нашем калькуляторе, которая часто помечается как SIN -1 . Нахождение ARCSIN нашего десятичного значения дает нам угол. Убедитесь, что калькулятор настроен на угловой режим, а не на радианный.
Мы можем повторить этот процесс, чтобы найти другой неизвестный угол в треугольнике, еще раз разделив его противоположную сторону на гипотенузу, а затем взяв ARCSIN.
Или мы могли бы продемонстрировать еще больше знаний о треугольниках, используя вычитание, чтобы найти его, поскольку мы знаем, что сумма внутренних углов треугольника должна составлять 180°. Вычитание угла, который мы только что нашли, из 180°, а затем вычитание нашего известного прямого угла (90°) также даст нам третий угол.
Этот калькулятор отлично подходит для получения всей этой информации только с двух сторон прямоугольного треугольника, но это забавная задача, чтобы попытаться найти стороны, углы, площадь и периметр самостоятельно без него.



Leave A Comment