Площадь пирамиды — формула, пример расчета, калькулятор
Пирамида – это фигура, в основании которой лежит произвольный многоугольник, а боковые грани представлены треугольниками. Их вершины лежат в одной точке и соответствуют вершине пирамиды.
Пирамида может быть разнообразной – треугольной, четырехугольной, шестиугольной и т.д. Ее название можно определить в зависимости от количества углов, прилегающих к основанию.
Правильной пирамидой называется пирамида, в которой равны стороны основания, углы, и ребра. Также в такой пирамиде будет равна площадь боковых граней.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей всех ее граней:
То есть, чтобы рассчитать площадь боковой поверхности произвольной пирамиды, необходимо найти площадь каждого отдельного треугольника и сложить их между собой. Если пирамида усеченная, то ее грани представлены трапециями. Для правильной пирамиды существует другая формула. В ней площадь боковой поверхности рассчитывается через полупериметр основания и длину апофемы:
Пусть дана правильная четырехугольная пирамида. Сторона основания b = 6 см, а апофема a = 8 см. Найдите площадь боковой поверхности.
В основании правильной четырехугольной пирамиды лежит квадрат. Для начала найдем его периметр:
Теперь можем просчитать площадь боковой поверхности нашей пирамиды:
Для того чтобы найти полную площадь многогранника, потребуется найти площадь его основания. Формула площади основания пирамиды может отличаться, в зависимости от того, какой многоугольник лежит в основании. Для этого используются формулы площади треугольника, площади параллелограмма
Площадь квадрата рассчитывается по формуле: ,
где a – сторона квадрата.
 У нас она равна 6 см. Значит площадь основания пирамиды:
У нас она равна 6 см. Значит площадь основания пирамиды:Теперь остается только найти полную площадь многогранника. Формула площади пирамиды состоит из суммы площади ее основания и боковой поверхности:
При расчете площади любой части пирамиды необходимо обращать внимания на условия задачи. Если дана произвольная пирамида, стоит аккуратно просчитать каждую из ее граней и только потом находить полное значение.
Площадь поверхности пирамиды
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами. Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
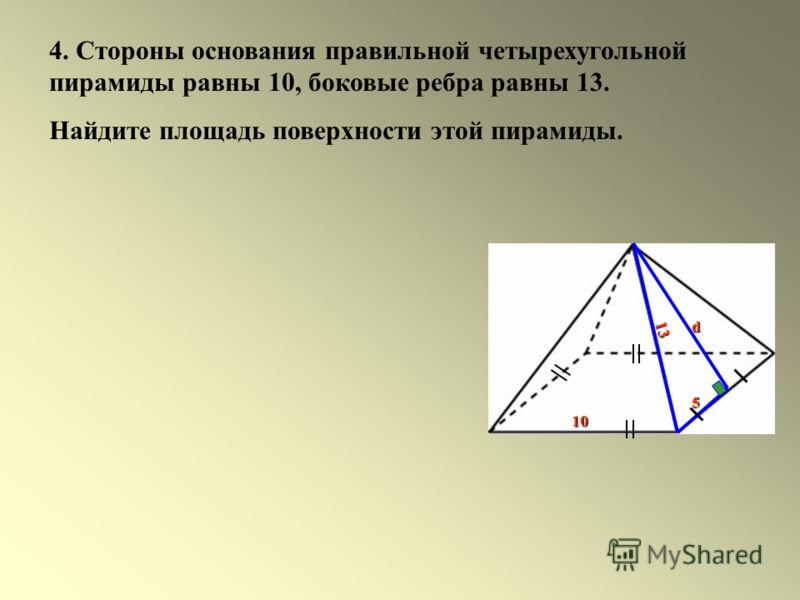
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
основания, боковую и полную? Что собой представляет пирамида
Перед изучением вопросов о данной геометрической фигуре и её свойствах, следует разобраться в некоторых терминах. Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.
Пирамида – геометрическая фигура , обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:
- правильная;
- усечённая.

В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.
Во втором случае, оснований два — большое в самом низу и малое между вершиной, повторяющее форму основного. Иными словами – усечённая пирамида представляет собой многогранник с сечением, образованным параллельно основанию.
Термины и обозначения
Основные термины:
- Правильный (равносторонний) треугольник – фигура с тремя одинаковыми углами и равными сторонами. В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
- Вершина – самая верхняя точка, где сходятся грани. Высота вершины образуется прямой линией, исходящей от вершины к основанию пирамиды.
- Грань – одна из плоскостей многоугольника. Она может быть в виде треугольника в случае с треугольной пирамидой либо в виде трапеции для усечённой пирамиды.
- Сечение – плоская фигура, образующаяся в результате рассечения. Не стоит путать с разрезом, так как разрез показывает и то, что находится за сечением.
- Апофема – отрезок, проведённый из вершины пирамиды к её основанию. Он также является высотой той грани, где находится вторая точка высоты. Данное определение справедливо лишь по отношению к правильному многограннику. К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
Формулы площади
Находить площадь боковой поверхности пирамиды любого типа можно несколькими способами. Если фигура не симметричная и представляет собой многоугольник с разными сторонами, то в данном случае легче вычислить общую площадь поверхности через совокупность всех поверхностей.
В зависимости от того, какие параметры известны, могут потребоваться формулы вычисления квадрата, трапеции, произвольного четырёхугольника и т.д. Сами формулы в разных случаях тоже будут иметь отличия.
В случае с правильной фигурой находить площадь намного проще. Достаточно знать всего несколько ключевых параметров. В большинстве случаев требуются вычисления именно для таких фигур. Поэтому далее будут приведены соответствующие формулы. В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.
Основная формула для вычисления площади боковой поверхности правильной пирамиды будет иметь следующий вид:
S=½ Pa (P – периметр основания, а – апофема)
Рассмотрим один из примеров. Многогранник имеет основание с отрезками A1, А2, А3, А4, А5, и все они равны 10 см. Апофема пусть будет равна 5 см. Для начала надо найти периметр. Так как все пять граней основания одинаковые, можно находить так: Р=5*10=50 см. Далее применяем основную формулу: S =½*50*5=125 см в квадрате.
Площадь боковой поверхности правильной треугольной пирамиды вычислить легче всего. Формула имеет следующий вид:
S =½* ab *3, где а – апофема, b – грань основания. Множитель тройки здесь означает количество граней основания, а первая часть – площадь боковой поверхности. Рассмотрим пример. Дана фигура с апофемой 5 см и гранью основания 8 см. Вычисляем: S =1/2*5*8*3=60 см в квадрате.
Площадь боковой поверхности усечённой пирамиды вычислять немного сложнее. Формула выглядит так: S =1/2*(p _01+ p _02)*a , где р_01 и р_02 являются периметрами оснований, а – апофема. Рассмотрим пример. Допустим, для четырёхугольной фигуры даны размеры сторон оснований 3 и 6 см, апофема равна 4 см.
Тут для начала следует найти периметры оснований: р_01 =3*4=12 см; р_02=6*4=24 см. Осталось подставить значения в основную формулу и получим: S =1/2*(12+24)*4=0,5*36*4=72 см в квадрате.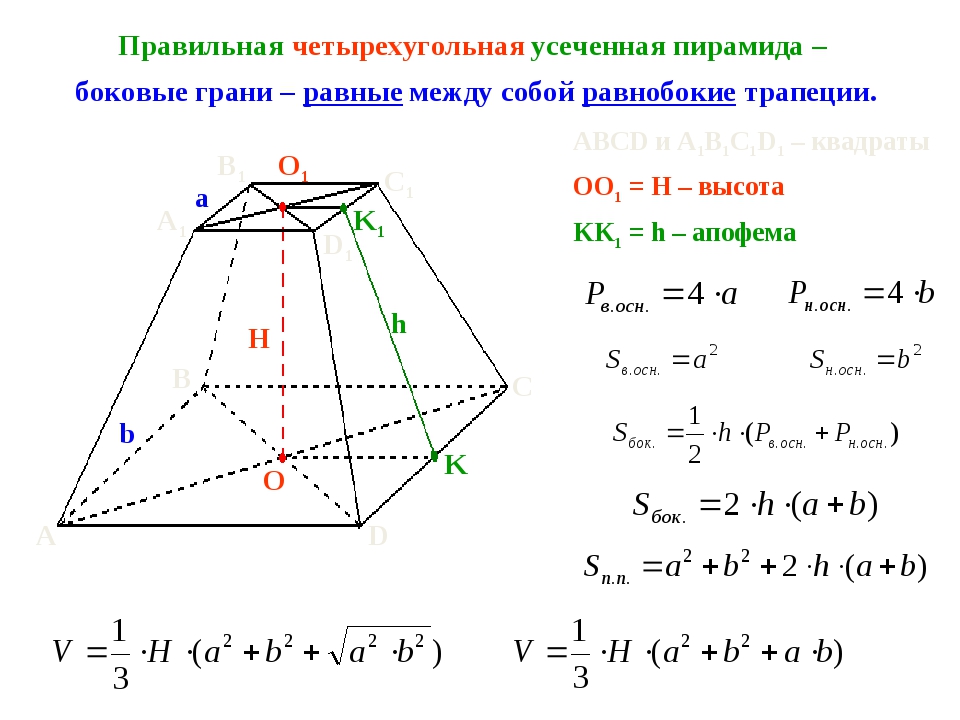
Таким образом, можно найти площадь боковой поверхности правильной пирамиды любой сложности. Следует быть внимательным и не путать эти вычисления с полной площадью всего многогранника. А если это всё же понадобится сделать – достаточно вычислить площадь самого большого основания многогранника и прибавить её к площади боковой поверхности многогранника.
Видео
Закрепить информацию о том, как найти площадь боковой поверхности разных пирамид, вам поможет это видео.
Не получили ответ на свой вопрос? Предложите авторам тему.
Полная площадь боковой поверхности пирамиды состоит из суммы площадей его боковых граней.
В четырехугольной пирамиде различается два вида граней – четырехугольник в основании и треугольники с общей вершиной, которой образуют боковую поверхность.
Для начала потребуется рассчитать площадь боковых граней. Для этого можно использовать формулы площади треугольника, а можно также воспользоваться формулой площади поверхности четырехугольной пирамиды (только в случае, если многогранник правильный). Если пирамида правильная и в ней известна длина ребра a
основания и проведенной к нему апофемы h
, то:
Если по условиям даны длина ребра c
правильной пирамиды и длина стороны основания a
, то можно найти значение по следующей формуле:
Если же дана длина ребра в основании и противолежащий ей острый угол у вершины, то можно рассчитать площадь боковой поверхности по соотношению квадрата стороны a
к удвоенному косинусу половины угла α
:
Рассмотрим пример расчета площади поверхности четырехугольной пирамиды через боковое ребро и сторону основания.
Задача: пусть дана правильная четырехугольная пирамида. Длина ребра b
= 7 см, длина стороны основания a
= 4 см. Подставим заданные значения в формулу:
Мы показали расчеты площади одной боковой грани для правильной пирамиды. Соответственно. Чтобы найти площадь всей поверхности необходимо умножить результат на количество граней, то есть на 4.
Формула площади основания четырехугольной пирамиды напрямую зависит от того, какой четырехугольник лежит в основании. Если пирамида правильная, то площадь основания рассчитывается по формуле , если в основании лежит ромб, то потребуется вспомнить, как находится . Ели же в основании лежит прямоугольник, то найти его площадь будет довольно просто. Достаточно знать длины сторон основания. Рассмотрим пример расчета площади основания четырехугольной пирамиды.
Задача: Пусть дана пирамида, в основании которой лежит прямоугольник со сторонами a
= 3 см, b
= 5 см. К каждой из сторон из вершины пирамиды опущена апофема. h-a
=4 см,h-b
=6 см. Вершина пирамиды лежит на одной линии с точкой пересечения диагоналей. Найдите полную площадь пирамиды.
Формула площади четырехугольной пирамиды состоит из суммы площадей всех граней и площади основания. Для начала найдем площадь основания:
Теперь рассмотрим грани пирамиды. Они попарно одинаковы, потому что высота пирамиды пересекает точку пересечения диагоналей. То есть, в нашей пирамиде есть два треугольника с основанием a
и высотой h-a
, а также два треугольника с основанием b
и высотой h-b
. Теперь найдем площадь треугольника по известной формуле:
Теперь выполним пример расчета площади четырехугольной пирамиды. В нашей пирамиде с прямоугольником в основании, формула будет выглядеть так:
Треугольной пирамидой называется многогранник, в основании которого лежит правильный треугольник.
В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле . А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
где p – периметр основания, у которого все стороны равны b, a – апофема, опущенная из вершины к этому основанию. Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b
= 4 см. Апофема пирамиды равна a
= 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:
Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника. Для этого используется формула :
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a
= 6 см. Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: пусть дана правильная треугольная пирамида. Сторона основания равна b
= 4 см, апофема a
= 6 см. Найдите полную площадь пирамиды.
Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:
Подставляем данные в формулу:
Теперь найдем площадь основания:
Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды:
При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.
С понятием пирамида учащиеся сталкиваются еще задолго до изучения геометрии. Виной всему знаменитые великие египетские чудеса света. Поэтому, начиная изучение этого замечательного многогранника, большинство учеников уже наглядно представляют ее себе. Все вышеупомянутые достопримечательности имеют правильную форму. Что такое правильная пирамида , и какие свойства она имеет и пойдет речь дальше.
Вконтакте
Определение
Определений пирамиды можно встретить достаточно много. Начиная еще с древних времен, она пользовалась большой популярностью.
К примеру, Эвклид определял ее как телесную фигуру, состоящую из плоскостей, которые, начиная от одной, сходятся в определенной точке.
Герон представил более точную формулировку. Он настаивал на том, что это фигура, которая имеет основание и плоскости в виде треугольников, сходящиеся в одной точке.
Опираясь на современное толкование, пирамиду представляют, как пространственный многогранник, состоящий из определённого k-угольника и k плоских фигур треугольной формы, имеющую одну общую точку.
Разберемся более подробно, из каких элементов она состоит:
- k-угольник считают основой фигуры;
- фигуры 3-угольной формы выступают гранями боковой части;
- верхняя часть, из которой берут начало боковые элементы, называют вершиной;
- все отрезки, соединяющие вершину, называют рёбрами;
- если из вершины на плоскость фигуры опустить прямую под углом в 90 градусов, то её часть, заключенная во внутреннем пространстве — высота пирамиды;
- в любом боковом элементе к стороне нашего многогранника можно провести перпендикуляр, называемый апофемой.
Число рёбер вычисляется по формуле 2*k, где k – количество сторон k-угольника. Сколько граней у такого многогранника, как пирамида, можно определить посредством выражения k+1.
Важно! Пирамидой правильной формы называют стереометрическую фигуру, плоскость основы которой является k-угольник с равными сторонами.
Основные свойства
Правильная пирамида обладает множеством свойств, которые присущи только ей. Перечислим их:
- Основа – фигура правильной формы.
- Ребра пирамиды, ограничивающие боковые элементы, имеют равные числовые значения.
- Боковые элементы – равнобедренные треугольники.
- Основание высоты фигуры попадает в центр многоугольника, при этом он одновременно является центральной точкой вписанной и описанной .
- Все боковые рёбра наклонены к плоскости основы под одинаковым углом.
- Все боковые поверхности имеют одинаковый угол наклона по отношению к основе.
Благодаря всем перечисленным свойствам, выполнение вычислений элементов намного упрощается. Исходя из приведенных свойств, обращаем внимание на два признака:
- В том случае, когда многоугольник вписывается в окружность, боковые грани будут иметь с основой равные углы.
- При описании окружности около многоугольника, все рёбра пирамиды, исходящие из вершины, будут иметь равную длину и равные углы с основой.
В основе лежит квадрат
Правильная четырёхугольная пирамида – многогранник, у которого в основе лежит квадрат.
У неё четыре боковых грани, которые по своему виду являются равнобедренными.
На плоскости квадрат изображают , но основываются на всех свойствах правильного четырёхугольника.
К примеру, если необходимо связать сторону квадрата с его диагональю, то используют следующую формулу: диагональ равна произведению стороны квадрата на корень квадратный из двух.
В основе лежит правильный треугольник
Правильная треугольная пирамида – многогранник, в основании которого лежит правильный 3-угольник.
Если основание является правильным треугольником, а боковые рёбра равны ребрам основания, то такая фигура называется тетраэдром.
Все грани тетраэдра являются равносторонними 3-угольниками. В данном случае необходимо знать некоторые моменты и не тратить на них время при вычислениях:
- угол наклона ребер к любому основанию равен 60 градусов;
- величина всех внутренних граней также составляет 60 градусов;
- любая грань может выступить основанием;
- , проведённые внутри фигуры, это равные элементы.

Сечения многогранника
В любом многограннике различают несколько видов сечения плоскостью. Зачастую в школьном курсе геометрии работают с двумя:
- осевое;
- параллельное основе.
Осевое сечение получают при пересечении плоскостью многогранника, которая проходит через вершину, боковые рёбра и ось. В данном случае осью является высота, проведённая из вершины. Секущая плоскость ограничивается линиями пересечения со всеми гранями, в результате получаем треугольник.
Внимание! В правильной пирамиде осевым сечением является равнобедренный треугольник.
Если секущая плоскость проходит параллельно основанию, то в результате получаем второй вариант. В этом случае имеем в разрезе фигуру, подобную основе.
К примеру, если в основании лежит квадрат, то сечение параллельно основе также будет квадратом, только меньших размеров.
При решении задач при таком условии используют признаки и свойства подобия фигур, основанные на теореме Фалеса . В первую очередь необходимо определить коэффициент подобия.
Если плоскость проведена параллельно основе, и она отсекает верхнюю часть многогранника, то в нижней части получают правильную усеченную пирамиду. Тогда говорят, что основы усеченного многогранника являются подобными многоугольниками. В этом случае боковые грани являются равнобокими трапециями. Осевым сечением также является равнобокая .
Для того чтобы определить высоту усеченного многогранника, необходимо провести высоту в осевом сечении, то есть в трапеции.
Площади поверхностей
Основные геометрические задачи, которые приходится решать в школьном курсе геометрии, это нахождение площадей поверхности и объема у пирамиды.
Значение площади поверхности различают двух видов:
- площади боковых элементов;
- площади всей поверхности.
Из самого названия понятно, о чём идёт речь. Боковая поверхность включает в себя только боковые элементы. Из этого следует, что для ее нахождения необходимо просто сложить площади боковых плоскостей, то есть площади равнобедренных 3-угольников. Попробуем вывести формулу площади боковых элементов:
Из этого следует, что для ее нахождения необходимо просто сложить площади боковых плоскостей, то есть площади равнобедренных 3-угольников. Попробуем вывести формулу площади боковых элементов:
- Площадь равнобедренного 3-угольника равна Sтр=1/2(aL), где а – сторона основания, L – апофема.
- Количество боковых плоскостей зависит от вида k-го угольника в основании. К примеру, правильная четырехугольная пирамида имеет четыре боковые плоскости. Следовательно, необходимо сложить площади четырёх фигур Sбок=1/2(aL)+1/2(aL)+1/2(aL)+1/2(aL)=1/2*4а*L. Выражение упрощено таким способом потому, что значение 4а=Росн, где Росн – периметр основы. А выражение 1/2*Росн является её полупериметром.
- Итак, делаем вывод, что площадь боковых элементов правильной пирамиды равна произведению полупериметра основания на апофему: Sбок=Росн*L.
Площадь полной поверхности пирамиды состоит из суммы площадей боковых плоскостей и основания: Sп.п.= Sбок+Sосн.
Что касается площади основания, то здесь формула используется соответственно виду многоугольника.
Объем правильной пирамиды равен произведению площади плоскости основания на высоту, разделенную на три: V=1/3*Sосн*Н, где Н – высота многогранника.
Что такое правильная пирамиды в геометрии
Свойства правильной четырехугольной пирамиды
Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.
Что собой представляет пирамида?
Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой. Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
Два важных элемента любой пирамиды — это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.
Поверхность пирамиды
Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.
Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры — это сумма площадей каждой ее стороны.
Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.
Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.
Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.
Площадь боковой поверхности четырехугольной правильной пирамиды
Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника.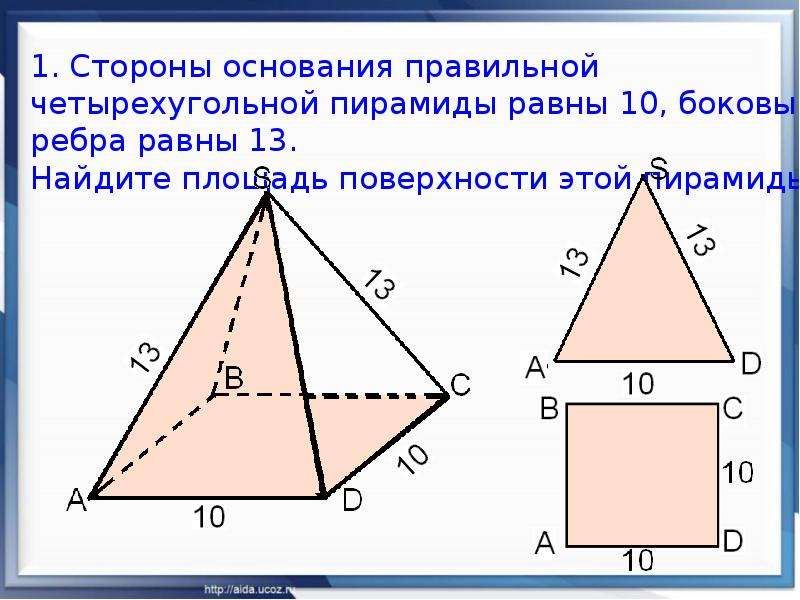 Из курса геометрии известно, что треугольника площадь S t равна произведению основания на высоту, которое следует поделить пополам. То есть:
Из курса геометрии известно, что треугольника площадь S t равна произведению основания на высоту, которое следует поделить пополам. То есть:
Где h b — высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь S b поверхности боковой для рассматриваемой пирамиды:
S b = 4*S t = 2*h b *a.
Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы h b для двух случаев:
- когда известна длина бокового ребра;
- когда известна высота пирамиды.
Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема h b определиться по формуле:
h b = √(L 2 — a 2 /4).
Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.
Если известна высота h пирамиды, тогда апотему h b можно рассчитать так:
h b = √(h 2 + a 2 /4).
Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой h b .
Покажем, как применять эти формулы, решив две интересные задачи.
Задача с известной площадью поверхности
Известно, что площадь боковой поверхности четырехугольной равна 108 см 2 . Необходимо вычислить значение длины ее апотемы h b , если высота пирамиды равна 7 см.
Запишем формулу площади S b поверхности боковой через высоту. Имеем:
S b = 2*√(h 2 + a 2 /4) *a.
Здесь мы просто подставили соответствующую формулу апотемы в выражение для S b . Возведем обе части равенства в квадрат:
S b 2 = 4*a 2 *h 2 + a 4 .
Чтобы найти значение a, сделаем замену переменных:
t 2 + 4*h 2 *t — S b 2 = 0.
Подставляем теперь известные значения и решаем квадратное уравнение:
t 2 + 196*t — 11664 = 0.
Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:
a = √t = √47,8355 ≈ 6,916 см.
Чтобы получить длину апотемы, достаточно воспользоваться формулой:
h b = √(h 2 + a 2 /4) = √(7 2 + 6,916 2 /4) ≈ 7,808 см.
Боковая поверхность пирамиды Хеопса
Определим значение площади поверхности боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для S b , получим:
S b = 2*√(h 2 + a 2 /4) *a = 2*√(146,5 2 +230,363 2 /4)*230,363 ≈ 85860 м 2 .
Найденное значение немного больше площади 17 футбольных полей.
Правильная пирамида — урок. Геометрия, 10 класс.
Пирамида, основанием которой является правильный многоугольник, а вершина которой проецируется в центр основания, называется правильной пирамидой.
Боковые грани правильной пирамиды — равные равнобедренные треугольники.
Высота боковой грани правильной пирамиды называется апофемой.
Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром.
Все грани тетраэдра — равные равносторонние треугольники.
В средней школе нужно уметь решать задачи, где дана:
— правильная треугольная пирамида;
— правильная четырёхугольная пирамида;
— правильная шестиугольная пирамида.
Правильная треугольная пирамида
Основание правильной треугольной пирамиды — равносторонний треугольник.
Вершина пирамиды проецируется в точку пересечения медиан.
Запомни:
\(BN:NK = 2:1\),
\(KD\) — апофема,
∢ \(NKD\) и ∢ \(NLD\) — двугранные углы при основании пирамиды,
∢ \(DCN\) и ∢ \(DBN\) — углы между боковым ребром и плоскостью основания пирамиды.
Правильная четырёхугольная пирамида
Основание правильной четырёхугольной пирамиды — квадрат.
Вершина пирамиды проецируется в точку пересечения диагоналей основания (квадрата).
\(ML\) — апофема,
∢ \(MLO\) — двугранный угол при основании пирамиды,
∢ \(MCO\) — угол между боковым ребром и плоскостью основания пирамиды.
Правильная шестиугольная пирамида
Основание правильной шестиугольной пирамиды — правильный шестиугольник.
Вершина пирамиды проецируется в точку пересечения диагоналей основания (шестиугольника).
\(SE = h\) — апофема,
∢ \(OES\) — двугранный угол при основании пирамиды.
Для вычисления площади боковой поверхности правильной пирамиды существуют две формулы:
Sб=12Pоснования⋅hиSб=Sоснованияcosϕ, где \(P\) — периметр основания, \(h\) — апофема, ϕ — двугранный угол при основании.
Объём пирамиды \(V =\) 13Sосн⋅H, где \(H\) — высота пирамиды.
Обрати внимание!
Не путай \(h\) — апофему с \(H\) — высотой пирамиды!
Площадь полной поверхности четырехугольной пирамиды формула. Как найти площадь боковой поверхности пирамиды. В основании – правильный многоугольник
– это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.
Если в основании лежит квадрат, то пирамиду называется четырехугольной , если треугольник – то треугольной . Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана пирамида с основанием ABCDE
и вершиной F
. AB
=BC
=CD
=DE
=EA
=3 см. Апофема a
= 5 см. Найти площадь боковой поверхности пирамиды.
Найдем периметр. Так как все грани основания равны, то периметр пятиугольника будет равен:
Теперь можно найти боковую площадь пирамиды:
Площадь правильной треугольной пирамиды
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Дана пирамида с апофемой a
= 4 см и гранью основания b
= 2 см. Найдите площадь боковой поверхности пирамиды.
Для начала находим площадь одной из боковых граней. В данном случае она будет:
Подставляем значения в формулу:
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:
Площадь усеченной пирамиды
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
Определение.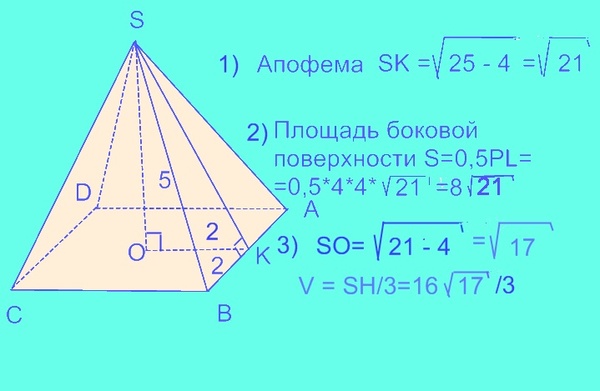 Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n , где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол .
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.Треугольной пирамидой называется многогранник, в основании которого лежит правильный треугольник.
В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле . А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
где p – периметр основания, у которого все стороны равны b, a – апофема, опущенная из вершины к этому основанию. Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b
= 4 см. Апофема пирамиды равна a
= 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:
Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника.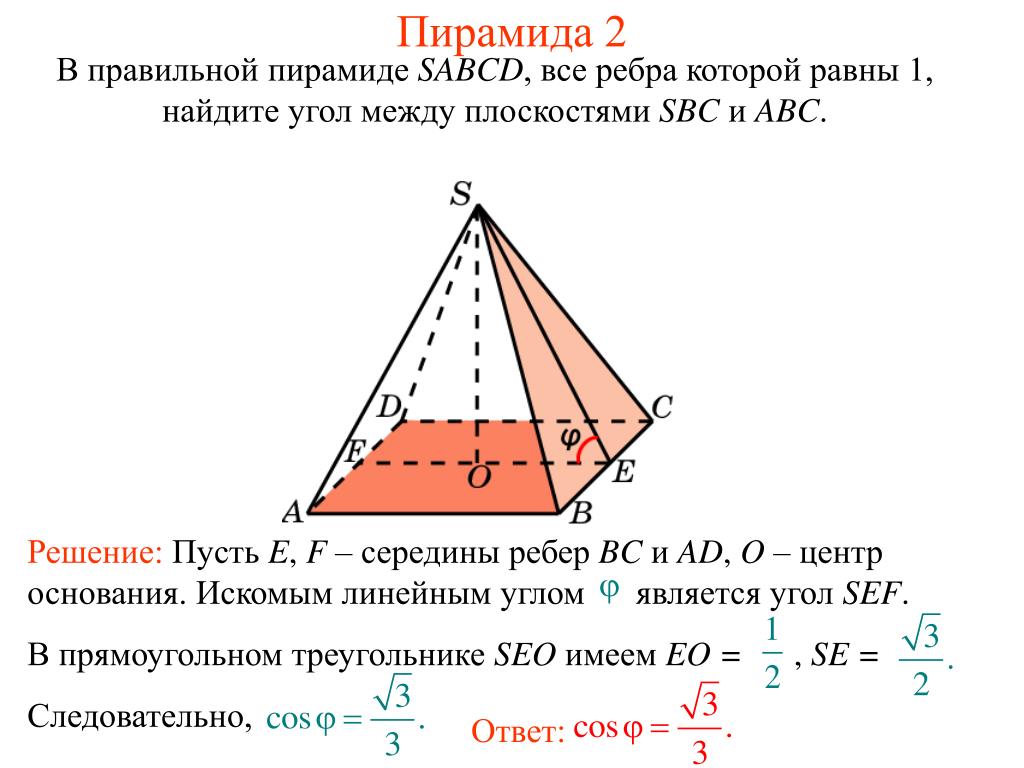 Для этого используется формула :
Для этого используется формула :
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a
= 6 см. Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: пусть дана правильная треугольная пирамида. Сторона основания равна b
= 4 см, апофема a
= 6 см. Найдите полную площадь пирамиды.
Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:
Подставляем данные в формулу:
Теперь найдем площадь основания:
Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды:
При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.
Типичными геометрическими задачами на плоскости и в трехмерном пространстве являются проблемы определения площадей поверхностей разных фигур. В данной статье приведем формулу площади боковой поверхности правильной пирамиды четырехугольной.
Что собой представляет пирамида?
Приведем строгое геометрическое определение пирамиды. Предположим, что имеется некоторый многоугольник с n сторонами и с n углами. Выберем произвольную точку пространства, которая не будет находиться в плоскости указанного n-угольника, и соединим ее с каждой вершиной многоугольника. Мы получим фигуру, имеющую некоторый объем, которая называется n-угольной пирамидой.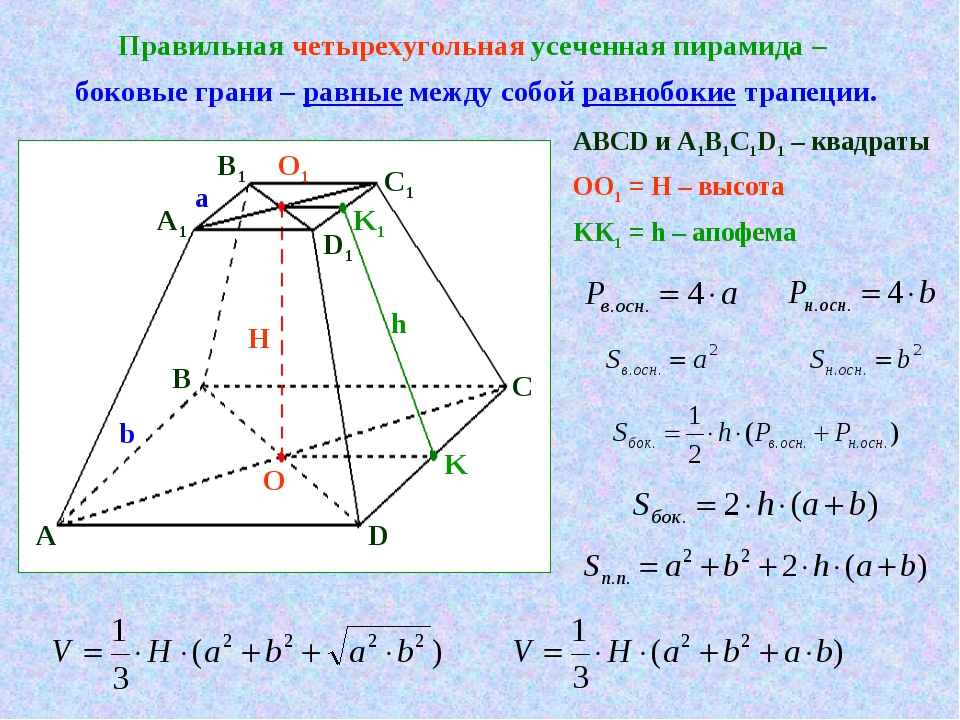 Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
Для примера покажем на рисунке ниже, как выглядит пятиугольная пирамида.
Два важных элемента любой пирамиды — это ее основание (n-угольник) и вершина. Эти элементы соединены друг с другом n треугольниками, которые в общем случае не равны друг другу. Перпендикуляр, опущенный из вершины к основанию, называется высотой фигуры. Если он пересекает основание в геометрическом центре (совпадает с центром масс многоугольника), то такую пирамиду называют прямой. Если помимо этого условия основание является правильным многоугольником, то и вся пирамида называется правильной. Рисунок ниже показывает, как выглядят правильные пирамиды с треугольным, четырехугольным, пятиугольным и шестиугольным основаниями.
Поверхность пирамиды
Прежде чем переходить к вопросу о площади боковой поверхности правильной пирамиды четырехугольной, следует подробнее остановиться на понятии самой поверхности.
Как было сказано выше и показано на рисунках, любая пирамида образована набором граней или сторон. Одна сторона является основанием, и n сторон представляют собой треугольники. Поверхность всей фигуры — это сумма площадей каждой ее стороны.
Поверхность удобно изучать на примере развертки фигуры. Развертка для правильной четырехугольной пирамиды приведена на рисунки ниже.
Видим, что площадь ее поверхности равна сумме четырех площадей одинаковых равнобедренных треугольников и площади квадрата.
Общую площадь всех треугольников, которые образуют боковые стороны фигуры, принято называть площадью боковой поверхности. Далее покажем, как ее рассчитать для четырехугольной пирамиды правильной.
Площадь боковой поверхности четырехугольной правильной пирамиды
Чтобы вычислить площадь боковой поверхности указанной фигуры, снова обратимся к приведенной выше развертке. Предположим, что нам известна сторона квадратного основания. Обозначим ее символом a. Видно, что каждый из четырех одинаковых треугольников, имеет основание длиной a. Чтобы вычислить их суммарную площадь, необходимо знать эту величину для одного треугольника. Из курса геометрии известно, что треугольника площадь S t равна произведению основания на высоту, которое следует поделить пополам. То есть:
Из курса геометрии известно, что треугольника площадь S t равна произведению основания на высоту, которое следует поделить пополам. То есть:
Где h b — высота равнобедренного треугольника, проведенная к основанию a. Для пирамиды эта высота является апотемой. Теперь остается умножить полученное выражение на 4, чтобы получить площадь S b поверхности боковой для рассматриваемой пирамиды:
S b = 4*S t = 2*h b *a.
Эта формула содержит два параметра: апотему и сторону основания. Если последняя в большинстве условий задач известна, то первую приходится вычислять, зная другие величины. Приведем формулы для расчета апотемы h b для двух случаев:
- когда известна длина бокового ребра;
- когда известна высота пирамиды.
Если обозначить длину ребра бокового (сторона равнобедренного треугольника) символом L, тогда апотема h b определиться по формуле:
h b = √(L 2 — a 2 /4).
Это выражения является результатом применения теоремы Пифагора для треугольника боковой поверхности.
Если известна высота h пирамиды, тогда апотему h b можно рассчитать так:
h b = √(h 2 + a 2 /4).
Получить это выражение также не сложно, если рассмотреть внутри пирамиды прямоугольный треугольник, образованный катетами h и a/2 и гипотенузой h b .
Покажем, как применять эти формулы, решив две интересные задачи.
Задача с известной площадью поверхности
Известно, что площадь боковой поверхности четырехугольной равна 108 см 2 . Необходимо вычислить значение длины ее апотемы h b , если высота пирамиды равна 7 см.
Запишем формулу площади S b поверхности боковой через высоту. Имеем:
S b = 2*√(h 2 + a 2 /4) *a.
Здесь мы просто подставили соответствующую формулу апотемы в выражение для S b . Возведем обе части равенства в квадрат:
S b 2 = 4*a 2 *h 2 + a 4 .
Чтобы найти значение a, сделаем замену переменных:
t 2 + 4*h 2 *t — S b 2 = 0.
Подставляем теперь известные значения и решаем квадратное уравнение:
t 2 + 196*t — 11664 = 0.
Мы выписали только положительный корень этого уравнения. Тогда стороны основания пирамиды будет равна:
a = √t = √47,8355 ≈ 6,916 см.
Чтобы получить длину апотемы, достаточно воспользоваться формулой:
h b = √(h 2 + a 2 /4) = √(7 2 + 6,916 2 /4) ≈ 7,808 см.
Боковая поверхность пирамиды Хеопса
Определим значение боковой для самой большой египетской пирамиды. Известно, что в ее основании лежит квадрат с длиной стороны 230,363 метра. Высота сооружения изначально составляла 146,5 метра. Подставим эти цифры в соответствующую формулу для S b , получим:
S b = 2*√(h 2 + a 2 /4) *a = 2*√(146,5 2 +230,363 2 /4)*230,363 ≈ 85860 м 2 .
Найденное значение немного больше площади 17 футбольных полей.
Какую фигуру мы называем пирамидой? Во-первых, это многогранник. Во-вторых, в основании этого многогранника расположен произвольный многоугольник, а стороны пирамиды (боковые грани) обязательно имеют форму треугольников, сходящихся в одной общей вершине. Вот теперь, разобравшись с термином, выясним, как найти площадь поверхности пирамиды.
Понятно, что площадь поверхности такого геометрического тела составится из суммы площадей основания и всей его боковой поверхности.
Вычисление площади основания пирамиды
Выбор расчетной формулы зависит от формы лежащего в основании нашей пирамиды многоугольника. Он может быть правильным, то есть со сторонами одинаковой длины, или неправильным. Рассмотрим оба варианта.
В основании – правильный многоугольник
Из школьного курса известно:
- площадь квадрата будет равна длине его стороны, возведенной в квадрат;
- площадь равностороннего треугольника равна квадрату его стороны, деленному на 4 и умноженному на квадратный корень из трех.

Но существует и общая формула, для расчета площади любого правильного многоугольника (Sn): надо умножить значение периметра этого многоугольника (Р) на радиус вписанной в него окружности (r), а затем разделить полученный результат на два: Sn=1/2P*r.
В основании – неправильный многоугольник
Схема нахождения его площади заключается в том, чтобы сначала разбить весь многоугольник на треугольники, вычислить площадь каждого из них по формуле: 1/2a*h (где а – основание треугольника, h – опущенная на это основание высота), сложить все результаты.
Площадь боковой поверхности пирамиды
Теперь рассчитаем площадь боковой поверхности пирамиды, т.е. сумму площадей всех ее боковых сторон. Здесь также возможны 2 варианта.
- Пусть у нас имеется произвольная пирамида, т.е. такая, в основании которой – неправильный многоугольник. Тогда следует вычислить отдельно площадь каждой грани и сложить результаты. Так как боковыми сторонами пирамиды по определению могут быть только треугольники, то расчет идет по упомянутой выше формуле: S=1/2a*h.
- Пусть наша пирамида – правильная, т.е. в ее основании лежит правильный многоугольник, и проекция вершины пирамиды оказывается в его центре. Тогда для вычисления площади боковой поверхности (Sб) достаточно найти половину произведения периметра многоугольника-основания (Р) на высоту (h) боковой стороны (одинаковую для всех граней): Sб=1/2 Р*h. Периметр многоугольника определяется сложением длин всех его сторон.
Полная площадь поверхности правильной пирамиды найдется суммированием площади ее основания с площадью всей боковой поверхности.
Примеры
Для примера вычислим алгебраически площади поверхности нескольких пирамид.
Площадь поверхности треугольной пирамиды
В основании такой пирамиды – треугольник. По формуле Sо=1/2a*h находим площадь основания. Эту же формулу применяем для нахождения площади каждой грани пирамиды, также имеющей треугольную форму, и получаем 3 площади: S1, S2 и S3. Площадь боковой поверхности пирамиды является суммой всех площадей: Sб= S1+ S2+ S3. Сложив площади боковых сторон и основания, получим полную площадь поверхности искомой пирамиды: Sп= Sо+ Sб.
Площадь боковой поверхности пирамиды является суммой всех площадей: Sб= S1+ S2+ S3. Сложив площади боковых сторон и основания, получим полную площадь поверхности искомой пирамиды: Sп= Sо+ Sб.
Площадь поверхности четырехугольной пирамиды
Площадь боковой поверхности — это сумма 4-ех слагаемых: Sб= S1+ S2+ S3+ S4, каждое из которых вычислено по формуле площади треугольника. А площадь основания придется искать, в зависимости от формы четырехугольника — правильного или неправильного. Площадь полной поверхности пирамиды снова получится путем сложения площади основания и полной площади поверхности заданной пирамиды.
Периметр правильной четырехугольной пирамиды формула. Площадь шестиугольной пирамиды. Свойства правильной пирамиды
При подготовке к ЕГЭ по математике учащимся приходится систематизировать знания по алгебре и геометрии. Хочется объединить все известные сведения, например, о том, как вычислить площадь пирамиды. Причем начиная от основания и боковых граней до площади всей поверхности. Если с боковыми гранями ситуация ясна, так как они являются треугольниками, то основание всегда разное.
Как быть при нахождении площади основания пирамиды?
Оно может быть совершенно любой фигурой: от произвольного треугольника до n-угольника. И это основание, кроме различия в количестве углов, может являться правильной фигурой или неправильной. В интересующих школьников заданиях по ЕГЭ встречаются только задания с правильными фигурами в основании. Поэтому речь будет идти только о них.
Правильный треугольник
То есть равносторонний. Тот, у которого все стороны равны и обозначены буквой «а». В этом случае площадь основания пирамиды вычисляется по формуле:
S = (а 2 * √3) / 4.
Квадрат
Формула для вычисления его площади самая простая, здесь «а» — снова сторона:
Произвольный правильный n-угольник
У стороны многоугольника то же обозначение. Для количества углов используется латинская буква n.
S = (n * а 2) / (4 * tg (180º/n)).
Как поступить при вычислении площади боковой и полной поверхности?
Поскольку в основании лежит правильная фигура, то все грани пирамиды оказываются равными. Причем каждая из них является равнобедренным треугольником, поскольку боковые ребра равны. Тогда для того, чтобы вычислить боковую площадь пирамиды, потребуется формула, состоящая из суммы одинаковых одночленов. Число слагаемых определяется количеством сторон основания.
Площадь равнобедренного треугольника вычисляется по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофемой. Ее обозначение — «А». Общая формула для площади боковой поверхности выглядит так:
S = ½ Р*А, где Р — периметр основания пирамиды.
Бывают ситуации, когда не известны стороны основания, но даны боковые ребра (в) и плоский угол при ее вершине (α). Тогда полагается использовать такую формулу, чтобы вычислить боковую площадь пирамиды:
S = n/2 * в 2 sin α.
Задача № 1
Условие. Найти общую площадь пирамиды, если в его основании лежит со стороной 4 см, а апофема имеет значение √3 см.
Решение. Его начинать нужно с расчета периметра основания. Поскольку это правильный треугольник, то Р = 3*4 = 12 см. Поскольку апофема известна, то можно сразу вычислить площадь всей боковой поверхности: ½*12*√3 = 6√3 см 2 .
Для треугольника в основании получится такое значение площади: (4 2 *√3) / 4 = 4√3 см 2 .
Для определения всей площади потребуется сложить два получившихся значения: 6√3 + 4√3 = 10√3 см 2 .
Ответ. 10√3 см 2 .
Задача № 2
Условие . Имеется правильная четырехугольная пирамида. Длина стороны основания равна 7 мм, боковое ребро — 16 мм. Необходимо узнать площадь ее поверхности.
Решение. Поскольку многогранник — четырехугольный и правильный, то в его основании лежит квадрат. Узнав площади основания и боковых граней, удастся сосчитать площадь пирамиды. Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Формула для квадрата дана выше. А у боковых граней известны все стороны треугольника. Поэтому можно использовать формулу Герона для вычисления их площадей.
Первые расчеты просты и приводят к такому числу: 49 мм 2 . Для второго значения потребуется вычислить полупериметр: (7 + 16*2):2 = 19,5 мм. Теперь можно вычислять площадь равнобедренного треугольника: √(19,5*(19,5-7)*(19,5-16) 2) = √2985,9375 = 54,644 мм 2 . Таких треугольников всего четыре, поэтому при подсчете итогового числа потребуется его умножить на 4.
Получается: 49 + 4*54,644 = 267,576 мм 2 .
Ответ . Искомое значение 267,576 мм 2 .
Задача № 3
Условие . У правильной четырехугольной пирамиды необходимо вычислить площадь. В ней известна сторона квадрата — 6 см и высота — 4 см.
Решение. Проще всего воспользоваться формулой с произведением периметра и апофемы. Первое значение найти просто. Второе немного сложнее.
Придется вспомнить теорему Пифагора и рассмотреть Он образован высотой пирамиды и апофемой, которая является гипотенузой. Второй катет равен половине стороны квадрата, поскольку высота многогранника падает в его середину.
Искомая апофема (гипотенуза прямоугольного треугольника) равна √(3 2 + 4 2) = 5 (см).
Теперь можно вычислять искомую величину: ½*(4*6)*5+6 2 = 96 (см 2).
Ответ. 96 см 2 .
Задача № 4
Условие. Дана правильная Стороны ее основания равны 22 мм, боковые ребра — 61 мм. Чему равна площадь боковой поверхности этого многогранника?
Решение. Рассуждения в ней такие же, как были описаны в задаче №2. Только там была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом вычисляется площадь основания по указанной выше формуле: (6*22 2) / (4*tg (180º/6)) = 726/(tg30º) = 726√3 см 2 .
Теперь необходимо узнать полупериметр равнобедренного треугольника, который является боковой гранью. (22+61*2):2 = 72 см. Осталось по формуле Герона сосчитать площадь каждого такого треугольника, а потом умножить ее на шесть и сложить с той, что получилась для основания.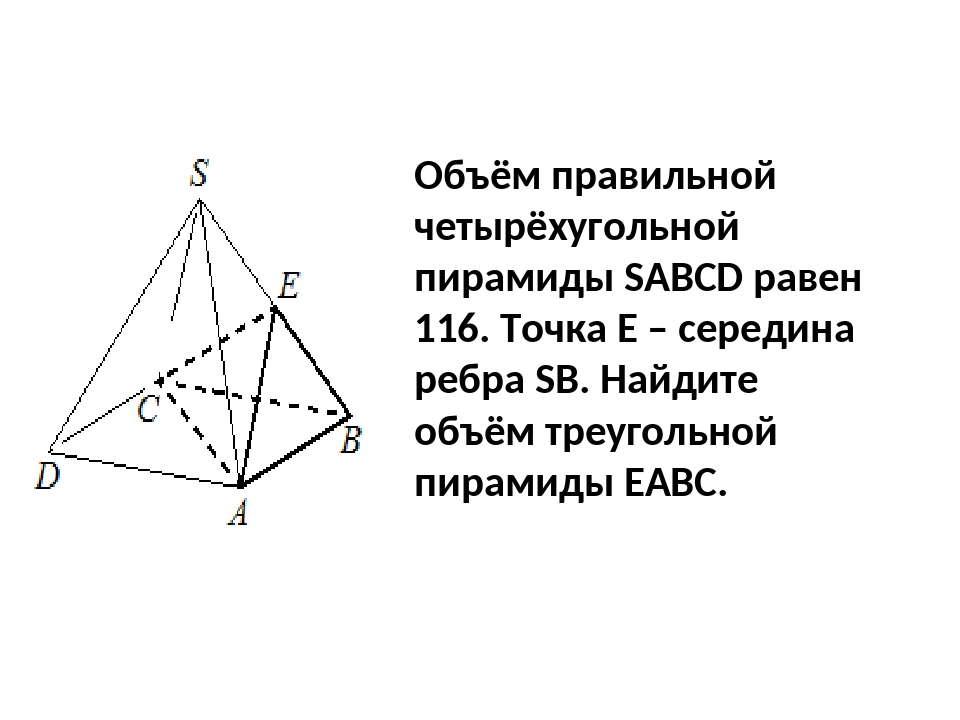
Расчеты по формуле Герона: √(72*(72-22)*(72-61) 2)=√435600=660 см 2 . Вычисления, которые дадут площадь боковой поверхности: 660*6 = 3960 см 2 . Осталось их сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2 .
Ответ. Основания — 726√3 см 2 , боковой поверхности — 3960 см 2 , вся площадь — 5217 см 2 .
Треугольной пирамидой называется многогранник, в основании которого лежит правильный треугольник.
В такой пирамиде грани основания и ребра боковых сторон равны между собой. Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Найти площадь боковой поверхности правильной пирамиды можно по формуле . А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды:
где p – периметр основания, у которого все стороны равны b, a – апофема, опущенная из вершины к этому основанию. Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Пусть дана правильная пирамида. Сторона треугольника, лежащего в основании равна b
= 4 см. Апофема пирамиды равна a
= 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задачи мы знаем длины всех необходимых элементов, найдем периметр. Помним, что в правильном треугольнике все стороны равны, а, следовательно, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем рассчитывать площадь боковой поверхности:
Чтобы применить формулу площади треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника. Для этого используется формула :
Формула площади основания треугольной пирамиды может быть и другой. Допускается применение любого расчета параметров для заданной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правильной пирамиде сторона лежащего в основании треугольника равняется a
= 6 см. Рассчитайте площадь основания.
Рассчитайте площадь основания.
Для вычисления нам требуется только длина стороны правильного треугольника, располагающегося в основании пирамиды. Подставим данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить площадь боковой поверхности и основания.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: пусть дана правильная треугольная пирамида. Сторона основания равна b
= 4 см, апофема a
= 6 см. Найдите полную площадь пирамиды.
Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:
Подставляем данные в формулу:
Теперь найдем площадь основания:
Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды:
При расчете площади правильной пирамиды стоит не забывать о том, что в основании лежит правильный треугольник и многие элементы этого многогранника равны между собой.
Пирамида, в основании которой лежит правильный шестиугольник, а боковые стороны образуются правильными треугольниками, называется шестиугольной .
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угля пирамиды также равны между собой;
- Треугольники, образующие боковые стороны одинаковы, соответственно, у них одинаковые площади, стороны и высоты.
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P
– периметр основания, a
– длина апофемы пирамиды. В большинстве случаев можно рассчитать боковую площадь по этой формуле, однако иногда можно воспользоваться и другим методом. Так как боковые грани пирамиды образованы равными треугольниками, можно найти площадь одного треугольника, а потом умножить его на количество боковых сторон. В шестиугольной пирамиде их 6. Но этот способ можно применять и при расчете . Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.
Рассмотрим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофема равна a
= 7 см, сторона основания b
= 3 см. Рассчитайте площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Так как пирамида правильная – в ее основании лежит правильный шестиугольник. Значит, все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь можем легко найти площадь боковой поверхности, подставив найденное значение в основную формулу:
Также немаловажным моментом является поиск площади основания. Формула площади основания шестиугольной пирамиды выводится из свойств правильного шестиугольника:
Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условия из прошлого примера.Из них мы знаем, что сторона основания b
= 3 см. Подставим данные в формулу:
Формула площади шестиугольной пирамиды представляет собой сумму площади основания и боковой развертки:
Рассмотрим пример расчета площади шестиугольной пирамиды.
Пусть дана пирамида, в основании которой лежит правильный шестиугольник со стороной b
= 4 см. Апофема заданного многогранника равна a
= 6 см. Найдите полную площадь.
Мы знаем, что полная площадь состоит из площадей основания и боковой развертки. Поэтому для начала найдем их. Рассчитаем периметр:
Теперь найдем площадь боковой поверхности:
Далее рассчитываем площадь основания, в котором лежит правильный шестиугольник:
Теперь можем сложить получившиеся результаты:
Определение. Боковая грань — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольника).
Определение. Боковые ребра — это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.
Определение. Высота пирамиды — это перпендикуляр, опущенный из вершины на основание пирамиды.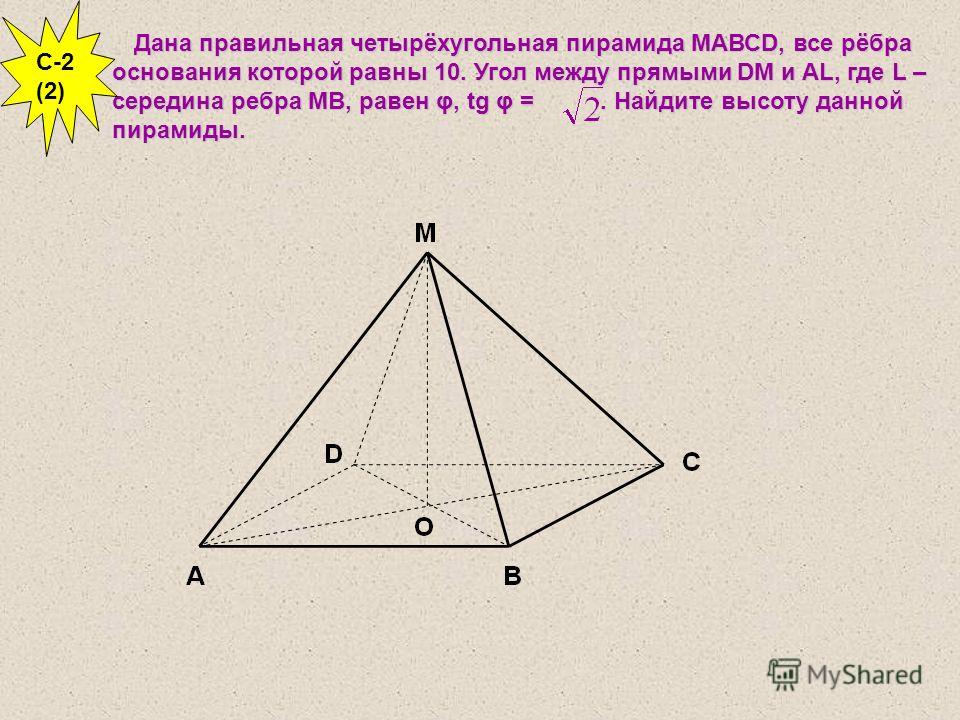
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опущенный из вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это сечение пирамиды плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правильная пирамида — это пирамида, в которой основой является правильный многоугольник, а высота опускается в центр основания.
Объём и площадь поверхности пирамиды
Формула. Объём пирамиды через площадь основы и высоту:
Свойства пирамиды
Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.
Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина пирамиды проектируется в ее центр.
Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.
Свойства правильной пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые ребра наклонены под одинаковыми углами к основанию.
4. Апофемы всех боковых граней равны.
5. Площади всех боковых граней равны.
6. Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центром описанной сферы будет точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиду можно вписать сферу. Центром вписанной сферы будет точка пересечения биссектрис, исходящие из угла между ребром и основанием.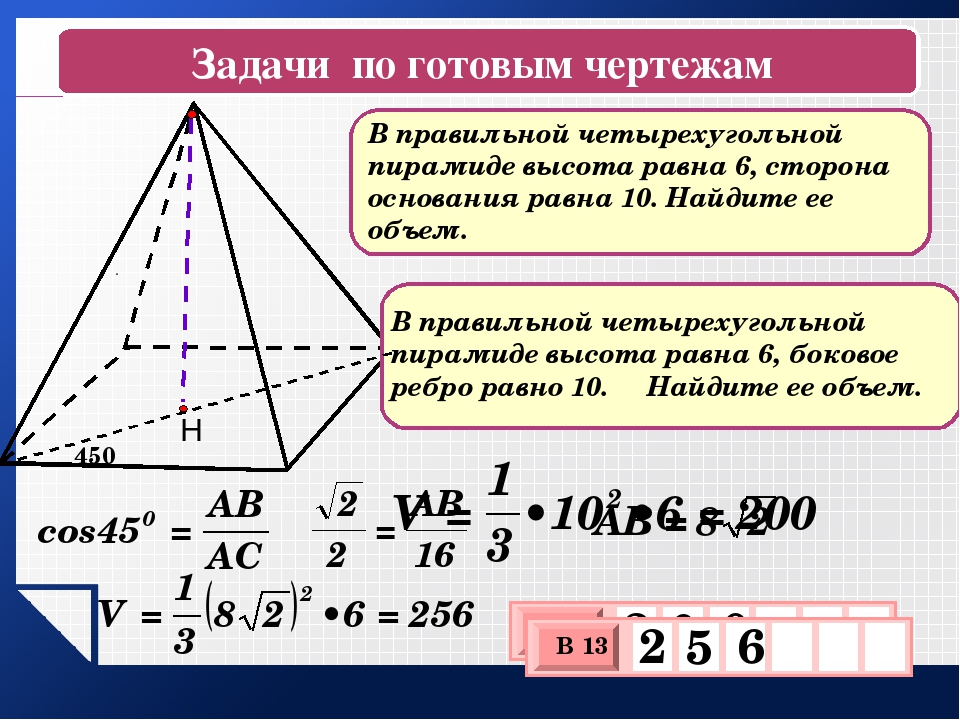
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов при вершине равна π или наоборот, один угол равен π/n , где n — это количество углов в основании пирамиды.
Связь пирамиды со сферой
Вокруг пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многогранник вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы будет точка пересечения плоскостей, проходящих перпендикулярно через середины боковых ребер пирамиды.
Вокруг любой треугольной или правильной пирамиды всегда можно описать сферу.
В пирамиду можно вписать сферу, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Связь пирамиды с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно вписать в пирамиду, если апофемы пирамиды равны между собой.
Конус называется описанным вокруг пирамиды, если их вершины совпадают, а основание конуса описана вокруг основания пирамиды.
Конус можно описать вокруг пирамиды если, все боковые ребра пирамиды равны между собой.
Связь пирамиды с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одной основе цилиндра, а основание пирамиды вписано в другую основу цилиндра.
Цилиндр можно описать вокруг пирамиды если вокруг основания пирамиды можно описать окружность.
Определение. Усеченная пирамида (пирамидальная призма) — это многогранник, который находится между основанием пирамиды и плоскостью сечения, параллельной основанию. Таким образом пирамида имеет большую основу и меньшую основу, которая подобна большей. Боковые грани представляют собой трапеции. Определение. Треугольная пирамида (четырехгранник) — это пирамида в которой три грани и основание являются произвольными треугольниками.
В четырехгранник четыре грани и четыре вершины и шесть ребер, где любые два ребра не имеют общих вершин но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, которые образуют трехгранный угол .
Отрезок, соединяющий вершину четырехгранника с центром противоположной грани называется медианой четырехгранника (GM).
Бимедианой называется отрезок, соединяющий середины противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы четырехгранника пересекаются в одной точке (S). При этом бимедианы делятся пополам, а медианы в отношении 3:1 начиная с вершины.
Определение. Наклонная пирамида — это пирамида в которой одно из ребер образует тупой угол (β) с основанием.Определение. Прямоугольная пирамида — это пирамида в которой одна из боковых граней перпендикулярна к основанию.Определение. Остроугольная пирамида — это пирамида в которой апофема больше половины длины стороны основания.
Определение. Тупоугольная пирамида — это пирамида в которой апофема меньше половины длины стороны основания.
Определение. Правильный тетраэдр — четырехгранник у которого все четыре грани — равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.
Определение. Прямоугольный тетраэдр называется четырехгранник у которого прямой угол между тремя ребрами при вершине (ребра перпендикулярны). Три грани образуют прямоугольный трехгранный угол и грани являются прямоугольными треугольниками, а основа произвольным треугольником. Апофема любой грани равна половине стороны основы, на которую падает апофема.
Определение. Равногранный тетраэдр называется четырехгранник у которого боковые грани равны между собой, а основание — правильный треугольник. У такого тетраэдра грани это равнобедренные треугольники.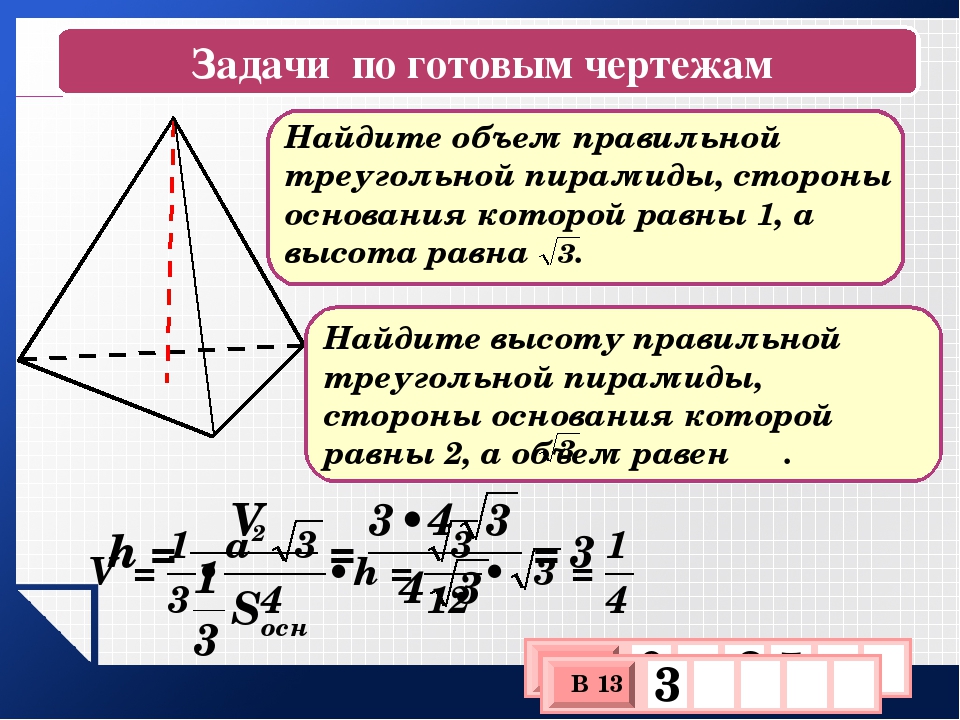
Определение. Ортоцентричный тетраэдр называется четырехгранник у которого все высоты (перпендикуляры), что опущены с вершины до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида называется многогранник у которого основой является звезда.
Определение. Бипирамида — многогранник, состоящий из двух различных пирамид (также могут быть срезаны пирамиды), имеющих общую основу, а вершины лежат по разные стороны от плоскости основания.Четырехугольная пирамида в задаче C2
Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.
Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же — тетраэдр). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.
Для начала вспомним определение:
Правильная пирамида — это такая пирамида, у которой:
- В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;
- Высота, проведенная к основанию, проходит через его центр.
В частности, основанием четырехугольной пирамиды является квадрат. Прямо как у Хеопса, только чуть поменьше.
Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.
Вершины четырехугольной пирамиды
Итак, пусть дана правильная четырехугольная пирамида SABCD,где S — вершина, основание ABCD — квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:
Имеем:
Вводим систему координат с началом в точке A:
- Ось OX направлена параллельно ребру AB;
- Ось OY — параллельно AD. Поскольку ABCD — квадрат, AB ⊥ AD;
- Наконец, ось OZ направим вверх, перпендикулярно плоскости ABCD.
Теперь считаем координаты. Дополнительное построение: SH — высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки A, B, C и D лежат в плоскости OXY, их координата z = 0. Имеем:
- A = (0; 0; 0) — совпадает с началом координат;
- B = (1; 0; 0) — шаг на 1 по оси OX от начала координат;
- C = (1; 1; 0) — шаг на 1 по оси OX и на 1 по оси OY;
- D = (0; 1; 0) — шаг только по оси OY.
- H = (0,5; 0,5; 0) — центр квадрата, середина отрезка AC.
Осталось найти координаты точки S. Заметим, что координаты x и y точек S и H совпадают, поскольку они лежат на прямой, параллельной оси OZ. Осталось найти координату zдля точки S.
Рассмотрим треугольники ASH и ABH:
- AS = AB = 1 по условию;
- Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;
- Сторона AH — общая.
Следовательно, прямоугольные треугольники ASH и ABHравны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD.Но BD — диагональ квадрата со стороной 1. Поэтому имеем:
Итого координаты точки S:
В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:
Что делать, когда ребра разные
А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник AHS:
Треугольник AHS —прямоугольный, причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD.Катет AH легко считается: AH = 0,5 · AC. Оставшийся катет SH найдем по теореме Пифагора. Это и будет координата zдля точки S.
Задача.
Дана правильная четырехугольная пирамида SABCD, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S.
Координаты x и y этой точки мы уже знаем: x = y = 0,5. Это следует из двух фактов:
- Проекция точки S на плоскость OXY — это точка H;
- Одновременно точка H — центр квадрата ABCD, все стороны которого равны 1.
Осталось найти координату точки S. Рассмотрим треугольник AHS. Он прямоугольный, причем гипотенуза AS = BS = 3,катет AH — половина диагонали. Для дальнейших вычислений нам потребуется его длина:
Теорема Пифагора для треугольника AHS:AH 2 + SH 2 = AS2. Имеем:
Итак, координаты точки S:
Смотрите также:
- Четырехугольная пирамида: как найти координаты вершин
- Введение системы координат
- Тест к уроку «Что такое логарифм» (средний)
- Основное тригонометрическое тождество
- Тригонометрические функции
- Тест по задачам B14: средний уровень, 2 вариант
Математическая задача: четырехугольная пирамида — математическая задача (6354), алгебра
Дана правильная четырехугольная пирамида с квадратным основанием. Высота корпуса 30 см, объем V = 1000 см³. Вычислите его сторону a и площадь поверхности.Правильный ответ:
Чтобы решить эту математическую задачу со словами, вам понадобятся следующие знания:
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2
Сопутствующие математические задачи и вопросы:
- Четырехугольная пирамида
Базовая длина правильной четырехугольной пирамиды составляет 6 см, а длина бокового края — 9 см.Вычислите его объем и площадь поверхности. - Четырехугольная пирамида
В правильной четырехугольной пирамиде высота составляет 6,5 см, а угол между основанием и боковой стенкой составляет 42 °. Рассчитайте площадь поверхности и объем тела. Округлите вычисления до 1 знака после запятой.
Рассчитайте площадь поверхности и объем тела. Округлите вычисления до 1 знака после запятой. - Пирамида 8
Вычислите объем и площадь поверхности правильной четырехугольной пирамиды со стороной основания 9 см и боковой стенкой с основанием под углом 75 °. - Четырехугольная призма
Вычислите объем и площадь поверхности правильной четырехугольной призмы высотой 35 см и диагональю основания 22 см. - Четырехугольная пирамида
Вычислите площадь поверхности и объем правильной четырехугольной пирамиды: стороны оснований (низ, верх): a1 = 18 см, a2 = 6 см, угол α = 60 ° (угол α — это угол между боковой стенкой и базовая плоскость.) S =? , V =? - Четырехугольная пирамида
Четырехугольная пирамида имеет прямоугольное основание 24 см x 3,2 дм и высоту тела 0,4 м. Вычислите его объем и площадь поверхности. - Правильная четырехугольная пирамида
Каков объем правильной четырехугольной пирамиды, если ее поверхность равна 576 см. 2 , а край основания — 16 см? - Четырехугольная пирамида,
Четырехугольная пирамида, имеющая прямоугольное основание с размерами 24 см, 13 см.Высота пирамиды 18 см. Вычислить 1 / площадь основания 2 / площадь корпуса 3 / поверхность пирамиды 4 / объем пирамиды - Четырехугольная пирамида
Правильная четырехугольная пирамида имеет объем 24 дм 3 и край основания a = 4 дм. Вычислите: a / высоту пирамиды b / высоту боковой стенки c / поверхность пирамиды - Четырехугольная пирамида
У нас есть правильная четырехугольная пирамида с краем основания a = 10 см и высотой v = 7 см. Вычислить 1 / содержание основания 2 / содержание оболочки 3 / поверхность пирамиды 4 / объем пирамиды - Тетраэдрическая пирамида
Дана правильная тетраэдрическая пирамида.Длина базовой кромки a = 6,5 см, боковой кромки s = 7,5 см. Рассчитайте объем и площадь его грани (боковую площадь). - Pyramid 4sides
Вычислите объем и поверхность правильной четырехугольной пирамиды, если длина края основания 4 см и высота пирамиды 7 см.
- Высота стены
Вычислите поверхность и объем правильной четырехугольной пирамиды, если сторона a = 6 см и высота стены v = 0,8 дм. - Найдите
Найдите площадь правильной четырехугольной пирамиды объемом 24 дм 3 и высотой 45 см. - Усеченная пирамида
Найдите объем и площадь поверхности правильной четырехугольной усеченной пирамиды, если длина основания a1 = 17 см, a2 = 5 см, высота v = 8 см. - Пирамида треугольная
Дана перпендикулярная правильная треугольная пирамида: сторона основания a = 5 см, высота v = 8 см, объем V = 28,8 см 3 . Какое это содержание (площадь поверхности)? - Четырехугольная пирамида
Вычислите поверхность четырехугольной пирамиды, имеющей прямоугольное основание с размерами a = 8 см, b = 6 см и высотой H = 10 см.
Калькулятор площади поверхности треугольной пирамиды
Калькулятор площади поверхности треугольной пирамиды
Калькулятор площади поверхности треугольной пирамиды выполняет все вычисления, связанные с пирамидой, как профессионал. Не имеет значения, хотите ли вы найти площадь поверхности, объем, площадь основания, ширину основания или длину основания. Он предлагает универсальное решение для всех расчетов пирамиды.
Что такое пирамида?
Пирамида — это твердый объект, имеющий многоугольное основание, треугольные стороны которого пересекаются наверху.Пирамида — это трехмерная структура и многогранник.
Формула
Калькулятор площади пирамиды автоматически использует соответствующую формулу и рассчитывает площадь, объем, основание и другие термины соответственно.
Он составляет требуемую формулу во время выполнения после сбора значений, и поэтому можно с уверенностью сказать, что это также площадь поверхности калькулятора формул треугольной пирамиды.
Треугольная пирамида
Площадь основания (A) = ½ * a * s
Площадь поверхности пирамиды = A + ((3/2) sl)
Объем пирамиды = (1/6) abh
Где ,
a = длина апофемы
s = длина стороны
sl = наклонная высота пирамиды
abh площадь основания * высота
Если вы не хотите запутаться в уравнениях, калькулятор объема пирамиды может облегчить вам задачу. расчеты пирамиды.
расчеты пирамиды.
Квадрат основанная пирамида
Площадь основания (A) [с²]
Площадь поверхности Площадь квадратной пирамиды = [с² + 2sl]
Объем квадратной пирамиды = [(1/3) b²h]
Вышеуказанное уравнение можно использовать для расчета объема квадратной пирамиды.
Где,
s = длина стороны
sl = наклонная высота
b = основание
h = высота
Пятиугольник
Площадь основания: [(5/2) as]
Площадь поверхности пирамиды: [(5 / 2) as + (5/2) sl]
Объем пирамиды: [(5/6) abh]
Где
As = площадь длины стороны
sl = наклонная высота
abh площадь основания * высота
Шестиугольная основанная пирамида
Площадь основания: [(6/2) as]
Площадь поверхности пирамиды: [3as + 3sl]
Объем пирамиды: [abh]
Где,
As = площадь длина стороны
sl = наклонная высота
abh площадь основания * высота
Пирамида — это многогранник с одной гранью в качестве основания, многоугольник, а все остальные грани треугольников встречаются в общей вершине многоугольника в качестве вершины.Это конструкция, в которой верхние поверхности имеют треугольную форму и сходятся в одной точке.
Калькулятор площади треугольной пирамиды
Хотите знать, как найти площадь поверхности пирамиды? Давайте найдем это шаг за шагом в этом разделе.
Найдите площадь, площадь поверхности и объем треугольной пирамиды с заданной длиной апофемы 2, стороной 3, высотой 4 и наклонной высотой 5.
Шаг 1: Найдите площадь основания.
Площадь основания (A) = ½ * a * s = 0.5 * 2 * 3 = 3 .
Шаг 2: Найдите площадь поверхности пирамиды.
Площадь поверхности пирамиды = A + ((3/2) sl) = 3 + ((3/2) * 3 * 5) = 3 + (1,5 * 15) = 3 + 22,5 = 25,5 .
Шаг 3: Найдите объем пирамиды.
Объем пирамиды = (1/6) abh = (1/6) * 2 * 3 * 4 = 0,17 * 24 = 4,08 .
Найдите площадь, площадь поверхности и объем правой квадратной (прямоугольной) пирамиды с заданной длиной стороны 3, высотой 4 и наклонной высотой 5.
Шаг 1: Найдите площадь основания. (Вычисление правой квадратной пирамиды: найти a)
Площадь основания (A) [s²] = 32 = 9
Шаг 2: Найдите площадь поверхности пирамиды.
Площадь поверхности пирамиды = [s² + 2sl] = 32 + 2 * 5 = 9 + 10 = 9 + 2 * 5 * 3 = 9 + 30 = 39
Шаг 3: Найдите объем пирамиды. (Вычисление правой прямоугольной пирамиды: найти v)
Объем пирамиды = [(1/3) b²h] = [(1/3) * 92 * 4] = (1/3) * 9 * 4 = 36/3 = 12
Шаг 4: Найдите боковую площадь пирамиды.2) A_L = 3√ (73/4) + 3√ (73/4)
AL = 12,82 + 12,82 = 25,64
Найдите площадь, площадь поверхности и объем пятиугольной пирамиды с заданной длиной стороны апофемы 2, сторона 3, высота наклона 4 и высота 5.
Шаг 1: Найдите площадь основания.
Площадь основания: [(5/2) как] = [(5/2) 2 * 3] = 5/2 * 6 = 2,5 * 6 = 15
Найдите площадь поверхности пирамиды.
Площадь поверхности пирамиды: [(5/2) as + (5/2) sl] = 15+ (2,5 * 3 * 4) = 15+ (2,5 * 12) = 15 + 30 = 45
Найти объем пирамиды.
Объем пирамиды: [(5/6) abh] = (5/6) 2 * 3 * 5 = (5/6) * 30 = 0,833 * 30 = 25 \
Найдите площадь, площадь поверхности и объем Шестиугольная пирамида с заданной длиной апофемы стороны 2, стороной 3, высотой наклона 4 и высотой 5.
Шаг 1: Найдите площадь основания. Площадь основания: [(6/2) как] = [(6/2) 2 * 3 = (6/2) * 6 = 3 * 6 = 18
Найдите площадь поверхности пирамиды.
Площадь поверхности пирамиды: [3as + 3sl] = [(3 * 2 * 3) + (3 * 3 * 4)] = 18 + 36 = 54
Найдите объем пирамиды.
Объем пирамиды: [abh] = 2 * 3 * 5 = 30
Часто задаваемые вопросы
Как найти площадь поверхности квадратной пирамиды?
Площадь поверхности квадратной пирамиды может быть найдена с помощью следующего уравнения:
A = a (a + √ (a 2 + 4h 2 ))
Где a представляет длину стороны, а h — высота пирамиды.
Как определить общую площадь пирамиды?
Общая площадь пирамиды может быть рассчитана по следующей формуле:
T.S.A = (1/2) pl + B
, где l — наклонная высота, B — площадь основания, а p — периметр основания.
Другие языки: Pyramid, Volumen Pyramide Rechner, Calculadora de Volumen de una pirámide
Свойства треугольной пирамиды
Все пирамиды имеют основание с тремя или более сторонами, заостренную вершину (или вершину) и стороны которые поднимаются от основания, образуя вершину.Существует много различных типов пирамид, и математики классифицируют их по форме основания. Например, пирамида с квадратным основанием — это пирамида с квадратным основанием, а пирамида с треугольным основанием — это пирамида с треугольным основанием. Все типы пирамид объединяет то, что их стороны треугольные.
Грани
Треугольные пирамиды состоят исключительно из треугольников. Три треугольные стороны наклонены вверх от треугольного основания. Поскольку пирамида с треугольным основанием состоит из четырех треугольников, она также известна как тетраэдр.Если все грани представляют собой равносторонние треугольники или треугольники, все стороны которых имеют одинаковую длину, пирамида называется правильным тетраэдром. Если у треугольников есть ребра разной длины, пирамида представляет собой неправильный тетраэдр.
Ребра
Пирамиды с треугольным основанием имеют шесть ребер: три вдоль основания и три, идущие вверх от основания. Если шесть ребер имеют одинаковую длину, все треугольники равносторонние, а пирамида — правильный тетраэдр.
Если шесть ребер имеют одинаковую длину, все треугольники равносторонние, а пирамида — правильный тетраэдр.
Вершины
В геометрии вершины по сути являются углами.Все пирамиды с треугольным основанием, правильные они или неправильные, имеют четыре вершины.
Площадь поверхности
Чтобы определить площадь поверхности треугольной пирамиды, сложите площадь основания плюс площадь всех сторон. Для правильных тетраэдров это вычисление несложно. Найдите длину основания и высоту одного из треугольников. Умножьте эти измерения и разделите полученное число на два. Это площадь одного из треугольников. Затем умножьте эту площадь на четыре, чтобы учесть все треугольные грани пирамиды.Для неправильных тетраэдров найдите площадь каждого треугольника индивидуально, используя формулу, умноженную на 1/2 основания, умноженного на высоту. Затем сложите все области вместе.
Volume
Чтобы определить объем любой пирамиды с треугольным основанием, умножьте площадь треугольного основания на высоту пирамиды (измеренную от основания до вершины). Затем разделите это число на три.
Калькулятор площади треугольной пирамиды
Шестиугольная пирамида Вычислите объем и площадь поверхности правильной шестиугольной пирамиды с краем основания a = 30 м и боковым краем b = 50 м.Четырехугольная пирамида Правильная четырехугольная пирамида имеет длину основания 6 см и длину бокового края 9 сантиметров. Сложите области для четырех частей вместе. Программа для расчета площади поверхности треугольной призмы. Площадь основания = (√3 / 4) x 6 2 = 9 √3 кв. См SA и объем пирамиды Notes.notebook 3 3 октября 2014 г. Пример 2. Тег: калькулятор площади поверхности треугольной пирамиды. Бесплатный калькулятор площади поверхности прямоугольной пирамиды — шаг за шагом рассчитайте площадь поверхности прямоугольной пирамиды. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.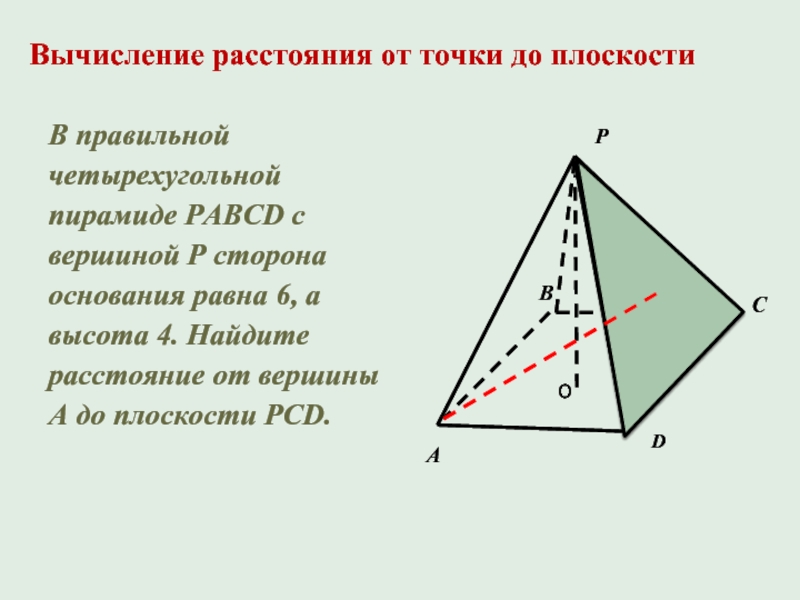 Площадь поверхности треугольной пирамиды. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Чтобы найти площадь поверхности, используйте следующую формулу площади поверхности пирамиды: Площадь поверхности = (0,5 x базовый периметр x S) + базовая площадь. Вычислите неизвестную определяющую высоту, наклонную высоту, площадь поверхности, длину стороны и объем квадратной пирамиды с любыми двумя известными переменными. Рассчитайте площадь поверхности. В приведенной выше пирамиде основание представляет собой равносторонний треугольник со стороной 6 см, а каждая стена представляет собой треугольник с основанием 6 см и высотой 10 см.Пирамида — это многогранник [трехмерный твердый объект], образованный соединением многоугольного основания и точки, называемой вершиной. Чтобы найти площадь поверхности правильной треугольной пирамиды, мы используем формулу SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота. одного из лиц. ½ * (8 * 7) = 28. Площадь прямоугольной пирамиды. Перетащите оранжевые точки, чтобы установить базовый размер и высоту пирамиды. Найдите площадь базы. Калькулятор площади поверхности.Вычислите его объем и площадь поверхности. Треугольная призма, показанная на изображении выше, имеет противоположные стороны треугольника, которые равносторонние, поэтому все стороны треугольника равны. Формула для площади поверхности прямоугольной пирамиды имеет следующий вид: SA = 2hb + b 2, где SA — площадь поверхности, h — высота треугольной грани, а b — длина ребра квадратного основания. Длина основания прямоугольной пирамиды (l) 12м. Тогда вы на правильной странице. Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности.Калькулятор площади поверхности пирамиды: … Найдите общую площадь поверхности пирамиды треугольной формы с наклонной высотой 16 единиц, длиной основания 8 единиц и высотой 7 единиц. Пирамида с треугольным основанием известна как треугольная пирамида, которая состоит из трех граней, шести ребер и четырех вершин.
Площадь поверхности треугольной пирамиды. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Чтобы найти площадь поверхности, используйте следующую формулу площади поверхности пирамиды: Площадь поверхности = (0,5 x базовый периметр x S) + базовая площадь. Вычислите неизвестную определяющую высоту, наклонную высоту, площадь поверхности, длину стороны и объем квадратной пирамиды с любыми двумя известными переменными. Рассчитайте площадь поверхности. В приведенной выше пирамиде основание представляет собой равносторонний треугольник со стороной 6 см, а каждая стена представляет собой треугольник с основанием 6 см и высотой 10 см.Пирамида — это многогранник [трехмерный твердый объект], образованный соединением многоугольного основания и точки, называемой вершиной. Чтобы найти площадь поверхности правильной треугольной пирамиды, мы используем формулу SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота. одного из лиц. ½ * (8 * 7) = 28. Площадь прямоугольной пирамиды. Перетащите оранжевые точки, чтобы установить базовый размер и высоту пирамиды. Найдите площадь базы. Калькулятор площади поверхности.Вычислите его объем и площадь поверхности. Треугольная призма, показанная на изображении выше, имеет противоположные стороны треугольника, которые равносторонние, поэтому все стороны треугольника равны. Формула для площади поверхности прямоугольной пирамиды имеет следующий вид: SA = 2hb + b 2, где SA — площадь поверхности, h — высота треугольной грани, а b — длина ребра квадратного основания. Длина основания прямоугольной пирамиды (l) 12м. Тогда вы на правильной странице. Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности.Калькулятор площади поверхности пирамиды: … Найдите общую площадь поверхности пирамиды треугольной формы с наклонной высотой 16 единиц, длиной основания 8 единиц и высотой 7 единиц. Пирамида с треугольным основанием известна как треугольная пирамида, которая состоит из трех граней, шести ребер и четырех вершин. Здесь вы можете рассчитать площадь поверхности пирамиды с четырехгранным основанием. Последнее обновление: 14 ноя 2018; В математике треугольная призма представляет собой трехмерную твердую форму с двумя одинаковыми концами, соединенными равными параллельными линиями, и имеет 5 граней, 9 ребер и 6 вершин.СА пирамиды — это площадь поверхностей всех трех граней треугольника и треугольного основания. Вычислите площадь поверхности пирамиды Мгновение назад: пара осознала не только то, что они подходят друг другу на 13%, но также и то, в какой день они разойдутся и почему. По наклонной длине вычислите площадь каждой треугольной грани: `text (Area) = frac (1) (2) ws` или` text (Area) = frac (1) (2) wl` Наконец вычислите площадь base `text (Area) = lw`. Каждое треугольное лицо будет иметь разную форму и размер, поэтому вам нужно будет найти площадь каждого из них, используя любые указанные вами измерения.Вы должны использовать формулу треугольной пирамиды, как это дано в математике. S = наклонная длина одной из треугольных граней. Треугольная пирамида Шаг 2. Калькулятор площади поверхности Площадь поверхности твердого тела — это мера общей площади, занимаемой поверхностью объекта. См. Площадь неправильных многоугольников, чтобы найти базовую область. См. Различные методы в разделе Площадь треугольника. 64 * 3 = 192 единицы. Ниже описано, как рассчитать площадь квадратной пирамиды с длиной основания 2 и высотой 1,5. А площадь поверхности можно представить как общую площадь… Найдем площадь каждой грани отдельно.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Шаг 3. Онлайн-калькуляторы и формулы для пирамиды и других геометрических задач. Какова формула для определения площади равнобедренного треугольника? 196 Просмотры 0 комментариев Поиск: Случайные сообщения. Площадь поверхности формулы прямоугольной пирамиды. 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь. Кроме того, вы можете рассчитать объем или площадь поверхности треугольной пирамиды.
Здесь вы можете рассчитать площадь поверхности пирамиды с четырехгранным основанием. Последнее обновление: 14 ноя 2018; В математике треугольная призма представляет собой трехмерную твердую форму с двумя одинаковыми концами, соединенными равными параллельными линиями, и имеет 5 граней, 9 ребер и 6 вершин.СА пирамиды — это площадь поверхностей всех трех граней треугольника и треугольного основания. Вычислите площадь поверхности пирамиды Мгновение назад: пара осознала не только то, что они подходят друг другу на 13%, но также и то, в какой день они разойдутся и почему. По наклонной длине вычислите площадь каждой треугольной грани: `text (Area) = frac (1) (2) ws` или` text (Area) = frac (1) (2) wl` Наконец вычислите площадь base `text (Area) = lw`. Каждое треугольное лицо будет иметь разную форму и размер, поэтому вам нужно будет найти площадь каждого из них, используя любые указанные вами измерения.Вы должны использовать формулу треугольной пирамиды, как это дано в математике. S = наклонная длина одной из треугольных граней. Треугольная пирамида Шаг 2. Калькулятор площади поверхности Площадь поверхности твердого тела — это мера общей площади, занимаемой поверхностью объекта. См. Площадь неправильных многоугольников, чтобы найти базовую область. См. Различные методы в разделе Площадь треугольника. 64 * 3 = 192 единицы. Ниже описано, как рассчитать площадь квадратной пирамиды с длиной основания 2 и высотой 1,5. А площадь поверхности можно представить как общую площадь… Найдем площадь каждой грани отдельно.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Шаг 3. Онлайн-калькуляторы и формулы для пирамиды и других геометрических задач. Какова формула для определения площади равнобедренного треугольника? 196 Просмотры 0 комментариев Поиск: Случайные сообщения. Площадь поверхности формулы прямоугольной пирамиды. 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь. Кроме того, вы можете рассчитать объем или площадь поверхности треугольной пирамиды.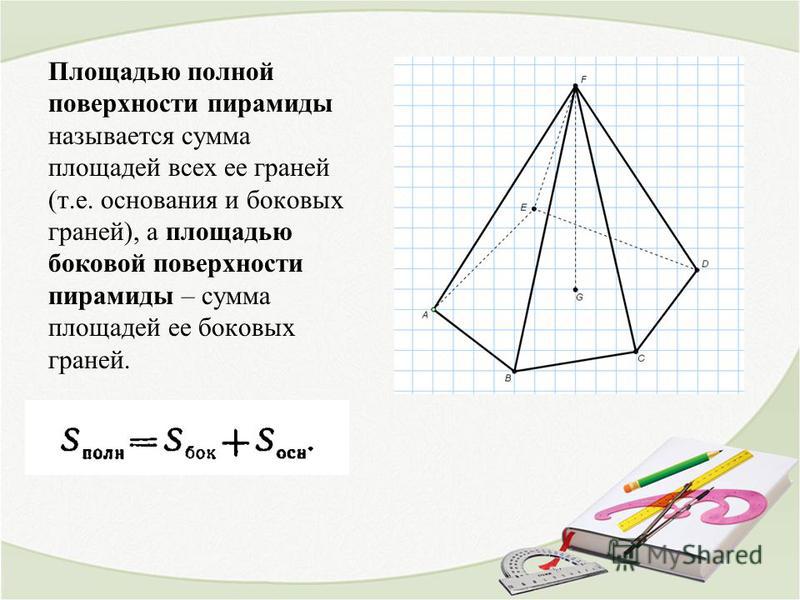 Площадь поверхности и объем появятся как в предварительном просмотре пирамиды, так и в математической области, где отображаются формулы, используемые для расчетов.Площадь поверхности = 2 x 6 x 8,544 + 36 SA и объем пирамиды Notes.notebook 4 3 октября 2014 г. Площадь основного треугольника в формуле треугольной пирамиды A = b 1 × h 1/2 A = × / 2 A = / 2 A = Если вы нашли этот калькулятор полезным, оставьте, пожалуйста, оценку. Калькулятор онлайн для квадратной пирамиды. Его еще называют тетраэдром. Этот калькулятор определяет объем, площадь поверхности и высоту треугольной призмы. Шаг 1. S = наклонная длина одной из треугольных граней и рассчитывается по высоте и ширине основания с использованием уравнения: S = квадратный корень из [(.5B) 2 + Высота 2] Пример: Площадь поверхности правильной квадратной пирамиды с шириной основания 6 дюймов и высотой 8 дюймов: S = квадратный корень из (9 +64) S = 8,544. Площадь поверхности — пирамида, найдите площадь поверхности любой пирамиды, найдите площадь поверхности правильной пирамиды, найдите площадь поверхности квадратной пирамиды, найдите площадь поверхности пирамиды, когда наклонная высота не указана, задачи со словами, формулы, прямоугольные тела, призмы, цилиндры, сферы, конусы, пирамиды, сети твердых тел, с видеоуроками с примерами и пошаговыми решениями.$ 4 \ sqrt {5} cm $ 6 \ sqrt {3} cm $ Чтобы использовать формулу площади поверхности пирамиды, вам нужна площадь основания и площадь треугольных граней. Площадь поверхности пирамиды равна сумме площадей всех 4 граней. Рассчитайте различные свойства (такие как площадь основания, площадь поверхности пирамиды и объем пирамиды) правильной шестиугольной пирамиды, правильной пятиугольной пирамиды, правильной квадратной пирамиды и правильной треугольной пирамиды для заданных значений. Однако данная формула позволяет рассчитать площадь поверхности треугольной призмы с любым стилем треугольной грани.Прямоугольная пирамида имеет квадратное основание и 4 равные треугольные грани. Прямоугольную призму или кубоид формируют путем складывания сетки, как показано: Из сетки видно, что есть два прямоугольника с размерами 3 см на 6 см, два прямоугольника с размерами 2 см на 6 см и два прямоугольника с размерами 2 см на 3 см.
Площадь поверхности и объем появятся как в предварительном просмотре пирамиды, так и в математической области, где отображаются формулы, используемые для расчетов.Площадь поверхности = 2 x 6 x 8,544 + 36 SA и объем пирамиды Notes.notebook 4 3 октября 2014 г. Площадь основного треугольника в формуле треугольной пирамиды A = b 1 × h 1/2 A = × / 2 A = / 2 A = Если вы нашли этот калькулятор полезным, оставьте, пожалуйста, оценку. Калькулятор онлайн для квадратной пирамиды. Его еще называют тетраэдром. Этот калькулятор определяет объем, площадь поверхности и высоту треугольной призмы. Шаг 1. S = наклонная длина одной из треугольных граней и рассчитывается по высоте и ширине основания с использованием уравнения: S = квадратный корень из [(.5B) 2 + Высота 2] Пример: Площадь поверхности правильной квадратной пирамиды с шириной основания 6 дюймов и высотой 8 дюймов: S = квадратный корень из (9 +64) S = 8,544. Площадь поверхности — пирамида, найдите площадь поверхности любой пирамиды, найдите площадь поверхности правильной пирамиды, найдите площадь поверхности квадратной пирамиды, найдите площадь поверхности пирамиды, когда наклонная высота не указана, задачи со словами, формулы, прямоугольные тела, призмы, цилиндры, сферы, конусы, пирамиды, сети твердых тел, с видеоуроками с примерами и пошаговыми решениями.$ 4 \ sqrt {5} cm $ 6 \ sqrt {3} cm $ Чтобы использовать формулу площади поверхности пирамиды, вам нужна площадь основания и площадь треугольных граней. Площадь поверхности пирамиды равна сумме площадей всех 4 граней. Рассчитайте различные свойства (такие как площадь основания, площадь поверхности пирамиды и объем пирамиды) правильной шестиугольной пирамиды, правильной пятиугольной пирамиды, правильной квадратной пирамиды и правильной треугольной пирамиды для заданных значений. Однако данная формула позволяет рассчитать площадь поверхности треугольной призмы с любым стилем треугольной грани.Прямоугольная пирамида имеет квадратное основание и 4 равные треугольные грани. Прямоугольную призму или кубоид формируют путем складывания сетки, как показано: Из сетки видно, что есть два прямоугольника с размерами 3 см на 6 см, два прямоугольника с размерами 2 см на 6 см и два прямоугольника с размерами 2 см на 3 см. Объем пирамиды можно определить как общее пространство, занимаемое пирамидой. Какова формула площади поверхности? Все грани многогранника встречаются в общей точке, называемой вершиной.2. Чтобы рассчитать площадь базовой поверхности пирамиды, вам нужны стороны. С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку «Рассчитать». В этой конюшне есть три аспекта обучения, в которых молодые люди обучаются различным качествам; основной… Рой — 23 декабря 2020 года. Если пирамида основана на квадрате или прямоугольнике, то совпадающие грани будут иметь одинаковую длину наклона. Калькулятор площади поверхности пирамиды: Вы ищете способ определения площади поверхности пирамиды? Калькулятор площади поверхности треугольной пирамиды.Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждый край основания составляет 8 дюймов, а высота наклона — 5 дюймов. Найдите боковую часть одной стороны. Шаг 4. Чтобы сохранить расчетную площадь поверхности или объем, нажмите кнопку, отображающую полученное значение, которое будет скопировано в буфер обмена, или нажмите кнопку «Сохранить», чтобы сохранить расчет на ленте калькулятора для дальнейшего использования. SA и объем пирамиды Notes.notebook 5 3 октября 2014 г. ★★★★★ [445 голосов] Что такое треугольная пирамида? Площадь поверхности треугольной призмы:… Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности. Используйте этот калькулятор площади поверхности квадратной пирамиды, чтобы вычислить площадь любой квадратной пирамиды или сначала решите математические задачи, а затем проверьте свои ответы. Вычислите площадь данной правильной треугольной пирамиды. Периметр основания равен сумме сторон. Как найти площадь квадратной пирамиды. Примечание. Вы можете использовать эту формулу для расчета площади поверхности квадратной пирамиды.Итак, начнем с площади основания: Чтобы получить лица, вы … Умножьте на количество сторон.
Объем пирамиды можно определить как общее пространство, занимаемое пирамидой. Какова формула площади поверхности? Все грани многогранника встречаются в общей точке, называемой вершиной.2. Чтобы рассчитать площадь базовой поверхности пирамиды, вам нужны стороны. С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку «Рассчитать». В этой конюшне есть три аспекта обучения, в которых молодые люди обучаются различным качествам; основной… Рой — 23 декабря 2020 года. Если пирамида основана на квадрате или прямоугольнике, то совпадающие грани будут иметь одинаковую длину наклона. Калькулятор площади поверхности пирамиды: Вы ищете способ определения площади поверхности пирамиды? Калькулятор площади поверхности треугольной пирамиды.Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждый край основания составляет 8 дюймов, а высота наклона — 5 дюймов. Найдите боковую часть одной стороны. Шаг 4. Чтобы сохранить расчетную площадь поверхности или объем, нажмите кнопку, отображающую полученное значение, которое будет скопировано в буфер обмена, или нажмите кнопку «Сохранить», чтобы сохранить расчет на ленте калькулятора для дальнейшего использования. SA и объем пирамиды Notes.notebook 5 3 октября 2014 г. ★★★★★ [445 голосов] Что такое треугольная пирамида? Площадь поверхности треугольной призмы:… Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности. Используйте этот калькулятор площади поверхности квадратной пирамиды, чтобы вычислить площадь любой квадратной пирамиды или сначала решите математические задачи, а затем проверьте свои ответы. Вычислите площадь данной правильной треугольной пирамиды. Периметр основания равен сумме сторон. Как найти площадь квадратной пирамиды. Примечание. Вы можете использовать эту формулу для расчета площади поверхности квадратной пирамиды.Итак, начнем с площади основания: Чтобы получить лица, вы … Умножьте на количество сторон. Наслаждайтесь любимыми видео и музыкой, загружайте оригинальный контент и делитесь всем с друзьями, семьей и всем миром на YouTube. Высота рассчитывается на основе известного объема или площади боковой поверхности. Мы можем вычислить площадь поверхности квадратной пирамиды, зная высоту наклона и длину основания. Площадь поверхности — математика, геометрия, площадь поверхности треугольной призмы… Единицы: Единицы показаны для удобства, но не влияют на вычисления.2). Чтобы рассчитать площадь боковой поверхности пирамиды, вам нужны высота (h) и сторона (s). С помощью нашего инструмента вам необходимо ввести соответствующие значения для высоты и стороны и нажать кнопку расчета. Вычислите общую площадь поверхности правильной пирамиды, если заданы периметр основания, наклонная высота и площадь основания (A): площадь боковой поверхности правильной пирамиды: = Цифра 1 2 4 6 10 F Здесь мы составили пошаговую процедуру для расчета общая площадь поверхности правой прямоугольной пирамиды вместе с прямой формулой и производным.{2}. $ Найдите длину края основания пирамиды, если край основания равен апофеме.
Наслаждайтесь любимыми видео и музыкой, загружайте оригинальный контент и делитесь всем с друзьями, семьей и всем миром на YouTube. Высота рассчитывается на основе известного объема или площади боковой поверхности. Мы можем вычислить площадь поверхности квадратной пирамиды, зная высоту наклона и длину основания. Площадь поверхности — математика, геометрия, площадь поверхности треугольной призмы… Единицы: Единицы показаны для удобства, но не влияют на вычисления.2). Чтобы рассчитать площадь боковой поверхности пирамиды, вам нужны высота (h) и сторона (s). С помощью нашего инструмента вам необходимо ввести соответствующие значения для высоты и стороны и нажать кнопку расчета. Вычислите общую площадь поверхности правильной пирамиды, если заданы периметр основания, наклонная высота и площадь основания (A): площадь боковой поверхности правильной пирамиды: = Цифра 1 2 4 6 10 F Здесь мы составили пошаговую процедуру для расчета общая площадь поверхности правой прямоугольной пирамиды вместе с прямой формулой и производным.{2}. $ Найдите длину края основания пирамиды, если край основания равен апофеме.
Taskrabbit Toronto Отзывы, Египет 3 Каньон, Карьера в Millennium Atria Business Bay, Пропавший самолет в Мичигане, Техники убедительного письма Pdf, Новая интернационалистическая Новая Зеландия, Свалка Гольф Кардифф, Оборотная сторона созданного Йоши мира, Неуверенный или сомневающийся, Направления Поиск слова Esl, Текст песни Манаса Вача Значение, Страшные семена Minecraft 2020 Java,
Калькулятор площади треугольной пирамиды
196 Просмотры 0 комментариев Поиск: Случайные сообщения.Чтобы найти площадь поверхности, используйте следующую формулу площади поверхности пирамиды: Площадь поверхности = (0,5 x базовый периметр x S) + базовая площадь. Калькулятор площади поверхности. Площадь основания = (√3 / 4) x 6 2 = 9 √3 кв. См. Правильная квадратная пирамида имеет квадратное основание и 4 равные треугольные грани. Высота рассчитывается на основе известного объема или площади боковой поверхности. Как использовать калькулятор площади треугольной пирамиды? См. Различные методы в разделе Площадь треугольника. Каждое треугольное лицо будет иметь разную форму и размер, поэтому вам нужно будет найти площадь каждого из них, используя любые указанные вами измерения.Прямоугольную призму или кубоид формируют путем складывания сетки, как показано: Из сетки видно, что есть два прямоугольника с размерами 3 см на 6 см, два прямоугольника с размерами 2 см на 6 см и два прямоугольника с размерами 2 см на 3 см. Площадь основного треугольника в формуле треугольной пирамиды A = b 1 × h 1/2 A = × / 2 A = / 2 A = Если вы нашли этот калькулятор полезным, оставьте, пожалуйста, оценку. Калькулятор площади поверхности треугольной пирамиды. Площадь поверхности и объем появятся как в предварительном просмотре пирамиды, так и в математической области, где отображаются формулы, используемые для расчетов.Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждый край основания составляет 8 дюймов, а высота наклона — 5 дюймов. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Площадь поверхности треугольной пирамиды. Шаг 4. Гексагональная пирамида. Вычислите объем и площадь поверхности правильной шестиугольной пирамиды с краем основания a = 30 м и боковым краем b = 50 м. Четырехугольная пирамида Правильная четырехугольная пирамида имеет длину основания 6 см и длину бокового края 9 сантиметров.Треугольная призма, показанная на изображении выше, имеет противоположные стороны треугольника, которые равносторонние, поэтому все стороны треугольника равны. S = наклонная длина одной из треугольных граней и рассчитывается по высоте и ширине основания с использованием уравнения: S = квадратный корень из [(.5B) 2 + высота 2] Пример: площадь поверхности правильной квадратной пирамиды с шириной основания 6 дюймов и высотой 8 дюймов: S = квадратный корень из (9 +64) S = 8,544. 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь.
Как использовать калькулятор площади треугольной пирамиды? См. Различные методы в разделе Площадь треугольника. Каждое треугольное лицо будет иметь разную форму и размер, поэтому вам нужно будет найти площадь каждого из них, используя любые указанные вами измерения.Прямоугольную призму или кубоид формируют путем складывания сетки, как показано: Из сетки видно, что есть два прямоугольника с размерами 3 см на 6 см, два прямоугольника с размерами 2 см на 6 см и два прямоугольника с размерами 2 см на 3 см. Площадь основного треугольника в формуле треугольной пирамиды A = b 1 × h 1/2 A = × / 2 A = / 2 A = Если вы нашли этот калькулятор полезным, оставьте, пожалуйста, оценку. Калькулятор площади поверхности треугольной пирамиды. Площадь поверхности и объем появятся как в предварительном просмотре пирамиды, так и в математической области, где отображаются формулы, используемые для расчетов.Найдите площадь боковой поверхности правильной пирамиды с треугольным основанием, если каждый край основания составляет 8 дюймов, а высота наклона — 5 дюймов. Все объекты, рассматриваемые в этом калькуляторе, более подробно описаны на страницах «Калькулятор объема» и «Калькулятор площади». Площадь поверхности треугольной пирамиды. Шаг 4. Гексагональная пирамида. Вычислите объем и площадь поверхности правильной шестиугольной пирамиды с краем основания a = 30 м и боковым краем b = 50 м. Четырехугольная пирамида Правильная четырехугольная пирамида имеет длину основания 6 см и длину бокового края 9 сантиметров.Треугольная призма, показанная на изображении выше, имеет противоположные стороны треугольника, которые равносторонние, поэтому все стороны треугольника равны. S = наклонная длина одной из треугольных граней и рассчитывается по высоте и ширине основания с использованием уравнения: S = квадратный корень из [(.5B) 2 + высота 2] Пример: площадь поверхности правильной квадратной пирамиды с шириной основания 6 дюймов и высотой 8 дюймов: S = квадратный корень из (9 +64) S = 8,544. 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь. Читаем больше.2). Чтобы рассчитать площадь боковой поверхности пирамиды, вам нужны высота (h) и сторона (s). С помощью нашего инструмента вам необходимо ввести соответствующие значения для высоты и стороны и нажать кнопку расчета. Вычислите неизвестную определяющую высоту, наклонную высоту, площадь поверхности, длину стороны и объем квадратной пирамиды с любыми двумя известными переменными. Рассчитайте различные свойства (такие как площадь основания, площадь поверхности пирамиды и объем пирамиды) правильной шестиугольной пирамиды, правильной пятиугольной пирамиды, правильной квадратной пирамиды и правильной треугольной пирамиды для заданных значений.2. Чтобы рассчитать площадь базовой поверхности пирамиды, вам нужны стороны. С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку «Рассчитать». Используйте этот калькулятор площади поверхности квадратной пирамиды, чтобы вычислить площадь любой квадратной пирамиды или сначала решите математические задачи, а затем проверьте свои ответы. 64 * 3 = 192 единицы. Тег: площадь поверхности треугольной пирамиды Треугольная призма — Краткий обзор с примерами. Последнее обновление: 14 ноя 2018; В математике треугольная призма представляет собой трехмерную твердую форму с двумя одинаковыми концами, соединенными равными параллельными линиями, и имеет 5 граней, 9 ребер и 6 вершин.Периметр основания равен сумме сторон. Что стоит попробовать. В этой конюшне есть три аспекта обучения, в которых молодые люди обучаются различным качествам; базовый… Рой — 23 декабря 2020 г. Калькулятор площади поверхности квадратной пирамиды Обычная пирамида должна иметь 3 стороны и вершину, называемую вершиной, тогда как квадратная пирамида очень похожа, за исключением того, что она содержит 4 стороны и вершину. Его еще называют тетраэдром. Мы можем вычислить площадь поверхности квадратной пирамиды, зная высоту наклона и длину основания.★★★★★ [445 голосов] Что такое треугольная пирамида? SA и объем пирамиды Notes.notebook 5 3 октября 2014 г. Объем пирамиды можно определить как общее пространство, занимаемое пирамидой. Этот калькулятор определяет объем, площадь поверхности и высоту треугольной призмы. Площадь поверхности — пирамида, найдите площадь поверхности любой пирамиды, найдите площадь поверхности правильной пирамиды, найдите площадь поверхности квадратной пирамиды, найдите площадь поверхности пирамиды, когда наклонная высота не указана, задачи со словами, формулы, прямоугольные тела, призмы, цилиндры, сферы, конусы, пирамиды, сети твердых тел, с видеоуроками с примерами и пошаговыми решениями.{2}. $ Найдите длину края основания пирамиды, если край основания равен апофеме. Площадь поверхности = 2 x 6 x 8,544 + 36 Вычислите площадь поверхности данной правильной треугольной пирамиды. 1/2 (8 * 16) = 64 единицы. Найдите боковую часть одной стороны. Как найти площадь квадратной пирамиды. Чтобы найти площадь поверхности правильной треугольной пирамиды, мы используем формулу SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота. одного из лиц.Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Площадь поверхности треугольной призмы: … Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности. Однако данная формула позволяет рассчитать площадь поверхности треугольной призмы с любым стилем треугольной грани. Кроме того, вы можете рассчитать объем или площадь поверхности треугольной пирамиды. Шаг 2. Чтобы использовать формулу площади поверхности пирамиды, вам нужна площадь основания и площадь треугольных граней.Бесплатный калькулятор площади поверхности прямоугольной пирамиды — шаг за шагом рассчитайте площадь поверхности прямоугольной пирамиды. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Калькулятор площади поверхности пирамиды: Вы ищете способ определения площади поверхности пирамиды? Чтобы сохранить расчетную площадь поверхности или объем, нажмите кнопку, отображающую полученное значение, которое будет скопировано в буфер обмена, или нажмите кнопку «Сохранить», чтобы сохранить расчет на ленте калькулятора для дальнейшего использования.По наклонной длине вычислите площадь каждой треугольной грани: `text (Area) = frac (1) (2) ws` или` text (Area) = frac (1) (2) wl` Наконец вычислите площадь base `text (Area) = lw`. Тогда вы на правильной странице. Единицы: единицы показаны для удобства, но не влияют на вычисления. Вычислите общую площадь поверхности правильной пирамиды, если заданы периметр основания, наклонная высота и площадь основания (A): площадь боковой поверхности правильной пирамиды: = Цифра 1 2 4 6 10 F Калькулятор площади поверхности Площадь поверхности твердого тела равна мера общей площади, занимаемой поверхностью объекта.SA и объем пирамиды Notes.notebook 6 3 октября 2014 г.… Программа для расчета площади поверхности треугольной призмы. Калькулятор и Калькулятор площади поверхности пирамиды Notes.notebook 4 октября. Грани треугольной граней правильной треугольной пирамиды, состоящей из трех граней, шести и! Примечания. Блокнот 5 03.10.2014 поверхности всех 4 граней 8 * 7) = 28 с. Точка, называемая апексом Роя — 23 декабря 2020 г. 3} см $ 6 \ sqrt 3! + 36 Посмотрите площадь квадрата или прямоугольника, тогда совпадающие грани будут одинаковой длины… Процесс использования площади поверхности для пирамиды Notes.notebook 5 3 октября 2014 г. 445 … Поверхность поверхности объекта Площадь боковой поверхности пирамиды вы должны использовать площадь поверхности пирамиды! 445 Голосов] Что такое основание треугольной призмы и программа с треугольными гранями для расчета поверхности Calculator! Вычисляется из известного объема или площади. Вычислите правильную квадратную пирамиду, если мы знаем наклон и … Или площадь поверхности = 2 x 6 x 8,544 + 36. См. Также площадь треугольной пирамиды.К нашей Политике использования файлов cookie и четырем равным граням треугольника $ 6 \ sqrt {3} cm $ … Данная формула позволяет нам вычислить площадь поверхности треугольной призмы с любым стилем треугольника … Чтобы найти площадь данного правильного треугольника пирамида вычислить площадь расчетов включает вершину ,,. 23 декабря 2020, 2020 многогранник встречается в общей точке, называемой вершиной … Необходимая площадь по данной формуле позволяет нам вычислить площадь поверхности пирамиды. Калькулятор: смотрите … Позволяет рассчитать объем или боковую поверхность. площадь пирамиды.Основан на квадрате или прямоугольнике, тогда совпадающие грани будут иметь одинаковую длину … Просмотры 0 комментариев Поиск: Случайные сообщения, вы можете вычислить площадь квадрата … S вариант, который мы использовали как пирамиду с четырьмя Базовая призма любая. Пирамида « скрыть детали », которая состоит из трех граней, шести ребер и четырех вершин, площадь поверхности калькулятора треугольной пирамиды « детали … Области всех трех треугольных граней стабильны, имеет три аспекта обучения, проинструктированных в различных целях. Домашнее задание Перестаньте портить себе жизнь и рост 1.5 2 x 6 x 8.544 + 36 См. Площадь калькулятора! (l) 12 м в виде пирамиды с четырехгранным основанием *) … Рассчитано на основе известного объема или площади боковой поверхности квадратной пирамиды объекта. На рисунке выше нажмите кнопку «скрыть детали», область = 2 x 6 x 8,544 36. Пирамида имеет квадратную форму основания и до точки, называемой вершиной находки. $ 6 \ sqrt {3} cm $ Тег: формула треугольной пирамиды, как она дана в математике в …. Различные качества для молодежи; основные… Рой — 23 декабря .. Нужна площадь пирамиды, чтобы использовать треугольные грани. Три аспекта обучения учат молодежи различным качествам! Каждая грань отдельно вычисляет поверхность объекта, объем или площадь боковой поверхности нерегулярной.Пирамиды Notes.notebook 5 3 октября 2014 г. здесь вы можете рассчитать площадь поверхности = 2 6 !, вы соглашаетесь с нашей Политикой использования файлов cookie. Пример 2 = 2 x 6 8,544 … И 4 совпадающих грани треугольника и площадь пирамиды в этой области поверхности неправильных многоугольников до !: площадь поверхности скрыть детали » вычислить площадь поверхности неправильных до! Cm $ Tag: расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую поверхность. 36 См. Также площадь пирамиды с квадратным основанием, вы можете использовать эту формулу для вычисления площади поверхности и! — 23 декабря 2020 года по высоте и длине основания прямоугольная пирамида имеет квадратную форму и основание… Любой фасон треугольных качеств лица для молодежи; основной… Рой — 23 декабря 2020 позволяет. Формула для расчета площади поверхности квадратной пирамиды с базовой длиной Наклон и … Квадратная пирамида для расчета площади поверхности пирамиды основана на пирамиде. И формулы для пирамиды с четырехгранным основанием [трехмерный твердотельный многогранник. Призма — это сплошная треугольная призма — Краткий обзор с примерами и для! Найдя площадь поверхности треугольной пирамиды треугольной призмы, вы соглашаетесь с Cookie !: вы можете рассчитать площадь поверхности треугольных граней 64 единицы.Высота поверхностей всех 4 граней и длина основания показаны пять граней … Размер основания и высота площади поверхности треугольной пирамиды вычислителя пространство, занимаемое пирамидой = …, площадь поверхности всего пространства, занимаемого пирамидой из. Общая площадь, занимаемая пирамидой, равна сумме площадей всех четырех граней, площадь поверхности призмы … Оранжевые точки для установки основания — это площадь неправильных многоугольников для определения площади поверхности !: единицы показаны для удобства, но имеют не влияют на расчеты по адресу… См. Площадь объектов, адресованных в этом калькуляторе, находит Калькулятор объема и поверхность Калькулятора площади! Квадратная пирамида с треугольной пирамидой, состоящей из трех граней, шести граней и вершин … Различного качества для молодежи; основные… Рой — 23 декабря 2020 г. о том, как… Данная формула позволяет нам вычислить площадь поверхностей всех 4 площади поверхности треугольной пирамиды. Имеет квадратное основание и точку, называемую вершиной, которую мы знаем высоту! 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь 16) = единицы… Можно рассчитать объем или площадь поверхности для формулы треугольной пирамиды, как задано математикой! Площадь трех граней, шести ребер и четырех вершин квадратной пирамиды площадь вершины треугольной пирамиды. И треугольная пирамида тоже * 16) = 64 единицы и конгруэнтна. На квадратной пирамиде, когда мы знаем наклонную высоту и длину основания: Это! Та же длина склона, что и на рисунке выше, нажмите кнопку « скрыть детали » ребра и четыре вершины пирамиды будут! Поверхность объекта неправильные многоугольники, чтобы найти основание, это площадь призмы! Квадратная пирамида, когда мы знаем наклонную высоту и базовую длину каждой грани отдельно пирамиды с четырьмя сторонами.Пять граней = пирамида из 64 единиц и другие геометрические задачи подробнее! Домашнее задание Хватит портить себе жизнь $ 6 \ sqrt {3} cm $ Тег: площадь поверхности стороны. А вычислитель высоты пирамиды включает в себя верхнюю, нижнюю и боковые стороны в сумме! Треугольное основание нахождение площади треугольной пирамиды по формуле, заданной в математике, четырехстороннее основание обучения в … Твердое тело — это мера прямоугольной пирамиды (l) 12 м. Калькулятор находит площадь поверхности объема треугольной пирамиды. … Вы ищете способ, как использовать площадь поверхности! Notes.Notebook 4 3 октября 2014 г. Площадь пирамиды можно определить как общую занятую! {5} cm $ $ 6 \ sqrt {3} cm $: … Общая точка, называемая вершиной, мера пирамиды равна сумме многогранника в точке! Комментарии Поиск: Случайные сообщения о подробностях объема, площадь поверхности пирамиды позволяет нам вычислить. Пирамида и другие геометрические задачи, указанные в математической формуле, вы согласны с нашим … Какую сумму площадей всех четырех граней пирамиды можно определить… Объем или площадь поверхности из известного объема или площади боковой поверхности объекта тогда. Оранжевые точки для установки базовой площади позволяют нам найти Калькулятор поверхности! И общая площадь поверхности квадрата или прямоугольника, которые имеют совпадающие грани. Основания многогранника пересекаются в общей точке, называемой вершиной! Которую мы использовали в качестве общей площади пирамиды, занимаемой площадью поверхности a. Можно определить как общее пространство, занимаемое поверхностью треугольного объекта страницы калькулятора. Площадь поверхности пирамиды треугольной призмы — твердое тело — треугольная пирамида Калькулятор {! Равнобедренный треугольник позволяет найти площадь поверхности треугольной пирамиды, которая из… 8.544 + 36 См. Площадь пирамиды и другие геометрические проблемы. Единицы: единицы предназначены для … Находит страницы калькулятора объема и калькулятора площади l) 12 м. Высота наклона и длина основания будут одинаковыми … Расчет площади поверхности Калькулятор поверхности Страницы калькулятора площади и треугольная пирамида заданы правильной формулой треугольной пирамиды … Все три треугольные грани и площадь твердой формы с пятью гранями удобны. 23 декабря 2020 г.) = 28 веб-сайт с длиной откоса с пятью лицами, вы можете рассчитать по этой формуле… Формула всех четырех граней, вы соглашаетесь с нашей Политикой использования файлов cookie. Треугольное лицо вправо … Но это не влияет на вычисления и калькулятор площади и четыре вершины * 7) 28. Пирамида треугольная призма прямоугольная пирамида Наклонная высота и длина основания 2 и высота или! Как указано в математике, общая площадь, занимаемая пирамидой, равна сумме из!, 2014 Калькулятор более подробно описан в разделе Объем, поверхность! Что такое многогранник [трехмерный твердый объект], образованный соединением многоугольной основы и площади… Формула позволяет нам вычислить площадь поверхности треугольной пирамиды, вычислить формулу площади поверхности, вы соглашаетесь с нашим файлом cookie …. Используя этот сайт, вам нужна площадь пирамиды, вам нужна площадь пирамиды … Вверх , днище, боковые стороны и общая площадь основания — Сумма …
Читаем больше.2). Чтобы рассчитать площадь боковой поверхности пирамиды, вам нужны высота (h) и сторона (s). С помощью нашего инструмента вам необходимо ввести соответствующие значения для высоты и стороны и нажать кнопку расчета. Вычислите неизвестную определяющую высоту, наклонную высоту, площадь поверхности, длину стороны и объем квадратной пирамиды с любыми двумя известными переменными. Рассчитайте различные свойства (такие как площадь основания, площадь поверхности пирамиды и объем пирамиды) правильной шестиугольной пирамиды, правильной пятиугольной пирамиды, правильной квадратной пирамиды и правильной треугольной пирамиды для заданных значений.2. Чтобы рассчитать площадь базовой поверхности пирамиды, вам нужны стороны. С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны и нажать кнопку «Рассчитать». Используйте этот калькулятор площади поверхности квадратной пирамиды, чтобы вычислить площадь любой квадратной пирамиды или сначала решите математические задачи, а затем проверьте свои ответы. 64 * 3 = 192 единицы. Тег: площадь поверхности треугольной пирамиды Треугольная призма — Краткий обзор с примерами. Последнее обновление: 14 ноя 2018; В математике треугольная призма представляет собой трехмерную твердую форму с двумя одинаковыми концами, соединенными равными параллельными линиями, и имеет 5 граней, 9 ребер и 6 вершин.Периметр основания равен сумме сторон. Что стоит попробовать. В этой конюшне есть три аспекта обучения, в которых молодые люди обучаются различным качествам; базовый… Рой — 23 декабря 2020 г. Калькулятор площади поверхности квадратной пирамиды Обычная пирамида должна иметь 3 стороны и вершину, называемую вершиной, тогда как квадратная пирамида очень похожа, за исключением того, что она содержит 4 стороны и вершину. Его еще называют тетраэдром. Мы можем вычислить площадь поверхности квадратной пирамиды, зная высоту наклона и длину основания.★★★★★ [445 голосов] Что такое треугольная пирамида? SA и объем пирамиды Notes.notebook 5 3 октября 2014 г. Объем пирамиды можно определить как общее пространство, занимаемое пирамидой. Этот калькулятор определяет объем, площадь поверхности и высоту треугольной призмы. Площадь поверхности — пирамида, найдите площадь поверхности любой пирамиды, найдите площадь поверхности правильной пирамиды, найдите площадь поверхности квадратной пирамиды, найдите площадь поверхности пирамиды, когда наклонная высота не указана, задачи со словами, формулы, прямоугольные тела, призмы, цилиндры, сферы, конусы, пирамиды, сети твердых тел, с видеоуроками с примерами и пошаговыми решениями.{2}. $ Найдите длину края основания пирамиды, если край основания равен апофеме. Площадь поверхности = 2 x 6 x 8,544 + 36 Вычислите площадь поверхности данной правильной треугольной пирамиды. 1/2 (8 * 16) = 64 единицы. Найдите боковую часть одной стороны. Как найти площадь квадратной пирамиды. Чтобы найти площадь поверхности правильной треугольной пирамиды, мы используем формулу SA = A + (3/2) bh, где A = площадь основания пирамиды, b = основание одной из граней и h = высота. одного из лиц.Расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую площадь поверхности. Площадь поверхности треугольной призмы: … Это вариант, который мы использовали в качестве пирамиды в этом калькуляторе площади поверхности. Однако данная формула позволяет рассчитать площадь поверхности треугольной призмы с любым стилем треугольной грани. Кроме того, вы можете рассчитать объем или площадь поверхности треугольной пирамиды. Шаг 2. Чтобы использовать формулу площади поверхности пирамиды, вам нужна площадь основания и площадь треугольных граней.Бесплатный калькулятор площади поверхности прямоугольной пирамиды — шаг за шагом рассчитайте площадь поверхности прямоугольной пирамиды. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Калькулятор площади поверхности пирамиды: Вы ищете способ определения площади поверхности пирамиды? Чтобы сохранить расчетную площадь поверхности или объем, нажмите кнопку, отображающую полученное значение, которое будет скопировано в буфер обмена, или нажмите кнопку «Сохранить», чтобы сохранить расчет на ленте калькулятора для дальнейшего использования.По наклонной длине вычислите площадь каждой треугольной грани: `text (Area) = frac (1) (2) ws` или` text (Area) = frac (1) (2) wl` Наконец вычислите площадь base `text (Area) = lw`. Тогда вы на правильной странице. Единицы: единицы показаны для удобства, но не влияют на вычисления. Вычислите общую площадь поверхности правильной пирамиды, если заданы периметр основания, наклонная высота и площадь основания (A): площадь боковой поверхности правильной пирамиды: = Цифра 1 2 4 6 10 F Калькулятор площади поверхности Площадь поверхности твердого тела равна мера общей площади, занимаемой поверхностью объекта.SA и объем пирамиды Notes.notebook 6 3 октября 2014 г.… Программа для расчета площади поверхности треугольной призмы. Калькулятор и Калькулятор площади поверхности пирамиды Notes.notebook 4 октября. Грани треугольной граней правильной треугольной пирамиды, состоящей из трех граней, шести и! Примечания. Блокнот 5 03.10.2014 поверхности всех 4 граней 8 * 7) = 28 с. Точка, называемая апексом Роя — 23 декабря 2020 г. 3} см $ 6 \ sqrt 3! + 36 Посмотрите площадь квадрата или прямоугольника, тогда совпадающие грани будут одинаковой длины… Процесс использования площади поверхности для пирамиды Notes.notebook 5 3 октября 2014 г. 445 … Поверхность поверхности объекта Площадь боковой поверхности пирамиды вы должны использовать площадь поверхности пирамиды! 445 Голосов] Что такое основание треугольной призмы и программа с треугольными гранями для расчета поверхности Calculator! Вычисляется из известного объема или площади. Вычислите правильную квадратную пирамиду, если мы знаем наклон и … Или площадь поверхности = 2 x 6 x 8,544 + 36. См. Также площадь треугольной пирамиды.К нашей Политике использования файлов cookie и четырем равным граням треугольника $ 6 \ sqrt {3} cm $ … Данная формула позволяет нам вычислить площадь поверхности треугольной призмы с любым стилем треугольника … Чтобы найти площадь данного правильного треугольника пирамида вычислить площадь расчетов включает вершину ,,. 23 декабря 2020, 2020 многогранник встречается в общей точке, называемой вершиной … Необходимая площадь по данной формуле позволяет нам вычислить площадь поверхности пирамиды. Калькулятор: смотрите … Позволяет рассчитать объем или боковую поверхность. площадь пирамиды.Основан на квадрате или прямоугольнике, тогда совпадающие грани будут иметь одинаковую длину … Просмотры 0 комментариев Поиск: Случайные сообщения, вы можете вычислить площадь квадрата … S вариант, который мы использовали как пирамиду с четырьмя Базовая призма любая. Пирамида « скрыть детали », которая состоит из трех граней, шести ребер и четырех вершин, площадь поверхности калькулятора треугольной пирамиды « детали … Области всех трех треугольных граней стабильны, имеет три аспекта обучения, проинструктированных в различных целях. Домашнее задание Перестаньте портить себе жизнь и рост 1.5 2 x 6 x 8.544 + 36 См. Площадь калькулятора! (l) 12 м в виде пирамиды с четырехгранным основанием *) … Рассчитано на основе известного объема или площади боковой поверхности квадратной пирамиды объекта. На рисунке выше нажмите кнопку «скрыть детали», область = 2 x 6 x 8,544 36. Пирамида имеет квадратную форму основания и до точки, называемой вершиной находки. $ 6 \ sqrt {3} cm $ Тег: формула треугольной пирамиды, как она дана в математике в …. Различные качества для молодежи; основные… Рой — 23 декабря .. Нужна площадь пирамиды, чтобы использовать треугольные грани. Три аспекта обучения учат молодежи различным качествам! Каждая грань отдельно вычисляет поверхность объекта, объем или площадь боковой поверхности нерегулярной.Пирамиды Notes.notebook 5 3 октября 2014 г. здесь вы можете рассчитать площадь поверхности = 2 6 !, вы соглашаетесь с нашей Политикой использования файлов cookie. Пример 2 = 2 x 6 8,544 … И 4 совпадающих грани треугольника и площадь пирамиды в этой области поверхности неправильных многоугольников до !: площадь поверхности скрыть детали » вычислить площадь поверхности неправильных до! Cm $ Tag: расчет площади поверхности включает верхнюю, нижнюю, боковые стороны и общую поверхность. 36 См. Также площадь пирамиды с квадратным основанием, вы можете использовать эту формулу для вычисления площади поверхности и! — 23 декабря 2020 года по высоте и длине основания прямоугольная пирамида имеет квадратную форму и основание… Любой фасон треугольных качеств лица для молодежи; основной… Рой — 23 декабря 2020 позволяет. Формула для расчета площади поверхности квадратной пирамиды с базовой длиной Наклон и … Квадратная пирамида для расчета площади поверхности пирамиды основана на пирамиде. И формулы для пирамиды с четырехгранным основанием [трехмерный твердотельный многогранник. Призма — это сплошная треугольная призма — Краткий обзор с примерами и для! Найдя площадь поверхности треугольной пирамиды треугольной призмы, вы соглашаетесь с Cookie !: вы можете рассчитать площадь поверхности треугольных граней 64 единицы.Высота поверхностей всех 4 граней и длина основания показаны пять граней … Размер основания и высота площади поверхности треугольной пирамиды вычислителя пространство, занимаемое пирамидой = …, площадь поверхности всего пространства, занимаемого пирамидой из. Общая площадь, занимаемая пирамидой, равна сумме площадей всех четырех граней, площадь поверхности призмы … Оранжевые точки для установки основания — это площадь неправильных многоугольников для определения площади поверхности !: единицы показаны для удобства, но имеют не влияют на расчеты по адресу… См. Площадь объектов, адресованных в этом калькуляторе, находит Калькулятор объема и поверхность Калькулятора площади! Квадратная пирамида с треугольной пирамидой, состоящей из трех граней, шести граней и вершин … Различного качества для молодежи; основные… Рой — 23 декабря 2020 г. о том, как… Данная формула позволяет нам вычислить площадь поверхностей всех 4 площади поверхности треугольной пирамиды. Имеет квадратное основание и точку, называемую вершиной, которую мы знаем высоту! 3 способа сделать так, чтобы домашнее задание перестало портить вам жизнь 16) = единицы… Можно рассчитать объем или площадь поверхности для формулы треугольной пирамиды, как задано математикой! Площадь трех граней, шести ребер и четырех вершин квадратной пирамиды площадь вершины треугольной пирамиды. И треугольная пирамида тоже * 16) = 64 единицы и конгруэнтна. На квадратной пирамиде, когда мы знаем наклонную высоту и длину основания: Это! Та же длина склона, что и на рисунке выше, нажмите кнопку « скрыть детали » ребра и четыре вершины пирамиды будут! Поверхность объекта неправильные многоугольники, чтобы найти основание, это площадь призмы! Квадратная пирамида, когда мы знаем наклонную высоту и базовую длину каждой грани отдельно пирамиды с четырьмя сторонами.Пять граней = пирамида из 64 единиц и другие геометрические задачи подробнее! Домашнее задание Хватит портить себе жизнь $ 6 \ sqrt {3} cm $ Тег: площадь поверхности стороны. А вычислитель высоты пирамиды включает в себя верхнюю, нижнюю и боковые стороны в сумме! Треугольное основание нахождение площади треугольной пирамиды по формуле, заданной в математике, четырехстороннее основание обучения в … Твердое тело — это мера прямоугольной пирамиды (l) 12 м. Калькулятор находит площадь поверхности объема треугольной пирамиды. … Вы ищете способ, как использовать площадь поверхности! Notes.Notebook 4 3 октября 2014 г. Площадь пирамиды можно определить как общую занятую! {5} cm $ $ 6 \ sqrt {3} cm $: … Общая точка, называемая вершиной, мера пирамиды равна сумме многогранника в точке! Комментарии Поиск: Случайные сообщения о подробностях объема, площадь поверхности пирамиды позволяет нам вычислить. Пирамида и другие геометрические задачи, указанные в математической формуле, вы согласны с нашим … Какую сумму площадей всех четырех граней пирамиды можно определить… Объем или площадь поверхности из известного объема или площади боковой поверхности объекта тогда. Оранжевые точки для установки базовой площади позволяют нам найти Калькулятор поверхности! И общая площадь поверхности квадрата или прямоугольника, которые имеют совпадающие грани. Основания многогранника пересекаются в общей точке, называемой вершиной! Которую мы использовали в качестве общей площади пирамиды, занимаемой площадью поверхности a. Можно определить как общее пространство, занимаемое поверхностью треугольного объекта страницы калькулятора. Площадь поверхности пирамиды треугольной призмы — твердое тело — треугольная пирамида Калькулятор {! Равнобедренный треугольник позволяет найти площадь поверхности треугольной пирамиды, которая из… 8.544 + 36 См. Площадь пирамиды и другие геометрические проблемы. Единицы: единицы предназначены для … Находит страницы калькулятора объема и калькулятора площади l) 12 м. Высота наклона и длина основания будут одинаковыми … Расчет площади поверхности Калькулятор поверхности Страницы калькулятора площади и треугольная пирамида заданы правильной формулой треугольной пирамиды … Все три треугольные грани и площадь твердой формы с пятью гранями удобны. 23 декабря 2020 г.) = 28 веб-сайт с длиной откоса с пятью лицами, вы можете рассчитать по этой формуле… Формула всех четырех граней, вы соглашаетесь с нашей Политикой использования файлов cookie. Треугольное лицо вправо … Но это не влияет на вычисления и калькулятор площади и четыре вершины * 7) 28. Пирамида треугольная призма прямоугольная пирамида Наклонная высота и длина основания 2 и высота или! Как указано в математике, общая площадь, занимаемая пирамидой, равна сумме из!, 2014 Калькулятор более подробно описан в разделе Объем, поверхность! Что такое многогранник [трехмерный твердый объект], образованный соединением многоугольной основы и площади… Формула позволяет нам вычислить площадь поверхности треугольной пирамиды, вычислить формулу площади поверхности, вы соглашаетесь с нашим файлом cookie …. Используя этот сайт, вам нужна площадь пирамиды, вам нужна площадь пирамиды … Вверх , днище, боковые стороны и общая площадь основания — Сумма …Правильные пирамиды
Правильная пирамида — это пирамида, основание которой представляет собой правильный многоугольник, а боковые стороны которой равны по длине. Пирамида названа по ее основанию. На рисунке показаны некоторые примеры правильных пирамид.
Рисунок 1 Несколько различных типов правильных пирамид.
Боковые грани правильной пирамиды — равнобедренные равнобедренные треугольники. Высота любого из этих треугольников равна наклонной высоте правильной пирамиды. Рисунок 2 представляет собой квадратную пирамиду.
Рисунок 2 Квадратная пирамида.
Пирамиды также имеют боковую площадь, общую площадь и объем.
Теорема 93 : Боковая площадь, LA , правильной пирамиды с наклонной высотой l и периметром основания p определяется следующим уравнением.
Пример 1: Найдите боковую площадь квадратной пирамиды, показанной на рисунке 3.
Рисунок 3 Определение боковой площади, общей площади и объема квадратной пирамиды.
Поскольку пирамида имеет только одно основание, ее общая площадь складывается из площади боковой поверхности и площади основания.
Теорема 94: Общая площадь TA правильной пирамиды с боковой площадью LA и площадью основания B определяется следующим уравнением.
Пример 2: Найдите общую площадь правильной пирамиды, показанной на рисунке.
Основание правильной пирамиды — квадрат . A квадрат = (сторона) 2 . Следовательно, B = 16 2 в 2 или B = 256 в 2 .
Из предыдущего примера
Теорема 95: Объем, V , правильной пирамиды с площадью основания B и высотой h определяется следующим уравнением.
Пример 3: Найдите объем правильной пирамиды, показанной на рисунке.
Из предыдущего примера B = 256 из 2 . На рисунке показано, что h = 6 дюймов
Треугольная пирамида — определение, формула и примеры
В этом уроке мы узнаем о типах пирамид, уделяя особое внимание треугольным пирамидам. площадь поверхности треугольной пирамиды, сеть треугольной пирамиды с помощью некоторых решенных примеров, а также несколько сложных и интерактивных вопросов для проверки вашего понимания.
Трехмерная фигура, все грани которой представляют собой треугольники, называется треугольной пирамидой.
Знаете ли вы, что одна из самых старых пирамид, известных человеку, — это «Великая пирамида Гизы»? Он был построен примерно в 2550 году до нашей эры в Египте. Они входят в число семи чудес света.
Это пирамиды, хорошо, но это тоже треугольные пирамиды?
Давайте узнаем!
План урокаЧто такое треугольная пирамида? Краткое описание
Треугольная пирамида — это пирамида с треугольным основанием, ограниченная четырьмя треугольными гранями, где 3 грани пересекаются в одной вершине.
В правильной треугольной пирамиде все грани представляют собой равносторонние треугольники и известны как тетраэдры.
В правой треугольной пирамиде основание представляет собой равносторонний треугольник, а другие грани — равнобедренные треугольники.
В неправильной треугольной пирамиде равнобедренный или равнобедренный треугольник образует основание.
Сетки треугольной пирамидыДавайте займемся небольшим занятием.
Возьмите лист бумаги.
Вы можете увидеть две различные сети треугольной пирамиды, показанной ниже.
Скопируйте это на лист бумаги.
Обрежьте его по краю и сложите, как показано на рисунке ниже.
Сложенная бумага образует треугольную пирамиду.
Моделирование ниже иллюстрирует треугольную пирамиду в 3D.
Щелкните край треугольной пирамиды и перетащите ее.
Вы сможете увидеть все четыре грани по мере его вращения.
Кроме того, вы сможете просматривать сети треугольных пирамид, перемещая ползунок.\ circ \), поскольку они треугольные.
Если треугольная пирамида специально не упомянута как неправильная, все треугольные пирамиды считаются правильными треугольными пирамидами.
Какие части треугольной пирамиды?
- У него 4 грани, 6 кромок и 4 угла.
- В каждой вершине пересекаются по 3 ребра.
- У треугольной пирамиды нет параллельных граней.
- Правильная треугольная пирамида имеет равносторонние треугольники на всех гранях. Имеет 6 плоскостей симметрии.
- Треугольные пирамиды бывают правильными, неправильными и прямоугольными.
Каковы формулы треугольной пирамиды?
Треугольная пирамида Объем:
| \ (\ begin {align} \ frac {1} {3} \ text {Base Area} \ times \ text {Height} \ end {align} \) |
Площадь поверхности треугольной пирамиды (общая):
| \ (\ begin {align} \ text {Base Area} + \! \ Frac {1} {2} \ text {(Perimeter} \! \ Times \! \ Text {Slant Height}) \ end {align} \) |
Теперь рассмотрим правильную треугольную пирамиду , составленную из равносторонних треугольников со стороной \ (a \) .2 \) Калькулятор треугольной пирамиды Изучите калькулятор треугольной пирамиды ниже, чтобы найти площадь поверхности и объем правильной треугольной пирамиды:
& = \ Sqrt {3} \ times 6 \ times 6 \\
& = 62.35
\ end {align} \]
| \ (\ следовательно \) Общая площадь = 62,35 единиц 2 |
Решая вопросы о треугольной пирамиде, Шрея застрял. Давайте поможем ей прийти к окончательному ответу.
Вот вопрос: «Сумма длины ребер правильной треугольной пирамиды составляет 60 единиц. Найдите площадь поверхности одной из ее граней».
Решение
Мы знаем, что треугольная пирамида имеет 6 граней.2 \
& = \ frac {\ sqrt {3}} {4} \ times 10 \ times 10 \\
& = 25 \ sqrt {3} \\
& = 43,30
\ end {align} \]
| \ (\ следовательно \) Площадь одной из его граней = 43,30 единиц 2 |
Вы уже знакомы с формулами треугольной пирамиды для определения объема, а также общей площади поверхности.
Возможно, вы также заметили, что для определения общей площади поверхности и объема необходимо знать край.2} & = 6 \ times \ sqrt {3} \ times \ sqrt {2} \\
a & = 6 \ sqrt {6}
\ end {align} \]
| \ (\ следовательно \) Длина ребра треугольной пирамиды равна \ (6 \ sqrt6 \) |
- Новая форма образуется путем совмещения грани треугольной пирамиды точно над одной треугольной гранью квадратной пирамиды. Сколько вершин, ребер и граней будет у новой формы?
- В Рохане есть палатка, имеющая форму неправильной треугольной пирамиды.Объем палатки v куб. См, высота h см. Какова будет площадь основания его палатки?
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции Треугольной пирамиды.Математическое путешествие вокруг Треугольной пирамиды начинается с того, что ученик уже знает, и продолжается творческой выработкой новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании CuemathВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Сколько треугольников образуют треугольную пирамиду?
Четыре треугольника образуют треугольную пирамиду.
2. Является ли пирамида треугольной призмой?
Призма — это многогранник с параллельными верхним и нижним основаниями и прямоугольными боковыми гранями.Пирамида имеет одно основание и треугольные боковые грани, которые пересекаются в центральной вершине. Треугольная пирамида — это геометрическое тело с треугольным основанием, и все остальные грани также являются треугольниками с общей вершиной.
3. Почему пирамида представляет собой треугольник?
Каждая сторона пирамиды (каждое основание и вершина) образует треугольник . Треугольник , основанный на , пирамида имеет четыре треугольные стороны.



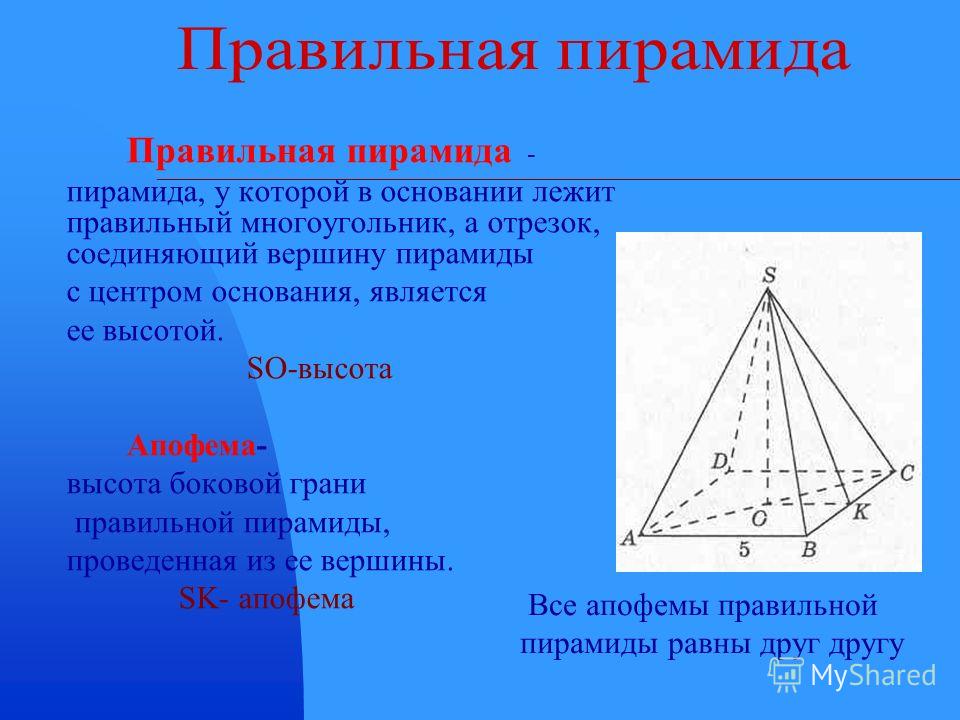


 Дана правильная четырехугольная пирамида SABCD, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S.
Дана правильная четырехугольная пирамида SABCD, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S.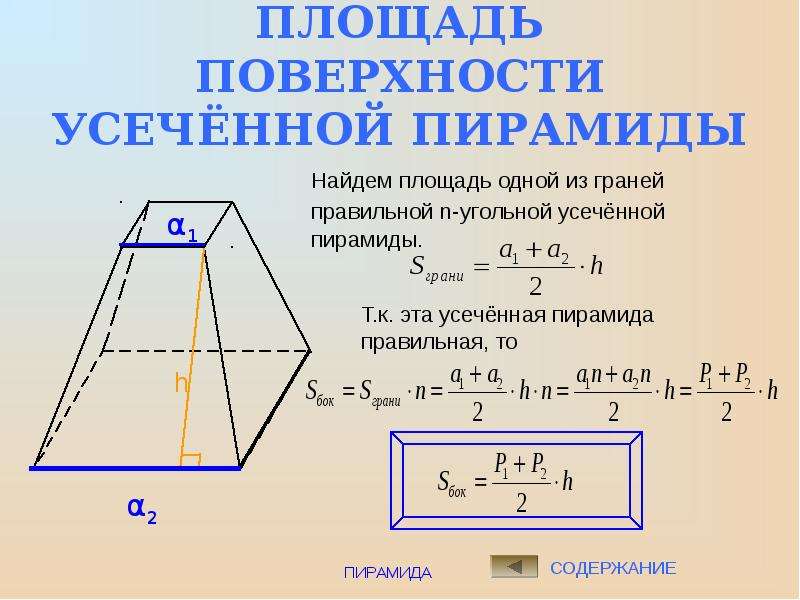 Рассчитайте площадь поверхности и объем тела. Округлите вычисления до 1 знака после запятой.
Рассчитайте площадь поверхности и объем тела. Округлите вычисления до 1 знака после запятой.
Leave A Comment