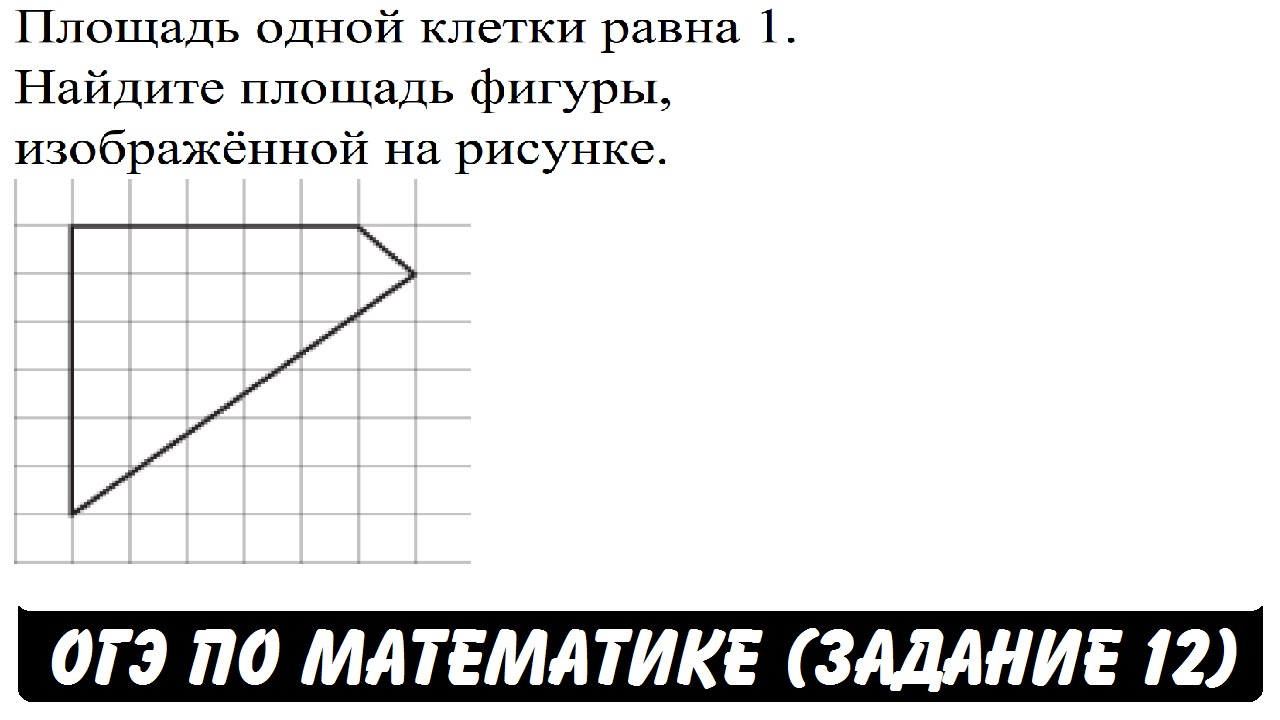
Главная → Видеоуроки → ОГЭ (ГИА) по математике. Задача 12. Описание видеоурока: Модуль «Алгебра», задача 12. Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке. 00:03:18Валерий Волков 8 25.01.2015 Будем рады, если Вы поделитесь ссылкой на этот видеоурок с друзьями! Новости образования | ЕГЭ по математике Профильный уровень Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18 Задание 19 Задание 20 Задание 21 ГИА по математикеЗадача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 Задача 13 Задача 14 Задача 15 Задача 16 Задача 17 Задача 18 Задача 19 Задача 20 Задача 21 Задача 22 Задача 23 Задача 24 Задача 25 Задача 26 Демонстрационные варианты ОГЭ по математике Математика. 5 класс.Натуральные числа Обыкновенные дроби Десятичные дроби Проценты Математика. 6 класс.Делимость чисел Сложение и вычитание дробей с разными знаменателями Умножение и деление обыкновенных дробей Отношения и пропорции Положительные и отрицательные числа Измерение величин Математика. 7 класс.Преобразование выражений Многочлены Формулы сокращенного умножения Математика. 8 класс.Модуль числа. Уравнения и неравенства. Квадратные уравнения Квадратные неравенства Уравнения с параметром Задачи с параметром Математика. 9 класс.Функции и их свойства Прогрессии Векторы Комбинаторика, статистика и теория вероятностей Математика. 10 — 11 класс.Числовые функции Тригонометрические функции Тригонометрические уравнения Преобразование тригонометрических выражений Производная Степенные функции Показательная функция Логарифмические функции Первообразная и интеграл Уравнения и неравенства Комбинаторика Создаёте видеоуроки?Если Вы создаёте авторские видеоуроки для школьников и учителей и готовы опубликовать их, то просим Вас связаться с администратором портала. Актуально Физкультминутки для школьников и дошкольников Подготовка к ЕГЭ Подготовка к ОГЭ |
Обобщающий урок геометрии для 8 класса «Решение задач по теме «Площадь»
#8 класс #Геометрия #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование
Решение задач по теме : « Площадь» Подготовила : Каровайцева Г.В.
Цель урока: обобщить, систематизировать и закрепить знания по теме: “Площади” Рассмотреть решение задач из ОГЭ.
Задачи урока:
образовательные: обеспечить условия для систематизации и обобщения знаний о четырехугольниках, их свойствах, признаках, площадях, закреплении основных понятий базового уровня , совершенствовать навыки решения задач на применение формул при вычислении площадей многоугольников;
развивающие: развитие логического мышления, математической речи, интуиции, сознательного восприятия материала; формирование у учащихся адекватной самооценки.
воспитательные: воспитание активности, самостоятельности, аккуратности, чувства ответственности, культуры общения, интереса к предмету и ответственность за общий результат.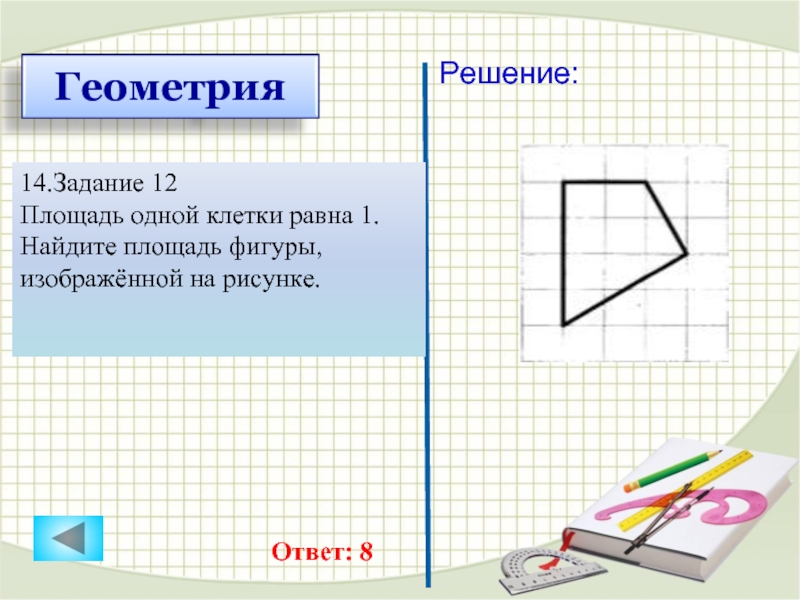
1.Противолежащие стороны параллельны у… 2.Все стороны равны у … 3. Только две стороны параллельны … 4. Противолежащие углы равны у … 5. Сумма соседних углов равна 180 у … 6.Все углы прямые у … 7.Диагонали точкой пересечения делятся пополам у … 8.Диагонали равны у … 9.Диагонали взаимно перпендикулярны у … 10. Диагонали являются биссектрисами его углов у … 11. Противолежащие стороны равны у … 12. Диагонали равны и являются биссектрисами у … 13. диагонали равны и перпендикулярны у… 14.Равны углы, прилежащие к одной стороне у … 15.Диагонали различны по длине у … 16. Какая фигура разбивается одной диагональю на 2 равных треугольника? 17. Какая фигура разбивается диагоналями на 4 равных треугольника? 18.Какая фигура разбивается диагоналями на 2 пары равных треугольника? 1 2 3 4 4 5 6 повторение
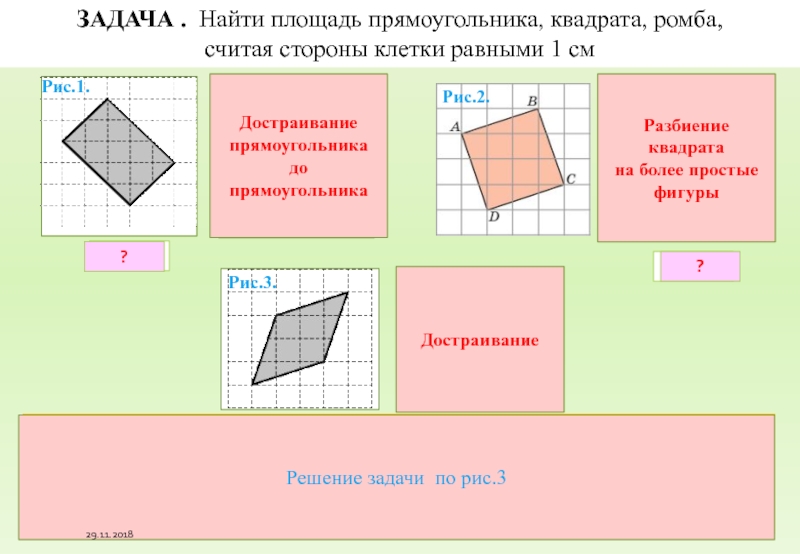
Повторение .
Для каждой фигуры выбрать нужную формулу
№ 1. Найдите площадь трапеции, изображённой на рисунке. № 2 Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке. Решите задачи В 8. В 9.
№ 3. № 4. Найдите площадь параллелограмма, изображённого на рисунке. Найдите площадь трапеции, изображённой на рисунке.
№ 5. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9. В равнобедренной трапеции основания равны 3 и 9 . Найдите площадь трапеции. № 6
№ 7. Найдите площадь треугольника, изображённого на рисунке. Найдите площадь ромба, если его диагонали равны 14 и 6. Периметр квадрата равен 160. Найдите площадь квадрата. № 8 № 9
Динамическая пауза
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
У каждого ученика имеется набор из 10 равнобедренных прямоугольных треугольников, катет которых равен 4 см . Построить, найти площадь и рассказать о применении фигур: 1) Квадрат, площадь которого 16 см2 2) Ромб, площадь которого 32 см2 3) Прямоугольник, площадь которого 32 см2
4.
Ребята, знание геометрии необходимо в различных областях человеческой деятельности. Формулы площадей плоских фигур нам приходится повторять на протяжении всей жизни. И сегодня мы рассмотрим значение геометрии в профессии дизайнера.
— Дизайнер – это специалист, имеющий художественное образование.
— В сферу деятельности дизайнера входит дизайн одежды, обуви, мебели, ткани, дизайн рекламы, ландшафтный дизайн, архитектурный дизайн.
1). Полиграфический дизайн (Красочное и яркое оформление визиток, открыток, буклетов)
2) Ландшафтный дизайн (оформление садов, парков, клумб)
3).
1. Представьте, что вы дизайнер интерьера. Поступил заказ «Подсчитать сколько краски потребуется для покраски стен комнаты, если её размеры 6 х 8 х 3 м, при этом учтите, что есть дверь размером 1м х 2м, три окна размерами 1 м х 1 м и шкаф размером 2м х2м (на 1кв.м. расходуется 200 г краски)? Сколько плиток паркета 0,5м х 0,5м нужно купить для пола?» 3 м «Дизайнер» 8 м 6 м 3 м 3 м 8 м 6 м 1 м 1 м 2 м 2 м 1 м 2 м 0,5 м 0,5 м
5
6
7
1
2
8
3
4
По горизонтали:
1.
Размер ячейки, площадь поверхности и объем
Размер ячейки, площадь поверхности и объемПочему клетки такие маленькие? Ответ на этот вопрос имеет столько же делать с математикой как с биологией. Представьте, что клетка имеет форму примерно куб.
По мере увеличения размера клетки отношение площади ее поверхности к объему
изменения.
Площадь поверхности и объем рассчитываются, как показано на
рисунок ниже:
площадь стороны равна длина x ширина . Мы можем записать это как A=L*W , а когда стороны одинаковой длины, мы можем написать A=L 2
Поскольку у куба шесть сторон, давайте также рассчитаем площадь поверхности всей внешней части ячейки как 6 * L 2
объем куба равен длине x ширине x высоте , или V=L*W*H , и когда стороны имеют одинаковую длину, мы можем написать В=Л 3
Вот где становится интересно. Поскольку мы продолжаем удваивать переменную L , от 1 до 2, от 4 до 8, площадь поверхности и объем не увеличиваются с одинаковой скоростью.
Вопросы :
1.
Перечислите некоторые вещества, проникающие через клеточную мембрану:
2. Почему важно, чтобы клетка имела большую площадь поверхности относительно его объема? (Другими словами, высокие площадь поверхности до соотношение объемов ?)
3. Представьте, что длина стороны ячейки может быть любого размера. Рассчитайте, что произойдет с отношением площади поверхности к объему, если клетка растет. Единицы здесь могут быть ничего, так как мы просто гипотезы.
Л | 6 л 2 | Л 3 | 6л 2 / л 3 | |
4.
Создайте свой собственный график x-y с помощью Create-A-Graph или Excel, где x — площадь поверхности, а y — объем, и подставьте диапазон значений. Что происходит с отношением площади поверхности к объему при увеличении размера клетки? (Если бы площадь поверхности и объем увеличивались с одинаковой скоростью, линия была бы диагональной с наклоном 1.) Что на самом деле происходит при малых размерах? В промежуточных размерах? В больших размерах? Загрузите электронную таблицу Excel, в которой я провел свои расчеты и создал эти графики: Surface_area_volume_graph.xlsx.
Рис. 2: График зависимости длины стороны клетки от отношения площади поверхности к объему. По мере уменьшения размера ячейки до нуля отношение SA:V приближается к бесконечности.
5. Поскольку транспорт материалов в клетку и из нее возможен только происходит на поверхности клетки, что происходит, когда клетки становятся больше? Как это накладывает ограничение на размер ячейки?
6. Таким образом масштабируются не только клетки. Целые животные тоже. Изучение размера тела в связи с анатомией, физиологией и поведением называется аллометрией. Для гомеотермных (животных, которые пытаются поддерживать постоянную температуру тела) необходимо производить тепло по мере его потери в окружающую среду, чтобы поддерживать равновесие. Если потеря тепла происходит только на открытых поверхностях, что бы вы предсказали относительно скорости метаболизма на единицу ткани тела крупного животного по сравнению с маленьким?
7. Возьмите то, что вы знаете об отношении площади поверхности к объему, и попробуйте
чтобы объяснить следующий график, который известен как «кривая мыши к слону». Предположим, что скорость метаболизма связана с теплотой
производство и что все эти животные пытаются сохранить свое
тела нагреваются в одинаковых условиях окружающей среды.
Обратите внимание, например
что слон имеет массу (и объем) более чем в 1000 раз больше
мыши, в то время как скорость ее метаболизма (и теплопродукция) всего лишь
примерно в 100 раз больше, чем у мыши. Другими словами, «Почему слон может больше нагреваться?
эффективно (на единицу массы), чем мышь?»
Кривая Броуди (1945) от мыши к слону
8. «Правило Аллена» предсказывает, что эндотермические животные (те, которые регулируют температуру своего тела внутренне) с одинаковым объемом тела должны иметь разные площади поверхности, предназначенные либо для помощи, либо для препятствия рассеиванию тепла, в зависимости от температуры их окружения. Объясните со ссылкой на площадь поверхности и объем. (Подумайте о необходимости удержания тепла в холодном климате или о теплоотдаче в жарком климате и сделайте предсказание о типах телосложения.)
9. «Правило Бергмана» гласит, что среди видов животных, имеющих
глобальное распространение, размер взрослого тела, как правило, самый большой в
полярные районы, средние в умеренном климате и наименьшие в тропическом
те.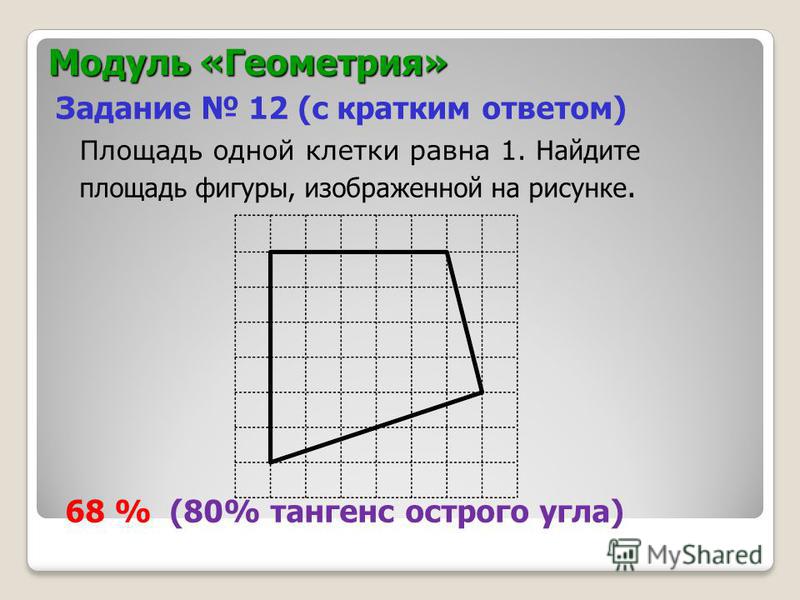
Хотя есть исключения, в целом это так. Почему
должно быть так?
10. Контрольный вопрос: В одном из моих любимых старых фильмов о монстрах Их , гигантские муравьи атакуют город. К сожалению, могло никогда не случится. Невероятная сила муравья зависит от его небольшой размер. Увеличьте его даже до человеческого размера, и он рухнет под собственным весом на этих тощих ножках. Объем (и поэтому вес) масштабируется до степени 3, а площадь поверхности (и размер) масштабируйте до степени 2. Создайте график, показывающий, почему гигантский муравей не может разрушить город, а вместо этого рухнет под собственным весом.
11. Контрольный вопрос: Как показано эмпирически на графике Броди, мощность пропорциональна массе в степени 0,734, примерно 3/4, однако отношение площади поверхности к объему дает значение только 2/3 или 0,67. Животные в реальном мире работают лучше, чем ожидалось, но животные в реальном мире не полностью полагаются на площадь поверхности для обогрева, охлаждения, газообмена и т.
д. Возможно, что система кровообращения позволяет более крупным организмам улучшать площадь поверхности. проблема с объемом? Объяснять.
Дополнительное чтение:
http://www.tiem.utk.edu/~gross/bioed/bealsmodules/area_volume.html
Как рассчитать отношение площади поверхности к объему (биология)
Все живые организмы состоят из клеток. Некоторые, как и люди, имеют множество клеток, в то время как другие имеют только одну. За некоторыми исключениями, отдельные клетки крошечные и их можно увидеть только в микроскоп. Почему клетки такие маленькие? Вот тут-то и появляется коэффициент отношения площади поверхности к объему .
Отношение площади поверхности к объему , также известное как sa/vol или SA:V, относится к величине площади поверхности объекта или набора объектов в единице объема.
В чем разница между размером, поверхностью и объемом клетки?
Итак, в чем разница между размером клетки, площадью поверхности и объемом? Давайте взглянем!
Площадь поверхности и объем определяют размер ячейки .
Большинство животных и растительных клеток имеют размер от 0,01 до 0,10 мм и не видны невооруженным глазом (наименьший размер, который вы сможете увидеть, составляет около 0,05 мм). Размер клеток обычно измеряется в микрометрах (мкм).
В геометрии площадь поверхности объекта — это площадь, занимаемая поверхностью объекта, а его объем — это пространство внутри него.
Площадь поверхности и объем
В биологии площадь поверхности и объем играют важную роль в обмене веществ в клетке. В этом случае площадь поверхности относится к общей площади организма, подвергающегося воздействию внешней среды. Объем относится к общему объему пространства внутри организма.
Отношение площади поверхности к объему (SA:Vol)
Отношение площади поверхности к объему (отношение S/V) относится к количеству поверхности объекта по отношению к его размеру. Чтобы вычислить отношение площади поверхности к объему (отношение S/V), вы можете разделить площадь поверхности на объем .
Чтобы помочь вам понять отношение поверхности к объему, мы будем использовать пример куба. По мере увеличения размера куба объем будет увеличиваться быстрее, чем площадь поверхности, и соотношение будет уменьшаться.
Рис. 1 – Отношение поверхности к объему куба
Расчет отношения куба (рис. 1):
SA = площадь одной стороны x 6 сторон (пример: 1 см x 1 см x 6 см) = 6 см2)
Объем = длина х ширина х высота (пример: 1 см х 1 см х 1 см = 1 см2)
Важное примечание: площадь всегда выражается в квадратах, а объем всегда быть в кубических единицах!
$$ \textbf{Отношение S/V} = \frac{\textbf{Площадь поверхности}}{\textbf{Объем}} $$ 9{2} $$
Примечание: π (пи) ~3,14 (3 ст.ф.)
По мере увеличения радиуса сферы площадь поверхности увеличивается как функция квадрата, а объем увеличивается в кубе. Таким образом, с увеличением радиуса объем будет увеличиваться быстрее. В какой-то момент при увеличении размера соотношение станет слишком низким, и вещества не смогут входить или выходить за достаточное время для выживания клетки.
Вещества не будут распределяться достаточно быстро путем диффузии внутри клетки.
Клетка перестанет расти, когда будет достаточно площади поверхности для эффективного распределения веществ внутри клетки и в окружающей среде.
Каково биологическое значение размера и отношения площади поверхности к объему?
Организмы переносят материалы между внутренней и внешней средой, чтобы выжить. Прокариотические и эукариотические клетки требуют меньшего размера. Это должно способствовать эффективному обмену веществ. Более мелкие одноклеточные организмы могут полагаться на диффузию газов и обмен веществ. Более высокое отношение площади поверхности к объему позволяет этим организмам быть более эффективными. Более крупные организмы, такие как животные, нуждаются в специализированных органах для облегчения обмена веществ.
Легкие — это органы, приспособленные к газообмену у человека.
За исключением тепла, обмен будет происходить двумя способами:
- Пассивный (энергия не требуется) путем диффузии (движение молекул) или осмоса (движение молекул воды).
- Активируется за счет активного транспорта (требуется метаболическая энергия).
Больше о движении энергии можно найти в наших статьях об активном транспорте, диффузии и осмосе.
Размер и скорость метаболизма организма влияют на количество обмениваемого материала. Организмы с более высокой скоростью метаболизма должны будут обмениваться большим количеством веществ и, в свою очередь, им потребуется более высокое соотношение SA:Vol.
Увеличение отношения площади поверхности к объему
Клетки и ткани, которые специализируются на газообмене и обмене веществ, будут иметь различные приспособления для облегчения эффективного обмена.
Мы можем использовать пример кишечной ткани. Тонкий кишечник имеет приспособления для всасывания питательных веществ и минералов из пищи. Внутренняя стенка тонкой кишки, слизистая оболочка выстлана простой цилиндрической эпителиальной тканью. Слизистая оболочка покрыта складками, которые являются постоянными чертами стенки, увеличивая площадь поверхности.
Складки выступают в виде пальцевидной ткани, называемой ворсинками , для дальнейшего увеличения площади поверхности. Ворсинки заполнены кровеносными капиллярами, чтобы увеличить количество растворенной, переваренной пищи, которая может всосаться в кровоток.
Рис. 3. Упрощенная структура кишечных ворсинок
Легкие имеют альвеолы, представляющие собой крошечные мешочки на концах бронхиол. Кровь и легкие обмениваются кислородом и углекислым газом в альвеолах. Стенки альвеол очень тонкие, и они также имеют перепончатые расширения, называемые микроворсинками, которые увеличивают общую поверхность мембраны.
Опасности увеличения площади поверхности
Мы установили, что клетка с большим объемом не выживет, поскольку это не будет способствовать эффективному перемещению материала внутри клетки и с внешней средой. Увеличенная поверхность тоже может вызвать проблемы. Большая площадь поверхности означает больший контакт с внешней средой, что приводит к большей потере воды, тепла и растворенных веществ.
Кроме того, особенно у экстремофилов , контроль температуры может нарушаться в неблагоприятных условиях.
Экстремофилы, организмы, живущие в экстремальных условиях, имеют небольшое отношение площади поверхности к объему. Они живут в сложных или невозможных условиях, таких как глубокое дно океана, геотермальные горячие источники и пустыни.
Например, белые медведи на Северном полюсе имеют небольшое отношение площади поверхности к объему, чтобы свести к минимуму потерю тепла из тканей, и толстый слой жира, чтобы согреться.
Отношение площади поверхности к объему – основные выводы
- Отношение площади поверхности к объему , также известный как sa/vol или SA:V, относится к , какова площадь поверхности объекта или набора объектов на единицу объема.
- Размер, площадь поверхности и объем клеток являются важными факторами обмена веществ. Площадь поверхности и объем определяют размер клетки.
- Соотношение между площадью поверхности и объемом будет определять скорость обмена веществом, рассчитываемую путем деления площади поверхности на объем.
Leave A Comment