Основные определения и свойства
| Фигура | Рисунок | Определения и свойства |
| Окружность |  | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |  | Часть окружности, расположенная между двумя точками окружности |
| Круг |  | Конечная часть плоскости, ограниченная окружностью |
| Сектор |  | Часть круга, ограниченная двумя радиусами |
| Сегмент |  | Часть круга, ограниченная хордой |
| Правильный многоугольник | 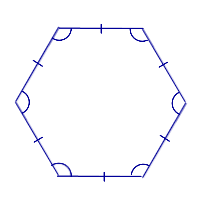 | Выпуклый многоугольник, у которого все стороны равны и все углы равны |
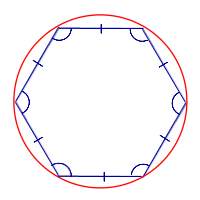 | Около любого правильного многоугольника можно описать окружность |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности |
| Дуга |
Часть окружности, расположенная между двумя точками окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |
Часть круга, ограниченная двумя радиусами |
| Сегмент |
Часть круга, ограниченная хордой |
| Правильный многоугольник |
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
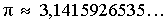
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
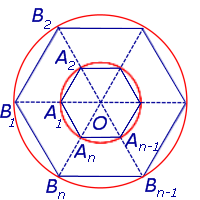
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
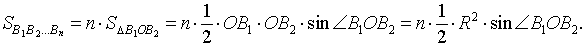
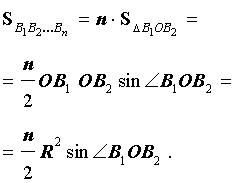
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
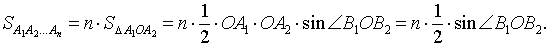
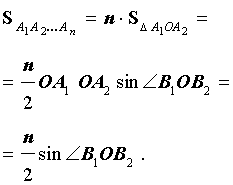
Следовательно,
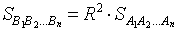
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
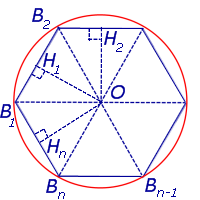
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
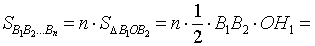
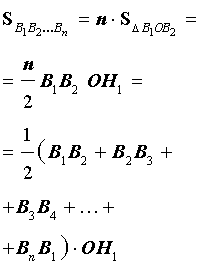
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
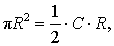
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
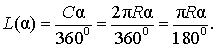
В случае, когда величина α выражена в радианах, справедлива пропорция
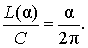
из которой вытекает равенство:
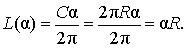
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
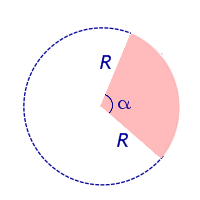
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
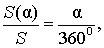
из которой вытекает равенство:
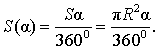
В случае, когда величина α выражена в радианах, справедлива пропорция
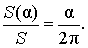
из которой вытекает равенство:
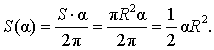
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
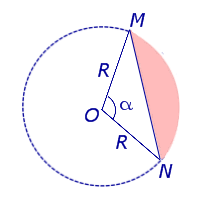
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
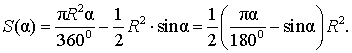
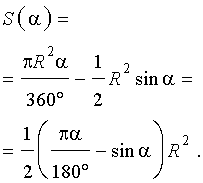
Следовательно,
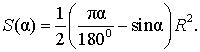
В случае, когда величина α выражена в в радианах, получаем
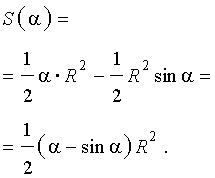
Следовательно,
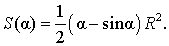
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Площадь круга
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке»).
Все, что требуется в таких заданиях — это найти радиус окружности R. Затем можно вычислить площадь круга по формуле S = πR2. Из этой формулы также следует, что для решения достаточно найти R2.
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
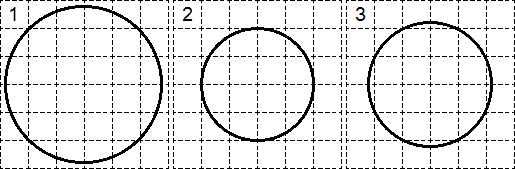
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
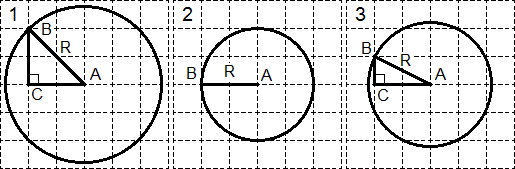
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R2 = AB2 = AC2 + BC2 = 22 + 22 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R2 = AB2 = AC2 + BC2 = 12 + 22 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
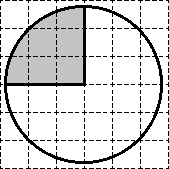
Задача. Найти площадь S закрашенного сектора. В ответе укажите S/π.
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · Sкруга.
Остается найти Sкруга — площадь круга. Для этого выполним дополнительное построение:
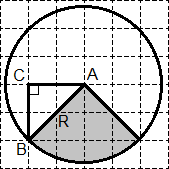
Треугольник ABC — прямоугольный. По теореме Пифагора имеем: R2 = AB2 = AC2 + BC2 = 22 + 22 = 8.
Теперь находим площади круга и сектора: Sкруга = πR2 = 8π; S = 0,25 · Sкруга = 2π.
Наконец, искомая величина равна S/π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010—2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
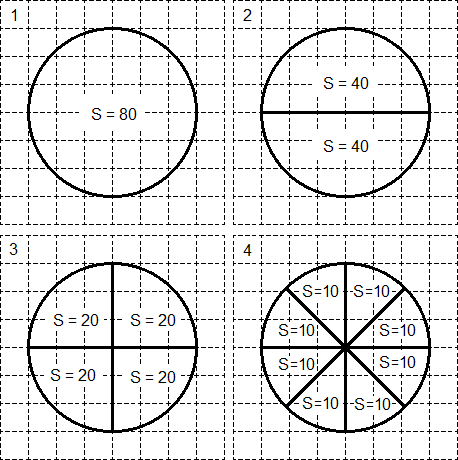
Пусть исходный круг имеет площадь Sкруга = 80. Тогда его можно разделить на два сектора площадью S = 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S = 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S = 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь Sкруга = 240, то «ошметки» имеют площадь S = 240 : 8 = 30;
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
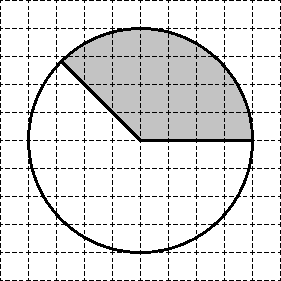
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40 : 5 = 8. Получим:
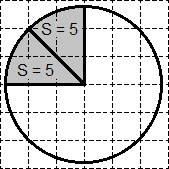
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64 : 8 = 8.
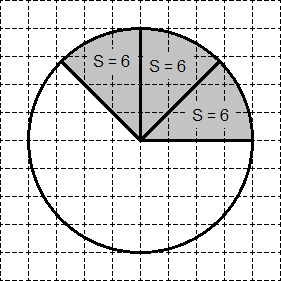
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S = 48 : 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
Смотрите также:
- Задача B5: площадь сектора
- Задача B5: площадь закрашенного сектора
- Схема Бернулли. Примеры решения задач
- Пробный ЕГЭ 2012. Вариант 10 (без логарифмов)
- Тригонометрические функции
- ЕГЭ-2014 по математике и открытый банк задач
Площадь круга
Формулы и калькулятор для вычисления площади круга для разных исходных данных. Таблица с формулами площади круга. Наш калькулятор поможет вам бесплатно в режиме онлайн вычислить площадь круга или проверить уже выполненные вычисления.
Таблица с формулами площади круга (в конце страницы)
— Вычисления (показано) (скрыто)
— примечания (показано) (скрыто)
1
Площадь круга через радиус
… подготовка …
r — радиус
2
Площадь круга через диаметр
… подготовка …
D — диаметр
3
Площадь круга по длине окружности
… подготовка …
— длина окружности
4
Площадь круга через вписанный в круг квадрат
… подготовка …
a — сторона
5
Площадь круга вписанного в квадрат
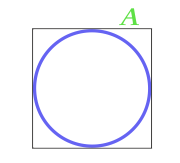
… подготовка …
A — сторона
6
Площадь круга описанного около произвольного треугольника
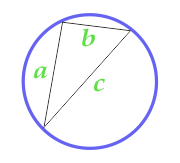
Данная формула применима только, если вокруг треугольника можно описать круг, то есть все три вершины треугольника должны лежать на линии окружности. Треугольник в данном случае может быть любым.
Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника
… подготовка …
a — сторона
b — сторона
c — сторона
7
Площадь круга описанного около равностороннего треугольника
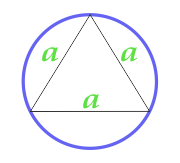
… подготовка …
a — сторона
8
Площадь круга описанного около равностороннего треугольника, вычисляемая по высоте треугольника
… подготовка …
h — высота
9
Площадь круга описанного около равнобедренного треугольника
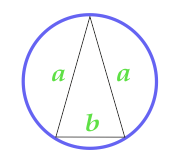
… подготовка …
a — сторона
b — основание
10
Площадь круга описанного около прямоугольного треугольника
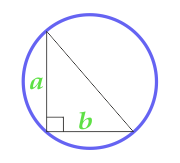
… подготовка …
a — сторона
b — сторона
11
Площадь круга вписанного в равнобедренный треугольник
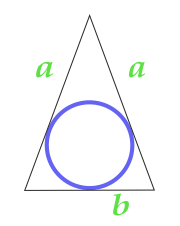
… подготовка …
a — сторона
b — основание
12
Площадь круга вписанного в равнобедренный треугольник, вычисляемая по боковым сторонам треугольника и углу между ними
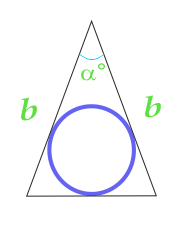
… подготовка …
b — сторона
α — угол между сторонами
13
Площадь круга вписанного в прямоугольный треугольник
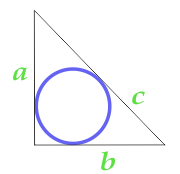
… подготовка …
a — сторона
b — сторона
c — сторона
14
Площадь круга вписанного в прямоугольный треугольник, вычисляемая по стороне и углу
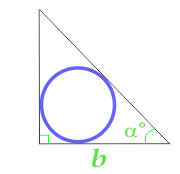
… подготовка …
b — сторона
α — угол при основании
15
Площадь круга вписанного в равносторонний треугольник
… подготовка …
a — сторона
16
Площадь круга вписанного в равнобедренную трапецию, вычисленная по основанию трапеции и углу при основании
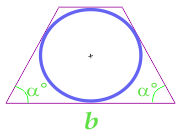
… подготовка …
b — сторона
α — угол при основании
17
Площадь круга описанного около равнобедренной трапеции, рассчитанная по боковым сторонам трапеции, ее диагонали и основанию
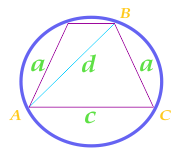
Для вычисления площади круга, предварительно рассчитаем полупериметр треугольника ABC
… подготовка …
a — сторона
c — сторона
d — диагональ
18
Площадь круга описанного около прямоугольника
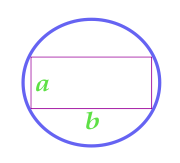
… подготовка …
a — сторона
b — сторона
19
Площадь круга описанного около правильного многоугольника
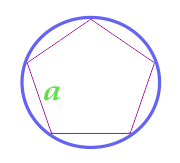
… подготовка …
a — сторона
N — количество сторон многоугольника
20
Площадь круга описанного около правильного шестиугольника
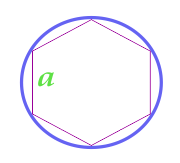
… подготовка …
a — сторона
Примечание:
Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°
Таблица с формулами площади круга
Определения
Круг – это геометрическая плоская фигура, ограниченная линией состоящей из множества точек равноудаленных от одной точки – центра круга. Кривая замкнутая линия проведенная через равноудаленные точки, образует окружность.
Диаметр круга – это отрезок в виде прямой линии, проходящей через центр окружности и соединяющий две точки лежащие на окружности.
Радиус круга – это прямой отрезок соединяющий центр окружности с любой точкой лежащей на окружности.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь круга — это численная характеристика, характеризующая размер плоскости, ограниченной линией окружности. Вычислить площадь круга можно с помощью числа Пи и радиуса окружности, или с помощью других известных исходных данных.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Площадь круга и его частей. Подробная теория.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Круг
 |
, — радиус, — число |
Производит впечатление? Представляешь, сколько времени математики думали, пока не додумались, что
 |
площадь круга радиуса ровно (!) в раз больше площади квадрата со стороной . |
Ну вот, а теперь площадь части круга.
Сектор
Смотри на картинку, это такая «хорошая» часть круга.
 |
, где: — величина угла сектора в радианах (т.е. в числах , , и т.д.) |
Подробнее о радианах смотри в теме «Окружность. Вписанный угол».
Сегмент
А это «плохая» часть круга – опять смотри на картинку:
 |
И даже не старайся запомнить ничего другого, хотя, конечно, можно написать сразу формулу
,
но это и есть
Площадь других частей круга
Иногда бывает, что нужно посчитать площадь какой-нибудь странной части круга. Эта часть может не быть ни сектором, ни сегментом. Как тогда быть?
Давай рассмотрим два примера.
Пример 1
Окружности радиусов и пересекаются по хорде, равной .
Найти площадь общей части кругов.
Решение
Обрати внимание, что общая часть кругов состоит из двух сегментов: красного и голубого.
Найдем площадь голубого сегмента.
Для этого нужно посмотреть на окружность с центром .
— правильный .
Значит,
(это по формуле ).
Если не помнишь, как считается площадь правильного треугольника, загляни в тему «Равносторонний треугольник».
Итак,
 |
|
А вот найти уже сложнее. Придется применять теорему косинусов!
Подставляем:
И теперь
Пример 2
На стороне треугольника как на диаметре построена окружность.
Найти площадь общей части треугольника и круга, если , , .
Решение
Проведем .
Опять наша непонятная фигура разделилась на две стандартные:
Сектор и .
, значит
(смотри тему «Окружность. Вписанный угол»)
Нужно найти
 |
|
И значит,
.
Это и есть ответ.
Что же общего в этих двух примерах, и есть ли общее правило?
Есть! И оно гласит:
| Непонятную фигуру нужно разделить на несколько стандартных, таких как сектор, сегмент, треугольник и т.д., потом посчитать площадь каждой стандартной фигуры и сложить все площади. |
ПЛОЩАДЬ КРУГА И ЕГО ЧАСТЕЙ. КОРОТКО О ГЛАВНОМ
Основные формулы:
|
|
|
Круг это плоская фигура, все точки которой, расположены на любом расстоянии от определенной точки (центр круга) но не больше заданной длины (радиус).
Радиус круга — отрезок, соединяющий центр окружности и любую, максимально удаленную от центра точку круга.
Диаметр круга — отрезок, соединяющий две любые точки максимально удаленные от центра круга и проходящий через этот центр. Диаметр, в два раза больше радиуса
Зная диаметр
или радиус круга или длину окружности, можно найти его площадь.
r — радиус круга
D — диаметр круга
π ≈ 3.14
Формула площади круга, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через радиус
Калькулятор для расчета площади круга через диаметр
L — длина окружности
О — центр круга
π ≈ 3.14
Формула площади круга если известна длина окружности, (S):
Решения задач
на тему: Площадь круга
Калькулятор для расчета площади круга через длину
- Подробности
- Автор: Сергей Кондратов
Площадь круга — формулы, примеры расчетов
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.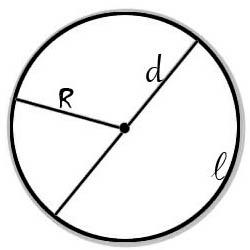 
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
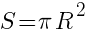
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
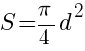
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.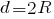
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
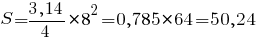
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: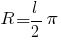 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу: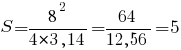
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
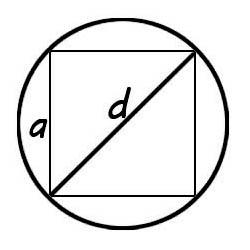
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 
отсюда 
.
После того, как найдем диагональ – мы сможем рассчитать радиус: 
.
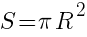
И после подставим все в основную формулу площади круга описанного вокруг квадрата: 
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
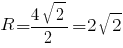
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Для того чтобы найти площадь круга, существует единственная формула, которую нужно запомнить – это произведение числа π на квадрат радиуса.
Доказательством этой формулы будет служить следующий расчет. На чертеже внутри и снаружи круга рисуем правильный многоугольник – многоугольник с равными сторонами.
Из центра круга проводим радиусы в указанные вершины многоугольников. Радиусы во вписанном многоугольнике делят его на определенное количество n одинаковых равнобедренных треугольников. Таким образом, площадь вписанного многоугольника – это n площадей треугольников Sв=nS∆. Тогда как площадь каждого треугольника, исходя из его свойств, равна 
. Так как конгруэнтные стороны a этого треугольника являются радиусами, то формула приобретает вид 
, а формула площади всего многоугольника – 
, считая сумму всех сторон nc, как периметр многоугольника P. Аналогично получаем площадь описанного многоугольника: 
. Если считать, что количество nc, как сторон многоугольника стремится к бесконечности, то его форма максимально приближается к кругу, и периметр становится близок по значению к длине окружности, а cosα стремится к 1. В этом случае обе формулы – и для вписанного, и для описанного многоугольника приобретают следующий вид:
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр или длину окружности.
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два. Так как в первоначальной формуле S=πr2 радиус возводится во вторую степень, полученная половина диаметра также должна будет быть в квадрате, и это уже будет выглядеть как 
.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель: 
. Подставляя это в основную формулу, не забываем возвести выражение во вторую степень, и получаем, что площадь круга через длину окружности равна 
.
Круглая форма
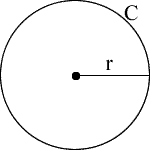
r = радиус
d = диаметр
C = окружность
A = площадь
π = pi = 3,1415926535898
√ = квадратный корень
Использование
Используйте этот калькулятор кругов, чтобы найти площадь, окружность, радиус или диаметр круга.Учитывая любую переменную A, C, r или d окружности, вы можете вычислить три других неизвестных.
Единицы: Обратите внимание, что единицы длины указаны для удобства. Они не влияют на расчеты. Единицы измерения установлены для указания порядка результатов, таких как футы, футы 2 или футы 3 . Любая другая базовая единица может быть заменена.
Формулы окружностей в терминах Pi π, радиуса r и диаметра d
радиус и диаметр:
р = д / 2
д = 2рПлощадь круга:
A = № 2 = № 2 /4
Окружность круга:
C = 2πr = πd
Круг Расчет:
С помощью приведенных выше формул и дополнительных формул вы можете вычислить свойства заданного круга для любой заданной переменной.2 \]
\ [C = 2 \ pi r \]
\ [d = 2r \]
Рассчитайте r, C и d | Учитывая A
По заданной площади круга рассчитать радиус, окружность и диаметр. Положив r, C и d в терминах A, получим следующие уравнения:
\ [r = \ sqrt {\ frac {A} {\ pi}} \]
\ [C = 2 \ pi r = 2 \ pi \ sqrt {\ frac {A} {\ pi}} \]
\ [d = 2r = 2 \ sqrt {\ frac {A} {\ pi}} \]
Рассчитайте A, r и d | Учитывая C
Учитывая окружность круга рассчитать радиус, площадь и диаметр.2} {4} \]
\ [C = 2 \ pi r = 2 \ pi \ frac {d} {2} = \ pi d \]
,Площадь сектора круга
Площадь сектора круга — Math Open ReferenceОпределение: количество квадратных единиц, необходимое для точного заполнения сектора круга.
Попробуйте это Перетащите одну из оранжевых точек, которые определяют конечные точки сектора. Площадь сектора пересчитывается при перетаскивании.
То, что делают формулы, это взять площадь всего круга, а затем взять часть этого в зависимости от того, какую долю круга заполняет сектор.Так, например, если бы центральный угол был 90 °, то сектор имел бы площадь, равную одной четверти всего круга.
Если вы знаете центральный угол
где:
C — центральный угол в
градусы
r — радиус круга, частью которого является сектор.
π — это Пи, приблизительно 3,142
Если вы знаете длину дуги
где:
L — длина дуги.
R — радиус круга, частью которого является сектор.
Площадь сектора пропорциональна длине дуги
Площадь, окруженная сектором, пропорциональна длине дуги сектора. Например, на рисунке ниже длина дуги AB составляет четверть всей окружности, а площадь сектора составляет четверть области круга.
Аналогично ниже длина дуги равна половине окружности, а площадь — половине общей окружности. 
Вы можете поэкспериментировать с другими пропорциями в апплете вверху страницы.Другие темы круга
General
Уравнения окружности
Углы по кругу
дуг
(C) 2011 Copyright Math Открытая ссылка.
Все права защищены
круговой сектор и сегмент
Ломтики
Есть два основных «кусочка» круга:
- Срез «пиццы» называется Сектор .
- И Сегмент , который отрезан от круга «хордой» (линия между двумя точками на круге).
Попробуйте!
Общих секторов
Квадрант и Полукруг — это два специальных типа Сектора:
Полукруг
Полукруг .
Четверть круга —
Квадрант .
Площадь сектора
Вы можете определить площадь сектора, сравнивая его угол с углом полного круга.
Примечание: мы используем радианы для углов.
Это рассуждение:
Круг имеет угол 2π и площадь: πr 2
Сектор имеет угол θ вместо 2π, поэтому его площадь составляет: θ 2π × πr 2
Что можно упростить до: θ 2 × r 2
Площадь сектора = θ 2 × r 2 (когда θ в радианах)
Площадь сектора = θ × π 360 × r 2 (когда θ в градусах)
Площадь сегмента
Площадь сегмента — это площадь сектора за вычетом треугольной фигуры (здесь показано синим цветом).
Существует длинная причина, но результатом является небольшое изменение формулы Сектора:
Площадь сегмента = θ — грех (θ) 2 × r 2 (когда θ в радианах)
Площадь сегмента = ( θ × π 360 — грех (θ) 2 ) × r 2 (когда θ в градусах)
Длина дуги
Длина дуги (из сектора или сегмента ):
L = θ × r (когда θ в радианах)
L = θ × π 180 × r (когда θ в градусах)
,Круг
Круг легко сделать: Нарисуйте кривую, которая находится в радиусе И так: Все точки находятся на одинаковом расстоянии от центра. |
Вы можете нарисовать сами
Вставьте булавку в доску, оберните вокруг нее петлю из ниток и вставьте в нее карандаш.Держите струну натянутой и нарисуйте круг!
играть с ним
Попробуйте перетащить точку, чтобы увидеть, как меняется радиус и окружность.
(посмотрите, сможете ли вы сохранить постоянный радиус!)
радиус, диаметр и окружность
Радиус — это расстояние от центра наружу.
Диаметр идет прямо через круг, через центр.
Окружность — это расстояние один раз вокруг круга.
И вот действительно крутая вещь:
Когда мы делим окружность на диаметр, мы получаем 3.141592654 …
, который является числом π (Pi)
Таким образом, когда диаметр равен 1, длина окружности равна 3,141592654 … |
Можно сказать:
Окружность = π × Диаметр
Пример: Вы идете по кругу диаметром 100 м, как далеко вы прошли?
Пройденное расстояние = Окружность = π × 100 м
= 314м (до ближайшего м)
Также обратите внимание, что диаметр в два раза больше радиуса:
Диаметр = 2 × Радиус
И так это тоже верно:
Окружность = 2 × π × Радиус
В итоге:
| × 2 | × № |
| Радиус | Диаметр | Окружность |
Вспоминая
Длина слов может помочь вам вспомнить:
- Радиус — самое короткое слово и самая короткая мера
- Диаметр длиннее
- Окружность самая длинная
Определение
Круг представляет собой плоскую форму (двумерную), а значит: |
Площадь
Площадь круга равна на радиуса в квадрате, на котором написано:
A = π r 2
где
- A — Район
- р радиус
Чтобы помочь вам вспомнить, подумайте «Пирог в квадрате» (хотя пироги обычно круглые):
Пример: какова площадь круга с радиусом 1.2 м?
Площадь = № 2
= π × 1,2 2
= 3,14159 … × (1,2 × 1,2)
= 4,52 (до 2 десятичных знаков)
Или, используя диаметр:
A = ( π /4) × D 2
Площадь по сравнению с площадью
У окружности около 80% площади квадрата одинаковой ширины.
Фактическое значение (π / 4) = 0.785398 … = 78,5398 …%
И что-то интересное для вас:
См. Круг по линиям
имен
Поскольку люди изучали кружки на протяжении тысячелетий, появились особые имена.
Никто не хочет сказать «та линия, которая начинается с одной стороны круга, проходит через центр и заканчивается на другой стороне» , когда они могут просто сказать «Диаметр».
Итак, вот наиболее распространенные специальные имена:
Линии
Линия, которая «просто касается» круга при прохождении, называется Tangent .
Линия, которая разрезает круг в двух точках, называется секцией .
Сегмент линии, проходящий от одной точки к другой на окружности круга, называется аккордом .
Если он проходит через центр, он называется Диаметр .
И часть окружности называется Arc .
Ломтики
Есть два основных «кусочка» круга.
Кусочек пиццы называется сектором.
И срез, сделанный аккордом, называется сегментом.
Общих секторов
Квадрант и Полукруг — это два специальных типа Сектора:
Четверть круга называется Квадрантом .
Полукруг называется Полукругом .
внутри и снаружи
У круга есть внутренняя и внешняя стороны (конечно!).Но он также имеет «вкл», потому что мы могли бы быть прямо на круге.
Пример: «A» находится вне круга, «B» находится внутри круга, а «C» находится на круге.
Эллипс
Круг — это «особый случай» эллипса.
,
Leave A Comment