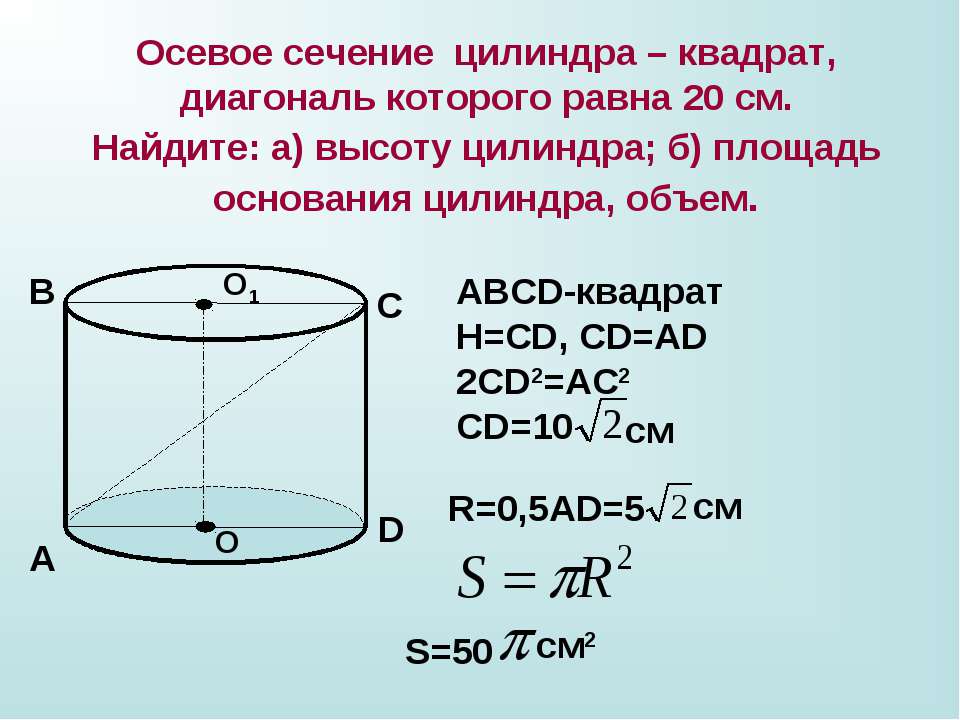
Дидактический материал по геометрии для 11 класса

Вариант I.

1.Радиус основания цилиндра равен 9,5, высота равна 4. Найдите площадь боковой поверхности цилиндра, деленную на  .

2. Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса.

3. Шар вписан в цилиндр. Объем шара равен 24. Найдите объем цилиндра.

4. Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

5. В сосуд, имеющий форму правильной треугольной призмы, налили 2300   воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в  .

6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке O. Площадь треугольника ABC равна 16, объем пирамиды равен 80. Найдите длину отрезка SС.

Вариант II.

1. Высота конуса равна 24, а длина образующей — 25. Найдите диаметр основания конуса.

2. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.

3. Шар вписан в цилиндр. Объем цилиндра равна 6. Найдите объем шара.

4. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

5. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.

6. Во сколько раз объём конуса, описанного около правильной четырёхугольной пирамиды, больше объёма конуса, вписанного в эту пирамиду?

Самостоятельная работа по теме «Цилиндр» и домашняя работа по теме «Цилиндр» 11 класс | Материал для подготовки к ЕГЭ (ГИА) по геометрии (11 класс) на тему:

Вариант 1.  Цилиндр

1.Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .

2. Длина окружности основания цилиндра равна 3, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3. Длина окружности основания цилиндра равна 14. Площадь боковой поверхности равна 182. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна 18, а диаметр основания равен 9. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 2. Найдите диаметр основания

6. Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?

7. Площадь осевого сечения цилиндра равна 7. Найдите площадь боковой поверхности цилиндра, деленную на .

Вариант 2 Цилиндр

1.Радиус основания цилиндра равен 7, высота равна 10. Найдите площадь боковой поверхности цилиндра, деленную на .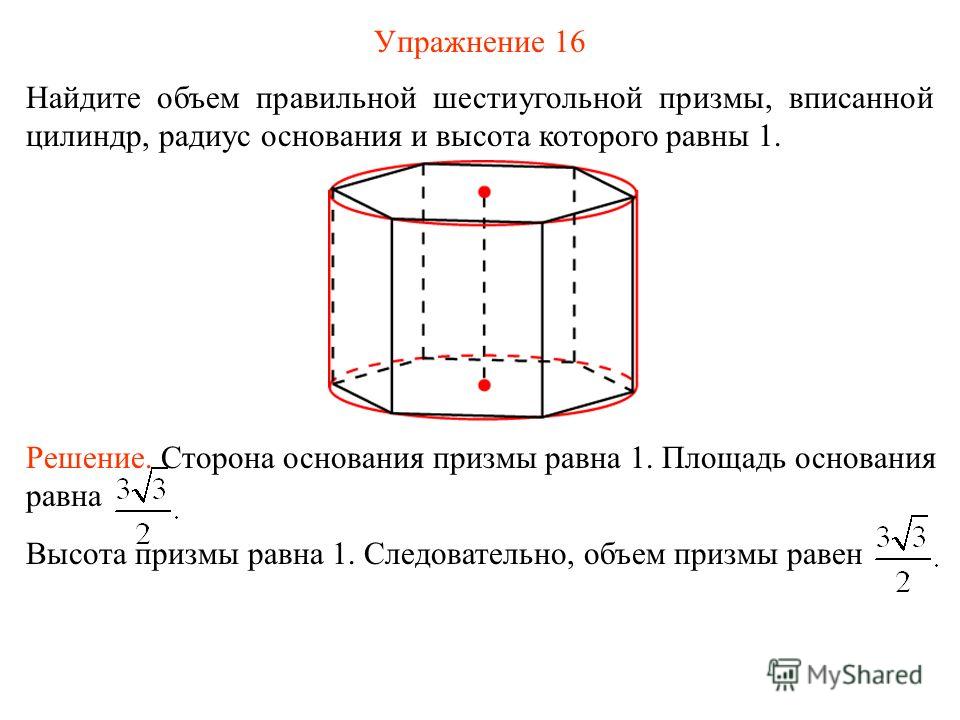

2. Длина окружности основания цилиндра равна 5, высота равна 2. Найдите площадь боковой поверхности цилиндра.

3. Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 12. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна 9, а диаметр основания равен 3. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 7. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 14. Найдите площадь боковой поверхности цилиндра, деленную на .

7. Даны два цилиндра. Радиус основания и высота первого равны соответственно 2 и 3, а второго — 12 и 5. Во сколько раз площадь боковой поверхности второго цилиндра больше площади боковой поверхности первого?

Вариант 3 Цилиндр

1.Радиус основания цилиндра равен 3, высота равна 6. Найдите площадь боковой поверхности цилиндра, деленную на .

2. Длина окружности основания цилиндра равна 3, высота равна 6. Найдите площадь боковой поверхности цилиндра.

3. Длина окружности основания цилиндра равна 5. Площадь боковой поверхности равна 70. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна 15, а диаметр основания равен 5. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 8. Найдите диаметр основания.

6. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

7.  Площадь осевого сечения цилиндра равна 23. Найдите площадь боковой поверхности цилиндра, деленную на .

Вариант 4 Цилиндр

1.Радиус основания цилиндра равен 10, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на .

2. Длина окружности основания цилиндра равна 5, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3.Длина окружности основания цилиндра равна 11. Площадь боковой поверхности равна 121. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 5. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 47. Найдите площадь боковой поверхности цилиндра, деленную на .

7. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

Вариант 5 Цилиндр

1.Радиус основания цилиндра равен 7, высота равна 2. Найдите площадь боковой поверхности цилиндра, деленную на .

2. Длина окружности основания цилиндра равна 2, высота равна 5. Найдите площадь боковой поверхности цилиндра.

3. Длина окружности основания цилиндра равна 12. Площадь боковой поверхности равна 180. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 5. Найдите диаметр основания.

6. Даны два цилиндра. Радиус основания и высота первого равны соответственно 15 и 6, а второго — 2 и 5. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

7. Площадь осевого сечения цилиндра равна 45. Найдите площадь боковой поверхности цилиндра, деленную на .

Вариант 6

1.Радиус основания цилиндра равен 6, высота равна 5. Найдите площадь боковой поверхности цилиндра, деленную на .
2. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

3. Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 20. Найдите высоту цилиндра.

4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 7. Найдите высоту цилиндра.

5. Площадь боковой поверхности цилиндра равна , а высота — 3. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 36. Найдите площадь боковой поверхности цилиндра, деленную на .

7. Даны два цилиндра. Радиус основания и высота первого равны соответственно 6 и 14, а второго — 7 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?

Домашняя работа. Цилиндр

1.Радиус основания цилиндра равен 10, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на .

2.Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3.Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 40. Найдите высоту цилиндра.

4.Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

5.Площадь боковой поверхности цилиндра равна , а высота — 7. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 1. Найдите площадь боковой поверхности цилиндра, деленную на .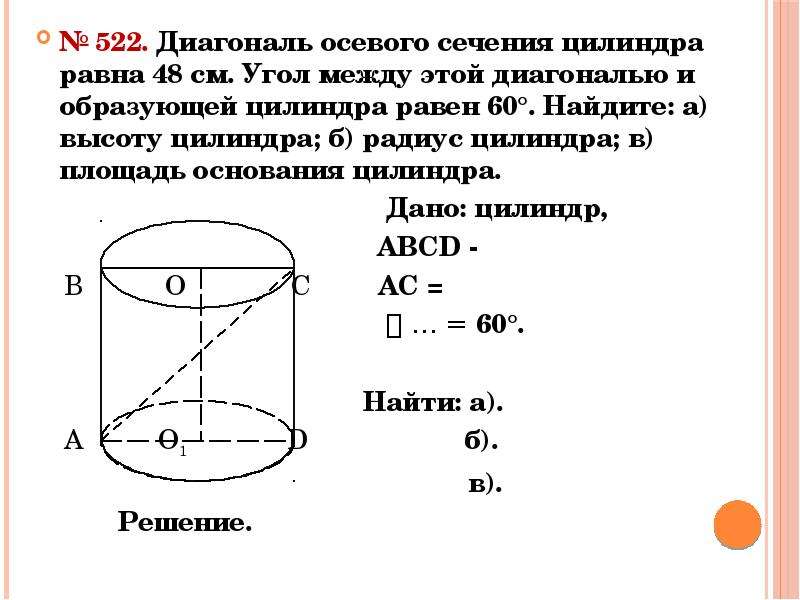

Домашняя работа. Цилиндр

1.Радиус основания цилиндра равен 10, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на .

2.Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3.Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 40. Найдите высоту цилиндра.

4.Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

5.Площадь боковой поверхности цилиндра равна , а высота — 7. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 1. Найдите площадь боковой поверхности цилиндра, деленную на .

Домашняя работа. Цилиндр

1.Радиус основания цилиндра равен 10, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на .

2.Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3.Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 40. Найдите высоту цилиндра.

4.Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

5.Площадь боковой поверхности цилиндра равна , а высота — 7. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 1. Найдите площадь боковой поверхности цилиндра, деленную на .

Домашняя работа. Цилиндр

1.Радиус основания цилиндра равен 10, высота равна 9. Найдите площадь боковой поверхности цилиндра, деленную на .

2.Длина окружности основания цилиндра равна 4, высота равна 4. Найдите площадь боковой поверхности цилиндра.

3.Длина окружности основания цилиндра равна 4. Площадь боковой поверхности равна 40. Найдите высоту цилиндра.

4.Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

5.Площадь боковой поверхности цилиндра равна , а высота — 7. Найдите диаметр основания.

6. Площадь осевого сечения цилиндра равна 1.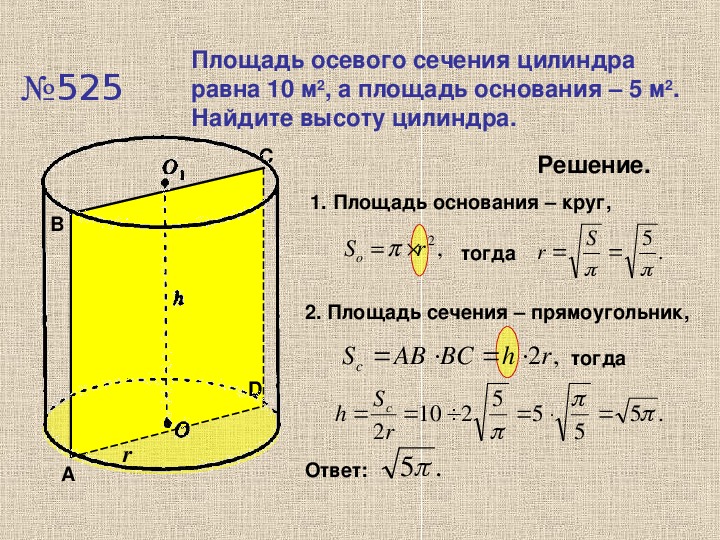 Найдите площадь боковой поверхности цилиндра, деленную на .

Практикум №8 по решению стереометрических задач

Практикум №8
по решению
стереометрических задач
Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной Геннадьевной
Конус
в заданиях
ЕГЭ

3. Содержание

Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
Задача №19
Задача №20
Задача №21
• Задачи для самостоятельного решения
Задача №22
Задача №23
Задача №24
Задача №25
Задача №26
Задача №27
Задача №28
Задача №29
Задача №30
Задача №31
Задача №32

4. Задача №1

Даны два конуса. Радиус основания и образующая первого
конуса равны соответственно 3 и 9, а второго — 6 и 9.
Во сколько
раз площадь боковой поверхности второго конуса больше
площади боковой поверхности первого?
Решение.
Т.к. площадь боковой поверхности конуса: S=πrl.
Значит S1= π·3·9= 27π, S2= π·6·9= 54π.
Тогда S2: S1= 54π : 27π = 2

5. Задача №2

Объём конуса равен 135. Через точку, делящую высоту конуса в от
ношении 1:2, считая от вершины, проведена плоскость, парал
лельная основанию. Найдите объём конуса, отсекаемого от данно
го конуса проведённой плоскостью.
Отношение объемов конусов равно кубу их коэффициен
та подобия. Высоты конусов относятся как 1:3, поэтому их
объемы относятся как 1:27. Следовательно, объем отсекае
мого конуса равен 135 : 33 = 5.

6. К задаче №2

Объём конуса равен 32. Через середину высоты конуса
проведена плоскость, параллельная основанию.
Найдите объём конуса, отсекаемого от данного конуса
проведённой плоскостью.
Решение.
Отношение объемов конусов равно кубу их коэффициента
подобия k. Так как высоты конусов относятся как 1:2, то
k равно одной второй, а значит объем отсекаемого конуса
будет равен 32 : 2³ = 4.

7. Задача №3

Объём конуса равен 50π а его высота равна 6 .
Найдите радиус основания конуса.
Найдём радиус основания конуса по
формуле: V=1/3·πR²h
Откуда R²=3V:πh => R²= 150π : 6π
= 25. Тогда R=5

8. Задача №4

Во сколько раз уменьшится объем конуса, если его высоту
уменьшить в 3 раза?
Объем конуса вычисляется по
формуле V=1/3·Soc.·h .
Значит, если высоту увеличить в 3
раза, то и объём увеличится в 3
раза

9. Задача №5

Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 1,5 раза?
Объем конуса вычисляется по формуле
V=1/3·Soc.·h = 1/3·πR²·h.
Значит, если радиус основания увеличить
в 1,5 раза, то и объём конуса увеличится
в 2,25 раза

10. Задача №6

Во сколько раз увеличится площадь боковой
поверхности конуса, если его образующую
увеличить в 3 раза?
Площадь
боковой
поверхности
конуса вычисляется по формуле
S= πR·L, где L-образующая.
Значит если увеличить L в 3 раза,
то площадь боковой поверхности
конуса тоже увеличится в 3 раза.

11. Задача №7

Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 1,5 раза,
а образующая останется прежней?
Площадь боковой поверхности конуса вычисляется
по формуле S= πR·L. Значит, если радиус
основания уменьшится в 1,5 раза, то площадь
боковой поверхности конуса тоже уменьшится в 1,5
раза.

12. Задача №8

Высота конуса равна 4, а диаметр основания — 6.
Найдите образующую конуса.
По теореме Пифагора
2
36
d
L h 16
25 5
4
2
2

13. Задача №9

Высота конуса равна 4, а длина образующей — 5.
Найдите диаметр основания конуса.
По теореме Пифагора….
Ответ: 6.

14. Задача №10

Диаметр основания конуса равен 6, а длина
образующей — 5. Найдите высоту конуса.
По теореме Пифагора….
Ответ: 4.

15. Задача №11

В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 70 мл.
Сколько миллилитров жидкости нужно долить, чтобы
полностью наполнить сосуд?
Меньший конус подобен большему с
коэффициентом 0,5. Объемы подобных тел
относятся как куб коэффициента подобия.
Поэтому объем большего конуса в 8 раз
больше объема меньшего конуса, он равен 560
мл. Следовательно, необходимо долить 560 −
70 = 490 мл жидкости.

16. Задача №12

В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём сосуда 1600 мл. Чему равен
объём налитой жидкости? Ответ дайте в миллилитрах.

17. Решение

Пусть х — высота налитой
жидкости, у —
радиус
окружности в основании
конуса. Тогда 2х — высота
сосуда,
2у
—
радиус
окружности в основании
сосуда (так как поверхность
жидкости
отсекает
от
конического сосуда конус
подобный
данному).
Найдем отношения объёмов
конусов,
Решение
1
2
2 y 2x
V1 3
8
1
V2
2
y x
3
Таким образом, объём
сосуда в 8 раз больше
объёма налитой
жидкости: 1600 : 8 = 200

18. Задача №13

Объём конуса равен 96π, а его высота равна 8.
Найдите радиус основания конуса.
Найдём радиус основания конуса
из формулы: V=1/3·πR²h
Откуда R²=3V:πh =>
3Vk .
3 96
R
36 6
h
8

19. Задача №14

Даны два конуса. Радиус основания и образующая первого
конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во
сколько раз площадь боковой поверхности второго
конуса больше площади боковой поверхности первого?

20. Решение

1) Найдём площадь боковой поверхности
первого конуса:
S1=π·R1·L1 = π·2·4=8π
2) Найдём площадь боковой поверхности второго
конуса:
S2=π·R2·L2 = π·6·8=48π
3) Найдём отношение площадей этих конусов:
S2 : S1 = 48π : 8π = 6

21.

Задача №15 Цилиндр и конус имеют общие основание и высоту.
Высота цилиндра равна радиусу основания. Площадь
боковой поверхности цилиндра равна 3√2. Найдите
площадь боковой поверхности конуса.

22. Решение

1) Заметим, что конус и цилиндр имеют общую высоту
и равные радиусы основания. Площадь боковой
поверхности цилиндра равна Sб.п.= 2πR·h, но R=h
следовательно Sб.п.= 2πR² и =3√2 => πR² =1,5√2
2)
Площадь боковой поверхности конуса
равна S=πR·L, Но L² = R²+h², но R=h => L² =
2R² => L = R√2.
Значит Sб.п.= πR·L= πR· R√2 = πR²·√2 =
= 1,5√2·√2 = 3

23. Задача №16

Диаметр основания конуса равен 12, а длина образующей
— 10. Найдите площадь осевого сечения этого конуса.
Осевым
сечением
конуса
является
равнобедренный треугольник, основание
которого —это диаметр основания конуса, а
высота совпадает с высотой конуса.
Но L² = R²+h² => h = √100-36=√64=8
Следовательно, площадь осевого сечения
равна 0,5 · 12 · 8 = 48.

24. Задача №17

Высота конуса равна 8, а длина образующей — 10. Найдите
площадь осевого сечения этого конуса.
Осевым сечением конуса является равнобедренный
треугольник, основание которого — диаметр
основания конуса, а высота совпадает с высотой
конуса.
Но L² = R²+h² => R=√100-64=√36=6
Следовательно, диаметр осевого сечения
конуса равен 12, а площадь осевого
сечения равна 0,5 · 12 · 8 = 48.

25. Задача №18

Площадь основания конуса равна 18. Плоскость,
параллельная плоскости основания конуса, делит его
высоту на отрезки длиной 3 и 6, считая от вершины.
Найдите площадь сечения конуса этой плоскостью

26. Решние

Сечение
плоскостью,
параллельной
основанию, представляет собой круг, радиус
которого относится к радиусу основания
конуса как 3 : 9. Площади подобных фигур
относятся как квадрат коэффициента подобия,
поэтому площадь сечения в 9 раз меньше
площади основания.
Тем самым, она равна 2.

27. Задача №19

Площадь основания конуса равна 16π, высота — 6.
Найдите площадь осевого сечения конуса.
Осевым сечением конуса является равнобедренный
треугольник, высота которого совпадает с высотой
конуса, а основание является диаметром основания
конуса. Поэтому площадь осевого сечения равна
половине произведения высоты конуса на диаметр его
основания или произведению высоты конуса на радиус
основания R. Поскольку по условию πR²=16π, то
радиус основания конуса равен 4, а тогда искомая
площадь осевого сечения равна 24.

28. Задача №20

Около конуса описана сфера (сфера содержит окружность
основания конуса и его вершину). Центр сферы
совпадает с центром основания конуса. Радиус сферы
равен 10√2. Найдите образующую конуса.
Высота конуса перпендикулярна основанию и
равна радиусу сферы. Тогда по теореме
Пифагора получаем:
2
2
2
L R R
L R 2 10 2 2 20
L R 2

29.

Задача №21 Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем шара равен 28. Найдите объем
конуса.
Формулу для объёма шара:
V=4/3 ·πR³, а формула объёма
конуса: V=1/3 ·πR³.
Значит объём конуса в 4 раза
меньше объёма шара.
Тогда объём конуса равен 28 : 4 = 7

30. Задача №22

Площадь боковой поверхности конуса в два раза больше
площади основания. Найдите угол между образующей
конуса и плоскостью основания. Ответ дайте в градусах.

31. Решение

S осн r
2
Решение
Sб. r L
Sб. 2 S осн r L 2 r
2
L 2r
Значит, в прямоугольном треугольнике,
образованном высотой, образующей и радиусом
основания конуса, катет, равный радиусу, вдвое
меньше гипотенузы. Тогда он лежит напротив угла
30°. Следовательно, угол между образующей конуса
и плоскостью основания равен 60°.

32. Задача №23

Радиус основания конуса равен 3, высота равна 4. Найдите
площадь полной поверхности конуса, деленную на π .
Найдем образующую по теореме Пифагора:
L=√h²+R²=√16+9=√25=5
Площадь
полной
поверхности
конуса
S R RL R( L R) 3 8 24
2

33. Задача №24

Длина окружности основания конуса равна 3, образующая
равна 2. Найдите площадь боковой поверхности конуса.
Площадь
равна
боковой
поверхности
конуса
1
1
Sб. r L С L 2 3 3
2
2

34. Задача №25

Конус получается при вращении равнобедренного
прямоугольного треугольника АВС вокруг катета, равного
6. Найдите его объем, деленный на π .
Треугольник АВС– так же равнобедренный, т.к.
углы при основании АВ равны 45°. Тогда радиус
основания равен 6, и объем конуса, деленный на π:
V
1 Sh 1 R 2 h 1
1 3
2
R R 6 72
3
3
3
3

35. Задача №26

Диаметр основания конуса равен 6, а угол при вершине
осевого сечения равен 90°. Вычислите объем конуса,
деленный на π.

36.

Решение В треугольнике, образованном радиусом основания r,
высотой h и образующей конуса l, углы при
образующей равны, поэтому высота конуса равна
радиусу его основания: h = r. Тогда объем конуса,
деленный на
вычисляется следующим
образом:
V 1 Sh 1 R h 1 2
1 3
R R 3 9
3 3
3
3
2

37. Задача №27

Найдите объем конуса, образующая которого равна 2 и
наклонена к плоскости основания под углом 30° . В ответе
укажите V/π.
30°

38. Решение

Высоту конуса найдем по свойству стороны
прямоугольного
треугольника,
находящейся
напротив угла в
30° – она вдвое меньше
гипотенузы, которой в данном случае является
образующая конуса. Радиус основания найдем по
теореме Пифагора: R=√2²-1=√3
V 1 Sh 1 R h 1 2
1
R h 3 1 1
3 3
3
3
2

39. Задача №28

Конус описан около правильной четырехугольной
пирамиды со стороной основания 4 и высотой 6. Найдите
его объем, деленный на π.
Радиус основания конуса r равен половине
диагонали квадрата ABCD: r=√2/2·AB=2√2
Тогда объем конуса, деленный
на π :
V 1 Sh 1 R h 1 2
1
R h 8 6 16
3 3
3
3
2

40. Задача №29

Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .
Объем
равен
данной
части
конуса
90 1 2
1 2
R H 9 13 87,75
360 3
12

41. Задача №30

Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .
Объем
равен
данной
части
конуса
270 1
3 1
1 2
2
2
R H R H 9 12 234
360 3
4 3
4

42. Задача №31

Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .
Объем
равен
данной
части
конуса
60 1 2
1 1 2
1
2
R H R H 12 27 216
360 3
6 3
18

43.

Задача №32 Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .
Объем данной части конуса
равен
300 1 2
5 1 2
5 2
R H R H 9 27 607,5
360 3
6 3
18
Задачи
для самостоятельного
решения

45. Задача №2 Решить самостоятельно

1) Объём конуса равен 27. Через точку, делящую высоту конуса в
отношении 1:2, считая от вершины, проведена плоскость,
параллельная основанию. Найдите объём конуса, отсекаемого от
данного конуса проведённой плоскостью.
Ответ:1
2) Объем конуса равен 16. Через середину высоты параллельно
основанию конуса проведено сечение, которое является основанием
меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Ответ:2
3) Объем конуса равен 128. Через середину высоты параллельно
основанию конуса проведено сечение, которое является основанием
меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

46.

Задача №3 Решить самостоятельно 1) Объём конуса равен 9π, а его высота равна 3 . Найдите
радиус основания конуса.
Ответ:3
2) Объём конуса равен 25π, а его высота равна 3 .
Найдите радиус основания конуса.
Ответ:5

47. Задача №4 Решить самостоятельно

1) Во сколько раз уменьшится объем конуса, если его
высоту уменьшить в 18,5 раза?
2) Во сколько раз уменьшится объем конуса, если его
высоту уменьшить в 24 раза?
3) Во сколько раз уменьшится объем конуса, если его
высоту уменьшить в 10 раз?

48. Задача №5 Решить самостоятельно

1) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 40 раз?
2) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 22 раза?
3) Во сколько раз увеличится объем конуса, если его
радиус основания увеличить в 31 раз?

49. Задача №6 Решить самостоятельно

1) Во сколько раз увеличится площадь боковой
поверхности конуса, если его образующую
увеличить в 36 раз?
2) Во сколько раз увеличится площадь боковой
поверхности конуса, если его образующую
увеличить в 11 раз?
3) Во сколько раз увеличится площадь боковой
поверхности конуса, если его образующую
увеличить в 1,5 раза?

50.

Задача №7 Решить самостоятельно 1) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 8 раз, а
образующая останется прежней?
2) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 36 раз, а
образующая останется прежней?
3) Во сколько раз уменьшится площадь боковой поверхности
конуса, если радиус его основания уменьшится в 21 раз, а
образующая останется прежней?

51. Задача №8 Решить самостоятельно

1) Высота конуса равна 8, а диаметр основания —
30. Найдите образующую конуса. Ответ: 17
2) Высота конуса равна 5, а диаметр основания —
24. Найдите образующую конуса. Ответ: 13
3) Высота конуса равна 6, а диаметр основания —
16. Найдите образующую конуса. Ответ: 10

52. Задача №9 Решить самостоятельно

1) Высота конуса равна 72, а длина образующей —
90. Найдите диаметр основания конуса.
Ответ:108
2) Высота конуса равна 21, а длина образующей —
75. Найдите диаметр основания конуса.
3) Высота конуса равна 57, а длина образующей —
95. Найдите диаметр основания конуса.

53. Задача №10 Решить самостоятельно

1) Диаметр основания конуса равен 108, а длина
образующей — 90. Найдите высоту конуса. Ответ: 72
2) Диаметр основания конуса равен 42, а длина
образующей — 75. Найдите высоту конуса. Ответ: 72
3) Диаметр основания конуса равен 24, а длина
образующей — 13. Найдите высоту конуса. Ответ: 5

54. Задача №11 Решить самостоятельно

1) В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/3 высоты. Объём жидкости равен 14 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
Ответ: 364
2) В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/2 высоты. Объём жидкости равен 40 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
Ответ: 280
3) В сосуде, имеющем форму конуса, уровень жидкости
достигает 1/4 высоты. Объём жидкости равен 6 мл. Сколько
миллилитров жидкости нужно долить, чтобы полностью
наполнить сосуд?
Ответ:

55. Задача №19 Решить самостоятельно

1) Площадь основания конуса равна 36π, высота —10.
Найдите площадь осевого сечения конуса. Ответ:60
2)

56. Задача №21 Решить самостоятельно

1) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем шара равен 116. Найдите объем
конуса.
2) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем шара равен 160. Найдите объем
конуса.
3) Конус вписан в шар. Радиус основания конуса равен
радиусу шара. Объем шара равен 132. Найдите объем
конуса.

57. Задача №23 Решить самостоятельно

1) Радиус основания конуса равен 12, высота равна 16.
Найдите площадь полной поверхности конуса,
деленную на π .
2) Радиус основания конуса равен 28, высота равна 21.
Найдите площадь полной поверхности конуса,
деленную на π .
3) Радиус основания конуса равен 15, высота равна 36.
Найдите площадь полной поверхности конуса,
деленную на π .

58. Задача №24 Решить самостоятельно

1) Длина окружности основания конуса равна 6,
образующая равна 2. Найдите площадь боковой
поверхности конуса.
Ответ: 6
2) Длина окружности основания конуса равна 5,
образующая равна 8. Найдите площадь боковой
поверхности конуса.
3) Длина окружности основания конуса равна 8,
образующая равна 6. Найдите площадь боковой
поверхности конуса.

59. Задача №25 Решить самостоятельно

1) Конус получается при вращении равнобедренного
прямоугольного треугольника АВС вокруг катета,
равного 15. Найдите его объем, деленный на π .
2) Конус получается при вращении равнобедренного
прямоугольного треугольника АВС вокруг катета,
равного 120. Найдите его объем, деленный на π .
3) Конус получается при вращении равнобедренного
прямоугольного треугольника АВС вокруг катета,
равного 60. Найдите его объем, деленный на π .

60. Задача №26 Решить самостоятельно

1) Диаметр основания конуса равен 66, а угол при
вершине осевого сечения равен 90°. Вычислите объем
конуса, деленный на π.
2) Диаметр основания конуса равен 12, а угол при
вершине осевого сечения равен 90°. Вычислите объем
конуса, деленный на π.
3) Диаметр основания конуса равен 36, а угол при
вершине осевого сечения равен 90°. Вычислите объем
конуса, деленный на π.

61. Задача №27 Решить самостоятельно

1) Найдите объем конуса, образующая которого равна 44
и наклонена к плоскости основания под углом 30° . В
ответе укажите V/π.
Ответ: 10 648
2) Найдите объем конуса, образующая которого равна 51
и наклонена к плоскости основания под углом 30° . В
ответе укажите V/π.
3) Найдите объем конуса, образующая которого равна 34
и наклонена к плоскости основания под углом 30° . В
ответе укажите V/π.

62. Задача №28 Решить самостоятельно

1) Конус описан около правильной четырехугольной
пирамиды со стороной основания 3 и высотой 13.
Найдите его объем, деленный на π.
Ответ:19,5
2) Конус описан около правильной четырехугольной
пирамиды со стороной основания 8 и высотой 12.
Найдите его объем, деленный на π.
3) Конус описан около правильной четырехугольной
пирамиды со стороной основания 4 и высотой 9.
Найдите его объем, деленный на π.

63. Задача №29 Решить самостоятельно

1) Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .

64. Задача №30 Решить самостоятельно

Задача №30
Найдите объем V
укажите V/π .
Решить
самостоятельно
части
конуса, изображенной на рисунке. В ответе

65. Задача №31 Решить самостоятельно

Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .

66. Задача №32 Решить самостоятельно

Найдите объем V части конуса, изображенной на
рисунке. В ответе укажите V/π .

67. Используемые ресурсы

• Шаблон подготовила учитель русского языка и литературы
Тихонова Надежда Андреевна
«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ
и ОГЭ. Режим доступа: http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
Автор и источник заимствования неизвестен
http://belmathematics.by/images/teorija/konys3.jpg
https://im1-tub-ru.yandex.net/i?
id=72aa47f9b7dce12424f069f72b9a
3c2a&n=33&h=215&w=158
http://900igr.net/datai/geometrija/Konus-geometrija/0001-001-G-11-urok-1.png
http://www.k6-geometric-shapes.com/image-files/3d-t3-cone.jpg
http://900igr.net/datai/geometrija/Osnovy-stereometrii/0040-033-Obem-konusa.png

Площадь боковой поверхности цилиндра равна 21 п, а диаметр основания равен 7. Найти высоту циллиндра.

10⁵¹ мне кажется.
________________

15/3=5 утят у хозяйки

                                                                                                        —
Первый брат — ?, но сказано, что поровну со своим братом   |
                                                                                                            | 1 конфета
Второй брат — ?, но сказано, что поровну со своим братом     |
                                                                                                        —

Решение: 

1) 1 : 2 = 0,5(конф) — досталось каждому брату, то есть половина

Ответ: 0,5 конфеты — половина 

1. 0,2 * (5/7 х — 1,2) = 3/7 х — 0,642. 0,4 * (1,3 + 5/9 х) = 7/9 х — 1,483. 7/20 : 3 х = 0,007 : 0,724. 0,375 : 1,04 = 3 11/13 LIT VLETU 1.    0,2 * (5/7 х — 1,2) = 3/7 х — 0,64
       1/7x  — 0,24 = 3/7x — 0,64
       0,4 = 2/7x
       x = 0,4:2/7 = 0,4*7/2=  1,4

2.    0,4 * (1,3 + 5/9 х) = 7/9 х — 1,48
       0,52 + 2/9x = 7/9x — 1,48
         5/9x = 2
         x = 2:5/9= 2 * 9/5 = 18/5 = 3 3/5

3.    7/20 : 3 х = 0,007 : 0,72
        x =  7/20 : (7/100 : 72/100) = 7/20 : 7/72 = 7/20*72/7 = 72/20 = 3,6

4.    0,375 : 1,04 = 3 11/13 : 4 х
         375/1000 : 104/100 = 375/1000* 100/104 = 75/208
           4x  = 3 11/13 : 75/208
           4x = 50/13 : 75/208
           4x = 50/13*208/75 = 32/3
             x = 32/3:4 = 8/3 = 2 2/3
 


дробь равна нулю, если числитель равен нулю:

 

Ответ: x=-10

1.

Диа­метр ос­но­ва­ния ко­ну­са равен 6, а длина об­ра­зу­ю­щей — 5. Най­ди­те вы­со­ту ко­ну­са. 1. Диа­метр ос­но­ва­ния ко­ну­са равен 6, а длина об­ра­зу­ю­щей — 5. Най­ди­те вы­со­ту ко­ну­са.

1. Диа­метр ос­но­ва­ния ко­ну­са равен 6, а длина об­ра­зу­ю­щей — 5. Най­ди­те вы­со­ту ко­ну­са.

2. Объем ко­ну­са равен 16. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

3. Най­ди­те тан­генс угла мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

4. Даны две пра­виль­ные четырёхуголь­ные пи­ра­ми­ды. Объём пер­вой пи­ра­ми­ды равен 9. У вто­рой пи­ра­ми­ды вы­со­та в 1,5 раза боль­ше, а сто­ро­на ос­но­ва­ния в 2 раза боль­ше, чем у пер­вой. Най­ди­те объём вто­рой пи­ра­ми­ды.

5. Во сколь­ко раз уве­ли­чит­ся пло­щадь по­верх­но­сти шара, если ра­ди­ус шара уве­ли­чить в 45 раз?

6. Конус впи­сан в ци­линдр. Объем ко­ну­са равен 5. Най­ди­те объем ци­лин­дра.

 

7. Пра­виль­ная че­ты­рех­уголь­ная приз­ма опи­са­на около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 5. Пло­щадь бо­ко­вой по­верх­но­сти приз­мы равна 40. Най­ди­те вы­со­ту ци­лин­дра.

8. Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы на­хо­дит­ся в цен­тре ос­но­ва­ния ко­ну­са. Об­ра­зу­ю­щая ко­ну­са равна . Най­ди­те ра­ди­ус сферы.

9. Ци­линдр и конус имеют общие ос­но­ва­ние и вы­со­ту. Най­ди­те объем ко­ну­са, если объем ци­лин­дра равен 138.

10. Около шара опи­сан ци­линдр, пло­щадь по­верх­но­сти ко­то­ро­го равна 69. Най­ди­те пло­щадь по­верх­но­сти шара.

 

11. Пра­виль­ная че­ты­рех­уголь­ная приз­ма опи­са­на около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 6. Пло­щадь бо­ко­вой по­верх­но­сти приз­мы равна 48.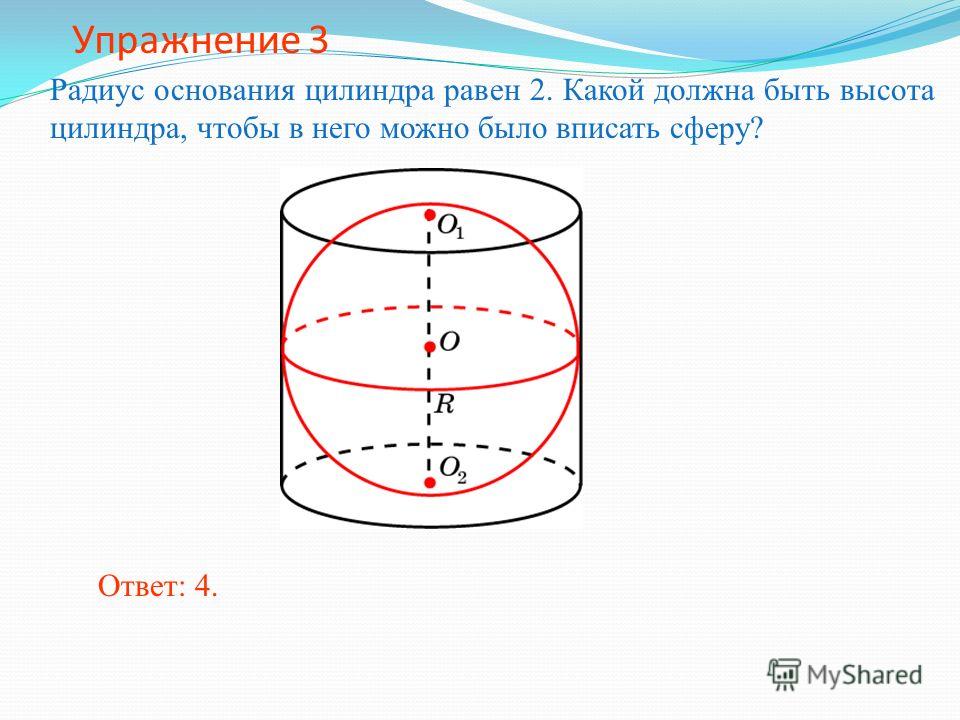 Най­ди­те вы­со­ту ци­лин­дра.

12. Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 13. Объем па­рал­ле­ле­пи­пе­да равен 676. Най­ди­те вы­со­ту ци­лин­дра.

13. Конус впи­сан в ци­линдр. Объем ко­ну­са равен 21. Най­ди­те объем ци­лин­дра.

 

14. Вы­со­та ко­ну­са равна 72, а диа­метр ос­но­ва­ния — 108. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

15. Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния ко­то­ро­го равен 3,5. Объем па­рал­ле­ле­пи­пе­да равен 24,5. Най­ди­те вы­со­ту ци­лин­дра.



16. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми и мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

17. Конус впи­сан в ци­линдр. Объем ко­ну­са равен 27. Най­ди­те объем ци­лин­дра.

18. Ци­линдр и конус имеют общее ос­но­ва­ние и общую вы­со­ту. Вы­чис­ли­те объем ци­лин­дра, если объем ко­ну­са равен 25.

19. Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, опи­сан­но­го около сферы, равен 1331. Най­ди­те ра­ди­ус сферы.

20. Вы­со­та ко­ну­са равна 4, а диа­метр ос­но­ва­ния — 6. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

 

21. Во сколь­ко раз уве­ли­чит­ся пло­щадь по­верх­но­сти пи­ра­ми­ды, если все ее ребра уве­ли­чить в 2 раза?

22. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­но, что Най­ди­те длину ребра .

23. Во сколь­ко раз уве­ли­чит­ся пло­щадь по­верх­но­сти ок­та­эд­ра, если все его ребра уве­ли­чить в 3 раза?

 

24. Най­ди­те объем мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

25. . Если каж­дое ребро куба уве­ли­чить на 1, то его объем уве­ли­чит­ся на 19. Най­ди­те ребро куба.

26. В куб впи­сан шар ра­ди­у­са 3. Най­ди­те объем куба.

27. Через сред­нюю линию ос­но­ва­ния тре­уголь­ной приз­мы, объем ко­то­рой равен 52, про­ве­де­на плос­кость, па­рал­лель­ная бо­ко­во­му ребру. Най­ди­те объем от­се­чен­ной тре­уголь­ной приз­мы.

28. Най­ди­те пло­щадь по­верх­но­сти мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

 

29. В ци­лин­дри­че­ском со­су­де уро­вень жид­ко­сти до­сти­га­ет 128 см. На какой вы­со­те будет на­хо­дить­ся уро­вень жид­ко­сти, если ее пе­ре­лить во вто­рой сосуд, диа­метр ко­то­ро­го в 8 раз боль­ше пер­во­го? Ответ вы­ра­зи­те в сан­ти­мет­рах.

30. Пло­щадь по­верх­но­сти куба равна 2592. Най­ди­те его диа­го­наль.

31. Объем па­рал­ле­ле­пи­пе­да равен 9. Най­ди­те объем тре­уголь­ной пи­ра­ми­ды

.

32. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де из­вест­но, что , , Най­ди­те длину диа­го­на­ли

33. Най­ди­те тан­генс угла мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

34. . Гра­нью па­рал­ле­ле­пи­пе­да яв­ля­ет­ся ромб со сто­ро­ной 1 и ост­рым углом 45°. Одно из ребер па­рал­ле­ле­пи­пе­да со­став­ля­ет с этой гра­нью угол в 45° и равно 5. Най­ди­те объем па­рал­ле­ле­пи­пе­да.

35. Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна 18 , а диа­метр ос­но­ва­ния равен 9. Най­ди­те вы­со­ту ци­лин­дра.

36. Най­ди­те пло­щадь по­верх­но­сти мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

37. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 1,5 раза?

38. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми и мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке. Все дву­гран­ные углы мно­го­гран­ни­ка пря­мые.

39. Объем па­рал­ле­ле­пи­пе­да равен 4,5. Най­ди­те объем тре­уголь­ной пи­ра­ми­ды .

40. Ос­но­ва­ни­ем пи­ра­ми­ды яв­ля­ет­ся пря­мо­уголь­ник со сто­ро­на­ми 3 и 4. Ее объем равен 16. Най­ди­те вы­со­ту этой пи­ра­ми­ды.

41. Диа­метр ос­но­ва­ния ко­ну­са равен 12, а длина об­ра­зу­ю­щей — 10. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

42.
Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1, 2. Объем па­рал­ле­ле­пи­пе­да равен 6. Най­ди­те пло­щадь его по­верх­но­сти.

43. Сто­ро­ны ос­но­ва­ния пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды равны 10, бо­ко­вые ребра равны 13. Най­ди­те пло­щадь по­верх­но­сти этой пи­ра­ми­ды.

44. Ос­но­ва­ни­ем пи­ра­ми­ды слу­жит пря­мо­уголь­ник, одна бо­ко­вая грань пер­пен­ди­ку­ляр­на плос­ко­сти ос­но­ва­ния, а три дру­гие бо­ко­вые грани на­кло­не­ны к плос­ко­сти ос­но­ва­ния под углом 60 . Вы­со­та пи­ра­ми­ды равна 6. Най­ди­те объем пи­ра­ми­ды.

45. В пра­виль­ной тре­уголь­ной приз­ме ABCA1B1C1 сто­ро­ны ос­но­ва­ний равны 2, бо­ко­вые рёбра равны 5. Най­ди­те пло­щадь се­че­ния приз­мы плос­ко­стью, про­хо­дя­щей через се­ре­ди­ны рёбер AB, AC, A1B1 и A1C1.

46. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD вы­со­та SO равна 13, диа­го­наль ос­но­ва­ния BD равна 8. Точки К и М— се­ре­ди­ны рёбер CD и ВСсо­от­вет­ствен­но. Най­ди­те тан­генс угла между плос­ко­стью SMK и плос­ко­стью ос­но­ва­ния ABC.

47. Най­ди­те объем части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те .

48. Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен 24. Одно из его ребер равно 3. Най­ди­те пло­щадь грани па­рал­ле­ле­пи­пе­да, пер­пен­ди­ку­ляр­ной этому ребру.

49. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­деABCDA1B1C1D1 ребро BC = 4, ребро ребро BB1 = 4. Точка K — се­ре­ди­на ребра CC1. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через точки B1, A1 и K.

50. Ос­но­ва­ни­ем пря­мой тре­уголь­ной приз­мы слу­жит пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми 3 и 5. Объем приз­мы равен 30. Най­ди­те ее бо­ко­вое ребро.

51. Най­ди­те угол пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, для ко­то­ро­го =4, =3, =5. Дайте ответ в гра­ду­сах.

52. В пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­де вы­со­та равна 12, объем равен 200. Най­ди­те бо­ко­вое ребро этой пи­ра­ми­ды.

53. Диа­метр ос­но­ва­ния ко­ну­са равен 10, а длина об­ра­зу­ю­щей равна 13. Най­ди­те вы­со­ту ко­ну­са.

54. Объем тре­уголь­ной пи­ра­ми­ды равен 30. Плос­кость про­хо­дит через сто­ро­ну ос­но­ва­ния этой пи­ра­ми­ды и пе­ре­се­ка­ет про­ти­во­по­лож­ное бо­ко­вое ребро в точке, де­ля­щей его в от­но­ше­нии 7:8, счи­тая от вер­ши­ны пи­ра­ми­ды. Най­ди­те боль­ший из объ­е­мов пи­ра­мид, на ко­то­рые плос­кость раз­би­ва­ет ис­ход­ную пи­ра­ми­ду.

55. Диа­метр ос­но­ва­ния ко­ну­са равен 6, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на π.

56. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­деABCDA1B1C1D1 ребро CD = 2, ребро ребро CC1 = 2. Точка K — се­ре­ди­на ребра DD1. Най­ди­те пло­щадь се­че­ния, про­хо­дя­ще­го через точки C1, B1 и K.

57. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 2 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 30 . В от­ве­те ука­жи­те .

58. В пра­виль­ной ше­сти­уголь­ной приз­ме все ребра равны 1. Най­ди­те угол . Ответ дайте в гра­ду­сах.

 

59. Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Ра­ди­ус сферы равен Най­ди­те об­ра­зу­ю­щую ко­ну­са.

Дата добавления: 2015-08-29; просмотров: 223 | Нарушение авторских прав


mybiblioteka.su — 2015-2021 год. (0.017 сек.)

Задания В Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.

Все прототипы задания В11 (2013)

Все прототипы задания В11 (2013) ( 25541) Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). ( 25561) Найдите площадь поверхности многогранника, изображенного

Подробнее

Задание 13. Задачи по стереометрии

Задание 13 Задачи по стереометрии 1.Диагональ куба равна Куб. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см

Подробнее

Стереометрия: конус, цилиндр.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: конус, цилиндр. 27052. Объем конуса равен

Подробнее

Задание 8 Стереометрия.

Задание 8 Стереометрия. Куб 1. Площадь поверхности куба равна 18. Найдите его диагональ. 2. Объем куба равен 8. Найдите площадь его поверхности. 3. Если каждое ребро куба увеличить на 1, то его площадь

Подробнее

Задание 16 Задачи по стереометрии

Задание 16 Задачи по стереометрии Куб 1.Диагональ куба равна 12. Найдите его объем. 2. Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30

Подробнее

Тригонометрические уравнения

Тригонометрические уравнения С б) Укажите корни, принадлежащие отрезку. а) Решите уравнение б) Укажите корни уравнения, принадлежащие отрезку а) Решbте уравнение. б) Укажите корни этого уравнения, принадлежащие

Подробнее

Все прототипы задания В9 (2013)

Все прототипы задания В9 (2013) ( 245359) Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. ( 245360) Найдите расстояние между вершинами и прямоугольного параллелепипеда,

Подробнее

Все прототипы В года

1. Прототип задания B9 ( 245359) Все прототипы В5 2013 года Найдите квадрат расстояния между вершинами и прямоугольного параллелепипеда, для которого,,. 2. Прототип задания B9 ( 245360) Найдите расстояние

Подробнее

Подготовка к ЕГЭ по математике

2015 2016 Подготовка к ЕГЭ по математике Прототипы задач из открытого банка заданий ЕГЭ по математике (профильный уровень) http://mathege.ru Стереометрия: конус, цилиндр. Александр и Наталья Крутицких

Подробнее

Прямоугольный параллелепипед

ЗАДАНИЕ 10 Стереометрия Куб 1.Площадь поверхности куба равна 18. Найдите его диагональ. 2. Диагональ грани куба равна 2 6. Найдите диагональ куба. 3. Диагональ грани куба равна 6. Найдите диагональ куба.

Подробнее

Стереометрия: комбинации тел.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: комбинации тел. 27041. Прямоугольный параллелепипед

Подробнее

Все прототипы заданий В года

1. Прототип задания B13 ( 27054) выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины. Все прототипы заданий В13

Подробнее

Все прототипы заданий года

1. Прототип задания 12 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий 12

Подробнее

Все прототипы заданий В года

1. Прототип задания B13 ( 27064) Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы. Все прототипы заданий

Подробнее

Стартовая контрольная работа

Стартовая контрольная работа Контрольная работа 1(на 20 мин) 1. Найдите координаты вектора АВ, если А (5; 1; 3), В (2; 2; 4). 2. Даны векторы b (3; 1; 2) и c 2b c (1; 4; 3). Найдите. 3. Изобразите систему

Подробнее

Куб. Прямоугольный параллелепипед

Куб 1. Задание 16 27098. Диагональ куба равна. Найдите его объем. О т в е т : 8 2. Задание 16 500957. Во сколько раз увеличится объем куба, если все его рѐбра увеличить в 5 раз? О т в е т : 1 2 5 3. Задание

Подробнее

Стереометрия: призма.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: призма. 27047. В сосуд, имеющий форму

Подробнее

Куб. 3. Найдите объем многогранника, вершинами которого являются точки,,,,, прямоугольного параллелепипеда, у которого,,.

Куб. 1. Диагональ куба равна. Найдите его объем. 2.Во сколько раз увеличится объем куба, если все его рёбра увеличить в 5 раз? 3. Ящик, имеющий форму куба с ребром 30 см без одной грани, нужно покрасить

Подробнее

7. Задачи по стереометрии

РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ 7 Задачи по стереометрии методические указания для абитуриентов физического факультета Ростов-на-Дону 00 Печатается по решению учебнофакультета РГУ методической комиссии

Подробнее

Задание 8.

h, 2000 S осн. V дет Ответ: 1500.

Вебинар 9 Тема: Тела вращения. Комбинация фигур. Подготовка к ЕГЭ (задание 8; 4) Задание 8.. В цилиндрический сосуд налили 000 см воды. Уровень жидкости оказался равным см. В воду полностью погрузили деталь.

Подробнее

Тест по теме 60 «Параллелепипед и куб»

Тест по теме 60 «Параллелепипед и куб» 1. Существует ли параллелепипед, у которого только одна боковая грань перпендикулярна основанию?, если в основании квадрат 2. Существует ли параллелепипед, у которого

Подробнее

Задачи по с т е р е о м е т р и и

Задачи по с т е р е о м е т р и и Ермак Елена Анатольевна, доктор педагогических наук, профессор кафедры математического анализа и методики обучения математике Псковского государственного университета

Подробнее

Геометрия.

Тренировочный вариант 1

Геометрия. Тренировочный вариант 1 1. Найдите площадь трапеции, изображённой на рисунке. 2. Около треугольника MNP описана окружность с центром О. Найдите угол РОМ, если угол PNM равен 17. Ответ дайте

Подробнее

Тест 250. Отрезок. Длина

Тест 250. Отрезок. Длина Длина отрезка равна 1, если он является: 1. высотой равностороннего треугольника со стороной 2; 2. третьей стороной треугольника, в котором две другие стороны равны 1 и 2, а угол

Подробнее

ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ)

И.М. Смирнова, В.А. Смирнов ГОТОВИМСЯ К ЕГЭ (ГЕОМЕТРИЯ) ОБЪЕМЫ И ПЛОЩАДИ ПОВЕРХНОСТЕЙ ПРОСТРАНСТВЕННЫХ ФИГУР Москва 2008 1 ВВЕДЕНИЕ В настоящем пособии собраны задачи на нахождение объемов и площадей поверхностей

Подробнее

Многогранники.

Призма

Справка В9 Многогранники Многогранник это такое тело, поверхность которого состоит из конечного числа плоских многоугольников. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников,

Подробнее

УДК 373:51 ББК 22.1я72 С50

УДК 373:5 ББК 22.я72 С50 Смирнов В. А. ЕГЭ 205. Математика. Задача 2. Геометрия: объем, площадь поверхности. Рабочая тетрадь Под ред. И. В. Ященко Электронное издание М.: МЦНМО, 205 64 с. ISN 978-5-4439-24-3

Подробнее

1 Расстояние от точки до прямой

1 Расстояние от точки до прямой 1 1 1 1 1.1. В единичном кубе 1 1 1 1 найдите расстояние от точки до прямой 1. 1 1.2. В правильной треугольной призме 1 1 1, все ребра которой равны 1, найдите расстояние

Подробнее

Стереометрия: пирамиды.

А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.ru Стереометрия: пирамиды. 27069. Стороны основания правильной

Подробнее

Тест по теме «Задачи стереометрии»

Тест по теме «Задачи стереометрии» Тест составлен на основе учебника «Геометрия, 10-11 класс (базового и профильного уровней ) / Л.С. Атанасян и др. — М.: «Просвещение», 2010. Аннотация: Задачи теста соответствуют

Подробнее

ID_7154 1/10 neznaika.pro

1 Задачи по стереометрии Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. Найдите объём

Подробнее

Домашние работы по алгебре и геометрии, 10-11 класс, ФГОС

Домашняя работа тела вращения.

1. Пло­щадь боль­шо­го круга шара равна 3. Най­ди­те пло­щадь по­верх­но­сти шара.

2.

Дано два шара. Ра­ди­ус пер­во­го шара в 2 раза боль­ше ра­ди­у­са вто­ро­го. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти вто­ро­го?

3. Во сколь­ко раз уве­ли­чит­ся объем шара, если его ра­ди­ус уве­ли­чить в три раза?

4. Ра­ди­у­сы трех шаров равны 6, 8 и 10. Най­ди­те ра­ди­ус шара, объем ко­то­ро­го равен сумме их объ­е­мов.

5. Объем од­но­го шара в 27 раз боль­ше объ­е­ма вто­ро­го. Во сколь­ко раз пло­щадь по­верх­но­сти пер­во­го шара боль­ше пло­ща­ди по­верх­но­сти вто­ро­го?

6. Ра­ди­у­сы двух шаров равны 6 и 8. Най­ди­те ра­ди­ус шара, пло­щадь по­верх­но­сти ко­то­ро­го равна сумме пло­ща­дей по­верх­но­стей двух дан­ных шаров.

7. Объем шара равен 288 . Най­ди­те пло­щадь его по­верх­но­сти, де­лен­ную на .

8. Объем ко­ну­са равен 16. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са.

9. Най­ди­те объем V ко­ну­са, об­ра­зу­ю­щая ко­то­ро­го равна 2 и на­кло­не­на к плос­ко­сти ос­но­ва­ния под углом 30. В от­ве­те ука­жи­те .

10. Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­та умень­шит­ся в 3 раза, а ра­ди­ус ос­но­ва­ния оста­нет­ся преж­ним?

11. Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если ра­ди­ус его ос­но­ва­ния уве­ли­чит­ся в 1,5 раза, а вы­со­та оста­нет­ся преж­ней?

15. Вы­со­та ко­ну­са равна 6, об­ра­зу­ю­щая равна 10. Най­ди­те его объем, де­лен­ный на .

16. Диа­метр ос­но­ва­ния ко­ну­са равен 6, а угол при вер­ши­не осе­во­го се­че­ния равен 90°. Вы­чис­ли­те объем ко­ну­са, де­лен­ный на π.

17. Конус по­лу­ча­ет­ся при вра­ще­нии рав­но­бед­рен­но­го пря­мо­уголь­но­го тре­уголь­ни­ка  во­круг ка­те­та, рав­но­го 6. Най­ди­те его объем, де­лен­ный на .

18. Длина окруж­но­сти ос­но­ва­ния ко­ну­са равна 3, об­ра­зу­ю­щая равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са.

19. Во сколь­ко раз уве­ли­чит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если его об­ра­зу­ю­щая уве­ли­чит­ся в 3 раза, а ра­ди­ус ос­но­ва­ния оста­нет­ся преж­ним?

20. Во сколь­ко раз умень­шит­ся пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са, если ра­ди­ус его ос­но­ва­ния умень­шит­ся в 1,5 раза, а об­ра­зу­ю­щая оста­нет­ся преж­ней?

21.  Вы­со­та ко­ну­са равна 6, об­ра­зу­ю­щая равна 10. Най­ди­те пло­щадь его пол­ной по­верх­но­сти, де­лен­ную на .

22. Пло­щадь бо­ко­вой по­верх­но­сти ко­ну­са в два раза боль­ше пло­ща­ди ос­но­ва­ния. Най­ди­те угол между об­ра­зу­ю­щей ко­ну­са и плос­ко­стью ос­но­ва­ния. Ответ дайте в гра­ду­сах.

23. Пло­щадь пол­ной по­верх­но­сти ко­ну­са равна 12. Па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, де­ля­щее вы­со­ту в от­но­ше­нии 1:1, счи­тая от вер­ши­ны ко­ну­са. Най­ди­те пло­щадь пол­ной по­верх­но­сти отсечённого ко­ну­са.

24. Ра­ди­ус ос­но­ва­ния ко­ну­са равен 3, вы­со­та равна 4. Най­ди­те пло­щадь пол­ной по­верх­но­сти ко­ну­са, де­лен­ную на .

29.Вы­со­та ко­ну­са равна 4, а диа­метр ос­но­ва­ния — 6. Най­ди­те об­ра­зу­ю­щую ко­ну­са.

 

30.  Вы­со­та ко­ну­са равна 4, а длина об­ра­зу­ю­щей — 5. Най­ди­те диа­метр ос­но­ва­ния ко­ну­са.

 

31.Диа­метр ос­но­ва­ния ко­ну­са равен 6, а длина об­ра­зу­ю­щей — 5. Най­ди­те вы­со­ту ко­ну­са.

32. В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет  вы­со­ты. Объём жид­ко­сти равен 70 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд?


 

33. Пло­щадь ос­но­ва­ния ко­ну­са равна 16π, вы­со­та — 6. Най­ди­те пло­щадь осе­во­го се­че­ния ко­ну­са.

34. Пло­щадь ос­но­ва­ния ко­ну­са равна 18. Плос­кость, па­рал­лель­ная плос­ко­сти ос­но­ва­ния ко­ну­са, делит его вы­со­ту на от­рез­ки дли­ной 3 и 6, счи­тая от вер­ши­ны. Най­ди­те пло­щадь се­че­ния ко­ну­са этой плос­ко­стью.

35.  Вы­со­та ко­ну­са равна 8, а длина об­ра­зу­ю­щей — 10. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

36. Диа­метр ос­но­ва­ния ко­ну­са равен 12, а длина об­ра­зу­ю­щей — 10. Най­ди­те пло­щадь осе­во­го се­че­ния этого ко­ну­са.

 

37. В сосуд ци­лин­дри­че­ской формы на­ли­ли воду до уров­ня 80 см. Ка­ко­го уров­ня до­стиг­нет вода, если её пе­ре­лить в дру­гой ци­лин­дри­че­ский сосуд, у ко­то­ро­го ра­ди­ус ос­но­ва­ния в 4 раза боль­ше, чем у пер­во­го? Ответ дайте в см.

38. Около ко­ну­са опи­са­на сфера (сфера со­дер­жит окруж­ность ос­но­ва­ния ко­ну­са и его вер­ши­ну). Центр сферы сов­па­да­ет с цен­тром ос­но­ва­ния ко­ну­са. Ра­ди­ус сферы равен  Най­ди­те об­ра­зу­ю­щую ко­ну­са.

41. В ци­лин­дри­че­ский сосуд на­ли­ли 2000 см3 воды. Уро­вень воды при этом до­сти­га­ет вы­со­ты 12 см.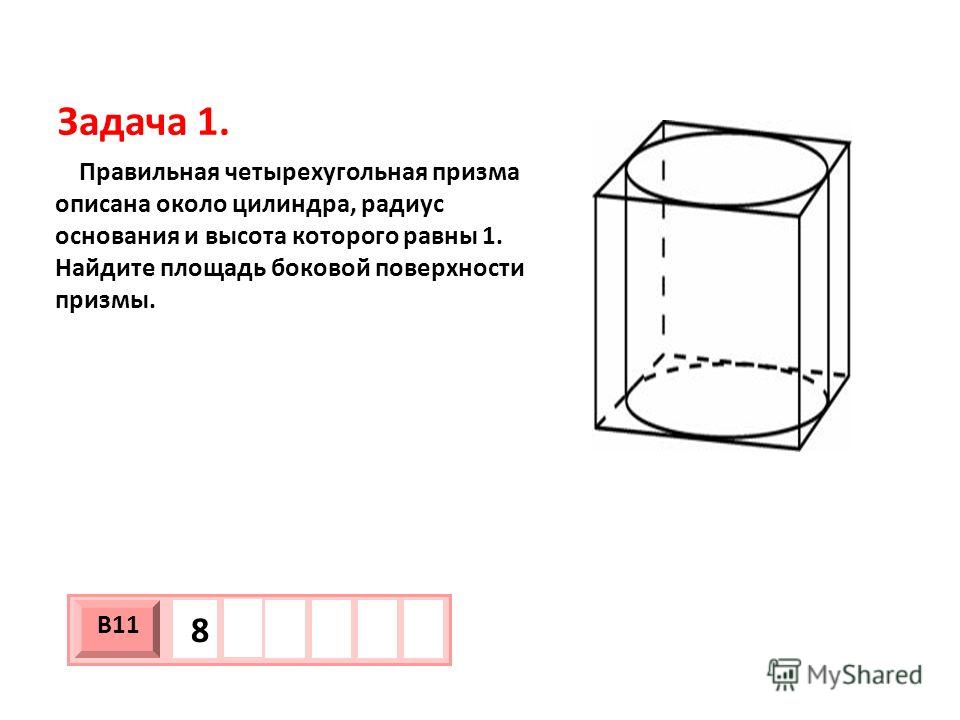 В жид­кость пол­но­стью по­гру­зи­ли де­таль. При этом уро­вень жид­ко­сти в со­су­де под­нял­ся на 9 см. Чему равен объем де­та­ли? Ответ вы­ра­зи­те в см3.

 

42. В ци­лин­дри­че­ском со­су­де уро­вень жид­ко­сти до­сти­га­ет 16 см. На какой вы­со­те будет на­хо­дить­ся уро­вень жид­ко­сти, если ее пе­ре­лить во вто­рой сосуд, диа­метр ко­то­ро­го в  раза боль­ше пер­во­го? Ответ вы­ра­зи­те в см.

43. Объем пер­во­го ци­лин­дра равен 12 м3. У вто­ро­го ци­лин­дра вы­со­та в три раза боль­ше, а ра­ди­ус ос­но­ва­ния — в два раза мень­ше, чем у пер­во­го. Най­ди­те объем вто­ро­го ци­лин­дра. Ответ дайте в ку­би­че­ских мет­рах.

44. Ра­ди­ус ос­но­ва­ния ци­лин­дра равен 2, вы­со­та равна 3. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра, де­лен­ную на .

45.

В ци­лин­дри­че­ский сосуд на­ли­ли 6 куб. см воды. В воду пол­но­стью по­гру­зи­ли де­таль. При этом уро­вень жид­ко­сти в со­су­де уве­ли­чил­ся в 1,5 раза. Най­ди­те объём де­та­ли. Ответ вы­ра­зи­те в куб. см.

46. Одна ци­лин­дри­че­ская круж­ка вдвое выше вто­рой, зато вто­рая в пол­то­ра раза шире. Най­ди­те от­но­ше­ние объ­е­ма вто­рой круж­ки к объ­е­му пер­вой.

47. Длина окруж­но­сти ос­но­ва­ния ци­лин­дра равна 3, вы­со­та равна 2. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра.

48. Пло­щадь осе­во­го се­че­ния ци­лин­дра равна 4. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра, де­лен­ную на .

50 . Длина окруж­но­сти ос­но­ва­ния ци­лин­дра равна 3. Пло­щадь бо­ко­вой по­верх­но­сти равна 6. Най­ди­те вы­со­ту ци­лин­дра.

 51. Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна , а диа­метр ос­но­ва­ния — 1. Най­ди­те вы­со­ту ци­лин­дра.

52. Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна , а вы­со­та — 1. Най­ди­те диа­метр ос­но­ва­ния.

53. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 20. Найдите объем шара.

54.Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 81 Найдите объем конуса.

55. Цилиндр описан около шара. Объем шара равен 144. Найдите объем цилиндра.

56. В сосуде, имеющем форму конуса, уровень жидкости достигает высоты. Объём жидкости равен 21 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?

Как найти площадь цилиндра

Пояснение:

Нам нужно найти выражения для площади поверхности и объема цилиндра. Площадь поверхности цилиндра складывается из суммы площадей двух оснований плюс площадь боковой поверхности.

площадь поверхности цилиндра = площадь основания + площадь боковой поверхности

Основанием цилиндра будут две окружности радиусом r . Таким образом, площадь каждого будет составлять πr 2 , а их общая площадь поверхности будет 2 πr 2 .

Площадь боковой поверхности цилиндра равна длине окружности круглого основания, умноженной на высоту. Длина окружности равна 2 πr , а высота — h , поэтому поперечная площадь равна 2 πrh .

площадь поверхности цилиндра = 2 πr 2 + 2 πrh

Далее нам нужно найти выражение для объема. Объем цилиндра равен произведению высоты на площадь одного из оснований.Площадь основания πr 2 , а высота h , поэтому объем цилиндра πr 2 h .

объем = πr 2 ч

Затем мы должны установить выражения для объема и площади поверхности равными друг другу и решить для r через h .

2 πr 2 + 2 πrh = πr 2 h

Во-первых, вынесем 2 πr из левой части.

2 πr ( r + h ) = πr 2 h

Мы можем разделить обе части на π.

2 r ( r + h ) = r 2 h

Мы также можем разделить обе стороны на r , потому что радиус не может равняться нулю.

2 ( r + h ) = rh

Давайте теперь распределим 2 на левой стороне.

2 r + 2 h = справа

Вычтите 2 r с обеих сторон, чтобы получить все r с одной стороны.

2 ч = правая -2 правая

r ч — 2 r = 2 ч

Выносим за скобки r с левой стороны.

r ( ч — 2) = 2 ч

Разделим обе стороны на h -2

r = 2 ч / ( ч — 2)

Ответ: r = 2 h / ( h — 2).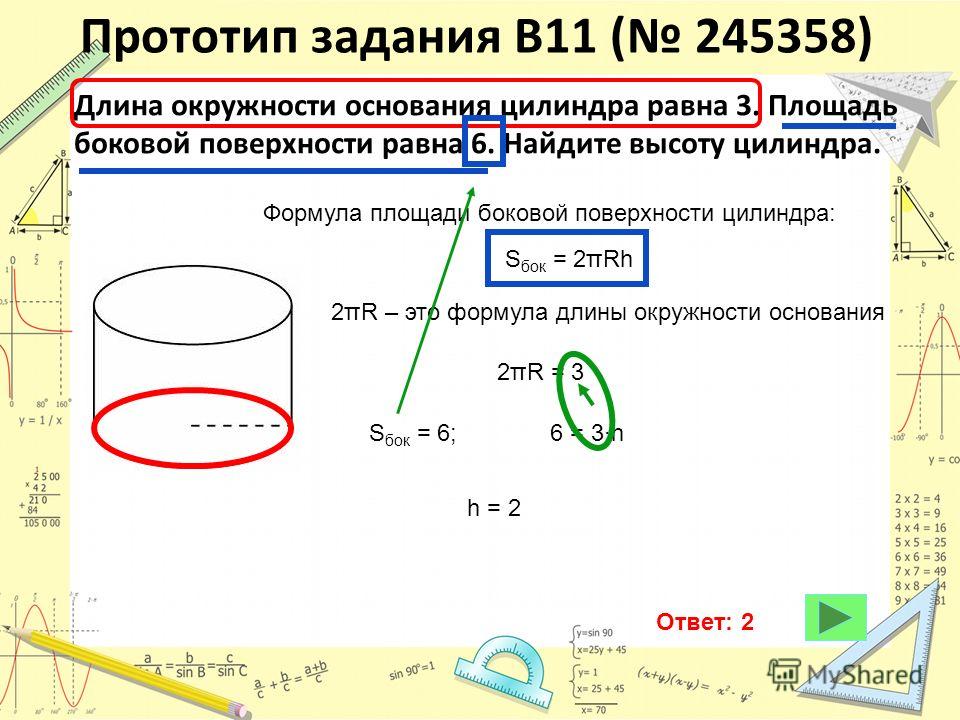

Видео с вопросом: Определение площади боковой поверхности цилиндра по радиусу основания и высоте

Стенограмма видео

Определите с точностью до 10-ю площадь боковой поверхности показанного цилиндра.

Площадь боковой поверхности будет площадью поверхности этого цилиндра, за исключением оснований. Итак, мы будем исключать круги. Итак, если мы подумаем о цилиндре, мы можем представить его как банку для супа.А площадь боковой поверхности — это этикетка для суповой банки, опять же без крышки и дна.

Итак, если мы представим себе, как снимают этикетку с консервной банки, и эта этикетка представляет собой прямоугольник, длина которого умножена на ширину, это наша формула площади боковой поверхности для цилиндра. И это потому, что это, опять же, прямоугольник.

Теперь в прямоугольнике ширина. Но в цилиндре ширину мы бы считали высотой. И длина, это расстояние, это будет расстояние, охватывающее крышку. А расстояние по кругу — это длина окружности. А длина окружности в два раза больше радиуса в 𝜋 раза.

Итак, в нашей формуле мы можем заменить на удвоенный, умноженный на радиус, и ширину на высоту. Итак, известная нам высота — 23 фута. Теперь радиус — это расстояние от центра круга до точки на окружности, которая будет здесь. И это говорит нам, что расстояние составляет 13 футов. Итак, дважды 13 равно 26. Итак, 26𝜋 футов, умноженные на 23 фута, будут равны 598𝜋 футов в квадрате.

Теперь нам нужно умножить на. И мы получаем примерно 1878,67 футов в квадрате. Но нам нужно округлить до ближайшего 10-го. Итак, нам нужно округлить, где находится шестерка. Таким образом, мы либо оставим шесть на шесть, либо округлим до семи.

Итак, если посмотреть на число справа, семь, которое больше или равно пяти, это означает, что мы округлим шесть до семи. Следовательно, площадь боковой поверхности показанного цилиндра составит 1878,7 квадратных футов.

Площадь поверхности цилиндра — объяснение и примеры

Прежде, чем мы перейдем к теме площади поверхности цилиндра, давайте рассмотрим цилиндр. В геометрии цилиндр — это трехмерная фигура с двумя параллельными друг другу круглыми основаниями и изогнутой поверхностью.

Как найти площадь поверхности цилиндра?

Площадь поверхности цилиндра складывается из двух параллельных и конгруэнтных круглых граней и площади изогнутой поверхности.

В этой статье мы обсудим , как найти общую площадь поверхности и площадь боковой поверхности цилиндра .

Чтобы вычислить площадь поверхности цилиндра , вам нужно найти площадь основания (B) и площадь криволинейной поверхности (CSA).Следовательно, площадь поверхности или общая поверхность цилиндра равна сумме площади основания, умноженной на два, и площади изогнутой поверхности.

Изогнутая поверхность цилиндра равна прямоугольнику, длина которого составляет 2 πr , а ширина — h.

где r = радиус круглой грани и h = высота цилиндра.

Площадь изогнутой поверхности = Площадь прямоугольника = lxw = πdh

Площадь основания, B = Площадь круга = πr 2

Формула площади цилиндра

Формула для общей площади поверхности цилиндра имеет следующий вид:

Общая площадь поверхности цилиндра = 2πr 2 + 2πrh

TSA = 2πr 2 + 2πrh

Где 2πr 2 равно площадь верхней и нижней круглой грани, а 2πrh — площадь изогнутой поверхности.

Принимая 2πr в качестве общего множителя из RHS, мы получаем;

TSA = 2πr (h + r) ……………………………………. ( Формула площади поверхности цилиндра )

Давайте решим примерные задачи, касающиеся площади поверхности цилиндра.

Пример 1

Найдите общую площадь поверхности цилиндра с радиусом 5 см и высотой 7 см.

Решение

По формуле

TSA = 2πr (h + r)

= 2 x 3.14 x 5 (7 + 5)

= 31,4 x 12

= 376,8 см 2

Пример 2

Найдите радиус цилиндра с общей площадью поверхности 2136,56 квадратных футов и высотой 3 ноги.

Решение

Дано:

TSA = 2136,56 квадратных футов

Высота, h = 3 фута

Но, TSA = 2πr (h + r)

2136,56 = 2 x 3,14 xr (3 + r)

2136,56 = 6,28r (3 + r)

По распределительному свойству умножения на правой стороне имеем,

2136. 56 = 18,84r + 6,28r 2

Разделите каждый член на 6,28

340,22 = 3r + r 2

r 2 + 3r — 340,22 = 0 ……… ( квадратное уравнение )

Решая уравнение по формуле корней квадратного уравнения, получаем:

r = 17

Следовательно, радиус цилиндра составляет 17 футов.

Пример 3

Стоимость окраски цилиндрической емкости составляет 0,04 доллара США за см 2 .Найдите стоимость покраски 20 контейнеров радиусом 50 см и высотой 80 см.

Раствор

Рассчитайте общую площадь поверхности 20 контейнеров.

TSA = 2πr (h + r)

= 2 x 3,14 x 50 (80 + 50)

= 314 x 130

= 40820 см 2

Общая площадь 20 контейнеров = 40820 см 2 x 20

= 816400 см 2

Стоимость покраски = 816400 см 2 x 0 руб.04 за см 2

= 32 656 долларов США.

Следовательно, стоимость покраски 20 контейнеров составляет 32 656 долларов США.

Пример 4

Найдите высоту цилиндра, если его общая площадь поверхности составляет 2552 дюйма 2 и радиус 14 дюймов

Решение

Дано:

TSA = 2552 дюйма 2

Радиус, r = 14 дюймов

Но, TSA = 2πr (h + r)

2552 = 2 x 3,14 x 14 (14 + h)

2552 = 87.92 (14 + h)

Разделите обе стороны на 87,92, чтобы получить,

29,026 = 14 + h

Вычтем на 14 с обеих сторон.

h = 15

Следовательно, высота цилиндра составляет 15 дюймов.

Площадь боковой поверхности цилиндра

Как указывалось ранее, площадь изогнутой поверхности цилиндра называется боковой поверхностью площадь. Проще говоря, площадь боковой поверхности цилиндра — это площадь поверхности цилиндра без учета площади основания и дна (круговой поверхности).

Площадь боковой поверхности цилиндра определяется по формуле;

LSA = 2πrh

Пример 5

Найдите следующую площадь поверхности цилиндра диаметром 56 см и высотой 20 см.

Решение

Дано:

Диаметр = 56 см, следовательно, радиус, r = 56/2 = 28 см

Высота, h = 20 см

По формуле

LSA = 2πrh

= 2 х 3,14 х 28 х 20

= 3516.8 см 2 .

Таким образом, площадь боковой поверхности цилиндра составляет 3516,8 см 2 .

Пример 6

Площадь боковой поверхности цилиндра составляет 144 фута 2 . Если радиус цилиндра 7 футов, найдите высоту цилиндра.

Решение

Дано;

LSA = 144 фута 2

Радиус, r = 7 футов

144 = 2 x 3,14 x 7 x h

144 = 43,96h

Разделить на 43.96 с обеих сторон.

3,28 = h

Итак, высота цилиндра составляет 3,28 фута.

Предыдущий урок | Главная страница | Следующий урок

Rd Sharma 2019 2020 for Class 8 Math Chapter 22

Страница № 22.
10:
Вопрос 1:

Найдите площадь криволинейной поверхности и общую площадь поверхности цилиндра, диаметр основания которого равен 7 см, а высота — 60 см.

Ответ:

Пусть r и h — радиус и высота цилиндра. Дано: r = 72 см, h = 60 см. Площадь изогнутой поверхности цилиндра = 2π × r × h = 2 × 227 × 72 × 60 = 22 × 60 = 1320 см2. площадь поверхности цилиндра = 2π × r × (r + h) = 2 × 227 × 72 × (72 + 60) = 22 × 1272 = 11 × 127 = 1397 см2

Стр. № 22.10:
Вопрос 2:

Площадь криволинейной поверхности цилиндрической дороги составляет 132 см. 2 . Найдите его длину, если радиус равен 0,35 см.

Ответ:

Считаем h высотой цилиндрического стержня. Дано: Радиус, r = 0,35 см Площадь изогнутой поверхности = 132 см2 Мы знаем: Площадь изогнутой поверхности = 2 × π × r × h 132 = 2 × 227 × 0,35 × h = 132 × 72 × 22 × 0. 35 h = 60, следовательно, длина цилиндрического стержня 60 см.

Страница № 22.10:
Вопрос 3:

Площадь основания правого кругового цилиндра — 616 см. 2 , высота — 2,5 см. Найдите площадь криволинейной поверхности цилиндра.

Ответ:

Дано: Площадь основания правого кругового цилиндра = 616 см2, высота = 2.5 см Пусть r — радиус основания правого кругового цилиндра. Πr2 = 616⇒r2 = 616 × 722⇒r2 = 196⇒r = 14 см Площадь изогнутой поверхности правого кругового цилиндра = 2πrh = 2 × 227 × 14 × 2,5 = 220 см2

Страница № 22.10:
Вопрос 4:

Окружность дна цилиндра 88 см, высота 15 см. Найдите площадь изогнутой поверхности и общую площадь поверхности.

Ответ:

Дано: Высота, h = 15 см Окружность основания цилиндра = 88 см2 Пусть r будет радиусом цилиндра. Окружность основания цилиндра = 2πr88 = 2 × 227 × rr = 88 × 72 × 22 = 14 см Площадь изогнутой поверхности = 2 × π × r × h = 2 × 227 × 14 × 15 = 1320 см2 Общая площадь поверхности = 2 × π × r × (r + h) = 2 × 227 × 14 × (14 + 15) = 2552 см2

Страница № 22.10:
Вопрос 5:

Прямоугольная полоса 25 см × 7 см повернута вокруг длинной стороны. Найти общую площадь поверхности сгенерированного таким образом твердого тела.

Ответ:

Поскольку прямоугольная полоса размером 25 см × 7 см вращается вокруг более длинной стороны, мы имеем: Высота, h = 25 см Радиус, r = 7 см ∴Общая площадь поверхности = 2πr (r + h) = 2π (7) (25+ 7) = 14π (32) = 448πcm² = 448 × 227cm² = 1408 см²

Стр. № 22.10:
Вопрос 6:

Прямоугольный лист бумаги размером 44 см × 20 см свернут по всей длине, образуя цилиндр. Найдите общую площадь поверхности сформированного цилиндра.

Ответ:

Прямоугольный лист бумаги размером 44 см × 20 см свернут по своей длине в виде цилиндра. Высота цилиндра 20 см, окружность 44 см. Имеем: Высота, h = 20 см, Окружность = 2πr = 44 см∴ Общая площадь S = 2πrh = 44 × 20 см² = 880 см²

Стр. № 22.10:
Вопрос 7:

Радиусы двух цилиндров находятся в соотношении 2: 3, а их высота — в соотношении 5: 3. Вычислите соотношение площадей их криволинейных поверхностей.

Ответ:

Пусть радиусы двух цилиндров равны 2r и 3r соответственно, а их высота равна 5h и 3h соответственно. Пусть S1 и S2 — площади криволинейной поверхности двух цилиндров. S1 = площадь криволинейной поверхности цилиндра высотой 5h и радиус 2rS2 = площадь криволинейной поверхности цилиндра высотой 3h и радиусом 3r∴ S1: S2 = 2 × π × r × h: 2 × π × r × h = 2 × π × 2r × 5h 2 × π × 3r × 3h = 10: 9

Стр.
№ 22.10:
Вопрос 8:

Соотношение между площадью криволинейной поверхности и общей площадью поверхности правильного кругового цилиндра составляет 1: 2. Докажите, что его высота и радиус равны.

Ответ:

Пусть S1 и S2 — площадь криволинейной поверхности и общая площадь поверхности кругового цилиндра, соответственно. Тогда S1 = 2πrh, S2 = 2πrr + h Согласно вопросу: S1: S2 = 1: 22πrh: 2πrr + h = 1: 2 h: r + h = 1: 2 hr + h = 12 2h = r + h h = r Следовательно, высота и радиус равны.

Страница № 22.11:
Вопрос 9:

Площадь криволинейной поверхности цилиндра 1320 см. 2 , диаметр основания 21 см. Найдите высоту цилиндра.

Ответ:

Пусть h будет высотой цилиндра. Дано: Площадь изогнутой поверхности, S = 1320 см2 Диаметр, d = 21 см Радиус, r = 10,5 S = 2πrh2320 = 2π × 10,5 × h h = 13202π × 10.5 h = 20 см

Страница № 22.11:
Вопрос 10:

Высота правого кругового цилиндра 10,5 см. Если трехкратная сумма площадей его двух круглых граней будет в два раза больше площади изогнутой поверхности. Найдите радиус его основания.

Ответ:

Пусть r — радиус кругового цилиндра. Высота, h = 10,5 см. Площадь изогнутой поверхности, S1 = 2πrh. Сумма площадей его двух круговых граней, S2 = 2πr2. Согласно вопросу: 3S2 = 2S13 × 2πr2 = 2 × 2πrh 6r = 4h 3r = 2h r = 23 × 10.5 см = 7 см

Страница № 22.11:
Вопрос 11:

Найдите стоимость оштукатуривания внутренней поверхности колодца из расчета 9,50 рупий за м. 2 , если глубина колодца 21 м, а диаметр кровли 6 м.

Ответ:

Дано: Высота, h = 21 м, диаметр, d = 6 м, радиус, r = 3 м, площадь внутренней поверхности колодца, S = 2πrh = 2π × 3 × 21 м2 = 2 × 227 × 3 × 21 м2 = 396 м2 Согласно вопрос, стоимость м2 9 рупий.50. ∴ Стоимость внутренней поверхности составляет 396 рупий × 9,50 = 3762

рупий.
Страница № 22.11:
Вопрос 12:

Открытый сверху цилиндрический сосуд имеет диаметр 20 см и высоту 14 см. Найдите стоимость лужения изнутри из расчета 50 пайс за сотку.

Ответ:

Дано: Диаметр, d = 20 см Радиус, r = 10 см Высота, h = 14 см Площадь внутри цилиндрического сосуда, подлежащего лужению = SS = 2πrh + πr2 = 2π × 10 × 14 + π × 102 = 280π + 100π = 380 × 227 см2 = 83607 см2 Согласно вопросу: Стоимость за 100 см2 = 50 пайсов Стоимость за см2 = 0 рупий.005 Стоимость лужения внутри цилиндрической емкости = 0,005 рупий × 83607 = 41,87 рупий = 5,97 рупий

Страница № 22.11:
Вопрос 13:

Внутренний диаметр круглого колодца — 3,5 м. Его глубина 10 м. Найдите стоимость оштукатуривания его внутренней криволинейной поверхности в 4 рупия за квадратный метр.

Ответ:

Дано: Внутренний диаметр круглого колодца = 3.5 м Внутренний радиус круглого колодца, r = 1,75 м Глубина круглого колодца, h = 10 м Площадь внутренней криволинейной поверхности, S = 2πrhS = 2π × 1,75 × 10 м2 = 2 × 227 × 1,75 × 10 м2 = 110 м2 Стоимость оштукатуривание площади 1м2 = 4 рупий Стоимость оштукатуривания площади 110 м2 = 110 рупий × 4 = 440

рупий
Страница № 22.11:
Вопрос 14:

Диаметр ролика 84 см, длина 120 см. Чтобы выровнять игровую площадку, требуется 500 полных оборотов.Какая площадь у детской площадки?

Ответ:

Дано: Диаметр ролика = 84 см Радиус, r = Диаметр2 = 42 см За 1 оборот он покрывает расстояние своей площади боковой поверхности. Ролик представляет собой цилиндр высотой, h = 120 см Радиус = 42 см Площадь боковой поверхности цилиндр = 2πrh = 2 × 227 × 42 × 120 = 31680 см2 Для выравнивания игровой площадки требуется 500 полных оборотов. Площадь поля = 31680 × 500 = 15840000 см2 1 см2 = 110000 м2 ∴ 15840000 см2 = 1584 м2.Таким образом, площадь поля в м2 составляет 1584 м2.

Страница № 22.11:
Вопрос 15:

Двадцать одна цилиндрическая опора Дома Парламента подлежит очистке. Если диаметр каждой колонны составляет 0,50 м, а высота — 4 м, сколько будет стоить их очистка из расчета 2,50 рупий за квадратный метр?

Ответ:

Дано: Диаметр столбов = 0.5 м Радиус столбов, r = 0,25 м Высота столбов, h = 4 м Количество столбов = 21 Скорость очистки = 2,50 рупий за квадратный метр Площадь изогнутой поверхности одной опоры = 2πrh = 2 × 227 × 0,25 × 4 = 2 × 227 = 447 м2∴ Площадь изогнутой поверхности одной опоры = 447 м2 Стоимость очистки 21 стойки из расчета 2,50 рупий за м2 = 2,5 × 21 × 447 = 7,5 × 44 Стоимость очистки 21 стойки из расчета 2,50 рупий за м2 = 330

рупий
Страница № 22.11:
Вопрос 16:

Общая площадь полого цилиндра, открытого с обеих сторон, составляет 4620 кв.см, площадь базового кольца 115,5 см2, высота 7 см. Найдите толщину цилиндра.

Ответ:

Дано: Общая площадь поверхности цилиндра = 4620 см2 Площадь базового кольца = 115,5 см2 Высота, h = 7 см Пусть R будет радиусом внешнего кольца, а r будет радиусом внутреннего кольца. Площадь базового кольца = πR2- πr2115,5 = πR2- r2R2- r2 = 115,5 × 722 (R + r) (Rr) = 36,75 ……….. (i) Общая площадь поверхности = Площадь внутренней криволинейной поверхности + Площадь внешней криволинейной поверхности + Площадь нижнего и верхнего колец 4620 = 2πrh + 2πRh + 2 × 115.52πh (R + r) = 4620-231R + r = 4389 × 72 × 22 × 7R + r = 3994 ……….. (ii) Подставляя значение R + r из уравнения (ii ) В (i): 3994 (Rr) = 36,75 (Rr) = 36,75 × 4399 = 0,368 см Толщина цилиндра = (Rr) = 0,368 см

Страница № 22.11:
Вопрос 17:

Сумма радиуса основания и высоты сплошного цилиндра составляет 37 м. Если общая площадь твердого цилиндра равна 1628 м 2 , найдите длину окружности его основания.

Ответ:

Пусть r и h будут радиусом и высотой твердого цилиндра. Дано: r + h = 37 м Общая площадь поверхности, S = 2πrr + h2628 = 2π × r × 37 r = 16282π × 37 = 1628232. 477 = 7 м Окружность его основания , S1 = 2πr = 2 × 227 × 7 м = 44 м

Страница № 22.11:
Вопрос 18:

Найдите отношение между общей площадью поверхности цилиндра и площадью его криволинейной поверхности, учитывая, что его высота и радиус равны 7.5 см и 3,5 см.

Ответ:

Пусть S1 и S2 — общая площадь поверхности и площадь изогнутой поверхности, соответственно. Дано: Высота, h = 7,5 см Радиус, r = 3,5 см S1 = 2πrr + hS2 = 2πrh Согласно вопросу: S1S2 = 2πrr + h3πrhS1S2 = r + hhS1S2 = 3,5 + 7,57,5S1S2 = 117,5 = 11075 = 2215, следовательно, соотношение 22:15.

Страница № 22.11:
Вопрос 19:

Цилиндрический сосуд без крышки должен быть покрыт оловом с обеих сторон.Если радиус основания 70 см, а его высота 1,4 м, рассчитайте стоимость лужения из расчета 3,50 рупий за 1000 см 2 .

Ответ:

Пусть r см и h см будут радиусом цилиндрического сосуда. Дано: Радиус, r = 70 см Высота, h = 1,4 м = 140 см Стоимость лужения = 3,50 рупий за 1000 квадратных сантиметров Стоимость лужения цилиндрического сосуда на обе поверхности (внутренняя и внешняя): Общая площадь поверхности сосуда = Площадь внутренней и внешней стороны основания + Площадь внутренней и внешней криволинейной поверхности = 2πr2 + 2πrh = 2πrr + 2h = 2 × 227 × 70 × 70 + 2 × 140 = 44 × 10 × 350 = 154000 см2 Стоимость покраски из расчета 3 рупий.50 за 1000 см2 = 154000 × 3,501000 = 539 рупий Следовательно, стоимость покраски составляет 539 рупий

Страница № 22.25:
Вопрос 1:

Найдите объем цилиндра, у которого
(i) r = 3,5 см, h = 40 см
(ii) r = 2,8 м, h = 15 м

Ответ:

(i) Дано: r = 3,5 см, h = 40 см. Объем цилиндра, V = πr2h = 227 × 3.52 × 40 = 1540 см3 (ii) Дано: r = 2,8 м, h = 15 м Объем цилиндра, V = πr2h = 227 × 2,82 × 15 = 369,6 м3

Страница № 22.25:
Вопрос 2:

Найдите объем цилиндра, если диаметр его основания ( d ) и высота ( h ) равны:
(i) d = 21 см, h = 10 см
(ii) d = 7 м, h = 24 м

Ответ:

(i) Дано: d = 21 см, радиус, r = d2 = 10.5 см высота, h = 10 см Объем цилиндра, V = πr2h = 227 × 10,52 × 10 = 3465 см3 (ii) Дано: d = 7 м, радиус, r = d2 = 3,5 м высота h = 24 м Объем цилиндра, В = πr2h = 227 × 3,52 × 24 = 924 м3

Страница № 22.25:
Вопрос 3:

Площадь основания правого кругового цилиндра — 616 см. 2 , высота — 25 см. Найдите объем цилиндра.

Ответ:

Пусть площадь основания правильного кругового цилиндра равна S см2.Дано: S = 616 см2 Высота, h = 25 см Пусть радиус прямого кругового цилиндра равен r см. S = πr2616 = 227 × r2 r 2 = 616 × 722 r2 = 196 r = 14 см Объем цилиндра, V = πr2h = π × 142 × 25 = 15400 см3

Страница № 22.25:
Вопрос 4:

Окружность дна цилиндра 88 см, высота 15 см. Найдите объем цилиндра.

Ответ:

Пусть r см будет радиусом цилиндра.Окружность цилиндра, S = 2πr Дано: Высота, h = 15 см. Окружность, S = 88 см S = 2πr88 = 2 × 227 × r r = 88 × 744 r = 14 см. Объем цилиндра, V = πr2h = 227 × 142 × 15. = 9240 см3

Страница № 22.25:
Вопрос 5:

Полая цилиндрическая труба длиной 21 дм. Его внешний и внутренний диаметр составляют 10 см и 6 см соответственно. Найдите объем меди, из которой изготовлена ​​труба.

Ответ:

Пусть длина трубы баллона h = 21, dm = 210 см.Пусть внешний и внутренний радиус трубы равны R см и r см соответственно. 2R = 10 и 2r = 6R = 5 см и r = 3 см. Объем меди, использованной для изготовления трубы, V = πR2-r2h = 227 × 52-32 × 210 = 22 × 25-9 × 30 = 22 × 16 × 30 = 10560 см3

Страница № 22.25:
Вопрос 6:

Найдите (i) площадь изогнутой поверхности (ii) общую площадь поверхности и (iii) объем прямоугольного кругового цилиндра, высота которого составляет 15 см, а радиус основания равен 7 см.

Ответ:

Дано: Высота, h = 15 см Радиус, r = 7 см (i) Площадь изогнутой поверхности, S1 = 2πrh = 2 × 227 × 7 × 15 = 660 см2 (ii) Общая площадь поверхности, S2 = 2πrr + h = 2 × 227 × 7 × 7 + 15 = 44 × 22 = 968 см2 (iii) Объем правого кругового цилиндра, V = πr2h = 227 × 72 × 15 = 2310 см3

Страница № 22.25:
Вопрос 7:

Диаметр основания правого кругового цилиндра 42 см, высота 10 см.Найдите объем цилиндра.

Ответ:

Дано: Диаметр, d = 42 см Радиус, r = d2 = 21 см Высота, h = 10 см Объем цилиндра, V = πr2h = 227 × 212 × 10 = 13860 см3

Страница № 22.25:
Вопрос 8:

Найдите объем цилиндра, диаметр основания которого 7 см, а высота 60 см. Также найдите объем цилиндра в литрах.

Ответ:

Дано: Диаметр, d = 7 см Радиус, r = 3,5 см Высота, h = 60 см Объем цилиндра, V = πr2h = 227 × 3,52 × 60 = 2310 см3 Объем цилиндра в литрах = 23101000 1 литр = 1000 кубических см = 2,31 л

Страница № 22.25:
Вопрос 9:

Прямоугольная полоса 25 см × 7 см повернута вокруг длинной стороны. Найдите объем образовавшегося твердого тела.

Ответ:

Дано: прямоугольная полоса имеет радиус, r = 7 см, высоту, h = 25 см, объем твердого тела, V = πr2h = 227 × 72 × 25 = 3850 см3

Страница № 22.25:
Вопрос 10:

Прямоугольный лист бумаги размером 44 см × 20 см свернут по всей длине, образуя цилиндр. Найдите объем сформированного цилиндра.

Ответ:

Длина (l) и ширина (b) прямоугольного листа составляют 44 см и 20 см. Теперь лист прокатывают по длине, чтобы сформировать цилиндр.Пусть радиус цилиндра равен r см. Высота, h = b = 20 см. Окружность, S = 44 см 2πr = 44 см2 × 227 × r = 44 см r = 7 см. Объем цилиндра, V = πr2h = 227 × 72 × 20 см3 = 3080 см3

Страница № 22.25:
Вопрос 11:

Объем и площадь изогнутой поверхности цилиндра составляют 1650 см 3 и 660 см 2 соответственно. Найдите радиус и высоту цилиндра.

Ответ:

Площадь криволинейной поверхности цилиндра = 2π rh = 660 см 2 … (1)
Объем цилиндра = π r 2 h = 1650 см 3 … ( 2)

Из (1) и (2) мы можем вычислить радиус ( r ) и высоту цилиндра ( h) .
Нам известен объем цилиндра, т.е. 1650 см 3
∴ 1650 = π r 2 h

h = 1650πr2

Подставляя h в (1):
660 = 2πrh

660 = 2πr × 1650πr2
660r = 2 (1650)
r = 5 см

h = 1650πr2 = 1650227 × 52 = 21 см.

Следовательно, радиус и высота цилиндра равны 5 см и 21 см соответственно.

Страница № 22.25:
Вопрос 12:

Радиусы двух цилиндров находятся в соотношении 2: 3, а их высота — в соотношении 5: 3. Рассчитайте соотношение их объемов.

Ответ:

Здесь r 1 = Радиус цилиндра 1
h 1 = Высота цилиндра 1
r 2 = Радиус цилиндра 2
2 = Высота цилиндра 2
V 1 = Объем цилиндра 1
V 2 = Объем цилиндра 2
Соотношение радиусов двух цилиндров = 2: 3
Соотношение высот два цилиндра = 5: 3

Объем цилиндра = π r 2 h
V 1 / V 2 = (π r 1 2 h 1 ) / (π r 2 2 h 2 ) = (π (2 r ) 2 5 h ) / (π (3 r ) ) 2 3 ч )
V 1 / V 2 = (π4 r 2 5 h ) / (π9 r 2 3 h ) = 20/27
Следовательно, отношение их объем 20:27

Стр. № 22.25:
Вопрос 13:

Отношение между площадью криволинейной поверхности и общей площадью поверхности правильного кругового цилиндра составляет 1: 2. Найдите объем цилиндра, если его общая площадь поверхности равна 616 см. 2 .

Ответ:

Пусть r см будет радиусом и h см будет длиной цилиндра. Площадь криволинейной поверхности и общая площадь поверхности 1: 2.
Общая площадь поверхности 616 см 2 .
Площадь изогнутой поверхности составляет половину 616 см 2 , то есть 308 см 2 .

Изогнутая площадь = 2π rh

Итак, h = 3082πr
Общая площадь поверхности = Изогнутая поверхность + Верхняя и нижняя области
Верхняя и нижняя области = 616-308 = 308 см 2 = 2π r 2

r2 = 3082 × 227
r = 7 см

h = 3082 × π × 7 = 7 см

Тогда объем цилиндра можно рассчитать следующим образом:

V = 227 × 72 × 7 = 1078
Отсюда получаем, что объем цилиндра составляет 1078 см 3 .

Страница № 22.25:
Вопрос 14:

Площадь криволинейной поверхности цилиндра 1320 см. 2 , диаметр основания 21 см. Найдите объем цилиндра.

Ответ:

r см = Радиус цилиндра
h см = Высота цилиндра

Диаметр цилиндра 21 см.Таким образом, радиус составляет 10,5 см.
Поскольку площадь криволинейной поверхности известна, мы можем рассчитать h по приведенному ниже уравнению:

Площадь криволинейной поверхности цилиндра = 2πr h
1320 см 2 = 2πrh
1320 см 2 = 2 x 22 x (10,5 см) x h
7
h = 20 см

∴ Объем цилиндра ( V ) = π r 2 h
V = 22 (10.5 см) 2 (20 см)
7
V = 6930 см 3

Страница № 22.25:
Вопрос 15:

Отношение между радиусом основания и высотой цилиндра составляет 2: 3. Найдите общую площадь поверхности цилиндра, если его объем равен 1617 см. 3 .

Ответ:

Пусть r см будет радиусом и h см будет высотой цилиндра.Принято, что соотношение r и h равно 2: 3, поэтому h = 1,5r
Объем цилиндра ( V ) равен 1617 см 3 .

Итак, мы можем найти радиус и высоту цилиндра из приведенного ниже уравнения:
V = π r 2 h
1617 = π r 2 h
1617 = π r 2 (1,5 r )
r 3 = 343
r = 7 см и h = 10.5 см

Общая площадь поверхности = 2π r 2 + 2π rh
= 2 × 227 × 72 + 2 × 227 × 7 × 10,5 = 770 см2

Следовательно, общая площадь поверхности цилиндра составляет 770 см 2 .

Страница № 22.25:
Вопрос 16:

Площадь криволинейной поверхности цилиндрической опоры 264 м 2 , объем 924 м 3 .Найдите диаметр и высоту столба.

Ответ:

Здесь r м = радиус цилиндра
h м = высота цилиндра

Площадь криволинейной поверхности цилиндра = 2π rh … (1)
Объем цилиндра = π r 2 h … (2)
924 = π r 2 h
h = 924πr2

Затем подставьте h в уравнение (1):
264 = 2π rh
264 = 2πr924πr2
264 r = 2 (924)
r = 2 × 4
r = 7 м, поэтому d = 14 м

h = 924πr2

24 h = 6 м
Следовательно, диаметр и высота цилиндра равны 14 м и 6 м соответственно.

Страница № 22.25:
Вопрос 17:

Два круглых цилиндра равного объема имеют отношение высоты 1: 2. Найдите отношение их радиусов.

Ответ:

Здесь V 1 = Объем цилиндра 1
V 2 = Объем цилиндра 2
r 1 = Радиус цилиндра 1

7 r

= Радиус цилиндра 2
h 1 = Высота цилиндра 1
h 2 = Высота цилиндра 2

Объемы цилиндра 1 и 2 равны.
Высота цилиндра 1 равна половине высоты цилиндра 2.
∴ V 1 = V 2
(π r 1 8 2 h 8 2 h 8 1 ) = (π r 2 2 h 2 )
(π r 1 2 h ) = (π r 119 2 909 2 h )
r12r22 = 21
r1r2 = 21

Таким образом, соотношение их радиусов равно 2: 1.

Страница № 22.25:
Вопрос 18:

Высота правого кругового цилиндра 10,5 м. Трехкратная сумма площадей его двух круглых граней в два раза больше площади изогнутой поверхности. Найдите объем цилиндра.

Ответ:

Известно, что трехкратная сумма площадей двух круглых граней правого кругового цилиндра равна удвоенной площади изогнутой поверхности.
Следовательно, это можно записать по следующей формуле:
3 (2π r 2 ) = 2 (2π rh )
3π r 2 = 2π rh
3 r = 2 h
Известно, что высота цилиндра ( h) составляет 10,5 м.
Подставляя это число в уравнение:
3 r = 2 (10,5)
r = 7 м

Объем цилиндра = π r 2 h
= 22 (7 2 ) (10.5)
7
= 1617 м 3
Таким образом, объем цилиндра равен 1617 м 3 .

Страница № 22.25:
Вопрос 19:

Сколько кубических метров земли необходимо выкопать, чтобы вырыть колодец глубиной 21 м и диаметром 6 м?

Ответ:

Объем земли, который необходимо выкопать, аналогичен объему цилиндра, который равен π r 2 h.
Высота колодца = 21 м
Диаметр колодца = 6 м
∴ Объем земли, который необходимо выкопать = (π (3 2 ) (21)) м 3 = 594 м 3

Страница № 22.26:
Вопрос 20:

Ствол дерева цилиндрической формы, его окружность 176 см. Если длина ствола 3 м, найдите объем древесины, который можно получить из ствола.

Ответ:

Окружность дерева = 176 см = 2π r
Длина ствола, h = 3 м = 300 см
Итак, радиус (r ) можно рассчитать по формуле:
r = 1762 × 227 = 28 см
Таким образом, объем ( В) бруса можно рассчитать по следующей формуле:
В = π r 2 ( h ) = 22 (28) 2 (300) см 3 = 739200 см 3 = 0.74 кв.м 3

Страница № 22.26:
Вопрос 21:

Колодец вырыт глубиной 20 м и диаметром 7 м. Выкопанная земля раскинулась на прямоугольном участке длиной 22 м и шириной 14 м. Какова высота образованной платформы?

Ответ:

Высота колодца = ч м = 20 м
Диаметр колодца = d м = 7 м
Радиус колодца = r м = 3.5 м
Объем скважины = π r 2 ч = 22 (3,5) 2 (20) м 3 = 770 м 3
7
Объем скважины = Объем прямоугольный участок
Длина прямоугольного участка = 22 м
Ширина прямоугольного участка = 14 м
Объем прямоугольного участка = 770 м 3 = (Длина × Ширина × Высота) прямоугольного участка
Высота = 77022 × 14 = 2,5 м

Таким образом, высота площадки равна 2.5 мес.

Страница № 22.26:
Вопрос 22:

Вырыта скважина диаметром 14 м глубиной 8 м. Вынутый из него грунт был равномерно разложен вокруг него шириной 21 м, образуя насыпь. Найдите высоту насыпи.

Ответ:

Диаметр колодца = d м = 14 м
Высота колодца = ч м = 8 м
Радиус колодца = r м = 7 м
Объем колодца = π r 2 ч = π (7 м) 2 (8 м) = 1232 м 3
Объем колодца = Объем насыпи

Насыпь представляет собой полый цилиндр с толщиной.Его внутренний радиус будет равен радиусу колодца, т.е. r = 7 м, а его внешний радиус R = 7 + 21 = 28 м.

Объем насыпи = π h ( R 2 -r 2 )

Для определения высоты ( h ) воспользуемся тем фактом, что объем насыпи равен объем колодца.
1232 = π h ((28) 2 — (7) 2 )
h = 1232227 × [(28) 2- (7) 2] = 0,533 м
Следовательно, высота насыпи равна 0.533 м или 53,3 см.

Страница № 22.26:
Вопрос 23:

Цилиндрический контейнер с диаметром основания 56 см содержит достаточно воды, чтобы погрузить прямоугольное твердое тело из железа с размерами 32 см × 22 см × 14 см. Найдите подъем уровня воды, когда твердое тело полностью погружено в воду.

Ответ:

Диаметр цилиндрической емкости = d см = 56 см
Радиус цилиндрической емкости = r см = 28 см
Объем цилиндрической емкости = Объем прямоугольного тела
Длина прямоугольного тела = 32 см
Ширина прямоугольного тела = 22 см
Высота прямоугольного тела = 14 см
Объем прямоугольного тела = длина x ширина x высота = 32 см x 22 см x 14 см = 9856 см 3
Объем цилиндрического контейнера = 9856 см 3 = πr 2 h
9856 см 3 = 22 (28 см) 2 h
7
h = 4 см
Таким образом, когда твердое тело полностью погруженный, вода поднимется на 4 см.

Страница № 22.26:
Вопрос 24:

Прямоугольный лист бумаги размером 30 см × 18 см может быть преобразован в изогнутую поверхность правильного круглого цилиндра двумя способами: либо скатывая бумагу по ее длине, либо скручивая ее по ширине. Найдите соотношение объемов двух образованных цилиндров.

Ответ:

Корпус 1:
Высота = h см = 30 см
Диаметр = d см = 18 см
Радиус = r см = 9 см
∴ Объем = (π r 2 h ) или (π (9) 2 (30)) = 2430π см 3

Случай 2:
Высота = h см = 18 см
Диаметр = d см = 30 см,
Радиус = r см = 15 см
∴ Объем = (π r 2 h ) или (π (15) 2 (18)) = 4050π см 3

Следовательно, соотношение объемов образуются два цилиндра 3: 5.

Страница № 22.26:
Вопрос 25:

Дождь, падающий на крышу длиной 18 м и шириной 16,5 м, разрешается хранить в цилиндрическом резервуаре диаметром 8 м. Если в день идет дождь 10 см, что из-за этого поднимается уровень воды в резервуаре?

Ответ:

Длина воды на крыше = 18 м
Ширина воды на крыше = 16.5 м
Высота воды на крыше = 10 см = 0,1 м
Объем воды на крыше = длина × ширина × высота = 18 м × 16,5 м × 0,1 м = 29,7 м 3
Поскольку вода должна храниться в цилиндрическом резервуаре, объем воды на крыше равен объему цилиндрического резервуара.
Объем цилиндрического резервуара = π r 2 h = 29,7 м 3
h = 29,7227 × (4) 2 = 0,5906 м = 59,06 см
Таким образом, подъем уровня воды в резервуаре составляет 59 .06 см.

Страница № 22.26:
Вопрос 26:

Кусок пластичного металла имеет форму цилиндра диаметром 1 см и длиной 5 см. Он вытянут в проволоку диаметром 1 мм. Какой длины будет образованный таким образом провод?

Ответ:

Диаметр пластичного металла = 1 см
Радиус пластичного металла = 0,5 см
Объем пластичного металла = πr 2 (длина) = π (0.5 см) 2 (5 см) = 1,25π см 3
Пластичный металл вытягивают в проволоку диаметром 1 мм.
Радиус провода = 0,5 мм = 0,05 см
Длина провода = 1,25π см3π0,05 см2 = 500 см = 5 м
Таким образом, длина провода равна 5 м.

Страница № 22.26:
Вопрос 27:

Найдите длину 13,2 кг медной проволоки диаметром 4 мм, когда 1 кубический см меди весит 8,4 г.

Ответ:

Плотность меди = Вес / Объем = 8.4 грамм / 1 см 3 = 8,4 грамм / см 3
Объем = Вес / Плотность = 13,2 кг × 1000 грамм / кг / 8,4 грамм / см 3 = 1571,43 см 3

Таким образом, длина 13,2 кг меди 125 м.

Страница № 22.26:
Вопрос 28:

2,2 куб. Дм латуни втянуть в цилиндрическую проволоку диаметром 0,25 см. Найдите длину провода.

Ответ:

Диаметр цилиндрической проволоки = 0.25 см
Радиус цилиндрической проволоки = 0,125 см
Объем латуни = 2,2 дм 3 = 2200 см 3

Объем латуни = Объем цилиндрической проволоки
Длина проволоки = 2200 см 3227 × 0,125 см2 = 44800 см = 448 м
Таким образом, длина провода составляет 448 м.

Страница № 22.26:
Вопрос 29:

Разница между внутренней и внешней поверхностями цилиндрической трубки длиной 14 см составляет 88 кв.см. Если объем трубки составляет 176 куб. См, найдите внутренний и внешний радиусы трубки.

Ответ:

r = Внутренние радиусы трубки
R = Наружные радиусы трубки
h = Длина трубки

2π h ( R — r ) = 88 … ( 1)
π h ( R 2 — r 2 ) = 176… (2)

Подставив h = 14 см в уравнения (1) и (2):

π ( Rr ) = 88/28 … (1)
π ( Rr ) ( R + r ) = 176/14 … (2)

Упростим второе уравнение, заменив его первым уравнением:
R + r = 4 см или R = (4-r) см
Re -подставляя R = 4-r в уравнение (1):
22 (4-rr) = 88
7 28
4-2 r = 1
r = 1.5 см
R = 4-1,5 = 2,5 см

Следовательно, внутренний и внешний радиусы трубки равны 1,5 и 2,5 см соответственно.

Страница № 22.26:
Вопрос 30:

Вода вытекает по круглой трубе с внутренним диаметром 2 см со скоростью 6 метров в секунду в цилиндрический резервуар с радиусом основания 60 см. Найти подъем уровня воды за 30 минут?

Ответ:

Радиус круглой трубы = 0.01 м Длина водяного столба за 1 секунду = 6 м Объем воды, протекающей за 1 секунду = πr2 h = π (0,01) 2 (6) м3 Объем воды, протекающей за 30 минут = π (0,01) 2 (6) × 30 × 60 м3 Пусть h m — повышение уровня воды в цилиндрическом резервуаре. Объем цилиндрического резервуара, в котором течет вода, = π (0,6) 2 × h Объем воды, протекающей за 30 минут = Объем цилиндрического резервуара в какая вода течет π (0,01) 2 (6) × 30 × 60 = π (0,6) 2 × hh = 6 (0,01) 2 × 30 × 600,6 × 0,6h = 3 м

Страница № 22.26:
Вопрос 31:

Цилиндрическая трубка, открытая с обоих концов, сделана из металла.Внутренний диаметр трубки 10,4 см, длина 25 см. Толщина металла везде 8 мм. Рассчитайте объем металла.

Ответ:

Здесь r = внутренний радиус = 5,2 см
R = внешний радиус
t = толщина = 0,8 см
h = длина = 25 см

R = r + t = 5,2 см + 0,8 см = 6 см
Объем металла = π h ( R 2 — r 2 )
= 22 × (25) × ((6) 2 — (5 .2) 2 )
7
= 704 см 3
Таким образом, объем металла 704 см 3 .

Страница № 22.26:
Вопрос 32:

Из крана с внутренним радиусом 0,75 см вода течет со скоростью 7 м в секунду. Найдите объем воды в литрах, доставленный по трубе за один час.

Ответ:

Радиус водопроводного крана = 0.75 см = 0,0075 м Длина воды, текущей за 1 с = 7 м = 700 см Объем воды, текущей за 1 с = π (0,0075) 2 × 700 Объем воды, текущей за 1 час = π (0,0075) 2 × 700 × 60 × 60 Объем воды, протекающей за 1 час = 227 × (0,0075) 2 × 7 × 60 × 60 = 4,455 м3 = 4455 л (1000 л = 1 м3)

Страница № 22.26:
Вопрос 33:

Цилиндрический резервуар для воды диаметром 1,4 м и высотой 2,1 м питается по трубе диаметром 3.5 см, через которые вода течет со скоростью 2 метра в секунду. За сколько времени резервуар будет заполнен?

Ответ:

Радиус цилиндрического резервуара = 0,7 м Высота цилиндрического резервуара = 2,1 м Объем цилиндрического резервуара = π (0,7) 2 (2,1) м3 Длина водяного столба, истекающего из трубы за 1 с = 2 м Установите время, необходимое для полного заполнения резервуар для воды должен быть x сек. Длина водяного столба, вытекающего из трубы, в x сек = 2 x м Радиус трубы = 1.75 см = 0,0175 м Объем водяного столба, истекающего из трубы в x сек = π (0,0175) 2 (2 x) м3 Объем цилиндрического бака = Объем водяного столба, истекающего из трубы π (0,7) 2 (2,1) = π (0,0175) 2 (2 x) x = 0,7) 2 (2,1) 0,0175) 2 (2) = 1680 сек = 28 мин

Таким образом, время, необходимое для заполнения бака для воды, составляет 28 мин.

Страница № 22.26:
Вопрос 34:

Прямоугольный лист бумаги 30 см × 18 см может быть преобразован в изогнутую поверхность правильного кругового цилиндра двумя способами: i.е., скручивая бумагу по длине или по ширине. Найдите соотношение объемов двух образованных цилиндров.

Ответ:

Пусть h см будет длиной бумаги и r см будет радиусом бумаги.

Мы знаем, что прямоугольный лист бумаги размером 30 см х 18 см может быть преобразован в два типа цилиндров.

Тип 1:
Длина = 30 см
Диаметр = 18 см
Объем = (π r 2 h ) = (π (9 см) 2 (30 см)) = 2430π см 3

Тип 2:
Длина = 18 см
Диаметр = 30 см
Объем = (π r 2 h ) или (π (15 см) 2 (18 см)) = 4050π см 3

Следовательно, соотношение объемов двух образованных цилиндров составляет 3: 5.

Страница № 22.26:
Вопрос 35:

Сколько литров воды вытекает из трубы с поперечным сечением 5 см 2 за одну минуту, если скорость воды в трубе 30 см / сек?

Ответ:

Мы знаем:
Площадь поперечного сечения = 5 см 2
Скорость = 30 см / с и
Время = 1 мин
Итак, объем потока воды равен:
Объем = Объемный расход × Время = (30 см / с) (5 см 2 ) (60 с / мин) = 9000 см 3 = 9 литров

Таким образом, из трубы вытекает 9 литров воды.

Стр. № 22.26:
Вопрос 36:

Цельный цилиндр имеет общую площадь 231 см 2 . Площадь его криволинейной поверхности составляет 23% от общей площади поверхности. Найдите объем цилиндра.

Ответ:

Нам известно, что общая площадь поверхности цилиндра составляет 231 см. 2 , а площадь криволинейной поверхности составляет 2/3 общей площади поверхности.
Итак, площадь криволинейной поверхности равна:
2/3 × (231 см 2 ) = 154 см 2

Тогда радиус цилиндра можно рассчитать следующим образом:
Площадь криволинейной поверхности = 2π правая
154 см 2 = 2π правая … (1)
Здесь r см — радиус цилиндра, а h см — длина цилиндра.
2πr 2 = (231-154) см 2 = 77 см 2
77 см 2 = 2π r 2
Отсюда можно рассчитать радиус (r ) следующим образом:

r = 772 × 227
r = 3,5 см

Подставляя этот результат в уравнение (1):
154 см 2 = 2π (3,5 см) h
h = 154 см 2 / (2x 22 x (3.5 см))
7
h = 7 см

∴ V = π r 2 h = 227 x (3,5 см) 2 x (7 см) = 269,5 см 3

Следовательно, объем цилиндра 269,5 см 3 .

Страница № 22.27:
Вопрос 37:

Найдите стоимость прохождения колодца глубиной 280 м и диаметром 3 м из расчета 3 рупий.60 за кубометр. Найдите также стоимость цементирования его внутренней криволинейной поверхности в размере 2,50 рупий за квадратный метр.

Ответ:

Стоимость проходки трубчатого колодца = Объем трубчатого колодца × Стоимость проходки трубного колодца на кубический метр
= 22 x (1,5 2 ) x (280) м 3 x 3,6 рупий / м 3 = 7128 рупий
7
Стоимость цементирования = Площадь внутренней поверхности трубной скважины × Стоимость цементирования на квадратный метр
= ((2 x 22 x 1.5x 280) м 2 ) x 2,5 рупий / м 2 = 6600 рупий
7

Страница № 22.27:
Вопрос 38:

Найдите длину 13,2 кг медной проволоки диаметром 4 мм, когда 1 кубический см меди весит 8,4 г.

Ответ:

Так как мы знаем вес и объем меди, мы можем рассчитать ее плотность.
плотность меди = вес объем = 8,4 грамм1 см3 = 8,4 грамм см3
Если вес медной проволоки составляет 13,2 кг, а плотность меди составляет 8,4 г / см 3 , то:
Объем = Вес / Плотность = 13,2 кг x 1000 грамм / кг / 8,4 грамм / см 3 = 1571,43 см 3

Радиус медной проволоки составляет 2 мм или 0,2 см. Итак, длину провода можно определить следующим образом:
L = Vπr2 = 1571,43 м3π0,2 см2 = 125050,01 см = 125 м
Таким образом, длина 13,2 кг меди составляет 125 м.

Страница № 22.27:
Вопрос 39:

2,2 куб. Дм латуни втянуть в цилиндрическую проволоку диаметром 0,25 см. Найдите длину провода.

Ответ:

Пусть r см будет радиусом провода, а h см — длиной провода.
Объем латуни = Объем проволоки
Мы знаем, что объем латуни = 2.2 дм 3 = 2200 см 3
Объем проволоки = π r 2 h = (0,125 см) 2 ( h )
h = 2200 см3π0. 125 см2 = 44800 см = 448 м
Таким образом, длина провода составляет 448 м.

Страница № 22.27:
Вопрос 40:

Вырыт колодец внутренним диаметром 10 м глубиной 8,4 м. Земля, извлеченная из него, раскинулась вокруг него на ширину 7.5 м для создания набережной. Найдите высоту насыпи.

Ответ:

Пусть r м — это радиус, а d м — глубина вырытой скважины.
Объем колодца = π r 2 d = π (5 м) 2 (8,4 м) = 660 м 3

Насыпь имеет форму полого цилиндра с толщиной. Его внутренние радиусы равны радиусам скважины, т.е. r = 5 м, а внешние — R = (5 + 7.5) = 12,5 см.
Тогда объем насыпи = π ч ( R — r 2 )

Объем колодца = Объем насыпи
659,73 м 3 = π h ((12,5 м) 2 — (5 м) 2 )
h = 660 см 3227 × 12,5 м2-5 м2 = 1,6 м
Следовательно, высота насыпи составляет 1,6 м.

Страница № 22.27:
Вопрос 41:

Полый садовый каток шириной 63 см и обхватом 440 см изготовлен из железа толщиной 4 см.Найдите объем утюга.

Ответ:

Здесь R = Внешний радиус
r = Внутренний радиус
t = Толщина = 4 см
w = Ширина = 63 см

Обхват = 440 см = 2π R
R = 4402 × 227 = 70 см
r = R — t = 70 см — 4 см = 66 см

Объем утюга = π (R 2 — r 2 ) w = 227 — (70 2 — 66 2 ) — (63) = 107712 см 3

Следовательно, объем утюга составляет 107712 см 3 .

Страница № 22.27:
Вопрос 42:

Какую длину сплошного цилиндра диаметром 2 см необходимо взять, чтобы превратить в полый цилиндр длиной 16 см, внешним диаметром 20 см и толщиной 2,5 мм?

Ответ:

Здесь r = внутренний радиус
R = внешний радиус = 10 см
h = длина цилиндра
t = толщина = 0.25 см

Объем полого цилиндра = π ч ( R 2 — r 2 ) = π (16) (10 2 — (10-0,25) 2 ) = 79 π см 3

Объем твердого цилиндра = Объем полого цилиндра
Мы знаем, что радиус твердого цилиндра равен 1 см.
∴ π (1 2 ) h = 79 π
h = 79 см
Следовательно, длина сплошного цилиндра, который дает тот же объем, что и полый цилиндр, составляет 79 см.

Страница № 22.27:
Вопрос 43:

Посреди прямоугольного поля размером 30 м × 20 м вырыт колодец диаметром 7 м и глубиной 10 м. Удаленная таким образом земля равномерно распределяется по оставшейся части поля. Найдите высоту, на которую поднимается уровень поля.

Ответ:

Пусть r м — радиус, а h м — глубина вырытой колодца.
Объем колодца = π r 2 h = 22 × (3,5 м) 2 × (10 м) = 385 м 3
7
Объем колодца = Объем прямоугольное поле
Объем прямоугольного поля = 385 м 3 = 30 м × 20 м × высота
Высота = 385 см 230 м × 20 м = 0,641 м = 64,1 см

Следовательно, высота, через которую проходит уровень поля приподнято 64,1 см.

Просмотреть решения NCERT для всех глав класса 8

Боковая зона: определение, формула и примеры — бизнес-класс (видео)

Боковая поверхность правого кругового цилиндра

Найдем боковую поверхность правого кругового цилиндра.

В этом примере нам дан цилиндр высотой 6 см и диаметром 10 см. Помните, что в правом круговом цилиндре основания — это круги. Чтобы найти площадь боковой поверхности, мы находим периметр, который в данном случае является окружностью (расстояние по окружности), а затем умножаем его на высоту цилиндра.

Длина окружности находится по следующей формуле:

C обозначает окружность, d обозначает диаметр, а символ Пи округляется до 3.14. Итак, мы находим длину окружности основания, 3,14 * 10 = 31,4, а затем умножаем ее на высоту, 6.

Причина, по которой мы используем окружность при определении площади боковой поверхности, заключается в том, что когда мы открываем круговой цилиндр и кладем стороны ровно, мы получаем прямоугольник. Представьте бумажное полотенце. Рулон бумажных полотенец представляет собой цилиндр, но когда вы снимаете бумажное полотенце с рулона, у вас получается прямоугольник. Длина — это окружность, а ширина — это высота рулона.

Чтобы найти площадь сторон этого цилиндра, нам нужно умножить длину окружности на высоту.Итак, у нас есть формула для площади боковой поверхности правого кругового цилиндра:

Площадь боковой поверхности правого кругового цилиндра = окружность * высота

Площадь боковой поверхности прямоугольной призмы

Давайте попробуем другой пример, на этот раз с прямоугольной призмой.

Как видите, указаны длина, ширина и высота. Итак, боковые поверхности — это все поверхности по бокам. Нам нужно найти площадь каждой из четырех сторон … но есть более быстрый способ — вы его видите? Если бы мы нашли периметр основания, а затем умножили его на высоту, мы получили бы площадь боковой поверхности.

У нас есть две длины и две ширины. Как и в предыдущем примере, основная формула для площади боковой поверхности:

Точно так же, как круглый цилиндр, если мы положим прямоугольную призму плоско, она будет выглядеть так:

Итак, сложите длину и ширину и умножьте на высоту, чтобы найти площадь боковой поверхности.Более кратко это можно записать так:

Площадь боковой поверхности правого кругового цилиндра и правой прямоугольной призмы в основном одинакова; найти периметр основания и умножить на высоту фигуры.

Площадь боковой поверхности пирамиды

Далее мы собираемся найти площадь боковой поверхности пирамиды.

Пирамида — это фигура с многоугольным основанием и множеством сторон, называемых гранями, которые все соединяются в одной точке, называемой вершиной.Чтобы найти площадь боковой поверхности, найдем половину периметра основания и умножим ее на наклонную высоту боковых треугольников. Каждый треугольник имеет наклонную высоту. Наклонная высота — это высота каждого треугольника, а не высота пирамиды. Почему, спросите вы, мы находим половину периметра? Это потому, что каждая из сторон пирамиды представляет собой треугольник, а формула площади треугольника равна половине основания, умноженному на высоту.

Чтобы найти площадь боковой поверхности пирамиды, вы можете найти площадь каждого треугольника: A = 1/2 bh или A = 1/2 lw , а затем умножить на количество треугольников. , который будет зависеть от количества сторон основания; или можно взять половину периметра и умножить на высоту уклона.

Давайте попробуем оба варианта на этой пирамиде:

Определение площади боковой поверхности путем нахождения площади каждого треугольника и последующего умножения на количество треугольников: l обозначает высоту наклона:

Определение площади боковой поверхности по формуле: LSA = 1/2 периметра, умноженного на наклонную высоту:

Определение площади боковой поверхности конуса такое же, как у пирамиды, за исключением того, что наше основание представляет собой круг, поэтому мы используем половину длины окружности, умноженную на наклонную высоту.Итак, допустим, у нас есть конус с наклонной высотой 12.

Резюме урока

Площадь боковой поверхности — это площадь поверхности сторон любой трехмерной фигуры. Каждая фигура может иметь различное основание, но площадь боковой поверхности определяется одинаково. Найдите периметр основания, а затем умножьте его на высоту любой трехмерной призмы.

При нахождении площади боковой поверхности пирамиды или конуса формула:

Определение объема и площади цилиндра

Результаты обучения

  • Найдите объем и площадь цилиндра

Если вы когда-нибудь видели банку газировки, вы знаете, как выглядит баллон.Цилиндр — это сплошная фигура с двумя параллельными кругами одинакового размера вверху и внизу. Верх и низ цилиндра называются основаниями. Высота [латекс] h [/ латекс] цилиндра — это расстояние между двумя основаниями. Для всех цилиндров, с которыми мы будем работать здесь, стороны и высота [латекс] h [/ латекс] будут перпендикулярны основанию.

Цилиндр имеет два круглых основания одинакового размера. Высота — это расстояние между основаниями.


Прямоугольные твердые тела и цилиндры в чем-то похожи, потому что оба имеют два основания и высоту.{2} [/ латекс]. На изображении ниже показано, как формула [латекс] V = Bh [/ latex] используется для прямоугольных твердых тел и цилиндров.

Увидев, как цилиндр похож на твердое тело прямоугольной формы, можно легче понять формулу объема цилиндра.


Чтобы понять формулу площади поверхности цилиндра, представьте банку с овощами. У него три поверхности: верхняя, нижняя и часть, образующая боковые стороны банки. Если аккуратно отрезать этикетку со стороны банки и развернуть ее, вы увидите, что это прямоугольник.См. Изображение ниже.

Разрезав и развернув этикетку банки с овощами, мы можем увидеть, что поверхность цилиндра представляет собой прямоугольник. Длина прямоугольника — это окружность основания цилиндра, а ширина — это высота цилиндра.


Расстояние по краю банки — это длина окружности основания цилиндра, а также длина [латекс] L [/ латекс] прямоугольной этикетки. Высота цилиндра равна ширине [латекса] W [/ латекса] прямоугольной этикетки.{2} +2 \ pi rh [/ латекс]

Объем и площадь цилиндра

Для цилиндра радиусом [латекс] r [/ латекс] и высотой [латекс] h: [/ латекс]

пример

Цилиндр имеет высоту [латекс] 5 [/ латекс] сантиметров и радиус [латекс] 3 [/ латекс] сантиметра. Найдите 1. объем и 2. площадь поверхности.

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и подпишите

это с данной информацией.

2.
Шаг 2. Определите то, что вы ищете.{2} +2 \ влево (3,14 \ вправо) \ влево (3 \ вправо) 5 [/ латекс]

Шаг 5. Решить. [латекс] S \ около 150,72 [/ латекс]
Шаг 6. Проверка: Мы предоставляем вам проверить ваши расчеты.
Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] составляет приблизительно 150,72 [/ латекс] квадратных дюймов.

пример

Найдите 1.объем и 2. площадь поверхности банки соды. Радиус основы составляет [латекс] 4 [/ латекс] сантиметра, а высота [латекс] 13 [/ латекс] сантиметров. Предположим, банка имеет форму цилиндра.

Показать решение

Решение

Шаг 1. Прочтите проблему. Нарисуйте фигуру и

пометьте его данной информацией.

1.
Шаг 2.{2} \ cdot 13 [/ латекс]

Шаг 5. Решить. [латекс] V \ прибл. 653,12 [/ латекс]
Шаг 6. Проверка: Мы предоставляем вам возможность проверить.
Шаг 7. Ответьте на вопрос. Объем [латекс] примерно 653,12 [/ латекс] кубических сантиметров.
2.
Шаг 2. Определите то, что вы ищете.{2} +2 \ влево (3,14 \ вправо) \ влево (4 \ вправо) 13 [/ латекс]

Шаг 5. Решить. [латекс] S \ приблизительно 427,04 [/ латекс]
Шаг 6. Проверка: Мы предоставляем вам проверить ваши расчеты.
Шаг 7. Ответьте на вопрос. Площадь поверхности [латекс] составляет приблизительно 427,04 [/ латекс] квадратных сантиметров.

Извините! — Страница не найдена

Пока мы разбираемся, возможно, поможет одна из ссылок ниже.

Дома Назад
  • Класс
  • Онлайн-тесты
  • Онлайн-ускоренный курс JEE
  • Двухлетний курс для JEE 2021
  • Класс
  • Онлайн-курс NEET
  • Серия онлайн-тестов
  • Фонд Калифорнии
  • CA Средний
  • CA Финал
  • Программа CS
  • Класс
  • Серия испытаний
  • Книги и материалы
  • Тестовый зал
  • Умный взломщик BBA
  • Обучение в классе
  • Онлайн-коучинг
  • Серия испытаний
  • Умный взломщик IPM
  • Книги и материалы
  • GD-PI
  • CBSE, класс 8
  • CBSE, класс 9
  • CBSE, класс 10
  • Класс 11 CBSE
  • CBSE, класс 12
  • Обучение в классе
  • Онлайн-классы CAT
  • Серия испытаний CAT
  • MBA Жилой
  • Умный взломщик CAT
  • Книги и материалы
  • Онлайн-классы без CAT
  • Серия испытаний без CAT
  • Тестовый зал
  • GD-PI
  • Обучение в классе
  • Серия испытаний
  • Civils Интервью
  • Класс
  • Онлайн-классы
  • Серия испытаний SSC
  • Переписка
  • Практические тесты
  • электронных книг SSC
  • SSC JE Study Package
  • Класс
  • RBI, класс B
  • Банковский тест серии
  • Переписка
  • Банковские электронные книги
  • Банк ПДП
  • Онлайн-коучинг
  • Обучение в классе
  • Серия испытаний
  • Книги и материалы
  • Класс
  • Программа моста GRE
  • GMAT Онлайн-коучинг
  • Консультации по приему
  • GMAT Классные тренировки
  • Стажировка
  • Корпоративные программы
  • Студенты колледжа
  • Рабочие специалисты
  • Колледжи
  • школ
.