Пешеход прошел по шоссе 5 км с постоянной скоростью и 6 км по лесу: решите задачу: Печеход прошёл по шоссе 5км с постоянной скоростью и 6 кс по лесу…

Учимся решать задачи на движение

Уровень А.

А1.

а) Из двух городов, расстояние между которыми равно 363 км, навстречу друг другу выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 57 км/ч и 64 км/ч?

Ответ: 3 часа.

б) Из двух городов, расстояние между которыми равно 108 км, навстречу друг другу выехали два велосипедиста. Через сколько часов велосипедисты встретятся, если их скорости равны 15 км/ч и 12 км/ч?

Ответ: 4 часа.

А2.

а) Города А, В и С соединены прямолинейным шоссе, причем город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 23 км/ч больше скорости грузовика, а расстояние между городами А и В равно 92 км?

Ответ: 4 часа.

б) Города А, В и С соединены прямолинейным шоссе, причем город В расположен между городами А и С. Из города А в сторону города С выехал легковой автомобиль, и одновременно с ним из города В в сторону города С выехал грузовик. Через сколько часов после выезда легковой автомобиль догонит грузовик, если скорость легкового автомобиля на 17 км/ч больше скорости грузовика, а расстояние между городами А и В равно 102 км?

Ответ: 6 часов.

А3.

а) Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 52 км/ч, а вторую половину времени – со скоростью 62 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Ответ: 57 км/ч.

б) Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 48 км/ч, а вторую половину времени – со скоростью 68 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Ответ: 58 км/ч.

А4.

а) Первую половину трассы автомобиль проехал со скоростью 42 км/ч, а вторую – со скоростью 63 км/ч.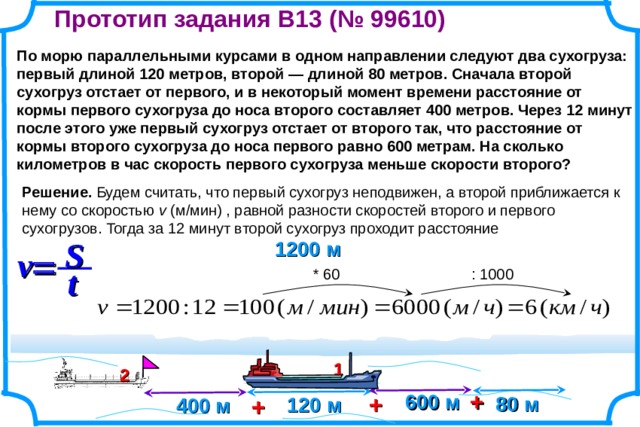 Найдите среднюю скорость автомобиля на протяжении всего пути.

Ответ: 50,4 км/ч.

б) Первую половину трассы автомобиль проехал со скоростью 46 км/ч, а вторую – со скоростью 69 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Ответ: 55,2 км/ч.

А5.

а) Путешественник переплыл океан на яхте со средней скоростью 17 км/ч. Обратно он летел на самолете со скоростью 561 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути.

Ответ: 33 км/ч.

б) Путешественник переплыл океан на яхте со средней скоростью 18 км/ч. Обратно он летел на самолете со скоростью 630 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути.

Ответ: 35 км/ч.

А6.

а) Расстояние от А до В первый автомобиль проезжает в 1 2/7раза быстрее второго автомобиля. Найдите скорости автомобилей, если известно, что скорость первого на 18 км/ч больше скорости второго.

Ответ: 81 км/ч, 63 км/ч.

б) Расстояние от А до В первый автомобиль проезжает в 1 2/5 раза медленнее второго автомобиля. Найдите скорости автомобилей, если известно, что скорость первого на 22 км/ч меньше скорости второго.

Ответ: 55 км/ч, 77 км/ч.

 

Уровень В.

В1.

а) Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой – со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдет их встреча?

Ответ: 3 км.

б) Два человека отправляются из одного и того же места на прогулку до лесной поляны, находящейся в 4 км от места отправления. Один идет со скоростью 3,3 км/ч, а другой – со скоростью 5,5 км/ч. Дойдя до поляны, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдет их встреча?

Ответ: 3 км.

В2.

а) Моторная лодка прошла против течения 8 км и вернулась обратно, затратив на обратный путь на 30 минут меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.

Ответ:

12 км/ч.

б) Моторная лодка прошла против течения 21 км и вернулась обратно, затратив на обратный путь на 20 минут меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 2 км/ч.

Ответ: 16 км/ч.

В3.

а) Теплоход, скорость которого в неподвижной воде равна 16 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт. Найдите расстояние, пройденное теплоходом за весь рейс, если скорость течения равна 4 км/ч, стоянка длится 2 часа, а в исходный пункт теплоход возвращается через 10 часов после отплытия из него.

Ответ: 120 км.

б)  Теплоход, скорость которого в неподвижной воде равна 12 км/ч, проходит по течению реки и после стоянки возвращается в исходный пункт.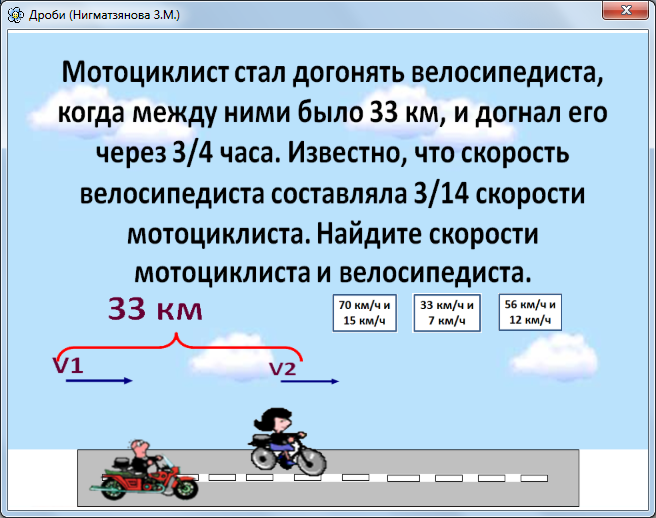

Найдите расстояние, пройденное теплоходом за весь рейс, если скорость течения равна 2 км/ч, стоянка длится 4 часа, а в исходный пункт теплоход возвращается через 16 часов после отплытия из него.

Ответ: 140 км.

В4.

а) Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 19 км. Пешеход прошел путь из А в В за 5 часов. Время его движения на спуске составило 4 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 1 км/ч?

Ответ:

4 км/ч.

б) Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 16 км. Пешеход прошел путь из А в В за 6 часов. Время его движения на спуске составило 2 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 2 км/ч?

Ответ: 4 км/ч.

В5.

а) Из пункта А круговой трассы, длина которой равна 80 км, одновременно в одном направлении стартовали два автомобилиста.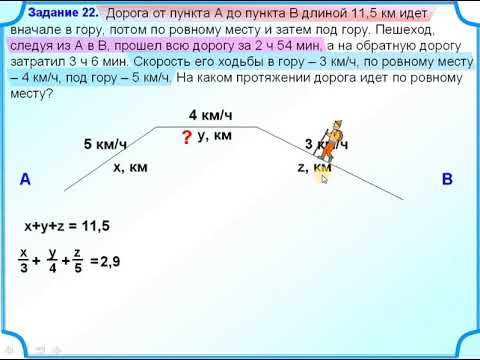 Скорость первого автомобилиста равна 92 км/ч, скорость второго автомобилиста равна 68 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?

Ответ: 3 часа 20 минут.

б) Из пункта А круговой трассы, длина которой равна 57 км, одновременно в одном направлении стартовали два автомобилиста. Скорость первого автомобилиста равна 81 км/ч, скорость второго автомобилиста равна 63 км/ч. Через сколько минут первый автомобилист будет опережать второго ровно на 1 круг?

Ответ: 3 часа 10 минут.

В6.

а) Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда.

Ответ: 9/10 км.

б) Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 24 секунды. Найдите длину поезда.

Ответ: 0,4 км.

 

Уровень С.

С1.

а) Из пункта А в пункт В, отстоящий от пункта А на 27 км, отправился пешеход со скоростью 5 км/ч. Через 36 минут после этого навстречу ему из В вышел другой пешеход со скоростью 3 км/ч. Найдите расстояние от пункта В до места их встречи.

Ответ: 9 км.

б) Из пункта А в пункт В, отстоящий от пункта А на 11 км, отправился пешеход со скоростью 4 км/ч. Через 15 минут после этого навстречу ему из В вышел другой пешеход со скоростью 6 км/ч. Найдите расстояние от пункта В до места их встречи.

Ответ: 6 км.

С2.

а) Из пункта А в пункт В по течению реки отправились одновременно моторная лодка и байдарка. Скорость течения реки равна 3 км/ч. Последнюю 1/13 часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 5 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.

Ответ: 10 км/ч.

б) Из пункта А в пункт В по течению реки отправились одновременно моторная лодка и байдарка.

Скорость течения реки равна 2 км/ч. Последнюю 1/9 часть пути моторная лодка шла с выключенным мотором, и ее скорость относительно берега была равна скорости течения. На той части пути, где моторная лодка шла с включенным мотором, ее скорость была на 7 км/ч больше скорости байдарки. Найдите скорость байдарки в неподвижной воде, если в пункт В байдарка и моторная лодка прибыли одновременно.

Ответ: 7 км/ч.

С3.

а) Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 2 часа пути вынужден был сделать остановку на 10 минут. После этого он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста из А в В.

Ответ: 22 км/ч.

б) Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 32 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 1 час пути вынужден был сделать остановку на 12 минут. После этого он продолжил путь в А, увеличив скорость на 4 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста из А в В.

Ответ: 16 км/ч.

С4.

а) Расстояние между пристанями А и В равно 70 км. Отчалив от пристани А в 7:00 утра, теплоход проплыл с постоянной скоростью до пристани В. После четырехчасовой стоянки у пристани В теплоход отправился в обратный рейс и прибыл в А в тот же день в 23:00. Найдите скорость теплохода в неподвижной воде, если скорость течения реки равна 2 км/ч.

Ответ: 12 км/ч.

б) Расстояние между пристанями А и В равно 45 км. Отчалив от пристани А в 8:00 утра, теплоход проплыл с постоянной скоростью до пристани В. После трехчасовой стоянки у пристани В теплоход отправился в обратный рейс и прибыл в А в тот же день в 19:00. Найдите скорость теплохода в неподвижной воде, если скорость течения реки равна 3 км/ч.

Ответ: 12 км/ч.

С5.

а) Иван и Алексей договорились встретится в N-ске. Они едут к N-ску разными дорогами. Иван звонит Алексею и узнает, что тот находится в 350 км от N-ска и едет с постоянной скоростью 70 км/ч. Иван в момент звонка находится в 399 км от N-ска и еще должен по дороге сделать 15-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем?

Ответ: 84 км/ч.

б) Сергей и Володя договорились встретится в N-ске. Они едут к N-ску разными дорогами. Сергей звонит Володе и узнает, что тот находится в 150 км от N-ска и едет с постоянной скоростью 50 км/ч. Сергей в момент звонка находится в 192 км от N-ска и еще должен по дороге сделать 20-минутную остановку. С какой скоростью должен ехать Сергей, чтобы прибыть в N-ск одновременно с Володей?

Ответ: 72 км/ч.

С6.

а) Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 0,4 минуты.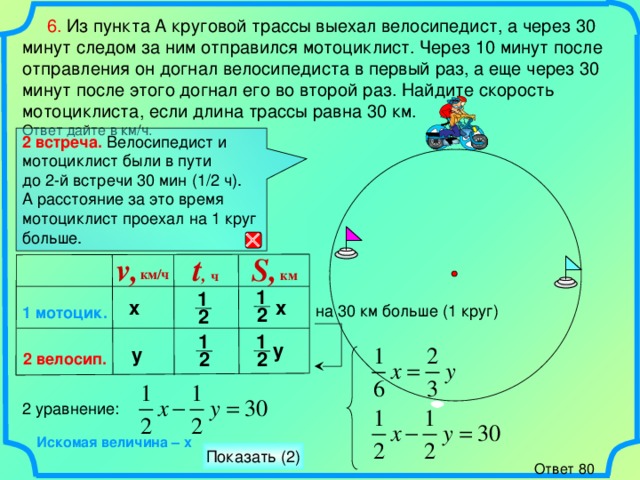 Найдите длину поезда.

Ответ: 200 метров.

б) Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 300 метрам, за 0,5 минуты. Найдите длину поезда.

Ответ: 200 метров.

С7.

а) Ходики показывают 9 часов. Какое время будут показывать ходики, когда минутная стрелка догонит часовую стрелку в третий раз?

Ответ: 12 часов.

б) Ходики показывают 4 часа. Какое время будут показывать ходики, когда минутная стрелка догонит часовую стрелку в восьмой раз?

Ответ: 12 часов.

С8.

а) Расстояние между пристанями А и В равно 18 км. Из А в В по течению реки отправился плот, а через 30 минут за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 9 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 50 м/мин.

Ответ: 25 км/ч.

б) Расстояние между пристанями А и В равно 14 км. Из А в В по течению реки отправился плот, а через 44 минуты за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошел 7 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 50 м/мин.

Ответ: 18 км/ч.

 

Уровень D.

D1.

а) Два бегуна одновременно стартовали из одного и того же места в одном направлении. Спустя 1 час, когда одному из них оставалось бежать 1 км до промежуточного финиша, ему сообщили, что второй бегун миновал промежуточный финиш 5 минут назад. Найдите скорость каждого бегуна, если известно, что скорость первого на 2 км/ч меньше скорости второго.

Ответ: 10 км/ч, 12 км/ч.

б) Два бегуна одновременно стартовали из одного и того же места в одном направлении. Спустя 1 час, когда одному из них оставалось бежать 1,5 км до промежуточного финиша, ему сообщили, что второй бегун миновал промежуточный финиш 5 минут назад. Найдите скорость каждого бегуна, если известно, что скорость первого на 3 км/ч меньше скорости второго.

Ответ: 15 км/ч, 18 км/ч.

D2.

а) Если велосипедист увеличит скорость на 5 км/ч, то получит выигрыш во времени 12 минут при прохождении некоторого пути. Если же он уменьшит скорость на 8 км/ч, то потеряет 40 минут на том же пути. Найдите скорость велосипедиста и длину пути.

Ответ: 20 км/ч, 20 км.

б) Если велосипедист увеличит скорость на 9 км/ч, то получит выигрыш во времени 27 минут при прохождении некоторого пути. Если же он уменьшит скорость на 5 км/ч, то потеряет 29 минут на том же пути. Найдите скорость велосипедиста и длину пути.

Ответ: 20 км/ч, 29 км.

D3.

а) Из пункта А в пункт В со скоростью 80 км/ч выехал первый автомобиль. Через некоторое время по тому же маршруту с постоянной скоростью отправился второй автомобиль. После остановки на 20 минут в пункте В второй автомобиль поехал с той же скоростью назад и через 48 км встретил первый автомобиль. В момент прибытия в В первого автомобиля второй автомобиль был в 120 км от В. Найдите расстояние от А до места первой встречи автомобилей, если расстояние между пунктами А и В равно 480 км.

Ответ: 80/3 км.

б) Из пункта А в пункт В с постоянной скоростью выехал первый автомобиль. Через некоторое время по тому же маршруту со скоростью 100 км/ч отправился второй автомобиль. Обогнав первый автомобиль через 150 км, второй автомобиль остановился на 1 час в В, затем поехал с той же скоростью назад и был на расстоянии 200 км от В в момент прибытия в В первого автомобиля. Найдите расстояние от В до места второй встречи автомобилей, если расстояние между пунктами А и В равно 600 км.

Ответ: 200/3км.

D4.

а) Велосипедист движется по пути АВ, состоящем из ровных участков, спусков и подъемов. На ровной дороге скорость велосипедиста равна 10 км/ч, на подъемах – 8 км/ч и на спусках – 16 км/ч. На дорогу из А в В велосипедист тратит 6 часов, а на обратный путь из В в А – 5 часов 30 минут. Известно, что ровная часть пути составляет 20 км. Найдите общую длину подъемов и спусков на пути из А в В.

Ответ: 40 км.

б) Велосипедист движется по пути АВ, состоящем из ровных участков, спусков и подъемов. На ровной дороге скорость велосипедиста равна 15 км/ч, на подъемах – 6 км/ч и на спусках – 18 км/ч. На дорогу из А в В велосипедист тратит 6 часов, а на обратный путь из В в А – 11 часов 20 минут. Известно, что ровная часть пути составляет 30 км. Найдите общую длину подъемов и спусков на пути из А в В.

Ответ: 60 км.

D5.

а) Мальчик сбежал вниз по движущемуся эскалатору и насчитал 20 ступенек. Затем он пробежал вверх по тому же эскалатору с той же скоростью относительно эскалатора и насчитал 60 ступенек. Сколько ступенек он насчитал бы, спустившись по неподвижному эскалатору?

Ответ: 30 ступенек.

б) Мальчик сбежал вниз по движущемуся эскалатору и насчитал 30 ступенек. Затем он пробежал вверх по тому же эскалатору с той же скоростью относительно эскалатора и насчитал 70 ступенек. Сколько ступенек он насчитал бы, спустившись по неподвижному эскалатору?

Ответ: 42 ступеньки.

D6.

а) Два бегуна одновременно стартуют из двух диаметрально противоположных точек А и В круговой дорожки стадиона. Они бегут в противоположных направлениях и встречаются в первый раз в точке М, находящейся в 50 метрах от В, во второй раз – в точке С, находящейся в 42 метрах от А. Найдите длину дорожки стадиона.

Ответ: 128 метров или 216 метров, или 384 метра.

б) Два бегуна одновременно стартуют из двух диаметрально противоположных точек А и В круговой дорожки стадиона. Они бегут в противоположных направлениях и встречаются в первый раз в точке М, находящейся в 70 метрах от В, во второй раз – в точке С, находящейся в 48 метрах от А. Найдите длину дорожки стадиона.

Ответ: 516 метров или 324 метра, или 172 метра.

МАОУ ДО ЦДТ. Усть-Илимск

Приветствуем Вас на новой информационной площадке Центра детского творчества! Мы постараемся сделать https://vk. com/maoudotsdt максимально удобным и информативным. Подпишитесь! Там Вам всегда рады! Центр детского творчества открывает запись на программы дополнительного образования на 2021-2022 учебный год. Подобрать программу вам поможет Навигатор дополнительного образования Иркутской области Консультации по телефону 89246034945   Вниманию родителей! В сентябре 2020 года в Иркутской области начнет работу система персонифицированного финансирования дополнительных занятий для детей.   Дополнительные сведения можно найти в информационном письме Информация о системе персонифицированного финансирования дополнительных занятий для дете Телефон для работы с Навигатором — 89246034945   Новые публикации Муниципальный фестиваль «С юбилеем, Усть-Илимск!» 02. 03.2023 1 марта в «ДК им. И.И. Наймушина» прошёл традиционный городской фестиваль, посвящённый празднованию 50-летнего юбилея нашего города. В фестивале приняли участие творческие коллективы школ города и МАУК «ДК им. И.И. Наймушина». «Наш герой» 02.03.2023 Победитель конкурса «Наш герой» Усть-Илимск — Родина моя 01.03.2023 В рамках XXVII месячника патриотического воспитания детей и молодёжи в Центре детского творчества прошла викторина «Усть- Илимск- Родина моя» Сценарный план профориентационного урока 16.02.2023 Сценарный план профориентационного урока «Технология выбора направления профессиональной подготовки» Сценарный план профориентационного урока 16.02.2023 Сценарный план профориентационного урока «Технология выбора направления профессиональной подготовки» Конспект занятия «Построение конструкций разной сложности» 14. 02.2023 Конспект занятия «Построение конструкций разной сложности»

Обращение граждан Отправить сообщение Порядок Порядок работы с обращениями граждан Портал Информация Минпросвещения Управление образования Усть-Илимска Cреднемесячная заработная плата Специальная оценка условий труда Телефоны экстренных и профилактических служб Безопасность Безопасное лето Дорожная безопасность О защите персональных данных Информационная безопасность Безопасность детей-пассажиров Информация для родителей Поддержка Фонд поддержки детей Анкетирование   Дополнительно

Обзор кинематики 1D — с ответами № 4

Перейдите к:

Обзорная сессия Главная — Список тем

1D Кинематика — Главная || Версия для печати || Вопросы и ссылки

Ответы на вопросы:  #1-7 || № 8– № 28 || № 29– № 42 || #43-#50

[ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50]

 

Часть E: Вычислительные задачи

43.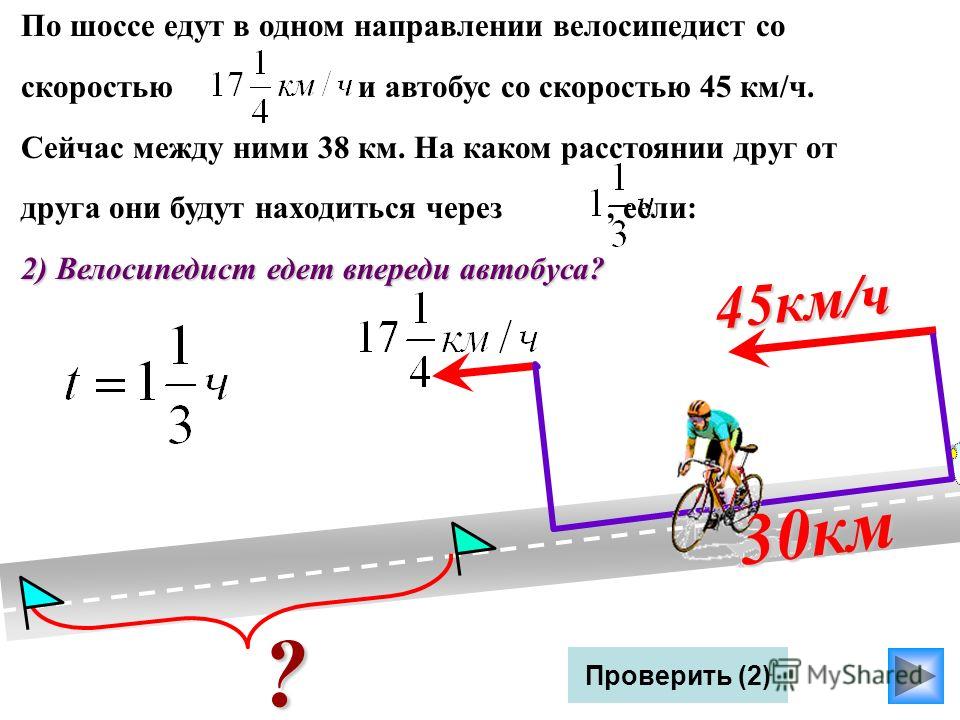 Определить ускорение (в м/с ² ) объекта, который … .

1. движется по прямой с постоянной скоростью 20,0 м/с в течение 12,0 секунд
2. меняет свою скорость с 12,1 м/с до 23,5 м/с за 7,81 секунды
3. изменяет свою скорость с 0,0 миль/час до 60,0 миль/час за 4,20 секунды
4. разгоняется с 33,4 м/с до 18,9 м/с на расстоянии 109 м

Ответ: См. ответы, пояснения и расчеты ниже.

а. Если скорость и направление объекта постоянны, то ускорение равно 0 м/с ² .

б. Ускорение представляет собой изменение скорости на отношение времени:

a = (Изменение скорости)/t = (23,5 м/с — 12,1 м/с) / (7,81 с) = 1,46 м/с ² .

в. Ускорение представляет собой изменение скорости на отношение времени:

a = (Изменение скорости)/t = (60,0 миль/ч — 0,0 миль/ч) / (4,20 с) = 14,3 миль/ч/с .

14,3 мили/ч/с * (1,0 м/с) / (2,24 мили/ч) = 6,38 м/с ² .

д. Значение ускорения также можно рассчитать с помощью кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v _o = 33,4 м/с; v _f = 18,9 м/с; и d = 109 м. Используя уравнение v _f ² = v _o ² + 2*a*d, можно вычислить ускорение.

а = (v _f ² — v _o ² ) / (2*d) = [(18,9 м/с) ² — (33,4 м/с) ² ] / (2 * 109 м) = -3,48 м/с ² . [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50 ]

44. Определить величину смещения (в метрах) объекта, который … .

1. движется из Туда в Йон (со средней скоростью 28,0 м/с), а затем обратно Туда (со средней скоростью 28,0 м/с), если путь туда и обратно занимает по 46 минут.
2. движется с постоянной скоростью 8,30 м/с по прямой в течение 15,0 секунд.
3. замедляется со скоростью -4,35 м/с/с со скорости 38,1 м/с до скорости 17,6 м/с
4. ускоряется из состояния покоя со скоростью 3,67 м/с ² за 12,1 секунды
5. движется со скоростью 12,2 м/с, а затем ускоряется со скоростью +1,88 м/с ² за 17,0 секунд

Ответ: См. ответы, пояснения и расчеты ниже.

а. Поскольку это рейс туда и обратно, общее перемещение равно 0 м.

б. Поскольку скорость постоянна, перемещение можно найти, умножив скорость на время.

d = v*t = (8,30 м/с) * (15,0 с) = 125 м

c. Значение смещения также можно рассчитать с помощью кинематических уравнений, если известны три другие кинематические величины. В этом случае известная информация: v _o = 38,1 м/с; v _f = 17,6 м/с; а = -4,35 м/с/с. Используя уравнение v _f ² = v _o ² + 2*a*d можно вычислить смещение.

d = (v _f ² — v _o ² ) / (2*a) = [(17,6 м/с) ² — (38,1 м/с) ^{1 2 ] / (2 * -4,35 м/с/с) = 131 м .}

д. Значение смещения можно рассчитать с помощью других кинематических уравнений, если известен другой набор кинематических величин. Здесь мы знаем, что: v _o = 0,0 м/с; т = 12,1 с; и а = 3,67 м/с/с. Используя уравнение d = v _o * t + 0,5*a*t ² , перемещение можно вычислить.

d = (0 м/с)*(12,1 с) + 0,5*(3,67 м/с/с)*(12,1 с) ² = 269 м .

эл. Здесь значение смещения рассчитывается с использованием того же кинематического уравнения. Мы знаем, что: v _o = 12,2 м/с; т = 17,0 с; а = 1,88 м/с/с. Используя уравнение d = v _o * t + 0,5*a*t ² , можно вычислить смещение.

d = (12,2 м/с)*(17,0 с) + 0,5*(1,88 м/с/с)*(17,0 с) ² = 479 м . [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50 ]

45. Заяц спит в локации в 1200 м от финиша. Черепаха проходит мимо него с постоянной скоростью 5,0 см/с. Если заяц наконец проснется через 6,5 часов, то какое минимальное ускорение (предполагаемое постоянным) он должен иметь, чтобы обогнать черепаху до финиша.

Ответ: 0,0067 м/с ²

Как и во многих текстовых задачах по физике, есть несколько путей к окончательному ответу. Во всех таких задачах решение требует размышлений и хороших стратегий решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. д.).

Черепаха, двигаясь с постоянной скоростью, пройдет 1200 м за время:

t _{черепаха} = d/v _{черепаха} = (1200 м) / (0,050 м/с) = 24000 s = 6,666… ​​hrs

Заяц будет спать 6,5 часа (23400 с) перед стартом, и поэтому у него будет только 0,1666… ​​часа (600 с), чтобы разогнаться до финиша. Таким образом, ускорение зайца можно определить с помощью кинематического уравнения. Известной информацией о движении зайца является: t = 600 с; д = 1200 м; v _или = 0 м/с. Лучшее уравнение: d = v _o * t + 0,5*a*t ² . Член v _o * t сокращается, и уравнение может быть алгебраически перестроено и решено для a:

a = 2*d / t ² = 2 * (1200 м) / (600 с) ² = 0,0067 м/с ² . [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50]

 

46. ​​А Золотой автомобиль , движущийся со скоростью 12,0 м/с, обгоняет зеленый автомобиль , в то время как зеленый автомобиль находится в состоянии покоя на светофоре. Зеленый автомобиль немедленно ускоряется со скоростью +1,80 м/с/с в течение 11,0 секунд, а затем поддерживает постоянную скорость. Через сколько времени (относительно начального времени старта) должна проехать Зеленая машина , прежде чем догнать Золотую машину .

Ответ: 14,0 с

(Как упоминалось в предыдущей задаче…) Как и во многих текстовых задачах по физике, существует более одного пути к окончательному ответу. Во всех таких задачах решение требует размышлений и хороших стратегий решения проблем (нарисуйте картинку, перечислите то, что вы знаете, перечислите соответствующие уравнения и т. д.).

Здесь золотой автомобиль движется с постоянной скоростью в течение времени t секунд (где t — общее время в пути для обоих автомобилей). Расстояние, пройденное золотой машиной, определяется уравнением кинематики d = v _o * t + 0,5*a*t ² . Второй член сокращается, и расстояние может быть выражено как

d = v _o * t + 0,5*a*t ² = (12,0 м/с)*t, или

d _золото = 12,0* t

Для зеленой машины есть период ускорения, а затем период постоянной скорости. Расстояние, пройденное за ускоренный период (d _{1зеленый} ), находится из того же кинематического уравнения. Для зеленой машины первый член сокращается, и расстояние равно

d _{1зеленая} = v _o * t + 0,5*a*t ² = 0,5*(1,80 м/с ² )*(11,0 у) ² или

d _{1зеленый} = 108,9 м

После того как зеленый автомобиль разогнался в течение 11 секунд, он сохраняет постоянную скорость в течение оставшегося времени, определяемого выражением t — 11 с.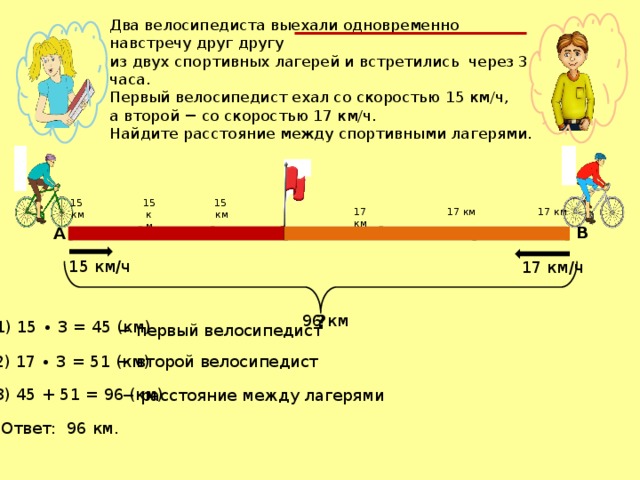 Скорость, с которой движется зеленый автомобиль в течение этого времени, можно вычислить по формуле:

v _{fзеленый} = v _o + a*t = (1,80 м/с ² ) *(11,0 с) = 19,8 м/с

Расстояние, пройденное зеленым автомобилем во время этой части движения с постоянной скоростью (d _2green ), можно рассчитать с помощью кинематического уравнения. д = v _или * т + 0,5*а*т ² . Второй член сокращается, и расстояние можно выразить как

d _{2зеленых} = v _o * t + 0,5*a*t ² = (19,8 м/с) * (t — 11 с) = 19,8* т — 217,8, или

d _{2зеленый} = 19,8*t — 217,8

Таким образом, общее расстояние, пройденное зеленым автомобилем, определяется выражением:

d _{зеленого цвета} = d _{1зеленого цвета} + d _{2зеленого цвета} = 108,9 + 19,8*t — 217,8

d _{зеленый} = 19,8*t — 108,9

Когда зеленая машина догонит золотую машину, их пройденное расстояние будет таким же.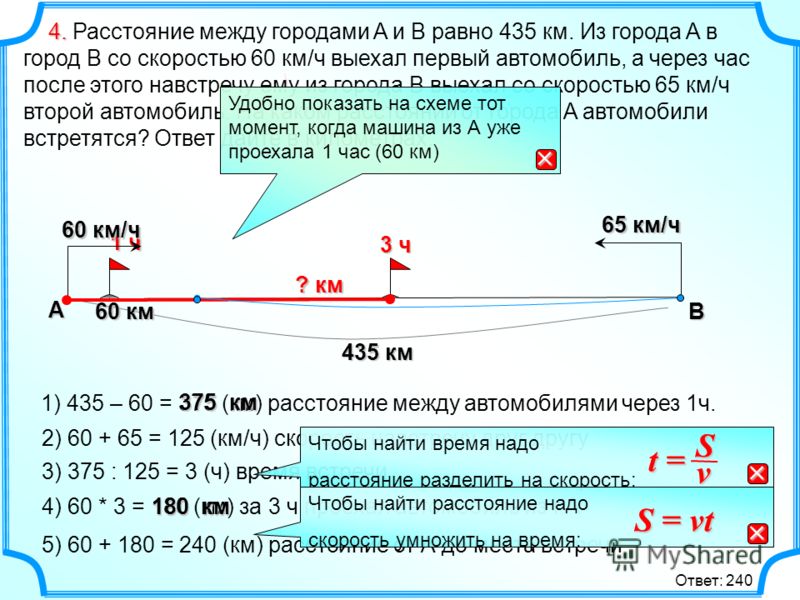 Таким образом, время t можно определить, установив два выражения для расстояния равными друг другу и найдя t.

12,0*т = 19,8*т — 108,9

108,9 = 7,80*t

т = (108,9) / (7,80)

t = 13,96 с = 14,0 с

[ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | #49| #50 ]

47. Ima Rilla Saari движется со скоростью 28,0 м/с по Лейк-авеню и через лесной заповедник. Она замечает, как олень прыгает на дорогу в 62,0 м перед ней. Има сначала реагирует на это событие, затем нажимает на тормоза и замедляется со скоростью -8,10 м/с ² и, в конце концов, останавливается в пикометре перед застывшим оленем. Какое время реакции Имы ? (т. е. сколько времени потребовалось Име, чтобы отреагировать на событие до замедления?)

Ответ: 0,486 с

Общее пройденное Имой расстояние (62,0 м) можно разбить на два сегмента — путь реакции (d _rxn ) и тормозной путь (d _{торможение} ). Расстояние реакции — это расстояние, которое Има проходит до торможения; она будет двигаться с постоянной скоростью в течение этого времени t _rxn . Тормозной путь — это расстояние, которое проходит Има, когда ее нога нажата на педаль тормоза, и она замедляется с 28,0 м/с до 0,0 м/с. Тормозной путь можно сначала рассчитать с помощью следующего кинематического уравнения: v _f ² = v _o ² + 2*a*d. Известная информация для этого периода торможения: v _o = 28 м/с; v _f = 0 м/с; а = -8,10 м/с/с. Замены и решение показаны ниже.

d _{торможение} = (v _f ² — v _o ² ) / (2*a) = [(0 м/с) ² — (28,0 м20) 28,0 м/с ] / (2 * -8,10 м/с/с) = 48,40 м .

Поскольку машине Имы требуется 48,40 м для торможения, она может проехать максимум 13,6 м за время реакции. Связь между временем реакции, скоростью и расстоянием реакции определяется уравнением 9. 0005

D _RXN = V * T _RXN

Заместитель 13,6 м для D _RXN и 28,0 м /с для V, время реакции может быть рассчитано:

T _RXN = (13,6 М) /М) /М) /М). (28,0 м/с) = 0,486 с [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50 ]

48. Двухступенчатая ракета разгоняется из состояния покоя со скоростью +3,57 м/с/с за 6,82 секунды. Затем он ускоряется со скоростью +2,98 м/с/с еще на 5,90 секунды. После второго этапа он входит в состояние свободного падения. Определить:

1. максимальная скорость
2. максимальная высота
3. высота полета ракеты через 20,0 секунд
4. общее время нахождения ракеты в воздухе (при условии запуска с земли)

Ответ: Смотрите ответы и пояснения ниже.

К этой проблеме можно подойти либо с помощью графика зависимости скорости от времени, либо с помощью кинематических уравнений (или их комбинации).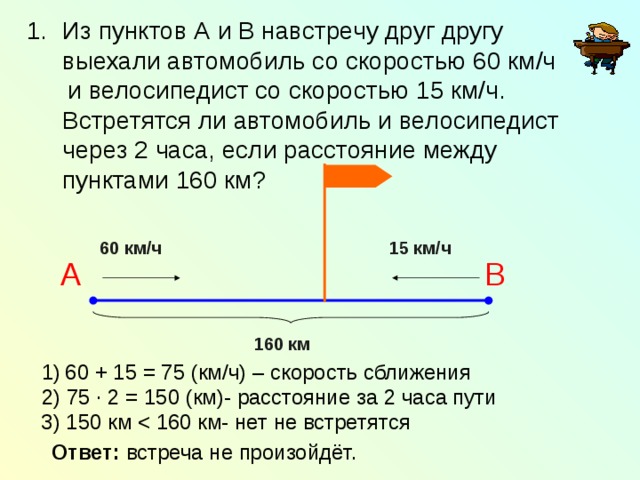 Каким бы ни был подход, необходимо разбить многоступенчатое движение на три различных периода ускорения. Использование кинематических уравнений подходит только для постоянных периодов ускорения. По этой причине сложное движение должно быть разбито на периоды времени, в течение которых ускорение постоянно. Эти три временных периода можно увидеть на графике скорость-время тремя линиями с отчетливо разным наклоном. Диаграмма справа дает изображение движения; отмечены стратегические точки. Эти точки будут упомянуты в решениях ниже. Приведенный ниже график зависимости скорости от времени будет использоваться во всем решении; обратите внимание, что на графике отмечены одни и те же стратегические точки.

а. Максимальная скорость достигается после второго этапа или периода ускорения (точка C). По истечении этого времени летящая вверх ракета начинает замедляться, поскольку гравитация становится единственной силой, действующей на нее. Для определения этой скорости (v _c ) кинематическое уравнение v _f = v _o + a*t будет использовано дважды — по одному разу для каждого периода ускорения.

Первая ступень: v _B = v _A + a*t = 0 м/с + (3,57 м/с/с) * (6,82 с) = 24,3 м/с

Второй этап: v _C = v _B + a*t = 24,3 м/с + (2,98 м/с/с) * (5,90 с) = 41,9 м/с

б. Максимальная высота достигается в точке D, через некоторое время после прекращения действия второй ступени, когда ракета, наконец, выдыхается . Скорость в этой точке равна 0 м/с (находится на пике траектории). Высота в этой точке представляет собой совокупное расстояние, пройденное от t = 0 с до t = t _D . Это расстояние представляет собой расстояние для первой ступени, второй ступени и периода замедления (от C до D). Эти расстояния соответствуют площади на графике v-t; они имеют маркировку A ₁ , A ₂ и A ₃ на графике. Они рассчитаны и суммированы ниже.

А ₁ = 0,5*b*h = 0,5 * (24,3 м/с) * (6,82 с) = 82,86 м

A ₂ = b*h + 0,5*b*h (треугольник на вершине квадрата)

A ₂ = (24,3 м/с) * (5,9 с) + 0,5 * (41,9 м/с — 24,3 м/с) * (5,9 с) = 195,42 м

Для определения A _{3 9 необходимо знать время от точки C до точки D0065 .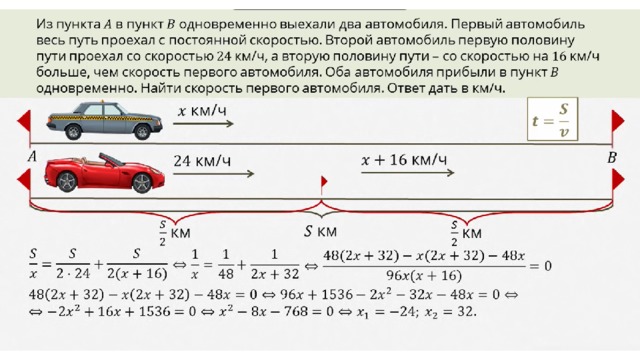 Это время можно определить с помощью кинематического уравнения v f = v o + a*t, для которого v f = 0 м/с и v o = 41,9 м/с и a = -9,8 м/с. SS.}

v _D = v _C + a*t

0 м/с = 41,9 м/с + (-9,8 м/с/с) * t

т = 4,28 с

Теперь A ₃ можно определить с помощью графика v-t. Площадь представляет собой треугольник и рассчитывается как

A ₃ = 0,5*b*h = 0,5 * (41,9м/с) * (4,82 с) = 89,57 м

Максимальная высота представляет собой сумму трех расстояний (площадей)

Макс. высота = 82,86 м + 195,42 м + 89,57 м = 368 м

c. Когда ракета достигает точки D, время составляет 17,0 секунд. Высота в 20,0 секунд будет равна 368 метрам подъема над стартовой площадкой из точки А в точку D минус расстояние падения от пика с 17,0 до 20,0 секунд. Это расстояние будет представлено отрицательной областью на графике скорость-время. Площадь представляет собой треугольник и может быть вычислена, если известна скорость в 20 секунд. Его можно рассчитать с помощью кинематического уравнения, а затем использовать для определения площади треугольника. В качестве альтернативы можно использовать кинематическое уравнение для определения расстояния, пройденного за эти 3,0 секунды. Работа представлена ​​ниже:

d = v _o * t + 0,5*a*t ² = 0,5 * (-9,8 м/с/с) * (3,0 с) ² = 44,1 м

Высота через 20 секунд равна следовательно, ~369 м, поднятые за первые 17 секунд, минус ~44 м, упавшие за следующие 3 секунды. Ответ: 325 м .

д. Ракета поднимается на 369 м за первые 17,0 с. За время после этого ракета должна упасть на 369 метров. Время падения с высоты 369 м можно найти из того же кинематического уравнения, что и в части c.

d = v _o * t + 0,5*a*t ²

-368 м = 0,5 * (-9,8 м/с/с) * т ²

т = 8,67 секунды

Это время можно добавить к 17,0 секундам, чтобы определить время приземления ракеты: 25,7 секунд .

[ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50 ]

49. В эстафете на 200,0 м (длина каждого этапа 50,0 м) один пловец имеет преимущество 0,450 с и плывет с постоянной скоростью 3,90 м/с в направлении противоположного конца бассейна. Какую минимальную скорость должен иметь второй пловец, чтобы догнать первого пловца к концу бассейна?

Ответ: 4,04 м/с

Оба пловца проплывают одинаковое расстояние (50 м) с постоянной скоростью. Пловец А (которого назвали произвольно) получает фору в 0,450 секунды. Таким образом, пловец В должен двигаться быстрее, чтобы закончить гонку за меньшее время, чем пловец А. Во-первых, время, необходимое пловцу А для прохождения 5010 м за 3,90 м/с можно вычислить. Время равно

t _A = d/v _A = (50,0 м) / (3,90 м/с) = 12,82 с

Таким образом, пловец B должен пробежать те же 50,0 м за 12,37 с (12,82 с — 0,45 с). Таким образом, скорость пловца B можно вычислить как

v _B = d/t _B = (50,0 м) / (12,37 с) = 4,04 м/с [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50 ]

50. Дрэг-гонщик разгоняется из состояния покоя со средней скоростью +13,2 м/с ² на расстояние 100 м. Водитель движется по инерции в течение 0,500 секунды, а затем использует тормоза и парашют для торможения до конца трассы. Если общая длина трассы составляет 180 м, какое минимальное замедление должен иметь гонщик, чтобы остановиться до конца трассы?

Ответ: -24 м/с/с

Эту задачу можно решить, сначала определив расстояние, на котором драгстер замедляется. Это расстояние будет меньше 80 метров на величину, равную расстоянию, которое драгстер преодолевает после пересечения финишной черты. См. схему.

Расстояние, пройденное драгстером до торможения, равно 100 м плюс расстояние накатом. Расстояние накатом можно определить, если определить скорость драгстера в конце 100 м. Итак, сначала будет использоваться кинематическое уравнение для определения скорости, а затем будет вычислено расстояние по инерции.

Используя уравнение v _f ² = v _o ² + 2*a*d, можно определить скорость через 100 м. Эта замена и решение показаны ниже.

v _f ² = v _o ² + 2*a*d = 2*(13,2 м/с/с)*(100, м) = 2640 м ² /с

v _f = 51,4 м/с

Движение по инерции со скоростью 51,38 м/с в течение 0,500 с приведет к пройденному расстоянию 25,7 м.

По окончании периода движения накатом остается небольшое расстояние до остановки. Это расстояние равно

180 м — 100 м — 25,7 м = 54 м

. Теперь то же кинематическое уравнение можно использовать для определения скорости замедления на последних 54 м пути. Известная информация: v _o = 51,4 м/с; v _f = 0 м/с; и d = 54 м. Используя уравнение v _f ² = v _o ² + 2*a*d, можно вычислить ускорение.

а = (v _f ² — v _o ² ) / (2*d) = = [(51,4 м/с) ² — (0 м/с) ^{1 2} ] / (2 * 54 м) = -24 м/с ² . [ #43 | № 44 | № 45 | № 46 | № 47 | № 48 | № 49 | #50]

 

Перейдите к:

Обзорная сессия Главная — Список тем

Одномерная кинематика — Главная || Версия для печати || Вопросы и ссылки

Ответы на вопросы:  #1-7 || № 8– № 28 || № 29– № 42 || #43-#50

Вам также может понравиться…

Пользователи The Review Session часто ищут учебные ресурсы, которые предоставляют им возможности для практики и обзора, включая встроенную обратную связь и инструкции. Если это то, что вы ищете, вам также может понравиться следующее:

1. Блокнот-Калькулятор

   Блокнот-Калькулятор включает задачи по физике, организованные по темам. Каждая проблема сопровождается всплывающим ответом и звуковым файлом, в котором подробно объясняется, как подходить и решать проблему. Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем.

   Посещение: Калькулятор Главная | Калькулятор — кинематика

    

2. Серия приложений Minds On Physics

   Приложение Minds On Physics («MOP the App») представляет собой серию интерактивных модулей вопросов для учащихся, которые серьезно относятся к улучшению своего концептуального понимания физики. Каждый модуль серии охватывает отдельную тему и далее разбит на подтемы. «Опыт MOP» предоставит учащемуся сложные вопросы, обратную связь и помощь по конкретным вопросам в контексте игровой среды. Он доступен для телефонов, планшетов, компьютеров Chromebook и Macintosh. Это идеальный ресурс для тех, кто хочет усовершенствовать свои способности к концептуальному мышлению. Часть 1 серии включает в себя кинематические концепции и кинематическую графику.

   Посещение: MOP Главная страница приложения || швабра приложение — часть 1
   

Решил? Головокружительные велосипедные пазлы | Математика

Сегодня в моем блоге головоломок я поставил перед вами следующие три задачи:

1) Царь гор поднимался по седловине со скоростью 15 км в час и спускался по ней со скоростью 45 км в час. В общей сложности на это у него ушло два часа. Предполагая, что расстояние, которое он прошел вверх и вниз, одинаково, как далеко он от основания до вершины седловины?

Решение

Единственное техническое знание, которое нам нужно здесь знать, это уравнение

скорость = расстояние/время

На пути вверх по седловине, следовательно, 15 = d / t , где d — это расстояние вверх, а t — это время, необходимое, чтобы добраться туда.

На пути вниз 45 = d / T , где T — время, необходимое для возвращения.

Другими словами, d = 15 t и d = 45T. Сложив их вместе, 15 t = 45 t или t = 3 t .

Мы также знаем, что t + T = 2. Итак, 3T + T = 2, что сводится к T = 1/2. Расстояние от основания до вершины седловины d равно 45/2 = 22,5 км.

2) Ксавье и Ив должны проехать 20 км и прибыть в одно и то же время. У них есть один велосипед, на котором они ездят по очереди. Каждый раз, когда всадник спешивается, он оставляет велосипед на обочине и идет дальше, а другой в конце концов подходит к велосипеду и запрыгивает на него. Ксавьер ходит со скоростью 4 км/ч и едет на велосипеде со скоростью 10 км/ч, а Ив ходит со скоростью 5 км/ч и едет на велосипеде со скоростью 8 км/ч.

Предполагая, что оба человека либо идут пешком, либо едут на велосипеде с такой скоростью и никогда не останавливаются на отдых, как они организуют свое путешествие?

Решение

Вот как я это решил. Пусть Ксавьер едет час, после чего он проедет 10 км. Пусть он бросит велосипед и продолжит идти пешком. Ив, который идет со скоростью 5 км/ч, доберется до велосипеда через два часа, на этом этапе Ксавьер уже будет на 14 км. Если Ив сейчас поедет на велосипеде, через час он будет на 18 км, что совпадает с прибытием Ксавьера. .

Однако наша цель состоит в том, чтобы пара прошла 20 км одновременно, а не 18 км. Если им нужно преодолеть оставшиеся 2 км так, чтобы они стартовали и прибыли в одно и то же время, им нужно и идти, и ехать. в девятый раз больше, чем раньше. Итак, пусть Ксавьер едет 1/9 часа (преодолевает 10/9 км), а затем идет пешком 2/9 часа. Ив будет ходить 2/9 часа, а остальное время будет ездить на велосипеде. Таким образом, полное путешествие составляет 3 часа и три девятых часа, или 3 часа 20 минут.

В моем решении Ксавьер едет 10 км, идет пешком 8 км, затем едет 1 и 1/9км, затем идет пешком, а Ив проезжает 8 км, когда впервые получает велосипед. Однако этот ответ является одним из нескольких решений. Ключевым моментом является то, что Ксавьер должен проехать первым, и что общее расстояние, которое он проедет, составляет 11 и 1/9 км. Он мог бы проехать всю партию за один раз, если бы захотел, или более короткими сегментами.

Дополнительный вопрос посложнее: к Ксавьеру и Иву присоединяется Зоя, которая идет со скоростью 3 км/ч, а едет на велосипеде со скоростью 12 км/ч. Как теперь троим организовать путешествие, чтобы они прибыли в одно и то же время?

Решение

Ответ заключается в том, что в пути Ксавьер должен проехать 7 и 11/27 км, Ив — 1 и 13/27 км, а Зоя — 11 и 3/27 км. Чтобы сэкономить место здесь и продемонстрировать свои навыки решения проблем, опубликуйте полный ответ с работами под строкой. Всем тем людям, которые не могут удержаться от публикации решений, когда я говорю БЕЗ СПОЙЛЕРОВ, это для вас!

3) Вот изображение велосипеда. Если вы прикрепите кусок веревки к нижней педали и потянете ее назад (как показано красной стрелкой), велосипед будет двигаться вперед или назад?

Решение

Велосипед движется назад (педаль движется против часовой стрелки). Или, по крайней мере, так будет почти на всех велосипедах, кроме тех, которые установлены на очень низкую передачу. Это контринтуитивный ответ, и он выглядит удивительным, когда вы попробуете его сами. Эта головоломка наделала много шума (извините!) пару лет назад благодаря следующему видео гениального Джорджа Харта.