| 1 | Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах. | Смотреть видеоразбор >> |
| 2 | Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота h горки равна 4,2 м. Ответ дайте в метрах. | Смотреть видеоразбор >> |
| 3 | Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 35 м и 65 м. Найдите длину забора (в метрах), которым нужно огородить участок, предусмотрев проезд шириной 3 м. | Смотреть видеоразбор >> |
| 4 | Участок земли под строительство санатория имеет форму прямоугольника, стороны которого равны 1000 м и 500 м. Одна из больших сторон участка идёт вдоль моря, а три остальные стороны нужно оградить забором. Найдите длину этого забора. Ответ дайте в метрах. | Смотреть видеоразбор >> |
| 5 | Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 17:00? | Смотреть видеоразбор >> |
| 6 | Человек стоит на расстоянии 12 м от столба, на котором висит фонарь, расположенный на высоте 9,5 м. Длина тени человека равна 3 м. Какого роста человек (в метрах)? | Смотреть видеоразбор >> |
| 7 | Диагональ прямоугольного телевизионного экрана равна 100 см, а высота экрана – 60 см. Найдите ширину экрана. Ответ дайте в сантиметрах. | Смотреть видеоразбор >> |
| 8 | План местности разбит на клетки. Каждая клетка обозначает квадрат 1м x 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 9 | Данный участок имеет форму прямоугольника, стороны которого равны 30 м и 20 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 6 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 10 | Дачный участок имеет форму прямоугольника со сторонами 20 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах. | Смотреть видеоразбор >> |
| 11 | Колесо имеет 5 спиц. Углы между соседними спицами равны. Найдите величину угла (в градусах), который образуют две соседние спицы. | Смотреть видеоразбор >> |
| 12 | Диагональ прямоугольного телевизионного экрана равна 80 см, а ширина экрана – 64 см. Найдите высоту экрана. Ответ дайте в сантиметрах. | Смотреть видеоразбор >> |
| 13 | План местности разбит на клетки. Каждая клетка обозначает квадрат 1м x 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 14 | Дачный участок имеет форму прямоугольника, стороны которого равны 40 м и 30 м. Дом, расположенный на участке, также имеет форму прямоугольника, стороны которого равны 9 м и 6 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 15 | Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин отгородил на участке квадратный вольер со стороной 15 м (см. рис.). Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 16 | На рисунке показано, как выглядит колесо с 7 спицами. Сколько будет спиц в колесе, если угол между соседними спицами в нём будет равен 30°? | Смотреть видеоразбор >> |
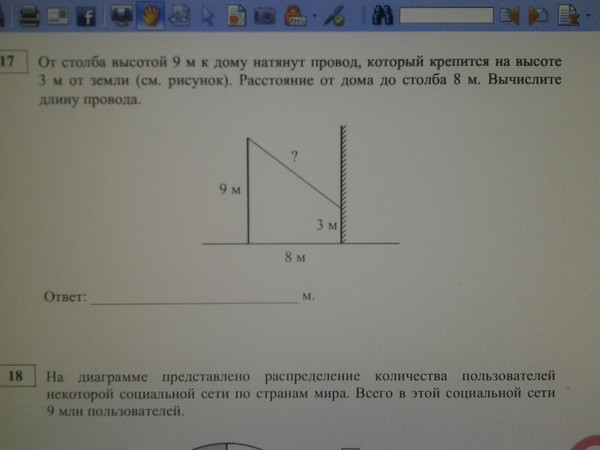
| 17 | От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Найдите длину провода. Ответ дайте в метрах. Найдите длину провода. Ответ дайте в метрах. | Смотреть видеоразбор >> |
| 18 | План местности разбит на клетки. Каждая клетка обозначает квадрат 1м x 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 19 | Дачный участок имеет форму квадрата, сторона которого равна 30 м. Дом, расположенный на участке, имеет на плане форму прямоугольника, стороны которого равны 8 м и 5 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 20 | Дачный участок имеет форму прямоугольника со сторонами 30 метров и 20 метров. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 12 м (см. рис.). Найдите суммарную длину изгороди в метрах. | Смотреть видеоразбор >> |
| 21 | Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах). При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах). | Смотреть видеоразбор >> |
| 22 | Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 0,7 м, а наибольшая h2 равна 1,5 м. Ответ дайте в метрах. | Смотреть видеоразбор >> |
| 23 | План местности разбит на клетки. Каждая клетка обозначает квадрат 1м x 1м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. | Смотреть видеоразбор >> |
| 24 | На плане указано, что прямоугольная комната имеет площадь 15,7 кв. м. Точные измерения показали, что ширина комнаты равна 3,2 м, а длина 5 м. На сколько квадратных метров площадь комнаты отличается от значения, указанного на плане? | Смотреть видеоразбор >> |
| 25 | Квартира состоит из комнаты, кухни, коридора и санузла (см.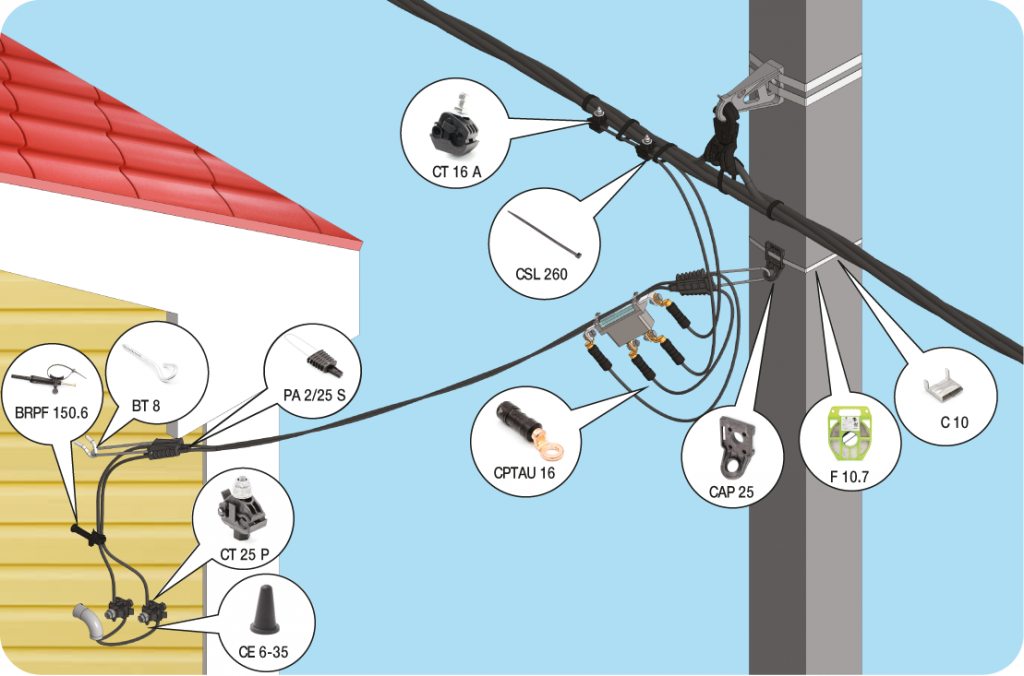 чертёж). Кухня имеет размеры 3 м x 4 м, санузел – 1,5 м x 2 м, длина коридора 6 м. Найдите площадь комнаты (в квадратных метрах). чертёж). Кухня имеет размеры 3 м x 4 м, санузел – 1,5 м x 2 м, длина коридора 6 м. Найдите площадь комнаты (в квадратных метрах). | Смотреть видеоразбор >> |
| 26 | На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м? | Смотреть видеоразбор >> |
|
Меню сайта Статистика Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
Геометрия 1.
2. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки А до точки О равно 6. 3. Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен . Найдите длину хорды АВ, если радиус окружности равен 8.
4. Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
5. В параллелограмме точка
середина стороны . Известно, что
. прямоугольник. 6. Точка О – центр окружности,
(см. рисунок). Найдите величину угла (в градусах).
7. В параллелограмме точка
середина стороны . Известно, что
. прямоугольник. 8. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен . Найдите площадь трапеции, если её основания равны 2 и 6. 9.
10. Сторона ромба равна 36, а острый угол равен .
11. Сторона ромба равна 30, а острый угол равен . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 12. На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
13. В параллелограмме диагонали и пересекаются в точке . Докажите, что площадь параллелограмма в четыре раза больше площади треугольника .14. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен , а расстояние от точки А до точки О равно 8. 15. От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см.
16. Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен , а радиус окружности равен 8. 17. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 15 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 8 м. Найдите длину троса.
18. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные и соответственно.
19. Медиана треугольника является диаметром окружности, пересекающей сторону в её середине. Длина стороны равна 4. Найдите радиус описанной окружности треугольника .20. Лестницу длиной 3 м прислонили к дереву.
21. В окружности с центром в точке проведены диаметры и , угол OAB равен . Найдите величину угла .
22. В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен . Найдите величину угла .
23. От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
24. Найдите площадь трапеции, изображённой на рисунке.
25. Диагональ BD параллелограмма и . Найдите меньший угол параллелограмма.
26. Найдите площадь трапеции, изображённой на рисунке.
27. В окружности с центром в точке О проведены диаметры AD и BC, угол равен . .
28.
29.
30. В треугольнике ABC угол C прямой,
,
.
31. В треугольнике ABC угол C прямой,
,
. Найдите AB.
32. Из вершины прямого угла треугольника проведена высота . Радиус окружности, вписанной в треугольник , равен , тангенс угла равен . Найдите радиус вписанной окружности треугольника . и соответственно.
34. Найдите площадь трапеции, изображённой на рисунке.
35. Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
36. Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
37.
38. Точка О – центр окружности,
(см. рисунок). Найдите величину угла (в градусах).
39.
40. Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
41. Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен . Найдите площадь трапеции, если её основания равны 2 и 7.
42.
43. Точка О – центр окружности,
(см. рисунок). Найдите величину угла (в градусах).
44. В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45 .
45. Точка О – центр окружности,
(см. рисунок). Найдите величину угла (в градусах).
46. В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45 .Найдите площадь трапеции.
47. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен . Найдите площадь трапеции, если её основания равны 3 и 9.
48. Точка О центр окружности,
(см. (в градусах).
|
Вход на сайт Календарь
Архив записей
Друзья сайта
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Электрический столб высотой 8 м.
 С его вершины к точке А на земле на расстоянии 8 м от подножия столба привязана стальная проволока. Какова длина провода?
С его вершины к точке А на земле на расстоянии 8 м от подножия столба привязана стальная проволока. Какова длина провода?ИКСЕ-ТРЕУГОЛЬНИК И ЕГО СВОЙСТВА-РЕМОНТ УПРАЖНЕНИЕ
16 видеоРЕКЛАМА
Аб Падхай каро бина адс ке
Хариэдо Д.Н. Про и дехо сари видео бина киси ад ки рукаават ке!
Пошаговое решение от экспертов, которое поможет вам избавиться от сомнений и получить отличные оценки на экзаменах.
Стенограмма
привет всем итак вопрос на сегодня в том, что электрический столб высотой 8 м и к его вершине привязана стальная проволока к точке а на земле на расстоянии 8 м от подножия столба то мы нужно найти, какова длина провода, поэтому теперь давайте построим диаграмму заземления на основании данного нам утверждения, что электрический столб получается M высотой, поэтому предположим, что это электрический столб 85 а стальная проволока устала от ноута до точки а это точка а давайте рассмотрим эту точку б и эту точку с покажите мне расстояние от подножия столба 8 м это 8 м а нам нужно
найдите значение x, которое является длиной стальной проволоки, поэтому давайте правильно, пусть длина проволоки x теперь, как вы можете видеть, что угол C равен 90 градусов, поскольку угол B равен 90 градусам, поэтому, применяя теорему Пифагора, мы можно сказать, что BC квадрат + AC квадрат равен
будет квадратом 9 букв Запланировано значение, которое является квадратом + b квадратом, равным x квадрату, что 464 плюс 64 равно x квадрату, поэтому значение x квадрата равно 128 поэтому X равно 8 корень 2 метра, поэтому делаем вывод, что длина 3 провода равна 88 руп до M
संबंधित वीडियो
Электрический
столб высотой 10 м. Стальная проволока, привязанная к вершине столба, закреплена в точке
на земле, чтобы держать шест в правильном положении. Если провод образует угол 45o
с
горизонтали через основание столба, найдите длину провода.
Стальная проволока, привязанная к вершине столба, закреплена в точке
на земле, чтобы держать шест в правильном положении. Если провод образует угол 45o
с
горизонтали через основание столба, найдите длину провода.
1413281
एक के खम खम्बे के शी выполнительный Расстояния до пола, высота над уровнем моря 1,5 м. दूर है और तार जमींन से 60∘ का कोंढ़ बनाता है । पोल की ऊचाई ज्ञात करे ।
21369201
18 M ऊँचे एक ऊ ऊ000 ऊ के ऊप ऊप000 खंभे के आधार से को कितनी दु दु000
52808322
एक बिजली का खम्भा 10 मीटर ऊँचा है| खम्भे को सीधा लम्बवत रखने के लिए एक तार का सिरा,खम्भे की चोटी से बंधा है तथा दूसरा सिरा भूमि पर स्थिर किया गया है|यदि तार खम्भे के आधार बिंदु से होकर जाने वाली क्षैतिज साथ 45∘ का कोण बनाये तो तार की लम्बाई ज्ञात कीजिए|
94852786
Электрический столб высотой 20 м стоит прямо на земле с помощью стальной проволоки к его вершине и прикрепленной к земле. Если стальная проволока составляет 60∘ с горизонтальной поверхностью земли, найдите длину стальной проволоки.
161136947
Мальчик наблюдал верхушку электрического столба под углом 60∘, когда точка наблюдения находилась на расстоянии 8 метров от подножия столба. Найдите высоту столба.
558735830
Провод длиной 18 м был привязан к электрическому столбу под углом возвышения 30∘ к земле. Поскольку он покрывал большое расстояние, его обрезали и привязали под углом 60∘ к земле. Какой длины провод был отрезан?
558735884
Мальчик наблюдал верхушку электрического столба под углом 60∘, когда точка наблюдения находилась на расстоянии 8 метров от подножия столба. Найдите высоту столба.
560943589
Провод длиной 18 м был привязан к электрическому столбу под углом 30° к земле. Поскольку он покрывал большое расстояние, его обрезали и привязали под углом 60∘ к земле. Какой длины провод был отрезан?
560943613
Артист цирка поднимается с земли по веревке, натянутой от вершины вертикального шеста и привязанной к земле на определенном расстоянии от подножия шеста. Высота столба 12 м, а угол, образуемый веревкой с землей, равен 30°. Найдите расстояние, которое преодолел художник, достигнув вершины шеста.
Высота столба 12 м, а угол, образуемый веревкой с землей, равен 30°. Найдите расстояние, которое преодолел художник, достигнув вершины шеста.
576999254
Электрический столб высотой 10 м. Стальная проволока, привязанная к вершине столба, закреплена в точке на земле, чтобы держать шест в правильном положении. Если провод образует угол 45∘ с горизонтали через основание столба, найдите длину провода.
642571062
Мальчик наблюдал верхушку электрического столба под углом 60∘, когда точка наблюдения находилась на расстоянии 8 метров от подножия столба. Найдите высоту столба.
642711859
Провод длиной 18 м был привязан к электрическому столбу под углом возвышения 30∘ к земле. Поскольку он покрывал большое расстояние, его обрезали и привязали под углом 60∘ к земле. Какой длины провод был отрезан?
642711877
Провод длиной 25 м был привязан к электрическому столбу под углом возвышения 30∘ с землей. Поскольку он покрывал большое расстояние, его разрезали и привязывали под углом 60∘ к земле на столько, сколько длина провода была отрезана.
6451
Стальной столб высотой 10 м. Чтобы столб оставался в вертикальном положении, один конец стальной проволоки привязывают к вершине столба, а другой конец закрепляют на земле. Если стальная проволока образует угол 45 с горизонталью через точку основания шеста, найдите длину стальной проволоки
6451
Напряжение и деформация) – x-Douglas College Physics 1107 Fall 2019 Custom учебник
Глава 4 Динамика: сила и законы движения Ньютона
Резюме
- Закон штата Гука.
- Объясните закон Гука, используя графическое изображение деформации и приложенной силы.
- Обсудите деформации, такие как изменение длины
- Определить изменение длины по массе, длине и радиусу.
Силы могут влиять на форму объекта. Если бульдозер втолкнет машину в стену, то машина не сдвинется с места, но заметно изменит форму. Изменение формы из-за приложения силы представляет собой деформацию . Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, т. е. при малых деформациях Закон Гука соблюдается. В форме уравнения закон Гука имеет вид
Известно, что даже очень малые силы вызывают некоторую деформацию. При малых деформациях наблюдаются две важные характеристики. Во-первых, объект возвращается к своей первоначальной форме при снятии силы, то есть деформация является упругой при малых деформациях. Во-вторых, величина деформации пропорциональна силе, т. е. при малых деформациях Закон Гука соблюдается. В форме уравнения закон Гука имеет вид
[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]
, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, которая зависит от формы и состава объект и направление силы. Обратите внимание, что эта сила является функцией деформации Δ L — не постоянна, как кинетическая сила трения. Иногда мы используем Δ x вместо Δ L. Деформация может быть вдоль любой оси. Переставить это на
Переставить это на
[латекс]\boldsymbol{\Delta{L}\: = }[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]
дает понять, что деформация пропорциональна приложенной силе. На рис. 1 показана зависимость по закону Гука между расширением Δ L пружины или человеческой кости. Для металлов или пружин прямолинейная область, к которой относится закон Гука, намного больше. Кости хрупкие, эластичная область мала, а перелом внезапный. В конце концов, достаточно большое напряжение на материале приведет к его разрыву или разрушению. Прочность на растяжение — это разрушающее напряжение, вызывающее необратимую деформацию или разрушение материала.
ЗАКОН ГУКА
[латекс]\boldsymbol{F = k\Delta{L},}[/латекс]
, где Δ L — величина деформации (например, изменение длины), вызванная силой F , а k — константа пропорциональности, зависящая от формы и состава объекта и направления силы.
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{F}{k}}[/латекс]
Рис. 1. График деформации Δ L в зависимости от приложенной силы Ф . Прямой отрезок — это линейный участок, на котором соблюдается закон Гука. Наклон прямолинейного участка равен 1/k . Для больших сил график искривлен, но деформация остается упругой — 90 102 Δ 90 111 L 90 112 90 103 вернется к нулю, если сила исчезнет. Еще большие силы постоянно деформируют объект, пока он окончательно не сломается. Форма кривой вблизи разрушения зависит от нескольких факторов, в том числе от того, как сила F применяется. Обратите внимание, что на этом графике наклон увеличивается непосредственно перед переломом, указывая на то, что небольшое увеличение F приводит к большому увеличению L вблизи перелома. Константа пропорциональности k зависит от ряда факторов для материала. Например, гитарная струна из нейлона растягивается при натяжении, причем удлинение Δ L пропорционально приложенной силе (по крайней мере, при малых деформациях). Более толстые нейлоновые струны и те, что сделаны из стали, меньше растягиваются при одном и том же приложенном усилии, что означает, что они имеют большее 9-кратное усилие.0111 к (см. рис. 2). Наконец, все три струны возвращаются к своей нормальной длине после снятия силы при условии, что деформация невелика. Большинство материалов ведет себя таким образом, если деформация составляет менее примерно 0,1% или примерно 1 часть на 10 3 .
Например, гитарная струна из нейлона растягивается при натяжении, причем удлинение Δ L пропорционально приложенной силе (по крайней мере, при малых деформациях). Более толстые нейлоновые струны и те, что сделаны из стали, меньше растягиваются при одном и том же приложенном усилии, что означает, что они имеют большее 9-кратное усилие.0111 к (см. рис. 2). Наконец, все три струны возвращаются к своей нормальной длине после снятия силы при условии, что деформация невелика. Большинство материалов ведет себя таким образом, если деформация составляет менее примерно 0,1% или примерно 1 часть на 10 3 .
НЕМНОГО ПОТЯНИТЕСЬ
Как бы вы измерили константу пропорциональности k резиновой ленты? Если резиновая лента растянулась на 3 см, когда к ней прикреплен груз массой 100 г, то насколько сильно она растянется, если две одинаковые резиновые ленты будут прикреплены к одной и той же массе, даже если их сложить параллельно или, наоборот, связать вместе последовательно?
Решения
Задачи и упражнения
1) 110 Н/м
2) 0,0101 м = 1,01 см
3) 1,11 ньютона
4) 6,0 см По соотношению и пропорции 12 Н/4,0 см? так ? = 18 х 4 / 12 =
Теперь рассмотрим тип деформации, вызывающий изменение длины (растяжение и сжатие). Существуют также боковые силы, вызывающие сдвиг (напряжение) и изменение объема, но мы не будем подробно останавливаться на них в этом курсе.
Изменение длины Δ L образуется при приложении к проволоке или стержню силы, параллельной его длине L 0 , либо растяжения (растяжение), либо сжатия. (См. рис. 3.)
(См. рис. 3.)
Эксперименты показали, что изменение длины ( Δ L ) зависит лишь от нескольких переменных. Как уже отмечалось, Δ L пропорциональна силе F и зависит от вещества, из которого сделан объект. Кроме того, изменение длины пропорционально исходной длине L 0 и обратно пропорциональна площади поперечного сечения проволоки или стержня. Например, длинная гитарная струна растянется больше, чем короткая, а толстая струна растянется меньше, чем тонкая. Мы можем объединить все эти факторы в одно уравнение для Δ L :
Мы можем объединить все эти факторы в одно уравнение для Δ L :
[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{\vec{\textbf{F}}}{A} }[/латекс][латекс]\boldsymbol{L_0},[/латекс]
где Δ L изменение длины, F приложенная сила, Y коэффициент, называемый модулем упругости или модулем Юнга, зависящий от вещества, 2 A A площадь поперечного сечения, а L 0 — исходная длина. В таблице 3 приведены значения Y для нескольких материалов. Говорят, что материалы с большим значением Y имеют большую жесткость при растяжении, поскольку они меньше деформируются при заданном растяжении или сжатии. 92)}[/латекс]
 Модули упругости 1 .
Модули упругости 1 .Модули Юнга для жидкостей и газов не указаны в таблице 3, поскольку они не могут растягиваться или сжиматься только в одном направлении. Обратите внимание, что существует предположение, что объект не ускоряется, так что на самом деле есть две приложенные силы величиной F действующие в противоположных направлениях. Например, струны на рисунке 3 тянут вниз под действием силы величиной w и удерживаются потолком, который также оказывает силу величиной w .
Пример 1: натяжение длинного троса
Подвесные тросы используются для перевозки гондол на горнолыжных курортах. (См. рис. 4) Рассмотрим подвесной трос с неподдерживаемым пролетом длиной 3 км. Рассчитайте величину растяжения стального троса. Предположим, что кабель имеет диаметр 5,6 см и максимальное натяжение, которое он может выдержать, равно 3,0 × 10 6 Н .
Стратегия
Сила равна максимальному натяжению, или F = 3,0 × 10 6 Н . Площадь поперечного сечения π r 2 = 2,46 × 10 -3 м 2 . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины. 92})(3020\textbf{ m})}[/latex]
[latex]\boldsymbol{=18\textbf{ m}}.[/latex]
Обсуждение
Это довольно натянуто, но только около 0,6% длины без поддержки. Влияние температуры на длину может быть важным в этих условиях.
Кости в целом не ломаются при растяжении или сжатии. Скорее, они обычно ломаются из-за бокового удара или изгиба, что приводит к сдвигу или хрусту кости. Поведение костей при растяжении и сжатии важно, поскольку оно определяет нагрузку, которую кости могут нести. Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.
Кости классифицируются как несущие конструкции, такие как колонны в зданиях и деревьях. Несущие конструкции имеют особенности; колонны в здании имеют стальные арматурные стержни, а деревья и кости — волокнистые. Кости в разных частях тела выполняют разные структурные функции и подвержены разным нагрузкам. Таким образом, кость в верхней части бедренной кости располагается тонкими пластинками, разделенными костным мозгом, тогда как в других местах кости могут быть цилиндрическими и наполненными костным мозгом или просто сплошными. Люди с избыточным весом склонны к повреждению костей из-за постоянного сжатия в суставах и сухожилиях.
Другой биологический пример закона Гука происходит в сухожилиях. Функционально сухожилие (ткань, соединяющая мышцу с костью) должно сначала легко растягиваться при приложении силы, но обеспечивать гораздо большую восстанавливающую силу при большем напряжении. На рис. 5 показана зависимость между напряжением и деформацией сухожилия человека. Некоторые сухожилия имеют высокое содержание коллагена, поэтому напряжение или изменение длины относительно невелики; другие, такие как опорные сухожилия (как в ноге), могут изменять длину до 10%.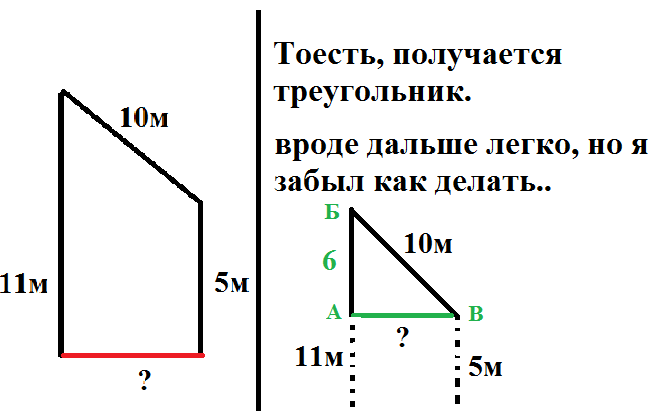 Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.0111 разжимной . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
Обратите внимание, что эта кривая напряжения-деформации нелинейна, поскольку наклон линии изменяется в разных областях. В первой части растяжения, называемой областью пальцев, волокна сухожилия начинают выстраиваться в направлении напряжения — это называется 9.0111 разжимной . В линейной области фибриллы будут растягиваться, а в области разрушения отдельные волокна начинают рваться. Простую модель этой взаимосвязи можно проиллюстрировать параллельными пружинами: разные пружины активируются при разной длине растяжения. Примеры этого приведены в задачах в конце этой главы. Связки (ткань, соединяющая кость с костью) ведут себя аналогичным образом.
В отличие от костей и сухожилий, которые должны быть прочными и эластичными, артерии и легкие должны быть очень растяжимыми. Эластические свойства артерий необходимы для кровотока.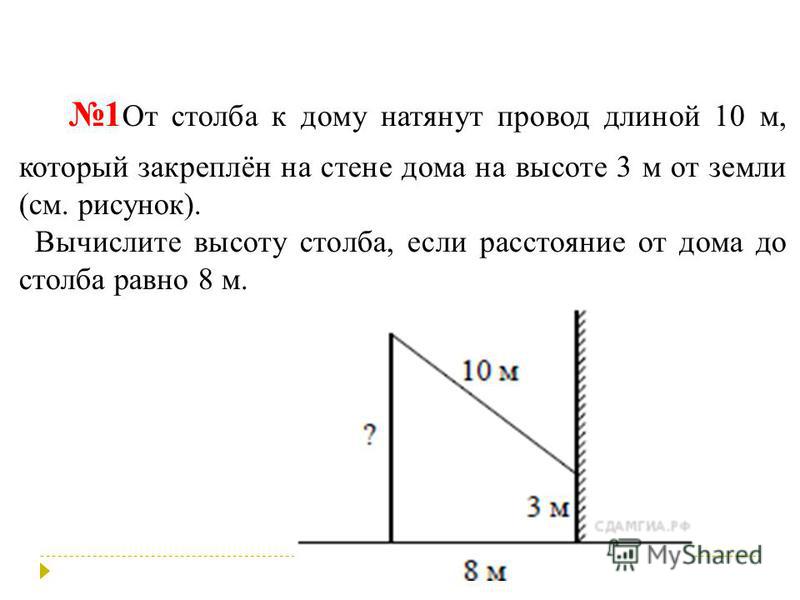 Давление в артериях увеличивается, и стенки артерий растягиваются, когда кровь выталкивается из сердца. Когда аортальный клапан закрывается, давление в артериях падает, и стенки артерий расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий по мере того, как кровь течет через них при каждом толчке сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластическими свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но свободно и эластично расслабляются, когда мы выдыхаем. Наша кожа особенно эластична, особенно у молодых. Молодой человек может похудеть со 100 кг до 60 кг без видимых провисаний кожи. Эластичность всех органов с возрастом снижается. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-летнего возраста.
Давление в артериях увеличивается, и стенки артерий растягиваются, когда кровь выталкивается из сердца. Когда аортальный клапан закрывается, давление в артериях падает, и стенки артерий расслабляются, чтобы поддерживать кровоток. Когда вы чувствуете свой пульс, вы чувствуете именно это — эластичное поведение артерий по мере того, как кровь течет через них при каждом толчке сердца. Если бы артерии были жесткими, вы бы не почувствовали пульс. Сердце также является органом с особыми эластическими свойствами. Легкие расширяются за счет мышечного усилия, когда мы вдыхаем, но свободно и эластично расслабляются, когда мы выдыхаем. Наша кожа особенно эластична, особенно у молодых. Молодой человек может похудеть со 100 кг до 60 кг без видимых провисаний кожи. Эластичность всех органов с возрастом снижается. Постепенное физиологическое старение за счет снижения эластичности начинается в начале 20-летнего возраста.
Пример 2. Расчет деформации: насколько укорачивается ваша нога, когда вы стоите на ней?
Рассчитайте изменение длины бедренной кости бедра, когда мужчина массой 70,0 кг поддерживает на ней 62,0 кг своего веса, принимая, что кость эквивалентна однородному стержню длиной 40,0 см и радиусом 2,00 см . 2) = 607.6\textbf{N}},[/латекс]
2) = 607.6\textbf{N}},[/латекс]
, а площадь поперечного сечения равна π r 2 = 1,257 × 10 -3 м 2 . Уравнение [латекс]\жирныйсимвол{\Delta{L} = \frac{1}{Y}\frac{F}{A}L_0}[/latex] можно использовать для определения изменения длины.
Раствор
Все количества, кроме Δ L , известны. Обратите внимание, что здесь необходимо использовать значение сжатия для модуля Юнга кости. Таким образом,
[латекс]\boldsymbol{\Delta{L}=(\frac{1}{9{-5}\textbf{ м}}.[/latex]
Обсуждение
Это небольшое изменение длины кажется разумным, согласующимся с нашим опытом, что кости жесткие. На самом деле, даже довольно большие силы, возникающие при напряженной физической работе, не сильно сжимают или сгибают кости. Хотя кость является жесткой по сравнению с жиром или мышцами, некоторые из веществ, перечисленных в таблице 3, имеют более высокие значения модуля Юнга Y .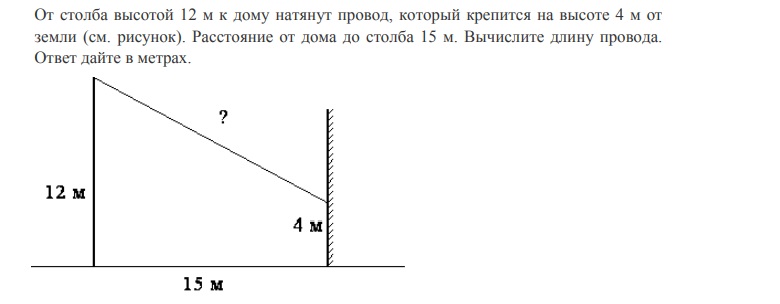 Другими словами, они более жесткие.
Другими словами, они более жесткие.
Уравнение изменения длины традиционно перестраивается и записывается в следующем виде:
[латекс]\boldsymbol{\frac{F}{A}}[/latex][латекс]\boldsymbol{=Y}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0 }}.[/латекс]
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение (измеряется в Н/м 2 ), а отношение изменения длины в длину,[латекс]\жирныйсимвол{\гидроразрыва{\Delta{L}}{L_0}},[/латекс]определяется как штамм (безразмерное количество). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
В этой форме уравнение аналогично закону Гука, где напряжение аналогично силе, а деформация аналогична деформации. Если мы снова перепишем это уравнение к виду
[латекс]\boldsymbol{F=YA}[/латекс][латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/latex]
видим, что это то же самое, что и закон Гука с константой пропорциональности
[латекс]\boldsymbol{k\:=}[/латекс][латекс]\boldsymbol{\frac{YA}{L_0}}. [/latex]
[/latex]
Эта общая идея о том, что сила и вызываемая ею деформация пропорциональны малым деформациям, применима к изменениям длины, боковому изгибу и изменениям объема.
НАПРЯЖЕНИЕ
Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение, измеренное в Н/м 2 .
НАПРЯЖЕНИЕ
Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как напряжение (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
- Закон Гука определяется выражением
[латекс]\boldsymbol{F=k\Delta{L}},[/latex] или [латекс]\boldsymbol{F=k\Delta{x}},[/latex]
, где Δ L — величина деформации (изменение длины), F — приложенная сила, а k — константа пропорциональности, зависящая от формы и состава объекта.
 и направление силы. Связь между деформацией и приложенной силой также можно записать как
и направление силы. Связь между деформацией и приложенной силой также можно записать как[латекс]\boldsymbol{\Delta{L}\:=}[/латекс][латекс]\boldsymbol{\frac{1}{Y}\frac{F}{A}}[/latex][латекс] \boldsymbol{L_0},[/латекс]
, где Y — это модуль Юнга , который зависит от вещества, A — площадь поперечного сечения, а L 0 — исходная длина.
- Отношение силы к площади [латекс]\boldsymbol{\frac{F}{A}},[/латекс] определяется как напряжение , измеренное в Н/м 2 .
- Отношение изменения длины к длине [латекс]\boldsymbol{\frac{\Delta{L}}{L_0}},[/латекс] определяется как штамм (безразмерная величина). Другими словами,
[латекс]\boldsymbol{\textbf{стресс}=Y\times\textbf{штамм}}.[/латекс]
Сноски
- 1 Приблизительные и средние значения. Модули Юнга Y для растяжения и сжатия иногда различаются, но здесь они усреднены.



 Докажите, что данный параллелограмм
Докажите, что данный параллелограмм 
 Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?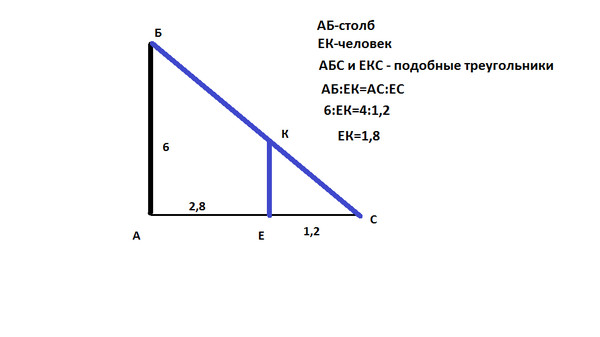
 На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?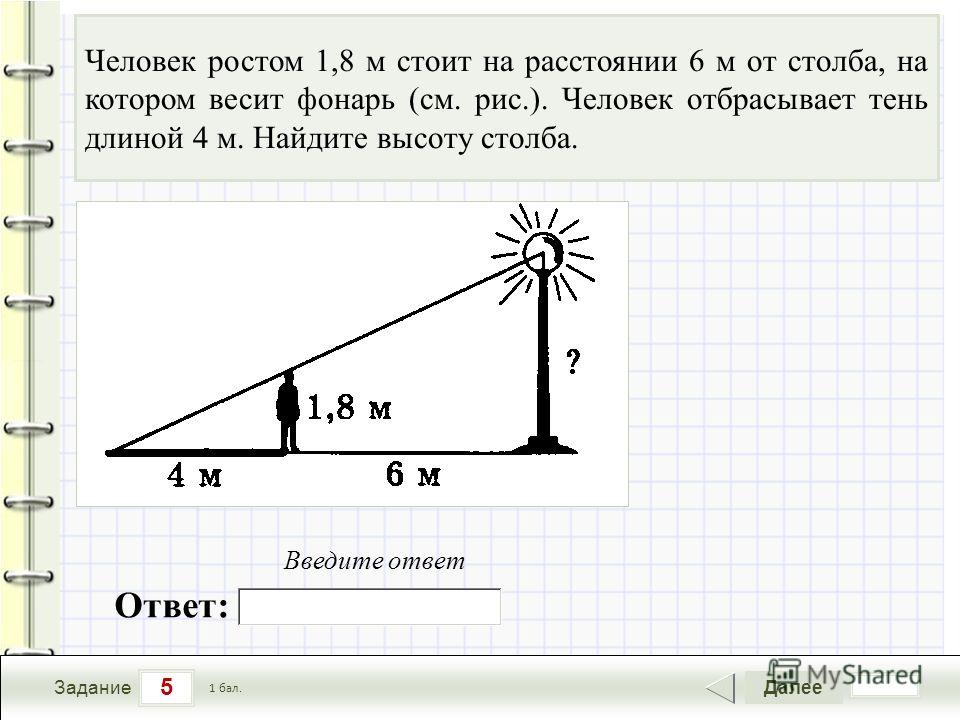 Найдите величину угла
Найдите величину угла 
 Найдите AB.
Найдите AB.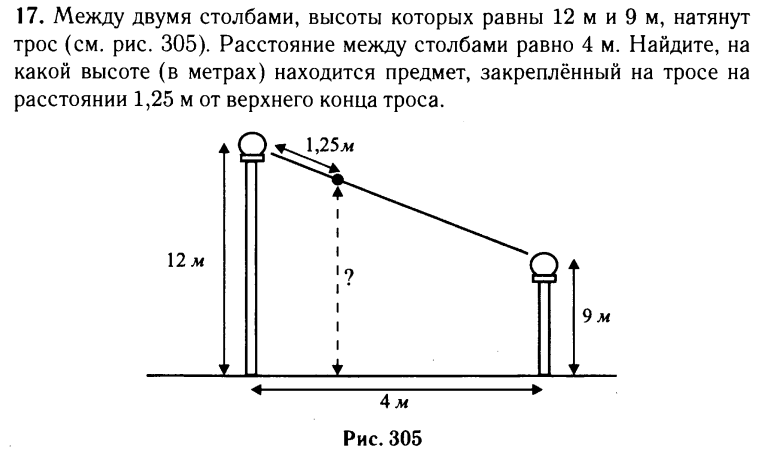 33. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные
33. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 

 Найдите площадь трапеции.
Найдите площадь трапеции. рисунок). Найдите величину угла
рисунок). Найдите величину угла 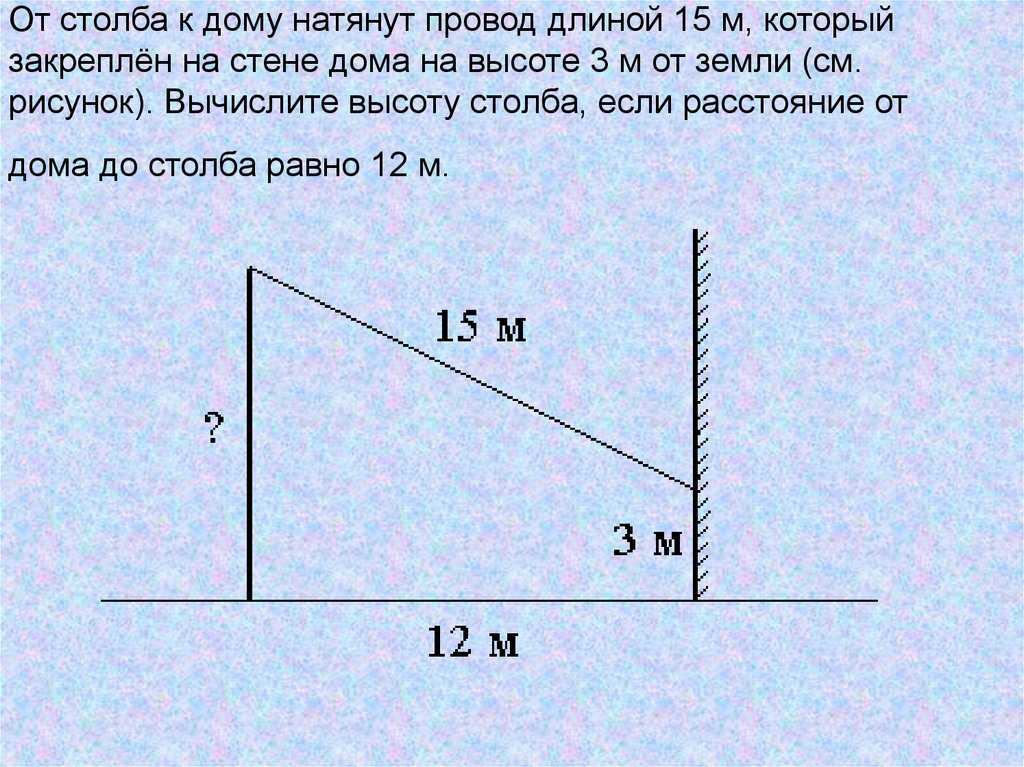 и направление силы. Связь между деформацией и приложенной силой также можно записать как
и направление силы. Связь между деформацией и приложенной силой также можно записать как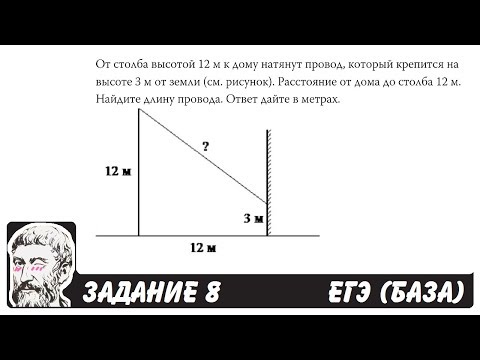
Leave A Comment