Основания трапеции равны 18 и 12, одна из боковых сторон 6, а тангенс …

Ответы
04. 09.15

Парень
Читать ответы

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука

Похожие вопросы

Для нумерации страниц книги использовано 1315 цифр. Сколько страниц проннумерованно, если нумерация страниц начинается с ее третьей страницы, с цифры три?

помогите решить задачу

Правда ли,что государство выделяет по 14000 первоклассникам?

скорость автомобиля лидера в гонке «фрмула-1» относительно следующего за ним автомобиля на прямолинейном участке трассы равна 3км/ч,относительно…

Как получить число 30 путем сложения ()+()+()=30. Из чисел 1,3,5,7,9,11,13,15. Числа могут овторяться

Пользуйтесь нашим приложением

Задачи 1 ЕГЭ профильная математика



Задачи 1 ЕГЭ профильная математика

MATHM >> ЕГЭ >> ЕГЭ профиль >>

Задача 1

ЗАДАЧА 1
сортировка
по темам

Сложность 1
Сложность 2
Сложность 3

Задачи разделены на уровни сложности.

Задачи из любого уровня вполне реально встретить на настоящем экзамене ЕГЭ, более сложные встретятся если «не повезло».
Сложность 1 (легкие задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

  12. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

    24. посмотреть ответ

    25. посмотреть ответ

    26. посмотреть ответ

    27. посмотреть ответ

    28. посмотреть ответ

    29. посмотреть ответ

    30. посмотреть ответ

    31. посмотреть ответ

    32. посмотреть ответ

    33. посмотреть ответ

  33. посмотреть ответ

    35. посмотреть ответ

    36. посмотреть ответ

    37. посмотреть ответ

    38. посмотреть ответ

    39. посмотреть ответ

    40. посмотреть ответ

    41. посмотреть ответ

    42. посмотреть ответ

    43. посмотреть ответ

    44. посмотреть ответ

    45. посмотреть ответ

    46. посмотреть ответ

    47. посмотреть ответ

    48. посмотреть ответ

    49. посмотреть ответ

    50. посмотреть ответ

    51. посмотреть ответ

    52. посмотреть ответ

    53. посмотреть ответ

  53. посмотреть ответ

    55. посмотреть ответ

    56. посмотреть ответ

    57. посмотреть ответ

    58. посмотреть ответ

    59. посмотреть ответ

    60. посмотреть ответ

    61. посмотреть ответ

    62. посмотреть ответ

    63. посмотреть ответ

    64. посмотреть ответ

    65. посмотреть ответ

    66. посмотреть ответ

    67. посмотреть ответ

    68. посмотреть ответ

    69. посмотреть ответ

    70. посмотреть ответ

    71. посмотреть ответ

  71. посмотреть ответ

  72. посмотреть ответ

    74. посмотреть ответ

    75. посмотреть ответ

    76. посмотреть ответ

    77. посмотреть ответ

    78. посмотреть ответ

    79. посмотреть ответ

    80. посмотреть ответ

    81. посмотреть ответ

    82. посмотреть ответ

    83. посмотреть ответ

    84. посмотреть ответ

    85. посмотреть ответ

    86. посмотреть ответ

    87. посмотреть ответ

    88. посмотреть ответ

    89. посмотреть ответ

  89. посмотреть ответ

    91. посмотреть ответ

Сложность 2 (средние по сложности задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

  12. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

    24. посмотреть ответ

    25. посмотреть ответ

    26. посмотреть ответ

    27. посмотреть ответ

    28. посмотреть ответ

    29. посмотреть ответ

    30. посмотреть ответ

    31. посмотреть ответ

    32. посмотреть ответ

  32. посмотреть ответ

    34. посмотреть ответ

    35. посмотреть ответ

    36. посмотреть ответ

    37. посмотреть ответ

    38. посмотреть ответ

    39. посмотреть ответ

    40. посмотреть ответ

    41. посмотреть ответ

    42. посмотреть ответ

    43. посмотреть ответ

    44. посмотреть ответ

    45. посмотреть ответ

    46. посмотреть ответ

    47. посмотреть ответ

    48. посмотреть ответ

    49. посмотреть ответ

    50. посмотреть ответ

    51. посмотреть ответ

    52. посмотреть ответ

  52. посмотреть ответ

    54. посмотреть ответ

    55. посмотреть ответ

    56. посмотреть ответ

    57. посмотреть ответ

    58. посмотреть ответ

    59. посмотреть ответ

    60. посмотреть ответ

    61. посмотреть ответ

    62. посмотреть ответ

    63. посмотреть ответ

    64. посмотреть ответ

    65. посмотреть ответ

    66. посмотреть ответ

    67. посмотреть ответ

    68. посмотреть ответ

    69. посмотреть ответ

    70. посмотреть ответ

    71. посмотреть ответ

    72. посмотреть ответ

  72. посмотреть ответ

    74. посмотреть ответ

    75. посмотреть ответ

Сложность 3 (более сложные задачи)

    2. посмотреть ответ

    3. посмотреть ответ

    4. посмотреть ответ

    5. посмотреть ответ

    6. посмотреть ответ

    7. посмотреть ответ

    8. посмотреть ответ

    9. посмотреть ответ

    10. посмотреть ответ

    11. посмотреть ответ

    12. посмотреть ответ

    13. посмотреть ответ

    14. посмотреть ответ

    15. посмотреть ответ

    16. посмотреть ответ

    17. посмотреть ответ

    18. посмотреть ответ

    19. посмотреть ответ

    20. посмотреть ответ

    21. посмотреть ответ

    22. посмотреть ответ

    23. посмотреть ответ

    24. посмотреть ответ

    25. посмотреть ответ

    26. посмотреть ответ

    27. посмотреть ответ

    28. посмотреть ответ

    29. посмотреть ответ

    30. посмотреть ответ

    31. посмотреть ответ

    32. посмотреть ответ

    33. посмотреть ответ

    34. посмотреть ответ

    35. посмотреть ответ

Площадь трапеций

Предоставил:

Диего Среда, 16 марта 2022 г. , 06:36 UTC

Этот PDF-файл включает трапецию, основание трапеции, высоту трапеции и площадь трапеции, а также некоторые решенные вопросы для них.

1. Страница 1 из 5
8.6 Площадь трапеций
Цель Напомним, что параллельные стороны трапеции являются основаниями, b1
Найдите площадь названных оснований трапеции, длина которой равна
трапеций. обозначаются b1 и b2. высота
Кратчайшее расстояние между основаниями равно основанию, b2
Ключевые слова высота трапеции .
• трапециевидный с. 332
• основание трапеции с. 332 Предположим, что две конгруэнтные трапеции с основаниями b1 и b2 и высотой
h образуют параллелограмм, как показано на рисунке.
• высота трапеции
b1 b2
h
b2 b1
Справка для учащихся Площадь параллелограмма равна h(b1 1 b2). Поскольку две трапеции
конгруэнтны, площадь одной из трапеций составляет половину площади параллелограмма
ОБРАТНО.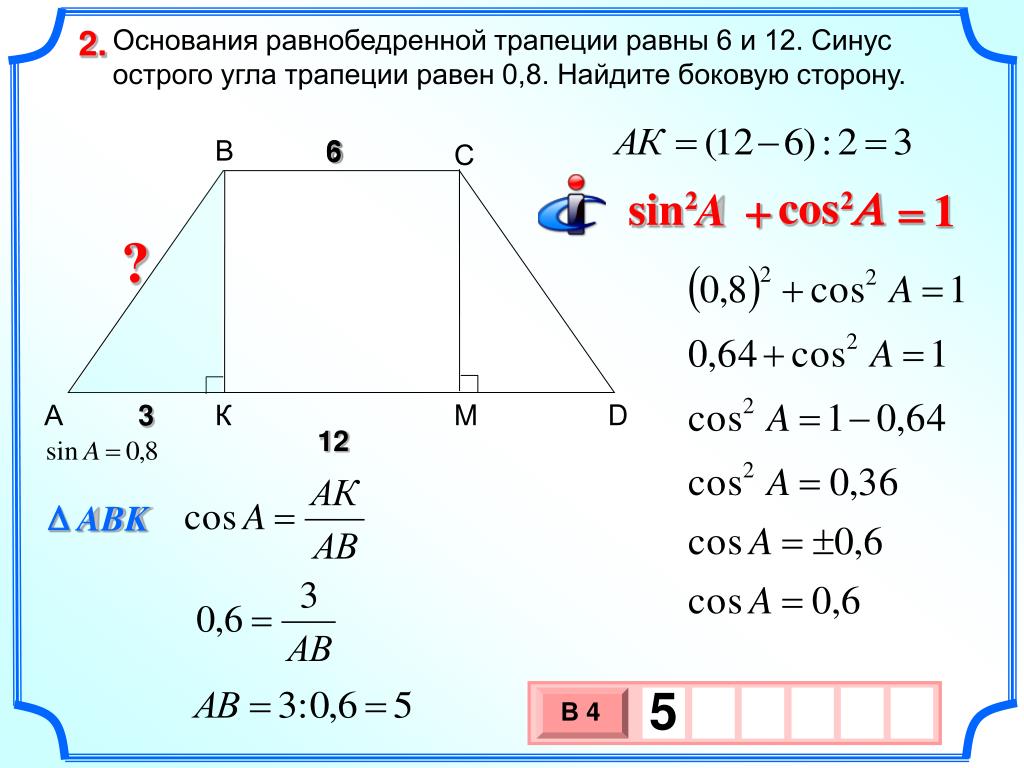
Чтобы узнать больше о трапециях
, см. стр. 332.
ПЛОЩАДЬ ТРАПЕЦИИ
1
Слова Площадь 5 }}(высота)(сумма оснований)
2
b1
1
Символы A 5 }}h(b1 1 b2)
2
b2
ПРИМЕР 1 Найдите площадь трапеции
Найдите площадь трапеции. 6 дюймов
Решение 8 дюймов
1
A 5 }}h(b1 1 b2) Формула площади трапеции
2
1
5 }}(5)(6 1 8) Подставим 5 вместо h, 6 для b1 и 8 для b2.
2
1
5 }}(5)(14) Упростить в скобках.
2
5 35 Упрощение.
ОТВЕТ © Площадь трапеции 35 квадратных дюймов.
446 Глава 8 Многоугольники и площади

2. Страница 2 из 5
Площадь трапеций
Найдите площадь трапеции.
1,7 м 2,16 футов 3,8 см
7 м 14 футов 5 см
12 см
11 м 10 футов
ПРИМЕР 2 Использование площади трапеции
Найдите значение b2, учитывая, что площадь 9м
трапеции равна 96 квадратных метров.
A 5 96 м2
Помощь учащимся b2
СОВЕТ ДЛЯ ИЗУЧЕНИЯ Решение
Уравнение проще
решить без формулы 1
A 5 }}h(b1 1 b2) для площади дроби трапеции
. Итак, перед числом
умножьте 2 
с каждой стороны на 2.распространение. 1
96 5 }}(8)(9 1 b2) Замените A на 96, h на 8 и b1 на 9.
2
192 5 8(9 1 b2) Умножьте каждую сторону на 2.
192 5 72 1 8b2 Используйте свойство распределения.
120 5 8b2 Вычтите 72 с каждой стороны.
15 5 b2 Разделите каждую сторону на 8.
ОТВЕТ © Значение b2 равно 15 метрам.
Использование площади трапеции
A дает площадь трапеции. Найдите недостающую меру.
4. A 5 77 футов2 5. A 5 39 см2 6. A 5 84 дюйма2
b1 13 дюймов
8 футов
h 6 см 8 дюймов
14 футов 8 см b2
7. Трапеция имеет площадь площадью 294 кв. Его высота 14 ярдов
, а длина одного основания 30 ярдов. Найдите длину другого основания
.
8.6 Площадь трапеций 447

3. Страница 3 из 5
8. 6 Упражнения
Практические занятия
Проверка словарного запаса 1. Нарисуйте трапецию. Обозначьте его высоту h и основания b1 и b2.
Проверка навыков Найдите высоту и длину оснований трапеции.
2. 3. 9 4.
7 11
13 12 10
6 8
3 7 5 19 6
Сопоставьте трапецию с уравнением, используемым для нахождения высоты.
1 1 1
A. A 5 }}h(5 1 13) B. A 5 }}h(8 1 13) C. A 5 }}h(5 1 8)
2 2 2
5. 5 6. 5 7. 8
h h h
8 5 8 13
Практика и применение
Дополнительная практика Площадь трапеции Найдите площадь трапеции.
См. с. 690. 8. 9. 10.
11 6 7
7 8
16
15 10
24
11. 12. 6.2 13.
14 15
13 19 4.6
8 14 8
4.4
Помощь в домашних условиях 14. Вы станете судьей, одноклассником. 6 9
, что если вы удвоите размеры
Пример 1: Exs. 8–13 6
Пример 2: Exs. 18–22 трапеции справа, то ее площадь удваивается.
Вы согласны? Поясните свой ответ.
9
448 Глава 8 Многоугольники и площади

4. Страница 4 из 5
15. Визуализируй это! Начертите три различные трапеции высотой
5 единиц и основаниями 3 и 7 единицами. Затем найдите площади
трапеций. Что ты заметил?
Технология помощи учащимся В упражнениях 16 и 17 используйте программное обеспечение для геометрии.
ПОСМОТРЕТЬ НАЗАД ●
1 Нарисуйте трапецию.
Для просмотра ●
2 Нарисуйте средний сегмент. B
средний сегмент A
трапеция, см. с. 333. 16. Найдите длину середины отрезка и F
высоту трапеции. Умножьте E
C
на две меры. D
17. Найдите площадь трапеции. Как площадь
соотносится с вашим ответом на
в упражнении 16?
Использование алгебры В упражнениях 18–20 A дает площадь трапеции
. Найдите недостающую меру.
18. А 5 135 см2 19. A 5 132 дюйма2 20. A 5 198 м2
b1 7 дюймов b2
10 см h 12 м
18 см 17 дюймов 15 м
I Справка для студентов 21. Площадь трапеции равна 50 квадратных единиц. Длина баз
ICLASSZONE.COM составляет 10 единиц и 15 единиц. Найдите высоту.
ПОМОЩЬ С ДОМАШНИМ ЗАДАНИЕМ
22. Площадь трапеции равна 24 квадратных единиц. Высота 3 единицы
Дополнительная помощь с задачей
и длиной одного из оснований 5 единиц. Найдите длину решения
в упр. 21–22 — это
на classzone.com
другая база.
Мосты В упражнениях 23–25 используйте следующую информацию.
Крыша моста внизу состоит из четырех сторон: двух конгруэнтных
трапеций и двух конгруэнтных треугольников.
137 футов 13 футов 2 дюйма
159 футов
Крытый мост через реку Доу в Элизабеттоне, штат Теннесси
23. Найдите общую площадь двух трапеций.
13 футов 7 дюймов.
24. Используйте диаграмму справа, чтобы найти
объединенную площадь двух треугольников.
21 фут
25. Какова площадь всей крыши? Деталь крыши
8.6 Площадь трапеций 449

5. Страница 5 из 5
Помощь учащимся Окна Найдите площадь окна.
ВИЗУАЛЬНАЯ СТРАТЕГИЯ 26. 16 дюймов 27. 28. 9 дюймов
Чтобы найти площадь сложного многоугольника 12 дюймов
, вы 12 дюймов
30 дюймов
можете добавить площади 21 дюймов
32 дюйма. 16 дюймов
более простые формы, которые 12 дюймов
составляют многоугольник,
16 дюймов 48 дюймов 20 дюймов
, как показано на стр. 410.
Используя теорему Пифагора Найдите высоту, используя
теорему Пифагора и калькулятор. Затем найдите площадь
трапеции.
29. 28 30. 100 31.
ч 17
ч 40 91 ч
11 25 8
24 35 120
Стандартизированный тест 32. Множественный выбор Какова площадь трапеции?
Практика X
A 25 дюймов2 X
B 42 дюйма2 8 дюймов
68 дюймов2 84 дюйма2 4 дюйма
X
C X
D
13 дюймов
33. Множественный выбор Какая площадь из трапеции?
X
F 88 ft2 X
G 128 ft2 16 ft
X
H 152 ft2 X
J 176 ft2 8 ft
6 ft
Смешанный обзор Область поиска Сопоставьте регион с формулой для его площади. Используйте каждую формулу
ровно один раз. (Уроки 8.3 – 8.6)
34. Область 1 A. A 5 s2
1
35. Область 2 B. A 5 }}d1d2 1
2
1 2
36. Область 3 C. A 5 }}bh
2 5
3
1
37. Область 4 D. A 5 }}h(b1 1 b2)
2 4
38. Область 5 E A 5 bh
Алгебра Навыки Действия с дробями Сложение и вычитание. Запишите ответ в виде дроби
в простейшей форме. (Обзор навыков, стр. 658)
3 5 5 2 3 1 4 1
39. }} 1 }} 40. }} 2 }} 41. }} 1 }} 42. }} 2 }}
8 8 9 9 4 12 7 5
450 Глава 8 Многоугольники и площадь

Площадь a Калькулятор трапеций [Простой в использовании + руководство по результатам]

a(основание)

b(основание)

h(высота)

Вернуться на страницу калькуляторов

двусторонняя геометрическая фигура. У него две параллельные стороны, а оставшиеся две стороны могут быть любой длины и под любым углом. Некоторые возможные формы трапеций показаны ниже, чтобы прояснить концепцию. Обратите внимание, что параллельные линии отмечены стрелками.

В реальной жизни существует множество объектов трапециевидной формы, которые вы могли не замечать. См. несколько примеров ниже. Вы удивлены?

Теперь, когда вы разобрались с формой трапеции, давайте обсудим параметры, которые вам нужно знать, чтобы найти ее площадь. Чтобы найти площадь трапеции, необходимо знать три важные длины: длины двух параллельных сторон «а» и «b» и высоту. Высота — это перпендикулярное расстояние между двумя параллельными сторонами. Под перпендикулярным расстоянием мы подразумеваем, что длина линии, соединяющей параллельные стороны «а» и «b», равна ровно 90 градусов им.

Площадь трапеции, A , определяется как:

Эта формула получена из понятия площади треугольника. Возможно, вы уже знаете, как вычислить площадь треугольника, но мы кратко рассмотрим его на тот случай, если вы забыли или не знаете. Два параметра, которые вам нужно знать, чтобы найти площадь треугольника, — это высота треугольника и основание треугольника. Высота треугольника определяется как расстояние по перпендикуляру от одного угла треугольника до уровня основания. Какую бы сторону треугольника вы ни выбрали в качестве «основания», измерьте высоту, считая угол, точно противоположный основанию. См. диаграммы ниже для большей ясности концепции высоты-базы.

Не запутайтесь, если форма треугольника отличается от той, которую вы обычно ожидаете. Помните о концепции основания и высоты и маркируйте соответственно.

Площадь треугольника определяется как:

Теперь, как это знание поможет нам вычислить формулу площади трапеции? Давайте посмотрим.

Посмотрите внимательно, и вы заметите, что трапецию можно разрезать по диагонали, чтобы образовались два треугольника:

Если мы найдем площади этих двух треугольников, а затем сложим их, мы получим площадь всей трапеции! Основание верхнего треугольника равно длине «а», а основание нижнего треугольника равно длине «b». Высота обоих треугольников одинакова.

Площадь верхнего треугольника равна:

Площадь нижнего треугольника равна:

Следовательно, площадь трапеции будет:

Принимая {2}\) в качестве общего множителя получаем:

Надеюсь, теперь вы полностью понимаете концепцию формулы площади трапеции. Давайте сделаем несколько примеров.

Пример 1:

Найти область трапеции, приведенная ниже:

Решение:

Из рисунка мы видим:

. 9 см

h = 5 см

Пусть площадь трапеции представлена ​​переменной ‘A’

А = ?

Примените формулу площади трапеции:

Пример 2:

Чему равно расстояние по перпендикуляру между двумя параллельными сторонами?

Решение:

Заданы следующие параметры:

Параллельная сторона 1 = a= 16 см

Параллельная сторона 2 = b= 12 см

Площадь трапеции = A = 98 см 2

Нам нужно найти расстояние по перпендикуляру между двумя параллельными сторонами. Как мы упоминали ранее в статье, это высота трапеции.

ч = ?

Вспомните формулу площади трапеции и найдите «h».

Теперь подставляем известные значения и находим высоту:

Пример 3:

Площадь приведенной ниже трапеции равна 100 см 2 . Найдите неизвестную длину параллельной стороны а.

Решение:

Одна сторона этой трапеции образует угол 90 градусов с обеими параллельными сторонами. Это означает, что высота трапеции и длина этой стороны одинаковы. Нам дается следующая информация:

Площадь трапеции = A = 100 см 2

Высота = h = 10 см

Параллельная сторона 2 = b = 11 см

Параллельная сторона 1 = a = ?

Чтобы найти «а», мы преобразуем формулу площади трапеции, чтобы найти «а»:

Теперь подставьте известные значения, чтобы получить окончательный ответ:

Заключительные мысли!

Мы попытались охватить почти все, что нужно знать о площади трапеции, от ее вывода до решения различных задач.