Определение точки максимума и минимума функции: Найдите точку максимума и точку минимума функции y=f(x),если известно ,что f'(x)=x^2-5x+6

Точки экстремума функции, необходимые и достаточные условия экстремума

Содержание:

• Необходимое условие экстремума
• Первое достаточное условие экстремума
• Второе достаточное условие экстремума

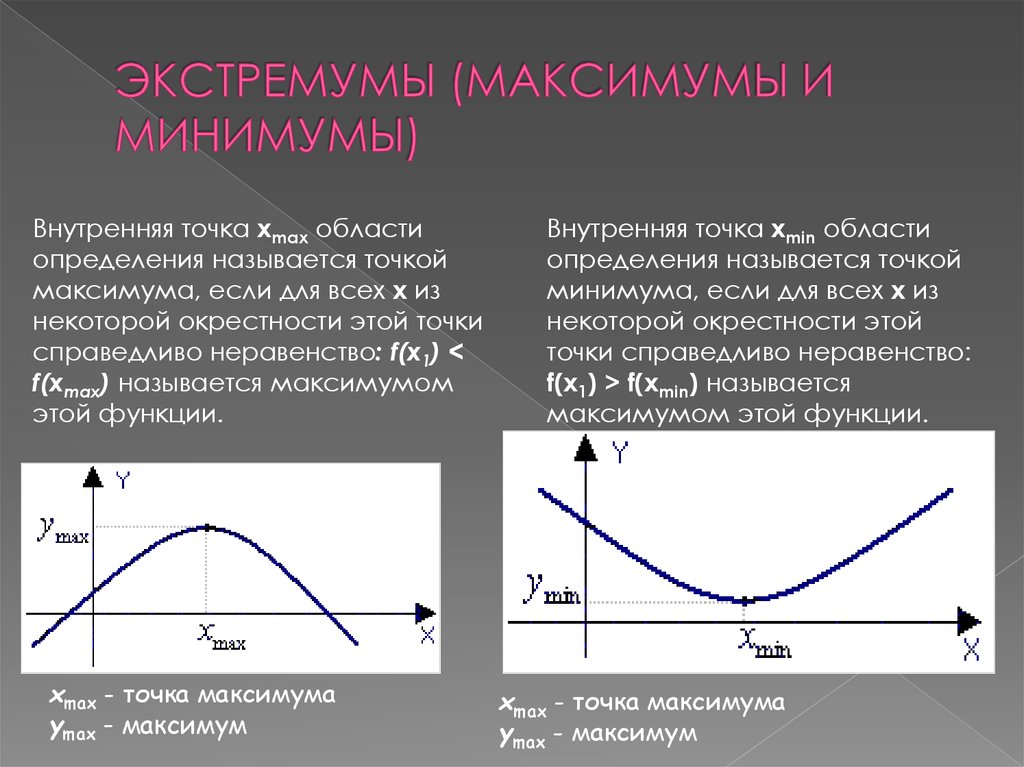
Определение

Точка $x_{0}$ называется точкой локального максимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности выполняется неравенство: $f(x) \leq f\left(x_{0}\right)$.

Точка $x_{0}$ называется точкой локального минимума функции $f(x)$, если существует такая окрестность этой точки, что для всех $x$ из этой окрестности $f(x) \geq f\left(x_{0}\right)$.

Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума — локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.

Точка $x_{0}$ называется точкой строгого локального максимума

функции $y=f(x)$, если для всех $x$ из окрестности этой точки будет справедливо строгое неравенство $f(x) \lt f\left(x_{0}\right)$. {2}+1}=-1$.

Ответ. $y_{\min }=y(0)=-1$

Остались вопросы?

Здесь вы найдете ответы.

Что подразумевается под понятием «экстремум»?

Экстремум представляет собой значение функции на определенном интервале в момент достижения им минимального или максимального показания. Под понятием «экстремумы» или по-другому минимумы/максимумы подразумевается значение функции (у).

Точка экстремума – что это такое?

Если в определенной точке достигается экстремум или, иными словами, максимальное/минимальное значение функции на заданном интервале, то эта точка носит название точки экстремума. Из этого следует, что при достижении минимума, точка экстремума будет названа точкой минимума, и, наоборот, при достижении максимума эта точка будет называться точкой максимума. В случае, когда указываются точки экстремумов (или минимумов/максимумов) подразумеваются иксы, в которых достигаются минимальные или максимальные значения.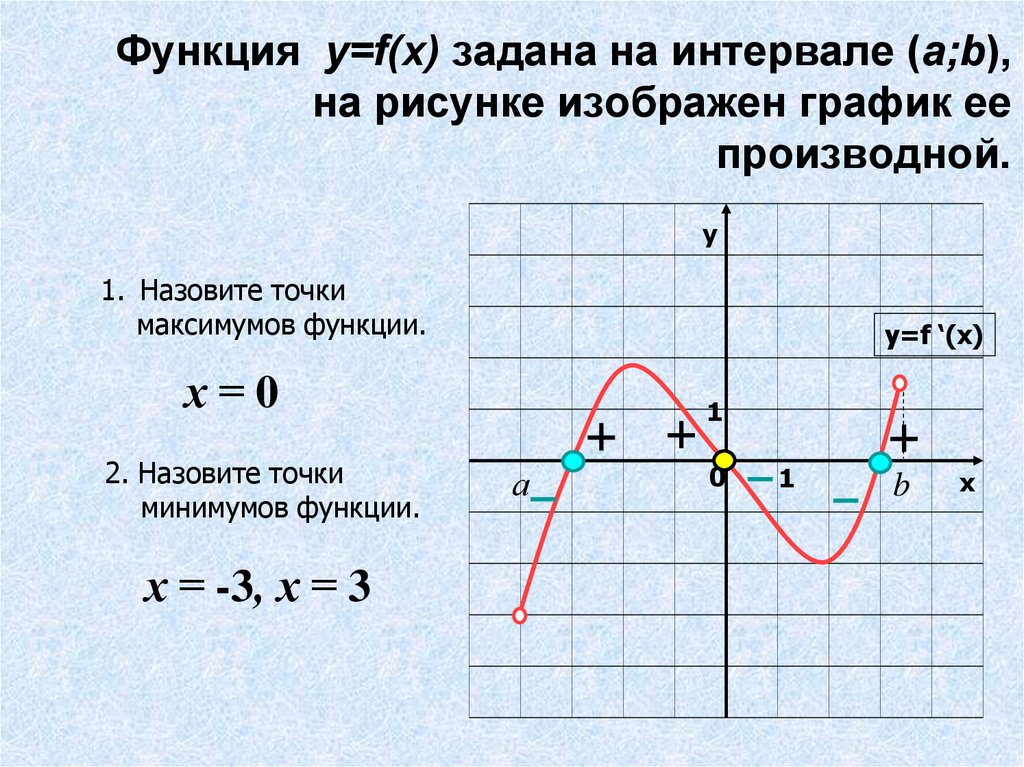

Что имеется в виду под понятием «точка минимума функции»?

Любая точка x₀ будет определена в качестве точки минимума функции y = f(x) при соблюдении условия о том, что имеется такая V, представляющая собой окрестность (x₀ — V; x₀+V) упомянутой ранее точки, из которой для каждого значения x x₀ действительно следующее неравенство:

f(x)>f(x₀).

Как описать точку минимума функции?

Под понятием «минимум функции» имеется в виду та точка на ней, в которой функция имеет значение, являющееся наименьшим среди всех значений, приобретаемых ею в любой из других соседних точек. Другими словами, это означает, что в случае, когда функция, достигнув определенной точки, прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и представляет собой точку ее минимума.

Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она достигает в точке своего минимума?

Для ответа на поставленный вопрос нужно отыскать точку минимума указанной функции, в которой ее значение перестает падать.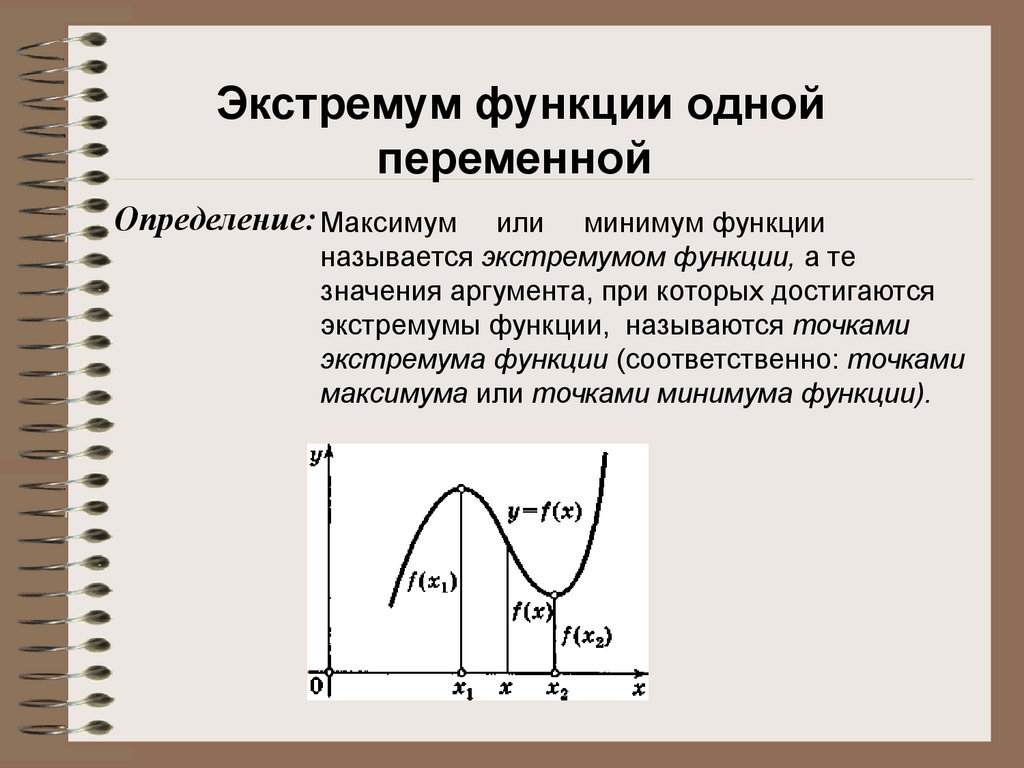 Это можно сделать следующим образом:

y’ = 4x³ — 12x² + 12x – 4

Предположив, что минимальное значение данной функции равно 0, можно переписать равенство в следующем виде:

4x³ — 12x² + 12x — 4 = 0

Сократим данное уравнение на 4:

x³ — 3x² + 3x — 1 = 0

Получившееся равенство также может быть записано в следующем виде после перемены местами слагаемых:

(x³ — 1) + (-3x² + 3x) = 0

Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:

(x — 1)(x² + x + 1) -3x(x — 1) = 0

Это же уравнение может выглядеть так:

(x -1)(x² + x + 1- 3x) = 0

Произведем сложение слагаемых х и -3х:

(x — 1) (x² -2x + 1) = 0

Теперь для упрощения можно переписать уравнение в таком виде:

(x — 1)(x-1)² = 0

Получившееся равенство:

(x — 1)³ = 0

В этом случае х = 1

-∞ 1 +∞

Знаками «+» и «-» обозначены значения производной.

После проведенных вычислений было установлено, что х = 1, что является точкой минимума функции:

у = 1⁴- 4*1³ + 6*1² — 4*1 = 1 — 4 +6 — 4 = -1

Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для функции y = -x/x²+484?

Точкой максимума называется то значение х, достигнув которого, производная начинает менять свой знак с плюса на минус.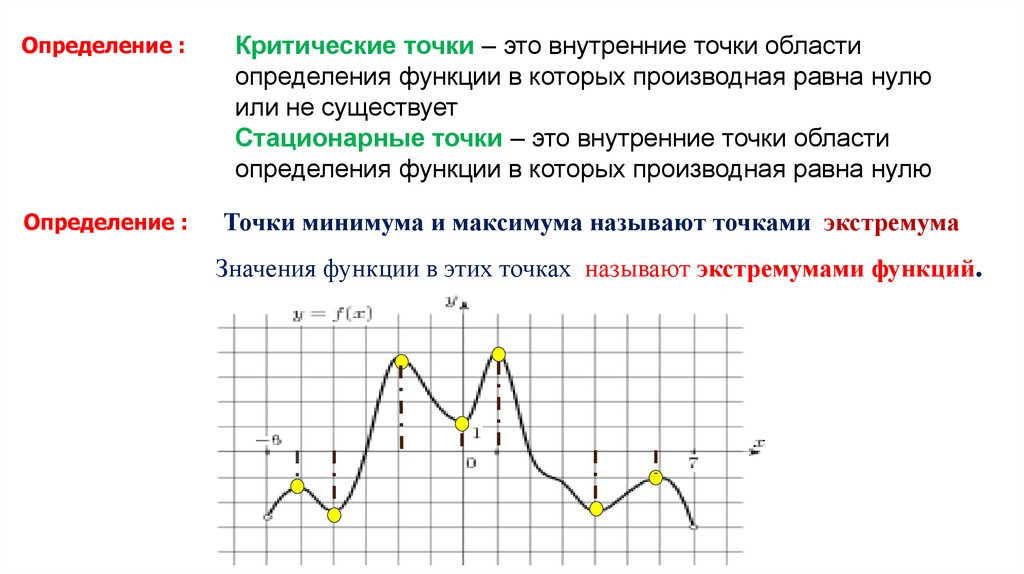 Зная это, можно перейти к поиску точки максимума для функции, указанной в задании.

Для этого нужно начать с поиска производной, используя следующую формулу:

(U/V)’ = (U’V — UV’)/V²

Подставляем приведенные в задании значения и получаем:

y’ = (-(x² + 484) — 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²

Теперь следует приравнять производную к 0 и начать решать получившееся уравнение:

(-x²-484 -2x)/(x² +484)² = 0

Упростим уравнение и получим:

(-x²-484 -2x) = 0

(x² +484)² ≠ 0

-x²-484 -2x = 0

Избавимся от минусов в уравнении:

x² + 2x +484 = 0

D

В результате вычислений стало ясно, что корней нет. Это значит, что невозможно поставить их на числовой прямой, для того чтобы проверить знаки производной по соседству с этими точками. На основании этого можно сделать вывод о том, что указанная в задании функция не имеет точек экстремума.

Что представляет собой точка максимума функции?

Под точкой максимума функции понимается та точка, в которой она достигает значения, являющегося наибольшим среди тех значений, что достигаются ею в соседних точках. Это означает, что в точке, при пересечении которой функция прекращает расти, и наблюдается ее падение, и достигается ее максимум.

Имеется график производной функции. Каким образом можно вычислить точки ее максимума и минимума?

В случае, если имеется график производной функции, и при этом требуется определить ее экстремумы, то необходимо вычислить точки пересечения этого графика производной с осью Ох. По-другому они называются «нулями» производной. В случае, когда, пересекая конкретную точку, график производной восходит из области со знаком «-» в область со знаком «+», и в это время производная меняет свой знак на противоположный, функция также изменяется с убывания на рост. В этом случае данная точка, которая пересекается графиком производной, представляет собой точку минимума. Если же при пересечении графиком производной какой-либо точки он идет из положительной в отрицательную область, а функция из возрастания меняется на убывание, то речь идет о точке ее максимума.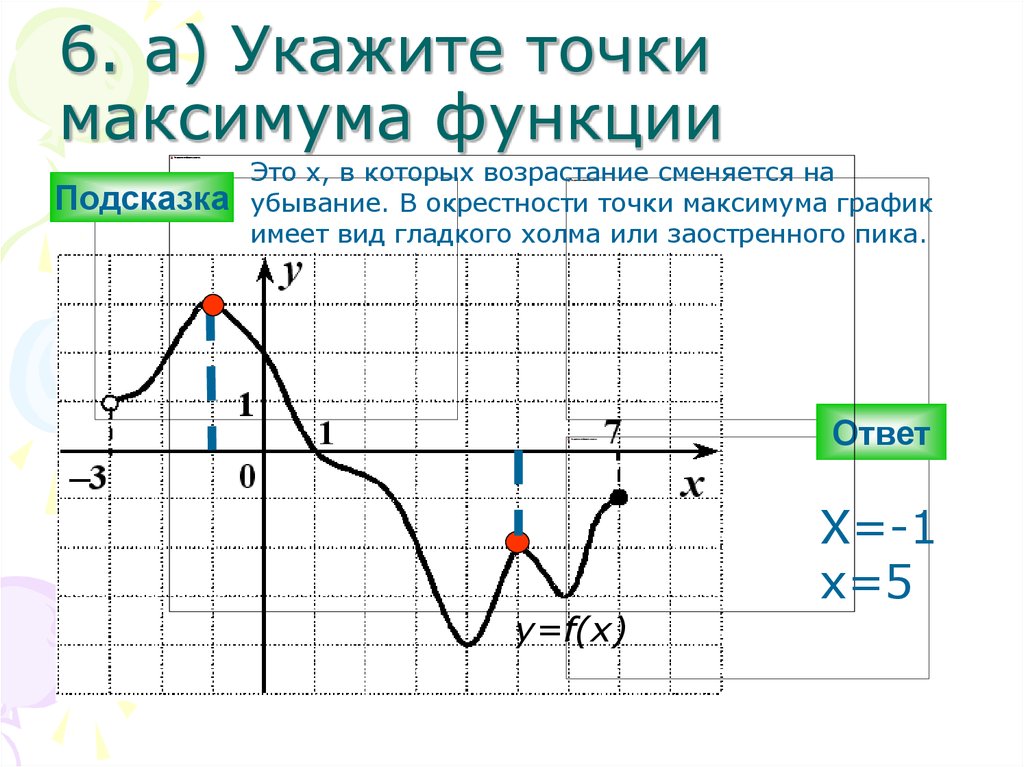

Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?

Для того чтобы найти ответ на поставленный вопрос, сначала нужно приравнять функцию к 0:

у = 0

Это же означает, что:

4X⁴ + 2X² + 1 = 0

Введем обозначения:

Х2 = А, при этом А больше 0.

С учетом введенных обозначений равенство будет иметь следующий вид:

4A² + 2A + 1 = 0

D = 4 — 4 = 0 ; √ D = 0

A = (- 2) : 4 = (- 0,5) (

Очевидно, что корней нет.

Ответ: х = 0, у = 1.

Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?

Имеется функция y = x² -3x+2, которую также можно переписать в следующем виде:

у = -0,25+ (x-1,5)²

Отсюда следует, что:

miny = — 0,25 при условии, что х-1,5 = 0

Можно сделать вывод о том, что х = 1,5.

Запишем производную данной функции:

y ‘= (x² -3x+2)’ =2x -3

А затем приравняем ее к 0:

y ‘ = 0, значит:

2x -3 = 0.

Это позволяет сделать вывод о том, что:

x = 3/2.

Получается, что, если x

Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.

x =3/2=1,5 – это единственная точка экстремума, которая является точкой минимума.

miny =(1,5)² -3*1,5+2 = -0,25.

Как раскрыть понятие «критическая точка функции»?

Критическая точка функции представляет собой ту точку, при пересечении с которой производная данной функции становится равной 0, либо она вовсе не существует.

Возможно ли привести доказательства того, что функция f(x) =2x — 3/x не может иметь критической точки?

Для начала нужно определить, что под критической точкой функции подразумевается та точка, при пересечении с которой производная приобретает нулевое значение, либо же эта производная просто не существует в этой точке, что означает, что функцию в данной точке невозможно дифференцировать.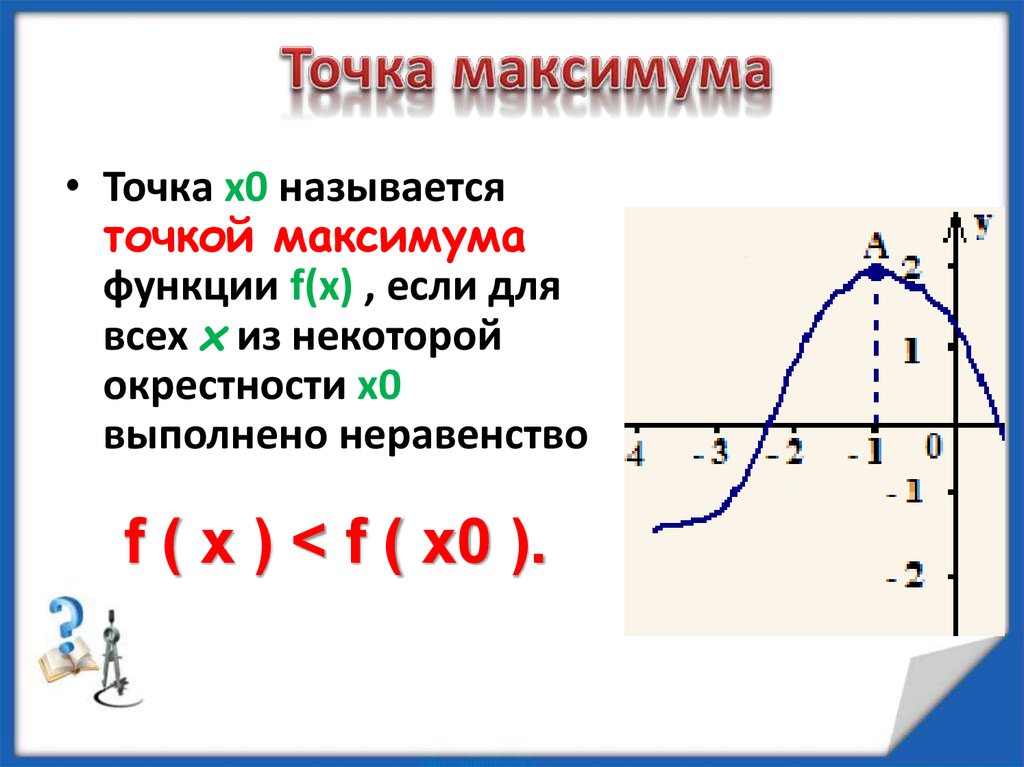

Проверим, применимо ли это утверждение к упомянутой в задании функции:

f ‘(x) =(sin2x — 3x)’ = 2sin2x-3

Приравняем производную функции к 0:

f ‘(x) = 0, это значит, что 2sin2x-3 = 0.

Следовательно:

sin2x= 3 2 не имеет решения

Ответ: заданная функция не имеет критических точек и существует при любых х.

Каким способом можно определить критические точки функции y=|x|/1+x²?

Под критическими точками функции понимаются те точки, в которых ее производная равна 0 или вовсе не существует.

В задании дана функция:

y=|x|/(1+x²)

Предположим, что x

y=-x/(1+x²)

Запишем производную функции и приравняем ее к 0:

y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0

х = 1 не соответствует условию, значит х = -1.

Теперь предположим, что x≥0.

Снова записываем производную имеющейся функции и приравниваем ее к 0:

y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0

х = — 1 не отвечает условию, значит х = 1.

Ответ: х = 1, х = -1.

Читать дальше: наибольшее и наименьшее значение функции.

Максимум, минимум и экстремумы функции. Необходимое условие существования экстремума.

Главная

» Общенаучные дисциплины

» Математика (1 семестр)

» Максимум, минимум и экстремумы функции. Необходимое условие существования экстремума.

Приведем точные определения точек экстремума. 

Определение. Точка x₀ называется точкой минимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≥ f(x₀.  

Это наглядно показано на рисунке 1: 

 
рисунок 1 

Определение. Точка x₀ называется точкой максимума функции f, если для всех x из некоторой окрестности x₀ выполняется неравенство f(x) ≤ f(x₀. 

Это наглядно показано на рисунке 2: 

 
рисунок 2 

По определению значение функции f в точке x₀ является наибольшим среди значений функции в окрестности этой точки, поэтому график функции в окрестности x₀ имеет обычно либо вид гладкого холма, либо вид острого пика (рис. 1 а) и б) соответственно). 

В окрестности точки минимума графики изображаются в виде загругленной или острой впадины (рис. 2 а) и б) соответственно). 

Другие примеры поведения графиков функций в точках максимума и минимума приведены на рисунке ниже: 

 

Слева направо: a — точка максимума; a — точка минимума; каждая точка из промежутка [-1; 0] является как точкой максимума, так и точкой минимума.  

Для точек минимума и максимума функции есть общее определение — точки экстремума. Значение функции в этих точках соответственно назывется максимумом или минимумом этой функции. Общее название — экстремум функции. Точки максимума обычно обозначают x_max, а точки минимума — x_min.

• Лемма Ферма. Пусть функция  дифференцируема в точке экстремума x₀. Тогда:

f‘(x₀) = 0.

• Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

 

---

Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.

Поиск по сайту

Поделиться

Дисциплины

• Информационные системы
• Проектирование ИС
• Интеллектуальные ИС
• Информационная безопасность и защита информации
• Информационные сети
• Моделирование систем
• Администрирование в ИС
• Информационные технологии
• Операционные системы
• Представление знаний в ИС
• Алгоритмизация
• Архитектура ЭВМ
• Управление данными
• Технология программирования
• Компьютерная геометрия и графика
• Информатика
• Агрегатор онлайн-курсов

• Самолетостроение
• Конструкция и проектирование самолетов
• Автоматизированное проектирование конструкций
• Основы теории управления
• Теория информационных процессов и систем
• Электротехника
• Физика
• Физика (3 семестр)
• Прикладная механика

• Общенаучные дисциплины
• Экономика
• Метрология
• Философия
• Математика (1 семестр)
• Математика (2 семестр)
• Математика (3 семестр)
• Культурология
• История
• Химия
• Биология
• Английский язык онлайн – быстро и просто
• Что делать, если по учёбе гора долгов?
• Помощь в поступлении в американский ВУЗ от Марии Гурьевой
• Полиграфическая продукция
• Бизнес школа
• Пожарная безопасность: виды инструктажей и требования
• Где записаться на курсы режиссуры монтажа?
• Особенности подготовки к ОГЭ по канадской методике
• Обучение профессии полиграфолога
• ПОИСК ЛУЧШИХ КУРСОВ В СЕТИ в сфере digital
• Курсы подготовки к ЕГЭ 2022 для 10-11 классов в Москве

---

Как найти максимальное и минимальное значение функции

Следующие шаги были бы полезны, чтобы найти максимальное и минимальное значение функции, используя первую и вторую производные.

Шаг 1: 

Пусть f(x) — функция. Найдите первую производную от f(x), которая равна f'(x).

Шаг 2 : 

Приравняйте первую производную f'(x) к нулю и найдите x, которые называются критическими числами.

Шаг 3 : 

Найдите вторую производную от f(x), которая равна f»(x). 

Шаг 4: 

Подставьте критические числа, найденные на шаге 2, во вторую производную f»(x).

Шаг 5:

Если f»(x) < 0 для некоторого значения x, скажем, x = a , то функция f(x) максимальна при x = a.

Если f»(x) > 0 для некоторого значения x, скажем, x = b, то функция f(x) минимальна при x = b. 

Шаг 6: 

Чтобы получить максимальное и минимальное значения замена функции x = a и x = b в f(x). 

Максимальное значение = f(a)

Минимальное значение = f(b)

Пример 1 :

Определить максимальное значение функции:

f(x) = 4x — x ² + 3

0 Найти решение первая производная f(x).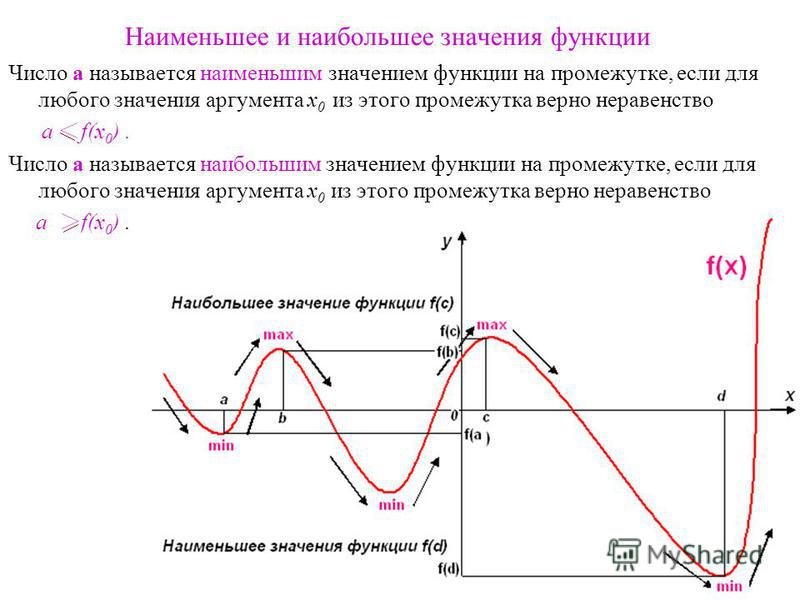

f'(x) = 4(1) — 2x + 0

= 4 — 2x

Приравняем первую производную к нулю, то есть f'(x) = 0.

4 — 2x = 0

2(2 — x) = 0

2 — x = 0

x = 2

Найдите вторую производную f(x).

f'(x) = 4 — 2x

f»(x) = 0 — 2(1)

f»(x) = -2

Подставить критическое число x = 2 в f»(x) .

f»(2) = -2 < 0

Итак, f(x) максимальна при x = 2.

Чтобы найти максимальное значение, подставьте x = 2 в f(x).

f(2) = 4(2) — 2 ² + 3

= 8 — 4 + 3

= 11 — 4

= 7

Следовательно, максимальное значение функции ) равно 7.

Обоснование :

Мы можем обосновать наш ответ, построив график функции f(x).

f(x) = 4x — x ² + 3

Данная функция является уравнением параболы. Замените f(x) на y.

y = -x ² + 4 x + 3

Запишите приведенное выше уравнение параболы в вершинной форме.

y = -(x ² — 4 x — 3)

y = -[x ²  — 2(x)(2) + 2 ²  — 2 ² 0 — 0 4] 9 0 0 4] = -[(x — 2) ²  — 4 — 3]

y = -[(x — 2) ²  — 7]

y = -(x — 2) ²  + 7

Приведенное выше уравнение имеет вид y = a(x — h) ²  + к.

a = -1

Вершина (h, k) = (2, 7)

Поскольку ‘a’ отрицательно, парабола раскрывается вниз. Итак, у нас есть только максимальное значение y, то есть координата y в вершине, равная 7.

Ответ обоснован.

Пример 2:

Определить максимальное и минимальное значения функции:

f(x) = 2x ³ + 3x ² — 36x + 1

Решение:

Найдите первую производную f(x).

f'(x) = 2(3x ² ) + 3(2x) — 36(1) + 0

= 6x ²  + 6x — 36 f'(x) = 0,

6x ²  + 6x — 36 = 0

Разделите обе части на 6.

x ²  + x — 6 = 0

Разложите на множители и решите.

(х — 2)(х + 3) = 0

х — 2 = 0 х = 2

х + 3 = 0 х = -3

Найдите вторую производную f(x).

f'(x) = 6x ² + 6x — 36

f»(x) = 6(2x) + 6(1) — 0

f»(x) = 12x + 6

Замена критические числа х = 2 и х = —3 в f»(x).

f»(2) = 12(2) + 6 = 24 + 6 = 30 > 0

f»(-3) = 12(-3) + 6 = -36 + 6 = -30 < 0

При x = 2, f»(x) > 0, функция f(x) минимальна при

x = 2 

При x = -3, f»(x) > 0, функция f (x) максимально при

x = -3

Чтобы найти максимальное и минимальное значения данной функции, подставьте x = -3 и x = 2 в f(x).

Максимальное значение:

f(-3) = 2(-3) ³  + 3(-3) ²  — 36(-3) + 1

= 2(-27) + 3(9) + 108 + 1

= -54 + 27 + 108 + 1

= 82

Минимальное значение:

f(2) = 2(2) ³  + 3(2) ²  — 36(2) + 1

= 2(8) + 3(4) — 72 + 1

= 16 + 12 — 72 + 1

= -43

Пожалуйста отправьте свой отзыв на v4formath@gmail.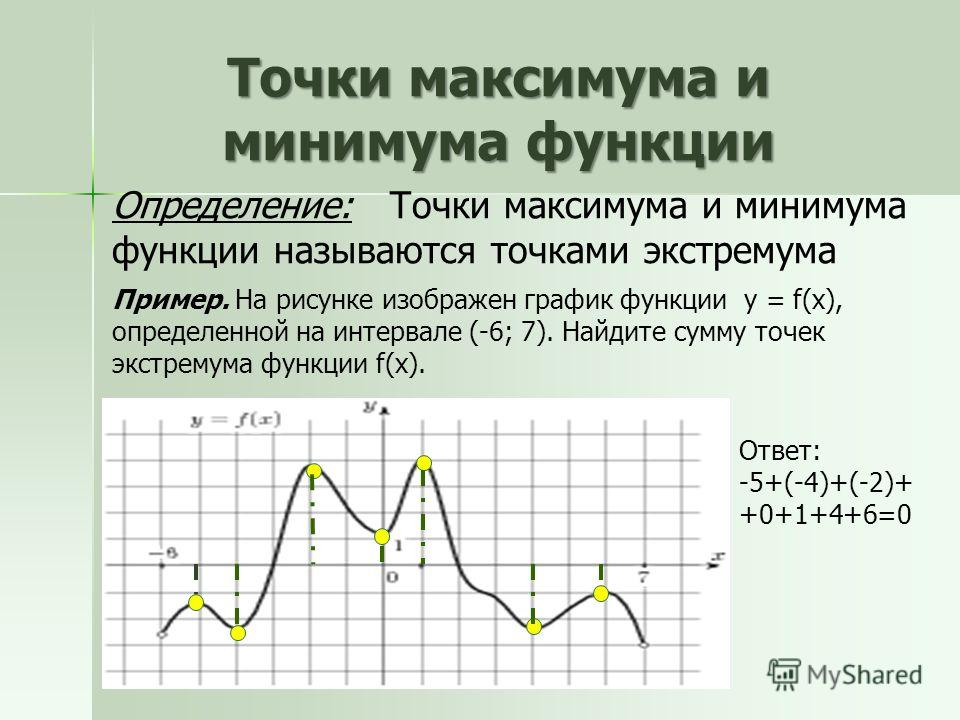 com

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Максимумы и минимумы | Superprof

Найти максимумы и минимумы на графике легко, если вы правильно понимаете. На самом деле нахождение относительных максимумов и относительных минимумов также со временем становится простым. Однако не у всех есть столько времени, чтобы нарисовать график только для того, чтобы вычислить максимумы и минимумы. Например, у исследователей не так много времени, они ищут короткие пути, один из коротких путей нахождения максимумов и минимумов — с помощью исчисления.

Исчисление — это раздел математики, а также один из наиболее часто используемых и наиболее сложных разделов. На самом деле, если вы студент инженерного факультета, вы знаете, насколько важен расчет. Исчисление используется для многих целей, и одна из них — найти максимальные и минимальные точки на графике. Использование дифференциалов может быть сложным, но как только вы поймете это правильно, вы сможете найти максимальное количество очков в кратчайшие сроки.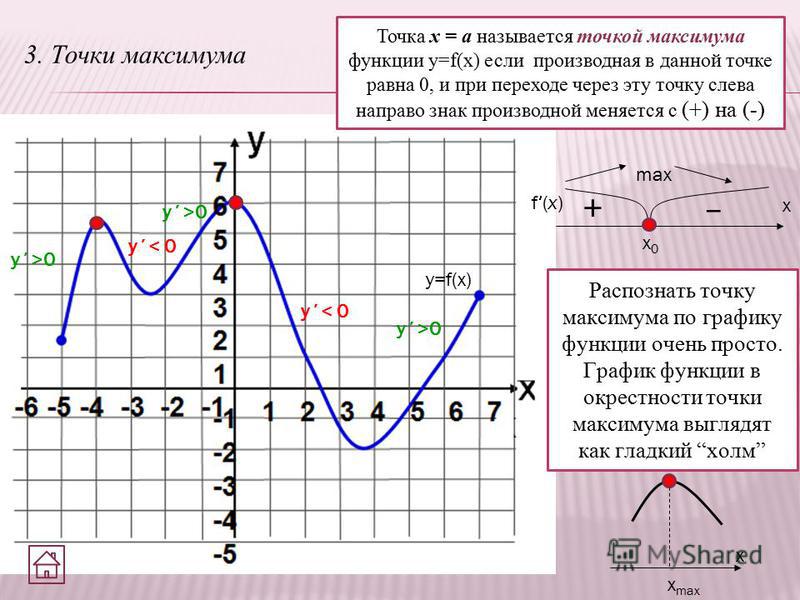

Допустим, у вас есть функция, дифференцируемая в точке и . Прежде чем найти максимальные точки, исчисление позволяет вам проверить, имеет ли функция максимальную точку / точки или нет? Точка «а» является локальным экстремумом, если:

Это означает, что при дифференцировании функции первая степень будет положена равной нулю. Информация, которую вы получите, является поворотной точкой графика. Это будет означать, что в этот момент график поворачивает свой курс. Эта информация ценна, но мы здесь не для того, чтобы найти точку поворота, мы хотим найти точки максимума и минимума. Чтобы получить эту информацию, вам нужно взять другую производную. Производная второго порядка будет определять, имеет ли функция точку максимума, минимума или и то, и другое.

Локальный максимум

Метод определения максимума и минимума одинаков. Сначала нужно продифференцировать функцию, а затем приравнять ее к нулю. Найдите значение переменной.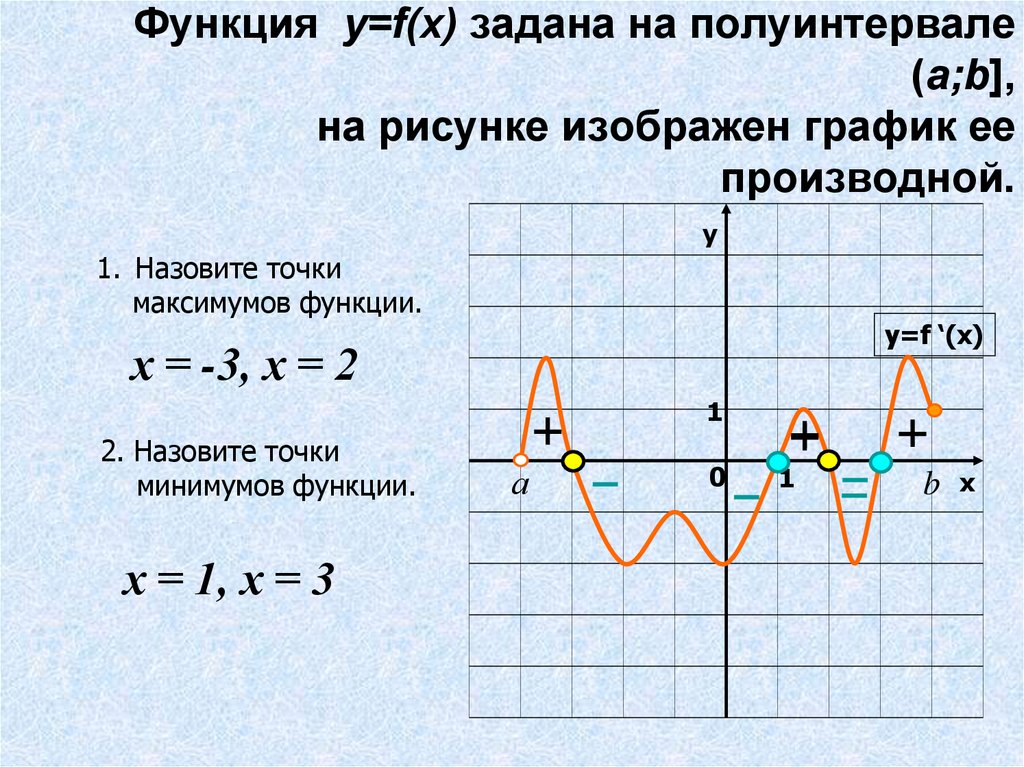 Затем вам нужно вывести функцию второй степени, а затем поместить значение переменной (которое вы нашли в первой степени) в производную второго порядка. Если значение производной второго порядка отрицательное, значит, в этой конкретной точке график имеет максимальное значение.

ШАГ 1:

ШАГ 2:

Лучшие репетиторы по математике

Поехали

Локальные минимумы

2 Возьмите первую производную, а затем найдите значение переменной от первой производной. Затем возьмите вторую производную, а затем поместите значение в переменную, и если значение положительное, это означает, что в этой конкретной точке график имеет минимальное значение.

Шаг 1:

Шаг 2:

Расчет максимального и минимального

Исследование. шагов:

1. Вычислить первую производную и ее корни.

2.