Данный калькулятор вычисляет значение выражения, подставляя туда значения переменных из таблицы. Удобно для проверки домашних заданий типа «Найдите значение выражения при a = 0.1, b = 2». Обозначения переменных в выражении должны совпадать с именами переменных в таблице. Если не совпадет — замены не будет и подсчитает неправильно, так что следите.
Вычисление выражений для заданных значений переменных
addimport_exportmode_editdeleteПеременные
Размер страницы: chevron_leftchevron_rightПеременные
Сохранить ОтменитьИмпортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;Lorem ipsum
Загрузить данные из csv файла
Импортировать Назад Отменить Точность вычисленияЗнаков после запятой: 2
Формула после подстановки
Результат расчета
save Сохранить extension Виджет
Для расчета после подстановки значений переменных используется Математический калькулятор.
- / — деление
- ^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
Онлайн калькулятор: Математический калькулятор
Калькулятор был создан в ответ на многочисленные запросы наших пользователей, которые желают воспользоваться нашим сервисом чтобы посчитать результат какого-либо математического выражения, например, что-нибудь сложить, вычесть, поделить возвести в степень, извлечь корень и т. п. Вводите последовательность математических выражений в поле математическое выражение и получайте результат.
Все тригонометрические функции принимают аргументы в радианах, а не в градусах. Обратные тригонометрические функции, также возвращают угол в радианах. Для преобразования градусов в радианы — умножайте градусы на pi/180, например, sin 30 градусов надо записывать как sin(30*pi/180).
Математический калькулятор
Допустимые операции: + — / * ^ Константы: pi Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точность вычисленияЗнаков после запятой: 10
Исходное выражение
Результат вычисления
save Сохранить extension Виджет
В математическом выражении допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34.biz
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Онлайн калькулятор: Вычисление значений функции
Данный онлайн калькулятор вычисляет значения функции одной переменной для заданных значений переменной . Функция задается при помощи формулы, в которой могут участвовать математические операции, константы и математические функции. Синтаксис описания формулы см. ниже.
Вычисление значений функции
Значения переменной x через запятую, для указания десятичной точки используйте точку.
Точность вычисленияЗнаков после запятой: 1
save Сохранить extension Виджет
В формуле допускается использование одной переменной (обозначается как x), числа пи ( pi), следующих математических операторов:
+ — сложение
— — вычитание
* — умножение
/ — деление
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) — кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
С помощью данного калькулятора онлайн вы можете умножить, вычесть, поделить, сложить и сократить числовые дроби с разными знаменателями.
Программа работает с правильными, неправильными и смешанными числовыми дробями.
Данная программа (калькулятор онлайн) умеет:
— выполнять сложение смешанных дробей с разными знаменателями
— выполнять вычетание смешанных дробей с разными знаменателями
— выполнять деление смешанных дробей с разными знаменателями
— выполнять умножение смешанных дробей с разными знаменателями
— приводить дроби к общему знаменателю
— преобразовывать смешанные дроби в неправильные
— сокращать дроби
Также можно ввести не выражение с дробями, а одну единственную дробь.
В этом случае дробь будет сокращена и из результата выделена целая часть.
Калькулятор онлайн для вычисления выражений с числовыми дробями не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс нахождения решения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода выражений с числовыми дробями, рекомендуем с ними ознакомиться.
Правила ввода выражений с числовыми дробями
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3 + 7/5
Результат: \( -\frac{2}{3} + \frac{7}{5} \)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&2/3 * 5&8/3
Результат: \( -1\frac{2}{3} \cdot 5\frac{8}{3} \)
Деление дробей вводится знаком двоеточие: :
Ввод: -9&37/12 : -3&5/14
Результат: \( -9\frac{37}{12} : \left( -3\frac{5}{14} \right) \)
Помните, что на ноль делить нельзя!
При вводе выражений с числовыми дробями можно использовать скобки.
Ввод: -2/3 * (6&1/2-5/9) : 2&1/4 + 1/3
Результат: \( -\frac{2}{3} \cdot \left( 6 \frac{1}{2} — \frac{5}{9} \right) : 2\frac{1}{4} + \frac{1}{3} \)
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
Калькулятор комплексных чисел позволяет вычислять арифметические выражения, содержащие комплексные числа, знаки арифметических действий (+, -, *, /, ^), а также некоторые математические функции.
Калькулятор комплексных чисел
7
8
9
+
—
*
/
^
4
5
6
i
(
)
π
e
1
2
3
sin
cos
tg
ctg
ln
.
0
√
sh
ch
th
cth
abs
Скрыть клавиатуру
Вычислено выражений: 46312
Как пользоваться калькулятором
- Введите в поле ввода выражение с комплексными числами
- Укажите, требуется ли вывод решения переключателем «С решением»
- Нажмите на кнопку «Построить»
Ввод комплексных чисел
комплексные числа можно вводить в следующих трёх форматах:
- Только действительная часть:
2, 2.5, -6.7, 12.25 - Только мнимая часть:
i, -i, 2i, -5i, 2.16i, -12.5i - Действительная и мнимая части:
2+i, -5+15i, -7+2.5i, -6+i - Математические константы:
π, e
Поддерживаемые операции и математические функции
- Арифметические операции:
+, -, *, /, ^ - Получение абсолютного значения числа:
abs - Базовые математические функции:
exp, ln, sqrt - Получение действительной и мнимой частей:
re, im - Тригонометрические функции:
sin, cos, tg, ctg - Гиперболические функции:
sh, ch, th, cth - Обратные тригонометрические функции:
arcsin, arccos, arctg, arcctg - Обратные гиперболические функции:
arsh, arch, arth, arcth
Примеры корректных выражений
- (2+3i)*(5-7i)
- sh(i)
- (4+i) / (3 — 4i)
- sqrt(2i)
- (-3+4i)*2i / exp(2i + (15 — 8i)/4 — 3.75)
Комплексные числа
Комплексные числа — это числа вида x+iy, где x, y — вещественные числа, а i — мнимая единица (специальное число, квадрат которого равен -1, то есть i2 = -1).
Так же, как и для вещественных чисел, для комплексных чисел определены операции сложения, разности, умножения и деления, однако комплексные числа нельзя сравнивать.
Примеры комплексных чисел
4+3i— действительная часть = 4, мнимая = 3-2+i— действительная часть = -2, мнимая = 1i— действительная часть = 0, мнимая = 1-i— действительная часть = 0, мнимая = -110— действительная часть = 10, мнимая = 0
Основные действия с комплексными числами
Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
- сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
- вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
- умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
- деление: = = + i
Примеры
Найти сумму чисел 5+7i и 5.5-2i:
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом:5+7i + 5.5-2i = 10.5 + 5i
Найти разность чисел 12-i и -2i:
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом:12-i — (-2i) = 12 + i
Найти произведение чисел 2+3i и 5-7i:
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом:2+3i * (5-7i) = 31 + i
Найти отношение чисел 75-50i и 3+4i:
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом:75-50i / (3+4i) = 1 - 18i
Другие действия над комплексными числами
Помимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:
- Получение действительной части числа:
Re(z) = a - Получение мнимой части числа:
Im(z) = b - Модуль числа:
|z| = √(a2 + b2) - Аргумент числа:
arg z = arctg(b / a) - Экспонента:
ez = ea·cos(b) + i·ea·sin(b) - Логарифм:
Ln(z) = ln |z| + i·arg(z) - Тригонометрические функции: sin z, cos z, tg z, ctg z
- Гиперболические функции: sh z, ch z, th z, cth z
- Обратные тригонометрические функции: arcsin z, arccos z, arctg z, arcctg z
- Обратные гиперболические функции: arsh z, arch z, arth z, arcth z
Примеры
Найти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i
Re(z) = Re(4 — 3i) = 4
Im(z) = Im(4 — 3i) = -3
|z| = √(42 + (-3)2) = √25 = 5
Формы представления комплексных чисел
Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.
- Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей:
x+iy, где x — действительная часть, а y — мнимая часть - Тригонометричкая форма — запись вида
r·(cos φ + isin φ), где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z)) - Показательная форма — запись вида
r·eiφ, где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))
Пример:
Переведите число 1+i в тригонометрическую и показательную формы:
Решение:
- Найдём радиус (модуль) комплексного числа r: r = √(12 + 12) = √2
- Найдём аргумент числа: φ = arctan() = = 45°
- Запишем результат в тригонометрической форме:
√2·(cos(45°) + isin(45°)) - Запишем результат в показательной форме:
√2·eπi/4
Вычисление логарифма числа онлайн | umath.ru
Онлайн калькулятор логарифмов
Калькулятор вычисляет логарифм числа онлайн. Можно вводить как десятичные дроби (в качестве разделителя для десятичных дробей можно использовать как точку, так и запятую), так и обычные (например, если нужно вычислить логарифм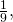 
то в поле «число» можете смело писать 1/9).
Помните, что операция взятия логарифма определена только для положительных чисел, а основание логарифма должно быть положительным и не должно равняться единице.
Что такое логарифм числа?
Примеры
Пример 2. Вычислить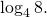
Решение. Воспользуемся следующим свойством логарифмов:
![\[\log_{a^{\alpha}}{b^{\beta}} = \frac{\beta}{\alpha}\log_a{b}.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-dedd0477895656027b8c3f5ea44a1ee9_l3.png)
Получаем:
![\[\log_4 8 = \log_{2^2}{2^3} = \frac{3}{2}\log_2 2.\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-3b4e2cd5f0c103ec094891b1fddd507a_l3.png)
Так как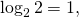 
то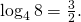 
Как видите, всё очень просто!
Логарифм числа 
по основанию 10 называют десятичным и обозначают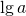 
, а логарифм числа по основанию 
называют натуральным и обозначают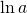 
.
Про свойства логарифмов читайте здесь.
выражений, значений и выражений let — PowerQuery M
- 5 минут, чтобы прочитать
В этой статье
Запрос языка формул Power Query M состоит из шагов формулы выражения , которые создают гибридный запрос.Выражение формулы можно вычислить (вычислить), получив значение. Выражение и инкапсулирует набор значений, которые необходимо вычислить, присвоить имена, а затем использовать в последующем выражении, которое следует за оператором в . Например, выражение let может содержать переменную Source , которая равна значению Text.Proper () и возвращает текстовое значение в надлежащем случае.
Пусть выражение
лет
Source = Text.Proper ("Привет, мир")
в
Источник
В приведенном выше примере текст.Правильный («привет мир») оценивается как «Привет, мир».
В следующих разделах описываются типы значений в языке.
Первобытное значение
Значение примитива — это однокомпонентное значение, например число, логическое значение, текст или ноль. Нулевое значение может использоваться для указания отсутствия каких-либо данных.
| Тип | Пример значения |
|---|---|
| Binary | 00 00 00 02 // количество баллов (2) |
| Дата | 23.05.2015 |
| DateTime | 23.05.2015, 00:00:00, |
| DateTimeZone | 23.05.2015 00:00:00 -08: 00 |
| Продолжительность | 15:35:00 |
| Logical | истинных и ложных |
| Нуль | ноль |
| номер | 0, 1, -1, 1.5 и 2.3e-5 |
| Текст | «abc» |
| Время | 12:34:12 |
Значение функции
A Функция — это значение, которое при вызове с аргументами создает новое значение. Функции записываются путем перечисления параметров функции в скобках, за которыми следует символ перехода к =>, а затем выражение, определяющее функцию. Например, чтобы создать функцию с именем «MyFunction», которая имеет два параметра и выполняет вычисление для параметра1 и параметра2:
лет
MyFunction = (параметр1, параметр2) => (параметр1 + параметр2) / 2
в
MyFunction
Вызов MyFunction () возвращает результат:
позволять
Источник = MyFunction (2, 4)
в
Источник
Этот код производит значение 3.
Структурированные значения данных
Язык M поддерживает следующие значения структурированных данных:
Список
Список — это упорядоченная последовательность значений, начинающаяся с нуля, заключенная в фигурные скобки {}. Символы фигурных скобок {} также используются для извлечения элемента из списка по позиции индекса. См. [Значение списка] (#_ List_value).
Примечание
Power Query M поддерживает бесконечный размер списка, но если список записывается в виде литерала, список имеет фиксированную длину.Например, {1, 2, 3} имеет фиксированную длину 3.
Ниже приведены некоторые Список примеров.
| Значение | Тип |
|---|---|
| {123, правда, «A»} | Список, содержащий число, логическое и текст. |
| {1, 2, 3} | Список номеров |
| { {1, 2, 3}, {4, 5, 6} } | Список списка номеров |
| { [CustomerID = 1, Name = «Bob», Phone = «123-4567»], [CustomerID = 2, Name = «Jim», Phone = «987-6543»] } | Список записей |
| {123, правда, «A»} {0} | Получить значение первого элемента в списке.Это выражение возвращает значение 123. |
| { {1, 2, 3}, {4, 5, 6} } {0} {1} | Получить значение второго элемента из первого элемента списка. Это выражение возвращает значение 2. |
Запись
A Record — это набор полей. Поле — это пара имя / значение, где имя — это текстовое значение, уникальное для записи поля. Синтаксис для значений записи позволяет писать имена без кавычек, форма также называется идентификаторами .Идентификатор может принимать следующие две формы:
Ниже приведена запись, содержащая поля с именами «OrderID», «CustomerID», «Item» и «Price» со значениями 1, 1, «Fishing rod» и 100.00. Квадратные скобки [] обозначают начало и конец выражения записи и используются для получения значения поля из записи. Следующие примеры показывают запись и как получить значение поля Item.
Вот пример записи:
лет Источник =
[
OrderID = 1,
CustomerID = 1,
Предмет = "Удочка",
Цена = 100.00
]
в источнике
Чтобы получить стоимость предмета, вы используете квадратные скобки в качестве источника [предмета]:
лет Источник =
[
OrderID = 1,
CustomerID = 1,
Предмет = "Удочка",
Цена = 100,00
]
в Source [Item] // равно "Удочка"
Стол
A Таблица — это набор значений, организованных в именованные столбцы и строки. Тип столбца может быть неявным или явным. Вы можете использовать #table для создания списка имен столбцов и списка строк.Таблица значений является списком в списке . Символы фигурных скобок {} также используются для извлечения строки из таблицы по позиции индекса (см. Пример 3 — получение строки из таблицы по позиции индекса).
Пример 1. Создание таблицы с неявными типами столбцов
лет
Source = #table (
{"OrderID", "CustomerID", "Item", "Price"},
{
{1, 1, «Удочка», 100,00},
{2, 1, "1 фунт. Черви", 5,00}
})
в
Источник
Пример 2. Создание таблицы с явными типами столбцов
лет
Source = #table (
таблица типов [OrderID = номер, CustomerID = номер, Item = текст, цена = номер],
{
{1, 1, «Удочка», 100.00},
{2, 1, "1 фунт. Черви", 5,00}
}
)
в
Источник
В обоих приведенных выше примерах создается таблица следующей формы:
| OrderID | CustomerID | Item | Цена |
|---|---|---|---|
| 1 | 1 | Удочка | 100,00 |
| 2 | 1 | 1 фунт червей | 5,00 |
Пример 3 — Получить строку из таблицы по позиции индекса
лет
Source = #table (
таблица типов [OrderID = номер, CustomerID = номер, Item = текст, цена = номер],
{
{1, 1, «Удочка», 100.00},
{2, 1, "1 фунт. Черви", 5,00}
}
)
в
Источник {1}
Это выражение возвращает следующую запись:
| OrderID | 2 |
| CustomerID | 1 |
| Товар | 1 фунт червей |
| Цена | 5 |
Дополнительные примеры структурированных данных
Структурированные данные могут содержать любое значение МВот несколько примеров:
Пример 1 — Список со значениями [Primitive] (#_ Primitive_value_1), [Function] (#_ Function_value) и [Record] (#_ Record_value)
лет
Источник =
{
1,
«Боб»,
DateTime.ToText (DateTime.LocalNow (), "гггг-ММ-дд"),
[OrderID = 1, CustomerID = 1, Item = "Удочка", Цена = 100.0]
}
в
Источник
Оценка этого выражения может быть визуализирована как:
Пример 2 — Запись, содержащая значения примитивов и вложенные записи
лет
Source = [CustomerID = 1, Name = "Bob", Phone = "123-4567", Orders =
{
[OrderID = 1, CustomerID = 1, Item = "Удочка", Цена = 100.0],
[OrderID = 2, CustomerID = 1, Item = "1 фунт. Черви", цена = 5.0]
}]
в
Источник
Оценка этого выражения может быть визуализирована как:
Примечание
Хотя многие значения могут быть записаны буквально как выражение, значение не является выражением. Например, выражение 1 оценивается как значение 1; выражение 1 + 1 оценивается как значение 2. Это различие тонкое, но важное. Выражения являются рецептами для оценки; значения являются результатами оценки.
Если выражение
Выражение , если выбирает между двумя выражениями на основе логического условия. Например:
если 2> 1 то
2 + 2
еще
1 + 1
Первое выражение (2 + 2) выбирается, если логическое выражение (2> 1) истинно, а второе выражение (1 + 1) выбирается, если оно ложно. Выбранное выражение (в данном случае 2 + 2) оценивается и становится результатом выражения , если (4).
,Исчисление II — Оценка стоимости серии
Пол Заметки ОнлайнНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Стратегия для серии
- Power Series
- глав
- Параметрические уравнения и полярные координаты
- Векторы
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Предварительные
Исчисление I — вычислительные ограничения
Пол Заметки ОнлайнНоты Быстрая навигация Скачать
- Перейти к
- Ноты
- Проблемы с практикой
- Проблемы с назначением
- Показать / Скрыть
- Показать все решения / шаги / и т. Д.
- Скрыть все решения / шаги / и т. Д.
- Разделы
- Limit Properties
- Бесконечные лимиты
- глав
- Обзор
- Производные
- Классы
- Алгебра
- Исчисление I
- Исчисление II
- Исчисление III
- Дифференциальные уравнения
- Дополнительно
- Обзор алгебры и триггеров
- Распространенные математические ошибки
- Комплексное число праймер
- Как изучать математику
- Шпаргалки и таблицы
- Разное
- Свяжитесь со мной
- Справка и настройка MathJax
- Мои ученики
- Примечания Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Практика Проблемы Загрузки
- Complete Book — Проблемы только
- Complete Book — Решения
- Текущая глава — только проблемы
- Текущая глава — Решения
- Текущий раздел — только проблемы
- Текущий раздел — Решения
- Проблемы с назначением Загрузки
- Полная книга
- Текущий Глава
- Текущий раздел
- Другие предметы
- Получить URL для загрузки элементов
- Распечатать страницу в текущей форме (по умолчанию)
- Показать все решения / шаги и распечатать страницу
- Скрыть все решения / шаги и распечатать страницу
- Дом
- Классы
- алгебра
- Предварительные
- Целочисленные экспоненты
- Рациональные экспоненты
- Радикалы
- полиномов
- Факторинг Полиномы
- Rational Expressions
- Комплексные числа
- Решение уравнений и неравенств
- Решения и комплекты решений
- линейных уравнений
- приложений линейных уравнений
- уравнений с более чем одной переменной
- Квадратичные уравнения — Часть I
- Квадратичные уравнения — Часть II
- Квадратичные уравнения: краткое изложение
- Приложения квадратичных уравнений Уравнения
- , приводимые к квадратичной форме
- Уравнения с радикалами
- линейных неравенств
- Полиномиальное неравенство
- Рациональное неравенство
- Уравнения абсолютной стоимости
- Абсолютное неравенство в значениях
- Графика и функции
- График
- Линии
- Круги
- Определение функции
- Графические функции
- Объединение функций
- Обратные функции
- общих графиков
- Линии, окружности и кусочные функции
- Параболы
- Эллипсы
- Гипербол
- Разные функции
- Преобразования
- Предварительные
Используйте выражения с условиями. — Power Automate
- 7 минут, чтобы прочитать
В этой статье
В этом пошаговом руководстве вы научитесь использовать выражения и условия для сравнения нескольких значений в расширенном режиме .
Когда вы создаете поток, вы можете использовать карту Условие в базовом режиме, чтобы быстро сравнить одно значение с другим значением. Однако бывают случаи, когда вам нужно сравнить несколько значений. Например, вы можете проверить значение нескольких столбцов в электронной таблице или таблице базы данных.
Вы можете использовать любую комбинацию следующих логических выражений в ваших условиях.
| Выражение | Описание | Пример |
|---|---|---|
| и | Принимает два аргумента и возвращает истину, если оба значения истинны. Примечание : оба аргумента должны быть логическими. | Это выражение возвращает false: и (больше (1,10), равно (0,0)) |
| или | Принимает два аргумента и возвращает истину, если любой из аргументов верен. Примечание : оба аргумента должны быть логическими. | Это выражение возвращает истину: или (больше (1,10), равно (0,0)) |
| равно | Возвращает true, если два значения равны. | Например, если параметр1 равен someValue, это выражение возвращает значение true: равно (параметры (‘parameter1’), ‘someValue’) |
| меньше | Принимает два аргумента и возвращает истину, если первый аргумент меньше второго аргумента. Примечание : Поддерживаемые типы: целое число, число с плавающей запятой и строка. | Это выражение возвращает истину: меньше (10 100) |
| меньшеОреальности | Принимает два аргумента и возвращает истину, если первый аргумент меньше или равен второму аргументу. Примечание : Поддерживаемые типы: целое число, число с плавающей запятой и строка. | Это выражение возвращает true: lessOrEquals (10,10) |
| больше | Принимает два аргумента и возвращает истину, если первый аргумент больше, чем второй аргумент. Примечание : Поддерживаемые типы: целое число, число с плавающей запятой и строка. | Это выражение возвращает ложь: больше (10,10) |
| БОЛЬШЕ ОБЕСПЕЧЕНИЙ | Принимает два аргумента и возвращает истину, если первый аргумент больше или равен второму аргументу. Примечание : Поддерживаемые типы: целое число, число с плавающей запятой и строка. | Это выражение возвращает ложь: большееOrEquals (10,100) |
| пусто | Возвращает true, если объект, массив или строка пустые. | Это выражение возвращает истину: пусто (») |
| не | Возвращает значение, противоположное логическому значению. | Это выражение возвращает true: not (содержит («200 Success», «Fail»)) |
| , если | Возвращает конкретное значение, если выражение приводит к true или false. | Это выражение возвращает «да»: , если (равно (1, 1), «да», «нет») |
Предпосылки
- Доступ к Power Automate.
- Таблица с таблицами, описанными далее в этом пошаговом руководстве. Обязательно сохраните электронную таблицу в таком месте, как Dropbox или Microsoft OneDrive, чтобы Power Automate мог получить к ней доступ.
- Microsoft Office 365 Outlook (хотя мы используем Office 365 Outlook, вы можете использовать любую поддерживаемую службу электронной почты в своих потоках.)
Используйте или выражение
Иногда ваш рабочий процесс должен предпринять действие, если значение элемента равно значению A или значениюB.Например, вы можете отслеживать состояние задач в таблице электронных таблиц. Предположим, что в таблице есть столбец с именем Статус и возможные значения в столбце Статус :
- завершено
- заблокирован
- ненужный
- не началось
Вот пример того, как может выглядеть электронная таблица:
Учитывая предыдущую электронную таблицу, вы хотите использовать Power Automate, чтобы удалить все строки со столбцом Статус , для которого установлено , завершено или необязательно .
Давайте создадим поток.
Начните с пустого потока
Войдите в систему Power Automate.
Выберите вкладку Мои потоки .
Выберите Создать с пустого .
Добавьте триггер к вашему потоку
Найдите расписание , а затем выберите расписание — триггер повторения
Установите расписание для запуска один раз в день.
Выберите таблицу и получите все строки
Выбрать Новый шаг > Добавить действие .
Найдите строк , а затем выберите Excel — Получить строки .
Примечание. Выберите действие «получить строки», соответствующее используемой электронной таблице. Например, если вы используете Google Sheets, выберите Google Sheets — Получить строки .
Выберите значок папки в поле Имя файла , найдите, а затем выберите электронную таблицу, содержащую ваши данные.
Выберите таблицу, содержащую ваши данные, из списка Имя таблицы .
Проверьте столбец состояния каждой строки
Выбрать Новый шаг > Подробнее > Добавить заявку к каждому .
Добавьте токен Value к Выберите выход из предыдущих шагов, окно .
Выберите Добавить условие > Редактировать в расширенном режиме .
Добавьте следующее выражение или . Это выражение или проверяет значение каждой строки в таблице (строка называется элементом при обращении к выражению). Если значение столбца состояния равно , завершено , или , не нужно, , выражение или оценивается как «истина».
Выражение или выглядит так, как показано здесь:
@ или (равно (элемент ()? ['Status'], 'ненужный'), равно (item ()? ['Status'], 'выполнено'))Ваша Условие карта похожа на это изображение:
Удалить соответствующие строки из таблицы
Выберите Добавьте действие в , ЕСЛИ ДА, НИЧЕГО не делайте из условия .
Поиск Удалить строку , а затем выберите Excel — Удалить строку .
В поле Имя файла найдите и выберите файл электронной таблицы, содержащий данные, которые вы хотите удалить.
В списке Имя таблицы выберите таблицу, содержащую ваши данные.
Поместите токен идентификатора строки в поле Идентификатор строки .
Назовите поток и сохраните его
Дайте вашему потоку имя, а затем нажмите кнопку Создать поток .
Запустите поток с выражением или
Поток запускается после его сохранения. Если вы создали электронную таблицу, показанную ранее в этом пошаговом руководстве, вот как она выглядит после завершения прогона:
Обратите внимание, что все данные из строк, которые были «заполнены» или «не нужны» в столбце «Состояние», были удалены.
Используйте и выражение
Предположим, у вас есть таблица с двумя столбцами. Имена столбцов: Статус и Назначено.Предположим также, что вы хотите удалить все строки, если значение столбца «Состояние» «заблокировано», а значение «Назначенный столбец» — «Джон Уандер». Чтобы выполнить эту задачу, выполните все шаги ранее в этом пошаговом руководстве, однако, когда вы редактируете карту Условие в расширенном режиме, используйте выражения и , показанные здесь:
@and (равно (элемент ()? ['Status'], 'заблокирован'), равно (item ()? ['Assigned'], 'John Wonder'))
Ваша Условие карта похожа на это изображение:
Запустите поток с и выражением
Если вы последовали, ваша таблица похожа на это изображение:
После запуска потока ваша таблица будет выглядеть примерно так:
Используйте пустое выражение
Обратите внимание, что в таблице есть несколько пустых строк.Чтобы удалить их, используйте пустое выражение , чтобы определить все строки, в которых нет текста в столбцах «Назначено» и «Состояние».
Для выполнения этой задачи выполните все шаги, перечисленные в . Используйте раздел и выражение ранее в этом пошаговом руководстве, однако при редактировании карты условия в расширенном режиме используйте пустое выражение следующим образом:
@and (пусто (item ()? ['Status']), пусто (item ()? ['Assigned']))
Ваша Условие карта похожа на это изображение:
После запуска потока таблица выглядит примерно так:
Обратите внимание, что дополнительные строки удалены из таблицы.
Используйте большее выражение
Представьте, что вы купили билеты на бейсбол для своих коллег и используете электронную таблицу, чтобы гарантировать, что вам заплатит каждый. Вы можете быстро создать поток, который отправляет ежедневное электронное письмо каждому человеку, который не заплатил всю сумму.
Используйте выражение больше , чтобы определить сотрудников, которые не заплатили полную сумму. Затем вы можете автоматически отправить дружеское напоминание по электронной почте тем, кто не заплатил полностью.
Вот вид таблицы:
Вот реализация большего выражения , которое идентифицирует всех людей, которые заплатили меньше, чем причитающаяся с них сумма:
@greater (item ()? ['Due'], item ()? ['Paid'])
Используйте меньшее выражение
Представьте, что вы купили билеты на бейсбол для своих коллег, и вы используете электронную таблицу, чтобы гарантировать, что каждый человек получит возмещение к дате, на которую все согласились.Вы можете создать поток, который отправит напоминание по электронной почте каждому человеку, который не заплатил полную сумму, если текущая дата меньше, чем за один день до срока оплаты.
Используйте выражение и вместе с выражением минус , поскольку проверяются два условия:
| Условие для подтверждения | выражение для использования | Пример |
|---|---|---|
| Была ли выплачена полная сумма? | больше | @greater (item ()? [‘Due’], item ()? [‘Paid’]) |
| Срок оплаты меньше одного дня? | меньше | @less (item ()? [‘DueDate’], addDays (utcNow (), 1)) |
Объедините большие и меньшие выражения в выражении и
Используйте выражение больше , чтобы определить сотрудников, которые заплатили меньше полной причитающейся суммы, и используйте выражение меньше , чтобы определить, не наступила ли дата платежа менее чем на один день от текущей даты.Затем вы можете отправить акцию по электронной почте , чтобы отправить дружеское напоминание по электронной почте тем, кто не оплатил полностью, а срок оплаты составляет менее одного дня.
Вот вид таблицы электронных таблиц:
Вот реализация выражений и , которая идентифицирует всех лиц, которые заплатили меньше, чем причитающаяся с них сумма, и срок оплаты составляет менее одного дня от текущей даты:
@and (больше (item ()? ['Due'], item ()? ['Paid']), меньше (item ()? ['DueDate'], addDays (utcNow (), 1)))
Использование функций в выражениях
Некоторые выражения получают свои значения от действий во время выполнения, которые могут еще не существовать, когда поток начинает выполняться.Чтобы ссылаться на эти значения или работать с ними в выражениях, вы можете использовать функции, предоставляемые языком определения рабочего процесса. Дополнительная информация: Справочник функций для языка определения рабочих процессов в Power Automate
,
Leave A Comment