Обратный и дополнительный коды числа
Назначение сервиса. Онлайн-калькулятор предназначен для представления чисел в обратном и дополнительном коде.- Решение онлайн
- Видеоинструкция
- Также решают
Число
Найти: прямой код обратный код дополнительный код
Вместе с этим калькулятором также используют следующие:
Операции с двоичными числами (сложение и вычитание)
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Алгебра и геометрия
Целые числа в ЭВМ могут быть представлены в виде:- прямого кода. Прямой код двоичного числа совпадает по изображению с записью самого числа.
- обратного кода
- дополнительного кода. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Прямой код числа кодирует только знаковую информацию и используется для хранения положительных и отрицательных чисел в ЭВМ. Прямой код двоичного числа совпадает по изображению с записью самого числа, но в знаковом разряде ставится 0, если число положительное и, 1 если число отрицательное.
Следует помнить, что положительные числа в обратном и дополнительном коде совпадают с прямым кодом.
1) Прямой код числа (кодируется только знаковая информация), “+”=0; ”-”=1.
Для прямого кода возможны два представления нуля, машинный положительный ноль, т.е. +0,110=0,110, машинный отрицательный ноль, т.е. -0,111=1,111.
Пример перевода
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение.
Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
Пример перевода
x1=10101-[x1]обр=010101
x2=-11101-[x2]обр=100010
x3=0,101-[x3]обр=0,101
x4=-0,111-[x4]обр=1,000
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1=10101-[x1]доп=010101
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.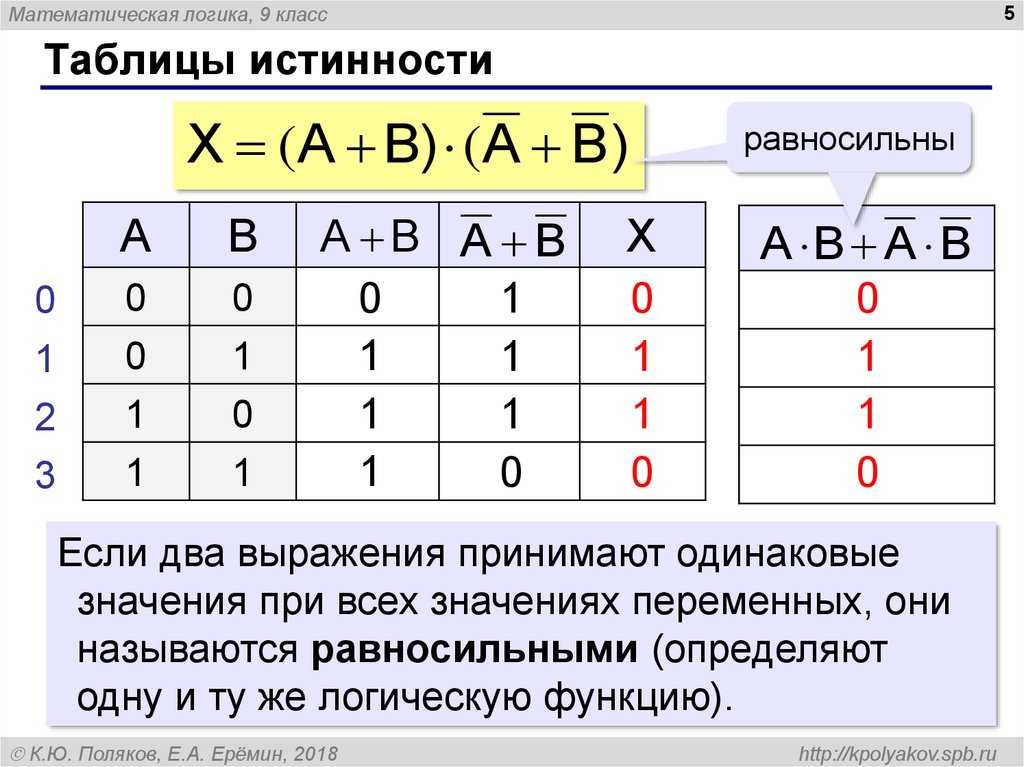
Как определить, положительное или отрицательное число? Знак числа определяет старший бит: 0 — положительное число, 1 — отрицательное число. Например, для числа 1,001 сразу можно определить, что оно отрицательное (меньше нуля).
Пример. Представить в дополнительном коде десятичные числа: -4.
Решение. Представим число в двоичном коде.
4 = 00001002
Инвертируем все разряды числа, а в знаковый разряд заносим 1
.
Добавляем к младшему разряду
1.
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Число -4 представляется в двоичном дополнительном коде как
11111100
tablica istinnosti ru
tablica istinnosti ruВы искали tablica istinnosti ru? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и алгебра логика калькулятор онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «tablica istinnosti ru».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как tablica istinnosti ru,алгебра логика калькулятор онлайн,алгебра логика онлайн калькулятор,алгебра логики калькулятор,алгебра логики калькулятор онлайн,алгебра логики онлайн,алгебра логики онлайн калькулятор,алгебра логики онлайн решение,алгебра логики решение онлайн,алгебра логики упростить выражение онлайн,булева алгебра калькулятор онлайн,булева алгебра онлайн,булева алгебра онлайн калькулятор,булевы функции онлайн калькулятор,булевых функций онлайн калькулятор,дискретная математика калькулятор онлайн,дискретная математика онлайн калькулятор,дискретная математика упростить выражение онлайн,днф и кнф онлайн,днф и кнф онлайн калькулятор,днф онлайн,днф онлайн калькулятор,доказать равносильность логических выражений онлайн,и таблица истинности,информатика упростить логическое выражение онлайн калькулятор,калькулятор алгебра логика,калькулятор алгебра логики,калькулятор алгебры логики,калькулятор алгебры логики онлайн,калькулятор булевой алгебры онлайн,калькулятор булевых функций,калькулятор булевых функций онлайн,калькулятор днф и кнф онлайн,калькулятор истинности,калькулятор истинности онлайн,калькулятор кнф онлайн,калькулятор логики,калькулятор логики онлайн,калькулятор логические операции,калькулятор логический,калькулятор логических выражений,калькулятор логических выражений онлайн,калькулятор логических выражений онлайн упрощение,калькулятор логических операций,калькулятор логических функций,калькулятор логических функций онлайн,калькулятор мат логика,калькулятор математической логики,калькулятор математической логики онлайн,калькулятор онлайн алгебра логика,калькулятор онлайн истинности,калькулятор онлайн сднф,калькулятор онлайн таблицы истинности,калькулятор онлайн упрощение логических выражений,калькулятор сднф,калькулятор сднф и скнф онлайн,калькулятор скнф и сднф онлайн,калькулятор таблиц истинности онлайн,калькулятор таблица истинности,калькулятор таблица истинности онлайн калькулятор,калькулятор таблицы истинности,калькулятор таблицы истинности онлайн,калькулятор упростить логическое выражение,калькулятор упрощение логических выражений онлайн,карта карно онлайн калькулятор,карты карно калькулятор онлайн,карты карно онлайн калькулятор,карты карно онлайн решение,карты карно решение онлайн,кнф и днф онлайн,кнф и днф онлайн калькулятор,кнф онлайн,логика алгебра онлайн калькулятор,логические выражения калькулятор онлайн,логические выражения онлайн,логические выражения онлайн калькулятор,логические выражения онлайн упростить,логические выражения упростить онлайн,логические операции калькулятор,логические операции калькулятор онлайн,логические операции онлайн,логические операции онлайн калькулятор,логические схемы онлайн,логические уравнения онлайн,логический калькулятор,логический калькулятор онлайн,мат логика калькулятор,мат логика онлайн,математическая логика калькулятор онлайн,математическая логика онлайн,математическая логика онлайн калькулятор,мднф онлайн,минимизация булевых функций онлайн,минимизация логических функций калькулятор онлайн,минимизация логических функций онлайн,минимизация логических функций онлайн калькулятор,минимизация онлайн,минимизация функции онлайн,минимизировать функцию онлайн,многочлен жегалкина онлайн калькулятор,онлайн алгебра логики,онлайн калькулятор алгебра логика,онлайн калькулятор алгебра логики,онлайн калькулятор алгебры логики,онлайн калькулятор булевой алгебры,онлайн калькулятор булевых функций,онлайн калькулятор дискретная математика,онлайн калькулятор днф,онлайн калькулятор истинности,онлайн калькулятор логики,онлайн калькулятор логические выражения,онлайн калькулятор логические операции,онлайн калькулятор логический,онлайн калькулятор логических выражений,онлайн калькулятор логических выражений упрощение,онлайн калькулятор логических функций,онлайн калькулятор математической логики,онлайн калькулятор полином жегалкина,онлайн калькулятор сднф,онлайн калькулятор таблиц истинности,онлайн калькулятор таблица истинности,онлайн калькулятор таблицы истинности,онлайн калькулятор упростить логическое выражение,онлайн калькулятор упростить логическое выражение информатика,онлайн калькулятор упрощение логических выражений,онлайн кнф,онлайн логические операции,онлайн логические схемы,онлайн логические уравнения,онлайн мат логика,онлайн математическая логика,онлайн минимизация,онлайн минимизация логических функций,онлайн минимизация функции,онлайн построение таблиц истинности,онлайн построение таблицы истинности,онлайн преобразование логических выражений,онлайн решение алгебра логики,онлайн решение карты карно,онлайн решение логических выражений,онлайн решение логических уравнений,онлайн решение таблиц истинности,онлайн решение таблицы истинности,онлайн сднф,онлайн составление таблиц истинности,онлайн составление таблицы истинности,онлайн упростите логическое выражение,онлайн упрощение логических выражений,онлайн упрощение логических функций,онлайн упрощение формул логики,полином жегалкина калькулятор онлайн,полином жегалкина онлайн,полином жегалкина онлайн калькулятор,построение онлайн таблиц истинности,построение онлайн таблиц истинности логических выражений,построение таблиц истинности логических выражений онлайн,построение таблиц истинности онлайн,построение таблицы истинности онлайн,построить логическое выражение по таблице истинности онлайн,построить логическую схему онлайн,построить онлайн таблицу истинности,построить таблицу истинности для логического выражения онлайн,построить таблицу истинности онлайн,преобразование логических выражений онлайн,привести к днф функцию онлайн,привести функцию к днф онлайн,решение алгебра логики онлайн,решение карты карно онлайн,решение логических выражений онлайн,решение логических операций онлайн,решение логических уравнений онлайн,решение онлайн логических выражений,решение онлайн таблица истинности,решение таблиц истинности онлайн,решение таблицы истинности онлайн,решить логическое уравнение онлайн,сднф и скнф онлайн,сднф и скнф онлайн калькулятор,сднф и скнф онлайн калькулятор с решением,сднф калькулятор,сднф калькулятор онлайн,сднф онлайн,сднф онлайн калькулятор,сднф по таблице истинности онлайн,скнф и сднф онлайн,скнф и сднф онлайн калькулятор,скнф онлайн,скнф упрощение онлайн,сократить днф онлайн,сокращение логических выражений онлайн,составить логическую схему онлайн,составить таблицу истинности,составить таблицу истинности онлайн,составить таблицу истинности онлайн с решением,составление таблиц истинности онлайн,составление таблицы истинности онлайн,составьте таблицу истинности,таблица истинности,таблица истинности калькулятор,таблица истинности калькулятор онлайн,таблица истинности логических операций онлайн,таблица истинности логических операций онлайн калькулятор,таблица истинности онлайн,таблица истинности онлайн калькулятор,таблица истинности онлайн решение,таблица истинности решение онлайн,таблица истинности ру,таблица истинности это,таблицы истинности калькулятор онлайн,таблицы истинности онлайн,таблицы истинности онлайн калькулятор,таблицы истинности онлайн решение,таблицы истинности решение онлайн,упростите логическое выражение онлайн,упростить выражение алгебра логики онлайн,упростить выражение дискретная математика онлайн,упростить выражение онлайн алгебра логики,упростить выражение онлайн дискретная математика,упростить логические выражения онлайн,упростить логическое выражение калькулятор,упростить логическое выражение калькулятор онлайн,упростить логическое выражение онлайн,упростить логическое выражение онлайн калькулятор,упростить логическое выражение онлайн калькулятор информатика,упростить логическое выражение онлайн калькулятор с решением,упростить логическую функцию онлайн,упростить формулу логики онлайн,упрощение булевых функций онлайн,упрощение логических выражений информатика онлайн калькулятор,упрощение логических выражений калькулятор онлайн,упрощение логических выражений онлайн,упрощение логических выражений онлайн калькулятор,упрощение логических выражений онлайн калькулятор информатика,упрощение логических функций онлайн,упрощение логического выражения онлайн,упрощение скнф онлайн,упрощение формул логики онлайн.
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и tablica istinnosti ru. Просто введите задачу в окошко и нажмите
«решить» здесь (например, алгебра логика онлайн калькулятор).
Решить задачу tablica istinnosti ru вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Генератор таблиц истинности— Мгновенное создание таблиц логической истинности
Генератор таблиц истинности — Мгновенное создание таблиц логической истинности
Логический инструмент для создания таблицы истинности онлайн
Введите логическое выражение
Поделиться
Твитнуть
Как использовать ?
- Введите свое логическое выражение в поле поиска
- Используйте буквы для переменных, символы для логических операторов
- Нажмите кнопку «Получить таблицу истинности»
- Таблица истинности будет отображаться
- Нажмите кнопку «Расширенная таблица истинности» для операций с пропозициональной логикой
| Оператор | Символ для ввода | Пример |
|---|---|---|
| ИЛИ | | | А | Б | С |
| И | и | А и В и С |
| НЕ | ! | ! А |
| И-НЕ (И + НЕ) 9 Б |
Таблица истинности
Таблица истинности представляет собой представление логического выражения в табличном формате.
Он в основном используется в математике и информатике.
Представление выполняется с использованием двухзначной логики — 0 или 1. Вы также можете ссылаться на них как на True (1) или False (0). Он используется для просмотра выходного значения, сгенерированного из различных комбинаций входных значений.
Символы логических вентилей
Эти входные значения представляют собой различные переменные и символы (обычно называемые ЛОГИЧЕСКИМИ ВОРОТАМИ). Ниже приведены ВОРОТ и символы
- И (символически: &)
- ИЛИ (символически: +)
- НЕ (символически: !)
- НО (обозначает: НЕ ИЛИ)
- НЕ-И (Обозначает: Не-И)
Примеры таблиц истинности
В каждой таблице истинности каждое утверждение обычно представлено двоичной цифрой или переменной.
Для лучшего понимания взгляните на приведенные ниже примеры.
Таблица истинности шлюза OR
| Символ | А | Б | А+В |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
Таблица истинности шлюзов И
| Символ | А | Б | АБ |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
Таблица истинности логических элементов NAND
| Символ | А | Б | !(А. Б) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
Таблица истинности шлюза NOR
| Символ | А | Б | !(А+В) |
|---|---|---|---|
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 0 |
Таблица истинности шлюза НЕ
| Символ | А | !А |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
Генератор таблиц истинности
Таблица истинности представляет собой математическую таблицу и основу для всех вычислительных нужд.
Он используется, чтобы выяснить, истинно ли пропозициональное выражение для всех допустимых входных значений.
Создание таблицы истинности включает в себя простую логику, но иногда это может замедлить работу, особенно когда вы работаете над последним проектом. Это когда вы можете использовать генератор таблиц истинности.
Генератор таблиц истинности — это онлайн-инструмент, который используется для мгновенного создания логических таблиц истинности. Вы можете вводить логические операторы в различных форматах и получать точные результаты в виде символов логической логики.
Расширенная таблица истинности
Этот инструмент генерирует таблицы истинности для формул пропозициональной логики. Вы можете вводить логические операторы в нескольких различных форматах. Например, пропозициональная формула p ∧ q → ¬r может быть записана как р/\ q -> ~г, как p и q => не r, или как p && q -> !r. Связки ⊤ и ⊥ можно вводить как T и F.
FAQ
Таблица, показывающая все возможные комбинации переменных в выражении в символьной логике с их окончательным результатом как истинным или ложным.
Таблица истинности представляет собой разбивку логической функции путем перечисления всех возможных значений, которые может получить функция.
0 представляет false в булевых логических выражениях. 1 считается Истинным. .
таблиц истинности, тавтологии и логические эквивалентности
таблицы истинности, тавтологии и логические эквивалентностиМатематики обычно используют двузначное число . логика : Каждое утверждение либо Истина , либо Ложь . Это называется Закон об исключенном среднем .
Утверждение в сентенциальной логике строится из простых утверждений с использованием логические связки , , , и . Правда или ложь утверждения, построенного с помощью этих связок, зависит от истинности или ложность его составляющих.
Например, составной оператор строится с использованием логических связок , и . Правда или
ложность зависит от истины
или ложность P, Q и R.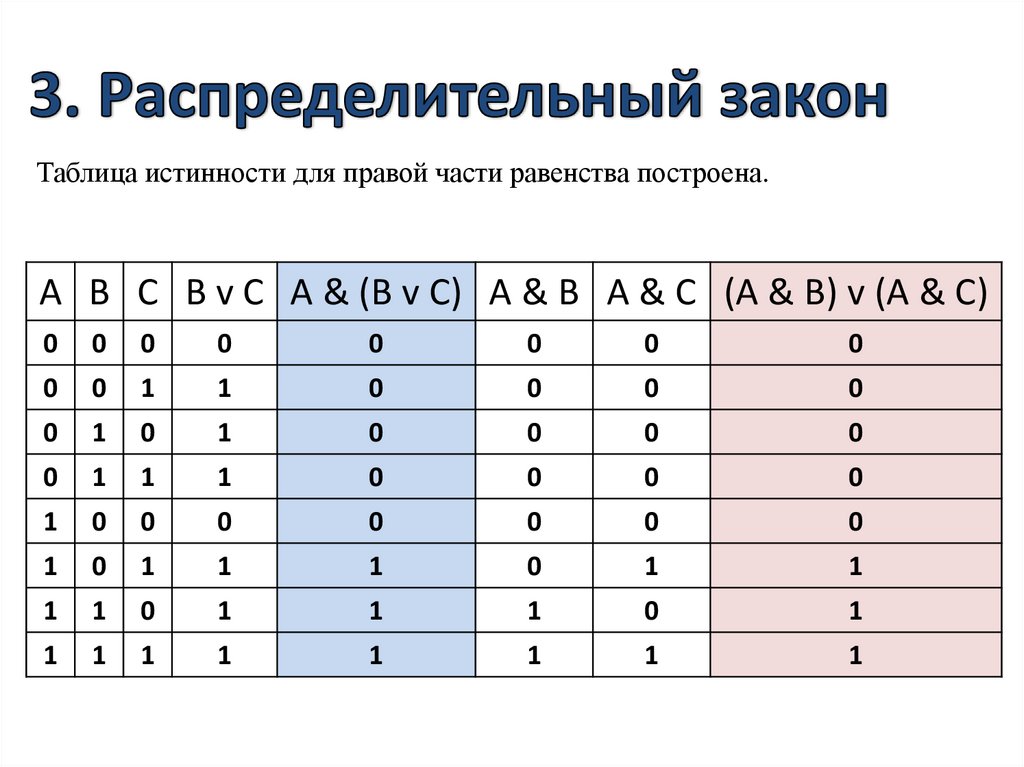
Таблица истинности показывает, как правда или ложь составного утверждения зависит от истинности или ложности простого утверждения, из которых он построен. Итак, мы начнем с рассмотрения таблицы истинности для пяти логических связок.
Вот таблица отрицания:
Эту таблицу легко понять. Если P равно true , его отрицание ложно . Если P равно false , то true .
должно быть true , когда оба P и Q true и false иначе:
является истинным , если либо P является истинным , либо Q является верно (или оба — помните, что мы используем «или» во включающем смысле). Только ложно , если оба P и Q ложно .
Вот таблица логических следствий:
Чтобы понять, почему эта таблица именно такая, рассмотрим следующее.
пример:
«Если ты получишь пятерку, я дам тебе доллар».
Утверждение будет верным , если я сдержу свое обещание и ложь если нет.
Предположим, что верно , что вы получаете пятерку, и это верно что я даю вам доллар. Поскольку я сдержал свое обещание, верно . Это соответствует первой строке таблицы.
Предположим, что верно , что вы получаете пятерку, но ложно что я даю вам доллар. Поскольку я не сдержал обещание , подразумевается false . Это соответствует второму строку в таблице.
Что, если это ложь, что вы получили пятерку? Независимо от того, дам ли я вам долларов, я не нарушил своего обещания. Таким образом, вывод не может быть ложно, поэтому (поскольку это двузначная логика) оно должно быть истинным. Этот объясняет последние две строки таблицы.
означает, что P и Q равны эквивалент .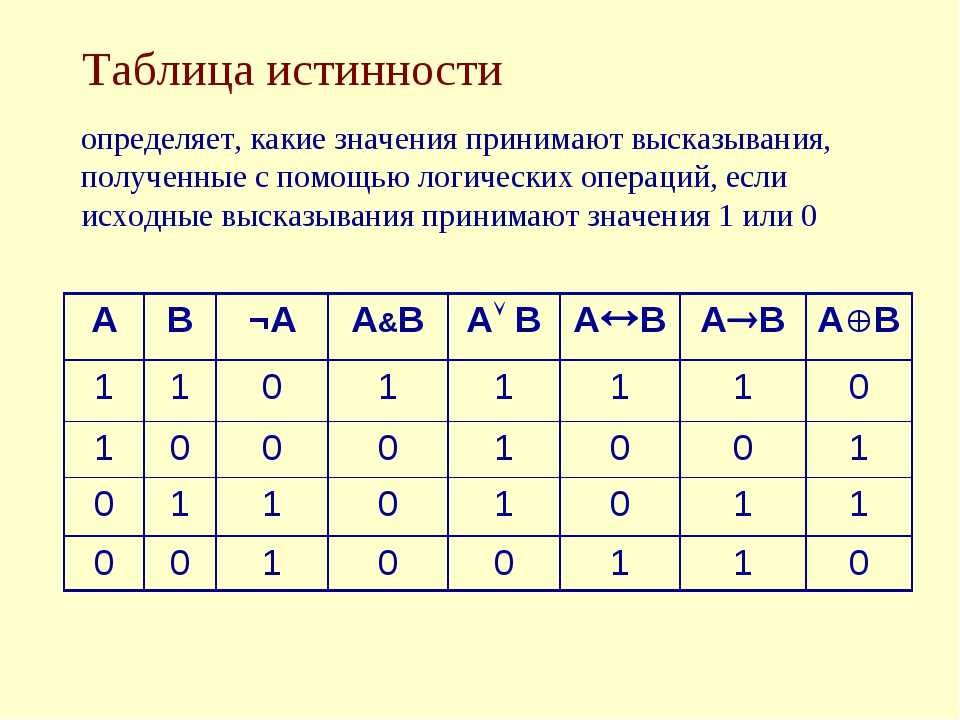
Таким образом, двойная импликация верна , если P и
Q оба истинны или если P и Q оба ложны ;
в противном случае двойная импликация ложна.
Вы должны помнить — или уметь составлять — таблицы истинности для логических связок. Вы будете использовать эти таблицы для построения таблицы для более сложных предложений. Легче продемонстрировать что делать, чем описать это словами, так вы увидите порядок выработано на примерах.
Примечание. (а) Когда вы строите правду таблице, вы должны рассмотреть все возможные назначения True (T) и False (F) для операторов компонента. Например, предположим, составные операторы — это P, Q и R. Каждый из этих операторов может быть либо правда, либо ложь, так что есть возможности.
Когда вы перечисляете возможности, вы должны присвоить значения истинности
к операторам компонентов систематическим образом, чтобы избежать дублирования
или упущение.
Самый простой подход — использовать лексикографический порядок . Таким образом, для составного оператора с
три компонента P, Q и R, я бы перечислил возможности этого
способ:
(б) Существуют различные способы составления таблиц истинности. Вы можете, для например, запишите значения истинности «под» логическим связки составного высказывания, постепенно дорастающие до столбец для «основной» связки.
Я буду записывать вещи длинным путем, создавая столбцы для каждого «кусочек» составного высказывания и постепенно наращивая к составному утверждению. Любой стиль хорош, пока вы показываете достаточно работы, чтобы оправдать ваши результаты.
Пример. Построить таблицу истинности для формула .
Во-первых, я перечисляю все альтернативы для P и Q.
Затем в третьем столбце я перечисляю значения на основе значений P. Я использую таблицу истинности для
отрицание: когда P истинно, ложно, а когда P ложно,
правда.
В четвертом столбце я перечисляю значения для . Проверьте сами, что это только ложь («F»), если P истинно («T»), а Q ложно («Ф»).
В пятом столбце приведены значения моего составного выражения. Это «и» из (третий столбец) и (четвертый столбец). «И» верно только в том случае, если обе части «и» верны; в противном случае оно ложно. Поэтому я смотрю на третья и четвертая колонки; если оба верны («T»), я ставлю T в пятой колонке, иначе ставлю F.
Тавтология есть формула, которая «всегда истинно» — то есть истинно для всякого присвоения истины значения его простых компонентов. Вы можете рассматривать тавтологию как правило логики .
Противоположностью тавтологии является число . противоречие , формула, которая «всегда ложна». В Другими словами, противоречие ложно для любого присвоения истины значения его простых компонентов.
Пример.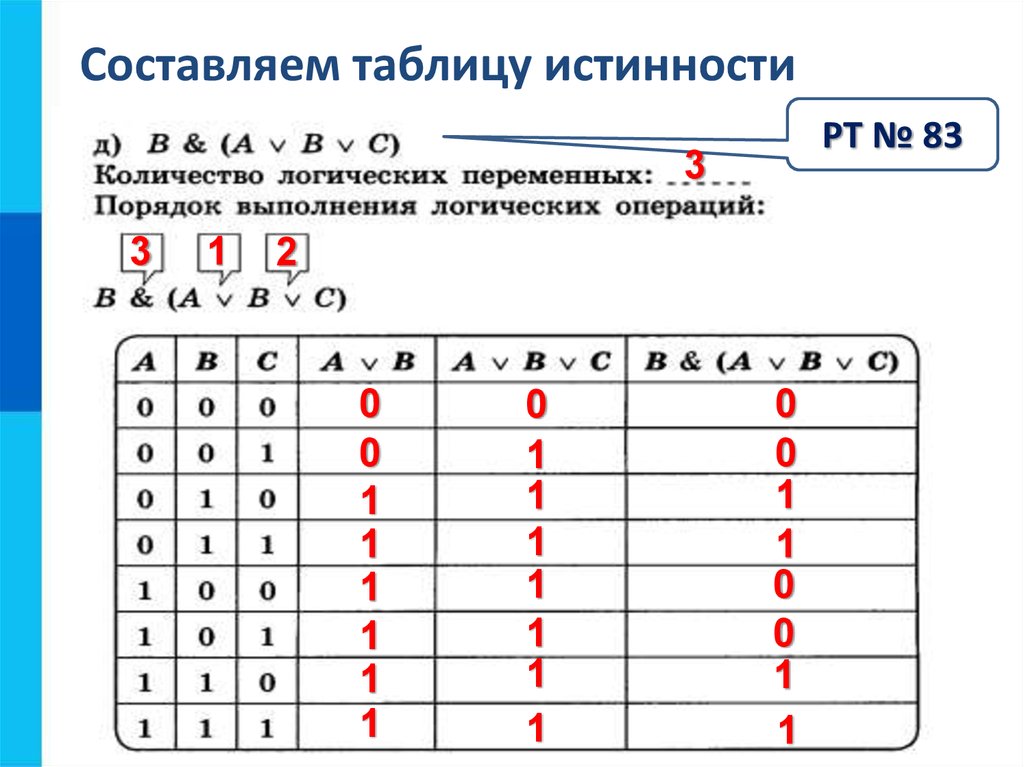
Покажите, что это тавтология.
Я строю таблицу истинности и показываю, что формула всегда верна.
Последний столбец содержит только Т. Следовательно, формула представляет собой тавтология.
Пример. Построить таблицу истинности для .
Вы можете видеть, что построение таблиц истинности для утверждений с большим количеством связок или большого количества простых утверждений довольно утомительно и подвержен ошибкам. Хотя могут быть некоторые приложения этого (например, для цифровые схемы), в какой-то момент лучше всего было бы написать программа для построения таблиц истинности (и это наверняка было сделано).
Суть здесь в том, чтобы понять, как значение истинности сложного
утверждение зависит от истинностных значений его простых утверждений и
его логические связи. В большинстве работ математики обычно не
операторы использования, которые очень сложны с логической точки зрения.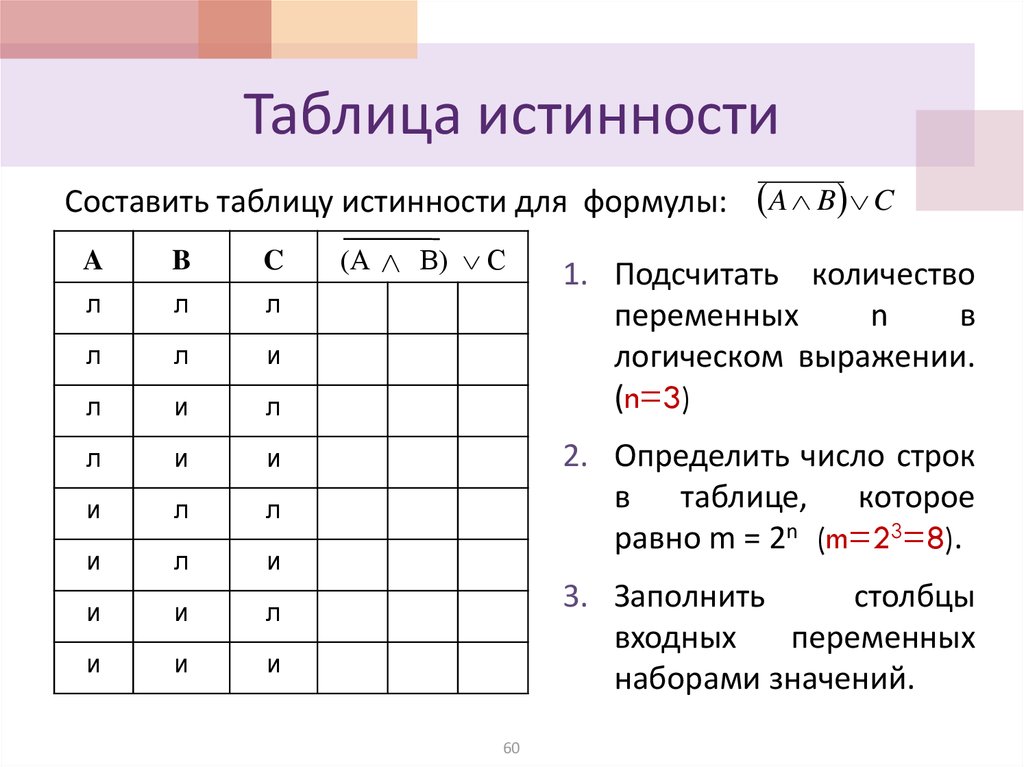
вид.
Пример. (a) Предположим, что P ложно и истинно. Скажите, является ли Q истинным, ложным или его истинной стоимость не может быть определена.
б) Предположим, что это неверно. Рассказывать является ли Q истинным, ложным или его истинностное значение не может быть определено.
а) Поскольку истинно, то либо Р истинно, либо истинно. Поскольку P ложно, оно должно быть истинным. Следовательно, Q должно быть ложным.
(b) Утверждение «если-то» ложно, когда часть «если» истина, а часть «тогда» ложна. Поскольку ложно, верно. Утверждение «и» истинно только когда обе части верны. В частности, должно быть истинным, поэтому Q ложно.
Пример. Предположим
» » правда.
» » неверно.
«У Кельвина Баттербола фиолетовые носки» — это правда.
Определить истинность утверждения
Для простоты пусть
П = «».
Q = «».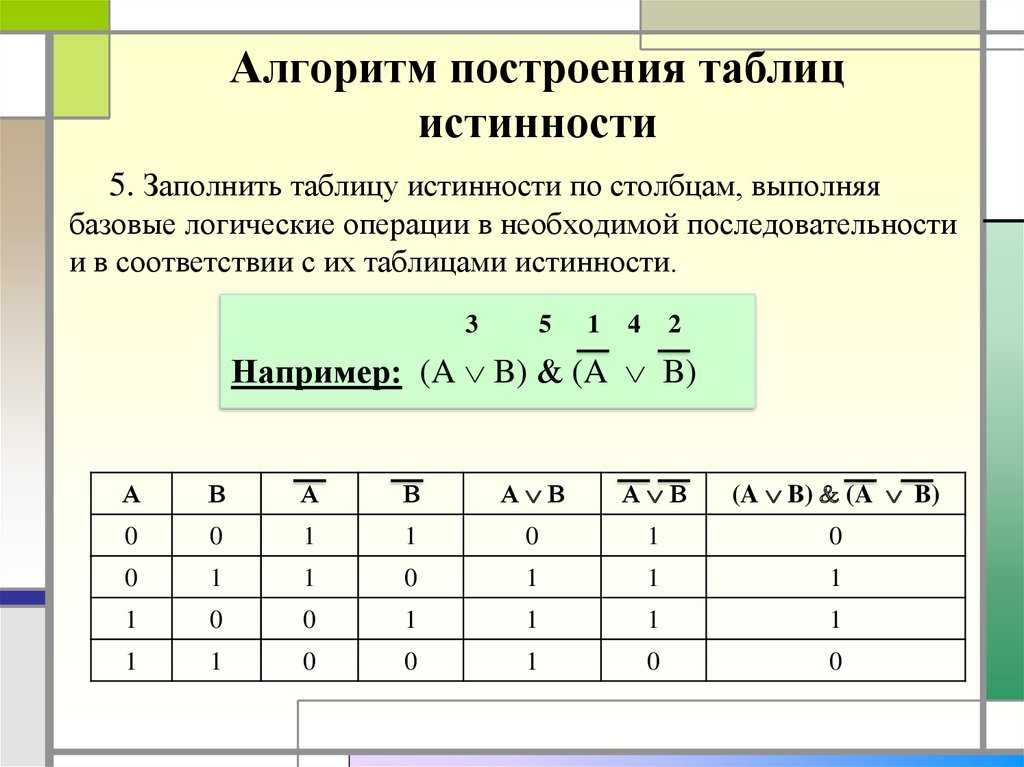
R = «У Кэлвина Баттербола фиолетовые носки».
Я хочу определить истинное значение . Поскольку мне были даны конкретные значения истинности для P, Q, и R, я составил таблицу истинности с одной строкой, используя данные значения для P, Q и R:
Следовательно, утверждение истинно .
Пример. Определить истинное значение заявление
Утверждение » » неверно. Вы не можете сказать действительно ли утверждение «Икабод Ксеркс ест шоколад кексы» истинны или ложны — но это не имеет значения. Если «если» часть утверждения «если-то» ложна, то утверждение «если-то» истинно. (Проверьте правду таблица для тех, кто не уверен в этом!) Так что данное утверждение должно быть истинным.
Два утверждения X и Y логически равны .
эквивалент , если это тавтология. Другой способ сказать
это: Для каждого присвоения значений истинности простым
операторы , составляющие X и Y, операторы X и Y имеют
одинаковые значения истинности.
С практической точки зрения вы можете заменить оператор в доказательство любым логически эквивалентным утверждением.
Чтобы проверить, являются ли X и Y логически эквивалентными, вы можете настроить таблица истинности, чтобы проверить, является ли тавтологией — что есть ли «все Т в столбце». Однако проще настроить таблицу, содержащую X и Y, а затем проверьте, совпадают ли столбцы для X и для Y.
Пример. Покажите, что и логически эквивалентны.
Поскольку столбцы для и идентичны, два оператора логически эквивалент. Эта тавтология называется Условное Разъединение . Вы можете использовать эту эквивалентность для замены условно дизъюнкцией.
Существует бесконечное количество тавтологий и логических эквивалентностей; Я перечислил несколько ниже; более обширный список приведен в конце эта секция.
Когда тавтология имеет форму бикондиционала, два утверждения
которые составляют бикондиционал, логически эквивалентны.
Следовательно, вы
можно заменить одну сторону другой без изменения логического
значение.
Вам часто придется отрицать математическое утверждение. К посмотрим, как это сделать, мы начнем с того, что покажем, как отрицать символические заявления.
Пример. Запишите отрицание следующие операторы, упрощая так, чтобы только простые операторы отрицается.
(а)
(б)
(a) Я отрицаю данное утверждение, затем упрощаю, используя логические эквивалентности. Я дал имена логических эквивалентностей на правильно, чтобы вы могли видеть, какие из них я использовал.
(б)
Я показал это и есть логически эквивалентны в предыдущем примере.
В следующих примерах мы будем отрицать утверждения, написанные словами.
Это более типично для того, что вам нужно делать в математике.
идея состоит в том, чтобы преобразовать слово-выражение в символическое высказывание, затем
используйте логические эквивалентности, как в предыдущем примере.
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Кэлвина нет дома или Бонзо в кино».
Пусть С будет утверждением «Кальвин дома», а В будет заявление «Бонзо в движении». Данное утверждение является . Я должен отрицать утверждение, затем упростите:
Результат: «Кальвин дома, а Бонзо нет на кино».
Пример. Используйте закон Де Моргана, чтобы написать отрицание следующего утверждения, упрощая так, что отрицаются только простые операторы:
«Если Фиби покупает пиццу, то Кэлвин покупает попкорн».
Пусть P будет утверждением «Фиби покупает пиццу», а C будет заявление «Кэлвин покупает попкорн». Данное утверждение является . Чтобы упростить отрицание, я буду использовать тавтологию условной дизъюнкции , которая гласит:
То есть я могу заменить на (или наоборот).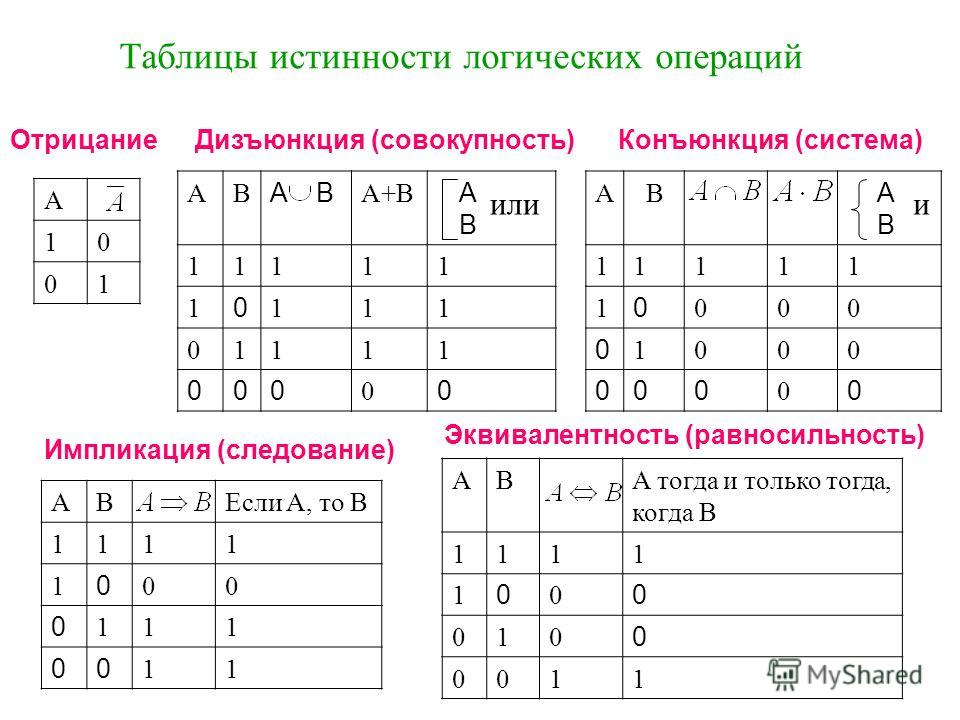
Вот вам и отрицание и упрощение:
Результат: «Фиби покупает пиццу, а Кэлвин не покупает». попкорн».
Далее мы применим нашу работу с таблицами истинности и отрицающими утверждениями к задачи на построение обратной, обратной и противопоставляется утверждению «если-то».
Пример. Замените следующий оператор на его противоположность:
«Если x и y рациональны, то рационально».
По контрапозитивной эквивалентности это утверждение совпадает с «Если не рационально, то это не так что и х, и у рациональны».
Этот ответ правильный в его нынешнем виде, но мы можем выразить его в немного лучший способ, который удаляет некоторые явные отрицания. Большинству людей позитивное утверждение легче понять, чем отрицательное утверждение.
По определению, действительное число равно 9.0411 иррациональный если
это не рационально. Поэтому я мог бы заменить часть «если»
противопоставляется слову «иррационально».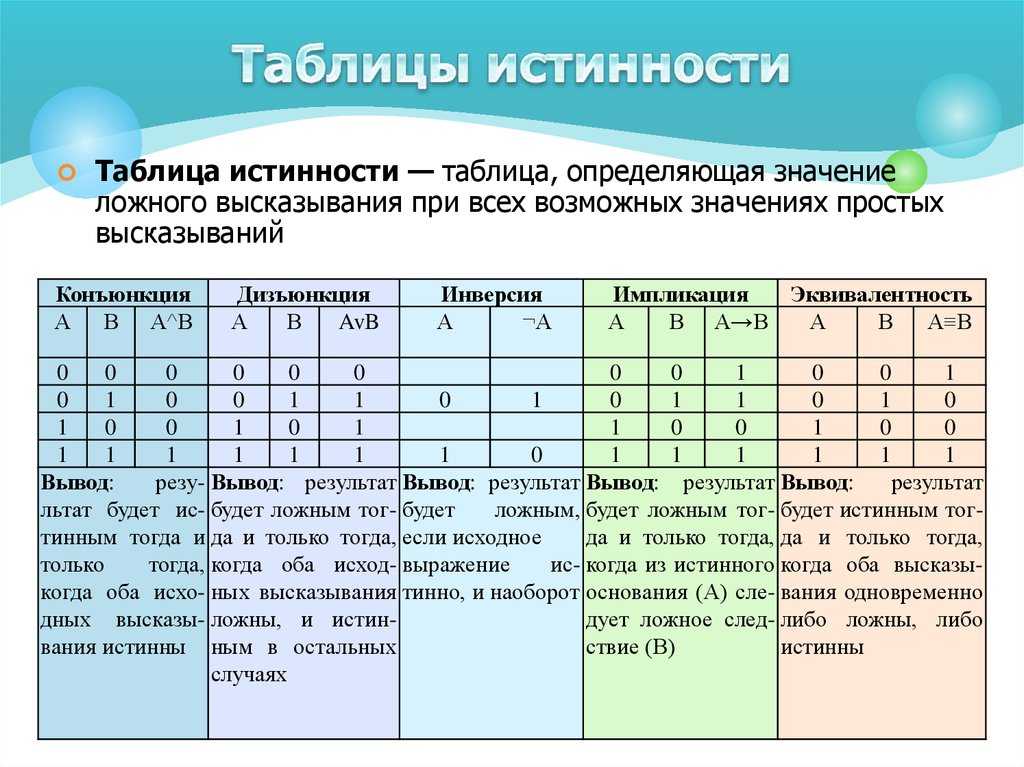
Часть противопоставления «тогда» есть отрицание утверждение «и». Вы могли бы переформулировать это так: «Это не случае, когда и x рационально, и y рационально». (Слово «оба» гарантируют, что отрицание применяется ко всему утверждение «и», а не только «х рационально».)
По закону Де Моргана это эквивалентно следующему: «x не является рациональным или y нерационально». В качестве альтернативы я мог бы сказать: «x есть иррационально или у иррационально».
Собрав все вместе, я мог бы выразить противоположное как: «Если иррационально, то либо х иррационально или у иррационально».
(Как обычно, я добавил слово «либо», чтобы было понятно, что часть «тогда» — это целое утверждение «или».)
Пример. Покажите, что обратное и обратные условные логически эквивалентны.
Пусть условно. Обратное есть. Обратное.
Я мог бы показать, что обратное и обратное эквивалентны
построение таблицы истинности для .
Leave A Comment