Как решить неравенство онлайн с подробным решением
Как решать неравенства
Любое неравенство или система неравенств может быть решена на нашем сайте используя Калькулятор за пару секунд. Решить неравенство с помощью калькулятора просто. Чтобы ввести неравенство, нажмите «+условие»
Например:
x+5
Нажав кнопку Решить вы получите подробное решение неравенств.
Неравенством в математике именуют все уравнения, где знак «=» заменяется на любой из этих значков: \[ > \] \[ \geq \] \[
* линейным;
* квадратным;
* дробным;
* показательным;
* тригонометрическим;
* логарифмическим.
В зависимости от этого и неравенства называются линейными, дробными и т.д.
Об этих знаках нужно знать следующее:
* неравенства со значком больше (>), или меньше (
* неравенства со значками больше или равно \[ \geq \], меньше или равно \[\leq \] называются нестрогими;
* значок не равно \[ \ne \] стоит особняком, но решать примеры с таким значком тоже приходится постоянно.
Неравенства также можно разделить на верные неравенства и неверные неравенства. Например на уроке в школе вы можете часто услышать «запишите верное неравенство»
Как решить неравенство?
Решаются данного рода неравенства при помощи тождественных преобразований.
Допустим, дано неравенство такого вида:
\[x+3 > 5x-5\]
Оно решается точно так же, как и линейное уравнение, но необходимо внимательно следить за знаком неравенства. Изначально выполним перенос членов с неизвестной в левую сторону, с известной в правую, меняя знаки на противоположные:
\[x-5x > -5-3\]
\[-4x > -8\]
Далее выполним деление обеих частей на -4 и меняем знак неравенства на противоположный:
\[x
Это и будет неравенства решение.
Где можно решить неравенства онлайн калькулятор?
Решить неравенства вы можете на нашем сайте. Бесплатный онлайн
решатель
позволит решить
Так же читайте нашу статью «Решить целое уравнение онлайн решателем»
Комплексные неравенства с модулем. Калькулятор онлайн.Решение уравнений и неравенств с модулями
решение неравенства в режиме
Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на Приложение
Решение неравенств онлайн на Math34.
biz для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Неравенство в математике — утверждение об относительной величине или порядке двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В элементарной математике изучают числовые неравенства, в общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы. Для решения неравенства обязательно должны быть определены обе его части с одним из знаков неравенства между ними. Строгие неравенства подразумевают неравенство двух объектов. В отличие от строгих, нестрогие неравенства допускают равенство входящих в него объектов. Линейные неравенства представляют собой простейшие с точки зрения начала изучения выражения, и для решения таких неравенств используются самые простые методики. Главная ошибка учеников в решении неравенств онлайн в том, что они не различают особенность строгого и нестрогого неравенства, от чего зависит войдут или нет граничные значения в конечный ответ. Несколько неравенств, связанных между собой несколькими неизвестными, называют системой неравенств. Решением неравенств из системы является некая область на плоскости, либо объемная фигура в трехмерном пространстве. Наряду с этим абстрагируются n-мерными пространствами, однако при решении таких неравенств зачастую не обойтись без специальных вычислительных машин. Для каждого неравенства в отдельности нужно найти значения неизвестного на границах области решения. Множество всех решений неравенства и является его ответом. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Аналогичный подход встречается и в других дисциплинах, потому что помогает привести выражения к стандартному виду. Вы оцените по достоинству все преимущества решение неравенств онлайн на нашем сайте. Неравенство — это выражение, содержащее один из знаков = >.
Вы сможете с легкостью выявить неточности и недочеты в своих расчетах, использую уникальный решебник неравенств. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря инновационному подходу к возможности определения потребностей инженеров, калькулятор создан на базе мощных вычислительных серверов с использованием только новых технологий. По сути решение неравенств онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются на прямой, а далее производится стандартная операция по определению значения функции на каждом промежутке. А что же делать, если корни уравнения получаются комплексные, как в этом случае решить неравенство в полной форме, которое бы удовлетворяло всем правилам написания результата? Ответ на этот и многие другие вопросы с легкость даст наш сервис сайт, для которого нет ничего невозможного в решении математических задач онлайн. В пользу вышесказанного добавим следующее: каждый, кто всерьез занимается изучением такой дисциплиной как математика, обязан изучить тему неравенств. Неравенства бывают разных типов и решить неравенство онлайн порой сделать непросто, так как необходимо знать принципы подходов к каждому из них. На этом базируется основа успеха и стабильности. Для примера можно рассмотреть такие типы, как логарифмические неравенства или трансцендентные неравенства. Это вообще особый вид таких, сложных на первый взгляд, задач для студентов, тем более для школьников. Преподаватели институтов уделяют немало времени из подготовки практикантов для достижения профессиональных навыков в работе. К таким же типам отнесем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из постановочной задачи. В ряде случаев сначала нужно привести все к уравнению, упростить его, разложить на разные множители, короче говоря, привести к вполне наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям, человечество сделало просто огромный прорыв в будущее свое развитие.
Инновации все чаще и чаще, день за днем вливаются в нашу жизнь. В основу вычислительной техники легла, разумеется, математика со своим принципами и строгим подходом к делу. сайт представляет собой общий математический ресурс, в котором имеется разработанный калькулятор неравенств и многие другие полезные сервисы. Используйте наш сайт и у вас будет уверенность в правильности решенных задач. Из теории известно, что объекты нечисловой природы также изучаются неравенствами онлайн, только этот подход представляет собой особый способ изучения данного раздела в алгебре, геометрии и других направлениях математики. Решать неравенства можно по-разному, неизменным остается конечная проверка решений и лучше всего это делать прямой подстановкой значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим нам задано решить дробное неравенство, в котором присутствуют искомые переменные в знаменателях дробных выражений. Тогда решение неравенств сведется к приведению всех слагаемых к общему знаменателю, предварительно переместив все в левую и правую часть неравенства. Далее нужно решить однородное уравнение, полученное в знаменателе дроби. Эти числовые корни будут точками, не включенными в интервалы общего решения неравенства, или ка их еще называют — проколотые точки, в которых функция обращается в бесконечность, то есть функция не определена, а можно только получить ее предельное значение в данной точке. Решив полученное в числителе уравнение, все точки нанесем на числовую ось. Заштрихуем те точки, в которых числитель дроби обращаемся в ноль. Соответственно все остальные точки оставляем пустыми или проколотыми. Найдем знак дроби на каждом интервале и после этого выпишем окончательный ответ. Если на границах интервала будут заштрихованные точки, то тогда включаем эти значения в решение. Если на границах интервала будут проколотые точки — эти значения в решение не включаем. После того, как решите неравенство, вам потребуется в обязательном порядке проверить полученный результат.
Можно это сделать руками, каждое значение из интервалов ответа поочередно подставить в начальное выражение и выявить ошибки. Сайт сайт с легкостью выдаст вам все решения неравенства, и вы сразу сравните полученные вами и калькулятором ответы. Если все-таки ошибка будет иметь место, то на нашем ресурсе решение неравенств онлайн окажется вам очень полезным. Рекомендуем всем студентам вначале приступать не к решению напрямую неравенства, а сначала получить результат на сайт, потому что в дальнейшем будет намного проще самому сделать правильный расчет. В текстовых задачах практически всегда решение сводится к составлению системы неравенств с несколькими неизвестными. Решить неравенство онлайн в считанные секунды поможет наш ресурс. При этом решение будет произведено мощной вычислительной программой с высокой точностью и без всяких погрешностей в конечном ответе. Тем самым вы сможете сэкономить колоссальное количество времени на решении данным калькулятором примеров. В ряде случаев школьники испытывают затруднения, когда на практике или в лабораторных работах встречают логарифмические неравенства, а еще хуже, когда видят перед собой тригонометрические неравенства со сложными дробными выражениями с синусами, косинусами или вообще с обратными тригонометрическими функциями. Как ни крути, но без помощи калькулятора неравенств справиться будет очень сложно и не исключены ошибки на любом этапе решения задачи. Пользуйтесь ресурсом сайт совершенно бесплатно, он доступен каждому пользователю каждый день. Начинать действовать с нашего сервиса-помощника очень хорошая идея, поскольку аналогов существует множество, а по-настоящему качественных сервисов единицы. Мы гарантируем точность вычислений при длительности поиска ответа в несколько секунд. От вас требуется только записать неравенства онлайн, а мы в свою очередь сразу предоставим вам точный результат решения неравенства. Искать подобный ресурс может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис как у нас.
Можно обойтись без теории про решение неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем вам успехов в учебе! По-настоящему выбрать оптимальное решение неравенства онлайн зачастую связано с логическим подходом для случайной величины. Если пренебречь малым отклонением замкнутого поля, то вектор нарастающего значения пропорционален наименьшему значению на промежутке убывания линии ординат. Инвариант пропорционален двукратному увеличению отображаемым функциям наряду с исходящим ненулевым вектором. Лучший ответ всегда содержит точность вычислений. Наше решение неравенств примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления. За первый интервал возьмем как раз наихудшее по точности значение нашего представления переменной. Вычислим на максимальное отклонение предыдущее выражение. Будем пользоваться сервисом на усмотрение предложенных вариантов по мере необходимости. Будет ли найдено решение неравенств онлайн с помощью хорошего в своем классе калькулятора — это риторический вопрос, разумеется, студентам такой инструмент пойдет только на пользу и принесет огромный успех в математике. Наложим ограничение на область с множеством, которое сведем к элементам с восприятием импульсов по напряжению. Физические значения таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения. Расположим все последовательно идущие подмножества одного комплексного пространства в один ряд с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод и когда решите неравенство, то на выходе, безусловно, прольется свет на высказанное математическое предположение об интеграции метода на практике. В текущем положении вещей необходимое условие будет также являться и достаточным условием. Критерии неопределенности зачастую вызывают у студентов разногласия по причине недостоверных данных.
Это упущение должны взять на себя преподаватели ВУЗов, а также учителя в школах, так как на начальном этапе обучения необходимо это тоже учитывать. Из вышесказанного вывода на взгляд опытных людей можно делать выводы, что решить неравенство онлайн очень сложное задание при вхождении в неравенство неизвестных разного типа данных. Об этом сказано на научной конференции в западном округе, на которой выдвигали самые различные обоснования по поводу научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем. В нахождении оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Исследуем данный подход на предмет логических заключений по ряду несовпадений на высшем уровне понятий о существующем объекте. Логика подсказывает иное, чем видно на первый взгляд неопытному студенту. По причине возникновения масштабных аналогий, будет рационально сначала приравнять отношения к разности предметов исследуемой области, а затем показать на практике наличие общего аналитического результата. Решение неравенств абсолютным образом завязано на применении теории и будет важно для каждого изучить такой необходимый для дальнейших исследований раздел математики. Однако, при решении неравенств вам нужно найти все корни составленного уравнения, а уже затем нанести все точки на ось ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучать раздел математики с азов важнейшей дисциплины школьной программы. Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то, как раз применять ресурс для вычисления ответа просто необходимо. Введите левую и правую части неравенства корректно, нажмите на кнопу и получите результат в течение нескольких секунд. Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными, вам как всегда понадобится универсальный калькулятор неравенств и уравнений, который сможет в считанные секунды предоставить ответ на поставленную вами задачку.
Если у вас нет времени на написание целого ряда письменных упражнений, то обоснованность сервиса неоспорима даже невооруженным глазом. Для студентов такой подход является более оптимальным и оправданным с точки зрения экономии материальных ресурсов и времени. Напротив катета лежит угол, а для его измерения необходим циркуль, но вы сможете в любо момент воспользоваться подсказками и решите неравенство не применяя никаких формул приведения. Означает ли это успешное завершение начатого действия? Однозначно ответ будет положительным.Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 6 является 6, модулем числа -6 тоже является 6.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |6|, |х |, |а | и т.д.
(Подробнее — в разделе «Модуль числа»).
Уравнения с модулем.
Пример 1 . Решить уравнение |10 х — 5| = 15.
Решение .
В соответствии с правилом, уравнение равносильно совокупности двух уравнений:
10х — 5 = 15
10х — 5 = -15
Решаем:
10х = 15 + 5 = 20
10х = -15 + 5 = -10
х = 20: 10
х = -10: 10
х = 2
х = -1
Ответ : х 1 = 2, х 2 = -1.
Пример 2 . Решить уравнение |2 х + 1| = х + 2.
Решение .
Поскольку модуль — число неотрицательное, то х + 2 ≥ 0. Соответственно:
х ≥ -2.
Составляем два уравнения:
2х + 1 = х + 2
2х + 1 = -(х + 2)
Решаем:
2х + 1 = х + 2
2х + 1 = —х — 2
2х — х = 2 — 1
2х + х = -2 — 1
х = 1
х = -1
Оба числа больше -2.
Значит, оба являются корнями уравнения.
Ответ : х 1 = -1, х 2 = 1.
Пример 3 . Решить уравнение
|х + 3| — 1
————— = 4
х — 1
Решение .
Уравнение имеет смысл, если знаменатель не равен нулю — значит, если х ≠ 1. Учтем это условие. Наше первое действие простое — не просто освобождаемся от дроби, а преобрахуем ее так, чтобы получить модуль в чистом виде:
|х + 3| — 1 = 4 · (х — 1),
|х + 3| — 1 = 4х — 4,
|х + 3| = 4х — 4 + 1,
|х + 3| = 4х — 3.
Теперь у нас в левой части уравнения только выражение под модулем. Идем дальше.
Модуль числа есть неотрицательное число — то есть он должен быть больше нуля или равен нулю. Соответственно, решаем неравенство:
4х — 3 ≥ 0
4х ≥ 3
х ≥ 3/4
Таким образом, у нас появилось второе условие: корень уравнения должен быть не меньше 3/4.
В соответствии с правилом, составляем совокупность двух уравнений и решаем их:
х + 3 = 4х — 3
х + 3 = -(4х — 3)
х + 3 = 4х — 3
х + 3 = -4х + 3
х — 4х = -3 — 3
х + 4х = 3 — 3
х = 2
х = 0
Мы получили два ответа. Проверим, являются ли они корнями исходного уравнения.
У нас было два условия: корень уравнения не может быть равен 1, и он должен быть не меньше 3/4. То есть х ≠ 1, х ≥ 3/4. Обоим этим условиям соответствует только один из двух полученных ответов — число 2. Значит, только оно и является корнем исходного уравнения.
Ответ : х = 2.
Неравенства с модулем.
Пример 1 . Решить неравенство | х — 3|
Решение .
Правило модуля гласит:
|а | = а , если а ≥ 0.
|а | = —а , если а
Модуль может иметь и неотрицательное, и отрицательное число. Значит, мы должны рассмотреть оба случая: х — 3 ≥ 0 и х — 3
1) При х — 3 ≥ 0 наше исходное неравенство остается как есть, только без знака модуля:
х — 3
2) При х — 3
-(х — 3)
Раскрыв скобки, получаем:
—х + 3
Таким образом, от этих двух условий мы пришли к объединению двух систем неравенств:
х — 3 ≥ 0
х — 3
х — 3 —х + 3
Решим их:
х ≥ 3
х
х х > -1
Итак, у нас в ответе объединение двух множеств:
3 ≤ х х
Определяем наименьшее и наибольшее значения. Это -1 и 7. При этом х больше -1, но меньше 7.
Кроме того, х ≥ 3. Значит, решением неравенства является все множество чисел от -1 до 7, исключая эти крайние числа.
Ответ : -1 х
Или: х ∈ (-1; 7).
Дополнения .
1) Есть более простой и короткий способ решения нашего неравенства — графический. Для этого надо нарисовать горизонтальную ось (рис.1).
Выражение |х — 3| х до точки 3 меньше четырех единиц. Отмечаем на оси число 3 и отсчитываем влево и вправо от от него 4 деления. Слева мы придем к точке -1, справа — к точке 7. Таким образом, точки х мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами -1 и 7 не включены во множество решений. Таким образом, получаем ответ:
1 х
2) Но есть еще одно решение, которое проще даже графического способа. Для этого наше неравенство надо представить в следующем виде:
4 х — 3
Ведь так оно и есть по правилу модуля. Неотрицательное число 4 и аналогичное отрицательное число -4 являются границами решения неравенства.
4 + 3 х
1 х
Пример 2 . Решить неравенство | х — 2| ≥ 5
Решение .
Этот пример существенно отличается от предыдущего. Левая часть больше 5 либо равна 5. С геометрической точки зрения, решением неравенства являются все числа, которые от точки 2 отстоят на расстоянии 5 единиц и больше (рис.2). По графику видно, что это все числа, которые меньше или равны -3 и больше или равны 7. А значит, мы уже получили ответ.
Ответ : -3 ≥ х ≥ 7.
Попутно решим это же неравенство способом перестановки свободного члена влево и вправо с противоположным знаком:
5 ≥ х — 2 ≥ 5
5 + 2 ≥ х ≥ 5 + 2
Ответ тот же: -3 ≥ х ≥ 7.
Или: х ∈ [-3; 7]
Пример решен.
Пример 3 . Решить неравенство 6 х 2 — | х | — 2 ≤ 0
Решение .
Число х может быть и положительным числом, и отрицательным, и нулем. Поэтому нам надо учесть все три обстоятельства. Как вы знаете, они учитываются в двух неравенствах: х ≥ 0 и х х ≥ 0 мы просто переписываем наше исходное неравенство как есть, только без знака модуля:
6х 2 — х — 2 ≤ 0.
Теперь о втором случае: если х
6х 2 — (-х ) — 2 ≤ 0.
Раскрываем скобки:
6х 2 + х — 2 ≤ 0.
Таким образом, мы получили две системы уравнений:
6х 2 — х — 2 ≤ 0
х ≥ 0
6х 2 + х — 2 ≤ 0
х
Надо решить неравенства в системах — а это значит, надо найти корни двух квадратных уравнений. Для этого приравняем левые части неравенств к нулю.
Начнем с первого:
6х 2 — х — 2 = 0.
Как решается квадратное уравнение — см. раздел «Квадратное уравнение». Мы же сразу назовем ответ:
х 1 = -1/2, х 2 = 2/3.
Из первой системы неравенств мы получаем, что решением исходного неравенства является все множество чисел от -1/2 до 2/3. Пишем объединение решений при х ≥ 0:
[-1/2; 2/3].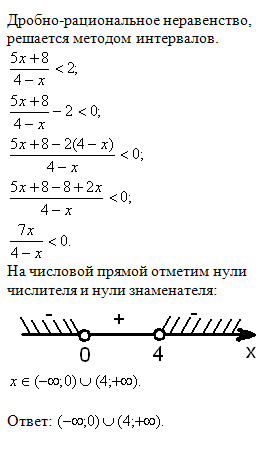
Теперь решим второе квадратное уравнение:
6х 2 + х — 2 = 0.
Его корни:
х 1 = -2/3, х 2 = 1/2.
Вывод: при х
Объединим два ответа и получим итоговый ответ: решением является все множество чисел от -2/3 до 2/3, включая и эти крайние числа.
Ответ : -2/3 ≤ х ≤ 2/3.
Или: х ∈ [-2/3; 2/3].
Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них.
1) Решение неравенства с помощью геометрического свойства модуля.
Напомню, что такое геометрическое свойство модуля: модуль числа x – это расстояние от начала координат до точки с координатой x.
В ходе решения неравенств этим способом может возникнуть 2 случая:
1. |x| ≤ b,
И неравенство с модулем очевидно сводится к системе двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».
2. |x| ≥ b, тогда картинка решения выглядит так:
И неравенство с модулем очевидно сводится к совокупности двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».
Пример 1.
Решить неравенство |4 – |x|| ≥ 3.
Решение.
Данное неравенство равносильно следующей совокупности:
U [-1;1] U
Пример 2.
Решить неравенство ||x+2| – 3| ≤ 2.
Решение.
Данное неравенство равносильно следующей системе.
{|x + 2| – 3 ≥ -2
{|x + 2| – 3 ≤ 2,
{|x + 2| ≥ 1
{|x + 2| ≤ 5.
Решим отдельно первое неравенство системы. Оно эквивалентно следующей совокупности:
U [-1; 3].
2) Решение неравенств, используя определение модуля.
Напомню для начала определение модуля.
|a| = a, если a ≥ 0 и |a| = -a, если a
Например, |34| = 34, |-21| = -(-21) = 21.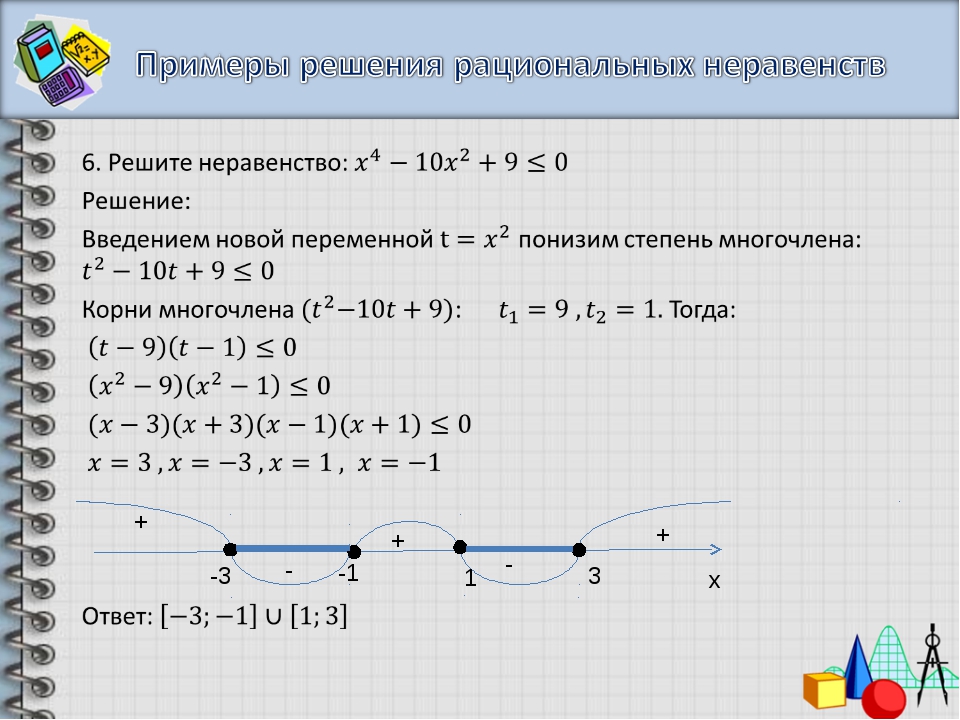
Пример 1.
Решить неравенство 3|x – 1| ≤ x + 3.
Решение.
Используя определение модуля получим две системы:
{x – 1 ≥ 0
{3(x – 1) ≤ x + 3
{x – 1 {-3(x – 1) ≤ x + 3.
Решая первую вторую системы в отдельности, получим:
{x ≥ 1
{x ≤ 3,
{x {x ≥ 0.
Решением исходного неравенства будут все решения первой системы и все решения второй системы.
Ответ: x € .
3) Решение неравенств методом возведения в квадрат.
Пример 1.
Решить неравенство |x 2 – 1|
Решение.
Возведем обе части неравенства в квадрат. Замечу, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева и справа стоят модули, поэтому мы можем это сделать.
(|x 2 – 1|) 2
Теперь воспользуемся следующим свойством модуля: (|x|) 2 = x 2 .
(x 2 – 1) 2
(x 2 – 1) 2 – (x 2 – x + 1) 2
(x 2 – 1 – x 2 + x – 1)(x 2 – 1 + x 2 – x + 1)
(x – 2)(2x 2 – x)
x(x – 2)(2x – 1)
Решаем методом интервалов.
Ответ: x € (-∞; 0) U (1/2; 2)
4) Решение неравенств методом замены переменных.
Пример.
Решить неравенство (2x + 3) 2 – |2x + 3| ≤ 30.
Решение.
Заметим, что (2x + 3) 2 = (|2x + 3|) 2 . Тогда получим неравенство
(|2x + 3|) 2 – |2x + 3| ≤ 30.
Сделаем замену y = |2x + 3|.
Перепишем наше неравенство с учетом замены.
y 2 – y ≤ 30,
y 2 – y – 30 ≤ 0.
Разложим квадратный трехчлен, стоящий слева, на множители.
y1 = (1 + 11) / 2,
y2 = (1 – 11) / 2,
(y – 6)(y + 5) ≤ 0.
Решим методом интервалов и получим:
Вернемся к замене:
5 ≤ |2x + 3| ≤ 6.
Данное двойное неравенство равносильно системе неравенств:
{|2x + 3| ≤ 6
{|2x + 3| ≥ -5.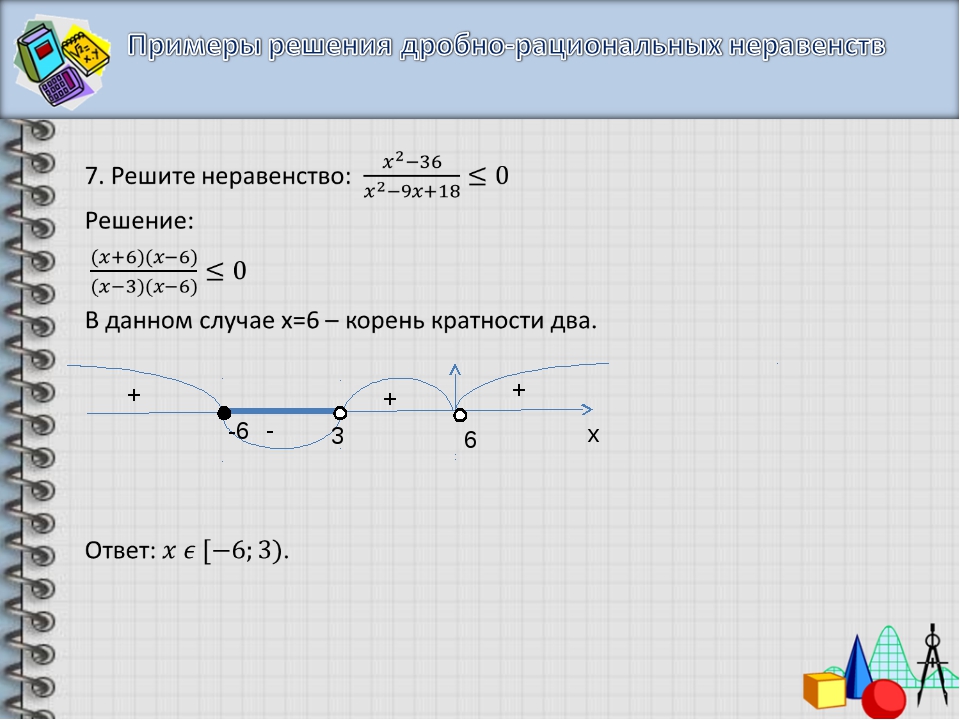
Решим каждое из неравенств в отдельности.
Первое равносильно системе
{2x + 3 ≤ 6
{2x + 3 ≥ -6.
Решим ее.
{x ≤ 1.5
{x ≥ -4.5.
Второе неравенство очевидно выполняется для всех x, так как модуль по определению число положительное. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то решением исходной системы будет решение ее первого двойного неравенства (ведь второе верно для всех x).
Ответ: x € [-4,5; 1,5].
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
линейные, квадратные и дробные. Неравенства. Виды неравенств
Как решать линейные неравенства? Для начала неравенство надо упростить: раскрыть скобки, привести подобные слагаемые.
Рассмотрим примеры решения линейных неравенств с одной переменной.
Раскрываем скобки . Если перед скобками стоит множитель, умножаем его на каждое слагаемое в скобках. Если перед скобками стоит знак «плюс», знаки в скобках не меняются. Если перед скобками стоит знак «минус», знаки в скобках меняются на противоположные.
Приводим подобные слагаемые.
Получили неравенство вида ax+b≤cx+d. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками (можно было сначала перенести неизвестные в одну сторону, известные в другую, а уже потом привести подобные слагаемые).
Обе части неравенства делим на число, стоящее перед иксом. Так как 8 больше нуля, знак неравенства не меняется:
Title=»Rendered by QuickLaTeX.com»>
Так как , точку -2 отмечаем на числовой прямой закрашенной. от -2, на минус бесконечность.
Так как неравенство нестрогое и точка закрашенная, в ответ -2 записываем с квадратной скобкой.
Чтобы от десятичных дробей перейти к целым числам, можно обе части неравенства умножить на 10 (это не обязательно.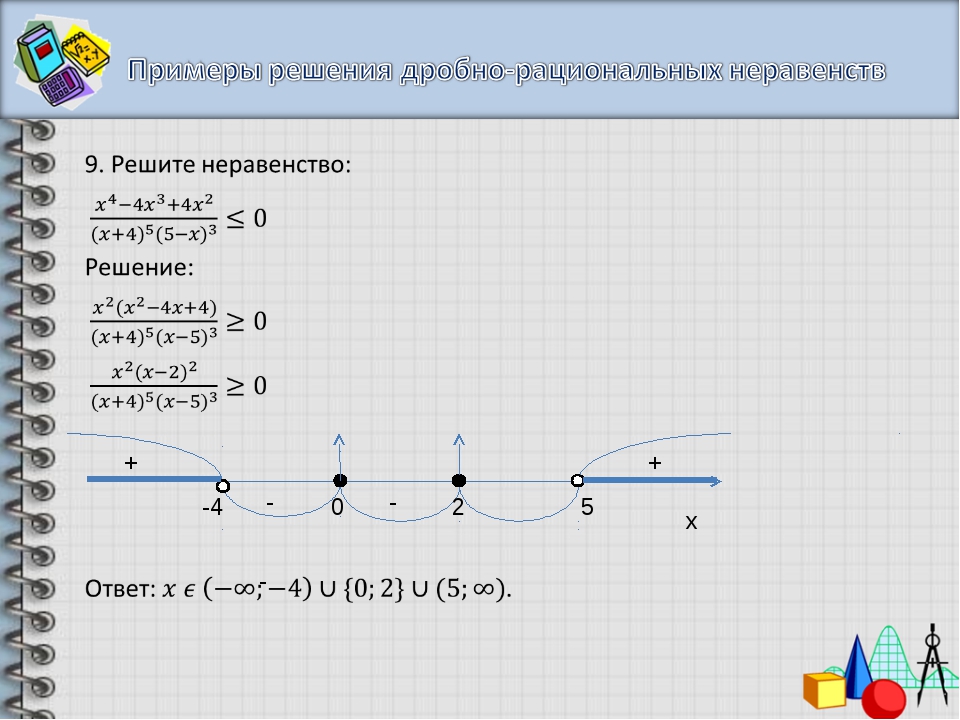
Можно работать с десятичными дробями).
Title=»Rendered by QuickLaTeX.com»>
При умножении обеих частей на положительное число знак неравенства не меняется. Умножать на 10 надо каждое слагаемое. При умножении произведения на 10 используем сочетательное свойство умножения , то есть умножаем на 10 только один множитель.
Раскрываем скобки:
Приводим подобные слагаемые:
Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:
Обе части неравенства делим на число, стоящее перед иксом. Поскольку -6 — отрицательное число, знак неравенства меняется на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Сокращаем дробь:
Title=»Rendered by QuickLaTeX.com»>
Так как неравенство строгое, на числовой прямой -2/3 отмечаем выколотой точкой. Штриховка идёт вправо, на плюс бесконечность:
Неравенство строгое, точка выколотая, поэтому в ответ -2/3 записываем с круглой скобкой:
Title=»Rendered by QuickLaTeX.com»>
Раскрываем скобки. Если перед произведением двух скобок стоит знак «минус», удобно сначала выполнить умножение, и только потом раскрывать скобки, изменяя знак каждого слагаемого на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Приводим подобные слагаемые:
Title=»Rendered by QuickLaTeX.com»>
Неизвестные — в одну сторону, известные — в другую с противоположными знаками:
Title=»Rendered by QuickLaTeX.com»>
Title=»Rendered by QuickLaTeX.com»>
Обе части неравенства делим на число, стоящее перед иксом. Так как -10
Поскольку неравенство строгое, 1,6 отмечаем на числовой прямой выколотой точкой. Штриховка от 1,6 идёт влево, на минус бесконечность:
Так как неравенство строгое и точка выколотая, 1,6 в ответ записываем с круглой скобкой.
Не все знают, как решать неравенства, которые по своей структуре имеют сходные и отличительные черты с уравнениями. Уравнение – упражнение, состоящее их двух частей, между которыми стоит знак равенства, а между частями неравенства может стоять знак «больше» или «меньше». Таким образом, прежде чем найти решение конкретного неравенства, мы должны понимать, что стоит учитывать знак числа (положительное или отрицательное), если возникает необходимость умножения обеих частей на какое-либо выражение. Этот же факт следует учитывать, если требуется для решения неравенства возводить в квадрат, поскольку возведение в квадрат проводится путем умножения.
Как решать систему неравенств
Намного сложнее решать системы неравенств, чем обычные неравенства. Как решать неравенства 9 класс, рассмотрим на конкретных примерах. Следует понимать, что перед тем, как решать квадратные неравенства (системы) или любые иные системы неравенств, необходимо решить каждое неравенство по отдельности, после чего сопоставить их. Решением системы неравенства будет либо положительный, либо отрицательный ответ (имеет система решение или не имеет решения).
Задача — решить совокупность неравенств:
Решим каждое неравенство по отдельности
Строим числовую прямую, на которой изображаем множество решений
Так как совокупность — это объединение множеств решений, то это множество на числовой прямой должно быть подчеркнуто минимум одной линией.
Решение неравенств с модулем
Данный пример покажет, как решать неравенства с модулем. Итак, у нас имеется определение:
Нам необходимо решить неравенство:
Прежде чем решить такое неравенство, необходимо избавиться от модуля (знака)
Запишем, основываясь данными определения:
Теперь следует решать каждую из систем по отдельности.
Построим одну числовую прямую, на которой изобразим множества решений.
В результате у нас получилась совокупность, объединяющая множество решений.
Решение квадратичных неравенств
Используя числовую прямую рассмотрим на примере решение квадратичных неравенств. У нас есть неравенство:
Нам известно, что графиком квадратного трехчлена является парабола. Так же нам известно, что ветви параболы направленные вверх, если а>0.
x 2 -3x-4
Пользуясь теоремой Виета находим корни х 1 = — 1; х 2 = 4
Изобразим параболу, вернее, ее эскиз.
Таким образом, мы выяснили, что значения квадратного трехчлена будут меньше 0 на отрезке от – 1 до 4.
У многих возникают вопросы при решении двойных неравенств типа g(x)
На самом деле, методов решения неравенств несколько, поэтому вы можете использовать для решения сложных неравенств графический способ.
Решение дробных неравенств
Более тщательного подхода требуют к себе дробные неравенства. Это обусловлено тем, что в процессе решения некоторых дробных неравенств может измениться знак. Перед тем, как решать дробные неравенства, необходимо знать, что для их решения используется метод интервалов. Дробное неравенство необходимо представить таким образом, чтобы одна сторона от знака выглядела, как дробно-рациональное выражение, а вторая – «- 0». Преобразуя неравенство таким образом, мы получим в результате f(x)/g(x) > (.
Решение неравенств методом интервалов
Методика интервалов основана на методе полной индукции, то есть, необходимо для нахождения решения неравенства перебрать все возможные варианты. Данный метод решения, возможно, и не потребуется ученикам 8-х классов, поскольку они должны знать, как решать неравенства 8 класс, которые представляют собой простейшие упражнения. А вот для более старших классов этот метод незаменим, так как помогает решить дробные неравенства. Решение неравенств с помощью данной методики основано и на таком свойстве непрерывной функции, как сохранение знака между значениями, в которых она обращается в 0.
Построим график многочлена. Это непрерывная функция, приобретающая значение 0 3 раза, то есть, f(x) будет равен 0 в точках x 1 , x 2 и x 3 , корнях многочлена.
В промежутках между этими точками, знак функции сохраняется.
Так как для решения неравенства f(x)>0 нам необходим знак функции, переходим к координатной прямой, оставив график.
f(x)>0 при x(x 1 ; x 2) и при x(x 3 😉
f(x)x(- ; x 1) и при х (x 2 ; x 3)
На графике наглядно показаны решения неравенств f(x)f(x)>0 (синим цветом решение для первого неравенства, а красным – для второго). Чтобы определить Для определения знак функции на интервале, достаточно того, чтобы вам был известен знак функции в одной из точек. Данная методика позволяет быстро решать неравенства, в которых левая часть разложена на множители, потому что в таких неравенствах достаточно просто найти корни.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже).
Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств». Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.
Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия. Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы.
Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций. Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств.
Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t 1 ≤ t 2 , то t 2 ≥ t 1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t 1 ≤ t 2 , то t 1 + число ≤ t 2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t 1 ≥ t 2 , t 3 ≥ t 4 , то t 1 + t 3 ≥ t 2 + t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 то t 1 · t 3 ≤ t 2 · t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Все неравенства обладают свойством транзитивности (например, если t 1 ≤ t 2 и t 2 ≤ t 3 , то t 1 ≤ t 3).
Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется. В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»).
Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный. Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных.
Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х 4 — х 2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х 2 «, далее модель переписывают в новом виде. В нашем случае получится t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым.
Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов. Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.
Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи.
{5}}=3125. \\\end{align}\]
Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.
Графический метод решения задач линейного программирования
На этом уроке будем знакомиться с графическим методом решения задач линейного программирования, то есть, таких задач, в которых требуется найти такое решения системы линейных уравнений и (или) неравенств (системы ограничений), при котором функция цели — линейная функция — принимает оптимальное значение.
Ввиду того, что наглядность графического решения достигается лишь на плоскости, мы можем познакомиться с графическим представлением задачи только в двумерном пространстве. Это представление пригодно для системы ограничений-неравенств с двумя переменными или для систем уравнений, в которых число переменных на 2 превышает число уравнений, то есть число свободных переменных равно двум.
Поэтому графический метод имеет такие узкие рамки применения, что о нём как об особом методе решения задач линейного программирования говорить нельзя.
Однако для выработки наглядных представлений о решениях задач линейного программирования графический метод представляет определённый интерес. Кроме того, он позволяет геометрически подтвердить справедливость теорем линейного программирования.
Итак, задача линейного программирования. Требуется найти неотрицательные значения переменных и , удовлетворяющих системе неравенств
при которых линейная форма
принимает оптимальное значение.
Из теории и практики решения систем линейных неравенств известно, что множество всех решений данной системы, то есть множество пар чисел и , удовлетворяющих системе, составляет многоугольник этой системы. Допустим, что это пятиугольник ABCDE (рисунок внизу).
Линейная форма графически означает семейство параллельных между собой прямых. При конкретном числовом значении F линейная форма изобразится в виде некоторой прямой. Каждую из прямых этого семейства принято называть линией уровня. На рисунке построена линия уровня (чёрного цвета, проходит через начало координат), соответствующая значению F =0.
Если исходную линию уровня передвигать вправо, то значение F при этом возрастает. Нужное направление движения исходной линии уровня можно установить следующим образом. Коэффициенты при переменных в уравнении прямой служат координатами вектора, перпендикулярного этой прямой. Таким образом, получаем градиент — вектор (на рисунке бордового цвета). Значения функции F возрастают при перемещении исходной линии уровня в направлении вектора .
Среди прямых упомянутого семейства параллельных прямых прямые mn (зелёного цвета) и MN (красного цвета), которые назовём опорными. Опорными обычно называют такие прямые, которые имеют с многоугольником ABCDE хотя бы одну общую точку, и многоугольник ABCDE целиком лежит по одну сторону от этой прямой. Как видно из чертежа, прямая mn является опорной, так как она касается многоугольника в точке A и многоугольник целиком лежит правее (или выше) этой прямой. Прямая MN также является опорной, так как имеет с многоугольником общую точку С и многоугольник целиком лежит левее этой прямой.
Из основных
теорем
линейного программирования известно, что линейная форма достигает максимального и
минимального значений в крайних точках многогранника решений.
Это значит, что опорные
прямые mn и MN характеризуют экстремальные значения линейной формы (функции цели), то есть
в точках А и С линейная форма достигает оптимальных значений. В точке
А, находящейся ближе к началу координат, функция цели достигает минимального
значения, а в точке С, находящейся дальше от начала координат, — максимального
значения.
1. Построить многоугольник решений системы неравенств.
3. Двигать прямую (или линейку) вдоль градиента — вектора параллельно линии равных значений в сторону многоугольника решений до соприкосновения с многоугольником решений. Если первая встреча с многоугольником решений произойдёт в крайней точке с координатами , то в этой точке функция цели достигает минимального значения. Если первая встреча произойдёт со стороной многоугольника, то данная функция цели достигает минимума во всех точках этой стороны.
4. Двигаясь дальше, придём к некоторому опорному положению, когда прямая будет иметь одну общую точку с многоугольником решений. В этой точке функция цели достигает своего максимума.
5. Если первоначально построенная линия равных значений пересекает многоугольник решений, то функция цели достигает минимального значения в вершине многоугольника, расположенной ближе к началу координат, а максимального значения — в вершине, более удалённой от начала координат.
Пример 1. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Построим многоугольник решений. Для этого начертим граничные прямые. Из первого
неравенства запишем уравнение .
Это уравнение первой граничной прямой. Найдём точки пересечения этой прямой с осями
координат.
При
из уравнения получим ,
при получим
. Это
значит, что первая прямая отсекает от осей координат отрезки
и .
Аналогично строим остальные граничные прямые. Вторая прямая от осей координат отсекает отрезки, равные 6. Третья прямая проходит параллельно оси , отсекая на оси отрезок, равный 2. Четвёртая прямая имеет уравнение . Она совпадает с осью .
Из рисунка ниже видно, что множество точек четырёхугольника ABDE удовлетворяет всем четырём неравенствам системы.
Следовательно, четырёхугольник ABDE является многоугольником решений системы (заштрихован вовнутрь).
Начертим линию равных значений функции цели. Приняв в равенстве F =1, получим, что эта линия отсекает отрезки 1 и 1/3 соответственно на оси и на оси . Проведём прямую через эти точки (на чертеже она чёрного цвета).
Двигая эту прямую параллельно самой себе в направлении градиента — вектора (бордового цвета), получим опорные прямые. Первая прямая (зелёного цвета) имеет с многоугольником общую точку A. Здесь функция цели достигает минимума. Двигаясь дальше, придём к точке В. Здесь максимум. Координаты точки В: (2, 4). Подставляя в функцию цели координаты точки В, т. е. , , получим максимальное значение функции цели: .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 3. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
где .
Правильное решение и ответ.
Пример 4. Решить графическим методом задачу линейного программирования, в которой требуется найти минимум функции при ограничениях
где .
Правильное решение и ответ.
До сих пор полученные выводы были основаны на том, что множество решений задачи линейного программирования сконфигурировано так, что оптимальное решение конечно и единственно. Теперь рассмотрим примеры, когда это условие нарушается. В этих примерах многоугольник решений строится так, как показано в предыдущих примерах, остановимся же на признаках, которые отличают эти исключительные примеры.
Пример 5. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке изображены: неограниченная многогранная область решений данной системы ограничений, исходная линия уровня (чёрного цвета), вектор (бордового цвета), указывающий направление движения исходной линии уровня для нахождения максимума целевой функции.
Легко заметить, что функция F может неограниченно возрастать при заданной системе ограничений, поэтому можно условно записать, что .
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Пример 6. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. Изображённая на рисунке ниже область не содержит ни одной общей точки, которая бы удовлетворяла всем неравенствам системы ограничений. То есть система ограничений противоречива и не может содержать ни одного решения, в том числе и оптимального.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
На сайте есть Онлайн калькулятор
решения задач линейного программирования симплекс-методом.
Пример 8. Решить графическим методом задачу линейного программирования, в которой требуется найти максимум функции при ограничениях
Решение. На рисунке ниже изображены область решений системы ограничений и линия уровня (чёрного цвета). Если передвигать линию уровня параллельно исходной в направлении вектора , то она выйдет из области решений не в одной точке, как это было в предыдущих примерах, а сольётся с прямой CD, которая является граничной линией области решений.
Все точки отрезка CD дают одно и то же значение функции цели, которое и служит её оптимальным значением: . Следовательно, имеется не одно, а бесчисленное множество оптимальных решений, совпадающих с точками отрезка CD, в частности, с двумя угловыми точками C и D. Этот пример показывает, что в некоторых случаях единственность оптимального решения нарушается.
На сайте есть Онлайн калькулятор решения задач линейного программирования симплекс-методом.
Напоследок следует заметить, что строить многогранник решений можно и другим способом, отличающимся о того, который мы рассматривали. А именно: можно не искать точки пересечения прямых с осями координат, а искать точки пересечения прямых. Для этого последовательно решаются системы из двух уравнений, так, чтобы решениями были точки пересечения всех прямых. Полученные точки и будут вершинами многогранника решений. Этот способ иногда бывает удобным в случаях, когда точки пересечения прямых с осями координат — дробные числа и, неправильно отложив точку пересечения, можно получить ошибку и в поиске точек пересечения самих прямых.
Начало темы «Линейное программирование»
Поделиться с друзьями
Топ-5 приложений для решения задач по математике
Мы отобрали для вас лучшие приложения для Android, которые созданы для решения практически любых задач по математике в два счета.
Математику по праву можно назвать царицей наук, которую в равной степени можно как любить, так и ненавидеть. Если задуматься всерьез, то мы используем знания по математике каждый день. Повсюду сталкиваемся с числами – на циферблате часов, на денежных банкнотах, в расписании уроков. Нам все время приходится выполнять простые и сложные математические операции – посчитать, через сколько минут начнется любимый фильм, сколько сдачи должны дать в магазине, когда приедет автобус.
Но для многих математика — это непонятные действия, числа, правила и задачи. Говорят, все познается в сравнении. Математика позволяет нам узнать, насколько что-то больше, длиннее, шире, дороже другого. Без знания математики невозможно построить дом, автомобиль. Если бы не математика, у нас бы никогда не было ни компьютеров, ни планшетов и смартфонов. Математическими расчетами пользуются все другие науки в мире.
Простая арифметика, превращающаяся в дальнейшем в сложную алгебру и геометрию, заставляла многих ненавидеть эти дисциплины. Кому-то математика в школе давалась легко, а для кого-то она так и осталась чем-то далеким и непостижимым. Как ни крути, иногда умение считать деньги не спасает от необходимости решения сложных математических уравнений и неравенств. «Смартфон» дословно переводится как «умный телефон», и благодаря стороннему софту ему можно доверить даже самые сложные задачи. В век информационных технологий дела с этим обстоят совсем иначе. На помощь школьникам и студентам пришли смартфоны и планшеты с «умными» приложениями-калькуляторами, речь о которых пойдет в этой статье. Оговоримся сразу, что приложения не могут быть панацеей. Вам всё равно придется учить математику, а они лишь помогут вам, подскажут ход решения. Пока что данные приложения не могут справляться со сложными заданиями, но кое-что умеют.
Photomath
Одно из самых известных приложений для решения математических задач с первого же дня назвали ужасом для учителей математики. А разработчики просто называют его «камерой-калькулятором».
Photomath интересно тем, что способно решить практически любую математическую задачу. Вам тяжело разобраться в решении логарифмических, квадратных, тригонометрических уравнений и неравенств? Трудно решать задачи с корнями, модулями, степенями, дробями, интегралами и факториалами? Теперь с помощью приложения Photomath решать такие задания не составит большого труда. Но самое интересно — приложение не просто решает математические задачи, а подробно расписывает ход расчетов. Это понравится не только учащимся и студентам, а также родителям, которые захотят проверить домашнее задание своего чада.
Пользователю понравится, что приложение Photomath способно работать в автоматическом режиме. Достаточно просто открыть его и сразу же активируется встроенный интерфейс камеры с заданной областью распознавания. Для того, что начать работу, необходимо расположить камеру так, чтобы математическая задача вместилась в эту область. Буквально через мгновение умные алгоритмы программы начнут анализировать данные на экране и практически моментально выдадут ответ. Если захотите увидеть весь ход решения вашей задачи, то просто нажмите на результат в красном прямоугольнике. В истории приложения сохраняются 10 последних записей, поэтому в любой момент сможете просмотреть решение предыдущей задачи.
Иногда случается, что программа некорректно распознала те или иные математические символы в задании, решив неправильно при этом задачу. Но не отчаивайтесь. В Photomath у вас есть возможность отредактировать их в режиме калькулятора. Стоит отметить, разработчики очень хорошо продумали эту функцию. Здесь доступен калькулятор со всевозможными операторами, есть цифровая, текстовая и символьная раскладки.
Долгое время приложение умело распознавать только напечатанное задание. Причем из книги было намного легче отсканировать его, чем с экрана ноутбука. Теперь же, наконец-то, появилась долгожданная функция распознавания рукописного текста. Все работает почти безупречно, но для лучшего результата желательно, чтобы запись была аккуратным почерком.
Мне очень понравилось пользоваться приложением. Оно практически справляется с любым заданием со всей школьной программы по математике и алгебре, включая старшую и высшую школы. Да, приложение стоящее, абсолютно бесплатное, не содержит рекламы, как обычно бывает с такими приложениями, есть русский язык интерфейса, способно работать без подключения к Интернету, но и ошибок предостаточно.
MalMath: Step by step solver
С помощью данного приложения вы сумеете решить математические задачи не только получив пошаговое описание процесса вычисления, но и построение необходимых графиков. Само приложение MalMath для Android полностью бесплатное, к тому же совершенно не содержит рекламы. Также у вас есть возможность использовать его без подключения к Интернету. Это является большим плюсом для него. Программа в первую очередь приглянется ученикам старших классов, студентам колледжей, а также университетов и академий. Дело в том, что MalMath умеет решать интегралы, производные, пределы, логарифмы, тригонометрические уравнения и неравенства, примеры с корнями и модулями. По крайней мере большую часть. Однако, вам придется в ручную вводить условие задания, так как функция распознавания с помощью камеры здесь не предусмотрена. Что касается его способностей, то они ограничиваются лишь задачами средней сложности с более скромным, чем у остальных приложений, описанием решений.
Интерфейс MalMath представлен на русском языке, выполнен в классическом стиле и оптимизирован под экраны смартфонов. У вас есть возможность в настройках изменить размер шрифта и скорость анимации. Открыв боковое меню, увидите, что оно включает пять пунктов: главный экран, рабочий лист, график, генератор задач, избранное. Но больше всего вам будет интересна функция «генератор задач». С ее помощью можно создавать случайные математические задачи с несколькими категориями и уровнями сложности, заданными в настройках. Все выражения и графики можно сохранять в избранном.
Сам процесс добавления задачи очень похож на вставку формул в Microsoft Word. Из собственного опыта отмечу, что, вроде бы все понятно и просто, но иногда довольно неудобно, особенно, что касается ввода сложных комбинаций с дробями и корнями. Придется потратить немного времени, чтобы привыкнуть к определенному принципу набора, но все же оно того стоит.
Mathway
Еще одно весьма заслуживающее внимания приложение, которое поможет справиться с математическими заданиями. Приложение является своеобразным инструмент для решения задач, который, помимо школьного курса математики, охватывает математический анализ, статистику, тригонометрию, линейную алгебру и даже химию. Если вы когда-то использовали веб-версию сервиса Mathway, то сразу же узнаете внешний вид и функциональные возможности данного приложения. Практически тот же интерфейс в виде мессенджера, в котором все действия происходят как бы в диалоге с виртуальным помощником.
Стоит заметить, что именно данное приложение из рассматриваемых в этой статье является одним из самых интересных в плане качества решения. Вам понравится, что получите, пожалуй, наиболее развернутые пошаговые решения задач, к тому же на понятном русском языке. Немного странным выглядит тот факт, что в описании указано, что для просмотра пошагового решения, нужна платная подписка, хотя все функциональные возможности приложения совершенно бесплатны. Mathway поможет вам не только с решением уравнений, неравенств и прочих сложных выражений, но также сумеет построить графики, может найти число молекул в определенной массе тела.
Mathway для Android тоже решает задачи с помощью камеры устройства, правда, реализована эта функция не самым лучшим образом. Для такого вывода у нас есть несколько веских причин. Во-первых, интерфейс камеры в программе крайне минималистичный, в нем почему-то нет даже области распознавания. Вам придется приловчится, чтобы выражение находилось по центру экрана, а рядом не должно быть других надписей, иначе приложение будет выдавать неправильное решение.
Часто на практике камера захватывала только часть приложения, отсюда и ошибки. К тому же камера автоматически настроена на макро-режим, поэтому алгоритмы распознавания часто плохо срабатывают и выдают неправильный ответ. Лично мне иногда было гораздо проще и быстрее ввести задачу вручную. К тому же для этого в приложении есть просто шикарные возможности. Дело в том, что выдвигающееся боковое меню позволит вам получить доступ аж к 10 разделам, у каждого из которых есть свой собственный калькулятор с определенными символами, операторами, константами и прочими функциями. Очень удобно и практично.
Мне очень понравилось, что Mathway предлагает пользователю самому выбрать способ решения задачи, в зависимости от этого результаты могут меняться. Если не подходит один из способов, достаточно снова тапнуть на математическое выражение и выбрать другой вариант решения. Скажем сразу, если вы хотите быстро и оперативно получить нужный ответ к задаче, то Mathway вряд ли подойдет вам. Но, если хотите точности и развернутости ответа, а также у вас есть терпение самостоятельно вводить математические символы и знаки, то данное приложение весьма вам понравится.
Mathpix
Mathpix — первое приложение, которое позволяет вам решать и визуализировать решения, распознавая рукописный текста, включая сложные формулы. Mathpix стремится заменить дорогие и устаревшие графические калькуляторы, чтобы обеспечить бесплатное и интересное учебное пособие для студентов-математиков по всему миру.
Я и вовсе хотел написать его первым среди всех приложений, так как это один из старожилов подобных приложений для решения математических задач. Оно намного раньше, в отличие от Photomath, получило способность распознавать рукописные математические задачи. Стоит заметить, что суть и принцип работы обоих приложений очень похожи, но в целом сервис Mathpix рассчитан на более взрослую аудиторию. Оно умеет решать простые и не очень квадратные уравнения, легко справляется с задачами, в которых есть дробные выражения, а также корнями, логарифмами, интегралами, производными и т.
д. То есть практически все, что есть в старших классах школы и первых курсов университета. Но особенно я бы отметил возможность построения графиков функций, благодаря интеграции с передовым графическим калькулятором Desmos. Этого нет ни у одного из представленных приложений, а это очень важно для решения задач алгебры и начала анализа.
Вам очень понравится работа алгоритмов распознавания текстов и условий у Mathpix. Программа практически в считанные секунды сканирует и считывает условие задачи. Тут же отправляет на сервер данные условия и почти мгновенно выдает ответ. Но ошибки тоже случаются, хотя довольно редко. При этом пользователю доступны инструменты для работы с задачами в режиме графика: редактирование вводных данных, добавление таблиц, заметок и дополнительных функций для нескольких графиков.
Я тут так пафосно расписал возможности приложения, но отмечу, что оно хорошо справляется только с несложными задачами. Если еще с построением элементарных графиков приложение справится, то с более сложными заданиями, которые включают тригонометрические и логарифмические уравнения, неравенства, а также уравнения с модулем, возникали большие проблемы. Приложение просто игнорировало их решение. Так что разработчикам еще необходимо потрудиться над возможностями своей программы.
Большинству пользователей не понравится, что отсутствует интерфейс на русском языке, а также подробное описания решения задач. Да и само приложение довольно-таки сложновато в использовании, элементы управления неудобны на смартфоне с небольшим экраном. Создалось впечатление,что это веб-версия приложения. Но решение всё же остается за вами.
MyScript Calculator
Ну и, наконец, самое интересное приложение MyScript Calculator, которое впервые появилось в начале 2013 года. К тому же, сразу получило признание на международной выставке CES и было отмечено за инновации. Мы привыкли, что в онлайн-калькуляторах либо роль считывателя играет камера устройства, либо вручную вводим данные.
В приложении MyScript Calculator принцип подхода к математическим вычислениям кардинально отличается. Особенность MyScript Calculator заключается в том, что приложение работает только с рукописным вводом данных. Здесь даже отсутствуют кнопки, как таковые, а все, что имеется — это чистое полотно на весь экран, имитирующее бумагу-миллиметровку. Примеры для вычисления пользователь пишет пальцем или с помощью стилуса. В данном случае предпочтительнее будет использование планшета или фаблета с цифровым пером.
Вам понравится, что приложение автоматически сумеет распознать написанное вручную, переведет записи в нормальный цифровой вид и буквально в то же мгновение выдаст результат. Стоит отметить, что алгоритмы распознавания MyScript Calculator просто великолепные. На практике программа умудряется определить даже самые откровенные каракули. Также вы сможете отменить или повторить последние действия и полностью очистить экран от написанного. К тому же вас определенно порадует довольно большой список поддерживаемых символов и операторов, который поможет решить даже сложные задания. Несмотря на все это, приложение вряд ли пригодится студентам университетов. Даже несмотря на возможность работать с дробями, квадратными корнями, константами, решать уравнения, находить переменные, MyScript Calculator решит школьную программу, не более.
Основным недостатком MyScript Calculator для Android можно считать отсутствие подробного описания решений, программа выдает только итоговый результат. Хотя, учитывая концепцию приложения, возможно оно было бы лишним. А вот то, что здесь не хватает различных удобных мелочей, так это скорее пожелание разработчикам на будущее. К примеру, хотелось бы увидеть историю вычислений, возможность масштабировать экран и сохранять введенные задачи. Но, если все это отбросить в сторону, приложение действительно полезное, простое и оригинальное.
Вместо тысячи слов…
Ну и в заключение все же хочется сказать, что хоть приведенные приложения и помогут вам справиться с математическими заданиями, но не забывайте, что это всего лишь программа.
(1/2))
Результат выражения
Действительная часть 0.66468285388895
Мнимая часть 1.0051451851734
Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.
- Уравнение пятой степени. Частное решение. >>
Калькулятор онлайн. Решение неравенств: линейные, квадратные и дробные
Понятие математического неравенства возникло в глубокой древности. Это произошло тогда, когда у первобытного человека появилась потребность при счёте и действиях с различными предметами сравнивать их количество и величину. Начиная с античных времён неравенствами пользовались в своих рассуждениях Архимед, Евклид и другие прославленные деятели науки: математики, астрономы, конструкторы и философы.
Но они, как правило, применяли в своих работах словесную терминологию. Впервые современные знаки для обозначения понятий «больше» и «меньше» в том виде, каком их сегодня знает каждый школьник, придумали и применили на практике в Англии. Оказал такую услугу потомкам математик Томас Гарриот. А случилось это около четырёх столетий назад.
Известно множество видов неравенств. Среди них простые, содержащие одну, две и больше переменных, квадратные, дробные, сложные соотношения и даже представленные системой выражений. А понять, как решать неравенства, лучше всего на различных примерах.
Не опоздать на поезд
Для начала представим себе, что житель сельской местности спешит на железнодорожную станцию, которая находится на расстоянии 20 км от его деревни. Чтобы не опоздать на поезд, отходящий в 11 часов, он должен вовремя выйти из дома. В котором часу это необходимо сделать, если скорость его движения составляет 5 км/ч? Решение этой практической задачи сводится к выполнению условий выражения: 5 (11 — Х) ≥ 20, где Х — время отправления.
Это понятно, ведь расстояние, которое необходимо преодолеть селянину до станции равно скорости движения, умноженной на количество часов в пути.
2-64
\(D=-4 \cdot 64
Когда выражение слева меньше нуля?
Всегда. Значит неравенство выполняется при любых \(x\).
Ответ: \(x∈(-∞;∞)\)
В этой статье собран материал, покрывающий тему «решение квадратных неравенств ». Сначала показано, что представляют собой квадратные неравенства с одной переменной, дан их общий вид. А дальше детально разобрано как решать квадратные неравенства. Показаны основные подходы к решению: графический способ, метод интервалов и путем выделение квадрата двучлена в левой части неравенства. Приведены решения характерных примеров.
Навигация по странице.
Что такое квадратное неравенство?
Естественно, прежде чем говорить о решении квадратных неравенств, надо отчетливо понимать, что такое квадратное неравенство. Иными словами, нужно по виду записи уметь отличать квадратные неравенства от неравенств других видов.
Определение.
Квадратное неравенство – это неравенство вида a·x 2 +b·x+c может быть любой другой знак неравенства ≤, >, ≥), где a , b и c – некоторые числа, причем a≠0 , а x – переменная (переменная может быть обозначена и любой другой буквой).
Сразу дадим еще одно название квадратных неравенств – неравенства второй степени . Это название объясняется тем, что в левой части неравенств a·x 2 +b·x+c
Также иногда можно слышать, что квадратные неравенства называют квадратичными неравенствами. Это не совсем корректно: определение «квадратичные» относится к функциям, заданным уравнениями вида y=a·x 2 +b·x+c . Итак, есть квадратные неравенства и квадратичные функции , но не квадратичные неравенства.
Покажем несколько примеров квадратных неравенств: 5·x 2 −3·x+1>0 , здесь a=5 , b=−3 и c=1 ; −2,2·z 2 −0,5·z−11≤0 , коэффициенты этого квадратного неравенства есть a=−2,2 , b=−0,5 и c=−11 ; , в этом случае .
Обратите внимание, что в определении квадратного неравенства коэффициент a
при x 2
считается отличным от нуля.
Это и понятно, равенство коэффициента a нулю фактически «уберет» квадрат, и мы будем иметь дело с линейным неравенством вида b·x+c>0
без квадрата переменной. А вот коэффициенты b
и c
могут быть равными нулю, причем как по отдельности, так и одновременно. Вот примеры таких квадратных неравенств: x 2 −5≥0
, здесь коэффициент b
при переменной x
равен нулю; −3·x 2 −0,6·x0
и b
, и c равны нулю.
Как решать квадратные неравенства?
Теперь можно озадачиться вопросом как решать квадратные неравенства. В основном для решения используются три основных метода:
- графический способ (или, как у А. Г. Мордковича, функционально-графический),
- метод интервалов,
- и решение квадратных неравенств через выделение квадрата двучлена в левой части.
Графическим способом
Сразу оговоримся, что метод решения квадратных неравенств, к рассмотрению которого мы приступаем, в школьных учебниках алгебры не называют графическим. Однако по сути это он и есть. Более того, первое знакомство с графическим способом решения неравенств обычно и начинается тогда, когда встает вопрос, как решать квадратные неравенства.
Графический способ решения квадратных неравенств a·x 2 +b·x+c, ≥) заключается в анализе графика квадратичной функции y=a·x 2 +b·x+c для нахождения промежутков, в которых указанная функция принимает отрицательные, положительные, неположительные или неотрицательные значения. Эти промежутки и составляют решения квадратных неравенств a·x 2 +b·x+c0 , a·x 2 +b·x+c≤0 и a·x 2 +b·x+c≥0 соответственно.
Методом интервалов
Для решения квадратных неравенств с одной переменной помимо графического метода достаточно удобен метод интервалов , который сам по себе очень универсален, и подходит для решения различных неравенств, а не только квадратных. Его теоретическая сторона лежит за пределами курса алгебры 8, 9 классов, когда учатся решать квадратные неравенства. Поэтому здесь мы не будем вдаваться в теоретическое обоснование метода интервалов, а сосредоточимся на том, как с его помощью решаются именно квадратные неравенства.
Суть метода интервалов, по отношению к решению квадратных неравенств a·x 2 +b·x+c, ≥), состоит в определении знаков, которые имеют значения квадратного трехчлена a·x 2 +b·x+c на промежутках, на которые разбивается координатная ось нулями этого трехчлена (при их наличии). Промежутки со знаками минус составляют решения квадратного неравенства a·x 2 +b·x+c0 , а при решении нестрогих неравенств к указанным промежуткам добавляются точки, отвечающие нулям трехчлена.
Познакомиться со всеми деталями этого метода, его алгоритмом, правилами расстановки знаков на промежутках и рассмотреть готовые решения типовых примеров с приведенными иллюстрациями Вы можете, обратившись к материалу статьи решение квадратных неравенств методом интервалов .
Путем выделения квадрата двучлена
Кроме графического метода и метода интервалов существуют и другие подходы, позволяющие решать квадратные неравенства. И мы подошли к одному из них, в основе которого лежит выделение квадрата двучлена в левой части квадратного неравенства.
Принцип этого способа решения квадратных неравенств состоит в выполнении равносильных преобразований неравенства , позволяющих перейти к решению равносильного неравенства вида (x−p) 2 , ≥), где p
и q
– некоторые числа.
А как осуществляется переход к неравенству (x−p) 2 , ≥) и как его решить разъясняет материал статьи решение квадратных неравенств путем выделения квадрата двучлена . Там же представлены примеры решения квадратных неравенств этим способом и даны необходимые графические иллюстрации.
Неравенства, сводящиеся к квадратным
На практике очень часто приходится сталкиваться с неравенствами, приводящимися с помощью равносильных преобразований к квадратным неравенствам вида a·x 2 +b·x+c
Начнем с примеров самых простых неравенств, которые сводятся к квадратным. Иногда, чтобы перейти к квадратному неравенству, достаточно переставить в данном неравенстве слагаемые или перенести их из одной части в другую.
Например, если перенести все слагаемые из правой части неравенства 5≤2·x−3·x 2
в левую, то получим квадратное неравенство в оговоренном выше виде 3·x 2 −2·x+5≤0
. Еще пример: переставив в левой части неравенства 5+0,6·x 2 −x
В школе на уроках алгебры, когда учатся решать квадратные неравенства, одновременно разбираются и с решением рациональных неравенств , сводящихся к квадратным. Их решение предполагает перенос всех слагаемых в левую часть с последующим преобразованием образовавшегося там выражения к виду a·x 2 +b·x+c путем выполнения . Рассмотрим пример.
Пример.
Найдите множество решений неравенства 3·(x−1)·(x+1).иррациональное неравенство равносильно квадратному неравенству x 2 −6·x−9логарифмическое неравенство – неравенству x 2 +x−2≥0 .
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. 2-21,5x-19 > 0$.
Калькулятор дробных неравенств
Наших пользователей:
Просто наблюдая, как мои студенты, один за другим, легко схватывают эти высшие математические концепции и действительно, по-настоящему понимают, что они делают, Алгебратор стоит платы за вход. Кроме того, для прибыли цена невероятно низкая!
Рик Паркер, МиссуриСпасибо создателям программы.Контекстно-зависимая помощь по любой теме алгебры дала мне ясное представление о моих основах математики. Очень полезный инструмент ..
J.R. Turnston, NYМне нужно было пройти тест по алгебре, чтобы соответствовать требованиям для поступления в школу. Алгебратор меня спас. Спасибо!
Мэри Джонс, Нью-ЙоркСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт.Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2015-04-12:
- Построение простых линейных уравнений с использованием целых чисел на плоскости
- сложение и вычитание целых чисел
- Практика сложения, вычитания, умножения и деления дробей
- процентных уравнений
- ВАЛЬТЕР РУДИН СОУЛЬШН
- как решить несколько уравнений с несколькими неизвестными в matlab nonlinear
- перестановочные и комбинированные ноты
- Упростите квадратный корень и степень с помощью калькулятора
- рабочих листов на основе формул перестановки
- harold r jacob геометрия домашнее задание ответы
- объяснение сложения и умножения дробей.com
- листов 1 разряда
- Онлайн-решатели математики
- Калькулятор кубического разложения
- набор заданий по математике бесплатно
- вертексная алгебра
- график гиперболы
- алгебра 1a математика прентис холла
- Использование квадратичной формулы сегодня
- как взять cube root ti-83 plus
- математический тест ks3 круги формулы числа шаблоны
- системы уравнений интерактивные игры Расчет коэффициента разницы
- Рабочие листы для детей в процентах
- Бесплатные рабочие листы по умножению и делению целых чисел
- КАЛЬКУЛЯТОР ОТРИЦАТЕЛЬНЫХ ИНТЕГЕРОВ
- математических задач. com
- десятичных знаков рабочего листа для девятого класса
- как упростить сложение и вычитание показателей Матричное дифференциальное уравнение
- в matlab
- умножение показателей нескольких переменных
- Элементарный лист научного метода
- объяснений по главе продвинутой математики Ричарда Дж. коричневый
- бесплатная распечатанная таблица умножения 1-20
- навык: умножение целых чисел расследование 3 страница ответа
- решающих комбинаций на калькуляторе
- упростить корни casio
- рабочий лист, площадь круга
- Решение сложных уравнений с дробями
- www.basicalgebra1.com
- преалгебра с творческими публикациями pizzazz
- как преобразовать десятичную дробь в дробь
- Шаги к решению полиномиальных уравнений
- Задачи с переменным сюжетом-Алгебра словесные задачи 5 класс игры
- Рабочий лист решения задач сложения и вычитания для шестиклассников
- Рабочие листы для умножения и деления целых чисел
- тесты на сложение и вычитание 4 класса
- Решение уравнения с использованием распределительного свойства
- как вы работаете со сложным рациональным выражением на TI-83
- Бесплатная программа для решения задач по алгебре и математике
- изучает элементарную алгебру
- преобразовать из погонных метров в квадратные
- Упростите решения алгебры
- программа для решения нелинейных уравнений
- Решатель энного члена
- + Алгебра; Почему при решении рационального уравнения необходимо проводить проверку?
- как решить квадратное уравнение с помощью Matlab
- Texas Instruments — калькулятор для решения задач Word
- решение максимальных и минимальных квадратичных формул
- макдугал литтелл руководство для учителей алгебры содержание
- Алгебратор
- вычитание дробей и целых чисел Фактор
- + калькулятор + трехчлен
- бесплатных онлайн уроков алгебры для начинающих для 4 гр.
- найти примеры уравнений и формул
- алгебра 1 ответы на множители по группировке
- сложение, вычитание, умножение и деление целых чисел
- упрощающий онлайн-калькулятор
- Excel решатель химия
- бесплатные рабочие листы по математике
- квадратичная по стандартной форме до вершины
- Рабочий лист первичной факторизации
- как вычислить квадратный корень из дроби
- вычислить 4 неизвестных
- Бесплатный рабочий лист по математике с неравенствами для 5-го класса
- находим кубический корень из чисел для 6 класса
- объединить похожие термины powerpoint
- решить уравнения и показать работу ti-83
- Калькулятор алгебраических выражений несколько переменных
- переменных квадратного корня
- математическая симметрия стихотворение
- решение для переменных в дробях Печатные математические игры
- , а также GCF и LCM
- Показатели по математике в 7 классе корни радикалы
- Рабочий лист преобразования алгебры
- Исследовательский проект по математике
- площадь круга рабочего листа
- корень 4-й степени из 2
- решение формулы для переменных листов
- Документы для тестирования способностей
- Учебники Химические уравнения для получения солей
- контрольная точка неравенства по математике
- Калькулятор очистки уравнений дробей
- решение уравнения 3 степени fortran
Онлайн-калькулятор неравенства
Наших пользователей:
Какой отличный дружественный интерфейс, полный цветов, ведьма делают программу Algebrator простой программой для работы, а также с ней так легко работать, что вам не нужно прерывать поток мыслей каждый раз, когда вам нужно взаимодействовать с программой.
Leeann Cook, NYЕсли кому-то нужна помощь по алгебре, я очень рекомендую «Алгебратор».
Мой сын использовал это, и он показал огромные успехи в этом предмете.
Кристофер Монтомери, ОгайоСуществуют и другие обучающие программы по математике, а также Алгебратор. Никакое другое программное обеспечение даже близко не может сравниться с этим!
Пол Д’Суза, Северная КаролинаУ меня были проблемы с изучением квадратных уравнений, пока я не купил вашу программу.Теперь я знаю, как делать не только квадраты, но и на пошаговых примерах научился составлять другие более сложные уравнения и неравенства. Отличный продукт!
M.H., ДжорджияЭтот продукт — величайшая вещь. Я всегда ходил в дом своих друзей, чтобы использовать ее, пока не смог убедить родителей купить его для меня. Ненавижу это говорить, но мне действительно нужна была помощь с алгеброй, и теперь я ее получил!
Sandy Ketchum, ALСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 31.07.2012:
- простой способ решения задачи о назначении
- калькулятор алгебры колледжа
- Подготовка седьмого класса к выпускному экзамену в Северной Каролине, практика седьмого класса и образец рабочей тетради
- герак линейный
- ПРОСТЫЕ ЗАДАЧИ АЛГЕБРЫ ДЛЯ НАЧИНАЮЩИХ
- наименьшее общее кратное 34 19
- делительная алгебра
- решение квадратной задачи со словами
- промежуточная матричная рабочая тетрадь ответ
- франшиза умножающая
- Жесткие уравнения GCSE
- бесплатных загрузок теста способностей
- стандартное выражение алгебры-6
- добавить средство решения уравнений в калькулятор ti 83
- творческих публикаций ответы по алгебре
- алгебраические уравнения
- бесплатный 7-й год онлайн-тест по математике
- квадратный корень собственность фракция
- Подготовка к экзамену IOWA по алгебре
- Репетитор по математике услуги по решению задач
- 1-й класс дополнительный powerpoint
- сложение и вычитание рациональных выражений планы уроков
- Решатель рациональных выражений умножения и деления
- ti-81 изготовление коробки и усов Примеры уклонов
- из реальной жизни
- объединение одинаковых терминов математика средней школы \
- дифференциальные уравнения со сложением и вычитанием
- Рабочие листы по математике для 7-го класса
- как преобразовать смешанную дробь в десятичные числа
- KS3 revision Maths Percentages + 10% online
- решатели системных уравнений Графический калькулятор
- рациональных выражений
- вычесть квадратные корни Ответы на экзамен regents по математике
- — глава 3 по интегрированной алгебре pearson
- сложнейших тригонометрических уравнений
- шаг 1 для решения квадратного уравнения
- как решить задачу о квадратном корне
- Эмулятор TI 84
- Решение задач системы линейных уравнений
- программное обеспечение предварительной алгебры
- ti-89 решить комплексные числа
- математические задачи
- График половинного логарифма VB6
- план урока, упрощающий тригонометрические выражения
- Задания по математике за 9 класс
- Пошаговое упрощение рациональных выражений
- онлайн-калькулятор подстановки алгебры
- радикалы онлайн-решения
- страниц бесплатных тестов по математике для шестого класса
- Алгебратор
- бесплатное пользование преподавателем зала Prentice Hall
- решение систем линейных уравнений по матрице + TI-83
- завершение квадратной математики
- 11 класс алгебра математические задачи
- Упражнение по дифференциальным уравнениям
- нечетные дроби
- Системные квадратные уравнения
- как создать путь данных в vhdl для сравнения двух значений
- решение онлайн-упражнений по алгебре 7 класс
- Рабочие листы закона Ньютона Формулы для 7-го класса
- предварительная алгебра Холта ответы
- ilaplace TI89
- образец бумаги для теста b. com (с отличием) тест на способности.
- макдугал / литтел алгебра 1 с отличием ответы
- бесплатные рабочие листы для оценки восьмого класса
- Тестовые листы по математике с дробями
- Онлайн-викторина по алгебре для 9 класса
- программа алгебры бесплатно
- код Фортрана уравнение третьего порядка решения
- Учебный лист по алгебре
- Высшая школа алгебры — это просто
- gcse математика алгебра линейные уравнения
- алгебра pdf
- план урока элементарной алегебры
- o level E-maths revision документы
- разница между абстрактной и логической алгеброй
- год 8 тест по алгебре
- mcdougallittell ответы
- как решить логарифмы
- математический круговой знак
- решение радикальных вопросов / 10 класс по математике
- многошаговая программа для решения уравнений
- рабочих листов с решением задач с двумя переменными
- Алжирба онлайн
- как построить круг на графике с помощью mathcad 5
- mcdougal littell math рабочий лист Учебник по общему знаменателю
- Практическая тетрадь для ответов на вопросы по алгебре
- упростить квадратный корень из суммы двух квадратов
- линейные уравнения и графики helf
- образец теста на корень квадратный из элементарной алгебры для 6-го класса
- промежуточная алгебра четвертое издание для студентов колледжей
- Скачать игры для ks2 бесплатно.
- чит научная бумага ks2 год 5
- как складывать линейные уравнения с дробями Символ
- для факториала в статистике
- программа сюжетная гипербола
- Excel уравнения
- Перепишите уравнение деления как умножение
Калькулятор неравенства
Наших пользователей:
Ваша программа сохранила мою оценку в этом семестре.Это не только помогло мне с домашним заданием, но и научило меня решать проблемы.
T.P., Нью-ЙоркМой сын Райан стал очень хорошо разбираться в алгебраических уравнениях благодаря использованию этого качественного программного обеспечения. Большое спасибо вам!
A.R., АрканзасАлгебратор — мой доктор алгебры. Уравнения и неравенство были двумя темами, над которыми я боролся, но использование программного обеспечения стерло мои проблемы с этим предметом.
Джули Саймонс, ДжорджияСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2012-12-05:
- Математические листы класса 3rs
- реши мои радикальные выражения
- уравнений алгебры для решения
- математическое приложение с использованием радикалов
- решение математического выражения с одной дробью
- рабочий лист и головоломки по экспонентам
- книга формул математики
- репетитор-сша.com рабочий лист отвечает на наклон-перехват формы
- Калькулятор перевода дробей в десятичные
- рабочие листы расчета уклонов
- Рабочий лист решения уравнений год 6
- фольга математика
- калькулятор решения любых задач
- ti-89 примеры программ
- + математические мелочи экспоненциальной функции
- разница между промежуточной алгеброй 4-го и 5-го изданий elayne
- Рабочий лист по математике макгроу-хилла
- преобразовать целое число в десятичное
- Альгибра
- задачи о степенях и квадратном корне, рабочие листы для 7 класса
- o уровень компьютерных исследований прошлые экзамены
- бесплатных листов для написания линейных уравнений Калькулятор дробей
- от наибольшей до наименьшей
- онлайн-калькулятор, используемый для нахождения квадратных корней и чисел с приведенным значением (ti 73)
- мелочи по математике
- синтетическое деление ти-89
- алгебра переставить журнал
- ti 89 из десятичного числа в квадратный корень
- ПОРЯДОК РАБОТЫ PDF ВЫБОР НЕСКОЛЬКИХ ЗАПИСЕЙ НАПИСАТЬ УРАВНЕНИЕ
- рабочие листы по базовой алгебре
- онлайн-калькулятор с целыми числами
- задач на слова с простыми дробями
- стандартный математический полином второго порядка неизвестен
- + фактор + практика + рабочий лист
- вопросов о способностях с решением и формулой
- как решать уравнения с показателями, содержащими деление и умножение
- рабочих листов для дошкольников
- сложение, вычитание, умножение и деление отрицательных чисел
- разница между операторами && и символами &, объясните простые примеры на java
- стандартная форма линейного уравнения + определение + алгебра средней школы
- рациональный решатель
- Целое число java 6
- Флорида математическая практика: рабочая тетрадь 7 класс
- онлайн-вычислитель
- промежуточный тест по алгебре
- Ti 84 plus онлайн-калькулятор
- факторинг трехчленов крестики-нолики
- рационализирующий знаменатель с использованием комплексных чисел
- сложных математических задач для шестиклассников
- конвертировать кубические метры в кубические футы TI 89
- Бесплатная игра сложения и вычитания
- Упрощение триггера
- преобразовать таблицу байтов в шестнадцатеричную Java
- возведение в квадрат квадратных уравнений
- РАБОЧИЕ ТАБЛИЦЫ ЛИНЕЙНЫХ УРАВНЕНИЙ КЛАСС 6
- факторизация тригонометрических выражений
- Алгебра практика система уравнений бесплатный рабочий лист
- Бесплатные бухгалтерские игры для старших классов
- рабочих листов 7-го класса техасских исследований и ответов
- hrw Словарь современной биологии
- общие вопросы по работе
- решение уравнений сложения и вычитания онлайн
- смешанных дробей, преобразованных в десятичные дроби калькулятор
- сложнейшая математическая задача с решением Калькулятор знаменателя
- пример уравнения алегры
- уравнение центров в гиперболе
- Решение задач алгебры с 2-мя переменными
- Факторинг математических задач
- Рабочий лист по переводу алгебраических выражений
- бесплатный решатель предалгебрных неравенств
- прентис холл алгебра 2 учителя издание
- семиступенчатый план уроков по математике / первый класс
- запись уравнений графов окружностей, гипербол, эллипсов и обратных вариаций
- как решать нелинейные уравнения
- Рабочие тетради McDougal Littell Концепция
- НАБОР АЛГЕБРЫ
- факторинг с кубическим членом
- онлайн-калькулятор фольги
- десятичных знаков в квадрате
- Методы математики CAS TI 89 Помощь репетитора
- Упростить кубический корень
Калькулятор дробей
Учитесь складывать, вычитать, умножать и делить дроби.Сократите дроби до наименьших значений, упростите, сравните и упорядочите дроби. Преобразуйте дроби в десятичные дроби и проценты, работайте со смешанными числами и неправильными дробями и решайте для X в уравнениях дробей с помощью онлайн-калькуляторов дробей CalculatorSoup ® .
Операции с дробями и манипуляции
Калькулятор дробей
Операции над правильными и неправильными дробями.Включает формулы для сложения, вычитания, умножения и деления дробей.
Сложение и вычитание дробей.
Сложите или вычтите до 10 дробей за раз и посмотрите, как найти ответ.
Смешанные числа новые решения
Смешанные числа, целые числа и дроби .Операции с целыми числами, целыми числами, смешанными числами, правильными дробями и неправильными дробями. Показывает уравнения и результаты работы калькулятора.
Смешанные фракции новые решения
(То же, что и для смешанных номеров.)
Упрощение дробей
Преобразование неправильных дробей в смешанные числа.Упростите правильные и неправильные дроби, показывая работу и ответ в виде дроби или смешанного числа.
Упрощение калькулятора сложных дробей
Упростите дроби, задав числители и знаменатели любых двух смешанных чисел (смешанные дроби), правильные дроби, неправильные дроби или целые числа.
Калькулятор комплексных дробей новый
Сложение, вычитание, умножение и деление сложных дробей, содержащих смешанные числа, дроби или целые числа.
Десятичная дробь
Преобразование десятичной дроби в дробь.
Дробь в десятичную новые решения
Преобразует дробь в десятичную.
Доля к процентам
Преобразование дробей в проценты.
Процент в фракцию
Преобразование процента в дробь.
Наименьший общий знаменатель ( LCD )
Находит ЖК-дисплей дробей, целых и смешанных чисел. Показывает дроби и эквивалентные дроби с ЖК-дисплей .
Наименьшее общее кратное ( LCM )
Находит LCM целых и целых чисел.
Наибольший общий коэффициент ( GCF )
Находит GCF набора чисел, показывающих работу с использованием факторизации, разложения на простые множители и алгоритма Евклида.
Калькулятор соотношения
Решите задачи соотношения и пропорции для пропущенного значения соотношения в форме A: B = C: D (или эквивалентного A / B = C / D). Сравните два отношения эквивалентности: ИСТИНА или ЛОЖЬ.
Калькулятор отношения к дроби новый
Преобразование отношений в дроби.Введите частичное или частичное отношение к целому и найдите дробные эквиваленты.
Ratio Simplifier
Упростите и уменьшите соотношение в форме A: B. Показывает работу с шагом.
Золотое сечение
Введите одно значение в формулу золотого сечения (A + B: A = A: B), и другие значения будут сгенерированы с геометрическим представлением.
Эквивалентные дроби
Создает набор дробей, эквивалентных заданной дроби, смешанному числу или целому числу.
Неправильные дроби для смешанных чисел
Преобразуйте неправильные дроби в смешанные числа и посмотрите, как выполняется преобразование. Упростите дроби и сведите к минимуму.
Смешанные числа в неправильные дроби
Преобразуйте смешанные числа в неправильные дроби и посмотрите, как выполняется преобразование.
Преобразование смешанных чисел в десятичную
Преобразуйте смешанные числа, дроби или целые числа в десятичные числа и просмотрите работу, связанную с преобразованием.
Смешанные числа в процентах
Преобразуйте смешанные числа, дроби или целые числа в проценты и просмотрите работу, связанную с преобразованием.
Порядок дробей
Упорядочивание и сортировка дробей, целых и смешанных чисел, чтобы определить, равны ли они, больше или меньше друг друга ( = или > или <). Показывает проделанную работу и преобразует входные данные в эквивалентные дроби с ЖК-дисплей .
Сравнение дробей
Сравнение дробей, целых и смешанных чисел, чтобы показать равенство или неравенство ( = или < или > ).Показывает входные данные, преобразованные в эквивалентные дроби с ЖК-дисплей .
Решение для X в дробях
Решить для неизвестного X , например X / 12 = 4/16 . Этот калькулятор может решить для Х в долях как равенства и неравенства: <или ≤ или> или ≥ или = .Показывает работу по перекрестному умножению.
Оценка сумм и различий
Оцените суммы и разности для положительных собственных дробей, n / d, где n ≤ d и 0 ≤ n / d ≤ 1. Включает таблицу дробей для дробей порядка половин, четвертей, восьмых и шестнадцатых с их десятичными эквивалентами.
Усреднение дробей новинка
Вычисляет среднее значение набора дробей.Находит среднее значение положительных и отрицательных, правильных и неправильных дробей, целых и смешанных чисел. Включает возможность показать работу, связанную с вычислением результата.
Таблица фракций
Дроби в порядке от 0 до 1, от половин до шестнадцатой. Включает десятичные эквиваленты дробей.
Строка числа дробей
Дробные части размером с шестнадцатую.
Преобразование дробей, десятичных знаков и процентов
Конвертер десятичных дробей в дробные
Конвертер десятичных чисел в проценты
Конвертер дробей в десятичные
Конвертер дробей в проценты
Конвертер процентов в десятичные
Конвертер процентов в доли
Конвертер смешанных чисел в десятичную
Конвертер смешанных чисел в проценты
Смешанные числа в неправильные дроби
Неправильные дроби для смешанных чисел
Калькулятор неравенств
Введите выражение, например.2б Пример задачи Найдите LCM Калькулятор алгебраических неравенств
Наших пользователей:
Удивительно знать, что это программное обеспечение охватывает так много вопросов по алгебре. Это не ограничивает вас заранее заданными автоматически созданными проблемами, вы просто вводите свои собственные.Это обязательно для всех студентов. Я очень рекомендую этот пакет всем.
Шарлотта Бичем, INНовая версия ооочень крутая! Это действительно отличный инструмент, чтобы рассказать об этом другим родителям … Больше не надо чесать голову, пытаясь помочь детям, когда я возвращаюсь домой с работы после долгого дня, особенно когда старый мозг начинает превращаться в кашу после 10-часового рабочего дня.
J.F., АляскаМой четырнадцатилетний сын Брэдли считался в школе подверженным риску.Но я не мог заставить его слушать меня. Затем, когда учитель в его школе, мистер Киндлер, благословил его сердце, заставил его попробовать внешкольную программу, это было похоже на чудо! Я бы не сказал, что Брэдли стал образцовым учеником, но он больше не пропускал уроки математики. Поэтому, когда я узнал, что мистер Киндлер основал всю свою программу на использовании Алгебратора, мне просто пришлось написать это письмо, чтобы поблагодарить вас! Представьте себе, что!
Патрик Оушен, ФлоридаМогу я просто сказать тебе, какая ты замечательная? Вам может показаться простым делом, но вы только что восстановили мою веру в человечество (немалое).Спасибо за добрый и быстрый ответ.
Билл Рейли, МассачусетсСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2009-11-26:
- куб ti калькулятор
- free mcdougal littel ответы
- РЕШЕНИЕ МАТЕМАТИЧЕСКОГО УРАВНЕНИЯ И ОТВЕТ
- холт / математические листы
- факторизация многочлена от нескольких переменных
- бесплатный онлайн-калькулятор радикалов Таблица эквивалентных дробей
- + ks2
- gcd контроллер
- Почему мы берем обратное рациональному выражению в задаче деления, но не в задаче умножения?
- решатель составных фракций
- как набирать радикальные знаки в компьютерной алгебре
- упрощение задачи о квадратном корне с показателями
- Написание уравнения стандартной формы в вершинной форме
- Однородное дифференциальное уравнение второго порядка
- триг., sin, cos, tan glencoe, рабочий лист
- ПРЕОБРАЗОВАТЬ ДЕСЯТИЧНОЕ ЧИСЛО В СМЕШАННОЕ ЧИСЛО
- Упростить кубические корни
- ДЕЯТЕЛЬНОСТЬ С УМНОЖЕНИЕМ ЦЕЛОГО ЧИСЛА
- Калькулятор упрощенных радикальных выражений
- ответы на листы макдугала литтел
- УРАВНЕНИЕ ПЕРПЕНДИКУЛЯРНОЙ ЛИНИИ
- пошагово упрощаем радикалы дроби
- Рабочие листы по энергетике и химии Рабочий лист
- от десятичной до дробной
- «стандартная форма» квадратичные «задачи со словами»
- системных уравнений в Mathcad
- как выучить коллажную алгебру
- Программа на C ++ для упрощения радикалов
- Excel онлайн-калькулятор с графиком
- обзорный лист для экзамена по математике штата Нью-Йорк для 3-го класса
- Glencoe Algebra 1 powerpoints
- Таблица для построения графиков алгебры
- поиск продукта по химическому уравнению
- квадратное уравнение для уравнений с несколькими переменными
- вопросов о способностях с решениями
- Рабочие листы по алгебре и преобразованию формул
- «Примеры программирования» и ШАГ 7 и ученик
- Калькулятор физических формул для баскетбола
- онлайн-упрощение квадратного корня
- ti-83 плюс десятичная дробь
- Вводная и промежуточная алгебра
- математические ответы по алгебре 2
- CLEP онлайн-тестирование колледж алебра
- кросс-мультипликация при решении неравенства
- тесты способностей pdf
- Калькулятор рационализации выражений
- корень квадратный из дроби
- математическое доказательство индукции тип файла swf
- задачи часов с использованием квадратных уравнений
- запись квадратного уравнения в вершинной форме
- порядок решения онлайн-математики от наименьшего до наибольшего целых чисел
- Изучить алгебру 1
- уравнение с рациональным показателем Калькулятор
- ti-83 как найти кубический корень
- скачать бесплатно программу решения алгебраических уравнений
- ответов и вопросов по физике для 8 класса
- преобразование десятичного числа в двоичное в TI 89
- год 6 квадратных чисел ресурсы
- Практикум IX
- ti 84 как упростить алгебраические выражения
- онлайн-тест на факторинг по алгебре
- clericalaptitude загрузить материал Калькулятор квадратного корня
- как решать уравнения с более чем одной переменной с помощью графического калькулятора
- КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ ДЛЯ 3-ГО КЛАССА
- смешанные числа в виде десятичных знаков
- Упрощающий логический калькулятор загрузить
- Рабочие листы по бесплатной алгебре
- листы на подшипник
- программа вычисления дроби наименьшего общего знаменателя
- квадрат двух разностей
- решение трехчленов
- ежедневных заданий по математике
- Калькулятор рациональных выражений
- gcd коды в vhdl
- преобразование десятичных знаков в дроби диаграмма
- рабочие листы поиска похожих терминов
- «квадратный корень» 140
- Калькулятор наименьших общих кратных алгебраических уравнений
- онлайн-калькулятор для уравновешивания уравнений
- математика elipce
- история умножения и деления негиев и положительных чисел
- писать программы для алгебры FX 2.0 плюс
Калькулятор неравенств
Наших пользователей:
Ваша программа сохранила мою оценку в этом семестре. Это не только помогло мне с домашним заданием, но и научило меня решать проблемы.
Кристин Тейлор, ВашингтонЭто было очень полезно.
Кэтрин Цайун, МассачусетсС алгебратором не может быть проще математики. Спасибо!
Коллин Д.Лестер, ПенсильванияСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2010-10-30:
- Сортировка неравенств с помощью алгебры
- скачать бесплатно абстрактную книгу по алгебре
- рабочие листы по периметру ks2
- Решатель третьего корня
- Функции, соотношения, пропорции и алгебра логарифмов ii просто ответ
- Уроки предварительной алгебры
- книга Лагранжа pdf скачать
- ответ по математической алгебре 1 книга
- Преобразовать целое число в процентном соотношении
- java решать одновременные уравнения
- бесплатных примеров вопросов для ks3 mental maths
- смешать фракции
- пол а.алгебра Фёрстера и тригонометрия Companiton web
- справка с algibra
- формулы дробей
- Решите рабочие листы уравнения сложения
- бесплатных игр, чтобы узнать многочлены 9 класса
- радикалы упрощения
- бесплатный калькулятор algrebra 2
- ks2 параллельный перпендикулярный лист
- поиск наклона на Ti 83
- скачать тестовую базу ks3
- рабочий лист многоступенчатых уравнений
- решатель алгебры колледжа
- уравнение с рациональными показателями
- делящих многочленов ti 83
- преобразование bigdecimal в два десятичных
- распечатанный дискриминантный лист
- Пробный тест по математике для 6-го класса + PA
- рабочие листы сложения и вычитания для печати
- Распечатки для пятого и шестого классов бесплатно
- учебники по математике для предварительного просмотра алгебры бесплатно онлайн для печати
- «Помощь с домашним заданием для третьего класса»
- Математическая поэма
- процедура решения квадратного уравнения путем факторизации
- окружность с алгеброй
- ks3 sats наука прошлые работы
- Практические задачи умножения и деления десятичных знаков
- характеристика неофициальных наблюдений и вопросов
- КАК ДЕЛАТЬ АЛГЕБРУ
- решение сложных линейных равенств
- рабочих листов со средним арифметическим
- рабочий лист расширений для печати
- mathtrivia.
2-21,5x-19 > 0$.
com
Мой сын использовал это, и он показал огромные успехи в этом предмете. 
com (с отличием) тест на способности.
Leave A Comment