Задание №24 ОГЭ по математике
геометрические задачи на доказательство
Первичный бал: 2 Сложность (от 1 до 3): 3 Среднее время выполнения: 10 мин.
Доказываем геометрические гипотезы.
Задание 24OM21R Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке N, лежащей на стороне ВС. Докажите, что N – середина ВС.Сделаем чертеж параллелограмма и покажем на нем биссектрисы углов, которые пересекаются в точке N.
Угол ANB равен углу NАD как накрест лежащие при параллельных прямых ВС и АD и секущей AN. А по условию углы BАN и NАD равны (AN биссектриса). Следовательно, углы BАN и BNА равны. Значит, треугольник ABN является равнобедренным, у него АВ= BN.
Аналогично, через равенство углов CND, ADN и CDN доказывается, что треугольник CND является равнобедренным, у него CN=DC.
По условию задачи мы имеем параллелограмм, а по свойству параллелограмма – противолежащие стороны равны, т.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2505o В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC= ED. Докажите, что данный параллелограмм — прямоугольник.Рассмотрим треугольники BEC и AED. BE = EA, так как E – середина стороны AB по условию. EC= ED по условию, а BC = AD по свойству параллелограмма (противолежащие стороны равны). Таким образом, BE = EA, EC= ED, BC = AD. Следовательно, треугольники BEC и AED равны по трём сторонам.
В равных треугольниках – равные элементы. Значит, углы CBE и DAE равны. Так как их сумма равна 180° по свойству параллелограмма , то углы равны 90° (180 / 2 = 90 ) .
Следовательно, данный параллелограмм — прямоугольник.
Ответ: доказаноpазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2504o В выпуклом четырёхугольнике ABCD углы ВСА и BDA равны.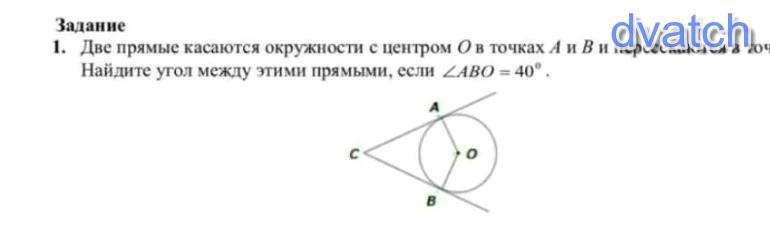 Докажите, что углы ABD и ACD также равны.
Докажите, что углы ABD и ACD также равны.Алгоритм решения:
- Выполняем рисунок по условию задачи.
- Устанавливаем подобие треугольников BOC и AOD.
- Записываем соотношение для сторон.
- Устанавливаем подобие треугольников AOB и DOC.
- Делаем вывод.
Решение:
1. Выполняем чертеж по условию задачи: 2. Рассматриваем треугольники BOC и AOD.У них: углы ВСА и BDA равны по условию задачи, углы BOC и AOD равны как вертикальные. Значит, треугольники BOC и AOD подобны по двум углам. 3. Для подобных треугольников BOC и AOD записываем соотношение соответствующих сторон: 4. Рассматриваем треугольники AOB и DOC. У них: углы AOB и DOC равны как вертикальные. Следовательно, данные треугольники подобны.По свойству подобных фигур соответствующие углы в треугольниках равны. Значит, , а поскольку эти углы совпадают с углами ABD и ACD , то .
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2503o Окружности с центрами в точках М и N пересекаются в точках S и Т, причём точки М и N лежат по одну сторону от прямой ST. Докажите, что прямые MN и ST перпендикулярны.
Докажите, что прямые MN и ST перпендикулярны.Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники SMN и TMN и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника SMT.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж согласно условия задачи.2. Рассмотрим треугольники SMN и TMN. Они равны по трем сторонам:
SM=TM как радиусы окружности с центром в точке М,
SN=TN как радиусы окружности с центром в точке N,
а MN – общая сторона (см. рисунок выше).
3. По свойству равных фигур, , как соответствующие углы в равных треугольниках.
4. Рассмотрим треугольник SMT.
В нем по доказанному выше , а значит MN – биссектриса угла M. Данный треугольник равнобедренный с равными сторонами SM и TM.
Следовательно, MN – высота по свойству биссектрисы равнобедренного треугольника.
pазбирался: Даниил Романович | обсудить разбор | оценить
Задание OM2502o Окружности с центрами в точках Е и F пересекаются в точках С и D, причём точки Е и F лежат по одну сторону от прямой CD. Докажите, что прямые CD и EF перпендикулярны.Алгоритм решения:
- Делаем чертеж по условию задачи.
- Рассмотрим треугольники CEF и DEF и установим их равенство.
- Воспользуемся свойством равных фигур для определения вида треугольника CED.
- Используем свойство равнобедренного треугольника и делаем вывод.
Решение:
1. Делаем чертеж по условию задачи:2. Рассмотрим треугольники CEF и DEF и установим их равенство:
У них CE=DE, как радиусы окружности с центром в точке Е,
Аналогично, CF = DF, как радиусы окружности с центром в точке F.
EF – общая сторона.
Значит, данные треугольники равны.
Тогда по свойству равных фигур .
Рассмотрим треугольник CED. У него CE=DE, поскольку это соответствующие стороны равных фигур. Значит, треугольник равнобедренный.
EF – биссектриса угла E. следовательно, EF – высота по свойству равнобедренного треугольника. Отсюда следует, что .
Ответ: доказаноАлгоритм решения:
- Делаем чертеж.
- Определяем место расположения точек I и J.
- Используем свойство серединного перпендикуляра.
- Делаем вывод.
Решение:
1. Делаем чертеж, согласно условия:2. Определяем место расположения точек I и J:
Точка I равноудалена от точек A и B. Аналогично, точка J равноудалена от концов отрезка AB.
3. По свойству геометрического места точек, равноудаленных от концов отрезка, эти точки расположены на серединном перпендикуляре к отрезку AB.
А если две точки I и J лежат на серединном перпендикуляре, прямая IJ совпадает с ним. Следовательно, прямые IJ и АВ перпендикулярны.
Ответ: доказаноpазбирался: Даниил Романович | обсудить разбор | оценить
👀 9.3k |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
геометрия — Окружность $\Gamma_2$ с центром в $C$ и радиусом $CN$ пересекает $\Gamma_1$ в точках $P$ и $Q$, а отрезки $PQ$ и $CD$ пересекаются в точке $M$
спросил
Изменено 2 года, 3 месяца назад
Просмотрено 97 раз
$\begingroup$
Пусть $CD$ — хорда окружности $\Gamma_1$, а $AB$ — диаметр, перпендикулярный $CD$ в точке $N$, где $AN > NB$. Окружность $\Gamma_2$ с центром в точке $C$ и радиусом $CN$ пересекает $\Gamma_1$ в точках $P$ и $Q$, а отрезки $PQ$ и $CD$ пересекаются в точке $M$.
Учитывая, что радиусы $\Gamma_1$ и $\Gamma_2$ равны $61$ и $60$ соответственно, найдите $AM$.
Что я пробовал : Вот картинка:-
Я не смог правильно понять вопрос, так как написано что $AB\perp CD$ но я не могу понять в какой точке проведена перпендикулярная линия . Проблема в целом также кажется сложной, поэтому я все равно не могу понять, с чего начать ее решать.
Кто-нибудь может мне помочь? Спасибо.
Редактировать :- Как упомянул @cosmos5 в комментариях, мой рисунок и мои мысли были совершенно неправильными. Вот новая картинка: —
Как обычно, проблема кажется сложной, и я не могу придумать, с чего начать, однако я вижу, что мы могли бы использовать теорему Пифагора в той или иной форме, но я не могу понять как, поскольку я не знаю никаких длин, кроме радиусов кругов.
- геометрия 92} = 78$
$\endgroup$
геометрия — $4$ точки в порядке $A,B,C,D$ лежат на окружности с расширением $AB$, пересекающимся с расширением $DC$ в точке $E$ и с расширениями $AD$ и $BC$ в $F$.

спросил
Изменено 2 года, 4 месяца назад
Просмотрено 537 раз
$\begingroup$
$4$ точки в порядке $A,B,C,D$ лежат на окружности с расширением $AB$, пересекающимся с расширением $DC$ в точке $E$ и с расширением $AD$ и $BC$ в точке $F $. Пусть $EP$ и $FQ$ касаются этой окружности с точками касания $P$ и $Q$ соответственно. Предположим, что $EP = 60$, $FQ = 63$. Найдите $EF$.
Что я пробовал : Вот картинка :-
Использована сила очка, чтобы получить :- $$EA * EB = ED * EC = 3600$$ $$FA * FD = FB * FC = 3969$$ Однако это не помогает продолжить и не находит значение $EF$ .
Однажды я подумал о теореме Пифагора.
 Соедините OP и OQ и пусть они будут по $x$ каждый. Тогда мы можем найти $OE$ и $OF$ через $x$. Хотя не уверен, что это поможет решить проблему.
Соедините OP и OQ и пусть они будут по $x$ каждый. Тогда мы можем найти $OE$ и $OF$ через $x$. Хотя не уверен, что это поможет решить проблему.Кто-нибудь может мне помочь? Спасибо.
- геометрия
- треугольники
- решение задач
- сила точки
$\endgroup$
$\begingroup$ 92=7569\если и только если EF=87$$
$\endgroup$
1
$\begingroup$
Проективная геометрия Хаттона , стр. 156 дает две версии теоремы:
[T] он квадрат расстояния между парой сопряженных точек с относительно окружности равна сумме степеней точек.
и
Если четырехугольник вписать в окружность, то квадрат расстояния между двумя его диагональными точками, внешними по отношению к окружности, равно сумма квадратов касательных из этих точек.


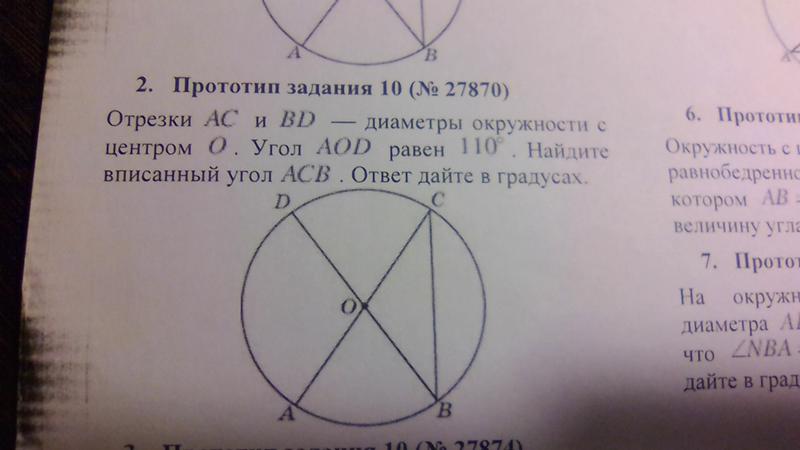

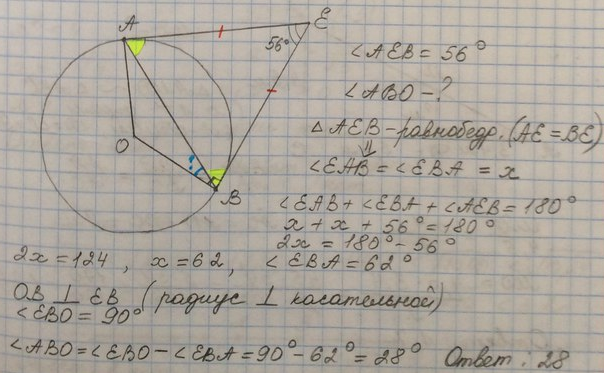 Теория вероятностей
Теория вероятностей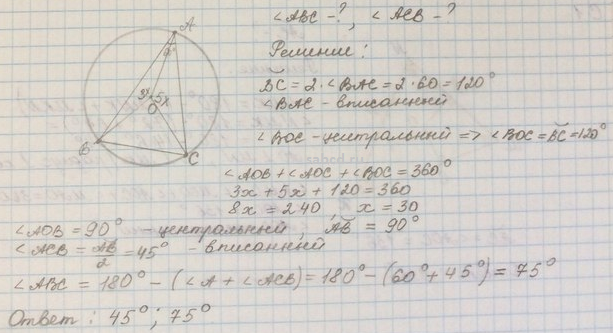 Учитывая, что радиусы $\Gamma_1$ и $\Gamma_2$ равны $61$ и $60$ соответственно, найдите $AM$.
Учитывая, что радиусы $\Gamma_1$ и $\Gamma_2$ равны $61$ и $60$ соответственно, найдите $AM$.
 Соедините OP и OQ и пусть они будут по $x$ каждый. Тогда мы можем найти $OE$ и $OF$ через $x$. Хотя не уверен, что это поможет решить проблему.
Соедините OP и OQ и пусть они будут по $x$ каждый. Тогда мы можем найти $OE$ и $OF$ через $x$. Хотя не уверен, что это поможет решить проблему.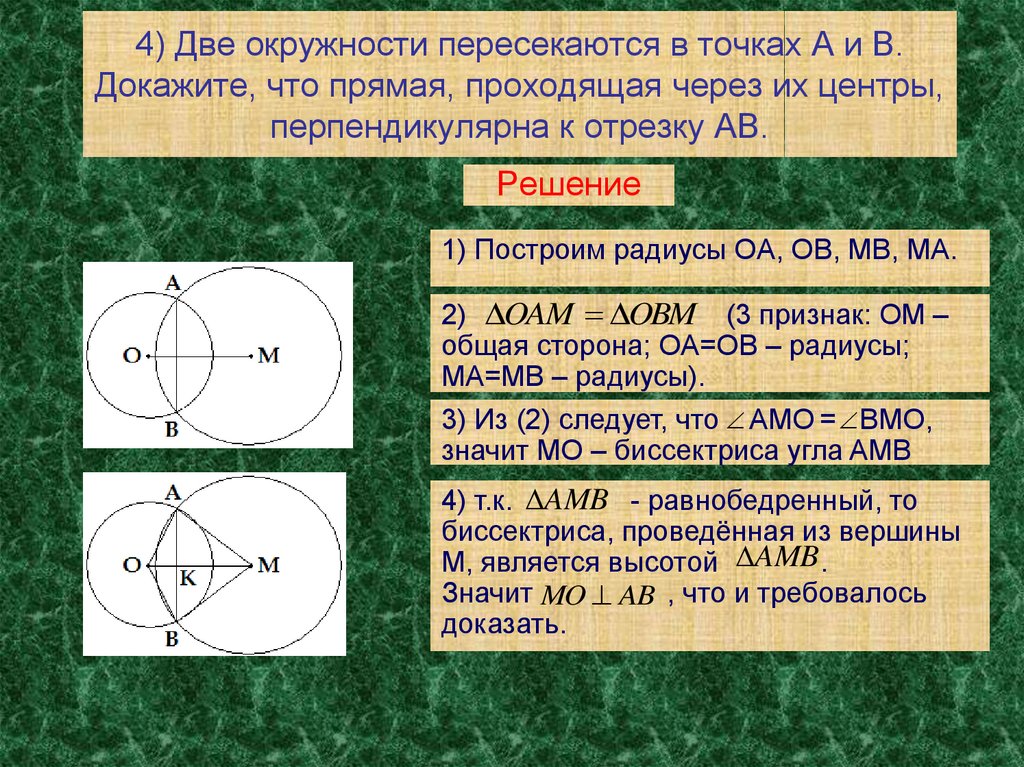
Leave A Comment