Окружность с центром о вписана в треугольник авс касается его сторон ав: Если окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС соответственно в точках K, L, M, а угол ВАС равен [math]varphi[/math], то угол KLM равен [math]90 ^{circ}

Вписанная окружность 8 класс онлайн-подготовка на Ростелеком Лицей

Тема: Окружность

Урок: Вписанная окружность

1. Опорные определения

Начнем с напоминания важных опорных фактов, и первый факт – это касание прямой и окружности.

Задана окружность с центром О и радиусом r (см. Рис. 1). А – общая точка прямой и окружности. Если такая точка единственная, то прямая р – касательная к окружности. Радиус ОА, проведенный в точку касания, перпендикулярен касательной р.

Справедливо обратное: если А – общая точка прямой и окружности, и радиус, проведенный в эту точку, перпендикулярен прямой, то общая точка единственная, и прямая р – касательная.

Рис. 1

Рассмотрим касание окружности сторонами угла (см. Рис. 2).

Помним, что биссектриса угла – это геометрическое место точек, равноудаленных от сторон данного угла.

Точка О лежит на биссектрисе: перпендикуляр ОА к прямой а, ОВ – к прямой В, .

Построим окружность радиусом ОА.

Рис. 2

Утверждаем, что окружность касается прямой а, т.к. А – общая точка прямой а и окружности, и она единственная (радиус ОА перпендикулярен прямой). Аналогично прямая b касается окружности.

Таким образом, имеем окружность, вписанную в угол.

Многоугольник имеет несколько углов и несколько сторон, мы готовы дать определение вписанной в него окружности.

2. Определение вписанной окружности

Окружность называется вписанной в многоугольник, если касается всех его сторон.

Мы будем рассматривать только выпуклые многоугольники, рассмотрим пример – окружность вписана в выпуклый четырехугольник:

Как получить центр и радиус вписанной окружности?

Мы знаем, что точка О – центр, лежит на биссектрисе угла А, вписана в угол А, аналогично точка О лежит на биссектрисе каждого угла и вписана в каждый угол.

Таким образом, все биссектрисы четырехугольника пересекаются в одной точке – точке О.

Строим биссектрисы, на их пересечении получаем центр окружности. Из точки О опускаем перпендикуляры к сторонам

Рис. 3

четырехугольника в точки K, L, M, N. Касательные, проведенные к окружности из одной точки, равны между собой, таким образом, из каждой вершины выходит пара равных касательных – , , , .

3. Теоремы о четырехугольниках, описанных около окружности

В описанном четырехугольнике суммы противоположных сторон равны.

Дано: окружность с центром О вписана в четырехугольник ABCD. Четырехугольник ABCD описан около окружности. Таким образом, описанный четырехугольник – это такой четырехугольник, в который можно вписать окружность (см. Рис. 4)_.

Доказать:

Рис. 4

Доказательство:

Запишем равенство через отрезки касательных:

; ; ; ;

;

Раскроем скобки:

;

Таким образом, суммы противоположных сторон четырехугольника, описанного около окружности, равны, что и требовалось доказать.

Итак, если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.

Справедлива обратная теорема.

Теорема

Если суммы противоположных сторон выпуклого четырехугольника равны, в него можно вписать окружность.

Это важная теорема, так как центр вписанной окружности находится на пересечении биссектрис. Отсюда, если суммы противоположных сторон четырехугольника равны, его биссектрисы пересекутся в одной точке.

Данную теорему мы доказывать не будем.

Прямую и обратную теоремы можно объединить.

Теорема

В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

4. Примеры четырехугольников, в которые можно и нельзя вписать окружность

Приведем конкретные примеры четырехугольников, в которые можно вписать окружность и в которые нельзя вписать окружность.

Ромб

У ромба все стороны равны, отсюда суммы противоположных сторон равны, значит, в ромб можно вписать окружность (см.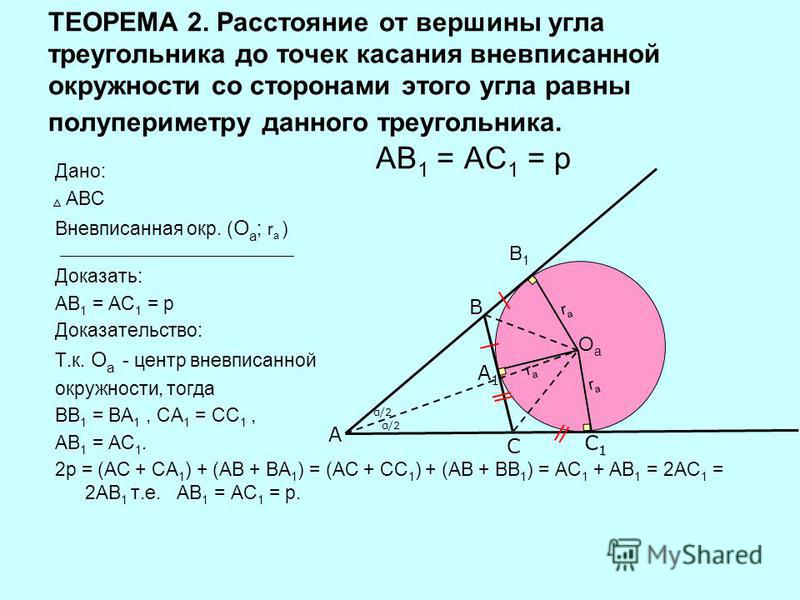 Рис. 5). Кроме того, мы знаем, что диагонали ромба перпендикулярны и делят углы ромба пополам. Значит, каждая диагональ – это биссектриса, биссектрисы всех четырех углов пересеклись в одной точке – точке О. О – центр вписанной окружности.

Рис. 5

Квадрат

Квадрат – частный случай ромба, в него также можно вписать окружность (см. Рис. 6).

Рис. 6

Прямоугольник

В прямоугольник нельзя вписать окружность (см. Рис. 7), это очевидно из рисунка – суммы противоположных сторон не равны, т.к. противоположные стороны равны между собой, а соседние не равны:

Рис. 7

5. Теорема об окружности, вписанной в треугольник

В любой треугольник можно вписать окружность, и только одну (см. Рис. 8).

Рис. 8

Доказательство:

Мы знаем, что все биссектрисы треугольника пересекаются в одной точке – пусть в точке О. Проведем биссектрисы АО, ВО, СО. Точка их пересечения О равноудалена от сторон треугольника. Она равноудалена от сторон угла  – АС и АВ, так как принадлежит биссектрисе этого угла. Аналогично она равноудалена от сторон углов  и , таким образом, от трех сторон треугольника.

Опустим перпендикуляры из точки О на стороны треугольника – ОМ на сторону АС, OL – на ВС, ОК – на АВ. Эти перпендикуляры и будут расстояниями от точки О до сторон треугольника, и они равны:

.

Обозначим расстояние от точки О до сторон треугольника за r и рассмотрим окружность с центром в точке О и радиусом r.

Окружность касается прямой АВ, т.к. имеет с ней общую точку К, и радиус ОК, проведенный в эту точку, перпендикулярен прямой АВ. Аналогично окружность касается прямых АС и ВС. Таким образом, окружность касается всех тех сторон треугольника, значит, она вписана в треугольник.

Докажем, что данная вписанная окружность единственная. Если бы была вторая окружность, ее центр был бы равноудален от всех сторон треугольника и лежал бы на пересечении всех биссектрис. Но все биссектрисы пересекаются в единственной точке – точке О, таким образом, и вписанная окружность в треугольник единственная.

6. Выводы по уроку

Итак, мы ознакомились с понятием вписанной окружности и доказали некоторые важные теоремы. В следующем уроке мы рассмотрим описанную окружность.

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Mschool.kubsu.ru (Источник).
3. Ege-study.ru (Источник).

Домашнее задание

1. Задание 1 – в треугольник  вписана окружность с центром О. Найдите угол , если угол .
2. Задание 2 – на сторонах АВ и АС треугольника АВС, описанного около окружности с центром О, отмечены точки D и E таким образом, что , . Доказать, что .
3. Задание 3 – найдите радиус окружности, вписанной в прямоугольный треугольник, периметр которого 24 см, а гипотенуза 10 см.

Вписанная окружность | ЮКлэва

Ну что, юнга, уверен, что знаешь все про окружности?

Пров вписанную точно знаешь. А про вневписанную слышал?

Ничего страшного, сейчас ты во всём разберешься!

Поехали!

Вписанная окружность и отрезки сторон треугольника

Давай представим, что мы откуда-то узнали все три стороны треугольника.

Можно ли найти как-то отрезочки \( \displaystyle AK\), \( \displaystyle KC\), \( \displaystyle BL\) и.д. –отрезки, на которые точки касания разбивают стороны треугольника?

Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).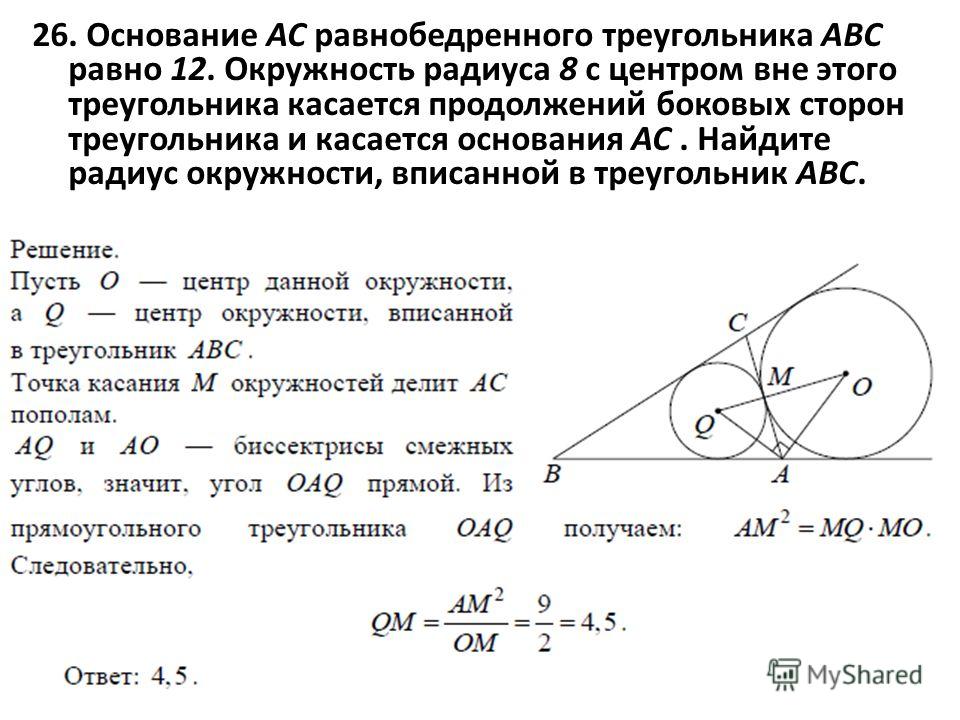

Итак, начнём поиск!

Посмотри внимательно: из точки \( \displaystyle A\) проведено две касательных, значит их отрезки \( \displaystyle AK\) и \( \displaystyle AM\) равны.

Мы обозначим их «\( \displaystyle x\)».

Далее, точно так же:

\( \displaystyle BM=BL=y\) (обозначили).

\( \displaystyle CK=CL=z\) (обозначили).

Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «\( \displaystyle a\)», «\( \displaystyle b\)», «\( \displaystyle c\)» – смотри на рисунок. Что же теперь получилось?

А вот, например, отрезок «\( \displaystyle a\)» состоит из двух отрезков «\( \displaystyle y\)» и «\( \displaystyle z\)», да и отрезки «\( \displaystyle b\)» и «\( \displaystyle c\)» тоже из чего-то состоят. Запишем это всё сразу:

\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\)

Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!

Сложим первые два уравнения и вычтем третье:

\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.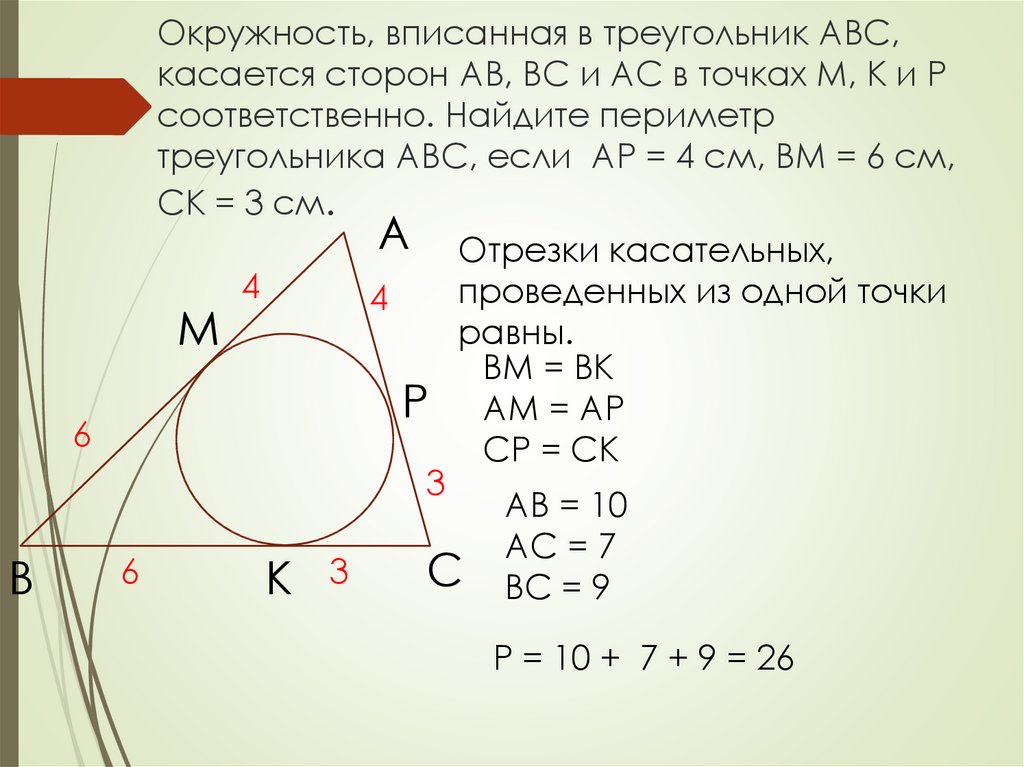 \Rightarrow x+y+2z-\left( x+y \right)=a+b-c\), то есть:

\( \displaystyle z=\frac{a+b-c}{2}\)

А теперь сложим первое и третье уравнение и вычтем второе:

\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\Rightarrow y+z+x+y-\left( x+z \right)=a+c-b\), то есть:

\( \displaystyle y=\frac{a+c-b}{2}\)

И последний шаг: сложим второе и третье, а потом вычтем первое.

\( \displaystyle \left\{ \begin{array}{l}y+z=a\\x+z=b\\x+y=c\end{array} \right.\Rightarrow x=\frac{b+c-a}{2}\) \( \displaystyle x=\frac{b+c-a}{2}\)

Ну вот, всё нашли:

\( \displaystyle x=\frac{b+c-a}{2};y=\frac{a+c-b}{2};~z=\frac{a+b-c}{2}\)

Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.

\( \displaystyle x=\frac{b+c-a}{2}\)

Секрет вот в чём: те стороны, на которых есть «\( \displaystyle x\)» («\( \displaystyle b\)» и «\( \displaystyle c\)») будут с плюсом, а та сторона, где нет «\( \displaystyle x\)» (это «\( \displaystyle a\)»), будет с минусом.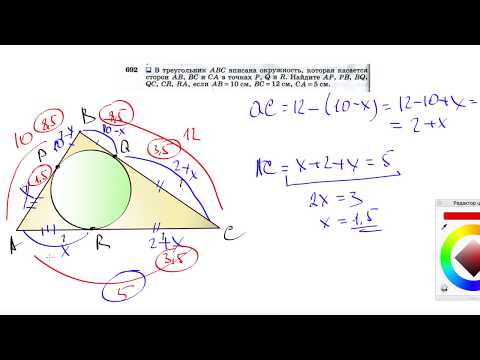

Ну, а пополам поделить всё хозяйство. С другими буквами точно так же

\( \displaystyle y=\frac{a+c-b}{2}\)

На «\( \displaystyle a\)» и «\( \displaystyle c\)» есть «\( \displaystyle y\)» – они с плюсом, на «\( \displaystyle b\)» нет «\( \displaystyle y\)» – она с минусом

\( \displaystyle z=\frac{a+b-c}{2}\)

На «\( \displaystyle a\)» и «\( \displaystyle b\)» есть «\( \displaystyle z\)» – они с плюсом, на «\( \displaystyle c\)» нет «\( \displaystyle z\)» – она с минусом.

На фигуре окружность, вписанная в треугольник ABC, касается его сторон AB, BC и AC в точках D, E и F соответственно. Если AB=12 см, BC=8 см и AC=10 см, найдите длины AD, BE и CF.

Последняя обновленная дата: 02 -й апрель 2023

•

Общее представление: 275.1K

•

Просмотры сегодня: 2,49K

Ответ

Проверено

275. 1K+ Просмотры

HINT:

275.1K+

HINT:

202020202020202020202020202 касательные, проведенные от внешнего к окружности, равны по длине. Мы видим, что AD и AF являются касательными, проведенными из точки A. Точно так же BE и BD являются касательными, проведенными из точки B, а CF и CE касательными, проведенными из точки C. У нас есть длины сторон AB, AC и BC. Предположим, что длина касательной равна x, y и z. Из рисунка видно, что AB=AD+DB, BC=BE+EC и AC=AF+FC. Итак, мы можем найти значения AD, BE и CF.

Полное пошаговое решение:

У нас есть цифра, как указано выше,
Мы знаем, что касательные, проведенные от внешнего к окружности, равны по длине. Итак, из рисунка видно, что
$\begin{align}
  & \Rightarrow AF=AD \\
 & \Rightarrow CF=CE \\
 & \Rightarrow BE=BD \\
\end{align}$
Предположим, что
$\begin{align}
  & \Rightarrow AF=AD=x \\
 & \Rightarrow CF=CE=y \\
 & \Rightarrow BE=BD=z \\
\end{align}$
Из рисунка ясно видно, что
$\begin{align}
  & \Rightarrow AB=AD+DB \\
 & \Rightarrow BC=BE+EC \\
 & \Rightarrow AC=AF+FC \\
\end{align}$
Мы знаем значения AB, BC и AC, мы можем записать приведенное выше уравнение как
$\begin{ align}
  & \Стрелка вправо 12=x+z.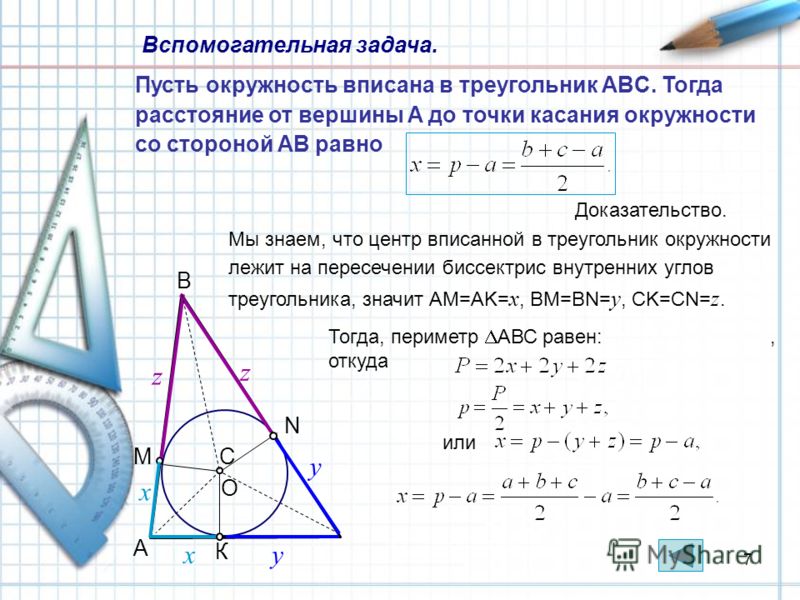 ……(i) \\
 & \Стрелка вправо 8=z+y……….(ii) \\
 & \ Стрелка вправо 10=x+y……..(iii) \\
\end{align}$
Добавим уравнения (i), (ii) и (iii), получим
$\begin{align}
  & \Rightarrow 2(x+y+z)=30 \ \
 & \Rightarrow x+y+z=15…….(iv) \\
\end{align}$
Подставим уравнение (iii) в уравнение (iv), получим,
$\begin{align}
  & \Rightarrow x+y+z=15 \\
 & \Rightarrow 10+z=15 \\
 & \Rightarrow z=5 \\
\end{align}$
Мы можем вычислить значение x и y, используя приведенный выше результат, мы получим
$\begin{align}
  & \Стрелка вправо x+z=12\Стрелка вправо x+5=12 \\
 & \Стрелка вправо x=7 \\
 & \Стрелка вправо x+y=10\Стрелка вправо 7+y=10 \\
 & \Rightarrow y=3 \\
\end{align}$
Мы это знаем,
$\begin{align}
  & \Rightarrow AF=AD=x \\
 & \Rightarrow CF=CE=y \\
 & \Rightarrow BE=BD=z \\
\end{align}$
Итак, AD=7см, BE=5см и CF=3см

Примечание: Прежде чем отвечать на этот вопрос, учащиеся должны знать понятия геометрии окружности. Для ученика важно правильно проанализировать рисунок, прежде чем делать выводы, половина вопроса может быть решена с использованием рисунка.

Недавно обновленные страницы

Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE

Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE

В любом треугольнике AB2 BC4 CA3 и D является средней точкой математики класса 11 JEE_Main

В Delta ABC 2asin dfracAB+C2 равно IIT Математика класса 11 JEE_Main

0002 Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол класса 11 по математике JEE_Main

Если пружина имеет период T и разрезана на n равный класс 11 по физике CBSE

Планета движется вокруг Солнца по почти круговой орбите класс 11 по физике CBSE

В любом треугольнике AB2 BC4 CA3 и D является средней точкой класса 11 по математике JEE_Main

C 60circ затем 11 класс математики JEE_Main

Если в треугольнике rmABC сторона равна sqrt 3 + 1rmcm и угол класс 11 математика JEE_Main

Тенденции сомнения

Математическая задача: Окружность в ромбе

Вписанный ромб. Точки касания делят стороны на части длиной 19 см и 6 см. Вычислите площадь круга.

Правильный ответ: