Глава 4
Задачи для повторения
165
Найдите площадь равнобедренной трапеции, если ее высота равна h, а боковая сторона видна из центра описанной окружности под углом а.
Площадь равнобедренной трапеции, описанной около окружности, равна S. Найдите длину средней линии трапеции, если градусная мера острого угла при ее основании равна ср.
В равнобедренную трапецию вписана окружность. Найдите длину диагонали трапеции, если длины ее оснований равны а и Ь.
Площадь равнобедренной трапеции, описанной около окружности, равна S, а боковая сторона трапеции в два раза больше ее высоты. Найдите площадь круга, вписанного в трапецию.

Площадь равнобедренной трапеции, описанной около окружности, равна 32 см2, а острый угол трапеции равен 30°. Вычислите длины сторон трапеции.
Около окружности описана прямоугольная трапеция с острым углом а. Найдите высоту трапеции, если ее периметр равен Р.
Диагонали равнобедренной трапеции взаимно перпендикулярны, а ее площадь равна S. Найдите высоту трапеции.
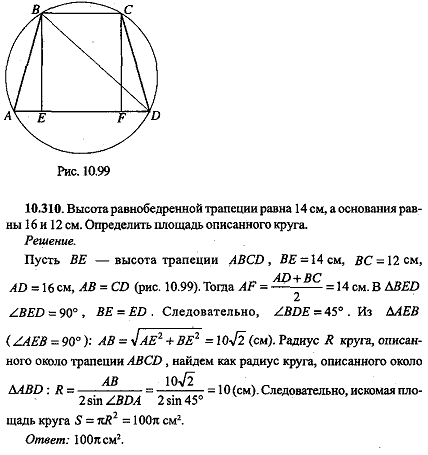
Высота равнобедренной трапеции равна 14 см, а длины оснований равны 16 см и 12 см. Вычислите площадь круга, ограниченного описанной около трапеции окружностью.
Вычислите площадь прямоугольной трапеции, если центр вписанной в нее окружности находится на расстоянии 1 см и 2 см от концов боковой стороны.

Длина диагонали равнобедренной трапеции равна 5 см, а площадь равна 12 см2. Вычислите высоту трапеции.
Длины боковых сторон АВ и CD трапеции ABCD равны 8 см и 10 см соответственно, а длина основания ВС равна 2 см. Биссектриса угла ADC проходит через середину стороны АВ. Вычислите площадь трапеции.
Скачено с Образовательного
38. Длины оснований
 Через
точку F, принадлежащую
стороне АВ и
делящую
ее
в
отношении т : п, считая
от
точки А, проведена
прямая,
параллельная
основаниям
трапеции,
пересекающая
сторону CD в
точке Т.
Через
точку F, принадлежащую
стороне АВ и
делящую
ее
в
отношении т : п, считая
от
точки А, проведена
прямая,
параллельная
основаниям
трапеции,
пересекающая
сторону CD в
точке Т.ап + Ьт
(рис. 122, а).
Дано: ABCD —
трапеция, AD = а,
AF : FB = т : п,
FT || AD, Тє CD.
Доказать:
™, an + bm 11 = .
Докажите, что FT
1 | С | Лт |
А | D | |
б)
а)
Рис. 122
122
Решение.
ОТ СТ
ED CD
„rr. an + bm г 1 = .
FT -b
п
Проведем отрезок СЕ, параллельный стороне
Так как AF : FB = m : п и FT || AD, то AF : FB = DT : ТС = m : п. Поскольку СЕ || АВ, то ОТ = ЕТ — Ь.
Треугольник СТО подобен треугольнику CDE, следовательно,
или
Отсюда получаем, что отрезок
Средняя линия трапеции имеет длину 10 см и делит площадь трапеции в отношении 3 : 5.
 Вычислите
длины
оснований
трапеции.
Вычислите
длины
оснований
трапеции.Длина средней линии равнобедренной трапеции, в которую вписана окружность, равна 5 см. Средняя линия делит трапецию на две части, отношение площадей которых равно 7 : 13. Вычислите высоту трапеции.
Длины оснований трапеции равны 1 см и 7 см. Вычислите длину отрезка, параллельного основаниям и делящего трапецию на равновеликие части.
портала www.adu.by
Решение варианта №190 ОГЭ по математике. Ларин
Contents
- 1 Задание №1
- 1.1 Решение
- 2 Задание №2. Решение варианта №190 ОГЭ по математике. Ларин
- 2.1 Решение
- 3 Задание №3. Решение варианта №190 ОГЭ по математике. Ларин
- 3.1 Решение
- 4 Задание №4
- 4.1 Решение
- 5 Задание №5. Решение варианта №190 ОГЭ по математике.
 Ларин
Ларин- 5.1 Решение
- 6 Задание №6
- 6.1 Решение
- 7 Задание №7. Решение варианта №190 ОГЭ по математике. Ларин
- 7.1 Решение
- 8 Задание №8. Решение варианта №190 ОГЭ по математике. Ларин
- 8.1 Решение
- 9 Задание №9. Решение варианта №190 ОГЭ по математике. Ларин
- 9.1 Решение
- 10 Задание №10. Решение варианта №190 ОГЭ по математике. Ларин
- 10.1 Решение
- 11 Задание №11. Решение варианта №190 ОГЭ по математике. Ларин
- 11.1 Решение
- 12 Задание №12
- 12.1 Решение
- 13 Задание №13
- 13.1 Решение
- 14 Задание №14. Решение варианта №190 ОГЭ по математике. Ларин
- 14.1 Решение
- 15 Задание №15. Решение варианта №190 ОГЭ по математике. Ларин
- 15.1 Решение
- 16 Задание №16. Решение варианта №190 ОГЭ по математике. Ларин
- 16.1 Решение
- 17 Задание №17
- 17.
 1 Решение
1 Решение
- 17.
- 18 Задание №18
- 18.1 Решение
- 19 Задание №19. Решение варианта №190 ОГЭ по математике. Ларин
- 19.1 Решение
- 20 Задание №20. Решение варианта №190 ОГЭ по математике. Ларин
- 20.1 Решение
- 21 Задание №21
- 21.1 Решение
- 22 Задание №22. Решение варианта №190 ОГЭ по математике. Ларин
- 22.1 Решение
- 23 Задание №23. Решение варианта №190 ОГЭ по математике. Ларин
- 23.1 Решение
- 24 Задание №24. Решение варианта №190 ОГЭ по математике. Ларин
- 24.1 Решение
- 25 Задание №25
- 25.1 Решение
- 26 Задание №26. Решение варианта №190 ОГЭ по математике. Ларин
- 26.1 Решение
- 27 Видео: Разбор Варианта ОГЭ Ларина №190 (№1-20)
- 28 Видео: Разбор Варианта ОГЭ Ларина №190 (№21-26)
Задание №1
Найдите значение выражения:
Решение
Ответ: -3.
Задание №2. Решение варианта №190 ОГЭ по математике. Ларин
Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья.
| Категория | Масса одного яйца, не менее, г |
| Высшая | 75,0 |
| Отборная | 65,0 |
| Первая | 55,0 |
| Вторая | 45,0 |
| Третья | 35,0 |
Используя данные, представленные в таблице, определите, к какой категории относится яйцо, массой 63,5 г.
Варианты ответа: 1. высшая 2. отборная 3. первая 4. вторая.
Решение
63,5 ∈ (55;65) следовательно, первая категория.
Ответ: 3.
Задание №3. Решение варианта №190 ОГЭ по математике. Ларин
Одно из чисел √5, √7, √11, √14 отмечено на прямой точкой A.
Какое это число? 1.√5 2. √7 3.√11 4.√14
√7 3.√11 4.√14
Решение
2 = √4; 3 = √9.
ТогдаA = √5 илиA = √7.
Так как число А ближе к 2, то оно равно √5, что соответствует 1 варианту.
Ответ: 1.
Задание №4
Представьте выражение:
в виде степени с основанием m.
Варианты ответа
- 1. m12 .
- 2.m-12 .
- 3.18 .
- 4.-4.
Решение
соответствует 3 варианту ответа.
Ответ: 3.
Задание №5. Решение варианта №190 ОГЭ по математике. Ларин
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости.
По горизонтальной оси откладывается скорость (в км/ч), по вертикальной — тормозной путь (в метрах).
Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 30 км/ч. Ответ дайте в метрах.
Ответ дайте в метрах.
Решение
Координате v=30 соответствует S=10.
Ответ: 10.
Задание №6
Решите уравнение:
Решение
Ответ: -3.
Задание №7. Решение варианта №190 ОГЭ по математике. Ларин
В поселке в настоящее время 40824 жителя. Известно, что население этого поселка увеличивалось ежегодно на 8%.
Сколько жителей было в поселке два года назад?
Решение
Пусть x –два года назад, тогда x*1,08 –год назад и (x*1,08)*1,08 в этом году.
x∗1,08² = 40824.
x = 40824/1,08 = 35000.
Ответ: 35000.
Задание №8. Решение варианта №190 ОГЭ по математике. Ларин
На диаграмме показан религиозный состав населения Германии.
Определите по диаграмме, в каких пределах находится доля католиков.
- 1. 0-10%
- 2. 10-15%
- 3. 15-25%
- 4. 25-45%
Решение
Сегмент католиков составляет третью часть круга, то есть около 33%, что попадает в 4 вариант ответа.
Ответ: 4.
Задание №9. Решение варианта №190 ОГЭ по математике. Ларин
На олимпиаде по математике 250 участников разместили в трёх аудиториях. В первых двух удалось разместить по 95 человек, оставшихся перевели в запасную аудиторию в другом корпусе.
Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение
В запасной аудитории 250-2*95=60 человек.
Следовательно вероятность попасть:
P = 60/250 = 0,24.
Ответ: 0,24.
Задание №10. Решение варианта №190 ОГЭ по математике. Ларин
График какой из приведенных ниже функций изображён на рисунке?
- y = x²+2.
- y = −x²+2.
- y = x²+4.
- y = −x²+4.
Решение
Ветви вниз, значит a<0. Вершина смещена на 4 вверх, значит b=4 (рассматриваем квадратичную функцию y=ax²+b), следовательно, ответ 4.
Ответ: 4.
Задание №11. Решение варианта №190 ОГЭ по математике. Ларин
Арифметическая прогрессия задана условием:
an = -29 + 5.8n.
Найдите a10.
Решение
a10 = −29 + 5,8∗10 = −29 + 58 = 29.
Ответ: 29.
Задание №12
Найдите значение выражения:
при а = — 18.
Решение
Ответ: 0,2.
Задание №13
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле T=2√l , где l — длина нити в метрах. Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 4 секунды.
Решение
Ответ: 4.
Задание №14. Решение варианта №190 ОГЭ по математике. Ларин
Решите неравенство 3x — 5(x+2) > -2.
Варианты ответа:
- (−4;+∞).
- (−12;+∞).
- (−∞;−4).
- (∞;−12).

Решение
3x−5(x+2) > −2.
3x−5x−10+2 > 0.
−2x−8 > 0.
−2x > 8.
x < 4x < 4, что соответствует ответу 3.
Ответ: 3.
Задание №15. Решение варианта №190 ОГЭ по математике. Ларин
Человек ростом 1,6 м стоит на расстоянии 6 шагов от столба, на котором висит фонарь. Тень человека равна четырём шагам.
На какой высоте (в метрах) расположен фонарь?
Решение
Ответ: 4.
Задание №16. Решение варианта №190 ОГЭ по математике. Ларин
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBA=44°.
Найдите угол NMB. Ответ дайте в градусах.
Решение
- ∠NBA = ½∪AN ⇒ ∪AN = 44∗2 = 88.
- ∪NB = 180−∪NA = 180−88 = 92.
- ∠NMB = ½∪NB = 92/2 = 46.
Ответ: 46.
Задание №17
Длина хорды окружности равна 24, а расстояние от центра окружности до этой хорды равно 5.
Найдите диаметр окружности.
Решение
Ответ: 26.
Задание №18
На клетчатой бумаге с размером клетки 1*1 изображена фигура.
Найдите её площадь.
Решение
Площадь одного квадрата составляет 1*1=1, тогда площадь фигуры равна 1*10=10.
Ответ: 10.
Задание №19. Решение варианта №190 ОГЭ по математике. Ларин
В треугольнике ABC угол C равен 90°, BC=9, sinA=0,6.
Найдите AB.
Решение
Ответ: 15.
Задание №20. Решение варианта №190 ОГЭ по математике. Ларин
Какие из следующих утверждений верны?
- 1. Высота прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
- 2. Диагонали параллелограмма равны.
- 3. Радиус окружности равен половине диаметра этой окружности.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Решение
- нет — так как половине гипотенузы равна медиана, к ней проведенная.
- нет — только в прямоугольнике и квадрате.
- верно.
Ответ: 3.
Задание №21
Решите уравнение:
Решение
Ответ: 0; 1; 2.
Задание №22. Решение варианта №190 ОГЭ по математике. Ларин
В первую поездку автомобиль израсходовал 10% бензина, имеющегося в баке, затем во вторую поездку — 25% остатка. После этого в баке осталось на 13 л меньше, чем было первоначально. Сколько литров бензина находилось в баке первоначально?
Решение
Пусть изначально было литров.
Израсходовал 0,1x , осталось 0,9x.
Затем израсходовал:
25% от 0,9x = 0,25*0,9x = 0,225x.
Тогда всего израсходовали:
0,1x + 0,25x = 13.
0,325x = 13 ⇔ x = 40 (литров) было в баке.
Ответ: 40.
Задание №23. Решение варианта №190 ОГЭ по математике.
 Ларин
ЛаринПостройте график функции:
и определите, при каких значениях а прямая y=а будет иметь с графиком единственную общую точку.
Решение
y = a — прямая, параллельная оси Ox, тогда одну точку будет иметь при a∈[0;4).Ответ: [0;4).
Задание №24. Решение варианта №190 ОГЭ по математике. Ларин
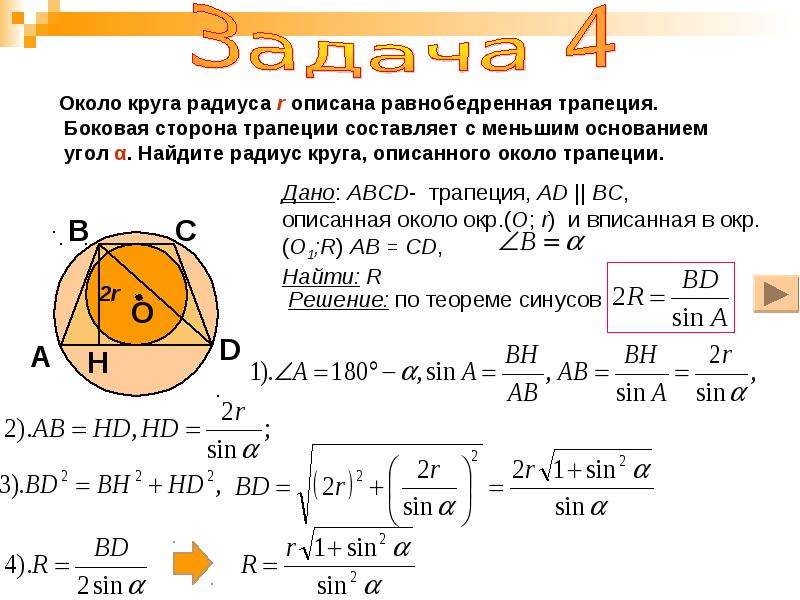
Около круга радиуса 2 см описана равнобедренная трапеция с острым углом 30°.
Найдите длину средней линии трапеции.
Решение
Ответ: 8.
Задание №25
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD.
Докажите, что МА2 + МВ2 + МС2 + МD2 = 8R2
Решение
Внутри параллелограмма ABCD взята точка K так, что треугольник CKD равносторонний. Известно, что расстояния от точки K до прямых AD, AB и BC равны соответственно 3, 6 и 5. Найдите периметр параллелограмма.



 Вычислите
длины
оснований
трапеции.
Вычислите
длины
оснований
трапеции. Ларин
Ларин 1 Решение
1 Решение

Leave A Comment