определение, примеры, формулы / Справочник :: Бингоскул
Объем правильной шестиугольной призмы: определение, примеры, формулыдобавить в закладки удалить из закладок
Содержание:
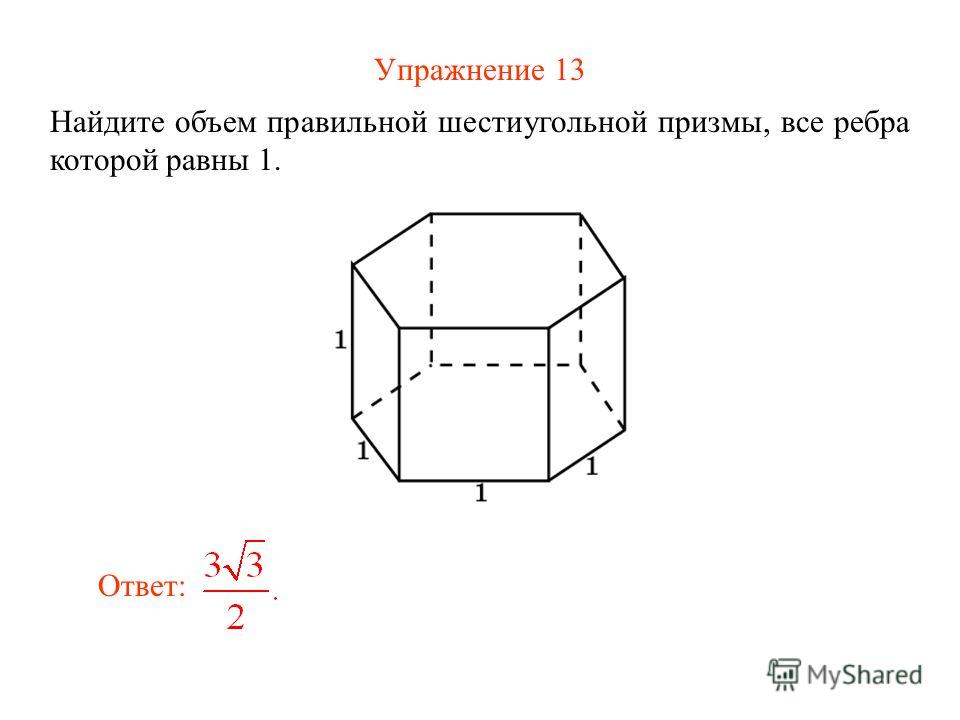
Призмой называется многогранник с многоугольниками в основаниях, которые находятся в параллельных плоскостях. Поверхности или боковые грани геометрического тела представлены параллелограммами или прямоугольниками. Плоская фигура, которая лежит в основании призмы, определяет ее название: треугольник – треугольная, шестиугольник – шестиугольная. Рассмотрим, как найти объем правильной шестиугольной призмы, ее особенности и свойства.
Характеристика правильной призмы
Геометрическое тело состоит из пары равносторонних 6-угольников, расположенных параллельно. После соединения точек многоугольников параллельными прямыми получается правильная шестиугольная призма. Шестиугольники называются основаниями, проходящие между ними линии – ребрами, образовавшиеся прямоугольники – боковыми гранями.
Отрезки, соединяющие расположенные в разных плоскостях вершины, называются диагоналями.
Свойства призмы:
- Боковые ребра равны по длине и параллельны.
- Грани – это равные прямоугольники, основания – 6-угольники.
- Боковая поверхность равна произведению периметра лежащего у ее основания шестиугольника на высоту.
Что такое объем призмы, как его определить
Геометрические тела занимают определенное место в пространстве. Объем шестиугольной призмы показывает, сколько жидкости или кубиков с длиной грани в единицу поместится внутри нее. Измеряется в кубических единицах: кубический сантиметр – см3, кубический метр – м3.
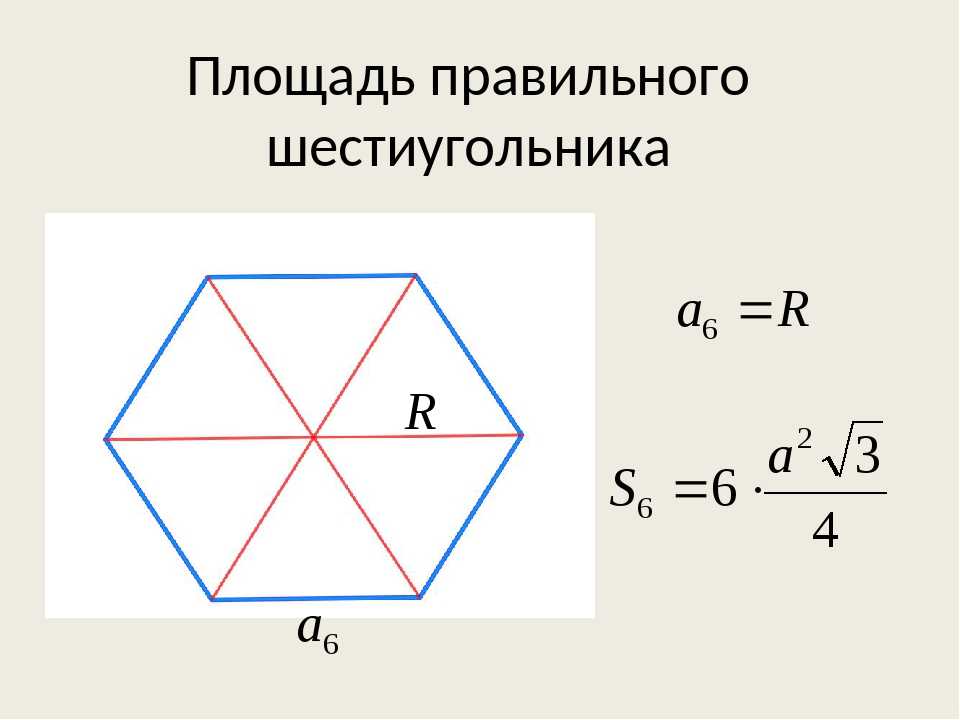
Формула вычисления объема правильной шестиугольной призмы следующая:
V = S * h, где:
- S – площадь основания – шестиугольника;
- h – высота геометрического тела или расстояние между расположенными в разных плоскостях точками, которые соединяются ребрами.

В большинстве задач известны высота призмы (h) и длина стороны многоугольника (a). Площадь последнего вычисляется по формуле:
После подстановки значений получаем:
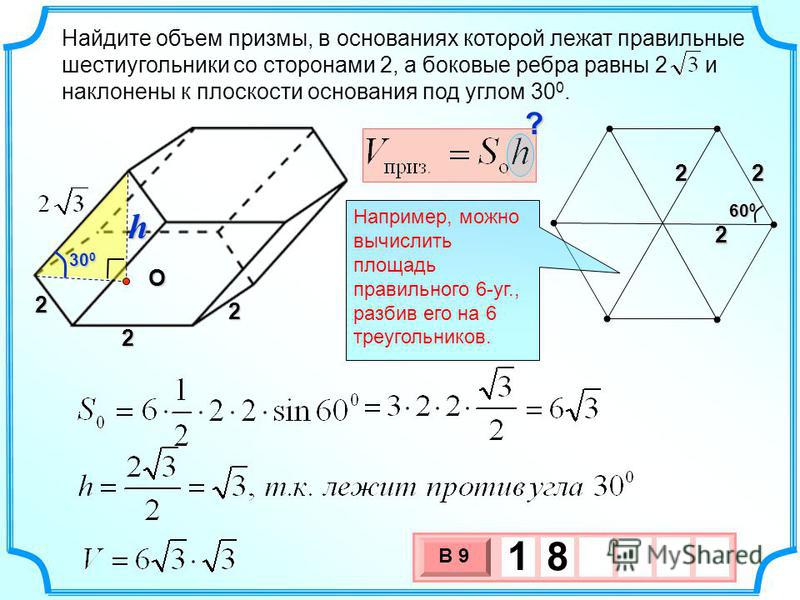
Определим объем 6-угольной призмы на живом примере, если известны:
- длина основания a = 6 см;
- высота призмы h = 14 см.
Площадь основания – шестиугольника – определим отдельно.
или 93,53 см2. Если не требуется точное значение, достаточно выражения
Подставим в формулу:
V = S * h.
В задачах повышенной сложности иногда дается не длина ребра, а, например, диагонали (большой или малой). Для определения длины основания нужно помнить: большая диагональ вдвое длиннее стороны многоугольника, меньшая – в раз.
Поделитесь в социальных сетях:
9 октября 2021, 08:27
Геометрия
Could not load xLike class!
Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4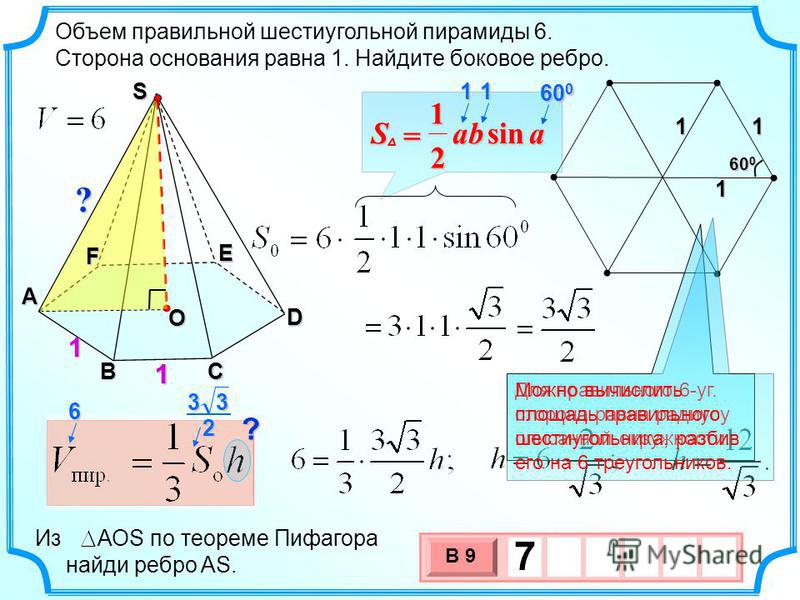 {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение] {\circ}$ больше вписанного угла ACB, опирающегося на ту же дугу. Ответ дайте в градусах. [посмотреть решение]В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Объем шестиугольной призмы – формула, определение и примеры
Объем шестиугольной призмы – это занимаемое ею пространство. Призма представляет собой трехмерную фигуру с одинаковыми основаниями, плоскими прямоугольными боковыми гранями и одинаковым поперечным сечением по всей длине. Призмы подразделяются на разные типы и называются по форме их основания. Шестиугольная призма, как следует из названия, представляет собой трехмерное тело, имеющее два шестиугольных основания, нижнее и верхнее. Боковые грани шестиугольной призмы имеют прямоугольную форму. Существует формула для нахождения объема шестиугольной призмы. Давайте изучим и изучим в деталях!
Существует формула для нахождения объема шестиугольной призмы. Давайте изучим и изучим в деталях!
| 1. | Что такое объем шестиугольной призмы? |
| 2. | Объем шестиугольной призмы Формула |
| 3. | Как рассчитать объем шестиугольной призмы? |
| 4. | Часто задаваемые вопросы по объему шестиугольной призмы |
Что такое объем шестиугольной призмы?
Объем шестиугольной призмы определяется как вместимость шестиугольной призмы. В геометрии шестиугольная призма представляет собой трехмерную фигуру с двумя шестиугольными основаниями и шестью прямоугольными гранями. Шестиугольная призма представляет собой многогранник с 8 гранями, 18 ребрами и 12 вершинами, где из 8 граней 6 граней имеют форму прямоугольников, а 2 грани имеют форму шестиугольников. Верх и низ шестиугольной призмы имеют форму шестиугольника и конгруэнтны друг другу.
Объем шестиугольной призмы Формула
Мы увидим формулы для расчета объемов различных типов шестиугольных призм. Объем любой призмы можно найти, найдя произведение площади ее основания на высоту. т. е. объем призмы = площадь основания × высота. Мы также будем использовать эту формулу для расчета объема шестиугольной призмы. Мы знаем, что основанием шестиугольной призмы является шестиугольник. Применяя приведенную выше формулу к шестиугольной призме. Таким образом, объем шестиугольной призмы = площадь основания × высота.
Объем шестиугольной призмы определяет вместимость призмы. Согласно общей формуле объема призмы, то есть объем = площадь основания × высота, формула объема шестиугольной призмы = площадь шестиугольной грани x высота призмы.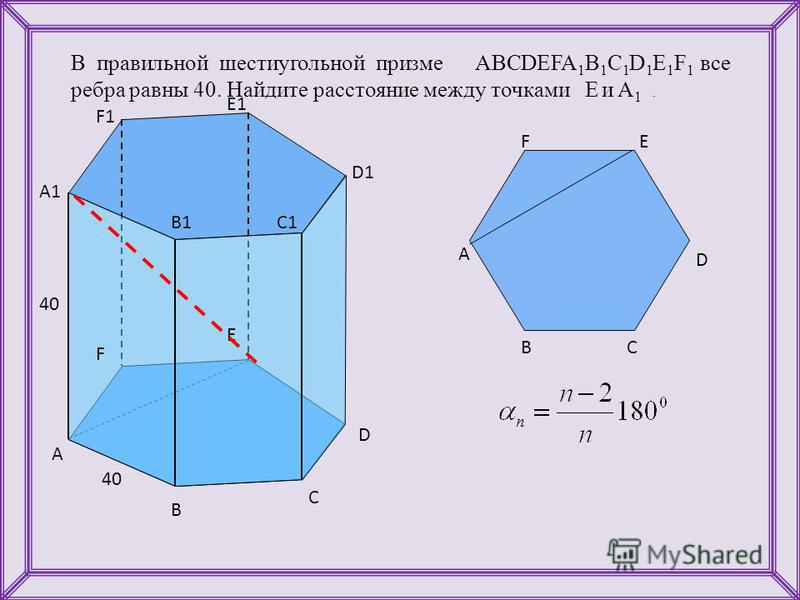
- а — базовая длина
- h высота призмы
Мы также можем использовать формулу V = 3abh, где
- a = длина апофемы
- b = длина стороны основания
- h = высота призмы.
Существует 2 различных типа шестиугольных призм: правильные шестиугольные призмы и неправильные шестиугольные призмы.
- Неправильная шестиугольная призма — это призма, у которой все стороны шестиугольного основания не имеют одинаковой длины. Углы тоже не те.
Как рассчитать объем шестиугольной призмы?
Вот шаги для расчета объема (обычной) шестиугольной призмы.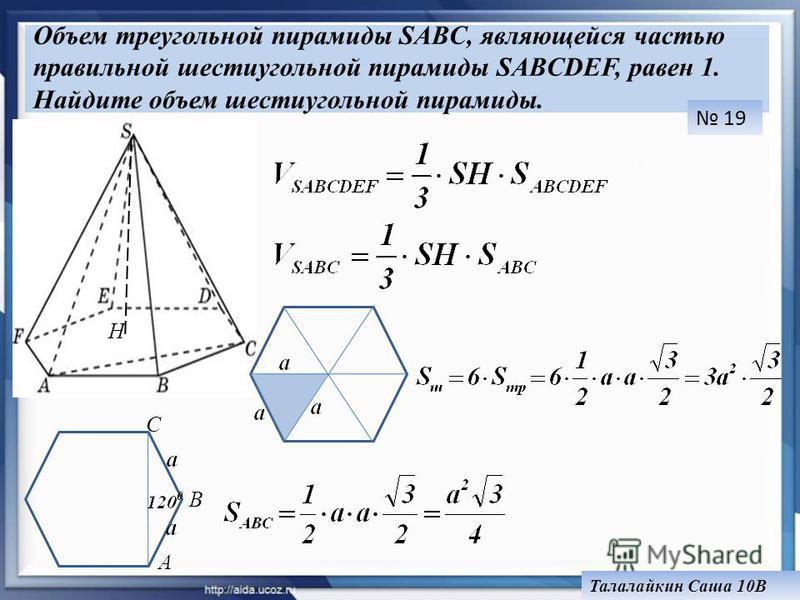 Мы должны быть уверены, что все измерения в одних и тех же единицах.
Мы должны быть уверены, что все измерения в одних и тех же единицах.
- Шаг 1: Определите ребро основания a и найдите площадь основания призмы по формуле a 2 .
-
- Шаг 3: Подставьте соответствующие значения в формулу, v = [(3√3)/2]a 2 h
- Шаг 4: Запишите полученное значение объема шестиугольной призмы с соответствующими кубическими единицами.
Теперь обратитесь к приведенному ниже примеру для большей ясности.
Пример: Вычислите объем шестиугольной призмы с ребром основания 4 фута и высотой 8 футов.
Решение: Учитывая, что базовое ребро а = 4 фута, а высота h = 8 футов. Объем шестиугольной призмы определяется по формуле V = площадь основания × высота или [(3√3)/2]a 2 h. Шаги для определения объема шестиугольной призмы:
- Шаг 1: Площадь основания шестиугольной призмы находится по формуле [(3√3)/2]a 2 = [ (3√3)/2](4) 2 = 41,568 квадратных футов.

- Шаг 2: Высота призмы 8 футов
- Шаг 3: Объем шестиугольной призмы = площадь основания × высота = 332,544 × 8 = 332,544 кубических фута.
Таким образом, объем шестиугольной призмы составляет 332,544 кубических фута.
Связанные темы
Ниже перечислены несколько интересных тем, связанных с объемом шестиугольной призмы, взгляните.
- Объем шестигранного цилиндра
- Площадь поверхности шестиугольной призмы
- Шестиугольная пирамида
Примеры объема шестиугольной призмы
Пример 1: Найдите объем шестиугольной призмы с длиной основания 20 единиц и высотой 10 единиц. Округлите ответ до ближайших десятых.
Решение:
Дано, длина основания = a = 20 единиц и высота = h = 10 единиц
У нас есть все значения, необходимые для непосредственного ввода формулы объема. Подставьте значения заданных размерностей в формулу v = [(3√3)/2]a 2 ч
V = 3√3(20) 2 (10)/2 = 10 392,3 кубических единицОтвет: Объем шестиугольной призмы равен 10 392,3 кубических единиц.

Пример 2: Определите высоту шестиугольной призмы, если ее объем и площадь основания даны как 450 кубических дюймов и 50 квадратных дюймов.
Решение:
Дано, объем = 450 кубических дюймов и площадь основания = 50 квадратных дюймов
Мы знаем, что объем шестиугольной призмы = площадь основания × высота.
Дан объем 450 кубических дюймов.
Таким образом, площадь основания x высота = 450. Следовательно, высота = объем/площадь основания = 450/50 = 9 дюймов.
Ответ : Высота шестиугольной призмы 9 дюймов.
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по объему шестиугольной призмы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по объему шестиугольной призмы
Каков объем шестиугольной призмы?
Объем шестиугольной призмы относится к вместимости шестиугольной призмы.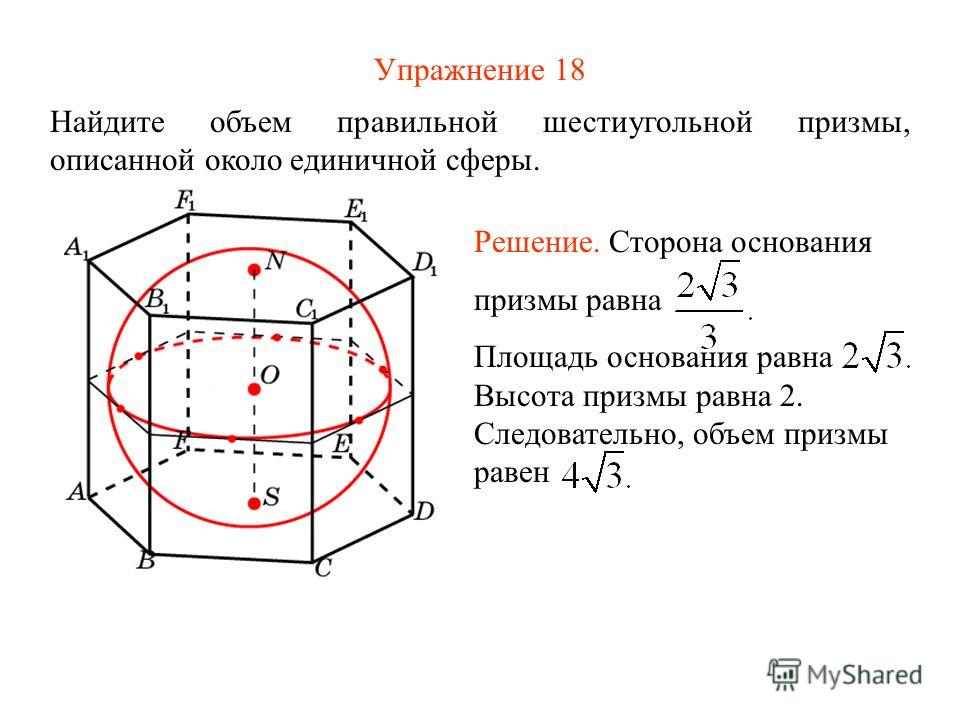 Это произведение площади основания и высоты призмы. Измеряется в кубических единицах.
Это произведение площади основания и высоты призмы. Измеряется в кубических единицах.
По какой формуле найти объем шестиугольной призмы?
Формула объема шестиугольной призмы: объем = [(3√3)/2]a 2 h кубических единиц, где a — длина основания, а h — высота призмы. Мы также можем использовать другую формулу V = 3abh, где a = длина апофемы, b = длина стороны основания и h = высота призмы.
Как найти объем шестиугольной призмы с площадью основания и высотой?
Поскольку объем любой призмы можно получить, умножив площадь ее основания на высоту, мы можем использовать эту формулу и для расчета объема шестиугольной призмы. Зная, что основанием шестиугольной призмы является шестиугольник, просто примените приведенную выше формулу к шестиугольной призме. Следовательно, объем шестиугольной призмы = площадь основания × высота.
Как найти объем наклонной шестиугольной призмы?
В любой наклонной призме основания не выровнены друг с другом. Кроме того, боковые грани являются параллелограммами. Как и объем любой другой призмы, объем косой призмы можно найти как произведение площади основания и высоты. Здесь высота — это перпендикулярное расстояние между двумя основаниями.
Кроме того, боковые грани являются параллелограммами. Как и объем любой другой призмы, объем косой призмы можно найти как произведение площади основания и высоты. Здесь высота — это перпендикулярное расстояние между двумя основаниями.
Как рассчитать объем шестиугольной призмы?
Чтобы рассчитать объем шестиугольной призмы, выполните следующие действия:
- Шаг 1: Найдите базовую площадь по соответствующей формуле.
- Шаг 2: Проверьте высоту заданной шестиугольной призмы.
- Шаг 3: Подставьте значения размеров в формулу v = [(3√3)/2]a 2 h
- Шаг 4: Запишите конечное значение в соответствующих кубических единицах.
Что произойдет с объемом шестиугольной призмы, если ее высоту удвоить?
Мы знаем, что формула объема шестиугольной призмы v = 3abh. Если ее высоту удвоить, высота станет равной 2h, тогда объем новой шестиугольной призмы будет равен 3ab(2h) = 2(3abh) = 2v. Таким образом, можно сказать, что объем также удвоится.
Что произойдет с объемом шестиугольной призмы, если длину ее основания увеличить вдвое, а высоту уменьшить вдвое?
Формула объема шестиугольной призмы: v = 3abh. Если длина его основания увеличится вдвое, новое основание станет равным 2b, а новая высота уменьшится вдвое, новая высота станет равной h/2. Тогда объем новой шестиугольной призмы будет 3a(2b)(h/2) = 3abh = v. Таким образом, можно сказать, что объем останется прежним.
Скачать БЕСПЛАТНЫЕ учебные материалы
Объем шестиугольной призмы Рабочий лист
Объем шестиугольного цилиндра – формула, примеры, определение
Объем шестиугольного цилиндра – это количество единичных кубов, которые могут в него поместиться. Единицей объема являются «кубические единицы». Шестиугольный цилиндр — это геометрический трехмерный объект, имеющий два параллельных шестиугольных основания и шесть боковых граней. Шестиугольник — это двумерный объект, и его эквивалентом в трехмерной плоскости становится шестиугольный цилиндр.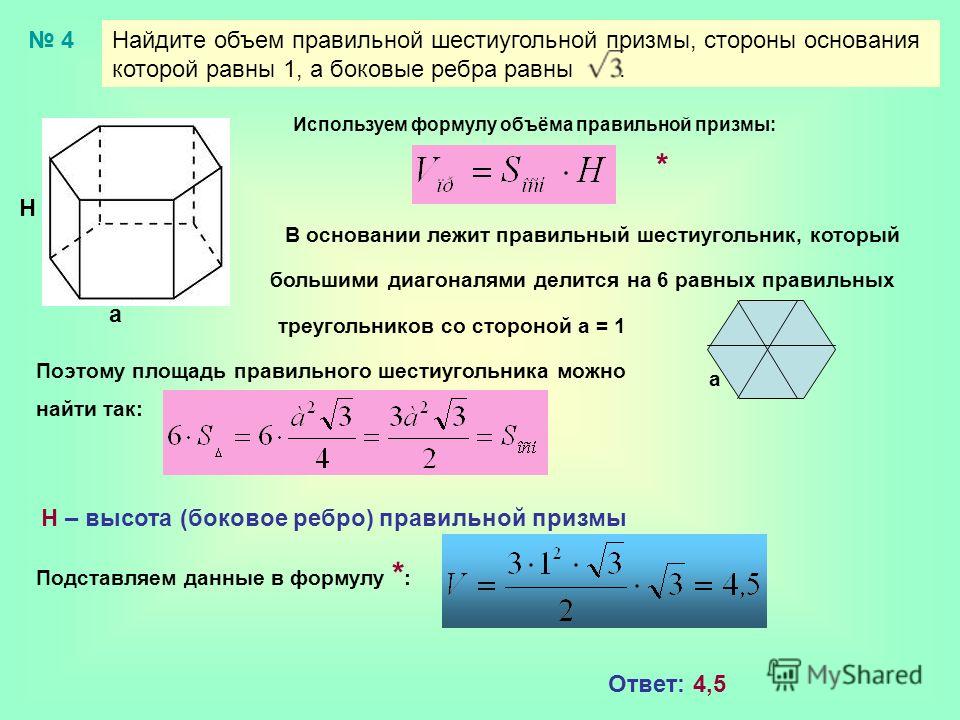 Шестиугольный цилиндр очень часто встречается в нашей повседневной жизни, и его можно увидеть во многих местах, таких как гири, гайки, карандаши, здания, вазы и т. д.
Шестиугольный цилиндр очень часто встречается в нашей повседневной жизни, и его можно увидеть во многих местах, таких как гири, гайки, карандаши, здания, вазы и т. д.
Существует два типа шестигранных цилиндров.
- Правильный шестигранный цилиндр. Правильный шестигранный цилиндр имеет в основании правильные шестиугольники.
- Неправильный шестиугольный цилиндр. Неправильный шестиугольный цилиндр имеет в основании неправильные шестиугольники.
| 1. | Что такое объем шестиугольного цилиндра? |
| 2. | Объем шестиугольного цилиндра Формула |
| 3. | Как найти объем шестигранного цилиндра? |
| 4. | Часто задаваемые вопросы по объему шестигранного цилиндра |
Что такое объем шестиугольного цилиндра?
Объем шестиугольного цилиндра – это полное пространство, заключенное в трехмерной плоскости. Цилиндр состоит из удлинения шестиугольной грани вверх на расстояние, называемое высотой шестиугольного цилиндра. В шестиугольном цилиндре есть два параллельных основания и шесть сторон, известных как грани. Кроме того, этот цилиндр имеет 18 ребер, 8 граней и 12 вершин. У него 6 прямоугольных граней и 2 шестиугольных грани из 8 граней, а противоположные грани одинаковы.
Цилиндр состоит из удлинения шестиугольной грани вверх на расстояние, называемое высотой шестиугольного цилиндра. В шестиугольном цилиндре есть два параллельных основания и шесть сторон, известных как грани. Кроме того, этот цилиндр имеет 18 ребер, 8 граней и 12 вершин. У него 6 прямоугольных граней и 2 шестиугольных грани из 8 граней, а противоположные грани одинаковы.
Объем шестиугольного цилиндра Формула
Рассмотрим шестиугольный цилиндр с длиной ребра основания «s», высотой «h» и объемом шестиугольного цилиндра «V». Поскольку основания шестиугольного цилиндра имеют шестиугольную форму, площадь которой равна (3√3/2)s 2 , а его высота считается «h». Мы знаем, что объем любого цилиндра равен произведению площади его основания на его высоту. Таким образом, объем шестиугольного цилиндра равен (3√3/2)s 2 × ч. Единицей объема являются «кубические единицы». Например, это может быть выражено как м 3 , см 3 , км 3 и т. д. в зависимости от данной единицы длины. Давайте посмотрим, как найти формулу объема шестиугольного цилиндра.
д. в зависимости от данной единицы длины. Давайте посмотрим, как найти формулу объема шестиугольного цилиндра.
Мы знаем, что основанием шестиугольного цилиндра является шестиугольная плоскость и, следовательно, его площадь равна (3√3/2)s 2 . Высота цилиндра равна «h». Таким образом, его объем равен
В = площадь основания × высота = (3√3/2) с 2 × h
По приведенной выше формуле мы можем сказать, что объем шестиугольного цилиндра равен (3√3/2) произведению квадрата длины его основания и его высоты.
Как найти объем шестиугольного цилиндра?
Как мы узнали из предыдущего раздела, объем любого цилиндра равен площади его основания, умноженной на его высоту, которая равна V = (3√3/2)s 2 × h. Таким образом, мы следуем шагам, показанным ниже, чтобы найти объем шестиугольного цилиндра.
- Шаг 1: Определите длину базовой кромки и назовите ее s или a; Определите его высоту и назовите его h.

- Шаг 2: Найдите объем по формуле V = (3√3/2)s 2 × h.
- Шаг 3: Представьте окончательный ответ в кубических единицах.
Пример
Найдите объем шестиугольного цилиндра с длиной основания 3 единицы и высотой 7 единиц.
Решение
Длина ребра основания, s = 3 ед.
Его высота, h = 7 ед.
Его объем равен,
V = (3√3/2)s 2 × h
V = (3√3/2)3 2 × 7
V = 163,67 кубических единиц.
Следовательно, объем данного шестигранного цилиндра равен 163,67 кубических единиц.
Примеры объема шестиугольного цилиндра
Пример 1: Объем шестигранного цилиндра составляет 70,14 кубических единиц. Найдите его высоту, если длина его основания равна 3 единицам.
Решение:
Объем шестиугольного цилиндра равен, (3√3/2)s 2 × h
Длина его основания, s = 3 единицы.

Предположим, что его высота равна «h».Подставьте эти значения в формулу, чтобы найти объем шестиугольного цилиндра:
V = (3√3/2)s 2 × h
70,14 = (3√3/2)3 2 × h
h = 70,14 × 2/(3√3 × 3 2 )
h ≈ 3 единицы
Ответ: Высота данного шестиугольного цилиндра составляет ок. 3 единицы.
Пример 2: Найдите объем шестиугольной вазы, площадь основания которой равна 93,53 квадратных дюйма. Его высота составляет 10 дюймов.
Решение:
Площадь основания шестиугольной вазы = 93,53 квадратных дюйма.
Высота шестиугольной вазы = 10 дюймов.
Подставьте эти значения в формулу, чтобы найти объем шестиугольной вазы:
V = площадь основания шестиугольной вазы × высота шестиугольной вазы
V = 93,53 × 10
V = 935,3 кубических единиц
Ответ: Объем шестиугольной вазы составляет 935,3 кубических единиц.

перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по объему шестиугольного цилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме шестиугольного цилиндра
Что означает объем шестигранного цилиндра?
Объем шестиугольного цилиндра — это общее пространство, занимаемое трехмерной фигурой. Объем шестиугольного цилиндра равен V = (3√3/2)s 2 × h, где s — длина ребра основания, а h — высота цилиндра.
Какая формула для объема шестиугольного цилиндра?
Объем шестигранного цилиндра можно рассчитать, используя площадь основания и высоту. Когда площадь основания умножается на высоту трехмерного объекта, получается формула объема любого объекта.
Какая единица используется для выражения объема шестиугольного цилиндра?
При измерениях объем шестигранного цилиндра выражается в кубических единицах. Используемые общие единицы измерения: 3 , м 3 , см 3 , фут 3 , ярд 3 и т. д.
Как изменится объем шестиугольного цилиндра при увеличении длины основания вдвое?
Объем шестигранного цилиндра пропорционален квадрату длины основания. Таким образом, объем увеличивается в четыре раза при удвоении радиуса.
Что такое апофема шестиугольного цилиндра?
Апофема шестигранного цилиндра представляет собой длину апофемы шестигранного основания. Правильный шестиугольник имеет шесть равных сторон. Апофема — это отрезок, проведенный от центра многоугольника к средней точке любой из сторон шестиугольника.
Формула для апофемы,
Апофема = s/[2tan(180/n)]
где
- ‘s’ — длина ребра основания.
- ‘n’ — количество сторон многоугольника.


 wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.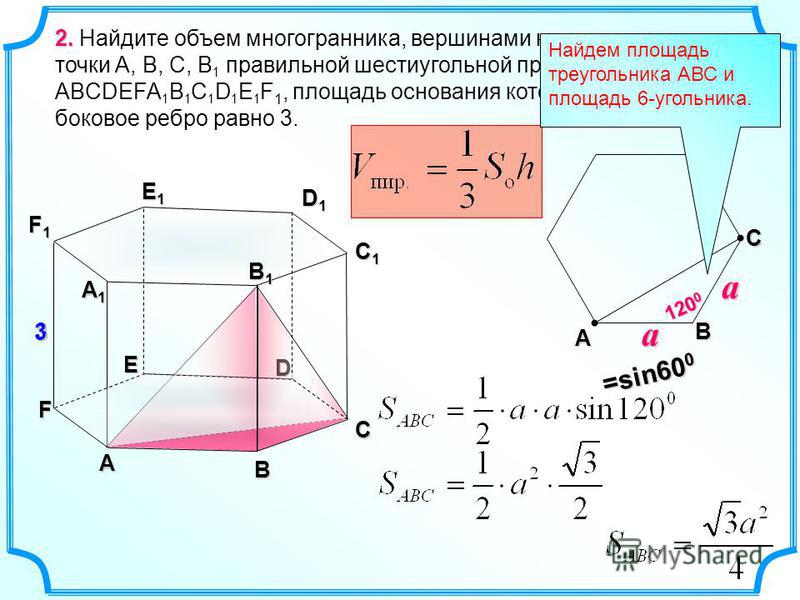 Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.


Leave A Comment