Напряженность электрического поля конденсатора –

Напряженность электрического поля

Задача

Условие: Плоский конденсатор емкостью С заполнен проводящим диэлектриком с проницаемостью ε и удельным сопротивлением ρ. Расстояние между пластинами равно d. Через резистор сопротивлением R конденсатор подключен к источнику с ЭДС Ɛ и внутренним сопротивлением r. Определите напряженность электрического поля в диэлектрике.

Решение:
Материалы, которые обладают обычно диэлектриками, в той или иной степени обладают электропроводностью. Если к источнику постоянного тока подключить конденсатор, заполненный проводящим диэлектриком, в цепи пойдет электрический ток (ток утечки). Между пластинами конденсатора будет существовать электрическое поле, напряженность которого Е можно определить, зная напряжение

U_C на обкладках конденсатора и расстояние между ними. Так как конденсатор является проводником, то это напряжение не равно ЭДС подключенного источника; чтобы его найти, нужно знать сопротивление конденсатора.

Если плоский конденсатор с площадью обкладок S и расстоянием между ними d заполнен проводящим диэлектриком с проницаемостью ε и удельным сопротивлением ρ, то емкость и сопротивление конденсатора равны соответственно:

Завдання

Умова: Плоский конденсатор ємністю

С заповнений проводним діелектриком з проникністю ε і питомим опором ρ. Відстань між пластинами дорівнює d. Через резистор опором R конденсатор підключений до джерела з ЕРС Ɛ і внутрішнім опором r. Визначте напруженість електричного поля в діелектрику.

Рішення:
Матеріали, які володіють зазвичай діелектриками, в тій чи іншій мірі володіють електропровідністю. Якщо до джерела постійного струму підключити конденсатор, заповнений проводним діелектриком, в ланцюзі піде електричний струм (струм витоку). Між пластинами конденсатора буде існувати електричне поле, напруженість якого

Е можна визначити, знаючи напругу U_C на обкладках конденсатора і відстань між ними. Так як конденсатор є провідником, то це напруження не дорівнює ЕРС підключеного джерела; щоб його знайти, потрібно знати опір конденсатора.

Якщо плоский конденсатор з площею обкладок S і відстанню між ними d заповнений проводним діелектриком з проникністю ε і питомим опором ρ, то ємність і опір конденсатора рівні відповідно:

profmeter.com.ua

Плоский конденсатор. Электризация. Электроёмкость, напряжённость конденсатора формулы

Рис. 1. Заряженный проводник

Представим себе отрицательно заряженный кусок проводника (рис. 1.1). Проводник в целом должен быть электронейтральным, т.е. его заряженность обеспечивается дополнительными электронами, которые помещены на проводник. Данный заряженный проводник организует вокруг себя электрические поле, напряженностью

. Добавим ещё один проводник (рис. 1.2). Во втором проводнике, из-за электрического поля первого проводника, происходит электризация через влияние — появление разделённого электрического заряда. Данный процесс проистекает из воздействия внешнего электрического поля (поле первого проводника) на свободные электроны внутри второго проводника, смещая их против направления поля (по закону Кулона). Тогда, в части, ближайшей к первому проводнику, остаётся несбалансированный положительный заряд (т.к. второй проводник изначально электронейтрален). Таким образом, мы получили систему, состоящую из двух заряженных разным по модулю, но одинаковым по значению зарядом. Такую систему и назовём конденсатором.

Рис. 2. Плоский конденсатор

Простейшим конденсатором, рассматриваемым в школе, является плоский конденсатор. Плоским конденсатором называется система из двух пластин, площадью

, помещённых на близком расстоянии () друг от друга (рис. 2). Пластины (обкладки конденсатора) заряжены одинаковым по модулю и различным по знаку зарядами ( и ). Между пластинами конденсатора чаще всего воздух (с диэлектрической проницаемостью ), тогда такой конденсатор называется воздушным. В случае заполнения пространства между обкладками конденсатора неким диэлектриком свойства конденсатора меняются и описываются диэлектрической проницаемостью данной среды ().

Нами были уже введены два параметра для плоского конденсатора:

(1)

(2)

где
- — заряд конденсатора.

Вывод: в принципе, конденсатором можно считать любые разнозаряженные тела, поднесённые близко друг к другу. Плоский конденсатор — это уже вполне определённая система, параметры которой достаточно просто рассчитать (1) и (2).

Поделиться ссылкой:

www.abitur.by

28. Электроемкость. Конденсаторы и их соединение. Энергия электрического поля заряженного конденсатора. Виды конденсаторов.

Электроемкость

Электроемкость уединенного проводника – отношение заряда проводника к его потенциалу.

Электроемкость характеризует способность тела накапливать электрические заряды.При большой электроемкоститело может накопить большой заряд при небольшом значении потенциала.

Единица измерения электроемкости Фарад, Ф.

Ф = Кл/В

1 мкФ = 10^-6Ф

1 нФ = 10

-9Ф

1 пФ = 10^-12Ф

Конденсатор – система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Плоский конденсатор –

две параллельные проводящие пластины, расположенные параллельно и разделенные

слоем диэлектрика.

Электрическое поле заряженного конденсатора

Вне пластин напряженность поля равна нулю

Напряженность поля внутри плоского конденсатора вдвое больше напряженности поля одной пластины

Электроемкость конденсатора –

отношение заряда на одной из обкладок к разности потенциалов между пластинами.

С = Q/U

Для однородного поля внутри конденсатора напряженность поля и разность потенциалов между обкладками связаны соотношением

U = Ed

электроемкость плоского конденсатора определятся формулой

Энергия заряженного конденсатора

Последовательное и параллельное соединение конденсаторов

Последовательное соединение

q=const

1/C =1/C₁+ 1/C₂

U = U₁₊U₂

Параллельное соединение

q=q₁₊q₂

U=const

C= С₁+С₂

При последовательном соединении емкость конденсаторов уменьшается

При параллельном соединении емкость конденсаторов увеличивается

29. Физические основы проводимости металлов. Постоянный электрический ток, его

характеристики. Закон Ома для участка цепи.

Согласно классической электронной теории,электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Электронный газ заполняет пространство между ионами, образующими кристаллическую решетку металла.

з-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев силы притяжения со стороны кристаллической решетки. Минимальная энергия, необходимая электрону для того, чтобы покинуть металл, называется работой выхода.

Допущения классической электронной теории являются весьма приближенными, однако она объясняетзаконы электрического тока в металлических проводниках.

При прохождении тока по проводнику переноса вещества не происходит

Электрическим током называется упорядоченное движение заряженных частиц.

Электрический ток возникает при упорядоченном перемещении свободных электронов или ионов.

При прохождении электрического тока через вещество всегда проявляется его магнитное действие. Могут проявляться также химическое и тепловое действия тока.

Направлением электрического тока считается направление упорядоченного движения положительно заряженных частиц.

Если ток образован движением отрицательных зарядов (например, электронов), то направление тока противоположно направлению движения частиц.

φА>φB;

Ток течет в сторону убывания потенциала.

Силой тока называется скалярная физическая величина I, равная электрическому заряду, который переносится через поперечное сечение проводника за единицу времени.

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Для постоянного тока

где Δq — заряд, который переносится сквозь поперечное сечение проводника за время Δt.

В самом общем случае сила тока определяется как производная от электрического заряда по времени.

I = q^/

Единица измерения силы тока Ампер, А – основная единица в системе СИ

Кл=А*с

Измерения показывают, что в металлах скорость электронов мала – порядка 10

^-5 м/с (для меди).

Условие протекания постоянного тока на участке электрической цепи: – наличие постоянной разности потенциалов (напряжения) на этом участке.

studfiles.net

Конденсатор: формулы для конденсаторов

Содержание:

Формула емкости конденсатора
Формула энергии конденсатора
Формула заряда конденсатора
Формула тока утечки конденсатора

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

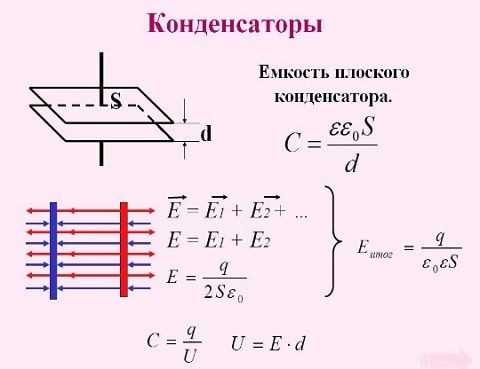
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε₀ = 8,854187817 х 10^-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU²/2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

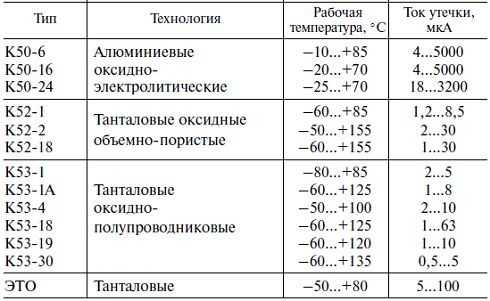
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

electric-220.ru

Ёмкость плоского конденсатора

Сообщим обкладкам плоского конденсатора заряды +Qи –Q. Плотность заряда на обкладках станет равной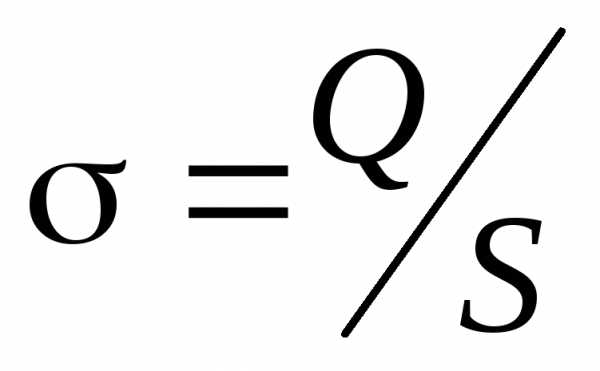, а напряжённость однородного электрического поля, возникшего в конденсаторе (см. 2.17):

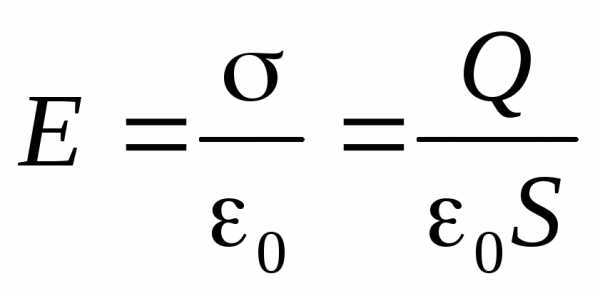Воспользовавшись связью напряжённости и потенциала в электрическом поле, вычислим разность потенциалов на обкладках конденсатора:

;

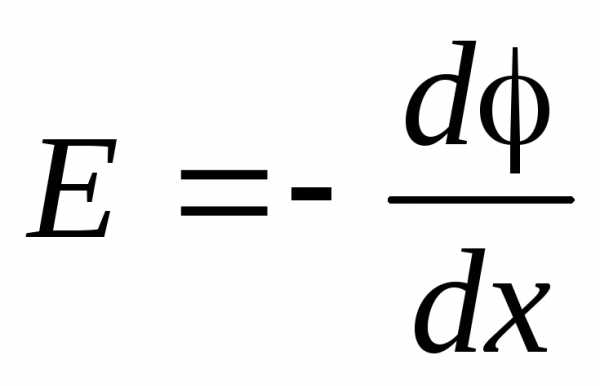.. (4.6)

Это соотношение и позволяет определить ёмкость плоского конденсатора

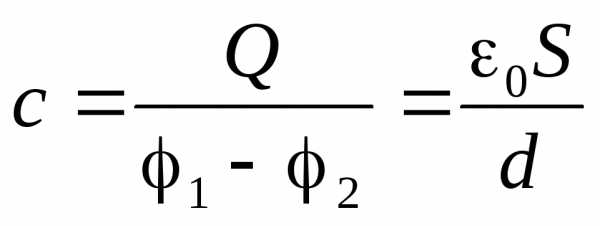(4.7)

Ёмкость этого конденсатора прямо пропорциональна площади его обкладок (S) и обратно пропорциональна расстоянию (d) между ними.

Напомним, что разность потенциалов между обкладками была вычислена в предположении, что поле между ними однородное. Это означает, что результат (4.7) в известном смысле идеализация. Мы вычислили ёмкость плоского конденсатора, пренебрегая краевыми искажениями поля.

Ёмкость сферического конденсатора

Обкладками такого конденсатора являются две концентрические сферы радиусами R₁иR₂(рис. 4.10,b).

На прошлой лекции была вычислена разность потенциалов между обкладками сферического конденсатора. Она оказалась пропорциональна заряду конденсатора (см. 3.27).

Ёмкость, равная по определению отношению заряда к разности потенциалов, для сферического конденсатора, составит следующую величину

(4.8)

Этот результат свидетельствует о том, что ёмкость сферического конденсатора зависит от размеров сфер (R₁иR₂) и от величины зазораd(d=R₁–R₂) между ними.

Интересно, что при достаточно малом зазоре d, когдаR₁R₂= R, можно записать ёмкость сферического конденсатора так:

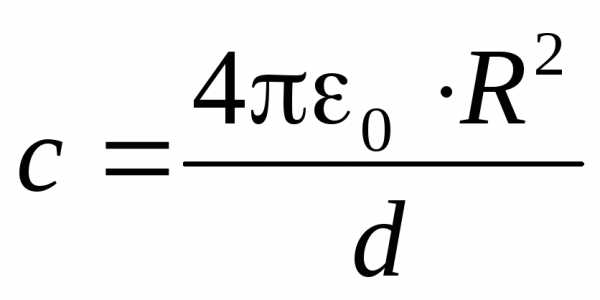
Но 4R²=S— площадь поверхности сферы. Поэтому

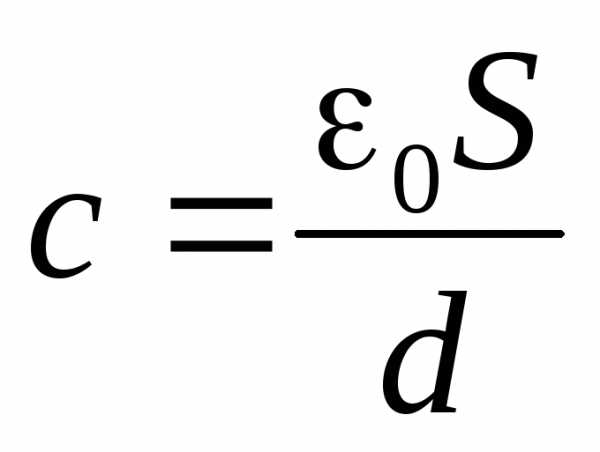
и ёмкость сферического конденсатора оказывается равной ёмкости «эквивалентного» плоского конденсатора.

Ёмкость цилиндрического конденсатора

Сообщим обкладкам цилиндрического конденсатора заряды (+q) и (–q) (рис. 4.11.). Вычислим напряжённость поля между обкладками. Для этого выберем гауссову замкнутую поверхность в виде цилиндра радиусомR₁<r<R₂и высотойl. Пренебрегая краевыми эффектами (!), запишем уравнение теоремы Гаусса

Рис. 4.11.

Из последнего равенства заключаем, что

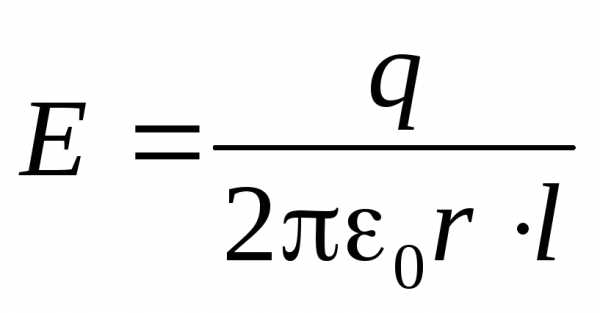(4.9)

Теперь, воспользовавшись связью напряжённости и потенциала электрического поля 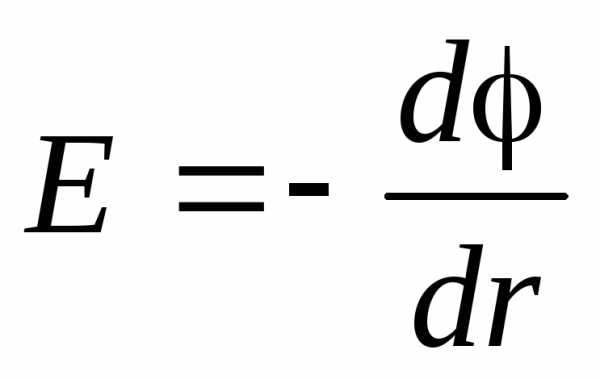, вычислим разность потенциалов между обкладками цилиндрического конденсатора

Как и в случае других конденсаторов, разность потенциалов на обкладках цилиндрического конденсатора оказалась пропорциональной заряду q. Поэтому ёмкость конкретного цилиндрического конденсатора оказывается величиной постоянной, зависящей только от размеров этого конденсатора

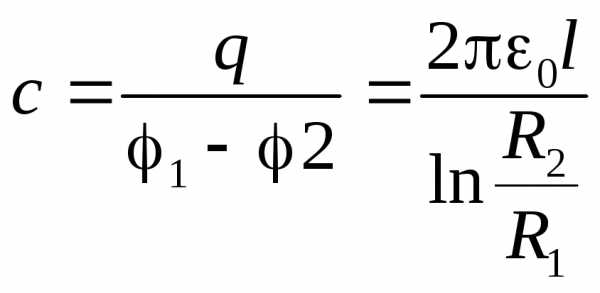(4.10)

Энергия электрического поля. Плотность энергии.

Будем заряжать плоский конденсатор, перенося малые порции заряда dqс одной обкладки на другую (рис. 4.12.) Для того чтобы перенести зарядdqмежду обкладками с разностью потенциалов (₁–₂) необходимо совершить работу

dA= (₁–₂)dq (4.11)

Рис. 4.12.

Учитывая, что 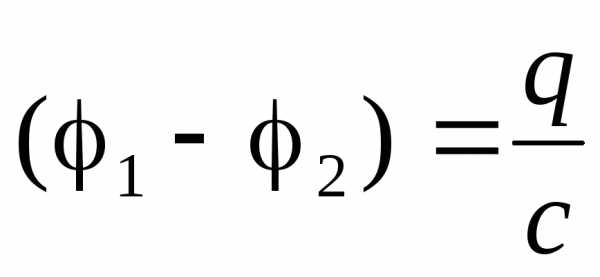, эту работу можно записать ещё и так

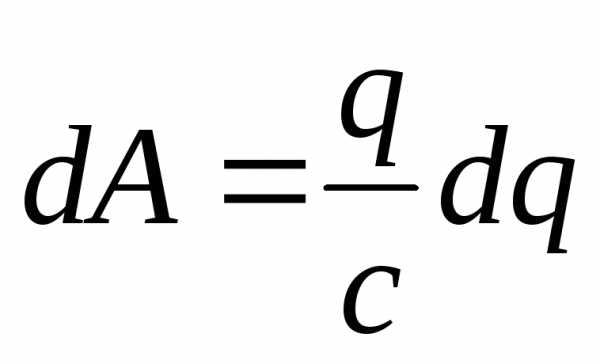
Для того чтобы первоначально незаряженному конденсатору сообщить заряд Q, необходимо совершить работу

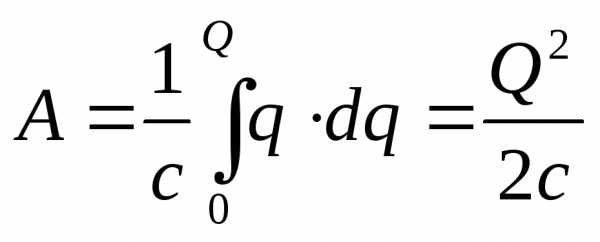
Эта работа равна энергии заряженного конденсатора

(4.12)

Здесь 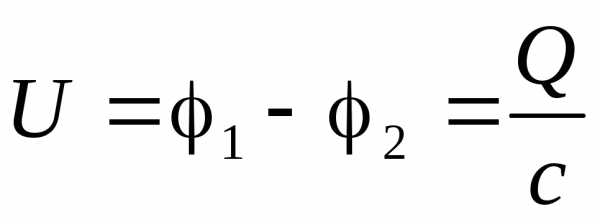— напряжение на конденсаторе, равное разности потенциалов на его обкладках.

Продолжим преобразования уравнения (4.12).

Вспомним, что ёмкость плоского конденсатора

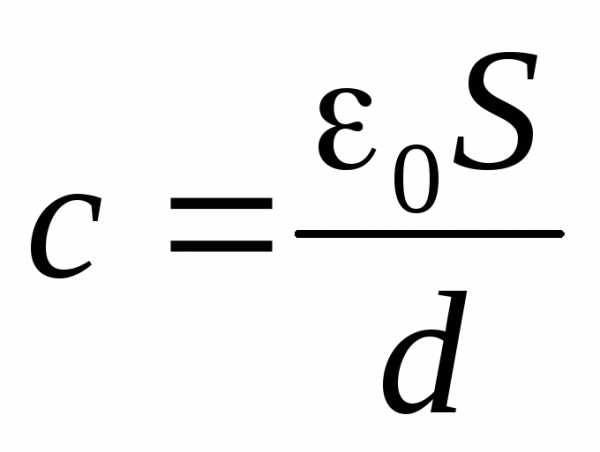а напряжение связано с напряжённостью электрического поля

U=E∙d

Воспользовавшись этими соотношениями, запишем энергию заряженного конденсатора в таком виде

(4.13)

Эти два выражения энергии конденсатора

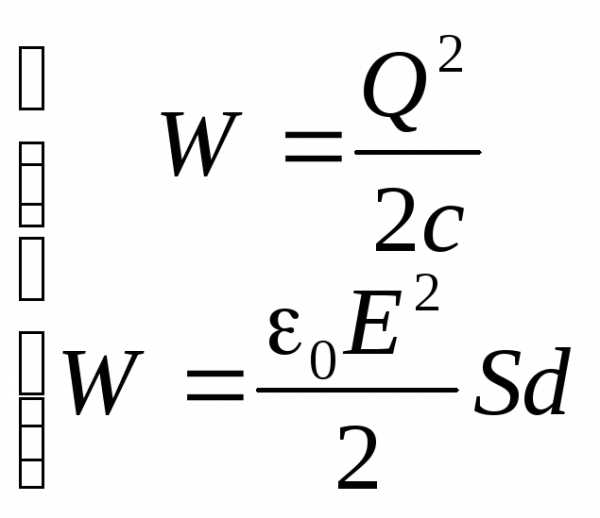
приводят к следующему принципиальному вопросу: где в конденсаторе располагается энергия? Где она «локализована»?

Если она связана с электрическими зарядами, то она находиться на обкладках конденсатора. Если же это энергия электрического поля, то она занимает пространство между обкладками, объем которого равен объему конденсатора V=S∙d.

Для ответа на этот вопрос нужно было бы заряд с обкладок убрать, а поле при этом оставить. Тогда можно было бы посмотреть: осталась энергия — значит, она связана с полем, исчезла — значит, она располагалась вместе с зарядом на обкладках.

Но проблема-то в том, что при удалении зарядов исчезает, конечно, и их электростатическое поле. Поэтому вопрос о локализации энергии в рамках электростатики не может быть решён.

В электродинамике переменныеэлектрические и магнитные поля, как известно, могут существовать и без электрических зарядов. Причем такие поля обладают энергией, что является прямым экспериментальным доказательством того, что эта энергия связана с электрическими полями и локализована в объёме, занятом полем. Теперь становиться понятнее последнее выражение энергии заряженного конденсатора:

Энергия конденсатора связана с его электрическим полем и поэтому пропорциональна объёму конденсатора (V), то есть объёму поля.

Отношение 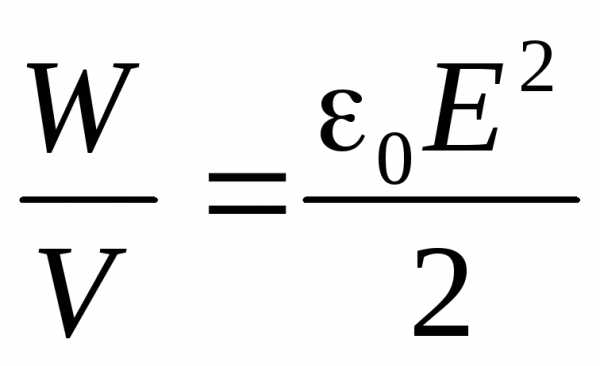представляет собой среднее значение энергии, приходящейся на единичный объём поля.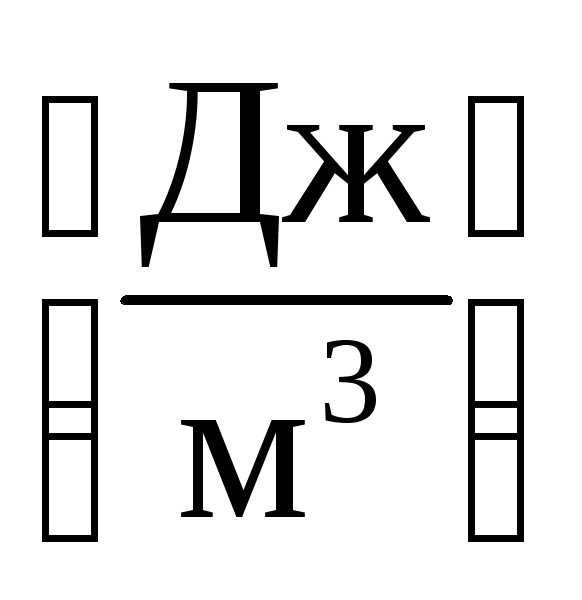

Эта характеристика энергетической насыщённости поля получила название «объёмная плотность энергии».

Обычно эта характеристика носит точечный, локальный характер. Вокруг заданной точки выбирают элементарный объём dVи вычисляют энергетическую плотность, деля энергию этой областиdWна её объём

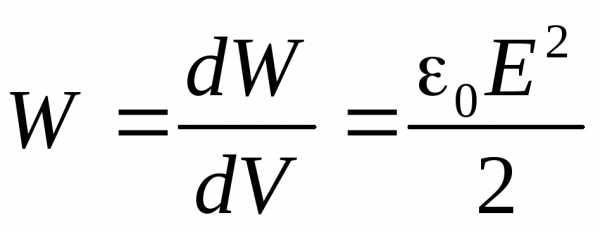(4.14)

Объёмная плотность энергии в заданной точке электрического поля пропорциональна квадрату напряжённости поля в этой точке. Измеряется объёмная плотность энергии, конечно, в Дж/м³:

Зная, как меняется плотность энергии в пространстве, можно вычислить энергию, сосредоточенную в объёме V, электрического поля:

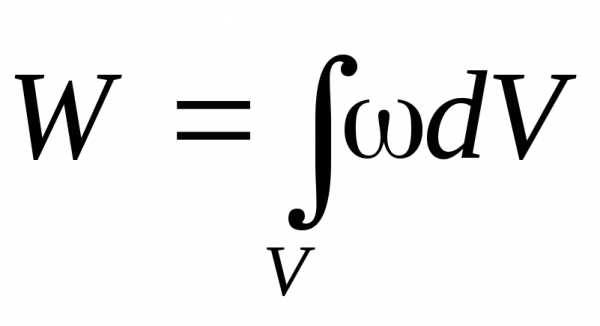Пример.

Проводящий шар радиусом Rнесет зарядQ. Какова энергия электрического поля этого шара?

Поле внутри заряженного шара отсутствует, а вне шара оно совпадает с полем точечного заряда:

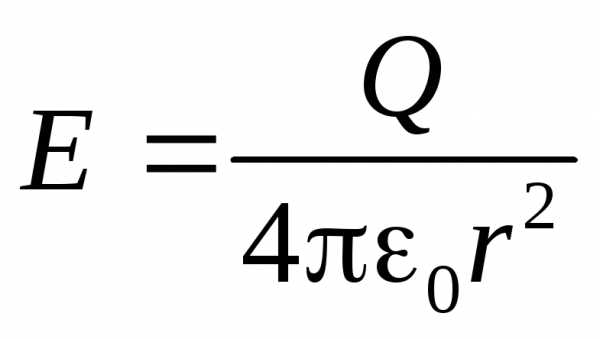,rR

Объёмная плотность энергии такого поля

Вычислим энергию, сосредоточенную в сферическом слое толщиной dr(рис. 4.13.)

Рис. 4.13.

Теперь просуммируем энергии всех слоёв от Rдо

Вспомним, что 4₀R=с— ёмкость шара (см. 4.4.), а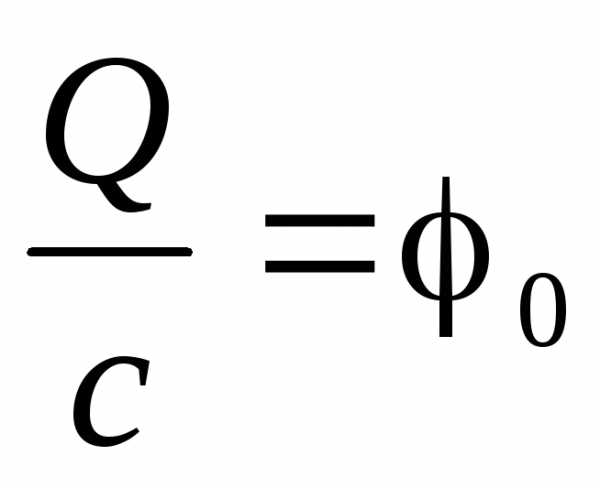— его потенциал. Тогда:

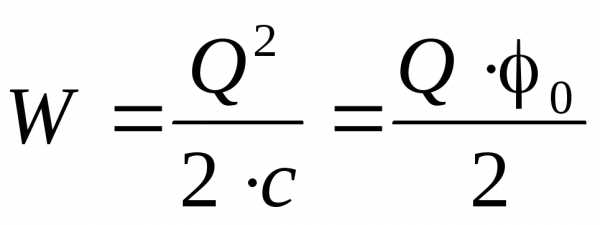. (4.15)

Эта энергия поля равна работе, которая была совершена при зарядке шара до потенциала ₀=. Покажем это.

Начнем заряжать шар, перенося на него из бесконечности электрические заряды малыми порциями dq. Если в некоторый момент времени заряд шара окажется равнымq, а его потенциал —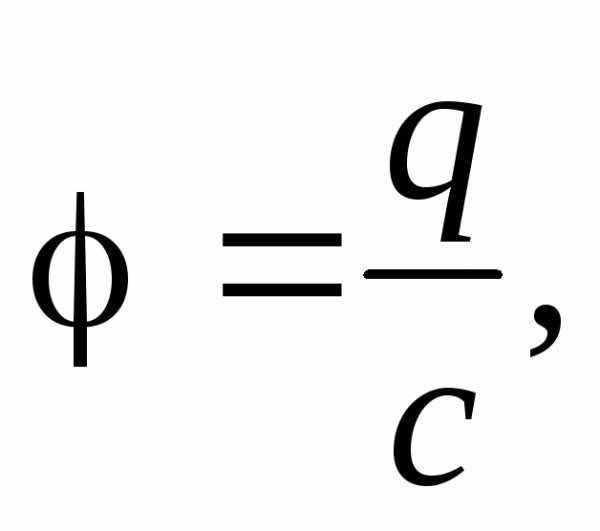то при переносе следующей порции зарядаdqпридется совершить работу против сил электрического поля

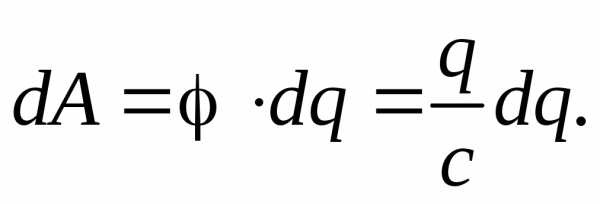
Теперь легко вычислить полную работу, которую необходимо проделать, чтобы передать первоначально незаряженному шару заряд Q:

Эта работа, как и ожидалось, равна энергии электрического поля, созданного нами при зарядке шара (см. 4.15).

studfiles.net

Энергия электрического поля конденсатора

Содержание:

Емкость – основное свойство конденсатора
Энергия электрического поля
Видео

Проводники и диэлектрики, по-отдельности помещенные в электрическое поле, проявляют собственные индивидуальные качества. Именно проявление этих качеств сделало возможным применить их совместно. В результате, к электротехническим элементам добавились специальные устройства – конденсаторы. При проведении дальнейших исследований были установлены основные физические свойства этих устройств, в том числе и энергия электрического поля конденсатора, выделяемая в процессе его разрядки. Эта величина представляет собой потенциальную энергию, возникающую при взаимодействии обкладок конденсатора, поскольку, заряженные разноименно, они создают взаимное притяжение.

Емкость – основное свойство конденсатора

Прежде чем рассматривать энергию конденсатора, следует остановиться на его основном свойстве – емкости. Когда двум проводникам, изолированным один от другого, сообщаются заряды q1 и q2, между ними наблюдается появление определенной разности потенциалов Δφ. Данная разность полностью зависит от величины зарядов и геометрической конфигурации проводников. Эта величина, возникающая в электрическом поле между двумя точками, известна также, как напряжение, обозначаемое символом U.

Наибольшее практическое значение имеют заряды проводников с одинаковым модулем и противоположными знаками: q1 = – q2 = q. С их помощью выводится такое понятие, как электрическая емкость системы, состоящей из двух проводников. Данная категория представляет собой физическую величину, в которой заряд q какого-либо проводника, соотносится с разностью потенциалов Δφ. В виде формулы это будет выглядеть следующим образом: Системой СИ в качестве единицы электроемкости установлен фарад, который равен: 1Ф = 1Кл/1В

Электроемкость может иметь разную величину, в зависимости от форм и размеров проводников, а также от свойств диэлектрика, разделяющего эти проводники. Изменение значения емкости позволяет определить, как изменится энергия электрического поля конденсатора при использовании некоторых конфигураций проводников возникает электрическое поле, сосредоточенное лишь на определенном участке. Подобные системы получили название конденсаторов, в которых функцию обкладок выполняют проводники.

Конструкция простейшего конденсатора включает в себя две плоские проводящие пластины, расположенные параллельно между собой на расстоянии, меньшем, чем толщина самих пластин. Обе пластины разделяет слой диэлектрика. Такая система получила название плоского конденсатора. Его электрическое поле локализуется преимущественно между пластинами. Кроме того, слабое поле возникает около краев пластин, а также в окружающем их пространстве. Оно называется полем рассеяния, которое не оказывает существенного влияния на многие решаемые задачи. Поэтому в большинстве случаев учитывается только электрическое поле, сосредоточенное только между обкладками конденсатора.

Модуль напряженности электрического поля, создаваемого заряженными пластинами плоского конденсатора, представляет собой соотношение: Е1 = Ϭ/2ε0. Соответственно, сумма напряженности каждой пластины, равна общей напряженности поля. Положительные и отрицательные векторы напряженности, расположены параллельно внутри конденсатора, поэтому напряженность суммарного поля будет равна: Е = 2Е1 = Ϭ/ε0. Вне пластин положительный и отрицательный векторы оказываются направленными в разные стороны, в связи с чем Е = 0.

Заряд пластин обладает поверхностной плотностью Ϭ, равной q/S. В данной формуле q является величиной заряда, а S – площадью пластин. Разность потенциалов (Δφ) однородного электрического поля будет равна Ed, где величина d является расстоянием между пластинами. После соединения всех этих соотношений, получается формула, определяющая электрическую емкость плоского конденсатора:

Из этой формулы видно, что между электроемкостью плоского конденсатора и площадью обкладок существует прямая пропорция, и обратная пропорция с расстоянием между этими обкладками.

Энергия электрического поля

Как показывает практика, все заряженные конденсаторы обладают определенным запасом энергии. Данная величина является равной работе внешних сил, затрачиваемой для зарядки конденсатора. Непосредственная зарядка конденсатора происходит в виде последовательного переноса зарядов небольшими порциями с одной пластины на другую. В это время осуществляется постепенная зарядка одной обкладки положительным зарядом, а другой – отрицательным.

Перенос каждой порции выполняется при наличии на обкладках некоторого заряда q. Между обкладками имеется определенная разность потенциалов. В связи с этим, в процессе переноса каждой порции заряда, внешними силами совершается работа: ΔА = UΔq = qΔq/C.

Существует максимальная энергия электрического поля конденсатора, формула которой отображается таким образом: We = A = Q2/2C, где We – энергия конденсатора, А – работа, C и Q – соответственно емкость и заряд конденсатора. Если использовать соотношение Q = CU, то формула энергии заряженного конденсатора может быть выражена в другой форме: We = Q2/2C = CU2 = QU/2

Электрическая энергия We по своим физическим качествам аналогична потенциальной энергии, накопленной в заряженном конденсаторе. Как уже отмечалось, локализация электрической энергии конденсатора осуществляется между его обкладками, то есть в электрическом поле. Поэтому она получила название энергия электрического поля конденсатора, формула которой выводится из нескольких понятий и определений.

Если в качестве примера взять плоский заряженный конденсатор, то напряженность его однородного поля составит E = U/d, а его емкость будет равна С = ε0 εS/d. В результате, энергия электрического поля будет выражена в следующем виде: We = CU2/2 = ε0 εSЕ2d2/2d = (ε0 εЕ2/2) x V. В этой формуле V является пространственным объемом между обкладками, заполненным электрическим полем. Таким образом, We в качестве физической величины представляет собой электрическую или потенциальную энергию единицы пространственного объема, в котором существует электрическое поле. Эта величина также известна, как объемная плотность электроэнергии.

electric-220.ru

Глава 20. Конденсаторы

Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.

Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):

(20.1)

Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.

Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):

(20.2)

Разность потенциалов между пластинами равна

(20.3)

где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора

(20.4)

Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает

(20.5)

Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.

Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов

(20.6)

Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .

Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов

(20.7)

Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна

(20.8)

С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:

(20.9)

Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.

Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).

Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).

Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4

(ответ 4).

Согласно определению электрической емкости имеем в задаче 20.1.5

(ответ 2).

Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).

При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул

где и — новый заряд конденсатора (ответ 3).

Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).

В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)

то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что

произведение от расстояния между пластинами не зависит (см. формулу (20.4)).

Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.

При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).

Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)

(1)

Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).

В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)

Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)

В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)

Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).

Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).

В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).

Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).

Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:

где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора

(ответ 4).

Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):

online.mephi.ru