Найти центростремительное ускорение с которым движется по круговой орбите: Найти центростремительное ускорение

StudyPort.Ru — Динамика

Страница 1 из 8

2.1. Какой массы m_хбалласт надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом m = 1600кг, подъемная сила аэростата F = 12kH. Считать силу сопротивления F_сопр воздуха одной и той же при подъеме и спуске.

Решение:

2.2. К нити подвешен груз массой m = 1 кг. Найти силу натяжения нити Т, если нить с грузом: а) поднимать с ускоре а = 5 м/с²; б) опускать с тем же ускорением а = 5 м/с².

Решение:

2.3. Стальная проволока некоторого диаметра выдерживает силу натяжения Т = 4,4 кН. С каким наибольшим ускорением можно поднимать груз массой m = 400 кг, подвешенный на этой проволоке, чтобы она не разорвалась.

Решение:

2.4. Масса лифта с пассажирами ш = 800кг. С каким ускорением а и в каком направлении движется лифт, если известно, что сила натяжения троса, поддерживающего лифт: а) Т = 12кН; б) T = 6кН.

Решение:

2.5. К нити подвешена гиря. Если поднимать гирю с ускоре а₁ = 2 м/с², то сила натяжения нити T, будет вдвое меньше той силы натяжения Т₂, при которой нить разорвется. С каким ускорением а₂надо поднимать гирю, чтобы нить разорвалась?

Решение:

2.6. Автомобиль массой m = 1020 кг, двигаясь равнозамедленно, остановился через время t = 5 с, пройдя путь S — 25 м. Найти начальную скорость V₀ автомобиля и силу торможе F.

Решение:

2.7. Поезд массой m = 500 т, двигаясь равнозамедленно, в течение времени t = 1 мин уменьшает свою скорость от v₁ = 40 км/ч до v₂ = 28 км/ч. Найти силу торможения F.

Решение:

2.8. Вагон массой m = 20 т движется с начальной скоростью v₀ = 54 км/ч. Найти среднюю силу F , действующую на вагон, если известно, что вагон останавливается в течение времени: а) t = 1 мин 40 с; б) t = 10 с; в) t = 1 с.

Решение:

2.9. Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t = 30 с прошел путь s = 11 м? Масса вагона т — 16 т. Во время движения на вагой действует сила трения F_тр, равная 0,05

действующей на него силы тяжести mg.

Решение:

2.10. Поезд массой m = 500т после прекращения тяги паро под действием силы трения F_тp = 98 кН останавливается че время t = 1 мин. С какой скоростью v₀ шел поезд?

Решение:

2.11. Вагон массой т = 20 т движется равнозамедленно, имея начальную скорость v₀ =54 км/ч и ускорение а = -0,3 м/с². Ка сила торможения F действует на вагон? Через какое время t вагон остановится? Какое расстояние s вагон пройдет до оста?

Решение:

2. 12. Тело массой т = 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути sот времени t дается уравнением s = А — Bt + Сt² — Dt³, где С = 5 м/с² и D = 1m/c^j. Найти силу Fi, действующую на тело в конце первой секунды движения.Решение:

 

2.13. Под действием силы F = 10 Н тело движется прямоли так, что зависимость пройденного телом пути s от време t дается уравнением s = A—Bt+Ct², где С = 1м/с². Найти массу т тела.

Решение:

2.14. Тело массой m = 0,5кг движется так, что зависимость пройденного телом пути s от времени t дается уравнением s = A sin w * t, где A =5 см и w=Pi рад/с. Найти силу F, дей на тело через время t = (l/б)с после начала движе.

Решение:

2.15. Молекула массой m = 4,65-10^-26 кг, летящая по нормали к стенке сосуда со скоростью v = 600 м/с, ударяется о стенку и упруго отскакивает от нее без потери скорости. Найти импульс силы Ft, полученный стенкой во время удара.

Решение:

2.16. Молекула массой m = 4,65 • 10^-26 кг, летящая со ско v = 600 м/с, ударяется о стенку сосуда под углом а = 60° к нормали и упруго отскакивает от нее без потери скорости. Най импульс силы Fdt, полученный стенкой во время удара.

Решение:

2.17. Шарик массой т = 0,1 кг, падая с некоторой высоты, ударяется о наклонную плоскость и упруго отскакивает от нее без потери скорости. Угол наклона плоскости к горизонту а = 30°. За время удара плоскость получает импульс силы Fdt = 1,73Н*с. Какое время t пройдет от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории?

Решение:

2. 18. Струя воды сечением S = 6 см² ударяется о стенку под углом а = 60° к нормали и упруго отскакивает от нее без потери скорости. Найти силу F, действующую на стенку, если из, что скорость течения воды в струе v = 12 м/с.

Решение:

2.19. Трамвай, трогаясь с места, движется с ускорением a = 0,5 м/с². Через время t = 12 с после начала движения мотор выключается и трамвай движется до остановки равнозамед-ленно. Коэффициент трения на всем пути k = 0,01. Найти наи скорость v и время t движения трамвая. Каково его ускорение а при его равнозамедленном движении? Какое рас s пройдет трамвай за время движения?

Решение:

2.20. На автомобиль массой m = 1т во время движения действует сила трения F , равная 0,1 действующей на него силе тяжести mg. Какова должна быть сила тяги F, развиваемая мотором автомобиля, чтобы автомобиль двигался: а) равно; б) с ускорением а = 2 м/с?

Решение:

Динамика.

Практика 9 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

При решении задач мы будем придерживаться нашей стандартной схемы решения, которую мы применяем к задачам курса физики.

 

1. Проанализировать условие. Определить, какие процессы происходят.
2. Определить закономерности, которым подчиняются происходящие процессы, записать эти закономерности в виде уравнений. Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ.
3. Математическая часть: решаем полученную систему уравнений. Получаем ответ, подставив численные значения переменных.

 

Задача 1

 

 

На столе в равномерно и прямолинейно движущемся поезде стоит легкий игрушечный автомобиль. При торможении поезда автомобиль без какого-либо внешнего воздействия покатился вперед. Выполняется ли закон инерции:

 

а) в системе отсчета, связанной с поездом во время его прямолинейного равномерного движения? Во время торможения?

б) в системе отсчета, связанной с Землей?

Анализ условия. Описан игрушечный автомобиль, который находится на столе поезда. В вопросе говорится о законе инерции – что это значит? Речь идет о том, что в отсутствии воздействия (или если оно компенсировано) тело сохраняет свою скорость, а сохранение скорости – это инерция. В первом законе Ньютона описывается эта закономерность и уточняется, что она справедлива для инерциальных систем отсчета. Так что для решения задачи нам нужно с применением первого закона Ньютона рассмотреть движение автомобиля в разных системах отсчета.

Физическая часть решения

а) Закон инерции выполняется в системе отсчета, связанной с поездом во время его прямолинейного движения: игрушечный автомобиль покоится относительно поезда, так как его притяжение к Земле компенсируется действием со стороны стола (реакцией опоры).

Торможение – это движение с ускорением, и поезд при торможении уже не является инерциальной системой отсчета, в ней закон инерции выполняться не должен. Проследим за автомобилем: так и есть, земное притяжение и реакция опоры те же, а автомобиль вдруг сам начал двигаться по ходу движения поезда (см. рис. 1).

Рис. 1. Движение игрушечного автомобиля (гифка)

б) В системе отсчета, связанной с Землей, закон инерции выполняется в обоих случаях. При равномерном движении поезда игрушечный автомобиль движется относительно Земли с постоянной скоростью (скоростью поезда), действия Земли и стола на него скомпенсированы. При торможении поезда автомобиль по инерции сохраняет свою скорость относительно Земли неизменной, здесь тоже выполняется закон инерции, а относительно поезда он катится вперед.

 

Задача 2

 

 

Тело движется прямолинейно под действием постоянной силы . Известно, что в первую секунду после начала движения тело прошло расстояние . Определить силу , если масса тела .

 

Анализ условия. В задаче описано прямолинейное движение под действием постоянной силы. По второму закону Ньютона ускорение тела прямо пропорционально действующей на него силе. Это значит, что постоянная сила создает постоянное ускорение – движение равноускоренное прямолинейное.

Физическая часть решения задачи

Запишем второй закон Ньютона:

В условии говорится о пройденном расстоянии, имеется в виду перемещение – расстояние от начальной точки движения до конечной. Перемещение при равноускоренном движении равно:

Начальная скорость тела . Сила, ускорение, перемещение – все направлено вдоль одной оси, в проекции на нее уравнения примут вид:

 

 

На этом физика закончилась, получили систему из двух уравнений, осталось ее решить – математическая часть решения (см. рис. 2).

Рис. 2. Задача 2

Выразим из второго уравнения ускорение:

Подставим в первое и определим силу:

Убедимся, что в ответе получатся Ньютоны:

Вычислим:

Задача решена.

 

Задача 3

 

 

Самолет выполняет «мертвую петлю», описывая в вертикальной плоскости окружность радиуса 250 м. Во сколько раз вес летчика в нижней части траектории больше, чем сила тяжести, если скорость самолета равна 100 м/с?

 

Анализ условия

В задаче описано движение летчика по окружности (вместе с самолетом), а это движение с центростремительным ускорением. На него действует сила тяжести и силы реакции опоры, ее модуль по третьему закону Ньютона равен весу летчика. Силы создают ускорение – будем применять второй закон Ньютона.

Физическая часть решения задачи

Изобразим на рисунке силы, которые действуют на летчика, и направление его ускорения. Выберем систему координат: нам достаточно одной оси, направим ее вертикально вверх (см. рис. 3).

Рис. 3. Силы, действующие на летчика во время выполнения мертвой петли

По второму закону Ньютона для летчика:

В проекции на ось OY:

По третьему закону Ньютона:

Центростремительное ускорение при движении по окружности равно:

Получили систему уравнений, которую осталось решить.

---

 

Математическая часть решения задачи 3

Выразим из первого уравнения силу реакции опоры:

Она по модулю равна весу:

Подставим центростремительное ускорение:

Найдем отношение веса к силе тяжести mg:

Мы ищем отношение сил, во сколько раз одна больше другой. Это безразмерная величина, проверим, получается ли это, так:

Вычислим отношение:

Задача решена, вес летчика больше силы тяжести в 5 раз: это еще называют пятикратной перегрузкой.

---

 

Задача 4

 

 

Спутник Земли движется по круговой орбите на высоте 1000 км от поверхности Земли. С какой скоростью движется спутник? За какое время спутник совершит один полный оборот вокруг Земли?

 

Анализ условия

В задаче описано движение спутника по круговой орбите (а значит, движение с центростремительным ускорением) под действием одной силы – силы притяжения к Земле. Будем использовать второй закон Ньютона, а силу гравитационного взаимодействия с Землей найдем по закону всемирного тяготения, массу и радиус Земли можно узнать из справочника (см. рис. 4).

Рис. 4. Задача 4

Физическая часть решения задачи

Запишем по второму закону Ньютона, как связана сила, действующая на спутник со стороны Земли, с его ускорением. С направлениями нам все понятно, они нас и не интересуют, запишем сразу по модулю:

Центростремительное ускорение мы умеем находить, оно равно:

Сила гравитационного притяжения, по закону всемирного тяготения, равна:

где m и M – массы спутника и Земли соответственно.

Так как спутник находится на некоторой высоте h над поверхностью Земли, расстояние от него до центра Земли:

где R – радиус Земли.

Условие задачи требует найти время полного оборота спутника вокруг Земли, то есть период вращения. Запишем, как связан период со скоростью спутника. Спутник за время T проходит путь, равный длине орбиты,  или . Значит, скорость, по определению, равна:

Получили систему уравнений, математическая часть решения – в ответвлении.

---

 

Математическая часть решения задачи 4

Перепишем уравнения для силы притяжения и для ускорения с учетом, что :

Подставим значение ускорения из второго уравнения и гравитационной силы из третьего в формулу для второго закона Ньютона (первое уравнение).

Разделим обе части на массу спутника  и умножим на :

Выразим скорость спутника:

Уже по этой формуле можно найти скорость. Теперь из четвертого уравнения системы выразим период:

Проверим единицы измерения и найдем значения искомых величин:

Ответ: спутник движется со скоростью 7,4 км/с; один полный оборот вокруг Земли спутник совершит за 1,7 ч.

---

 

Задача 5

 

 

Найдите минимальную скорость, которую следует придать подвешенному на нитке шарику, при котором он сможет осуществить полный оборот в вертикальной плоскости. Длина нитки равна 0,5 м; сопротивлением воздуха можно пренебречь.

 

Анализ условия

На нити подвешен шарик. Если его несильно толкнуть, придать ему небольшую скорость, он отклонится на какую-то высоту и будет двигаться обратно. Если придавать все большую скорость, он будет отклоняться все больше. Если шарик достигнет крайнего верхнего положения и его скорость в этот момент будет равна нулю, то он из этого положения упадет вниз под действием силы тяжести, которая сообщает ему ускорение свободного падения. Запишем по второму закону Ньютона:

Значит нужно, чтобы скорость шарика была еще больше, чтобы он в верхней точке продолжал двигаться по окружности с центростремительным ускорением , которое сообщает ему сила тяжести. Длина нитки – здесь это радиус окружности. Вот тогда шарик совершит оборот (см. рис. 5).

Рис. 5. Задача 5

Если скорость будет больше, большее центростремительное ускорение будут создавать сила тяжести и сила натяжения нити, то есть нить будет натянута. Нас, по условию задачи, интересует минимальная скорость, поэтому рассматриваем случай, когда нить еще не натянута и шарик движется только под действием силы тяжести.

В физической части решения задачи осталось связать начальную скорость шарика с его скоростью в верхней точке. Скорости тела  на разных высотах  удобно связать, применив закон сохранения энергии. Сила тяжести консервативная, сила натяжения нити работу не выполняет, т. к. направлена всегда перпендикулярно скорости, а трением воздуха по условию пренебрегаем, значит, можно применять закон сохранения механической энергии.

За нулевой уровень выберем самое низкое положение шарика.

В нижнем положении потенциальная энергия шарика равна нулю , а кинетическая .

В верхней точке на высоте, равной диаметру окружности или двум длинам нити, потенциальная энергия равна , а кинетическая – , где  – та самая скорость в верхней точке.

Получили систему уравнений, которую остается решить.

Математическая часть решения

Подставим центростремительное ускорение в первое уравнение:

Подставим квадрат скорости в верхней точке в третье уравнение системы, но перед этим для удобства умножим обе его части на 2:

И разделим на :

Следовательно,

Проверим единицы, найдем значения искомой величины:

Задача решена.

 

Задача 6

 

 

Два шарика массами 300 и 200 г, которые двигаются со скоростями 4 и 2 м/с соответственно, сталкиваются центрально абсолютно неупруго. Определите, сколько кинетической энергии шариков преобразуется во внутреннюю, если шарики двигаются друг за другом.

 

Анализ условия

В задаче описано столкновение шариков, они взаимодействуют только друг с другом – к такому процессу удобно применить закон сохранения импульса (см. рис. 6).

Рис. 6. Задача 6

Столкновение неупругое – о чем нам это говорит? При столкновении шариков не возникает силы упругости, которая бы растолкнула их, то есть они продолжат движение как одно целое, как бы «слипшись». Сила неупругой деформации – это неконсервативная сила, поэтому полная механическая энергия не сохраняется, нам как раз по условию нужно найти, какая энергия преобразуется во внутреннюю.

Физическая часть решения задачи

Шарики движутся горизонтально, изменения потенциальной энергии не происходит, запишем суммарную кинетическую энергию системы двух шариков до столкновения:

И после столкновения:

т. к. шарики двигаются вместе со скоростью .

Уменьшение кинетической энергии  – это и будет та энергия, перешедшая во внутреннюю, которую нам надо будет найти.

Применим закон сохранения импульса:

Ось ОХ направим вдоль движения шариков, они по условию задачи движутся в одном направлении. В проекции на ось ОХ запишем:

Получили систему уравнений, из которой осталось найти разность . Сделаем это в ответвлении.

---

 

Математическая часть решения задачи 6

Из второго уравнения найдем скорость после столкновения, все остальные величины в нем известны:

Подставим в уравнение для кинетической энергии после столкновения:

В уравнении для кинетической энергии до столкновения все известно. Можем найти их разность, но сначала проверим их единицы измерения:

И теперь найдем изменение общей кинетической энергии системы:

Ответ: во внутреннюю энергию преобразуется 0,24 Дж.

---

 

Задача 7

 

 

Два шарика одинаковой массы, которые двигаются со скоростями 4 и 2 м/с соответственно, сталкиваются центрально упруго. Определите скорости шариков после столкновения, если они двигаются навстречу друг другу.

 

Анализ условия

В задаче снова описано столкновение шариков, они также взаимодействуют только друг с другом – будем применять закон сохранения импульса.

Столкновение упругое – что это значит? При столкновении шариков возникнет сила упругости, которая растолкнет шарики, и они после столкновения будут двигаться раздельно с разными скоростями. Сила упругости – это консервативная сила, а к системе, где действуют только консервативные силы, можно применить закон сохранения полной механической энергии.

Физическая часть решения задачи

Выполним рисунок к задаче, шарики двигались навстречу друг другу, а потом разлетелись. Ось ОХ направим вдоль движения шариков (см. рис. 7).

Рис. 7. Задача 7

Применим закон сохранения импульса:

Запишем в проекциях на ось ОХ:

Применим закон сохранения кинетической энергии:

---

 

Математическая часть решения задачи 7

Учтем, что по условию , и после сокращения получим систему уравнений:

Перенесем скорости первого шарика в левую часть, а второго – в правую:

Во втором уравнении разность квадратов разложим на множители:

Поделим второе уравнение системы на первое и получим (первое уравнение просто перепишем):

Решим полученную систему методом сложения и найдем скорости шариков после столкновения:

Как видим, во время упругого центрального столкновения шарики одинаковой массы обменяются скоростями.

Ответ: .

---

 

Задача 8

 

 

Компоненты топлива в двигатель ракеты подаются со скоростью 200 м/с, а горючий газ выходит из сопла со скоростью 500 м/с. Массовый расход топлива двигателем 30 кг/с. Определите реактивную силу.

 

Анализ условия

В задаче описано реактивное движение ракеты. Это движение можно описать, применяя закон сохранения импульса. Если рассматривать движение на протяжении длительного времени, то масса ракеты будет уменьшаться, и это надо учитывать в уравнении. Но у нас описано только движение топлива и горючих газов. Опишем изменение импульса топлива под действием силы взаимодействия топлива и ракеты. По третьему закону Ньютона, эта сила как раз равна по модулю реактивной силе, с которой газы действуют на ракету и которую мы ищем (см. рис. 8).

Рис. 8. Задача 8

Физическая часть решения задачи

За некоторое время  израсходуется масса топлива . Изменение его импульса равно:

Как мы уже сказали, по модулю сила , подействовавшая на горючий газ, вырывающий из сопла ракеты, по модулю равна реактивной силе .

Из этого простого уравнения можно получить силу , сделаем это:

 – это заданная в условии скорость подачи топлива.

Проверим единицы, найдем значения искомой величины:

Задача решена.

 

Список литературы

1. Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е изд., передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «class-fizika.ru» (Источник)
2. Интернет-портал «class-fizika.ru» (Источник)

 

Домашнее задание

1. Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит на сиденье при прохождении положения равновесия со скоростью 6 м/с?
2. Под каким углом к горизонту нужно бросить камень, чтобы в верхней точке траектории кинетическая энергия камня была в три раза больше его потенциальной энергии?
3. В покоящийся шар массой 1 кг, подвешенный на стержне, попадает пуля массой 0,01 кг, летящая под углом 45° к стержню, и застревает в нем. После удара пуля с шаром откачнулись на высоту 0,02 м. Найти скорость пули.

 

 

Центростремительное ускорение | Brilliant Math & Science Wiki

Июль Томас, Шравант С., Джош Сильверман, и

способствовал

Содержимое

• Орбитальное движение
• Векторное изображение центростремительного ускорения
• Доказательство связи между двумя определениями
• Рекомендации

В теории гравитации Ньютона тела следуют траекториям, которые представляют собой конические сечения (например, эллипсы, параболы). Например, планеты в нашей Солнечной системе вращаются вокруг Солнца по траекториям, которые примерно представляют собой эллипсы. Для орбит, характеризующихся эксцентриситетом, близким к нулю, это довольно хорошее приближение к моделированию орбитального движения как равномерного кругового движения. 9{11} \text{м}.\)

1. Орбитальный период (время, за которое Земля совершает один оборот по орбите) составляет 365 земных суток.
2. 1 Земные сутки длятся 24 часа.

---

Для расчета центростремительного ускорения можно использовать либо орбитальную скорость \(v\), либо угловую скорость \(\omega\), но \(v\) проще с заданными переменными, поскольку

\[v = \frac{\Delta s}{\Delta t} = \frac{2\pi r}{T},\]

, где \(\Delta s\) — длина дуги, проходимой за один оборот, а \(T\) — период обращения. Мы можем вычислить орбитальную скорость \(v\) из предположений: 92?\)

На приведенном выше рисунке показана общая ситуация кругового движения в определенный момент времени.

Пусть \(r\) и \(r’\) — векторы положения, а \(v\) и \(v’\) — скорости объекта, когда он находится в точке \(P\) и \ (P’, \) соответственно, как показано выше. По определению, скорость находится в точке по касательной в этой точке в направлении движения. Поскольку путь круговой, \(v\) и \(v’\) перпендикулярны \(r\) и \(r’,\) соответственно. Таким образом, \(\Delta v \perp \Delta r\) . Поскольку среднее ускорение равно \(\Delta v\) \(\left(\text{since}\, \overline{a}=\dfrac{\Delta v}{\Delta t}\right)\), \ (\overline{a} \perp \Delta r\) . \(\Delta v\) направлена ​​к центру, расположенному на линии, делящей пополам угол между \(r\) и \(r’\) . Поскольку \(\Delta t \rightarrow 0\) ускорение становится мгновенным и всегда направлено к центру. Таким образом, величина ускорения по определению равна

\[|a|=\lim_{\Delta t \rightarrow 0} \dfrac{|\Delta v|}{\Delta t}.\]

Угол между векторами положения \(r\) и \(r’\) равен \(\Delta \theta\), а угол между \(v\) и \(v’\) также равен \(\Delta \ тета\).

Таким образом, \(\Delta CPP’ \sim \Delta GHI\) и поскольку соответствующие стороны подобных треугольников пропорциональны, мы имеем

\[\dfrac{\Delta v}{v}=\dfrac{\Delta r}{R} \Стрелка вправо \Delta v=v\dfrac{\Delta r}{R}. \]

Таким образом, величина ускорения становится равной

\[|a|=\lim_{\Delta t \rightarrow 0} \dfrac{|\Delta v|}{\Delta t}=\lim_{\Delta t \rightarrow 0} \dfrac{v|\Delta r |}{R\Delta t}=\dfrac{v}{R}\lim_{\Delta t \rightarrow 0} \dfrac{|\Delta r|}{\Delta t}. \]

Так как \(\Delta t\) мала, \(\Delta \theta\) также мала и мы можем взять \(PP’\) примерно равным \(|\Delta r|\) :

\[|\Дельта г| \ приблизительно v \ Delta t \ Rightarrow \ dfrac {\ Delta r} {\ Delta t} \ приблизительно v \ Rightarrow \ lim _ {\ Delta t \ rightarrow 0} \ dfrac {|\ Delta r |} {\ Delta t} = в. \] 92 р.\)

Чтобы рассчитать ускорение мотоциклиста, найдите изменение вектора скорости \(\Delta \vec{v} = \vec{v}(\theta+\Delta \theta) — \vec{v}(\theta)\), при движении велосипеда через угол \(\Delta \theta. \)

Увеличив небольшой участок траектории, проверьте векторы, использованные для расчета:

Чтобы найти разницу, выровняйте \(\vec{v}(\theta+\Delta \theta)\) и \(-\vec{v}(\theta)\) кончик к хвосту:

Во-первых, обратите внимание, что разность \(\Delta \vec{v}\) указывает прямо на центр окружности.

Далее, угол между двумя векторами, очевидно, равен \(\Delta \theta\).

Длина разности \(\Delta \vec{v}\) определяется (приблизительно) длиной дуги, заметаемой \(\vec{v}\) при вращении через \(\Delta \theta\). Используя \(s = \theta r,\)

\[\Delta \vec{v} \приблизительно \Delta \theta \lvert v \rvert.\] 92}{R}}\) и указывает прямо на центр кругового пути. \(_\квадрат\)

Хотя эта демонстрация показательна, она была несколько надуманной. На движение сохраняются многие ограничения: радиус остается постоянным, скорость изменения радиуса остается постоянной, углового ускорения нет.

На самом деле существует гораздо более простой метод вычисления всех четырех ускорений, которые могут возникать во вращающихся системах отсчета, который включает использование теоремы Муавра.

1. Садху, Д. Спиральная модель — вихревая анимация солнечной системы . Получено 4 мая 2016 г., от http://www.djsadhu.com/the-helical-model-vortex-solar-system-animation/
Процитировать как: Центростремительное ускорение. Brilliant.org . Извлекаются из https://brilliant.org/wiki/centripetal-acceleration-2/

4.4 Равномерное круговое движение – University Physics Volume 1

4 Движение в двух и трех измерениях

Цели обучения

К концу этого раздела вы сможете:

• Находить центростремительное ускорение объекта, движущегося по круговой траектории.
• Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
• Объясните разницу между центростремительным ускорением и тангенциальным ускорением в результате неравномерного кругового движения.
• Оцените центростремительное и тангенциальное ускорения при неравномерном круговом движении и найдите вектор полного ускорения.

Равномерное круговое движение — это особый тип движения, при котором объект движется по окружности с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах на самом деле ускоряются, хотя скорость вращения постоянна. Чтобы увидеть это, мы должны проанализировать движение с точки зрения векторов.

Центростремительное ускорение

В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или [latex]d\mathbf{\overset{\to }{v}}\text{/}dt\ne 0.[/latex] Это показано на рисунке. Когда частица движется против часовой стрелки во времени [латекс]\Delta t[/латекс] по круговой траектории, ее вектор положения перемещается из [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс] to [latex]\mathbf{\overset{\to }{r}}(t+\Delta t).[/latex] Вектор скорости имеет постоянную величину и касается пути при изменении от [latex]\mathbf{ \overset{\to }{v}}(t)[/latex] to [latex]\mathbf{\overset{\to }{v}}(t+\Delta t),[/latex] меняет только свое направление. Поскольку вектор скорости [латекс]\mathbf{\overset{\to }{v}}(t)[/latex] перпендикулярен вектору положения [латекс]\mathbf{\overset{\to }{r}}( t), [/latex] треугольники, образованные векторами положения и [latex]\Delta \mathbf{\overset{\to }{r}},[/latex] и векторами скорости и [latex]\Delta \mathbf {\overset{\to}}{v}}[/latex] похожи. Кроме того, поскольку [латекс]|\mathbf{\overset{\to }{r}}(t)|=|\mathbf{\overset{\to }{r}}(t+\Delta t)|[/latex] и [латекс]|\mathbf{\overset{\to }{v}}(t)|=|\mathbf{\overset{\to }{v}}(t+\Delta t)|,[/latex] два треугольника равнобедренные. Из этих фактов мы можем сделать утверждение

[латекс]\frac{\Delta v}{v}=\frac{\Delta r}{r}[/latex] или [латекс]\Delta v=\frac{v}{r}\Delta r. [/latex]

Рисунок 4.18  (a) Частица движется по окружности с постоянной скоростью, с векторами положения и скорости в моменты времени [latex]t[/latex] и [latex]t+\Delta t.[/ латекс] (б) Векторы скорости, образующие треугольник. Два треугольника на рисунке подобны. Вектор [латекс]\Delta \mathbf{\overset{\to }{v}}[/latex] указывает на центр окружности в пределе [latex]\Delta t\to 0.[/latex] 9{2}}{r}.[/latex]

Направление ускорения также можно найти, заметив, что as [latex]\Delta t[/latex] и, следовательно, [latex]\Delta \theta[/latex] приближается к нулю, вектор [латекс]\Delta\mathbf{\overset{\to }{v}}[/latex] приближается к направлению, перпендикулярному [латексу]\mathbf{\overset{\to }{v}}.[ /latex] В пределе [латекс]\Delta t\to 0,[/latex] [латекс]\Delta \mathbf{\overset{\to }{v}}[/latex] перпендикулярно [латексу]\mathbf {\ overset {\ to {v}}. [/latex] Поскольку [latex] \ mathbf {\ overset {\ to {v}} [/latex] касается окружности, ускорение [латекс] d \ mathbf{\overset{\to}}{v}}\text{/}dt[/latex] указывает на центр круга. Подводя итог, частица, движущаяся по окружности с постоянной скоростью, имеет ускорение величиной 9{2}}{r}.[/latex]

Вектор ускорения направлен к центру окружности (рисунок). Это радиальное ускорение называется центростремительным ускорением , поэтому мы даем ему индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (что означает искать) и, таким образом, принимает значение «искание центра».

Рисунок 4.19  Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Вектор скорости также показан и касается окружности.

Давайте рассмотрим несколько примеров, иллюстрирующих относительные величины скорости, радиуса и центростремительного ускорения. {2}?[/ латекс]

Show Solution

134,0 см/с

Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны кругового пути. Типичные центростремительные ускорения приведены в следующей таблице.

Типичные центростремительные ускорения

Объект	Центростремительное ускорение (м/с 2 или коэффициенты g )
Земля вокруг Солнца	[латекс]5. 9{22}[/латекс]

Уравнения движения для равномерного кругового движения

Частица, совершающая круговое движение, может быть описана ее вектором положения [латекс]\mathbf{\overset{\to }{r}}(t).[/latex] На рисунке показана частица совершая круговые движения против часовой стрелки. Когда частица движется по окружности, ее вектор положения образует угол [латекс]\тета[/латекс] с осью x-. Вектор [латекс]\mathbf{\overset{\to }{r}}(t)[/латекс], образующий угол [латекс]\тета[/латекс] с 9Ось 0145 x показана с ее компонентами вдоль осей x и y . Величина вектора положения равна [латекс] A = |\ mathbf {\ overset {\ to }{r}} (t) | [/ латекс], а также радиусу окружности, так что с точки зрения его компонентов ,

[латекс] \ mathbf {\ overset {\ to {r}} (t) = A \, \ text {cos} \, \ omega t \ mathbf {\ hat {i}} + A \, \ text{sin}\,\omega t\mathbf{\hat{j}}.[/latex]

Здесь [latex]\omega[/latex] — константа, называемая угловой частотой частицы.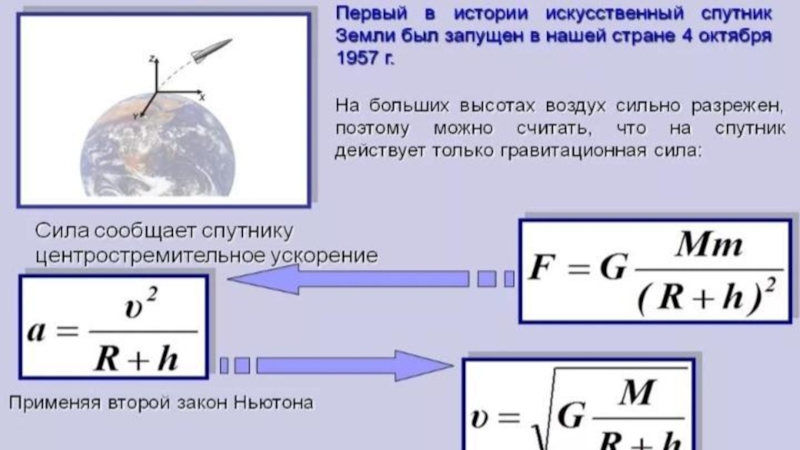 Угловая частота имеет единицы радианы (рад) в секунду и представляет собой просто число радиан угловой меры, через которое проходит частица в секунду. Угол [латекс]\тета[/латекс], который имеет вектор положения в любой конкретный момент времени, равен [латекс]\омега t[/латекс].

Если T — это период движения или время, необходимое для совершения одного оборота ([латекс]2\пи[/латекс] рад), то

[латекс]\омега =\фрак{2\пи }{ T}.[/latex]

Рисунок 4.20 Вектор положения частицы в круговом движении с его компонентами вдоль осей x и y. Частица движется против часовой стрелки. Угол [латекс]\тета[/латекс] — это угловая частота [латекс]\омега[/латекс] в радианах в секунду, умноженная на t.

Скорость и ускорение можно получить из функции положения дифференцированием:

[латекс] \ mathbf {\ overset {\ to {v}} (t) = \ frac {d \ mathbf {\ overset {\ to {r}} (t)} {dt} = \ text { −} A \ omega \, \ text {sin} \, \ omega t \ mathbf {\ hat {i}} + A \ omega \, \ text {cos} \, \ omega t \ mathbf {\ hat {j} }.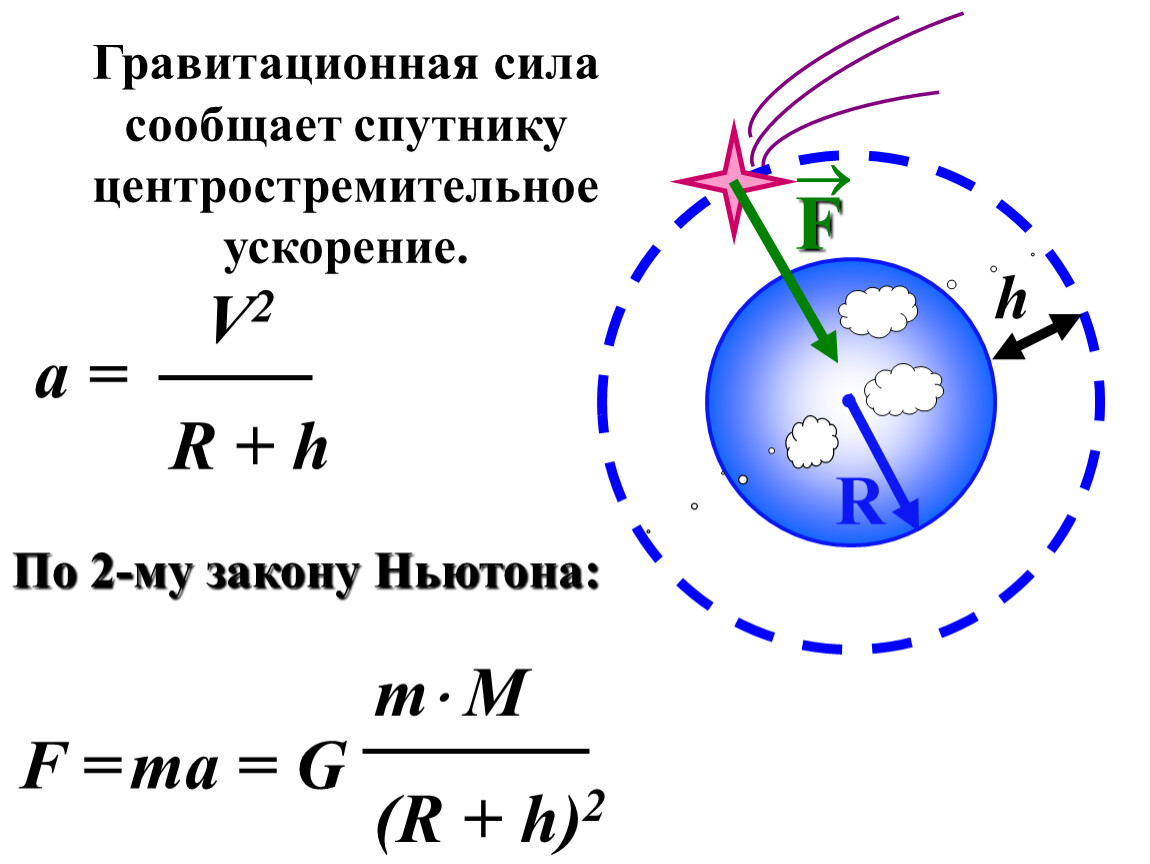 {2} \, \ text{sin}\,\omega t\mathbf{\hat{j}}.[/latex] 9{-7}\text{s}=200\,\text{ns}\text{.}[/latex] Показана траектория протона. Угол, под которым протон движется по окружности, равен 5,712 рад, что чуть меньше одного полного оборота.

Значение

Мы выбрали начальное положение частицы на оси x-. Это было совершенно произвольно. Если бы была задана другая начальная позиция, у нас была бы другая конечная позиция в t = 200 нс.

Неравномерное круговое движение

Круговое движение не обязательно должно быть с постоянной скоростью. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.

При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а окружность имеет фиксированный радиус. Если меняется и скорость частицы, то вводим дополнительное ускорение в направлении, касательном к окружности. Такие ускорения возникают в точке на волчке, меняющем скорость вращения, или на каком-либо ускоряющемся роторе. В разделе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы меняется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:

[латекс] {a} _ {\ text {T}} = \ frac {d | \ mathbf {\ overset {\ to } v}}|}{dt}.[/latex]

Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения направлено радиально внутрь к центру окружности. Таким образом, частица, движущаяся по окружности с тангенциальным ускорением, имеет полное ускорение , которое представляет собой векторную сумму центростремительного и тангенциального ускорений:

[латекс] \ mathbf {\ overset {\ to {a}} = {\ mathbf {\ overset {\ to {a}}} _ {\ text {C}} + {\ mathbf {\ overset { \to }{a}}}_{\text{T}}.[/latex]

Векторы ускорения показаны на рисунке. Обратите внимание, что два вектора ускорения {a}}}_{\text{T}}[/latex] перпендикулярны друг другу, при этом [latex]{\mathbf{\overset{\to}}{a}}}_{\text{C}} [/latex] в радиальном направлении и [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}[/latex] в тангенциальном направлении. Полное ускорение [латекс]\mathbf{\overset{\to }{a}}[/latex] указывает на угол между [латекс]{\mathbf{\overset{\to }{a}}}_{\text {C}}[/latex] и [latex]{\mathbf{\overset{\to}}{a}}}_{\text{T}}.[/latex]

Рисунок 4.22 Центростремительное ускорение направлено к центру окружности. Тангенциальное ускорение касается окружности в месте нахождения частицы. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений, которые перпендикулярны.

Пример

Полное ускорение при круговом движении

Частица движется по окружности радиусом r = 2,0 м. За интервал времени от t = 1,5 с до 9{2}},\enspace{c}_{1}=4.0\,\text{m}\text{/}\text{s,}\enspace{c}_{2}=6.0\,\text{ m}\cdot \text{s}\text{.}[/latex]

Чему равно полное ускорение частицы в точке t = 2,0 с?

Стратегия

Нам известны скорость частицы и радиус окружности, поэтому мы можем легко рассчитать центростремительное ускорение. Направление центростремительного ускорения направлено к центру окружности. Мы находим величину тангенциального ускорения, взяв производную по времени от [латекс]|v(t)|[/латекс] с помощью рисунка и оценив ее в 9\circ[/latex] от касательной к окружности. См. рисунок.

Рисунок 4.23 Векторы тангенциального и центростремительного ускорения. Чистое ускорение [латекс]\mathbf{\overset{\to }{a}}[/латекс] представляет собой векторную сумму двух ускорений.

Значение

Направления центростремительных и тангенциальных ускорений удобнее описывать в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, используемая для движения по криволинейным траекториям, подробно обсуждается далее в книге. 9{2}\text{/}р.[/латекс]

3. Неравномерное круговое движение возникает, когда существует тангенциальное ускорение объекта, совершающего круговое движение, так что скорость объекта изменяется. Это ускорение называется тангенциальным ускорением [latex]{\mathbf{\overset{\to }{a}}}_{\text{T}}. [/latex] величина скорости. Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Полное ускорение представляет собой векторную сумму тангенциального и центростремительного ускорений.
4. Объект, совершающий равномерное круговое движение, может быть описан уравнениями движения. Вектор положения объекта равен [латекс]\mathbf{\overset{\to}}{r}}(t)=A\,\text{cos}\,\omega t\mathbf{\hat{i}}+ A\,\text{sin}\,\omega t\mathbf{\hat{j}},[/latex], где A — величина [латекс]|\mathbf{\overset{\to }{r} }(t)|,[/latex], который также является радиусом окружности, а [latex]\omega[/latex] является угловой частотой.

Концептуальные вопросы

Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?

Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?

Показать решение

да

Проблемы

Маховик вращается со скоростью 30 об/с. {2} [/латекс]

Кэм Ньютон из команды «Каролина Пантерз» делает идеальную футбольную спираль со скоростью 8,0 об/с. Радиус профессионального футбольного мяча составляет 8,5 см посередине короткой стороны. Чему равно центростремительное ускорение шнурков футбольного мяча?

Ярмарочный аттракцион вращает своих обитателей внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют всадники, имеет радиус 8,00 м, при каком числе оборотов в минуту всадники испытывают центростремительное ускорение, равное силе тяжести? 9{2}=r\enspace{a}_{\text{C}}=78,4,\enspace v=8,85\,\text{m}\text{/}\text{s}[/latex]

[латекс]T=5,68\,\text{s,}[/latex], что составляет [латекс]0,176\,\text{rev}\text{/}\text{s}=10,6\,\text{rev }\текст{/}\текст{мин}[/латекс]

Бегун, участвующий в забеге на 200 м, должен обежать конец дорожки, имеющей дугу окружности с радиусом кривизны 30,0 м. Бегун начинает гонку с постоянной скоростью. Если она пробежит 200 м за 23,2 с и будет бежать с постоянной скоростью на протяжении всей гонки, каково будет ее центростремительное ускорение, когда она пробегает кривую часть трассы? 9{2}[/latex]

Экспериментальная реактивная ракета летит вокруг Земли вдоль ее экватора прямо над ее поверхностью.