Найти решение неравенства: Решение тригонометрических неравенств онлайн · Как пользоваться Контрольная Работа РУ

Неравенства, решение линейных неравенств, принцип решения неравенств

Неравенство это выражение с , ≤, или ≥. Например, 3x — 5 Решить неравенство означает найти все значения переменных, при которых это неравенство верно. Каждое из этих чисел является решением неравенства, а множество всех таких решений является его множеством решений. Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами.

Линейные неравенства

Принципы решения неравенств аналогичны принципам решения уравнений.

Принципы решения неравенств
Для любых вещественных чисел a, b, и c:
Принцип прибавления неравенств: Если a Принцип умножения для неравенств: Если a 0 верно, тогда ac Если a bc также верно.
Подобные утверждения также применяются для a ≤ b.

Когда обе стороны неравенства умножаются на отрицательное число, необходимо полностью изменить знак неравенства.
Неравенства первого уровня, как в примере 1 (ниже), называются

линейными неравенствами.

Пример 1 Решите каждое из следующих неравенств. Затем изобразите множество решений.
a) 3x — 5 b) 13 — 7x ≥ 10x — 4
Решение

3x — 5	Используя принцип прибавления для неравенств, прибавляем 2x
5x — 5	Используя принцип прибавления для неравенств, прибавляем 5
5x	Используя принцип умножения для неравенств, умножаем или делим на 5
x

Любое число, меньше чем 11/5, является решением.
Множество решений есть {x|x
Чтобы сделать проверку, мы можем нарисовать график y

1 = 3x — 5 и y₂ = 6 — 2x. Тогда отсюда видно, что для x 1 находится ниже графика y₂, или y₁2.

13 — 7x ≥ 10x — 4	вычитаем 10x
13 — 17x ≥ -4	вычитаем 13
-17x ≥ -17	Делим на 17 и меняем знак неравенства
x ≤ 1

Множеством решений есть {x|x ≤ 1}, или (-∞, 1]. График множества решений изображён ниже.

Двойные неравенства

Когда два неравенства соединены словом и, или, тогда формируется двойное неравенство. Двойное неравенство, как
-3 и 2x + 5 ≤ 7
называется соединённым, потому что в нём использовано и. Запись -3 Двойные неравенства могут быть решены с использованием принципов прибавления и умножения неравенств.

Пример 2 Решите -3 Решение У нас есть

Множество решений есть {x| — 4
Двойное неравенство, как 2x — 5 ≤ -7 или называется разделённым, потому что оно содержит или. В отличие от некоторых соединённых неравенств, оно не может быть сокращено; поэтому, оно не может быть записано без или.

Пример 3 Решите 2x — 5 ≤ -7 или 2x — 5 > 1. Постройте график множества решений.
Решение У нас есть

-3	Вычитаем 5
-8	Делим на 2
-4

2x — 5 ≤ -7 или 2x — 5 > 1.	Прибавляем 5
2x ≤ -2 или 2x > 6	Делим на 2
x ≤ -1 или x > 3.

Множество решений {x|x ≤ -1 или x > 3}. Мы можем также написать решение с использованием обозначения интервала и символ для объединения или включения обоих множеств: (-∞ -1] (3, ∞). График множества решений изображен ниже.

Для проверки, нарисуем y₁ = 2x — 5, y₂ = -7, и y₃ = 1. Заметьте, что для {x|x ≤ -1 или x > 3}, y₁ ≤ y₂или y₁ > y₃.

Неравенства с абсолютным значением (модулем)

Неравенства иногда содержат модули. Следующие свойства используются для их решения.
Для а > 0 и алгебраического выражения x:
|x| |x| > a эквивалентно x или x > a.
Подобные утверждения и для |x| ≤ a и |x| ≥ a.

Например,
|x| |y| ≥ 1 эквивалентно y ≤ -1 или y ≥ 1;
и |2x + 3| ≤ 4 эквивалентно -4 ≤ 2x + 3 ≤ 4.

Пример 4 Решите каждое из следующих неравенств. Постройте график множества решений.
a) |3x + 2| b) |5 — 2x| ≥ 1

Решение
a) |3x + 2|

-5Вычитаем 2 -7Делим на 3

-7/3 Множеством решением есть {x|-7/3
b) |5 — 2x| ≥ 1

|5 — 2x| ≤ -1 или 5 — 2x ≥ 1	Вычитаем 5
-2x ≤ -6 или -2x ≥ -4	Делим на -2 и меняем знак неравенства
x ≥ 3 или x ≤ 2

Множеством решением есть {x|x ≤ 2 или x ≥ 3}, или (-∞, 2] [3, ∞). График множества решений изображен ниже.

Использование неравенств

Пример 5 Планы выплат. За выполнение малярных работ, Эрику может быть выплачена заработная плата одним из двух способов:

План A: \$250 плюс \$10 в час;
План B: $20 в час.
Предположим, что работа занимает n часов. Для каких значений n план B лучше для Эрика?

Решение

1. Понимание задачи. Предположим, что работа отнимет 20 часов. Тогда n = 20, и согласно плану A, Эрик заработает \$250 + \$10,20, или \$250 + \$200, или \$450. Его заработок согласно плану B составит \$20,20, или \$400. Это показывает, что план A лучше для Эрика, если он будет работать 20 часов. Подобным образом, если он будет работать 30 часов, тогда n = 30, и согласно плану A, Эрик заработает \$250 + \$10,30, или \$250 + \$300, или \$550. При плане B, он заработает \$20,30, или \$600, поэтому план B лучше в этом смысле. Чтобы определить

все значения n, для которых план B является лучшим для Эрика, составим и решим неравенство.

2. Составление неравенства. Запишем это в виде неравенства.
Доход от плана B больше, чем доход от плана A.

20n > 250 + 10n

3. Решим неравенство:

20n > 250 + 10n	Вычитаем 10n из двух сторон
10n > 250	Делим на 10 обе стороны
n > 25

4. Проверка. Для n = 25 выплаты согласно плану A составят: \$250 + \$10,25, или \$250 + \$250, или \$500, и выплаты согласно плану B составят \$20,25, или \$500. То есть, для работы длительностью менее 25 часов, доход одинаков для каждого плана. Согласно плану B выплаты больше для работы, которая занимает больше 30-и часов. Так как 30 > 25, это обеспечивает частичную проверку результата, но мы не можем проверить все значения n.
5. Вывод . Для значений, n больше, чем 25 часов, план B является лучшим.

Алгебра. Урок 8. Неравенства, системы неравенств.

Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Неравенства

• Линейные неравенства

Таблица числовых промежутков
Алгоритм решения линейного неравенства
Примеры решения линейных неравенств

• Квадратные неравенства

Алгоритм решения квадратного неравенства
Примеры решения квадратных неравенств

• Дробно рациональные неравенства

Алгоритм решения дробно рационального неравенства
Примеры решения дробно рациональных неравенств

• Системы неравенств

Алгоритм решения системы неравенств
Примеры решения систем неравенств

 

Что такое неравенство? Если взять любое уравнение и знак     =     поменять на любой из знаков неравенства:

>    больше,

≥    больше или равно,

<    меньше,

≤    меньше или равно,

то получится неравенство.

Линейные неравенства

Линейные неравенства – это неравенства вида:

ax<bax≤bax>bax≥b

где a и b – любые числа, причем a≠0,x – переменная.

Примеры линейных неравенств:

3x<5x−2≥07−5x<1x≤0

Решить линейное неравенство – получить выражение вида:

x<cx≤cx>cx≥c

где c – некоторое число.

Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.

• Если знак неравенства строгий >,<, точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой.

Смысл выколотой точки в том, что сама точка в ответ не входит.

• Если знак неравенства нестрогий ≥,≤, точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной.

Смысл жирной точки в том, что сама точка входит в ответ.

• Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.

Таблица числовых промежутков

Неравенство	Графическое решение	Форма записи ответа
x<c		x∈(−∞;c)
x≤c		x∈(−∞;c]
x>c		x∈(c;+∞)
x≥c		x∈[c;+∞)

Алгоритм решения линейного неравенства

1. Раскрыть скобки (если они есть), перенести иксы в левую часть, числа в правую и привести подобные слагаемые. Должно получиться неравенство одного из следующих видов:

ax<bax≤bax>bax≥b

1. Пусть получилось неравенство вида ax≤b. Для того, чтобы его решить, необходимо поделить левую и правую часть неравенства на коэффициент a.

• Если a>0 то неравенство приобретает вид x≤ba.

• Если a<0, то знак неравенства меняется на противоположный, неравенство приобретает вид x≥ba.

1. Записываем ответ в соответствии с правилами, указанными в таблице числовых промежутков.

Примеры решения линейных неравенств:

№1. Решить неравенство    3(2−x)>18.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6−3x>18

−3x>18−6−3x>12|÷(−3)

Делим обе части неравенства на (-3) – коэффициент, который стоит перед  x. Так как    −3<0,  знак неравенства поменяется на противоположный. x<12−3⇒x<−4 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈(−∞;−4)

№2. Решить неравество    6x+4≥3(x+1)−14.

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x+4≥3x+3−14

6x−3x≥3−14−4

3x≥−15    |  ÷3 Делим обе части неравенства на (3) – коэффициент, который стоит перед  x. Так как 3>0,   знак неравенства после деления меняться не будет.

x≥−153⇒x≥−5 Остается записать ответ (см. таблицу числовых промежутков).

Ответ: x∈[−5;  +∞)

Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно).

Примеры:

№1. Решить неравенство    6x−1≤2(3x−0,5).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

6x−1≤6x−1

6x−6x≤−1+1

0≤0

Получили верное неравенство, которое не зависит от переменной x. Возникает вопрос, какие значения может принимать переменная x, чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа.

Ответ:

1. x – любое число
2. x∈(−∞;+∞)
3. x∈ℝ

 

 

 

 

№2. Решить неравенство    x+3(2−3x)>−4(2x−12).

Решение:

Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые.

x+6−9x>−8x+48

−8x+8x>48−6

0>42

Получили неверное равенство, которое не зависит от переменной x. Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ.

Ответ: x∈∅

Квадратные неравенства

Квадратные неравенства – это неравенства вида: ax2+bx+c>0ax2+bx+c≥0ax2+bx+c<0ax2+bx+c≤0 где a, b, c — некоторые числа, причем   a≠0,x — переменная.

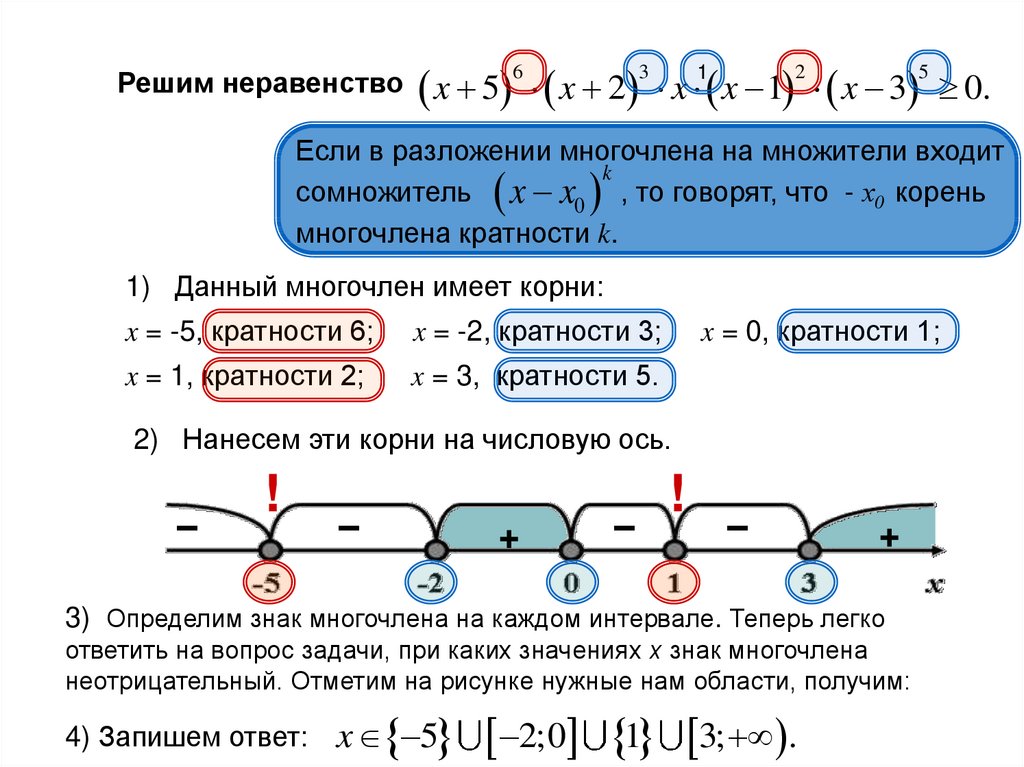
Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет.

Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4).

Алгоритм решения квадратного неравенства методом интервалов

1. Решить уравнение ax2+bx+c=0 и найти корни x1 и x2.
1. Отметить на числовой прямой корни трехчлена.

Если знак неравенства строгий >,<, точки будут выколотые.

Если знак неравенства нестрогий ≥,≤, точки будут жирные (заштрихованный).

1. Расставить знаки на интервалах. Для этого надо выбрать точку из любого промежутка (в примере взята точка A) и подставить её значение в выражение ax2+bx+c вместо x.

Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться.

Точки выколотые, если знак неравенства строгий.

Точки жирные, если знак неравенства нестрогий.

1. Выбрать подходящие интервалы (или интервал).

Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +.

Если знак неравенства < или ≤ в ответ выбираем интервалы со знаком -.

1. Записать ответ.

Примеры решения квадратных неравенств:

№1. Решить неравенство    x2≥x+12.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2≥x+12

x2−x−12≥0

x2−x−12=0

a=1,b=−1,c=−12

D=b2−4ac=(−1)2−4⋅1⋅(−12)=1+48=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−1)±492⋅1=1±72=[1+72=82=41−72=−62=−3

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6. Подставляем эту точку в исходное выражение:

x2−x−1=62−6−1=29>0

Это значит, что знак на интервале, в котором лежит точка 6 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪.

Точки -3 и 4 будут в квадратных скобках, так как они жирные.

Ответ:   x∈(−∞;−3]∪[4;+∞)

№2. Решить неравенство    −3x−2≥x2.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

−3x−2≥x2

−x2−3x−2≥0

−x2−3x−2=0

a=−1,b=−3,c=−2

D=b2−4ac=(−3)2−4⋅(−1)⋅(−2)=9−8=1

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±12⋅(−1)=3±1−2=[3+1−2=4−2=−23−1−2=2−2=−1

x1=−2,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение:

−x2−3x−2=−(0)2−3⋅0−2=−2<0

Это значит, что знак на интервале, в котором лежит точка 0 будет   −.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства   ≥, выбираем в ответ интервал со знаком   +.

Точки -2 и -1 будут в квадратных скобках, так как они жирные.

Ответ:   x∈[−2;−1]

№3. Решить неравенство   4<x2+3x.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

4<x2+3x

−x2−3x+4<0

−x2−3x+4=0

a=−1,b=−3,c=4

D=b2−4ac= (−3)2−4⋅(−1)⋅4=9+16=25

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−3)±252⋅(−1)=3±5−2=[3+5−2=8−2=−43−5−2=−2−2=1

x1=−4,x2=1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение:

−x2−3x+4=−(2)2−3⋅2+4=−6<0

Это значит, что знак на интервале, в котором лежит точка 2, будет   -.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства   <,  выбираем в ответ интервалы со знаком   −.

Точки -4 и 1 будут в круглых скобках, так как они выколотые.

Ответ:   x∈(−∞;−4)∪(1;+∞)

№4. Решить неравенство   x2−5x<6.

Решение:

Приводим неравенство к виду ax2+bx+c ≥0, а затем решаем уравнение ax2+bx+c=0.

x2−5x<6

x2−5x−6<0

x2−5x−6=0

a=1,b=−5,c=−6

D=b2−4ac=(−5)2−4⋅1⋅(−6)=25+25=49

D>0⇒ будет два различных действительных корня

x1,2=−b±D2a=−(−5)±492⋅1=5±72=[5+72=122=65−72=−22=−1

x1=6,x2=−1

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение:

x2−5x−6=102−5⋅10−6=100−50−6= 44>0

Это значит, что знак на интервале, в котором лежит точка 10 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства   <, выбираем в ответ интервал со знаком   -.

Точки -1 и 6 будут в круглых скобках, так как они выколотые

Ответ:   x∈(−1;6)

№5. Решить неравенство   x2<4.

Решение:

Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения.

x2<4

x2−4<0

x2−4=0

(x−2)(x+2)=0⇔[x−2=0x+2=0 [x=2x=−2

x1=2,x2=−2

Наносим точки на ось x. Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3. Подставляем эту точку в исходное выражение:

x2−4=32−4=9−4=5>0

Это значит, что знак на интервале, в котором лежит точка 3 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства   <,   выбираем в ответ интервал со знаком   −.

Точки -2 и 2 будут в круглых скобках, так как они выколотые.

Ответ:   x∈(−2;2)

№6. Решить неравенство   x2+x≥0.

Решение:

Выносим общий множитель за скобку, находим корни уравнения   x2+x=0.

x2+x≥0

x2+x=0

x(x+1)=0⇔[x=0x+1=0[x=0x=−1

x1=0,x2=−1

Наносим точки на ось x. Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1. Подставляем эту точку в исходное выражение:

x2+x=12+1=2>0

Это значит, что знак на интервале, в котором лежит точка 1 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

Поскольку знак неравенства   ≥,  выбираем в ответ интервалы со знаком   +.

В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные.

Ответ:   x∈(−∞;−1]∪[0;+∞)

Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже.

Дробно рациональные неравенства

Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов:

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю).

Примеры дробно рациональных неравенств:

x−1x+3<03(x+8)≤5×2−1x>0x+20x≥x+3

Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов.

Алгоритм решения дробно рациональных неравенств:

1. Привести неравенство к одному из следующих видов (в зависимости от знака в исходном неравенстве):

f(x)g(x)<0f(x)g(x)≤0f(x)g(x)>0f(x)g(x)≥0

1. Приравнять числитель дроби к нулю   f(x)=0.  Найти нули числителя.
1. Приравнять знаменатель дроби к нулю   g(x)=0.  Найти нули знаменателя.

В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.

1. Нанести нули числителя и нули знаменателя на ось x.

Вне зависимости от знака неравенства
при нанесении на ось xнули знаменателя всегда выколотые.

Если знак неравенства строгий,
при нанесении на ось x нули числителя выколотые.

Если знак неравенства нестрогий,
при нанесении на ось x нули числителя жирные.

1. Расставить знаки на интервалах.
1. Выбрать подходящие интервалы и записать ответ.

Примеры решения дробно рациональных неравенств:

№1. Решить неравенство   x−1x+3>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду  f(x)g(x)>0.
1. Приравниваем числитель к нулю  f(x)=0.

x−1=0

x=1 — это ноль числителя. Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.

1. Приравниваем знаменатель к нулю  g(x)=0.

x+3=0

x=−3 — это ноль знаменателя. При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение f(x)g(x):x−1x+3 = 2−12+3=15>0,

Это значит, что знак на интервале, в котором лежит точка 2 будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства   >,  выбираем в ответ интервалы со знаком   +.

В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые.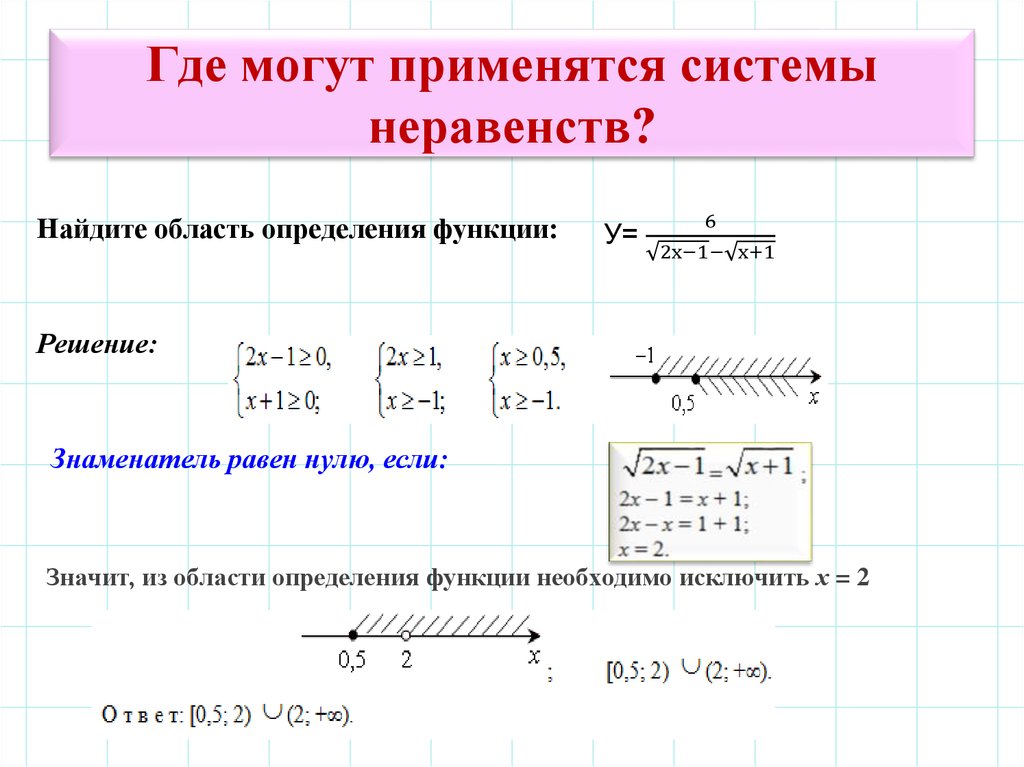

Ответ:   x∈(−∞;−3)∪(1;+∞)

№2. Решить неравенство   3(x+8)≤5.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Привести неравенство к виду  f(x)g(x)≤0.

3(x+8)≤5

3(x+8)−5\x+8≤0

3x+8−5(x+8)x+8≤0

3−5(x+8)x+8≤0

3−5x−40x+8≤0

−5x−37x+8≤0

1. Приравнять числитель к нулю  f(x)=0.

−5x−37=0

−5x=37

x=−375=−375=−7,4

x=−7,4 — ноль числителя. Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.

1. Приравнять знаменатель к нулю  g(x)=0.

x+8=0

x=−8 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0. Подставляем эту точку в исходное выражение  f(x)g(x):

−5x−37x+8=−5⋅0−370+8=−378<0

Это значит, что знак на интервале, в котором лежит точка 0 будет   -.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства   ≤,  выбираем в ответ интервалы со знаком   -.

В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная.

Ответ:   x∈(−∞;−8)∪[−7,4;+∞)

№3. Решить неравенство   x2−1x>0.

Решение:

Будем решать данное неравенство в соответствии с алгоритмом.

1. Первый шаг алгоритма уже выполнен. Неравенство приведено к виду  f(x)g(x)>0.
1. Приравнять числитель к нулю  f(x)=0.

x2−1=0

(x−1)(x+1)=0⇒[x−1=0x+1=0[x=1x=−1

x1=1,x2=−1  — нули числителя. Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.

1. Приравнять знаменатель к нулю g(x)=0.

x=0 — это ноль знаменателя. При нанесении на ось x, точка будет всегда выколотой (вне зависимости от знака неравенства).

1. Наносим нули числителя и нули знаменателя на ось x.

При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.

1. Расставляем знаки на интервалах.

Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2. Подставляем эту точку в исходное выражение  f(x)g(x):

x2−1x=22−12=4−12=32>0, Это значит, что знак на интервале, в котором лежит точка 2, будет   +.

Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.

1. Выбираем подходящие интервалы и записываем ответ.

Поскольку знак неравенства   >,  выбираем в ответ интервалы со знаком   +.

В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые.

Ответ:   x∈(−1;0)∪(1;+∞)

Системы неравенств

Сперва давайте разберёмся, чем отличается знак { системы от знака [ совокупности. Система неравенств ищет пересечение решений, то есть те точки, которые являются решением и для первого неравенства системы, и для второго. Проще говоря, решить систему неравенств — это найти пересечение решений всех неравенств этой системы друг с другом. Совокупность неравенств ищет объединение решений, то есть те точки, которые являются решением либо для первого неравенства, либо для второго, либо одновременно и для первого неравенства, и для второго. Решить совокупность неравенств означает объединить решения обоих неравенств этой совокупности. Более подробно об этом смотрите короткий видео-урок.

Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой.

Пример системы неравенств:

{x+4>02x+3≤x2

Алгоритм решения системы неравенств

1. Решить первое неравенство системы, изобразить его графически на оси x.
1. Решить второе неравенство системы, изобразить его графически на оси x.
1. Нанести решения первого и второго неравенств на ось x.
1. Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Примеры решений систем неравенств:

№1. Решить систему неравенств   {2x−3≤57−3x≤1

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

1. Решаем первое неравенство системы.

2x−3≤5 

2x≤8|÷2, поскольку  2>0,  знак неравенства после деления сохраняется.

x≤4;

Графическая интерпретация:

Точка 4 на графике жирная, так как знак неравенства нестрогий.

1. Решаем второе неравенство системы.

7−3x≤1

−3x≤1−7

−3x≤−6|÷(−3),  поскольку  −3<0,  знак неравенства после деления меняется на противоположный.

x≥2

Графическая интерпретация решения:

Точка 2 на графике жирная, так как знак неравенства нестрогий.

1. Наносим оба решения на ось x.
1. Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на отрезке от 2 до 4. Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные.

Ответ:   x∈[2;4]

№2. Решить систему неравенств   {2x−1≤51<−3x−2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

1. Решаем первое неравенство системы.

2x−1≤5

2x≤6|÷2, поскольку  2>0,  знак неравенства после деления сохраняется.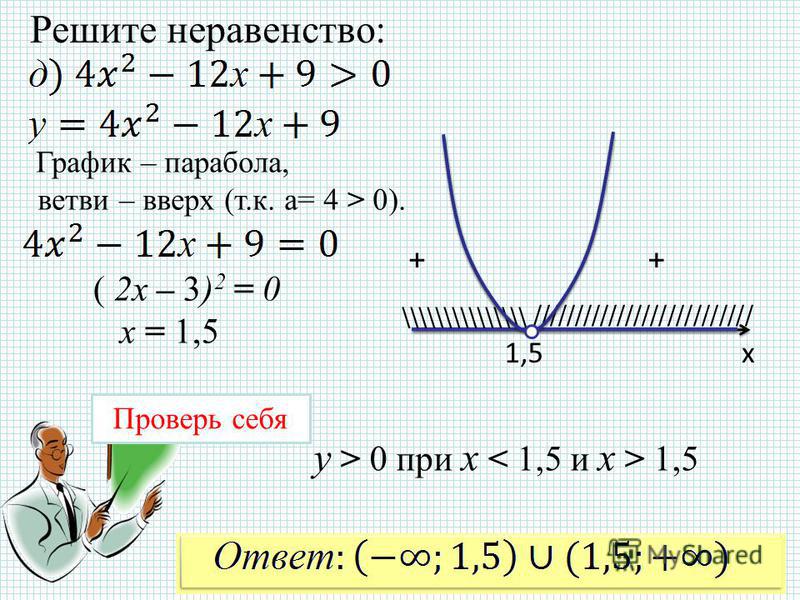

x≤3

Графическая интерпретация:

Точка 3 на графике жирная, так как знак неравенства нестрогий.

1. Решаем второе неравенство системы.

1<−3x−2

3x<−1−2

3x<−3|÷3,  поскольку  3>0,  знак неравенства после деления сохраняется.

x<−1

Графическая интерпретация решения:

Точка -1 на графике выколотая, так как знак неравенства строгий.

1. Наносим оба решения на ось x.
1. Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая.

Ответ:   x∈(−∞;−1)

№3. Решить систему неравенств   {3x+1≤2xx−7>5−x

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

1. Решаем первое неравенство системы.

3x+1≤2x

3x−2x≤−1

x≤−1

Графическая интерпретация решения:

1. Решаем второе неравенство системы

x−7>5−x

x+x>5+7

2x>12| ÷2,  поскольку  2>0,  знак неравенства после деления сохраняется.

x>6

Графическая интерпретация решения:

1. Наносим оба решения на ось x.
1. Выбираем подходящие участки и записываем ответ.

Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений.

Ответ:   x∈∅

№4. Решить систему неравенств   {x+4>02x+3≤x2

Решение:

Будем решать данную систему неравенств в соответствии с алгоритмом.

1. Решаем первое неравенство системы.

x+4>0

x>−4

Графическая интерпретация решения первого неравенства:

1. Решаем второе неравенство системы

2x+3≤x2

−x2+2x+3≤0

Решаем методом интервалов.

−x2+2x+3=0

a=−1,b=2,c=3

D=b2−4ac=22−4⋅(−1)⋅3=4+12=16

D>0 — два различных действительных корня.

x1,2=−b±D2a=−2±162⋅(−1)=−2±4−2=[−2−4−2=−6−2=3−2+4−2=2−2=−1

Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными.

Графическая интерпретация решения второго неравенства:

1. Наносим оба решения на ось x.
1. Выбираем подходящие участки и записываем ответ.

Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения  ∪.

Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные.

Ответ:   x∈(−4;−1]∪[3;+∞)

 

Скачать домашнее задание к уроку 8.

 

Поиск решений неравенства | Магазин развивающей математики

Результаты обучения

• Классифицировать решения и графики как уравнения или неравенства
• Определить, входит ли упорядоченная пара в набор решений линейного неравенства

Определите разницу между графиком линейного уравнения и линейным неравенством

Вспомните, что решениями линейных неравенств являются целые наборы чисел, а не одно число, как вы находите с решениями равенств (уравнений).

Вот пример из раздела о решении линейных неравенств:

Решить для с. [латекс] 4p+5<29[/латекс]

[латекс] \displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\ ,\,\,\,\,\,-5\,\,\,\,\,\,\,-5}\\\подчеркнуть{4p}\,\,\,\,\,\,\ ,\,<\,\,\подчеркнуть{24}\,\,\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,4\\\,\,\,\,\,\,\,\,\,\,\,p<6\end{массив}[ /latex]

Решение можно интерпретировать так, что p может быть любым числом меньше шести. Теперь вспомните, что мы можем построить уравнения линий, определив выходные данные [latex]y[/latex] и входные данные [latex]x[/latex] и написав уравнение.

Ранее мы показали, как изобразить линию, описываемую уравнением  [latex]y=2x+3[/latex]    , и обнаружили, что можем построить бесконечную таблицу значений, которые образуют точки на линии — это некоторые решения уравнения [латекс]у=2х+3[/латекс].

x значения	[латекс]2x+3[/латекс]	y значения
[латекс]0[/латекс]	[латекс]2(0)+3[/латекс]	[латекс]3[/латекс]
[латекс]1[/латекс]	[латекс]2(1)+3[/латекс]	[латекс]5[/латекс]
[латекс]2[/латекс]	[латекс]2(2)+3[/латекс]	[латекс]7[/латекс]
[латекс]3[/латекс]	[латекс]2(3)+3[/латекс]	[латекс]9[/латекс]

Кроме того, мы узнали, как изобразить линию, представляющую все точки, которые делают [латекс]у=2х+3[/латекс] верным утверждением.

Что, если мы объединим эти две идеи — линейные неравенства и графики линий? Сначала переведите строку [latex]y=2x+3[/latex] в слова:

Вы получите y, умножив [latex]x[/latex] на два и прибавив три. [latex]y=2x+3[/latex]

Как бы вы перевели это неравенство словами? [latex]y<2x+3[/latex]

Для каких значений [latex]x[/latex] вы получите результат, [latex]y[/latex], который меньше, чем [latex]2[ /латекс] умножить на [латекс]х[/латекс] плюс три?

ВАУ, это может показаться запутанным, но продолжайте читать, мы поможем вам разобраться.

Линейные неравенства отличаются от линейных уравнений, хотя вы можете применить свои знания об уравнениях, чтобы понять неравенства. Неравенства и уравнения — это математические операторы, которые сравнивают два значения. В уравнениях используется символ = ; помните, что неравенства представлены символами < , ≤ , > и ≥.

Один из способов визуализировать неравенства с двумя переменными — нанести их на координатную плоскость. Вот как выглядит неравенство [latex]x>y[/latex]. Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.

 

Здесь следует отметить несколько моментов. Во-первых, посмотрите на пунктирную красную граничную линию: это график соответствующего линейного уравнения [latex]x=y[/latex]. Затем посмотрите на светло-красную область справа от линии. Эта область (за исключением строки [latex]x=y[/latex]) представляет собой все множество решений неравенства [latex]x>y[/latex]. Помните, как все точки на прямой являются решениями линейного уравнения прямой? Ну, все точки в область являются решениями линейного неравенства , представляющего эту область.

Давайте задумаемся об этом на мгновение — если [латекс]x>y[/латекс], то график [латекс]х>у[/латекс] покажет все упорядоченные пары [латекс](х,у)[ /latex], для которого координата x- больше, чем координата y-.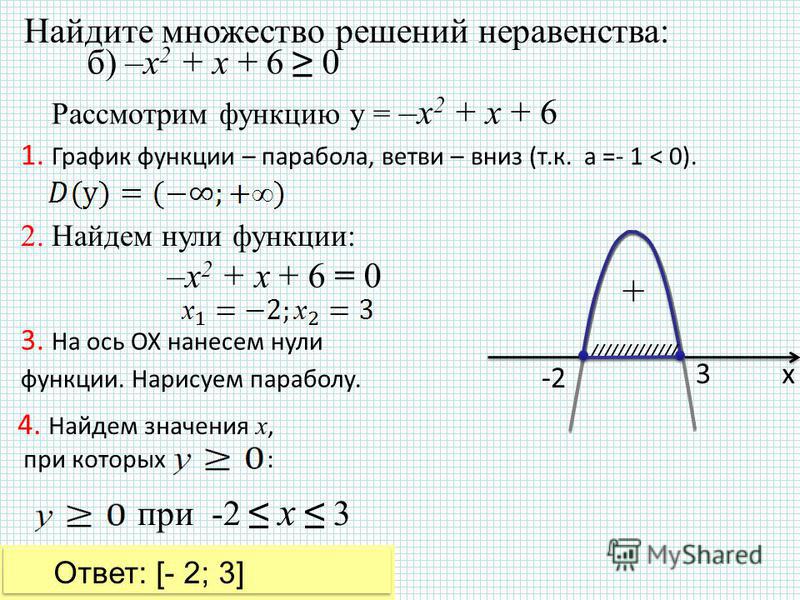

Определите упорядоченные пары, которые являются набором решений линейного неравенства

На приведенном ниже графике показана область [латекс]x>y[/латекс] , а также некоторые упорядоченные пары на координатной плоскости. Посмотрите на каждую заказанную пару. 9Координата 0105 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?

 

Упорядоченные пары [латекс](4,0)[/латекс] и [латекс](0,−3)[/латекс] лежат внутри заштрихованной области. В этих упорядоченных парах координата x- больше, чем координата y-. Эти упорядоченные пары входят в набор решений уравнения [латекс]х>у[/латекс].

Упорядоченные пары [латекс](−3,3)[/латекс] и [латекс](2,3)[/латекс] находятся за пределами заштрихованной области. В этих упорядоченных парах 9Координата 0105 x- на меньше , чем координата y-, поэтому они не включены в набор решений неравенства.

Упорядоченная пара [латекс](−2,−2)[/латекс] находится на граничной линии. Это не решение, так как [латекс]-2[/латекс] не больше, чем [латекс]-2[/латекс]. Однако если бы неравенство было [латекс]x\geq y[/латекс] (читается как « x больше или равно y »), то [латекс](−2,−2)[/латекс ] был бы включен (и линия была бы представлена ​​сплошной, а не пунктирной линией).

Посмотрите видео ниже, чтобы еще раз объяснить разницу между линейным уравнением и линейным неравенством.

Рассмотрим еще один пример: неравенство [латекс]3х+2у\leq6[/латекс]. На приведенном ниже графике показана область значений, которая делает это неравенство верным (заштрихована красным), граничная линия [латекс]3x+2y=6[/латекс], а также несколько упорядоченных пар. Граничная линия на этот раз сплошная, потому что точки на граничной линии [latex]3x+2y=6[/latex] делают неравенство [latex]3x+2y\leq6[/latex] истинным.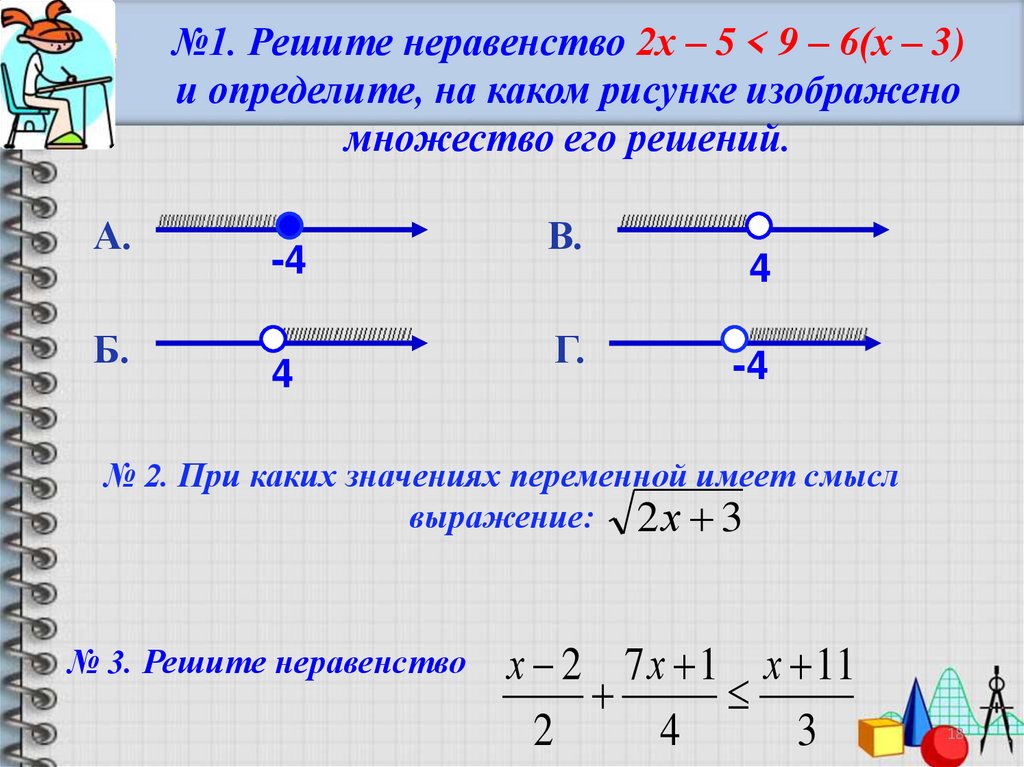

 

Как и в предыдущем примере, вы можете заменить значения [latex]x[/latex]– и [latex]y[/latex] в каждом из [latex](x,y)[/ латекс] упорядочил пары в неравенстве, чтобы найти решения. Хотя вы, возможно, смогли сделать это в уме для неравенства [latex]x>y[/latex], иногда создание таблицы значений имеет смысл для более сложных неравенств.

Заказная пара	Делает неравенство [латекс]3x+2y\leq6[/латекс] верное утверждение	Делает неравенство [латекс]3x+2y\leq6[/латекс] ложное заявление
[латекс](−5, 5)[/латекс]	[латекс]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array }[/латекс]
[латекс](−2,−2)[/латекс]	[латекс]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\ –10\leq6\end{массив}[/латекс]
[латекс](2,3)[/латекс]		[латекс]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/ латекс]
[латекс](2,0)[/латекс]	[латекс]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/ латекс]
[латекс](4,−1)[/латекс]		[латекс]\begin{массив}{r}3\влево(4\вправо)+2\влево(-1\вправо)\leq6\\12+\влево(-2\вправо)\leq6\\10\ leq6\end{массив}[/латекс]

Если подстановка [латекс](х,у)[/латекс] в неравенство дает верное утверждение, тогда упорядоченная пара является решением неравенства, и точка будет нанесена в заштрихованную область или точку будет частью сплошной граничной линии. Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.

Вы можете посмотреть следующее видео, чтобы увидеть больше примеров того, как определить, удовлетворяет ли упорядоченная пара линейному неравенству.

Посмотрите видео ниже, чтобы увидеть пример использования графика для определения того, является ли упорядоченная пара решениями линейного неравенства с двумя переменными

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

Графические неравенства | Начальная алгебра

Цели обучения

• Определение графиков и решений уравнений и неравенств
  • Определите сходства и различия между решениями линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
  • Определите сходства и различия между графиками линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
• График неравенства двух переменных
  • Определите и выполните шаги для построения графика линейного неравенства с двумя переменными

Определите разницу между графиком линейного уравнения и линейным неравенством

Вспомните, что решениями линейных неравенств являются целые наборы чисел, а не одно число, как вы находите с решениями равенств (уравнений).

Вот пример из раздела о решении линейных неравенств:

Решить для p . [латекс] 4p+5<29[/латекс]

[латекс] \displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\ ,\,\,\,\,\,-5\,\,\,\,\,\,\,-5}\\\подчеркнуть{4p}\,\,\,\,\,\,\ ,\,<\,\,\подчеркнуть{24}\,\,\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,4\\\,\,\,\,\,\,\,\,\,\,\,p<6\end{массив}[ /латекс]

Вы можете интерпретировать решение как p может быть любым числом меньше шести. Теперь вспомните, что мы можем построить уравнения линий, определив выходные данные y и входные данные x и написав уравнение.

Ранее мы показали, как изобразить линию, описываемую этим уравнением:  [latex]y=2x+3[/latex]    , и обнаружили, что можно построить бесконечную таблицу значений, которые образуют точки на линия — это некоторые решения уравнения [латекс]у=2х+3[/латекс].

x значения	[латекс]2x+3[/латекс]	y значения
0	[латекс]2(0)+3[/латекс]	3
1	[латекс]2(1)+3[/латекс]	5
2	[латекс]2(2)+3[/латекс]	7
3	[латекс]2(3)+3[/латекс]	9

Кроме того, мы узнали, как изобразить линию, представляющую все точки, которые делают [латекс]у=2х+3[/латекс] верным утверждением.

Что, если мы объединим эти две идеи — линейные неравенства и графики линий? Сначала переведите строку [latex]y=2x+3[/latex] в слова:

Вы получите y , умножив x на два и прибавив три. [latex]y=2x+3[/latex]

Как бы вы перевели это неравенство словами? [latex]y<2x+3[/latex]

Для каких значений x вы получите результат y, который на меньше, чем 2 умножить на x плюс три?

ВАУ, это может показаться запутанным, но продолжайте читать, мы поможем вам разобраться.

Линейные неравенства отличаются от линейных уравнений, хотя вы можете применить свои знания об уравнениях, чтобы понять неравенства. Неравенства и уравнения — это математические операторы, которые сравнивают два значения. В уравнениях используется символ = ; помните, что неравенства представлены символами < , ≤ , > и ≥.

Один из способов визуализировать неравенства с двумя переменными — нанести их на координатную плоскость. Вот что означает неравенство [latex]x>y[/latex]   выглядит так. Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.

 

Здесь следует отметить несколько моментов. Во-первых, посмотрите на пунктирную красную граничную линию: это график соответствующего линейного уравнения [latex]x=y[/latex]. Затем посмотрите на светло-красную область справа от линии. Эта область (за исключением строки [latex]x=y[/latex]) представляет собой все множество решений неравенства [latex]x>y[/latex]. Помните, как все точки на строки решения линейного уравнения линии? Итак, все точки в области являются решениями линейного неравенства , представляющего эту область.

Давайте задумаемся об этом на мгновение — если [латекс]x>y[/латекс], то график [латекс]х>у[/латекс] покажет все упорядоченные пары [латекс](х,у)[ /latex], для которого координата x- больше, чем координата y-.

На приведенном ниже графике показана область [латекс]x>y[/латекс], а также некоторые упорядоченные пары на координатной плоскости. Посмотрите на каждую заказанную пару. 9Координата 0105 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?

 

Упорядоченные пары [латекс](4,0)[/латекс] и [латекс](0,−3)[/латекс] лежат внутри заштрихованной области. В этих упорядоченных парах координата x- больше, чем координата y-. Эти упорядоченные пары входят в набор решений уравнения [латекс]х>у[/латекс].

Упорядоченные пары [латекс](−3,3)[/латекс] и [латекс](2,3)[/латекс] находятся за пределами заштрихованной области. В этих упорядоченных парах 9Координата 0105 x- на меньше , чем координата y-, поэтому они не включены в набор решений неравенства.

Упорядоченная пара [латекс](−2,−2)[/латекс] находится на граничной линии. Это не решение, так как [латекс]-2[/латекс] не больше, чем [латекс]-2[/латекс]. Однако если бы неравенство было [латекс]x\geq y[/латекс] (читается как « x больше или равно y »), то [латекс](−2,−2)[/латекс ] был бы включен (и линия была бы представлена ​​сплошной, а не пунктирной линией).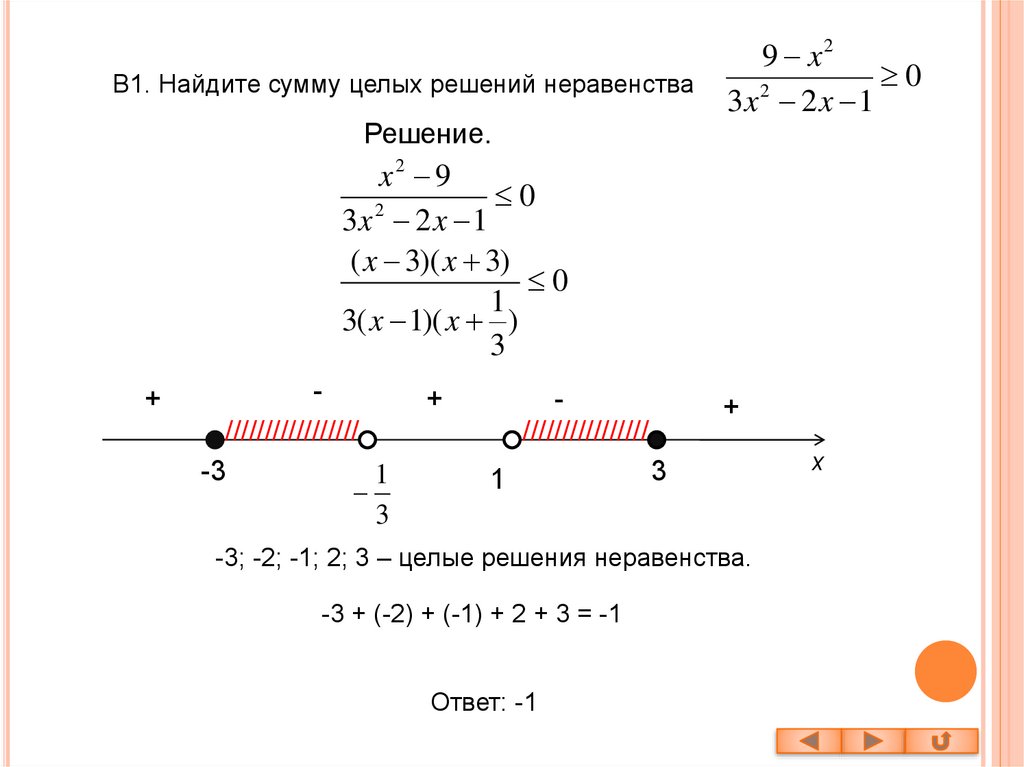

Разница между линейным уравнением и линейным неравенством (две переменные)

Рассмотрим еще один пример: неравенство [latex]3x+2y\leq6[/latex]. На приведенном ниже графике показана область значений, которая делает это неравенство верным (заштрихована красным), граничная линия [латекс]3x+2y=6[/латекс], а также несколько упорядоченных пар. Граничная линия на этот раз сплошная, потому что точки на граничной линии [latex]3x+2y=6[/latex] делают неравенство [latex]3x+2y\leq6[/latex] истинным.

 

Как и в предыдущем примере, вы можете подставить значения x- и y- в каждую из упорядоченных пар [латекс](х,у)[/латекс] в неравенство, чтобы найти решения . Хотя вы, возможно, смогли сделать это в уме для неравенства [latex]x>y[/latex], иногда создание таблицы значений имеет смысл для более сложных неравенств.

Заказная пара	Делает неравенство [латекс]3x+2y\leq6[/латекс] верное утверждение	Делает неравенство [латекс]3x+2y\leq6[/латекс] ложное заявление
[латекс](−5, 5)[/латекс]	[латекс]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array }[/латекс]
[латекс](−2,−2)[/латекс]	[латекс]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\ –10\leq6\end{массив}[/латекс]
[латекс](2,3)[/латекс]		[латекс]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/ латекс]
[латекс](2,0)[/латекс]	[латекс]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/ латекс]
[латекс](4,−1)[/латекс]		[латекс]\begin{массив}{r}3\влево(4\вправо)+2\влево(-1\вправо)\leq6\\12+\влево(-2\вправо)\leq6\\10\ leq6\end{массив}[/латекс]

Если подстановка [латекс](х,у)[/латекс] в неравенство дает верное утверждение, тогда упорядоченная пара является решением неравенства, и точка будет нанесена в заштрихованную область или точку будет частью сплошной граничной линии. Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.

Определите, удовлетворяют ли упорядоченные пары линейному неравенству

Использование графика Определение упорядоченных парных решений линейного неравенства с двумя переменными

 

Определение того, удовлетворяют ли упорядоченные пары линейному неравенству

10 Неравенство с двумя переменными в графе

Итак, как вы получаете от алгебраическая форма неравенства, например [latex]y>3x+1[/latex], к графику этого неравенства? Построить неравенство довольно просто, если вы выполните пару шагов.

Графические неравенства

Для построения графика неравенства:

• Начертите соответствующую граничную линию. Замените знак <, >, ≤ или ≥ в неравенстве на =, чтобы найти уравнение граничной линии.
• Определите хотя бы одну упорядоченную пару по обе стороны от линии границы и подставьте эти значения [латекс](х,у)[/латекс] в неравенство. Закрасьте область, содержащую упорядоченные пары, которые делают утверждение неравенства верным.  
• Если точки на граничной линии являются решениями, используйте сплошную линию для рисования граничной линии. Это произойдет для ≤ или ≥ неравенств.
• Если точки на граничной линии не являются решениями, используйте пунктирную линию для граничной линии. Это произойдет для < или > неравенств.

Построим график неравенства [latex]x+4y\leq4[/latex].

Чтобы построить граничную линию, найдите не менее двух значений, лежащих на линии [latex]x+4y=4[/latex]. Вы можете использовать точки пересечения x – и y для этого уравнения, подставив сначала 0 вместо x и найдя значение y ; затем подставьте 0 вместо y и найдите x .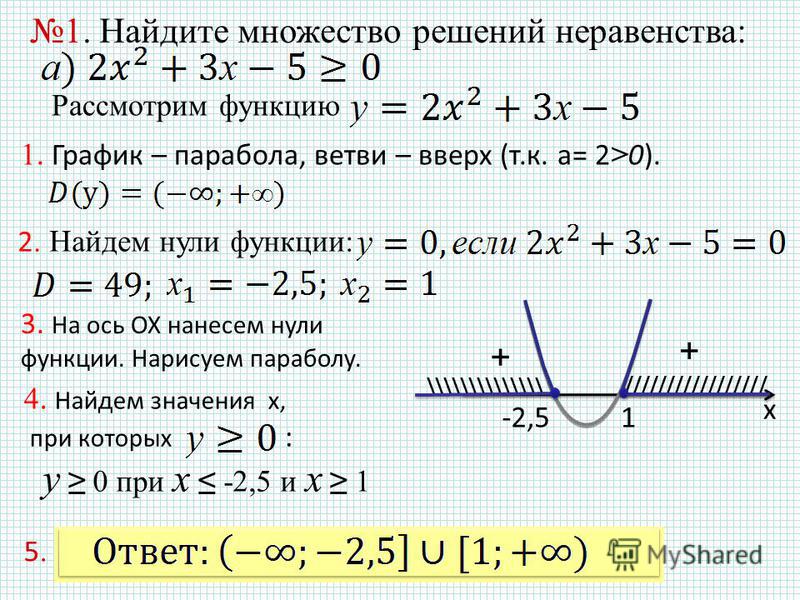

х	у
0	1
4	0

Нанесите точки [латекс](0,1)[/латекс] и [латекс](4,0)[/латекс] и проведите линию через эти две точки в качестве граничной линии. Линия сплошная, потому что ≤ означает «меньше или равно», поэтому все упорядоченные пары вдоль линии включаются в набор решений.

Следующий шаг — найти область, содержащую решения. Это выше или ниже границы? Чтобы определить область, в которой справедливо неравенство, вы можете протестировать пару упорядоченных пар, по одной с каждой стороны от граничной линии.

Если заменить [латекс](−1,3)[/латекс] на [латекс]x+4y\leq4[/латекс]:

[латекс]\begin{array}{r}−1+4\ left(3\right)\leq4\\−1+12\leq4\\11\leq4\end{array}[/latex]

Это неверное утверждение, поскольку 11 не меньше или равно 4.

С другой стороны, если вы замените [латекс](2,0)[/латекс] на [латекс]x+4y\leq4[/латекс]:

[латекс]\begin{array}{r}2 +4\left(0\right)\leq4\\2+0\leq4\\2\leq4\end{массив}[/latex]

Это правда! Область, включающая [латекс](2,0)[/латекс], должна быть заштрихована, так как это область решений.

Вот и все — график множества решений для [latex]x+4y\leq4[/latex].

Графики линейных неравенств с двумя переменными

Небольшое примечание к описанной выше проблеме: обратите внимание, что вы можете использовать точки [латекс](0,−3)[/латекс] и [латекс](2,1)[/латекс] для построения линии границы, но это эти точки не входят в область решений, так как область не включает граничную линию!

Графики линейных неравенств с двумя переменными (форма пересечения наклона)

Резюме

Когда неравенства изображаются на координатной плоскости, решения располагаются в области координатной плоскости, которая представлена ​​в виде заштрихованной области на самолет.