5х 60 найдите корень уравнения
Вы искали 5х 60 найдите корень уравнения? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найдите корень уравнения 5х 60, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «5х 60 найдите корень уравнения».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 5х 60 найдите корень уравнения,найдите корень уравнения 5х 60.
Где можно решить любую задачу по математике, а так же 5х 60 найдите корень уравнения Онлайн?
Решить задачу 5х 60 найдите корень уравнения вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
ГДЗ. Математика 5 класс Тарасенкова. Уравнения.
Категория: —>> Математика 5 класс Тарасенкова.
Задание: —>> 553 — 569 570 — 586
наверх
|
|
Задание 553.
Какое из чисел 4. 5, 8 и 10 является корнем уравнения:
Решение:
| 1) 5; | 2) 10; | 3) 4. |
Задание 554.
Решите уравнение устно:
Решение:
| 1) 15 + x: = 55, x = 40; | 3) 60 — y = 45, y = 15; | 5) 88 : x = 8, x = 11; |
| 2) х — 22 = 42, x = 64; | 4) у * 12 = 12, y = 1; | 6) у : 10 = 40, y = 400. |
Задание 555.
Можно ли решить уравнение:
| 1) 8x = 0; | 2) 0 : y = 25; | 3) 5х = 5 | 4) 12 : y = 0? |
Решение:
1) x = 0; 2) Не имеет решений; 3) x = 1; 4) Не имеет решений;
Задание 556.
Решите уравнение:
Решение:
1)28 + (45 + х) = 100;
| 11) 121 : (х — 45) = 11;

|
Задание 557.
Решите уравнение:
Решение:
1) 65 + (х + 23) = 105;
| 6) 9х + 50 = 86;

|
Задание 558.
Составьте уравнение, корнем которого является число:
| а) 8; | б) 14. |
Решение:
| а) 2y = 16; | б) x + 7 = 21. |
Задание 559.
Составьте уравнение, корнем которого является число.
| а) 5; | б) 9. |
Решение:
| а) 25 : x = 5; | б) 5x = 45. |
Задание 560.
Некоторое число увеличили на 67 и получили число 109. Найдите это число.
Решение:
- Некоторое число — x.
- x + 67 = 109;
- x = 109 — 67;
- x = 42.
- Ответ: число 42.
Задание 561.
К некоторому числу прибавили 38 и получили число 245. Найдите это число.
Решение:
- x + 38 = 245;
- x = 245 — 38;
- x = 207.

- Ответ: 207.
Задание 562.
Некоторое число увеличили в 24 раза и получили число 1968. Найдите это число.
Решение:
- 24x = 1968;
- x = 1968 : 24;
- x = 82.
- Ответ: 82.
Задание 563.
Некоторое число уменьшили в 18 раз и получили число 378. Найдите это число.
Решение:
- x : 18 = 378;
- x = 378 * 18;
- x = 6804.
- Ответ: 6408.
Задание 564.
Некоторое число уменьшили на 22 и получили число 105. Найдите это число.
Решение:
- x — 22 = 105;
- x = 105 + 22;
- x = 127.
- Ответ: 127.
Задание 565.
Из числа 128 вычли некоторое число и получили 79. Найдите это число.
Решение:
- 128 — x = 79;
- x = 128 — 79;
- x = 49.
- Ответ: 49.

Задание 566.
Составьте и решите уравнение:
- 1) сумма удвоенного числа х и числа 39 равна 81;
- 2) разность чисел 32 и y в 2 раза меньше числа 64;
- 3) частное суммы чисел х и 12 и числа 2 равно 40;
- 4) сумма чисел х и 12 в 3 раза больше числа 15;
- 5) частное разности чисел у и 12 и числа 6 равно 18;
- 6) утроенная разность чисел у и 17 равна 63.
Решение:
- 1) 2x + 39 = 81
- 2x = 81 — 39;
- 2x = 42;
- x = 42 : 2;
- x = 21;
- 2) (32 — y) * 2 = 64
- 32 — y = 64 : 2;
- 32 — y = 32;
- y = 32 — 32;
- y = 0;
- 3) (x + 12) : 2 = 40
- x + 12 = 40 * 2;
- x + 12 = 80;
- x = 80 — 12;
- x = 68;
- 4) (x + 12) : 3 = 15
- x + 12 = 15 * 3;
- x + 12 = 45;
- x = 45 — 12;
- x = 33;
- 5) (y — 12) : 6 = 18
- y — 12 = 18 * 6;
- y — 12 = 108;
- y = 108 + 12;
- y = 120;
- 6) (y — 17) * 3 = 63
- y — 17 = 63 : 3;
- y — 17 = 21;
- y = 21 + 17;
- y = 38;
Задание 567.

Составьте и решите уравнение:
- 1) разность утроенного числа у и числа 41 равна 64;
- 2) сумма чисел 9 и х в 5 раз меньше числа 80;
- 3) частное суммы чисел у и 10 и числа 4 равно 16;
- 4) разность утроенного числа х и числа 17 равна 10.
Решение:
- 1) 3y — 41 = 64
- 3y = 64 + 41;
- 3y = 105;
- y = 105 : 3;
- y = 15;
- 2) (9 + x) * 5 = 80
- 9 + x = 80 : 5;
- 9 + x = 16;
- x = 16 — 9;
- x = 7;
- 3) (y + 10) : 4 = 16
- y + 10 = 16 * 4;
- y + 10 = 64;
- y = 64 — 10;
- y = 54;
- 4) 3x — 17 = 10
- 3x = 10 + 17;
- 3x = 27;
- x = 27 : 3;
- x = 9;
Задание 568.
Некоторое число увеличили на 5 и полученное число удвоили. В результате получили число 22. Найдите неизвестное число.
В результате получили число 22. Найдите неизвестное число.
Решение:
- (x + 5) * 2 = 22;
- x + 5 = 22 : 2;
- x + 5 = 11;
- x = 11 — 5;
- x = 6;
Задание 569.
Некоторое число увеличили в 7 раз и полученное число уменьшили на 54. В результате получили число 100. Найдите неизвестное число.
Решение:
- 7x — 54 = 100;
- 7x = 100 + 54;
- 7x = 154;
- x = 154 : 7;
- x = 22;
Задание: —>> 553 — 569 570 — 586
8. Дано уравнение х4+х3-7х2-13х-60. Проверить, являются ли его корнями делители свободного члена уравнения. Проверочная работа №13.
Проверочная работа №13.Вариант1.
1. Из множества {1;-1;-2;3} выделить подмножество, состоящее из корней уравнения х2-6=х.
2. Даны уравнения: 5-2х=х-3 (А), 17(2х-5)=17(3-х)(Б), 13 QUOTE 1415(В), 2х-х=3-5(Г). Указать те, которые равносильны уравнению 2х-5=3-х. Ответ обосновать.
Указать те, которые равносильны уравнению 2х-5=3-х. Ответ обосновать.
3. Решить уравнения: а) -7х=4; б) 0,6у=-0,2; в) 0у=-2; г)0х=0.
4. Найти все целые значения параметра b, при которых уравнение bx=22 имеет целый корень.
5. Найти множество корней уравнения: а) |6x|=1,2: б) |-0,06y|=1,8; в) |6,07x|=0; г)|0,5y|=-1,2.
6. При каких значениях параметра а уравнение ах=а2+2а:
а) имеет единственный корень; б) не имеет корней; в) имеет бесконечно много корней.
7, Решить уравнение -2ny=а относительно переменной: а)у; б)n.
8. Дано уравнение х4+х3-7х2-13х-6=0. Проверить, являются ли его корнями делители свободного члена уравнения.
Проверочная работа №13.
Вариант2.
1. Из множества {1;-1;-5;-3} выделить подмножество, состоящее из корней уравнения х2+4х=5.
2. Даны уравнения: 5х-3=4-2х(А), 4-5х=2х-3(Б), 2,5х-2=1,5-х(В), 5х-2х=3-4(Г). Указать те, которые равносильны уравнению 5х-4=3-2х. Ответ обосновать.
Ответ обосновать.
3. Решить уравнения: а) 117х=17; б) 0,12у=-2,4; в) 0у=2,4; г)0х=0.
4.Найти множество В, состоящее из значений параметра b, при которых уравнение bx=-46 имеет натуральный корень.
5. Найти множество корней уравнения: а) |0,27x|=81; б) |-0,1y|=0,02; в) |-2,25x|=0; г)|0,7y|=-1,4.
6. При каких значениях параметра а уравнение ах=2+а:
а) имеет единственный корень; б) не имеет корней; в) имеет бесконечно много корней.
7, Решить уравнение kxy=p относительно переменной: а)у; б)x.
8. Дано уравнение х4- х3- х2- х- 2=0. Проверить, являются ли его корнями делители свободного члена уравнения.
15
Приложенные файлы
- 6543038
Размер файла: 29 kB Загрузок: 0
Уравнения. 6 класс | Тест з математики – «На Урок»
Запитання 1
Найдите корень уравнения 5х — 60 = 12 — х
варіанти відповідей
Запитання 2
Найдите корень уравнения 7х — 30 = 24 + х
варіанти відповідей
Запитання 3
Найдите сумму корней уравнения 5(10 — 4х) = 50 и -3( 2 — х) = — 9
варіанти відповідей
Запитання 4
Найдите сумму корней уравнений 5х + 10 = 15х + 40 и 2(- 5х + 10) = 80
варіанти відповідей
Запитання 5
Решите уравнение 2х + 4 = 4 — 2х
варіанти відповідей
Запитання 6
Решите уравнение 5х + 6 = 6 — 5х
варіанти відповідей
Запитання 7
Чему равно 5х, если 7(х — 4) — 2х = 2
варіанти відповідей
Запитання 8
Чему равно 5х, если 2( х — 5 ) + 3х = 15
варіанти відповідей
Запитання 9
Решите уравнение — 8( 3х + 2 ) = — 10 — 22х
варіанти відповідей
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook
Найдите корень уравнения А)5x=-60 Д)-9x=-3 И)42x-13 Б)-10x=8 Е)0,5x=1,2 В)7x=9 Ж)0,7x=0 Г)6x=-50 З)-1,5x=6
(∛3+ √2)¹⁵
C⁰₁₅ (∛3)¹⁵*(√2)⁰ +C¹₁₅(∛3)¹⁴*√2¹+C²₁₅ (∛3)¹³*√2² + C³₁₅ (∛3)¹²*√2³ +
+ C⁴₁₅ (∛3)¹¹*√2⁴ + C⁵₁₅ (∛3)¹⁰*√2⁵ …. .+ C¹²₁₅ (∛3)³*√2¹² +………
.+ C¹²₁₅ (∛3)³*√2¹² +………
15! 12!*13*14*15 C¹²₁₅ (∛3)³*√2¹² = C¹²₁₅ (3)*2⁶= ———— = ——————— *3*2⁶ = 3!*12! 3!*12!
13*14*15
= —————— *3* 64 = 87360 1*2*3
——————————————————————————————-
(∛x + (1/x))¹⁶ 16=15+1
T(n+1)= Cⁿ₁₆ (∛x)¹⁶⁻ⁿ * (1/x)ⁿ = Cⁿ₁₆ (x)⁽¹⁶⁻ⁿ⁾/³ * x⁻ⁿ =Cⁿ₁₆ (x) ⁽¹⁶⁻⁴ⁿ⁾/³
значение член разложения бинома не будет зависеть от переменной х ,если показатель степени х равен 0
(16-4n)/3=0 ⇒16-4n=0 n=4 T(n+1)=Т(4+1)=Т(5)
Значит пятый член разложения бинома не зависит от переменной х
Ответ ответ ответ ответ ответ
Сумма углов равна 180 градусов, значит угол KED будет равен
180-64=116 градусов, отсюда DEM=KED/4=116/4=29 градусов
ответ б
2)-4-4x+2=9-15x
-4x-2=9-15x
11x=11
x=1
ответ б
3)б
4)б
Пошаговое решение:
Шаг 1:
Уравнение в конце шага 1:
(5x 2 - 5x) - 60 = 0
Шаг 2:
Шаг 3:
Термины вытягивания:
3. 1 Факторы вытягивания:
1 Факторы вытягивания:
5x 2 — 5x — 60 = 5 • (x 2 — x — 12)
Попытка разложить на множители путем разделения среднего члена
3.2 Факторинг x 2 — x — 12
Первый член x 2 его коэффициент равен 1.
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен -12
Шаг-1: Умножьте коэффициент первого члена на константу 1 • -12 = -12
Шаг-2: Найдите два множителя -12, сумма которых равен коэффициенту среднего члена, который равен -1.
| -12 | + | 1 | = | -11 | ||
| -6 | + | 2 | = | -4 | ||
| -4 | + | 3 | = | -1 | Вот и все |
Шаг 3: Перепишите полином, разделяя средний член, используя два фактора, найденные на шаге 2 выше, -4 и 3
x 2 — 4x + 3x — 12
Шаг 4: сложите первые 2 члена, вычитая одинаковые множители:
x • (x-4)
Складываем последние 2 члена, вычитая общее факторы:
3 • (x-4)
Шаг-5: сложите четыре члена шага 4:
(x + 3) • (x-4)
Какой желаемый факторизат ion
Уравнение в конце шага 3:
5 • (x + 3) • (x - 4) = 0
Шаг 4:
Теория — Истоки продукта:
4. 1 Произведение нескольких членов равно нулю.
1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы один из членов должен быть равен нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении.
Любое решение условия = 0 также решает произведение = 0.
Уравнения, которые никогда не верны:
4.2 Решить: 5 = 0
У этого уравнения нет решения.
A ненулевая константа никогда не равна нулю.
Решение уравнения с одной переменной:
4.3 Решите: x + 3 = 0
Вычтите 3 из обеих частей уравнения:
x = -3
Решение уравнения с одной переменной:
4.4 Решите: x-4 = 0
Добавьте 4 к обеим сторонам уравнения:
x = 4
Дополнение: Непосредственное решение квадратного уравнения
Непосредственное решение x 2 -x-12 = 0
Ранее мы учли это полином путем разбиения среднего члена. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Парабола, найдя вершину:
5.1. Найдите вершину y = x 2 -x-12
Параболы имеют наибольшее или самая низкая точка называется вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (АКА абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину.Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх, через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна 0,5000
Подставив в формулу параболы 0,5000 для x, мы можем вычислить координату y:
y = 1,0 * 0,50 * 0,50 — 1,0 * 0,50 — 12,0
или y = -12,250
Парабола, Графическое изображение вершин и пересечений X:
Корневой график для: y = x 2 -x-12
Ось симметрии (пунктирная линия) {x} = {0,50}
Вершина в точке {x, y} = {0.50, -12.25}
x -Пересечения (корни):
корень 1 при {x, y} = {-3.00, 0.00}
корень 2 при {x, y} = {4.00, 0.00}
Решите квадратное уравнение с помощью Завершение квадрата
5.2 Решение x 2 -x-12 = 0 путем завершения квадрата.
Добавьте 12 к обеим сторонам уравнения:
x 2 -x = 12
Теперь умный бит: возьмите коэффициент при x, равный 1, разделите его на два, получив 1/2, и возведите его в квадрат. давая 1/4
давая 1/4
Добавьте 1/4 к обеим частям уравнения:
В правой части мы имеем:
12 + 1/4 или, (12/1) + (1/4)
Общий знаменатель две дроби равны 4. Сложение (48/4) + (1/4) дает 49/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 -x + (1/4) = 49/4
Сложение 1/4 превратила левую часть в полный квадрат:
x 2 -x + (1/4) =
(x- (1/2)) • (x- (1/2)) =
( x- (1/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x 2 -x + (1/4) = 49/4 и
x 2 -x + (1/4) = (x- (1/2)) 2
, то по закону транзитивности,
(x- (1/2)) 2 = 49/4
Мы будем называть это уравнение уравнением. # 5.2.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x- (1/2)) 2 равен
(x- (1/2)) 2/2 =
(x- (1/2)) 1 =
x- (1/2)
Теперь, применяя принцип квадратного корня к уравнению. # 5.2.1 получаем:
# 5.2.1 получаем:
x- (1/2) = √ 49/4
Добавляем 1/2 к обеим сторонам, чтобы получить:
x = 1/2 + √ 49/4
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 — x — 12 = 0
имеет два решения:
x = 1/2 + √ 49/4
или
x = 1/2 — √ 49/4
Обратите внимание, что √ 49/4 может быть записано как
√ 49 / √ 4, что равно 7/2
Решите квадратное уравнение с помощью квадратичной формулы
5.3 Решение x 2 -x-12 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = -1
C = -12
Соответственно B 2 — 4AC =
1 — (-48) =
49
Применение квадратичной формулы:
1 ± √ 49
x = —————
2
Можно ли упростить √ 49?
Да! Разложение 49 на простые множители равно
7 • 7
Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i. е. второй корень).
е. второй корень).
√ 49 = √ 7 • 7 =
± 7 • √ 1 =
± 7
Итак, теперь мы смотрим на:
x = (1 ± 7) / 2
Два реальных решения:
x = ( 1 + √49) / 2 = (1 + 7) / 2 = 4.000
или:
x = (1-√49) / 2 = (1-7) / 2 = -3.000
Были найдены два решения :
- x = 4
- x = -3
Алгебраическое решение уравнений
Алгебраическое решение уравненийСодержание: Эта страница соответствует § 2.4 (с. 200) текста.
Предлагаемые задачи из текста:
с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97
Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения
Квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0.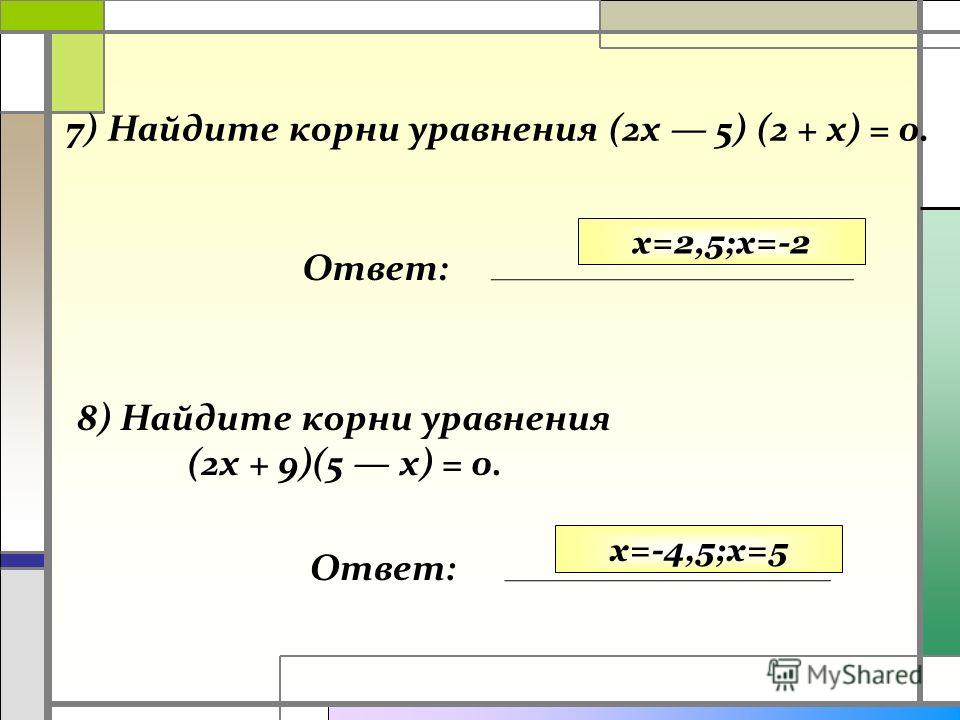
Факторинг
Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.
Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2, или x = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt (k).
Пример 2.
x 2 — 9 = 0.
x 2 = 9.
x = 3 или x = -3.
Пример 3.
Пример 4.
x 2 + 7 = 0.

х 2 = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.
Завершение квадрата
Идея завершения квадрата заключается в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.
Пример 5.
x 2 + 6x — 1 = 0.
x 2 + 6x = 1.
x 2 + 6x + 9 = 1 + 9.
9, прибавляемая к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Вот почему эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 .
Чтобы получить «а» нужно только разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
(x + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
х = -3 ± sqrt (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x 2 + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) 2 = 9/4.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x 2 + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня может быть перегруппирован и решен путем факторизации, как мы видим в следующем примере.
Пример 7.
x 2 = 16.
x 2 — 16 = 0.
(x + 4) (x — 4) = 0.
x = -4 или x = 4.
В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.
Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению
топор 2 + bx + c = 0.
Результатом завершения квадрата этого общего уравнения является формула для решений уравнения называется квадратной формулой.
Квадратичная формула
Решение уравнения ax 2 + bx + c = 0:
Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.
Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!
Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!
Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x 2 + 6x — 5.
Пример 9.
4x 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует отметить два момента.

- Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
- Решение упрощено, так что квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом. (Все квадратные уравнения могут быть решены путем разложения на множители ! Я имею в виду, что это могло быть решено легко факторингом.)
4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0.
х = -1/2.
Пример 10.
x 2 + x + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов функции f (x) = x 2 + x + 1. Таким образом, решения сложны, потому что график y = x 2 + x + 1 не имеет пересечений по x.

Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.
1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.
Примечания к проверке растворов
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко допустить ошибку.
Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.

Например, в предпоследнем примере, 4x 2 + 4x + 1 = 0, мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) 2 +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x 2 + 6x — 5 и проследите график, чтобы приблизительно определить, где x-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и сразу перешли к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако обнаружив (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, то вы, наверное, правы!
Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3x 2 -5x — 2 = 0. Ответ
(b) (x + 1) 2 = 3. Ответ
(c) x 2 = 3x + 2. Ответ
Вернуться к содержанию
Уравнения с участием радикалов
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.
д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.
Если в уравнении только один радикал, то перед возведением в степень вам следует договориться, чтобы радикальный член сам по себе на одной стороне уравнения.
Пример 11.
Теперь, когда мы изолировали радикальный член в правой части, возводим обе стороны в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является координата x точки пересечения графиков y = x и у = sqrt (х + 1) +1.

Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал. срок.
Это хуже, чем мы начали!
Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем на уменьшить количество радикальных членов на , возведя их в степень.
Если уравнение включает более одного радикального члена, то мы все же хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.
Пример 12.
Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член и возведите в квадрат снова обе стороны.
Чек:
Подстановка x = 5/4 в исходное уравнение дает
sqrt (9/4) + sqrt (1/4) = 2.

3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание по проверке решений:
В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение это координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).
Упражнение 2:
Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее. Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с помощью графической утилиты.
Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с помощью графической утилиты.
Нулевая постоянная
Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.
Пример 13.
2x 3 + 3x 2 -5x = 0.
x (2x 2 + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, поэтому у нас есть два более простых уравнения.
x = 0 или 2x 2 + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение можно решить путем факторизации. Примечание: Если бы мы не смогли разложить квадратичный коэффициент во втором уравнении, мы могли бы прибегнуть к к использованию квадратичной формулы.
[Убедитесь, что вы получили те же результаты, что и ниже.]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x 3 + 3x 2 -5x.
Фактор по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0.
Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа терминов один и два, а также три и четыре.
x 2 (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить на множители левую часть уравнения.
(x — 2) (x 2 — 9) = 0.
Когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.

x — 2 = 0 или x 2 — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x 3 -2x 2 -9x +18.
Квадратичная форма
Пример 15.
x 4 — x 2 — 12 = 0.
Этот многочлен неквадратичный, у него четвертая степень. Однако ее можно рассматривать как квадратичную по x 2 .
(x 2 ) 2 — (x 2 ) — 12 = 0.
Это может помочь вам фактически заменить z на x 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.
Теперь заменим z на x 2 и решите полученные уравнения.
x 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i или x = — i.
Итак, есть четыре решения, два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x 4 — х 2 — 12.
График f (x) = x 4 — x 2 -12 и увеличение, показывающее его локальное экстремумы.
Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения, содержащие дробные выражения или абсолютные значения
Пример 16.
Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.

Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).
Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (х — 1) = х + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.

Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Эта точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение становится
-5 (х — 1) = х + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по оси x, или вы можете найти решение как координаты x точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).
Упражнение 4:
(а) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ
Вернуться к содержанию
Свойства равенств (Алгебра 1, Как решать линейные уравнения) — Mathplanet
Два уравнения, которые имеют одно и то же решение, называются эквивалентными уравнениями e. г. 5 +3 = 2 + 6. И это, как мы узнали в предыдущем разделе, обозначается знаком равенства =. Обратная операция — это две операции, которые отменяют друг друга, например сложение и вычитание или умножение и деление. Вы можете выполнить ту же обратную операцию с каждой стороной эквивалентного уравнения без изменения равенства.
г. 5 +3 = 2 + 6. И это, как мы узнали в предыдущем разделе, обозначается знаком равенства =. Обратная операция — это две операции, которые отменяют друг друга, например сложение и вычитание или умножение и деление. Вы можете выполнить ту же обратную операцию с каждой стороной эквивалентного уравнения без изменения равенства.
$$ 5 + 3 \, {\ color {green} {- \, 2}} = 6 + 2 \, {\ color {green} {- \, 2}} $$
Это дает нам несколько свойств, которые верны для всех уравнений.
Свойство сложения равенства говорит нам, что добавление одного и того же числа к каждой стороне уравнения дает нам эквивалентное уравнение
$$ if \: ab = c, то \: ab \, {\ color {green} {+ \, b}} = c \, {\ color {green} {+ \, b}} или \: а = с + b $$
То же самое и со свойством вычитания равенства .
$$ if \: a + b = c, то \: a + b \, {\ color {green} {- \, b}} = c \, {\ color {green} {- \, b}} , или \: a = cb $$
Так же, как и для свойства умножения равенства . Если вы умножите каждую сторону уравнения на одно и то же ненулевое число, вы получите эквивалентное уравнение.
Если вы умножите каждую сторону уравнения на одно и то же ненулевое число, вы получите эквивалентное уравнение.
$$ если \: \ frac {a} {b} = c, и \: b \ neq 0, то \: \ frac {a} {b} \, \ cdot {\ color {green} b} = c \ cdot \, {\ color {green} b} или \: a = cb $$
И, естественно, это относится и к разделу , равному .Вы можете разделить каждую часть уравнения на одно и то же ненулевое число, чтобы получить эквивалентное уравнение
$$ if \: a \ cdot b = c и \: b \ neq 0, то \: \ frac {a \ cdot b} {{\ color {green} b}} \, = \ frac {c} {{\ color {green} b}} или \: a = \ frac {c} {b} $$
Это дает нам возможность изменить уравнение по своему усмотрению. Приемлемо все, что угодно, если вы делаете одно и то же с обеих сторон.
Есть несколько других свойств уравнений, о которых также может быть полезно знать
Пример
Джордж срубил дуб высотой 60 футов.Теперь он хочет разрезать его на более мелкие кусочки. Сначала он разрезает его на две части по 30 футов каждая. А затем он продолжает делать десять деталей длиной 6 футов, прежде чем погрузить их в свой грузовик.
Сначала он разрезает его на две части по 30 футов каждая. А затем он продолжает делать десять деталей длиной 6 футов, прежде чем погрузить их в свой грузовик.
Глядя на различные куски дерева, мы можем убедиться в следующем.
$$ 60 = 30 + 30 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 $$
Это называется рефлексивным свойством равенства и говорит нам, что любая величина равна самой себе
$$ a = a $$
Мы также можем использовать этот пример с кусками дерева, чтобы объяснить свойство симметрии равенства .Это свойство гласит, что если количество a равно количеству b, то b равно a.
$$, если \: a = b, \: then \: b = a $$
Или, если использовать наш пример
$$ if \: 60 = 30 + 30, \: then \: 30 + 30 = 60 $$
Еще одно свойство, которое можно объяснить этим, — это переходное свойство равенства . Он говорит нам, что если количество a равно количеству b, а b равно количеству c, то a и c также равны.
$$ если \: a = b \: и \: b = c, \: then \: a = c $$
Или в числах взятых из примера дуба
$$ if \: 60 = 30 + 30 $$
$$ и \: 30 + 30 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 $$
$$, тогда \: 60 = 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 $$
Поскольку мы знаем, что 30 + 30 = 20 + 40 и что 30 + 30 = 60, мы можем заменить 30 + 30 на 20 + 40 и получить 60 = 20 + 40.Это называется свойством замещения равенства .
Если a = b, тогда a можно заменить на b в любом выражении.
Видеоурок
Решите эти уравнения, используя обратные операции
$$ x + 8 = 10 $$
$$ x — 4 = 22 $$
$$ x \ div 3 = 6 $$
$$ 7x = 28 $$
Квадратные уравнения — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите квадратные уравнения, используя свойство нулевого произведения
- Решите квадратные уравнения, разложив на множители
- Решение приложений, моделируемых квадратными уравнениями
Перед тем, как начать, пройдите тест на готовность.
- Решить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решить:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Объедините похожие термины:.
Если вы пропустили эту проблему, просмотрите (рисунок). - Фактор полностью.
Если вы пропустили эту проблему, просмотрите (рисунок).
Мы уже решили линейные уравнения, уравнения вида. В линейных уравнениях у переменных нет показателей. Квадратные уравнения — это уравнения, в которых переменная возведена в квадрат.Ниже приведены некоторые примеры квадратных уравнений:
В последнем уравнении переменная не возведена в квадрат, но если мы упростим выражение слева, мы получим.
Общий вид квадратного уравнения.
Квадратное уравнение
Уравнение вида называется квадратным уравнением.
Для решения квадратных уравнений нам нужны методы, отличные от тех, которые мы использовали при решении линейных уравнений. Здесь мы рассмотрим один метод, а в следующей главе — несколько других.
Здесь мы рассмотрим один метод, а в следующей главе — несколько других.
Решите квадратные уравнения, используя свойство нулевого произведения
Сначала мы решим некоторые квадратные уравнения, используя свойство нулевого произведения. Свойство нулевого продукта говорит, что если произведение двух величин равно нулю, должно быть, что хотя бы одно из количеств равно нулю. Единственный способ получить продукт равный нулю — это умножить его на ноль.
Свойство нулевого продукта
Если, то либо, либо оба.
Теперь мы воспользуемся свойством нулевого произведения, чтобы решить квадратное уравнение.
Как использовать свойство нулевого произведения для решения квадратного уравнения
Решить:.
Решить:.
Решить:.
Обычно мы выполняем немного больше работы, чем в этом последнем примере, для решения линейных уравнений, возникающих в результате использования свойства нулевого произведения.
Решить:.
Решить:.
Решить:.
Обратите внимание, когда мы проверяли решения, каждое из них давало только один множитель, равный нулю.Но продукт был нулевым для обоих решений.
Решить:.
Решить:.
Решить:.
Может показаться, что в следующем примере есть только один фактор. Помните, однако, что это значит.
Решить:.
Решить:.
Решить:.
Решите квадратные уравнения множителем
У каждого из уравнений, которые мы решили до сих пор в этом разделе, была одна сторона в факторизованной форме.Чтобы использовать свойство нулевого произведения, квадратное уравнение должно быть разложено на множители с нулем на одной стороне. Поэтому обязательно начнем с квадратного уравнения в стандартной форме. Затем факторизуем выражение слева.
Как решить квадратное уравнение с помощью факторинга
Решить:.
Решить:.
Решить:.
Решите квадратное уравнение, вычислив множители.
- Запишите квадратное уравнение в стандартной форме,.
- Разложите квадратное выражение на множители.
- Используйте свойство нулевого продукта.
- Решите линейные уравнения.
- Проверить.
Прежде чем мы разложим на множители, мы должны убедиться, что квадратное уравнение имеет стандартную форму.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
При решении квадратных уравнений путем разложения на множители будут использоваться все методы разложения, которые вы изучили в этой главе! Узнаете ли вы особый рисунок продукта в следующем примере?
Решить:.
Решить:.
Решить:.
Левая часть в следующем примере разложена на множители, но правая часть не равна нулю. Чтобы использовать свойство нулевого произведения, одна сторона уравнения должна быть равна нулю. Мы умножим множители и запишем уравнение в стандартной форме.
Решить:.
Решение
Решить:.
Решить:.
Свойство нулевого продукта также применяется к произведению трех или более факторов.Если продукт равен нулю, по крайней мере один из факторов должен быть равен нулю. Мы можем решить некоторые уравнения степени выше двух, используя свойство нулевого произведения, точно так же, как мы решали квадратные уравнения.
Решить:.
Решить:.
Решить:.
Когда мы разложим квадратное уравнение на множители в следующем примере, мы получим три фактора. Однако первый фактор постоянен. Мы знаем, что этот коэффициент не может быть равен 0.
Решить:.
Решение
Решить:.
Решить:.
Решение приложений, моделируемых квадратными уравнениями
Стратегия решения проблем, которую мы использовали ранее для приложений, которые переводят в линейные уравнения, будет работать так же хорошо для приложений, которые переводят в квадратные уравнения. Мы скопируем здесь стратегию решения проблем, чтобы использовать ее для справки.
Используйте стратегию решения проблем для решения словесных задач.
- Прочтите проблему. Убедитесь, что все слова и идеи понятны.
- Определите то, что мы ищем.
- Имя то, что мы ищем. Выберите переменную для представления этого количества.
- Переведите в уравнение. Может быть полезно переформулировать проблему одним предложением со всей важной информацией.
 Затем переведите английское предложение в алгебраическое уравнение.
Затем переведите английское предложение в алгебраическое уравнение. - Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Мы начнем с числовой задачи, чтобы попрактиковаться в переводе слов в квадратное уравнение.
Произведение двух последовательных целых чисел. Найдите целые числа.
Произведение двух последовательных целых чисел. Найдите целые числа.
Произведение двух последовательных целых чисел.Найдите целые числа.
Были ли вы удивлены парой отрицательных целых чисел, которая является одним из решений предыдущего примера? Произведение двух положительных целых чисел и произведение двух отрицательных целых чисел дает 132.
В некоторых приложениях отрицательные решения будут результатом алгебры, но не будут реалистичными в данной ситуации.
Прямоугольный сад имеет площадь в квадратных футах. Длина сада на два фута больше ширины.Найдите длину и ширину сада.
Прямоугольный знак имеет площадь 30 квадратных футов. Длина знака на фут больше ширины. Найдите длину и ширину знака.
футов и
футовПрямоугольный внутренний дворик площадью 180 квадратных футов. Ширина патио на три фута меньше длины. Найдите длину и ширину патио.
футов и
футовВ предыдущей главе мы использовали теорему Пифагора.Это дало отношение между катетами и гипотенузой прямоугольного треугольника.
Мы будем использовать эту формулу для следующего примера.
Жюстин хочет поставить колоду в углу своего двора в форме прямоугольного треугольника, как показано ниже. Гипотенуза будет 17 футов в длину. Длина одной стороны будет на 7 футов меньше длины другой стороны. Найдите длины сторон колоды.
Парус лодки представляет собой прямоугольный треугольник. Длина одной стороны паруса на 7 футов больше, чем другой стороны. Гипотенуза равна 13. Найдите длины двух сторон паруса.
Длина одной стороны паруса на 7 футов больше, чем другой стороны. Гипотенуза равна 13. Найдите длины двух сторон паруса.
футов и
футовСад для медитации имеет форму прямоугольного треугольника с одной ногой 7 футов. Длина гипотенузы на единицу больше, чем длина одной из сторон. Найдите длины гипотенузы и другого отрезка.
футов и
футовКлючевые понятия
- Свойство нулевого произведения Если, то либо одно, либо оба.См. (Рисунок).
- Решите квадратное уравнение множителем Чтобы решить квадратное уравнение множителем: См. (Рисунок).
- Запишите квадратное уравнение в стандартной форме,.
- Разложите квадратное выражение на множители.
- Используйте свойство нулевого продукта.
- Решите линейные уравнения.
- Проверить.
- Используйте стратегию решения проблем для решения текстовых задач См.
 (Рисунок).
(Рисунок).
- Прочтите проблему.Убедитесь, что все слова и идеи понятны.
- Определите то, что мы ищем.
- Имя то, что мы ищем. Выберите переменную для представления этого количества.
- Переведите в уравнение. Может быть полезно переформулировать проблему одним предложением со всей важной информацией. Затем переведите английское предложение в алгебраическое уравнение.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в задаче и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Упражнения по разделам
Практика ведет к совершенству
Использовать свойство нулевого произведения
В следующих упражнениях решите.
Решите квадратные уравнения с помощью факторинга
В следующих упражнениях решите.
Решение приложений, моделируемых квадратными уравнениями
В следующих упражнениях решите.
Произведение двух последовательных целых чисел равно 56. Найдите целые числа.
Произведение двух последовательных целых чисел равно 42. Найдите целые числа.
Найдите целые числа.
Площадь прямоугольного ковра составляет 28 квадратных футов. Длина на три фута больше ширины. Найдите длину и ширину ковра.
Прямоугольная подпорная стена имеет площадь 15 квадратных футов. Высота стены на два фута меньше ее длины. Найдите высоту и длину стены.
Вымпел имеет форму прямоугольного треугольника с гипотенузой 10 футов. Длина одной стороны вымпела на два фута больше, чем длина другой стороны. Найдите длину двух сторон вымпела.
Отражающий бассейн имеет форму прямоугольного треугольника, одна ножка которого расположена вдоль стены здания. Гипотенуза на 9 футов длиннее, чем сторона вдоль здания. Третья сторона на 7 футов длиннее, чем сторона вдоль здания. Найдите длины всех трех сторон отражающего бассейна.
Смешанная практика
В следующих упражнениях решите.
Произведение двух последовательных целых чисел равно 110. Найдите целые числа.
Найдите целые числа.
Длина одного отрезка прямоугольного треугольника на три отрезка больше длины другого отрезка.Если гипотенуза равна 15, найдите длины двух катетов.
Повседневная математика
Площадь внутреннего дворика Если каждую сторону квадратного внутреннего дворика увеличить на 4 фута, площадь внутреннего дворика составит 196 квадратных футов. Решите уравнение для s , чтобы найти длину стороны внутреннего дворика.
Арбузная капля Арбуз падает с десятого этажа здания. Решите уравнение, чтобы найти количество секунд, в течение которых арбуз достигает земли.
Письменные упражнения
Объясните, как вы решаете квадратное уравнение. Сколько ответов вы ожидаете получить от квадратного уравнения?
Приведите пример квадратного уравнения, у которого есть ОКФ, и ни одно из решений уравнения не равно нулю.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении задач этого раздела.
ⓑ В целом, после просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?
Глава 7 Упражнения на повторение
7.1 наибольший общий множитель и фактор по группировке
Найдите наибольший общий множитель двух или более выражений
В следующих упражнениях найдите наибольший общий фактор.
Разложите на множители наибольший общий множитель из полинома
В следующих упражнениях разложите на множители наибольший общий делитель каждого полинома.
Фактор по группировке
В следующих упражнениях разложите по группам.
7.3 Факторинговые трехчлены формы
Полное распознавание предварительной стратегии факторных многочленов
В следующих упражнениях определите лучший метод разложения каждого многочлена на множители.
Факторные трехчлены формы с GCF
В следующих упражнениях учитывайте полностью.
Триномы на множители с использованием метода «ac»
В следующих упражнениях фактор.
Фактор трехчленов с GCF с использованием метода «ac»
В следующих упражнениях фактор.
7.4 Факторинг специальных продуктов
Фактор трехчлена идеального квадрата
В следующих упражнениях фактор.
Факторные разности квадратов
В следующих упражнениях фактор.
Факторные суммы и разности кубов
В следующих упражнениях фактор.
7.
 6 квадратных уравнений
6 квадратных уравнений
Использовать свойство нулевого произведения
В следующих упражнениях решите.
Решите квадратные уравнения с помощью факторинга
В следующих упражнениях решите.
Решение приложений, моделируемых квадратными уравнениями
В следующих упражнениях решите.
Произведение двух последовательных чисел равно. Найдите числа.
Площадь патио прямоугольной формы квадратных футов. Длина патио на фут больше его ширины. Найдите длину и ширину.
Практический тест
В следующих упражнениях найдите наибольший общий фактор в каждом выражении.
В следующих упражнениях учитывайте полностью.
В следующих упражнениях решите.
Произведение двух последовательных целых чисел. Найдите целые числа.
Площадь прямоугольного коврика составляет квадратные дюймы. Его длина на два дюйма больше ширины. Найдите длину и ширину салфетки.
Глоссарий
- квадратные уравнения
- — это уравнения, в которых переменная возведена в квадрат.
- Свойство нулевого продукта
- Свойство нулевого продукта утверждает, что, если произведение двух величин равно нулю, по крайней мере одно из количеств равно нулю.

Решите квадратное уравнение с помощью программы «Пошаговое решение математических задач»
Решение уравнений — центральная тема алгебры. Все приобретенные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения. В предыдущих главах мы решали уравнения первой степени.Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратные уравнения .
КВАДРАТИКА, РЕШЕННАЯ ФАКТОРИНГОМ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите квадратное уравнение.
- Приведите квадратное уравнение в стандартную форму.
- Решите квадратное уравнение факторизацией.
Квадратное уравнение — это полиномиальное уравнение, которое содержит вторую степень, но не более высокую степень переменной.
Стандартная форма квадратного уравнения: ax 2 + bx + c = 0, когда a ≠ 0 и a, b и c — действительные числа.
Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть преобразовано в стандартную форму, является квадратным уравнением. Другими словами, стандартная форма представляет все квадратные уравнения.
Решение уравнения иногда называют корнем уравнения .
| Эта теорема доказана в большинстве учебных пособий по алгебре. |
Важная теорема, которую невозможно доказать на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней». Использование этого факта говорит нам, что квадратные уравнения всегда будут иметь два решения. Возможно, что два решения равны.
| Квадратное уравнение будет иметь два решения, потому что оно имеет степень два. |
Самый простой метод решения квадратичных вычислений — факторинг. Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторинг возможен.
Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторинг возможен.
Метод решения с помощью факторизации основан на простой теореме.
Если AB = 0, то либо A = 0, либо B = 0.
| Другими словами, если произведение двух факторов равно нулю, то по крайней мере один из факторов равен нулю. |
Мы не будем пытаться доказывать эту теорему, но внимательно отметим, что в ней говорится. Мы никогда не сможем перемножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю. Конечно, оба числа могут быть нулевыми, поскольку (0) (0) = 0.
Решение Шаг 1 Приведите уравнение в стандартную форму.
| Мы должны вычесть 6 с обеих сторон. |
Шаг 2 Полностью разложить на множители.
| Напомним, как разложить на множители трехчлены. |
Шаг 3 Установите каждый коэффициент равным нулю и решите для x. Поскольку у нас есть (x — 6) (x + 1) = 0, мы знаем, что x — 6 = 0 или x + 1 = 0, и в этом случае x = 6 или x = — 1.
| Здесь применяется приведенная выше теорема, согласно которой хотя бы один из факторов должен иметь нулевое значение. |
Шаг 4 Проверьте решение в исходном уравнении. Если x = 6, то x 2 — 5x = 6 становится
| Проверка ваших решений — верный способ узнать, правильно ли вы решили уравнение. |
Следовательно, x = 6 — решение. Если x = — 1, то x 2 — 5x = 6 становится
Следовательно, — 1 — решение.
Решения могут быть указаны либо записью x = 6 и x = — 1, либо использованием обозначения набора и записи {6, — 1}, что мы читаем «набор решений для x равен 6 и — 1». В этом тексте мы будем использовать обозначения набора.
| В этом примере 6 и -1 называются элементами набора. |
| Обратите внимание, что в этом примере уравнение уже имеет стандартную форму. |
| Опять же, проверка решений убедит вас, что вы не допустили ошибки при решении уравнения. также называют корнями уравнения. |
| (x + 1) — наименьший общий знаменатель всех дробей в уравнении. Помните, что каждый член уравнения нужно умножить на (x + 1).  |
Проверьте решения в исходном уравнении.
| Проверьте исходное уравнение, чтобы убедиться, что знаменатель не равен нулю. |
| Обратите внимание, что здесь два решения равны.Это происходит только тогда, когда трехчлен является полным квадратом. |
НЕПОЛНАЯ КВАДРАТИКА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите неполное квадратное уравнение.
- Решите неполное квадратное уравнение.
Если уравнение представлено в стандартной форме ax 2 + bx + c = 0, либо b = 0, либо c = 0, уравнение будет неполным квадратичным .
Пример 1
5x 2 -10 = 0 является неполным квадратичным, так как средний член отсутствует и, следовательно, b = 0.
Когда вы встречаетесь с неполной квадратичной с c — 0 (отсутствует третий член), ее все же можно решить с помощью факторизации.
| x — общий множитель. Произведение двух факторов равно нулю. Поэтому воспользуемся теоремой из предыдущего раздела. Проверьте эти решения. |
Обратите внимание, что если член c отсутствует, вы всегда можете множить x из других членов. Это означает, что во всех таких уравнениях нуль будет одним из решений.
Неполная квадратичная с отсутствующим членом b должна быть решена другим методом, поскольку факторизация будет возможна только в особых случаях.
Пример 3 Решите относительно x if x 2 — 12 = 0.
Решение Поскольку x 2 — 12 не имеет общего множителя и не является разностью квадратов, его нельзя разложить на рациональные множители. Но из предыдущих наблюдений мы имеем следующую теорему.
| Обратите внимание, что есть два значения, которые в квадрате будут равны A. |
Используя эту теорему, имеем
| Проверьте эти решения. |
| Добавьте 10 с каждой стороны. Проверьте эти решения. |
| Здесь 7x — общий множитель. Проверьте эти решения. |
Обратите внимание, что в этом примере у нас есть квадрат числа, равного отрицательному числу. Это никогда не может быть правдой в реальной системе счисления, и поэтому у нас нет реального решения.
ЗАВЕРШЕНИЕ ПЛОЩАДИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите трехчлен полного квадрата.

- Завершите третий член, чтобы получить трехчлен в виде полного квадрата.
- Решите квадратное уравнение, заполнив квадрат.
Из вашего опыта факторизации вы уже понимаете, что не все многочлены факторизуемы. Следовательно, нам нужен метод решения квадратичных вычислений, которые не подлежат факторизации.Необходимый метод называется «завершение квадрата».
Сначала давайте рассмотрим значение «трехчлена полного квадрата». Когда мы возводим двучлен в квадрат, мы получаем полный квадрат трехчлена. Общая форма: (a + b) 2 = a 2 + 2ab + b 2 .
| Помните, возведение бинома в квадрат означает его умножение на само себя. |
Из общей формы и этих примеров мы можем сделать следующие наблюдения относительно трехчлена полного квадрата.
- Два из трех членов — полные квадраты. 4x 2 и 9 в первом примере, 25x 2 и 16 во втором примере и 2 и b 2 в общем виде.

Другими словами, первый и третий члены — это полные квадраты. - Другой член — это произведение квадратных корней из двух других членов, умноженное на два плюс или минус.
Член -7 сразу говорит о том, что это не может быть трехчлен полного квадрата.Задача при заполнении квадрата состоит в том, чтобы найти число, которое заменит -7 так, чтобы получился идеальный квадрат.
Рассмотрим эту задачу: заполните пробел так, чтобы «x 2 + 6x + _______» было трехчленом в виде полного квадрата. Из двух условий для трехчлена полного квадрата мы знаем, что пробел должен содержать полный квадрат и что 6x должно быть удвоенным произведением квадратного корня x 2 и числа в пробеле. Поскольку x уже присутствует в 6x и представляет собой квадратный корень из x 2 , то 6 должно быть в два раза больше квадратного корня из числа, которое мы помещаем в пробел. Другими словами, если мы сначала возьмем половину 6, а затем возведем в квадрат этот результат, мы получим необходимое число для бланка.
Другими словами, если мы сначала возьмем половину 6, а затем возведем в квадрат этот результат, мы получим необходимое число для бланка.
Следовательно, x 2 + 6x + 9 — это трехчлен полного квадрата.
Теперь давайте рассмотрим, как мы можем использовать завершение квадрата для решения квадратных уравнений.
Пример 5 Решите x 2 + 6x — 7 = 0, завершив квадрат.
| Напомним, что вместо -7, +9 сделает выражение идеальным квадратом. |
Решение Сначала мы замечаем, что член -7 необходимо заменить, если мы хотим получить трехчлен в виде полного квадрата, поэтому мы перепишем уравнение, оставив пустое место для нужного числа.
На этом этапе будьте осторожны, чтобы не нарушить никаких правил алгебры. Например, обратите внимание, что вторая форма появилась в результате добавления +7 к обеим сторонам уравнения. Никогда не добавляйте что-либо к одной стороне, не добавляя то же самое к другой стороне.
Никогда не добавляйте что-либо к одной стороне, не добавляя то же самое к другой стороне.
Теперь мы находим половину 6 = 3 и 3 2 = 9, чтобы получить число для пробела.Опять же, если мы поместим 9 в пустое поле, мы также должны добавить 9 к правой стороне.
| Помните, что если 9 добавляется к левой части уравнения, это также должно быть добавлено к правой части. |
Теперь разложите на множитель полного квадрата трехчлена, что дает
| Теперь x 2 + 6x + 9 можно записать как (x + 3) 2 . |
| Таким образом, 1 и -7 являются решениями или корнями уравнения. |
Пример 6 Решите 2x 2 + 12x — 4 = 0, заполнив квадрат.
Решение Эта проблема порождает еще одну трудность. Первый член, 2x 2 , не является полным квадратом.
Мы исправим это, разделив все члены уравнения на 2 и получим
| Другими словами, получите коэффициент 1 для члена x 2 . |
Теперь добавим 2 к обеим сторонам, получив
| Опять же, это более лаконично. |
Пример 7 Решите 3x 2 + 7x — 9 = 0, заполнив квадрат.
Решение Шаг 1 Разделите все термины на 3.
| Опять же, получите коэффициент 1 для x 2 , разделив на 3. |
Шаг 2 Перепишите уравнение, оставив пробел для члена, необходимого для завершения квадрата.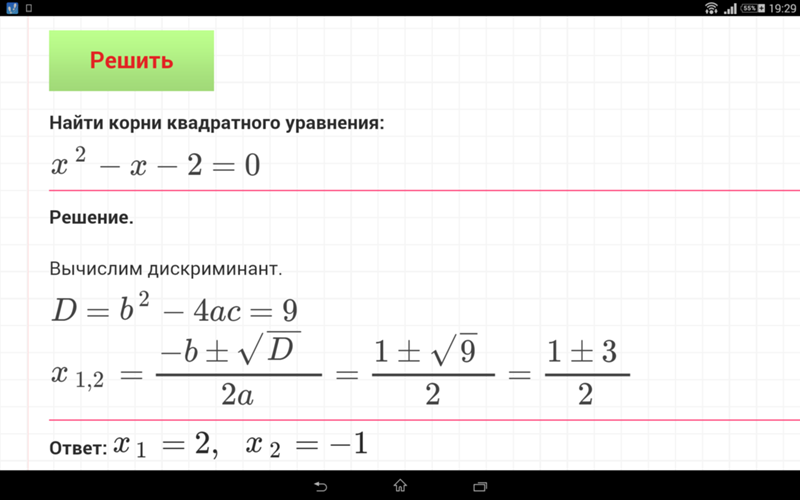
Шаг 3 Найдите квадрат половины коэффициента при x и прибавьте к обеим сторонам.
| Это выглядит сложно, но мы следуем тем же правилам, что и раньше. |
Шаг 4 Разложите квадрат на множители.
Разложение на множители никогда не должно быть проблемой, поскольку мы знаем, что у нас есть идеальный квадратный трехчлен, что означает, что мы находим квадратные корни из первого и третьего членов и используем знак среднего члена.
Если у вас возникнут какие-либо затруднения, вам следует еще раз повторить арифметические действия при сложении чисел справа.
Теперь у нас
Шаг 5 Извлеките квадратный корень из каждой части уравнения.
Шаг 6 Решите относительно x (два значения).
не может быть упрощено. Мы могли бы также записать решение этой проблемы в более сжатой форме как Мы могли бы также записать решение этой проблемы в более сжатой форме как |
Выполните шаги, описанные в предыдущем вычислении, а затем обратите особое внимание на последнее значение. Каков вывод, когда квадрат количества равен отрицательному числу? «Реального решения нет.«
| Какое действительное число возведем в квадрат и получим -7? |
Таким образом, чтобы решить квадратное уравнение, заполнив квадрат, выполните этот пошаговый метод.
Шаг 1 Если коэффициент при x2 не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x2 + bx + _______ = c + _______.
Шаг 3 Найдите квадрат половины коэффициента при x и прибавьте это количество к обеим сторонам уравнения.
Шаг 4 Разложите заполненный квадрат на множители и сложите числа в правой части уравнения.
Шаг 5 Найдите квадратный корень из каждой части уравнения.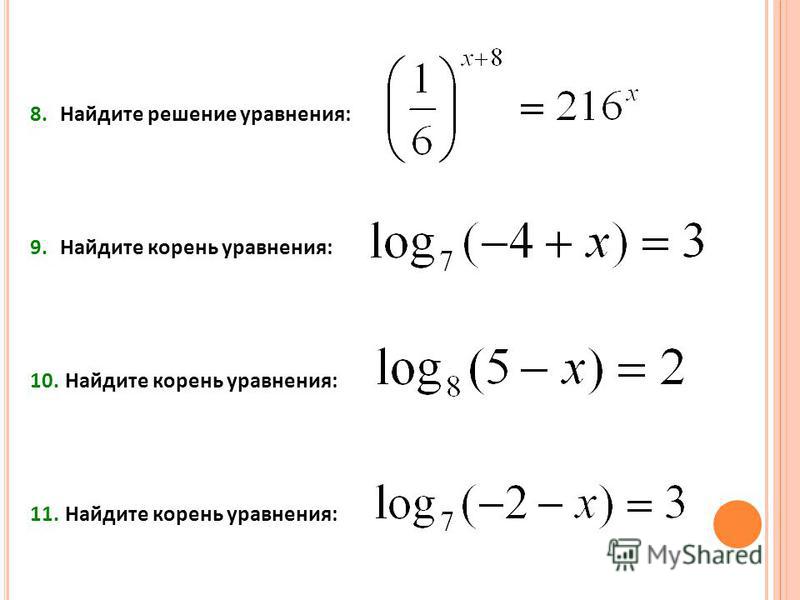
Шаг 6 Решите относительно x и упростите.
Если шаг 5 невозможен, уравнение не имеет реального решения.
| Эти шаги помогут решить уравнения в следующем упражнении. |
КВАДРАТИЧЕСКАЯ ФОРМУЛА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Решите общее квадратное уравнение, заполнив квадрат.
- Решите любое квадратное уравнение, используя формулу корней квадратного уравнения.
- Решите квадратное уравнение, заполнив квадрат.
Стандартная форма квадратного уравнения — ax 2 + bx + c = 0. Это означает, что каждое квадратное уравнение может быть представлено в этой форме. В некотором смысле ax 2 + bx + c = 0 представляет все квадратичные системы. Если вы сможете решить это уравнение, вы получите решение всех квадратных уравнений.
Решим общее квадратное уравнение методом завершения квадрата.
| Это необходимо для получения члена x 2 с коэффициентом 1. Это мы проделывали в предыдущем разделе много раз. |
| Надо прибавить с каждой стороны. |
Эта форма называется квадратной формулой и представляет собой решение всех квадратных уравнений.
| Запомните это выражение. |
Чтобы использовать формулу квадратного уравнения, вы должны указать a, b и c.Для этого данное уравнение всегда необходимо оформлять в стандартном виде.
| Осторожно подставьте значения a, b и c в формулу. |
Не каждое квадратное уравнение имеет реальное решение.
Это уравнение уже имеет стандартную форму. |
Реального решения нет, так как -47 не имеет действительного квадратного корня.
| Опять же, это уравнение в стандартной форме. |
Теперь это решение следует упростить.
ПРОБЛЕМЫ СО СЛОВОМ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите текстовые задачи, для решения которых требуется квадратное уравнение.
- Решайте текстовые задачи, связанные с квадратными уравнениями.
Некоторые типы словесных задач могут быть решены с помощью квадратных уравнений. Процесс обрисовки и постановки проблемы такой же, как описано в главе 5, но с проблемами, решаемыми квадратичными методами, вы должны быть очень осторожны, чтобы проверить решения в самой проблеме.Физические ограничения внутри проблемы могут устранить одно или оба решения.
Пример 1 Если длина прямоугольника на 1 единицу больше, чем в два раза больше ширины, а его площадь составляет 55 квадратных единиц, найдите длину и ширину.
Решение Формула площади прямоугольника: Площадь = Длина X Ширина. Пусть x = ширина, 2x + 1 = длина.
| Если x представляет ширину, то 2x представляет двойную ширину, а 2x + 1 представляет единицу более чем в два раза ширину. |
| Приведите квадратное уравнение в стандартную форму. Эта квадратичная величина может быть решена путем факторизации. |
На этом этапе вы можете видеть, что решение x = -11/2 недействительно, поскольку x представляет собой измерение ширины, а отрицательные числа не используются для таких измерений. Следовательно, решение —
ширина = x = 5, длина = 2x + 1 = 11.
| Результат измерения не может быть отрицательным. |
Значение x, обратное. Помните, что ЖК-дисплей означает наименьший общий знаменатель. Каждый член необходимо умножить в 10 раз. Опять же, эту квадратичную величину можно разложить на множители. |
Оба решения проверяют. Следовательно, набор решений есть.
| Есть два решения этой проблемы. |
Пример 3 Если определенное целое число вычитается из его квадрата, умноженного на 6, получается 15.Найдите целое число.
Решение Пусть x = целое число. Тогда
Поскольку ни одно из решений не является целым числом, проблема не имеет решения.
| У вас может возникнуть соблазн указать эти значения в качестве решения, если вы не обратили пристальное внимание на тот факт, что проблема запрашивала целое число. |
Пример 4 Управляющий фермой имеет под рукой 200 метров забора и желает оградить прямоугольное поле так, чтобы его площадь составляла 2400 квадратных метров. Какими должны быть размеры поля?
Какими должны быть размеры поля?
Решение Здесь задействованы две формулы. P = 2l + 2w для периметра и A = lw для площади.
Сначала используя P = 2l + 2w, получаем
Теперь мы можем использовать формулу A = lw и подставить (100 — l) вместо w, получив
Поле должно быть шириной 40 метров и длиной 60 метров.
| Мы могли бы точно так же решить для l, получив l = 100 — w. Тогда |
Обратите внимание, что в этой задаче мы фактически используем систему уравнений
P = 2 l + 2 w
A = l w.
Как правило, система уравнений, в которой участвует квадратичная функция, будет решаться методом подстановки. (См. Главу 6.)
РЕЗЮМЕ
Ключевые слова
- Квадратное уравнение — это полиномиальное уравнение от одного неизвестного, которое содержит вторую степень, но не более высокую степень переменной.

- Стандартная форма квадратного уравнения имеет вид ax 2 + bx + c = 0, когда a ≠ 0.
- Неполное квадратное уравнение имеет вид ax 2 + bx + c = 0, и либо b = 0, либо c = 0.
- Квадратичная формула — это
Процедуры
- Самый прямой и самый простой метод поиска решений квадратного уравнения — это факторизация. Этот метод основан на теореме: если AB = 0, то A = 0 или B = 0. Чтобы использовать эту теорему, мы приводим уравнение в стандартную форму, множители и устанавливают каждый множитель равным нулю.
- Чтобы решить квадратное уравнение, заполнив квадрат, выполните следующие действия:
Шаг 1 Если коэффициент при x 2 не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x 2 + bx + _____ = c + _____
Шаг 3 Найдите квадрат половины коэффициента члена x и прибавьте эту величину к обеим сторонам. уравнения.
уравнения.
Шаг 4 Разложите заполненный квадрат на множители и сложите числа в правой части уравнения.
Шаг 5 Найдите квадратный корень из каждой части уравнения.
Шаг 6 Решите относительно x и упростите. - Метод завершения квадрата используется для вывода формулы корней квадратного уравнения.
- Чтобы использовать формулу корней квадратного уравнения, напишите уравнение в стандартной форме, укажите a, b и c и подставьте эти значения в формулу. Все решения следует упростить.
MATH 110 EXAM I, FALL 98
Решения: MATH 110 EXAM I, FALL 98 Отделение математических наук, Университет Северного ИллинойсаРЕШЕНИЯ: МАТЕМАТИКА 110, ЭКЗАМЕН I, форма A, 25.09.98
Печать: Если вы распечатываете эту страницу, важно убедиться, что неравенства соответствуют тому, что вы видите на экране, потому что «меньше или равно» может быть напечатано как <вместо <.
-
Какое число нужно добавить, чтобы завершить квадрат выражения
x 2 — 6x ?
Решение: Разделите коэффициент при x на 2, а затем возведите в квадрат. Ответ: (б) 9.
Ответ: (б) 9.
-
Полностью множитель: 6x 2 — 4x — 16 .
Решение: Мы можем вынести 2, чтобы получить 2 (3x 2 -2x-8), а затем 3x 2 -2x-8 множителей как (3x + 4) (x-2), так что ответ будет (c) 2 (3x + 4) (x-2). -
Упростить
(24x 8 y 3 / 3x 2 y 5 ) 1/2 .Предположим, что все переменные положительны.
Решение: Во-первых, упростим дробь внутри квадратного корня, чтобы получить (8x 6 / y 2 ) 1/2 . Тогда извлечение квадратного корня из каждого члена в круглых скобках дает ответ (г) 2x 3 2 1/2 / у. -
Упростим (125/64) -2/3 .
Решение: Поскольку показатель степени отрицательный, мы можем инвертировать выражение в скобках, чтобы получить (64/125) 2/3 = 64 2/3 /125 2/3 . В дробном показателе знаменатель соответствует извлечению корня,
поэтому сначала нам нужно извлечь кубический корень из 64 и кубический корень из 125.
Затем каждый из них возводится в квадрат, чтобы получить ответ (b) 16/25.
В дробном показателе знаменатель соответствует извлечению корня,
поэтому сначала нам нужно извлечь кубический корень из 64 и кубический корень из 125.
Затем каждый из них возводится в квадрат, чтобы получить ответ (b) 16/25.
-
Найдите действительные решения уравнения
(1 — 2x) 1/3 = 1 .
Решение: Обведите кубом обе части уравнения, чтобы получить 1-2x = 1. Тогда 2x = 0, поэтому x = 0, и ответ (b) x = 0. -
Найдите площадь данного треугольника
с основанием 12, высотой 8 и стороной длиной 10.
Решение: Площадь равна 1/2 основания, умноженному на высоту, то есть 48. Ответ: (д) ничего из этого. -
В баскетбольном матче команда набрала 60 очков.
Он выполнил вдвое меньше штрафных бросков (по 1 очку)
в качестве бросков с игры (по 2 очка).
Сколько штрафных бросков они сделали?
Решение: Пусть x — количество штрафных бросков, а y — количество бросков с игры. Тогда имеем y = 2x и x + 2y = 60. Подстановка y дает 5x = 60, поэтому x = 12, и ответ будет (a).
Подстановка y дает 5x = 60, поэтому x = 12, и ответ будет (a). -
Уменьшить
(x 2 -4) / (x 2 + 5x + 6)
на самые низкие сроки.
Решение: Разделите числитель и знаменатель на множители, чтобы получить (x + 2) (x-2) / (x + 2) (x + 3). Тогда у нас есть произведение терминов в числителе и произведение терминов в знаменателе, так что любой общий термин можно отменить. Это позволяет нам отменить x + 2, поэтому ответ будет (b) (x-2) / (x + 3). -
Фактор полностью:
x 3 — 3x 2 — 4x + 12
Решение: Первые два члена имеют очевидный множитель x-3, так что мы можем попробовать это как фактор последних двух терминов.Это работает, и мы получаем x 2 (x-3) — 4 (x-3). Тогда (x 2 -4) (x-3) = (x + 2) (x-2) (x-3), поэтому ответ (b) правильный. -
Найдите решения неравенства
(x + 2) / (x-3) > 0 .
Решение: Числитель может быть равен нулю, а знаменатель — нет. В противном случае оба фактора должны быть положительными или оба фактора должны быть отрицательными.
Знаки факторов приведены в таблице ниже.
В противном случае оба фактора должны быть положительными или оба фактора должны быть отрицательными.
Знаки факторов приведены в таблице ниже.
х <-2 х = -2-2 <х <3 х = 3 3 <х х + 2 - 0 + + + х-3 - - - 0 + (х + 2) (х-3) + 0 - * + * здесь дробь не определенаОтвет: (b) x <-2 или 3- Упростить (16x 2 y 2/3 ) 3/2
Решение: (16x 2 y 2/3 ) 3/2 = 16 3/2 (x 2 ) 3/2 (y 2/3 ) 3/2 = 64x 3 г- Найдите действительные решения уравнения х - х 1/2 = 2 .
Решение: Перепишем уравнение в виде x-2 = x 1/2 и возведите обе стороны в квадрат, получая x 2 -4x + 4 = x.Поскольку теперь это квадратное уравнение, сгруппируйте термины слева и множитель. Получаем x 2 -5x + 4 = 0 или (x-4) (x-1) = 0.
Это дает два возможных решения x = 4 и x = 1.
Поскольку мы возводили обе части уравнения в квадрат,
возможно, мы ввели дополнительный корень, поэтому необходимо проверить оба ответа.
Только первый работает в исходном уравнении,
так что ответ (б) x = 4.
Получаем x 2 -5x + 4 = 0 или (x-4) (x-1) = 0.
Это дает два возможных решения x = 4 и x = 1.
Поскольку мы возводили обе части уравнения в квадрат,
возможно, мы ввели дополнительный корень, поэтому необходимо проверить оба ответа.
Только первый работает в исходном уравнении,
так что ответ (б) x = 4.- Решите для x: 1/3 <2/3
Решение: Сначала умножьте на общий знаменатель 6.
2 <4
2 <4
-1 <1
-1/3 <1/3- Решить относительно x: | х + 2 | <6
Решение:
-6 <х + 2 <6
-8 <х <4- Решить относительно x: 2 (2x + 3) -10 <6 (x-2)
Решение:
4x + 6-10 <6x-12
-2x <-8
x> 4- Сьюзан заработала 120 долларов в течение 1 года на счете, который приносил 20% интерес. Сколько было первоначальных вложений Сьюзан?
Решение: Если x - начальные инвестиции, то.2x = 120, поэтому x = 600.
- Напишите неравенства x > 4 И x <6 в интервальной записи.
Решение: (г) [4, 6)- Решите для x: | 2x - 3 | > 5
Решение:
2x - 3 > 5 OR 2x - 3 <-5
2x > 8 OR 2x <-2
x > 4 OR x <-1- Решить относительно x: x 2 + x - 1 = 0
Решение: Воспользуйтесь квадратным уравнением, чтобы получить (a) x = (-1 + 5 1/2 ) / 2 или x = (-1-5 1/2 ) / 2.- Упрощать
х 2 -4 х 2 -2x-3 ------- . ------- х 2 + 3x + 2 х 2 -5x + 6
Решение: Факторизуйте каждый член.(х + 2) (х-2) (х-3) (х + 1) -------------------- = 1 (х + 2) (х + 1) (х-2) (х-3)
- Упростить (16x 2 y 2/3 ) 3/2
Выразите многочлен как произведение линейных множителей
Объяснение: Мы начинаем с попытки найти любые рациональные корни, используя теорему о рациональных корнях, которая гласит, что возможные рациональные корни являются положительными или отрицательными версиями возможных дробных комбинаций, образованных путем помещения множителя постоянного члена в числитель и коэффициент ведущего коэффициента в знаменателе.
Это было много слов в одном предложении, так что давайте разберемся с этим. Начнем с нашего многочлена.
Постоянный член - это термин без переменной (просто число). В нашем случае константа 60. Каковы возможные множители 60?
Старший коэффициент - это число перед наибольшей степенью переменной. Когда члены перечислены в порядке убывания (от наибольшей к наименьшей степени), ведущим коэффициентом всегда является первое число.В нашем случае опережающий коэффициент определить сложно. Поскольку перед цифрой нет числа, по умолчанию коэффициент равен 1.
Это хорошо, потому что единственный множитель 1 - это хорошо ... 1.
Затем мы создаем все возможные дроби с коэффициентом константы в числителе и коэффициентом старшего коэффициента в знаменателе. На самом деле это не так плохо, как могло бы быть, поскольку наш единственный возможный знаменатель - 1. Любая дробь со знаменателем 1 является просто числителем.Следовательно, наши возможные «дроби» просто
Однако мы должны учитывать их положительные или отрицательные версии, поэтому наш окончательный список возможных рациональных корней составляет
К сожалению, именно здесь процесс (по крайней мере, без помощи графического калькулятора) становится менее увлекательным. Используя синтетическое деление, мы должны просто пробовать каждый возможный корень, пока не добьемся успеха. На самом деле нет единого правила, которое указывало бы нам, с чего начать. Обычно лучше начинать с меньших целых чисел, потому что синтетическое деление проще.Таким образом, мы могли бы начать с, а затем перейти к и т. Д.
Используя синтетическое деление, мы должны просто пробовать каждый возможный корень, пока не добьемся успеха. На самом деле нет единого правила, которое указывало бы нам, с чего начать. Обычно лучше начинать с меньших целых чисел, потому что синтетическое деление проще.Таким образом, мы могли бы начать с, а затем перейти к и т. Д.
Чтобы сделать это объяснение как можно короче, я перейду сразу к 2, где мы сначала добьемся успеха.
Следовательно, 2 - это корень. Однако всегда важно проверить, является ли корень на самом деле двойным корнем (это работает дважды). Поэтому попробуем еще раз.
2 действительно работает дважды и, таким образом, является двойным корнем. Поскольку у нас осталось только три члена, мы можем преобразовать синтетическое выражение обратно в алгебраическое.
Затем мы можем разложить на множители.
Запись корня из 2 в виде алгебраического выражения дает. Поскольку у нас есть двойной корень, нам понадобятся два из них.




 Чтобы получить «а» нужно только
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
Чтобы получить «а» нужно только
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]  Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат. 


 Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение. 

 [Убедитесь, что вы получили те же результаты, что и ниже.]
[Убедитесь, что вы получили те же результаты, что и ниже.] 
 Теперь заменим z на
x 2 и решите полученные уравнения.
Теперь заменим z на
x 2 и решите полученные уравнения. 

 Затем переведите английское предложение в алгебраическое уравнение.
Затем переведите английское предложение в алгебраическое уравнение.  (Рисунок).
(Рисунок).




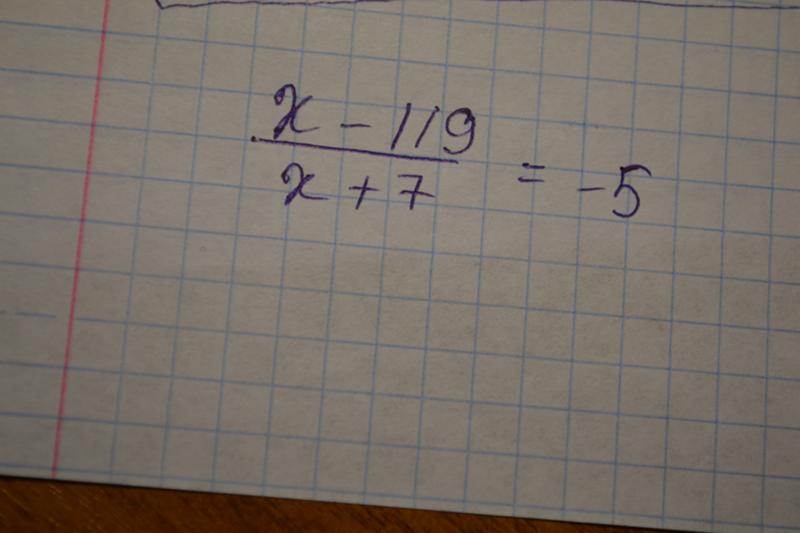 уравнения.
уравнения.  Ответ: (б) 9.
Ответ: (б) 9.
 В дробном показателе знаменатель соответствует извлечению корня,
поэтому сначала нам нужно извлечь кубический корень из 64 и кубический корень из 125.
Затем каждый из них возводится в квадрат, чтобы получить ответ (b) 16/25.
В дробном показателе знаменатель соответствует извлечению корня,
поэтому сначала нам нужно извлечь кубический корень из 64 и кубический корень из 125.
Затем каждый из них возводится в квадрат, чтобы получить ответ (b) 16/25.
 Подстановка y дает 5x = 60, поэтому x = 12, и ответ будет (a).
Подстановка y дает 5x = 60, поэтому x = 12, и ответ будет (a). В противном случае оба фактора должны быть положительными или оба фактора должны быть отрицательными.
Знаки факторов приведены в таблице ниже.
В противном случае оба фактора должны быть положительными или оба фактора должны быть отрицательными.
Знаки факторов приведены в таблице ниже.
 Получаем x 2 -5x + 4 = 0 или (x-4) (x-1) = 0.
Это дает два возможных решения x = 4 и x = 1.
Поскольку мы возводили обе части уравнения в квадрат,
возможно, мы ввели дополнительный корень, поэтому необходимо проверить оба ответа.
Только первый работает в исходном уравнении,
так что ответ (б) x = 4.
Получаем x 2 -5x + 4 = 0 или (x-4) (x-1) = 0.
Это дает два возможных решения x = 4 и x = 1.
Поскольку мы возводили обе части уравнения в квадрат,
возможно, мы ввели дополнительный корень, поэтому необходимо проверить оба ответа.
Только первый работает в исходном уравнении,
так что ответ (б) x = 4.
Leave A Comment