Как найти диагональ грани куба
Если шесть граней квадратной формы ограничивают некоторый объем пространства, то геометрическую форму этого пространства можно назвать кубической или гексаэдрической. Все двенадцать ребер такой пространственной фигуры имеют одинаковую длину, что значительно упрощает вычисления параметров многогранника. Длина диагонали куба — не исключение, ее можно найти многими способами.Инструкция
- Если длина ребра куба (a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них и диагонали грани, является прямоугольным. Ребра в этом случае — катеты, а рассчитать вам нужно длину гипотенузы. Согласно упомянутой выше теореме она равна квадратному корню из суммы квадратов длин катетов, а так как в данном случае они имеют одинаковые размеры, просто умножьте длину ребра на квадратный корень из двойки: l = √(a²+a²) = √(2*a²) = a*√2.
- Площадь квадрата тоже может быть выражена через длину диагонали, а так как каждая грань куба имеет именно такую форму, знания площади грани (s) достаточно для вычисления ее диагонали (l). Площадь каждой боковой поверхности куба равна возведенной в квадрат длине ребра, поэтому сторону квадрата грани можно выразить через нее как √s. Подставьте это значение в формулу из предыдущего шага: l = √s*√2 = √(2*s).
- Куб составлен из шести граней одинаковой формы, поэтому, если в условиях задачи дана общая площадь поверхности (S), для вычисления диагонали грани (l) достаточно немного изменить формулу предыдущего шага. Замените в ней площадь одной грани одной шестой общей площади: l = √(2*S/6) = √(S/3).
- Длину ребра куба можно выразить и через объем этой фигуры (V), а это позволяет формулу расчета длины диагонали грани (l) из первого шага использовать и в этом случае, внеся в нее некоторые поправки. Объем такого многогранника равен третей степени длины ребра, поэтому замените в формуле длину стороны грани кубическим корнем из объема: l = ³√V*√2.
- Радиус описанной около куба сферы (R) связан с длиной ребра коэффициентом, равным половине корня из тройки. Выразите сторону грани через этот радиус и подставьте выражение во все ту же формулу вычисления длины диагонали грани из первого шага: l = R*2/√3*√2 = R*√8/√3.
- Формула расчета диагонали грани (l) с использованием радиуса вписанной в куб сферы (r) будет еще проще, так как этот радиус составляет половину длины ребра: l = 2*r*√2 = r*√8.
completerepair.ru
Как найти диагональ куба если известна диагональ грани куба
Найти количество трехзначных чисел, сумма цифр которых равна А, а само число заканчивается цифрой В (А и В вводятся с клавиатуры) Pascal (Паскаль)
Что такое диагональ куба, и как ее найти
Что такое куб, и какие диагонали он имеет
Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Если известна площадь поверхности
Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см 2 . Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см 2 . Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a 2 , значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см 2 .
Если известна длина ребер куба
Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!
Как найти диагональ куба если известна диагональ грани куба
Что такое диагональ куба, и как ее найти
Что такое куб, и какие диагонали он имеет
Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см 2 . Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см 2 . Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a 2 , значит a=√S. Подставляем и получаем a=√12 (ребро куб
poiskvstavropole.ru
ДЛИНА ДИАГОНАЛИ КУБА — Как вычислить объем куба
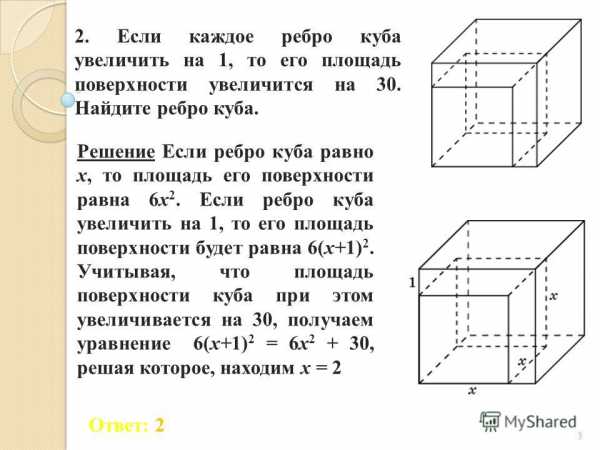 Отсюда боковое ребро равно диагонали основания, умноженной на тангенс угла между диагональю параллелепипеда и основанием. Диагональ прямоугольного параллелепипеда равна L и составляет с основанием параллелепипеда угол в 30 градусов, а с одной из боковой граней угол в 45 градусов. Длину диагонали определяем по теореме Пифагора и она равна квадратному корню из суммы квадратов сторон. Длину ребра куба можно выразить и через объем этой фигуры (V), а это позволяет формулу расчета длины диагонали грани (l) из первого шага использовать и в этом случае, внеся в нее некоторые поправки.
Отсюда боковое ребро равно диагонали основания, умноженной на тангенс угла между диагональю параллелепипеда и основанием. Диагональ прямоугольного параллелепипеда равна L и составляет с основанием параллелепипеда угол в 30 градусов, а с одной из боковой граней угол в 45 градусов. Длину диагонали определяем по теореме Пифагора и она равна квадратному корню из суммы квадратов сторон. Длину ребра куба можно выразить и через объем этой фигуры (V), а это позволяет формулу расчета длины диагонали грани (l) из первого шага использовать и в этом случае, внеся в нее некоторые поправки.
В куб можно вписать тетраэдр двумя способами. У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих кубических единицах.
Длина диагонали куба — не исключение, ее можно найти многими способами. Если длина ребра куба (a) известна из условий задачи, формулу расчета длины диагонали грани (l) можно вывести из теоремы Пифагора. В кубе любые два смежных ребра образуют прямой угол, поэтому треугольник, составленный из них и диагонали грани, является прямоугольным.

Объем такого многогранника равен третей степени длины ребра, поэтому замените в формуле длину стороны грани кубическим корнем из объема: l = ³√V*√2. Радиус описанной около куба сферы (R) связан с длиной ребра коэффициентом, равным половине корня из тройки. Прямоугольные четырехугольники (прямоугольник, квадрат) диагональ делит на два прямоугольных треугольника, в каждом из которых она будет гипотенузой.
Вычисление объема по диагонали
Если перед вами квадрат, то вычислить диагональ можно, зная одну из его сторон или площадь. Значит, квадрат гипотенузы (в фигуре квадрат) равен его удвоенной площади (a²=2S).Пример 2: площадь квадрата 16 см². Найдите длинудиагонали. В некоторых случаях для вычисления диагонали необходимо делать дополнительные построения.Пример 3: равносторонний многоугольник со стороной, равной 6 см, угол BCD прямой.

Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.В различных дисциплинах используются значения термина, имеющие отношения к тем или иным свойствам геометрического прототипа.
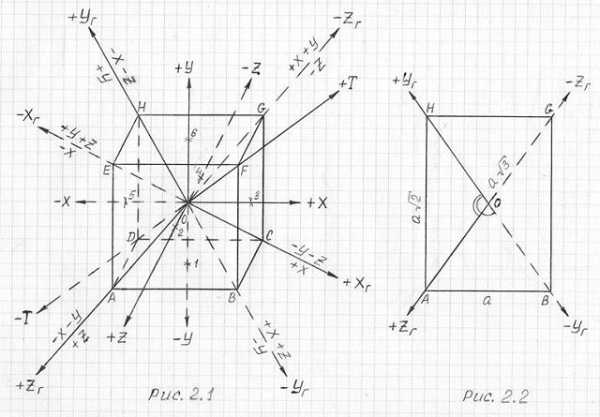
Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его диагоналям. Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми гранях октаэдра.
Рёбра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. И так, прямоугольный параллелепипед на картинке дает нам возможность увидеть вершины, ребра и диагонали. Вершины мы можем потрогать пальцем, ребра мы можем измерять, диагональ можем высчитать.
Возведение в куб ребра куба
Следующая фраза «… равны 1, 2, 3″ обозначает, что нам не нужно искать этот злополучный прямоугольный параллелепипед и свою линейку, чтобы измерить длины его граней, как это показано на рисунке. Кто есть кто в этом списке чисел? Где длина, ширина, высота нашего параллелепипеда? Теперь вопрос, в чём же конкретно измеряется наш прямоугольный параллелепипед и площадь его поверхности? Вот одна из этих формул нам как раз нужна. Разберемся в площадях на примере коробки для обуви. Площадь основания — это площадь донышка или крышки коробки.
Если уточнений типа «боковой» или «основания» нет, значит искать нужно полную площадь поверхности прямоугольного параллелепипеда. Длины трех граней у нас есть, формула тоже, можно произвести расчет. Как видим, полная площадь поверхности нашего прямоугольного параллелепипеда получилась равной 22 единицы в квадрате.
Вычисление объема по площади поверхности
Площадь поверхности этого создания равна, как и у всех призм, двум площадям оснований плюс площадь боковых граней (их четыре). В основании ромб. Его площадь равна половине произведения диагоналей. Делим диагонали пополам, возводим половинки в квадрат, складываем в кучку и выковыриваем из этого квадратный корень.
Площадь боковой поверхности равна периметру, умноженному на высоту прямоугольного параллелепипеда. В прямоугольном параллелепипеде стороны основания относятся как 2:3, а диагональное сечение есть квадрат с площадью 169. Найдите объем параллелепипеда.Ответ 1014. Интересно было бы решение. Методом научного тыка удалось выяснить, что диагональное сечение образовано диагональю основания и высотой. В прямом парпалелепипеде рёбра, выходящие из одной вершины, равны 1м 2м и 3м, причём два меньших образуют угол 60 градусов.Опредилить диагонали этого паралелепипеда.
Уравнения — это теоремы Пифагора для диагоналей. Получилось, что площадь поверхности стекла в таком аквариуме равна 4500 квадратных сантиметра. Чтобы найти стороны этого чудовища, нужно решить маленькую систему из трех уравнений с тремя неизвестными.
Четыре способа решения задач на нахождение расстояния между скрещивающимися прямыми
Нужно найти объем параллелепипеда. Третье можно найти по теореме Пифагора — квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех измерений (ребер). Размер диагонали известен по условию. Выражаем измерения «a», «b» и «c» через диагональ прямоугольного параллелепипеда. По правой картинке находим диагональ основания по теореме Пифагора.
Презентация к уроку
В этом случае площадь боковой грани равна 45/3=15, а её высота 2*15/3=10 Боковая грань представляет собой равнобедренный треугольник. 1) По теореме Пифагора треугольник в основании прямоугольный. Параллелепипед является разновидностью призмы, а у призмы объем равен произведению площади основания на высоту. Ребро со стороной основания образуют угол в 45 градусов, следовательно высота, сторона основания и ребро образуют равнобедренный треугольник.
Косинус угла определяется как отношение диагонали грани к диагонали куба (вместе с ребром они образуют прямоугольный треугольник). По теореме Пифагора можем найти сторону ромба 5 см, периметр составляет четыре стороны, т. е. 20 см. Площадь боковой поверхности 80 см в квадрате. Советую прочесть первую задачу с решением от 11 февраля 2013 года, они очень похожи и расположены выше в комментариях. Идем на эту страницу с диагоналями прямоугольного параллелепипеда и смотрим вторую картинку, зеленый треугольник справа — это наш случай.
Следовательно, синус — это отношение вертикального катета (высота параллелепипеда) к гипотенузе (диагональ параллелепипеда). Записуем циферки и получаем, что синус угла между диагональю параллелепипеда и плоскостью его основания равен корню из двух на два (если я не ошибся в вычислениях). При скольжении вдоль граней меньшая диагональ проходит через центр шестиугольника. Не трудно заметить, что одна меньшая диагональ равна двум радиусам вписанной окружности.
Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень. В нашей задаче мы измеряем всё в абстрактных единицах измерения длины. Соответственно, полученная нами площадь будет измеряться в этих же единицах измерения, возведенных в квадрат.
Предлагаю также ознакомиться:
kakbypridaser.ru
Что такое диагональ куба, и как ее найти
Образование 13 сентября 2013Что такое куб, и какие диагонали он имеет
Куб (правильный многогранник или гексаэдр) представляет собой объемную фигуру, каждая грань – это квадрат, у которого, как нам известно, все стороны равны. Диагональю куба является отрезок, который проходит через центр фигуры и соединяет симметричные вершины. В правильном гексаэдре имеется 4 диагонали, и все они будут равны. Очень важно не путать диагональ самой фигуры с диагональю ее грани или квадрата, который лежит на его основании. Диагональ грани куба проходит через центр грани и соединяет противоположные вершины квадрата.
Формула, по которой можно найти диагональ куба
Диагональ правильного многогранника можно найти по очень простой формуле, которую необходимо запомнить. D=a√3, где D обозначаем диагональ куба, а – это ребро. Приведем пример задачи, где необходимо найти диагональ, если известно, что длина его ребра равна 2 см. Здесь все просто D = 2√3, даже считать ничего не надо. Во втором примере, пусть ребро куба будет равно √3 см, то тогда получаем D = √3√3=√9=3. Ответ: D равен 3 см.
Формула, по которой можно найти диагональ грани куба
Диагональ грани можно также найти по формуле. Диагоналей, которые лежат на гранях, всего 12 штук, и они все равны между собой. Теперь запоминаем d=a√2, где d – это диагональ квадрата, а – это также ребро куба или сторона квадрата. Понять откуда взялась эта формула, очень просто. Ведь две стороны квадрата и диагональ образуют прямоугольный треугольник. В этом трио диагональ играет роль гипотенузы, а стороны квадрата — это катеты, которые имеют одинаковую длину. Вспомним теорему Пифагора, и все тут же встанет на свои места. Теперь задача: ребро гексаэдра равняется √8 см, необходимо найти диагональ его грани. Вставляем в формулу, и у нас получается d=√8 √2=√16=4. Ответ: диагональ грани куба равняется 4 см.
Если известна диагональ грани куба
По условию задачи, нам дана только диагональ грани правильного многогранника, которая равна, предположим, √2 см, а нам необходимо найти диагональ куба. Формула решения этой задачи немного сложнее предыдущей. Если нам известно d, то мы можем найти ребро куба, исходя из нашей второй формулы d=a√2. Получаем а= d/√2= √2/√2=1см (это наше ребро). А если известна эта величина, то найти диагональ куба не составит труда: D = 1√3= √3. Вот так мы решили нашу задачку.
Если известна площадь поверхности
Следующий алгоритм решения строится на нахождении диагонали по площади поверхности куба. Предположим, что она равна 72 см2. Для начала найдем площадь одной грани, а всего их 6. Значит, 72 необходимо поделить на 6, получаем 12 см2. Это площадь одной грани. Чтобы найти ребро правильного многогранника, необходимо вспомнить формулу S=a2, значит a=√S. Подставляем и получаем a=√12 (ребро куба). А если мы знаем это значение, то и диагональ найти не сложно D= a√3= √12 √3 = √36 = 6. Ответ: диагональ куба равна 6 см2.
Если известна длина ребер куба
Бывают такие случаи, когда в задаче дана только длина всех ребер куба. Тогда необходимо это значение разделить на 12. Именно столько сторон в правильном многограннике. Например, если сумма всех ребер равна 40, то одна сторона будет равна 40/12=3,333. Вставляем в нашу первую формулу и получаем ответ!
Источник: fb.rumonateka.com
Как найти ребро куба если известна его диагональ?
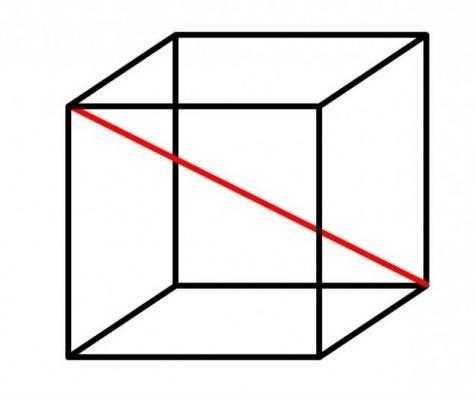
если сторона куба равна х, диаглналь стороны куба равна корень из 2х квадрат. теперь вычислить диагональ куба — гипотенуза прямоугольного треугольника со сторонами х и уже вычисленной стороной
через треугольники
у куба все стороны равны? или нет? я уже не помню)) если равны, то диагональ :2
ребро равно квадратный корень из квадрата диагонали деленного на 2
По теореме пифагора находите катеты, которые и являются ребрами.
touch.otvet.mail.ru


Leave A Comment