Банк ЕГЭ | Открытый банк заданий
Банк ЕГЭ Банк решенных | ЕГЭ по математике В1 ● В2 ● В3 ● В4 ● В5 ● В6 ● В7 |
Полезные советы | Лента задачек | |
| С4Дан параллелограмм $ABCD$, сторона которого $AB=13$. Из углов $А$ и $В$ проведены биссектрисы, которые пересекаются в точке $O$. Расстояние от точки $O$ до отрезка АВ равно $\frac{60}{13}$. В7Найдите, если $\operatorname{tg}\alpha=-4$ [посмотреть решение] |
Найдите тангенс угла между плоскостью основания и боковым ребром. Дополнительные задачи 312, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс
Найдите тангенс угла между плоскостью основания и боковым ребром. Дополнительные задачи 312, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/классШкола
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?В правильной n-угольной пирамиде боковые грани составляют с плоскостью основания угол φ.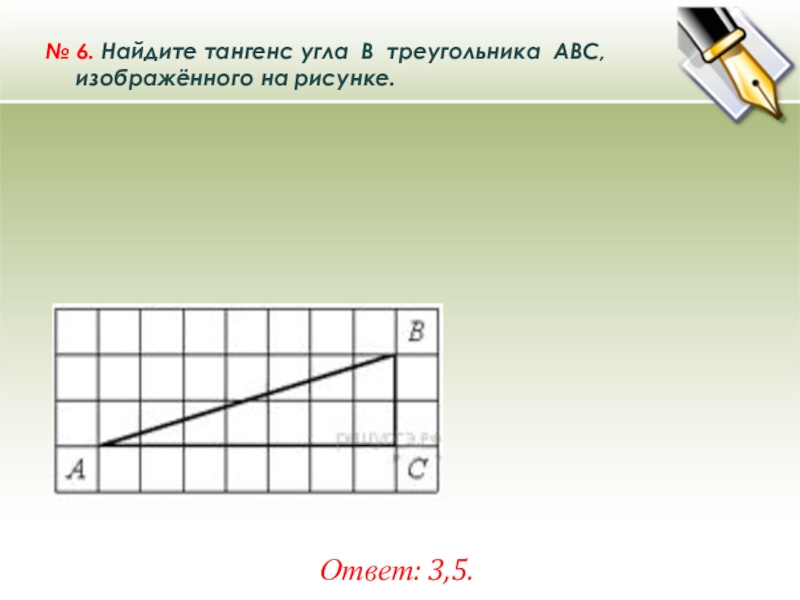 Найдите тангенс угла между плоскостью основания и боковым ребром.
Найдите тангенс угла между плоскостью основания и боковым ребром.
Кто-нибудь из присутствующих имеет решение к ней?
Лучший ответ
Да, у меня решено
Т.к. в основании пирамиды лежит правильный n-угольник, и вокруг пра вильного n-угольника можно описать окружность, то OA=OB=OC=…=R.
Пусть сторона правильного n-угольника равна а, значит,
Проведем ОК┴АВ и отрезок SK. SK┴AB по теореме о 3-х перпен дикулярах, ∟SKO — линейный угол двугранного угла между боковой гранью и плоскостью основания,
Из прямоугольного ΔSOK
Пусть искомый угол SBO равен х (другие углы будут равны ему)
еще ответы
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЮморОлимпиадыЕГЭКомпьютерные игрыпохожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный переносИспользуя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
Почему сейчас школьники такие агрессивные ?Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
Какой был проходной балл в вузы в 2017 году?Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)
Поступление11 классЕГЭНовости
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Тангенс (угла)
Горячая математикакасательная угла – это тригонометрическое соотношение между прилежащей стороной и противолежащей стороной прямоугольного треугольника, содержащего этот угол.
касательная «=» длина из в нога противоположный к в угол длина из в нога соседний к в угол сокращенно «загар»
Пример:
В показанном треугольнике
загар
(
А
)
«=»
6
8
или
3
4
и
загар
(
Б
)
«=»
8
6
или
4
3
.
Отношение тангенсов одинаково независимо от размера прямоугольного треугольника. Итак, часто проще всего рассмотреть прямоугольный треугольник с гипотенузой длины 1 .
Отношение тангенса также можно рассматривать как функцию, которая принимает разные значения в зависимости от меры угла. Вы можете измерить угол в градусах или радианы .
Обратная величина отношения тангенса известна как отношение котангенса угла, сокращенно «кроватка».
То есть,
котангенс «=» длина из в нога соседний к в угол длина из в нога противоположный к в угол
В приведенном выше примере
детская кроватка
(
А
)
«=»
7
4
и
детская кроватка
(
Б
)
«=»
4
7
.
Смотрите также: синус и косинус .
Калькулятор угла касательной
Создано Джоанной Сметаньской, докторантом
Отредактировано Стивеном Вудингом
Последнее обновление: 10 марта 2023 г.
Содержание:- Как найти угол касательной?
- Свойства функции тангенса
- Пример расчета тангенса угла
- Другие полезные тригонометрические калькуляторы
- Часто задаваемые вопросы
Этот быстрый калькулятор угла тангенса поможет вам, когда вы задаетесь вопросом 9000 3 как найти угол касательной . Неважно, указан ли угол в вашей домашней работе в градусах, радианах или пи-радианах. Читайте ниже, чтобы узнать больше полезной информации о тангенс угла .
Как найти угол касательной?
В тригонометрии или геометрии тангенс угла (обозначается просто как тангенс ) — это длина стороны , противоположной углу, деленная на прилежащую сторону . Обратите внимание, что это относится только к прямоугольному треугольнику . Звучит сложно? Не волнуйся. Давайте посмотрим на изображение, чтобы объяснить:
Обратите внимание, что это относится только к прямоугольному треугольнику . Звучит сложно? Не волнуйся. Давайте посмотрим на изображение, чтобы объяснить:
Если α\alphaα угол между сторонами bbb и ccc треугольника, то тангенс угла tan(θ)\tan(\theta)tan(θ) равен отношение между противоположной стороной aaa и соседней стороной bbb.
tan(θ)=ab\small{\tan(\theta) = \frac{a}{b}}tan(θ)=ba
Другое определение гласит, что тангенс представляет собой отношение функции синуса и функция косинуса , поэтому тангенс является отношением sin/cos .
Свойства функции тангенса
Функция тангенса является одной из основных тригонометрических функций. График функции тангенса имеет ту особенность, что он не имеет определенного значения при x = -π/2, π/2, -3π/2, 3π/2, 5π/2 и т. д. (или -90°, 90°, -270°, 270°, 450° и т.д. ).
В отличие от синуса или косинуса, функция тангенса имеет период π\piπ, поэтому ее значения повторяются через каждые π радиан .
💡 Проверьте сами! Попробуйте ввести угол π/2 (или 90° в градусах) в этот калькулятор угла тангенса и посмотрите, какое значение он вам даст.
Пример вычисления тангенса угла
Если вы хотите найти тангенс заданного угла , введите градус в наш калькулятор угла касательной или выполните следующие действия:
Определите гипотенузу в вашем треугольнике. Обычно это самая длинная сторона треугольника.
Измерьте две стороны , между которыми есть угол, и обозначьте их как aaa (противоположная) и bbb (прилежащая), например, a=21a = 21a=21 и b=8b = 8b=8.
Разделите aaa на bbb – a/b=21/8a/b = 21/8a/b=21/8 =2,63 = 2,63=2,63. Вы получите тангенс угла .
Другие полезные тригонометрические калькуляторы
Когда вы научитесь пользоваться калькулятором тангенса угла , ознакомьтесь с другими нашими тригонометрическими инструментами:
- Тригонометрический калькулятор;
- Калькулятор косинуса треугольника;
- Калькулятор триггерного треугольника;
- Калькулятор синус-косинус-тангенса; и
- Калькулятор отношения тангенса.


 wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье.
wolframalpha.com/. На этом сайте вы можете: решать не слишком сложные уравнения и системы уравнений (неравенств), брать производные от функций, стоить графики этих функций и так далее. Во время подготовки к ЕГЭ, этот сайт можно использовать для: проверки отсутствия арифметических ошибок, вычисления громоздких выражений, решения промежуточных систем уравнений, и еще для огромного количества других полезных вещей. Более подробную информацию о том, как пользоваться сайтом wolframalpha.com, можно получить в соответствующей статье. Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.
Мы рекомендуем просматривать этот форум именно через браузер Firefox, потому что отображение в нем MathML-формул самое лучшее.

Leave A Comment