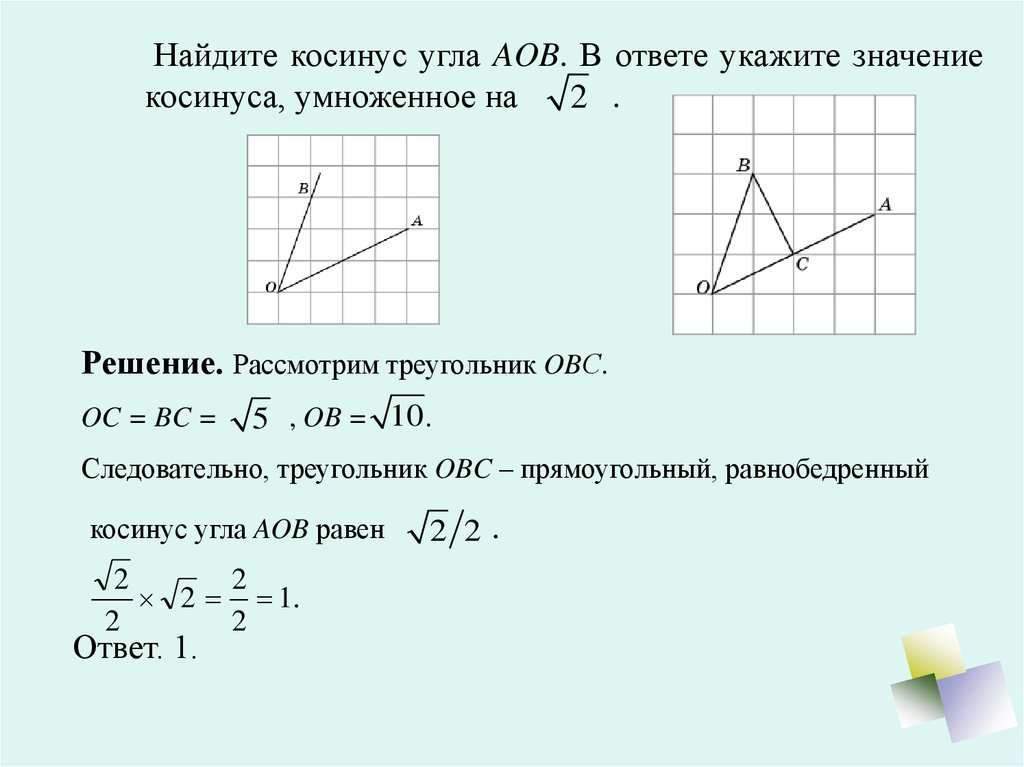
СРОЧНО, ДАЮ 100 БАЛЛОВ14.Найдите синус угла AOB, изображенного на рисунке.16.Найдите косинус угла MPK, изображенного на рисунке.№9 В прямоугольном треугольнике ABC гипотенуза BC=6,катет AB=3. Найдите угол АВС. Ответ дайте в градусах.17. Найдите тангенс угла MOD, изображенного на рисунке.
Ответы
Знаешь ответ? Добавь его сюда!
Последние вопросы
Математика
3 часа назад
ужас мне так лень сюда заходить
Химия
4 часа назад
Визначте масу калій гідроксиду ,що реагує з 5,6 л сульфур(IV) оксиду (н.у.).
Алгебра
9 часов назад
Найди первые пять членов геометрической прогрессии bn
= 256•(1/2).
 n
nХимия
12 часов назад
2. Визначте масу калій гідроксиду ,що реагує з 5,6 л сульфур(IV) оксиду (н.у.).
3. Яка кількіст речовини солі утворюється при взаємодії ферум(ІІІ) оксиду з сульфатною кислотою масою 2,94 г.
Другие предметы
1 день назад
Пользуясь определителем дикорастущих растений и опираясь на знания по курсу ботаники, определите, к какому виду, роду, семейству и классу относятся полезные растения, произрастающие в ближайшем лесу, поле или парке.
( Помогите срочно! )
2 дня назад
24.
Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг? 02.2022?
02.2022?Математика
2 дня назад
32) найдите область определение функции z = (1/x) + (1/y)2 дня назад
33) найдите область определение функции z = (y — 1) / (x² + y²)Математика
2 дня назад
31) найдите область определение функции z = 1 / (x-y)Геометрия
2 дня назад
100 баллов таму кто поможет2 дня назад
Subjunctive Mood
Test
I.
 Choose the right form:
Choose the right form:1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (

II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.

Английский язык
2 дня назад
Subjunctive Mood
Test
I. Choose the right form:
1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.

- Если бы не твоя помощь, я бы не смог закрепить
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Литература
2 дня назад
А где почему это напряжоный момент
Биология
3 дня назад
У голонасінних рослин уперше з’являєтся:
Математика
3 дня назад
Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140
Курс по подготовке к ОГЭ первая часть
Home » Курс по подготовке к ОГЭ первая часть
Задания по ОГЭ
6 задание (1 неделя):
- Сложение и вычитание обыкновенных дробей;
- Умножение и деление обыкновенных дробей;
- Доп.

- Домашняя работа.
6-8 задание (2 неделя):
- Сложение, вычитание, умножение и деление десятичных дробей;
- Степень с натуральным показателем. Свойства степени с натуральным показателем. Часть 1;
- Степень с натуральным показателем. Свойства степени с натуральным показателем. Часть 2;
- Доп.урок по ОГЭ практика. Сложение, вычитание, умножение и деление десятичных дробей;
- Контрольная работа;
- Домашняя работа.
8 задание (3 неделя):
- Степень с отрицательным показателем;
- Занесение общего множителя в скобки;
- Арифметический квадратный корень. Запись с вебинара;
- Домашняя работа.Степень с отрицательным показателем;
- Домашняя работа.Занесение общего множителя в скобки;
8 задание (4 неделя):
- Вынесение общего множителя за скобки;
- Формула сокращенного умножения.
 Часть 1;
Часть 1; - Дополнительный урок практика по ОГЭ;
8 задание (5 неделя):
- Видео отзыв;
- Формулы сокращенного умножения. Часть 2;
- Формула сокращенного умножения. Часть 3;
- Формула сокращенного умножения. Часть 4;
- Урок практика по ОГЭ;
9 задание (6 неделя):
- Линейные уравнения;
- Система линейных уравнений;
- Полные и неполные квадратные уравнения;
- Дополнительный урок полные и неполные квадратные уравнения;
9 и 13 задание (7 неделя):
- Линейные неравенства;
- Система линейных неравенств;
- Квадратные неравенства. Часть1;
- Квадратные неравенства. Часть2;
- Рациональные уравнения;
- Рациональные неравенства;
7 и 11 задание (8 неделя):
- Неравенства. Сравнение чисел. Числа на прямой.
 Выбор верного или неверного утверждения;
Выбор верного или неверного утверждения; - Линейная функция y=ax+b. Прямая;
- Квадратичная функция. Парабола;
11 и 14 задание (9 неделя):
- Гипербола;
- Другие функции;
- Арифметическая прогрессия;
- Геометрическая прогрессия;
- Задача №1: Рабочие прокладывают тоннель длиной 400 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля. Определите, сколько метров тоннеля проложили рабочие в последний день, если вся работа была выполнена за 10 дней.
- Задача №2: Игрок в компьютерной игре начинает с 0 очков и для перехода на следующий уровень ему нужно набрать не менее 8000 очков. После первой минуты игры игроку добавляется 2 очка, после второй минуты — 4 очка, после третьей — 8 очков и так далее. Через сколько минут игрок перейден на следующий уровень?
10, 11 и 12 задание (10 неделя):
- Вероятность;
- Комбинаторика;
- Статистика;
- 12 задание.
 Формулы;
Формулы; - Уравнение окружности;
- Задача. Из 900 новых флеш-карт в среднем 50 не пригодны для записи. Какова вероятность того, что случайно выбранная флеш-карта пригодна для записи?
15 и 16 задание (11 неделя):
- Виды треугольников. Биссектриса, высота, медиана. Периметр;
- Равнобедренный треугольник;
- Три признака равенства треугольников;
- Параллельные прямые. Признаки параллельности двух прямых;
- Углы в треугольнике;
- Прямоугольный треугольник;
- Геометрическое место точек;
- Окружность и круг;
- Окружность, диаметр и хорда;
- Описанная окружность;
- Вписанная окружность;
- Центральные и вписанные углы;
- Касательная к окружности;
- Свойство пересекающихся хорд;
- Теорема секущей и касательной;
- Окружность практика;
- Окружность практика;
- На окружности отмечены точки A и B так, что меньшая дуга AB равна 50°.
 Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
- Четырёхугольник ABCD описан около окружности,AB=5 ,BC =12 ,CD =16 . Найдите AD
15 и 17 задание (12 неделя):
- Четырехугольники;
- Выпуклые четырехугольники;
- Параллелограмм;
- Прямоугольник;
- Ромб;
- Квадрат;
- Длина окружности. Площадь круга. Площадь кругового сектора. Сегмент;
- Тригонометрия в прямоугольном треугольнике;
- Теорема Пифагора;
- Подобие треугольников;
- Свойства подобных треугольников;
- Теорема синусов;
- Теорема косинусов;
- Площадь квадрата;
- Площадь параллелограмма;
- Площадь прямоугольника;
- Площадь ромба;
- Площадь треугольника;
- Площадь четырехугольника;
- Практика треугольники;
- Практика четырехугольники;
- В треугольнике ABC известно, что BAC = 82° , AD – биссектриса.
 Найдите угол BAD. Ответ дайте в градусах.
Найдите угол BAD. Ответ дайте в градусах.
- Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O,AN = 6 ,CM= 9 . Найдите СO.
15 и 17 задание (13 неделя)
- Практика геометрия. Часть 1;
- Практика геометрия. Часть 2;
- Практика. Площади фигур;
- Домашнее задание. Высота равностороннего треугольника равна 6. Найдите его площадь, делѐнную на √3.
- В треугольнике ABC проведены медиана BM и высота BH. Известно,
что AC = 40 и BC = BM. Найдите AH
17, 18 и 19 задание (14 неделя)
- Площади фигур. Геометрия;
- Фигуры на квадратной решётке. Площади. Нахождение углов. Тригонометрия. Часть 1;
- Фигуры на квадратной решётке. Площади. Нахождение углов. Тригонометрия. Часть 2;
 Их необходимо прочитать несколько раз и постараться запомнить.
Их необходимо прочитать несколько раз и постараться запомнить.Анализ геометрических высказываний
Часть 1.
Задание. Укажите (обведите) номера верных утверждений.
I) Начальные геометрические сведения (отрезки, прямые и углы)
1. Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
2. Существуют три прямые, которые проходят через одну точку.
3. Смежные углы всегда равны.
4. Вертикальные углы равны.
5. Всегда один из двух смежных углов острый, а другой тупой.
6. Через заданную точку плоскости можно провести только одну прямую.
7. Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
8. Если угол острый, то смежный с ним угол также является острым.
II) Параллельные и перпендикулярные прямые
9. Две прямые, параллельные третьей прямой, перпендикулярны.
10. Две прямые, перпендикулярные третьей прямой, перпендикулярны.
11. Две различные прямые, перпендикулярные третьей прямой, параллельны.
12. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
13. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
III) Треугольник
14. Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
15. В любом тупоугольном треугольнике есть острый угол.
16. В тупоугольном треугольнике все углы тупые.
17. В остроугольном треугольнике все углы острые.
18. В треугольнике против большего угла лежит большая сторона.
19. Внешний угол треугольника больше не смежного с ним внутреннего угла.
20. Внешний угол треугольника равен сумме его внутренних углов.
21. Один из углов треугольника всегда не превышает 60 градусов.
22. Медиана треугольника делит пополам угол, из вершины которого проведена.
23. Отношение площадей подобных треугольников равно коэффициенту подобия.
24. Площадь треугольника меньше произведения двух его сторон.
25. Сумма углов любого треугольника равна 360 градусам.
26. Треугольник со сторонами 1, 2, 4 существует.
27. Треугольника со сторонами 1, 2, 5 не существует.
28. Биссектриса треугольника делит пополам сторону, к которой проведена.
29. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
30. Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
31. Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
32. Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.
33. Биссектрисы треугольника пересекаются в точке, которая является центром окружности, вписанной в треугольник.
34. Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
35. Все равнобедренные треугольники подобны.
36. Всякий равнобедренный треугольник является остроугольным.
37. Каждая из биссектрис равнобедренного треугольника является его высотой.
38. Каждая из биссектрис равнобедренного треугольника является его медианой.
39. Сумма углов равнобедренного треугольника равна 180 градусам.
40. Все высоты равностороннего треугольника равны.
41. Всякий равносторонний треугольник является равнобедренным.
42. Всякий равносторонний треугольник является остроугольным.
43. Любые два равносторонних треугольника подобны.
44. Все равносторонние треугольники подобны.
45. В прямоугольном треугольнике гипотенуза равна сумме катетов.
46. Все прямоугольные треугольники подобны.
47. В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов.
48. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
49. Площадь прямоугольного треугольника равна произведению длин его катетов.
50. Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету.
51. Сумма углов прямоугольного треугольника равна 90 градусам.
52. Тангенс любого острого угла меньше единицы.
53. Сумма острых углов прямоугольного треугольника равна 90 градусам.
IV) Четырехугольник
54. В любой четырёхугольник можно вписать окружность.
55. Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
56. Сумма углов выпуклого четырёхугольника равна 360 градусам.
V) Параллелограмм
57. Диагонали параллелограмма равны.
58. В параллелограмме есть два равных угла.
59. Площадь любого параллелограмма равна произведению длин его сторон.
60. Площадь параллелограмма равна половине произведения его диагоналей.
61. Диагональ параллелограмма делит его на два равных треугольника.
VI) Квадрат, прямоугольник
62. В любой прямоугольник можно вписать окружность.
63. Диагонали любого прямоугольника делят его на четыре равных треугольника.
64. Диагонали прямоугольника точкой пересечения делятся пополам.
65. Существует прямоугольник, диагонали которого взаимно перпендикулярны.
66. Если диагонали параллелограмма равны, то это прямоугольник.
67. Любой прямоугольник можно вписать в окружность.
68. Все углы прямоугольника равны.
69. В любом прямоугольнике диагонали взаимно перпендикулярны.
70. Площадь прямоугольника равна произведению длин всех его сторон.
71. Площадь прямоугольника равна произведению длин его смежных сторон.
72. Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.
73. Если диагонали параллелограмма равны, то этот параллелограмм является квадратом.
74. Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то этот четырёхугольник является квадратом.
75. Любой квадрат является прямоугольником.
76. Площадь квадрата равна произведению двух его смежных сторон.
77. Площадь квадрата равна произведению его диагоналей.
78. Существует квадрат, который не является прямоугольником.
79. Все квадраты имеют равные площади.
VII) Трапеция
80. Основания любой трапеции параллельны.
81. Основания равнобедренной трапеции равны.
82. Площадь трапеции равна произведению основания трапеции на высоту.
83. Средняя линия трапеции параллельна её основаниям.
84. Средняя линия трапеции равна сумме её оснований.
85. Средняя линия трапеции равна полусумме её оснований.
86. Боковые стороны любой трапеции равны.
87. В любой прямоугольной трапеции есть два равных угла.
88. Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
89. Диагонали прямоугольной трапеции равны.
90. Диагонали равнобедренной трапеции равны.
91. Диагональ равнобедренной трапеции делит её на два равных треугольника.
92. Диагональ трапеции делит её на два равных треугольника.
VIII) Ромб
93. В любой ромб можно вписать окружность.
94. Все углы ромба равны.
95. Диагонали ромба перпендикулярны.
96. Диагонали ромба равны.
97. Диагонали ромба точкой пересечения делятся пополам.
Диагонали ромба точкой пересечения делятся пополам.
98. Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
99. Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
100. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.
101. Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
102. Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
103. Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом
IX) Окружность
104. Вписанный угол, опирающийся на диаметр окружности, прямой.
105. Все диаметры окружности равны между собой.
106. Все хорды одной окружности равны между собой.
107. Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
108. Касательная к окружности параллельна радиусу, проведённому в точку касания.
109. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
110. Любой параллелограмм можно вписать в окружность.
111. Любые два диаметра окружности пересекаются.
112. Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
113. Точка пересечения двух окружностей равноудалена от центров этих окружностей.
114. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
115. Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
116. Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
117. Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
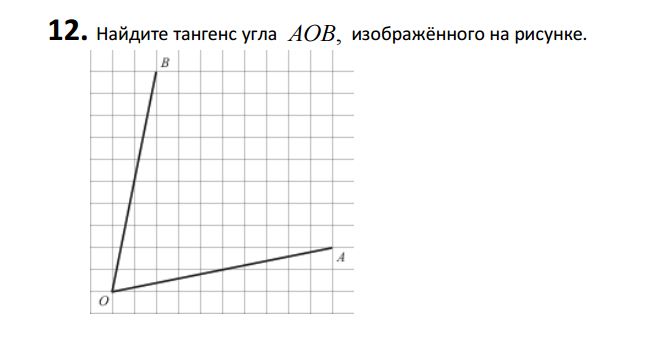
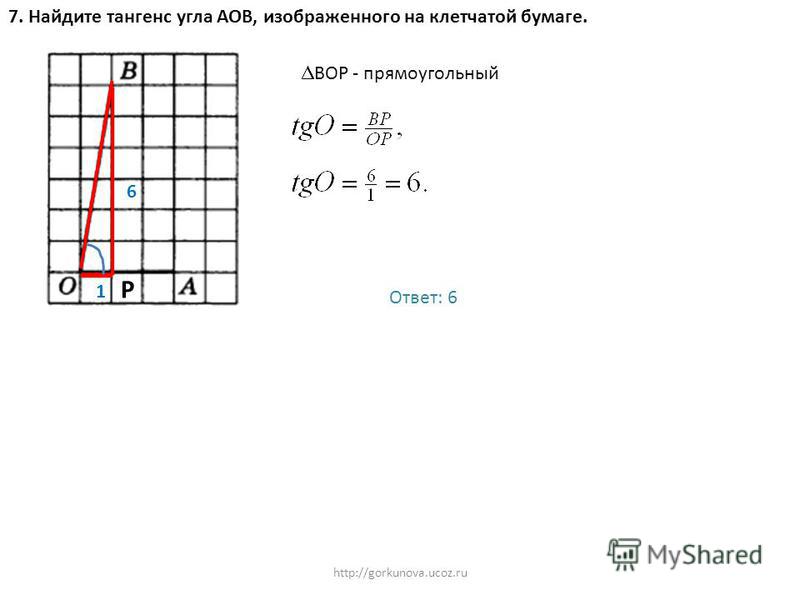
- Домашняя работа. Найдите тангенс угла AOB, изображенного на рисунке:
- Найдите угол ABC:
1-5 задания (15 неделя):
- Квартира;
- План местности;
- Теплица;
- Террасы;
- Шины;
- Домашняя работа на 2 недели.
 Решить вариант с 1-19 задание
Решить вариант с 1-19 задание
1-5 задания (16 неделя):
- Печи;
- Тарифы;
- Листы бумаги;
- ОСАГО;
- Зонт;
Видео-вопрос: Нахождение значения тригонометрической функции по координатам точки пересечения единичной окружности с конечной стороной угла в стандартном положении
Конечная сторона угла 𝐴𝑂𝐵 в стандартном положении пересекается с единичной окружностью в точке 𝐵 с координатами (−𝑥, −𝑥), где 𝑥 — положительное число. Найди грех 𝜃.
Стенограмма видео
Конечная сторона угла 𝐴𝑂𝐵 в стандартном положении пересекается с единичной окружностью в точке 𝐵 с координаты отрицательные 𝑥, отрицательные 𝑥, где 𝑥 — положительное число. Найдите грех 𝜃.
Сначала нарисуем единичный круг.
чтобы помочь нам визуализировать то, что здесь происходит. Единичный круг имеет центр в
начало и радиус один. Наша координата 𝐵 отрицательная 𝑥,
отрицательное 𝑥, где 𝑥 — положительное число. Это означает, что наша точка 𝐵 будет
находиться в третьем квадранте, на 𝑥 единиц слева от начала координат и на 𝑥 единиц ниже
источник. Так как угол 𝐴𝑂𝐵 стандартный
положение, его начальная сторона является положительной 𝑥-осью, а его конечная сторона будет идти
через точку 𝐵.
Единичный круг имеет центр в
начало и радиус один. Наша координата 𝐵 отрицательная 𝑥,
отрицательное 𝑥, где 𝑥 — положительное число. Это означает, что наша точка 𝐵 будет
находиться в третьем квадранте, на 𝑥 единиц слева от начала координат и на 𝑥 единиц ниже
источник. Так как угол 𝐴𝑂𝐵 стандартный
положение, его начальная сторона является положительной 𝑥-осью, а его конечная сторона будет идти
через точку 𝐵.
А для уголков в стандарте
позиции, они будут вычисляться против часовой стрелки от начала координат. Прежде чем мы сможем вычислить грех
𝜃, мы будем вычислять так называемый опорный угол от точки 𝐵. Это угол, созданный с помощью
точка 𝐵 и отрицательная ось 𝑥. Назовем этот угол 𝛼. Оттуда мы можем использовать наш
знание тригонометрии прямоугольного треугольника для нахождения угла 𝛼. У этого прямоугольного треугольника две стороны
длины, которые измеряют и 𝑥, и гипотенузу, равную единице. Мы знаем, что гипотенуза равна
потому что точка 𝐵 попадает на единичную окружность, а расстояние между 𝐵 и
центр этого круга один.
Мы знаем, что гипотенуза равна
потому что точка 𝐵 попадает на единичную окружность, а расстояние между 𝐵 и
центр этого круга один.
Чтобы найти 𝑥, мы можем использовать Теорема Пифагора, которая гласит, что 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате. В нашем треугольнике это 𝑥 в квадрате плюс 𝑥 в квадрате равно единице в квадрате. Два 𝑥 в квадрате равно единице. Разделив обе части на два, находим что 𝑥 в квадрате равно одному больше двух. Извлечение квадратного корня из обоих стороны, мы находим, что 𝑥 равно квадратному корню из одного из двух, что упрощается до один на квадратный корень из двух. Мы знаем, что коэффициент греха равен на длину противоположной стороны по гипотенузе. И поэтому грех 𝛼 будет быть равно 𝑥 больше единицы или просто 𝑥. Это делает грех 𝛼 на один больше квадратный корень из двух.
И это грех для нашего
опорный угол. Чтобы точно найти грех
нашего отношения 𝜃 с начальной стороной, являющейся осью 𝑥, и конечной стороной
будучи точкой 𝐵, мы используем диаграмму CAST. В первом квадранте все триггеры
значения положительные. Во втором квадранте только
значение синуса положительное. В третьем квадранте только
значение тангенса положительное. А в четвертом квадранте
значение косинуса положительное.
Чтобы точно найти грех
нашего отношения 𝜃 с начальной стороной, являющейся осью 𝑥, и конечной стороной
будучи точкой 𝐵, мы используем диаграмму CAST. В первом квадранте все триггеры
значения положительные. Во втором квадранте только
значение синуса положительное. В третьем квадранте только
значение тангенса положительное. А в четвертом квадранте
значение косинуса положительное.
Начиная с нашей точки 𝐵, наш терминал сторона находится в третьем квадранте, то грех угла 𝐴𝑂𝐵 будет отрицательным. Мы используем абсолютное значение нашего опорный угол, а диаграмма CAST говорит нам, что грех 𝜃 отрицателен. Грех 𝜃 равен отрицательной единице над квадратным корнем из двух.
Тригонометрические функции
Тригонометрические функцииПроизвольные углы и единичная окружность
До сих пор мы использовали единичный круг для определения тригонометрических функций для острых углов.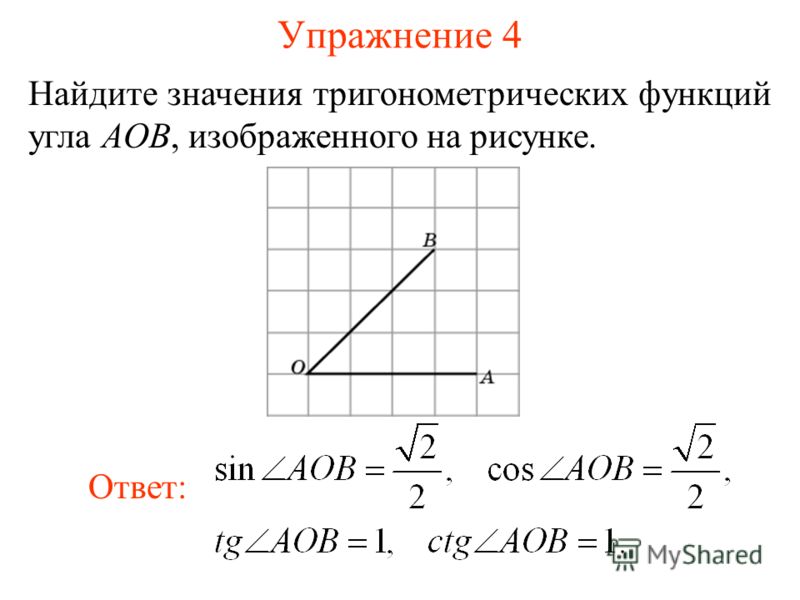 В следующем разделе, где мы рассмотрим косые треугольники, нам понадобятся не только острые углы. Некоторые косоугольные треугольники тупые, и нам нужно знать синус и косинус тупых углов. Пока мы это делаем, мы также должны определить триггерные функции для углов, превышающих 180°, и для отрицательных углов. Во-первых, нам нужно понять, что такое такие углы.
В следующем разделе, где мы рассмотрим косые треугольники, нам понадобятся не только острые углы. Некоторые косоугольные треугольники тупые, и нам нужно знать синус и косинус тупых углов. Пока мы это делаем, мы также должны определить триггерные функции для углов, превышающих 180°, и для отрицательных углов. Во-первых, нам нужно понять, что такое такие углы.Древнегреческие геометры рассматривали только углы между 0° и 180°, и они не считали ни прямой угол 180°, ни вырожденный угол 0° углами. Полезно не только рассматривать эти частные случаи как углы, но также включать углы между 180° и 360°, иногда называемые «рефлекторными углами». С применением тригонометрии к предметам исчисления и дифференциальных уравнений также стали приняты углы за пределами 360 ° и отрицательные углы.
Рассмотрим единичный круг. Обозначим его центр (0,0) как O, , а точку (1,0) на нем как A. В качестве движущейся точки B движется по единичной окружности, начиная с против часовой стрелки, угол AOB как угол 0° и увеличивается.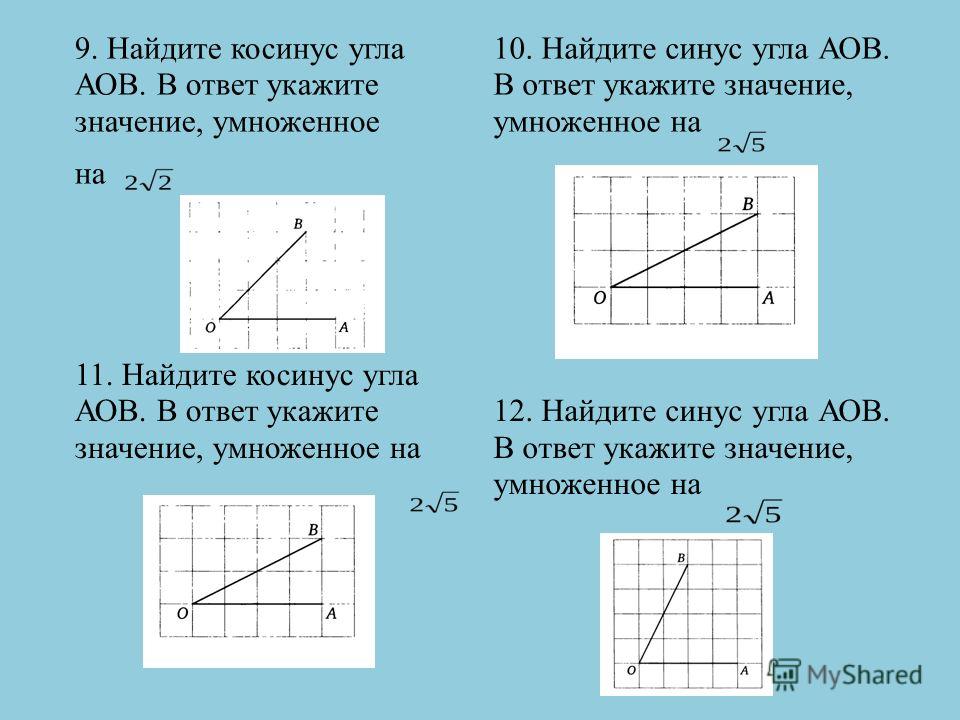 Когда B пройдет весь круг и вернется к A, , тогда угол AOB будет равен 360°. Конечно, это тот же угол, что и угол 0°, поэтому мы можем идентифицировать эти два угла. Как B продолжается второй раз по кругу, мы получаем углы от 360° до 720°. Это те же ракурсы, которые мы видели в первый раз, но у нас для них разные названия. Например, прямой угол называется либо 90°, либо 450°. Каждый раз по кругу мы получаем другое название углов. Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Когда B пройдет весь круг и вернется к A, , тогда угол AOB будет равен 360°. Конечно, это тот же угол, что и угол 0°, поэтому мы можем идентифицировать эти два угла. Как B продолжается второй раз по кругу, мы получаем углы от 360° до 720°. Это те же ракурсы, которые мы видели в первый раз, но у нас для них разные названия. Например, прямой угол называется либо 90°, либо 450°. Каждый раз по кругу мы получаем другое название углов. Таким образом, 90°, 450°, 810° и 1170° обозначают один и тот же угол.
Если B начинается в той же точке A и движется по часовой стрелке, то мы получим отрицательные углы, точнее, имена в отрицательных градусах для тех же углов. Например, если вы пройдете четверть круга по часовой стрелке, угол AOB обозначен как 90°. Конечно, это то же самое, что угол 270°.
Таким образом, любой угол имеет бесконечно много имен, но все они отличаются друг от друга на кратное 360°.
Синусы и косинусы произвольных углов
Теперь, когда мы задали произвольные углы, мы можем определить их синусы и косинусы.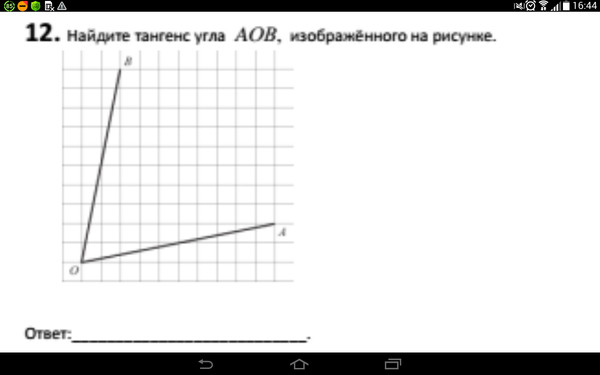 Пусть угол расположен так, что его вершина находится в центре единичной окружности O = (0,0), а первая сторона угла расположена вдоль x — ось. Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B для определения косинуса угла и синуса угла. В частности, координата x координаты B является косинусом угла, а координата y координатой B является синусом угла.
Пусть угол расположен так, что его вершина находится в центре единичной окружности O = (0,0), а первая сторона угла расположена вдоль x — ось. Пусть вторая сторона угла пересекает единичную окружность в точке B. Тогда угол равен углу AOB , где A равно (1,0). Мы используем координаты B для определения косинуса угла и синуса угла. В частности, координата x координаты B является косинусом угла, а координата y координатой B является синусом угла.Свойства синусов и косинусов, вытекающие из этого определения
Есть несколько свойств, которые мы можем легко вывести из этого определения. Некоторые из них обобщают тождества, которые мы уже видели для острых углов.- Синус и косинус являются периодическими функциями периода 360°, то есть периода 2. Это потому, что синус и косинус определяются в терминах углов, и вы можете добавить числа, кратные 360° или 2, и это не изменится угол.
 Таким образом,
Таким образом,sin ( t + 360°) = sin t, и cos ( t + 360°) = cos t.
Многие из современных приложений тригонометрии следуют из использования тригонометрического исчисления, особенно те приложения, которые имеют дело непосредственно с тригонометрическими функциями. Таким образом, мы должны использовать радианную меру, когда думаем о триггере с точки зрения триггерных функций. В радианах последняя пара уравнений читается как
sin ( t + 2) = sin т, и cos ( t + 2) = cos t.
- Синус и косинус дополняют друг друга:
cos t = sin (/2 t ) sin t = cos (/2 t )
Мы это уже видели, а теперь имеем для любого угла t. Это правда, потому что, когда вы отражаете плоскость через диагональную линию y = x, угол обменивается на его дополнение.
- Тождество Пифагора для синусов и косинусов следует непосредственно из определения.
 Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1. Но координаты косинус и синус, так что делаем вывод
Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1. Но координаты косинус и синус, так что делаем выводsin 2 t + cos 2 t = 1. Теперь мы готовы рассмотреть синус и косинус как функции.
- Синус — нечетная функция, а косинус — четная функция. Возможно, вы не сталкивались с этими прилагательными «нечетный» и «четный» применительно к функциям, но знать их важно. Функция f называется нечетной функцией , если для любого числа x, f ( x ) = f ( x ). Функция f называется функцией даже , если для любого числа x, f ( x ) = f ( x ). Большинство функций не являются ни нечетными, ни четными функциями, но важно обращать внимание на то, является ли функция четной или нечетной.
 Любой полином с только сроками нечетной степени является нечетной функцией, например, F ( x ) = x 5 +8 x 3 2 x. (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 3 x 2 5. (Константа 5 равна 5 x 90 143 0 , а 0 — четное число.)
Любой полином с только сроками нечетной степени является нечетной функцией, например, F ( x ) = x 5 +8 x 3 2 x. (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 3 x 2 5. (Константа 5 равна 5 x 90 143 0 , а 0 — четное число.)Синус — нечетная функция, а косинус — четная.
sin t = sin t, и cos t = cos t.
Эти факты следуют из симметрии единичного круга относительно оси x . Угол t — это тот же угол, что и t , за исключением того, что он находится по другую сторону оси x . Переворот точки ( x,y ) на другую сторону оси x превращает ее в ( x,y ), поэтому координата y инвертируется, то есть синус инвертируется , но x -координата остается прежней, то есть косинус не меняется.

- Очевидным свойством синусов и косинусов является то, что их значения лежат между 1 и 1. Каждая точка на единичной окружности удалена на 1 единицу от начала координат, поэтому координаты любой точки также находятся в пределах 1 от 0.
Графики функций синуса и косинуса
Продолжим использовать t в качестве переменного угла. Хороший способ для человека понять функцию — посмотреть на ее график. Начнем с графика sin t. Возьмите горизонтальную ось за ось t (а не ось x , как обычно), возьмите вертикальную ось за ось y и постройте уравнение y = sin t . Выглядит так. Во-первых, обратите внимание, что она периодична с периодом 2. Геометрически это означает, что если вы возьмете кривую и сдвинете ее 2 влево или вправо, то кривая вернется сама на себя. Во-вторых, обратите внимание, что график находится в пределах одной единицы оси t . Мало что еще очевидно, за исключением того, где оно увеличивается и уменьшается. Например, sin t растет от 0 до /2, так как y -координата точки B увеличивается с увеличением угла AOB увеличивается с 0 до /2.
Например, sin t растет от 0 до /2, так как y -координата точки B увеличивается с увеличением угла AOB увеличивается с 0 до /2.
Далее давайте посмотрим на график косинуса. Снова возьмем горизонтальную ось за ось t , но теперь возьмем вертикальную ось за ось x и построим уравнение x = cos t.
Обратите внимание, что он выглядит точно так же, как график sin t , за исключением того, что он сдвинут влево на /2. Это из-за тождества cos t = sin (/2 + т ). Хотя мы раньше не встречались с этим тождеством, оно легко следует из тех, что мы видели: т ).
Графики функций тангенса и котангенса
График функции тангенса имеет вертикальную асимптоту в точке x = /2. Это связано с тем, что тангенс стремится к бесконечности, когда t приближается к /2. (На самом деле она приближается к минус бесконечности как t приближается к /2 справа, как вы можете видеть на графике.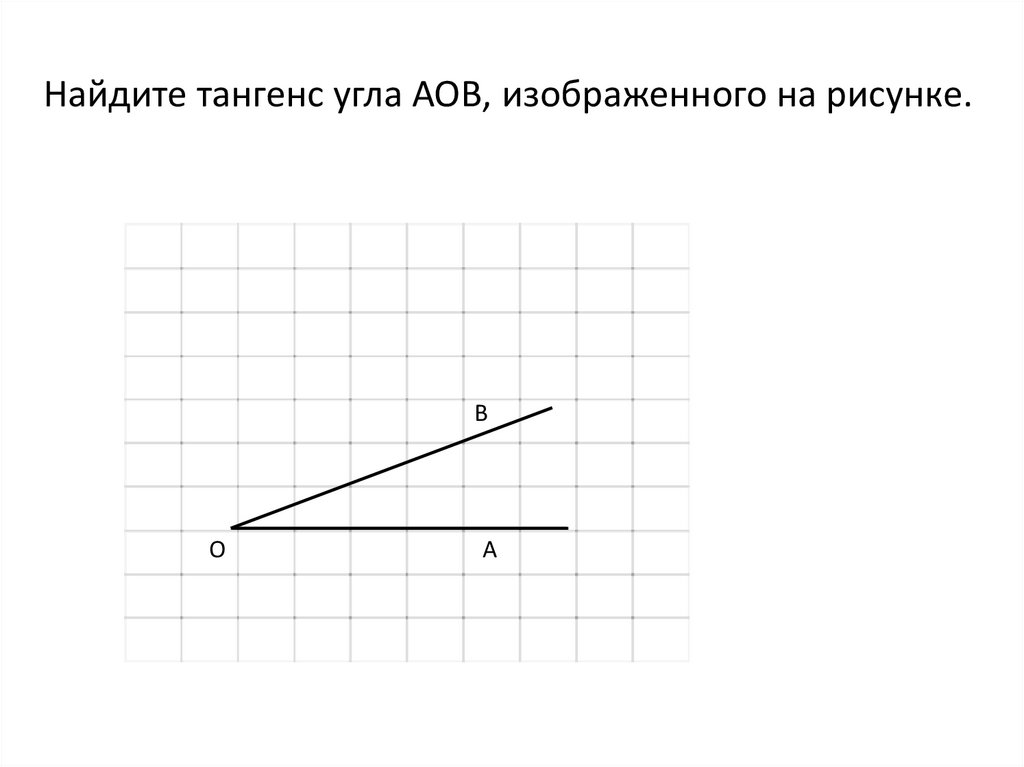
Вы также можете видеть, что тангенс имеет период; есть также вертикальные асимптоты через каждые единицы влево и вправо. Алгебраически эта периодичность выражается как тангенс ( t + ) = тангенс t.
График для котангенса очень похож.
Это сходство просто потому, что котангенс t — тангенс дополнительного угла t.
Графики функций секанса и косеканса
Секанс является обратной величиной косинуса, и поскольку косинус принимает значения только между 1 и 1, следовательно, секанс принимает значения только выше 1 или ниже 1, как показано на графике. Также секанс имеет период .Как и следовало ожидать, график косеканса очень похож на график секанса.
Оглавление. | Вернемся к прямоугольным треугольникам. | О косых треугольниках.
© 1997.
Дэвид Э.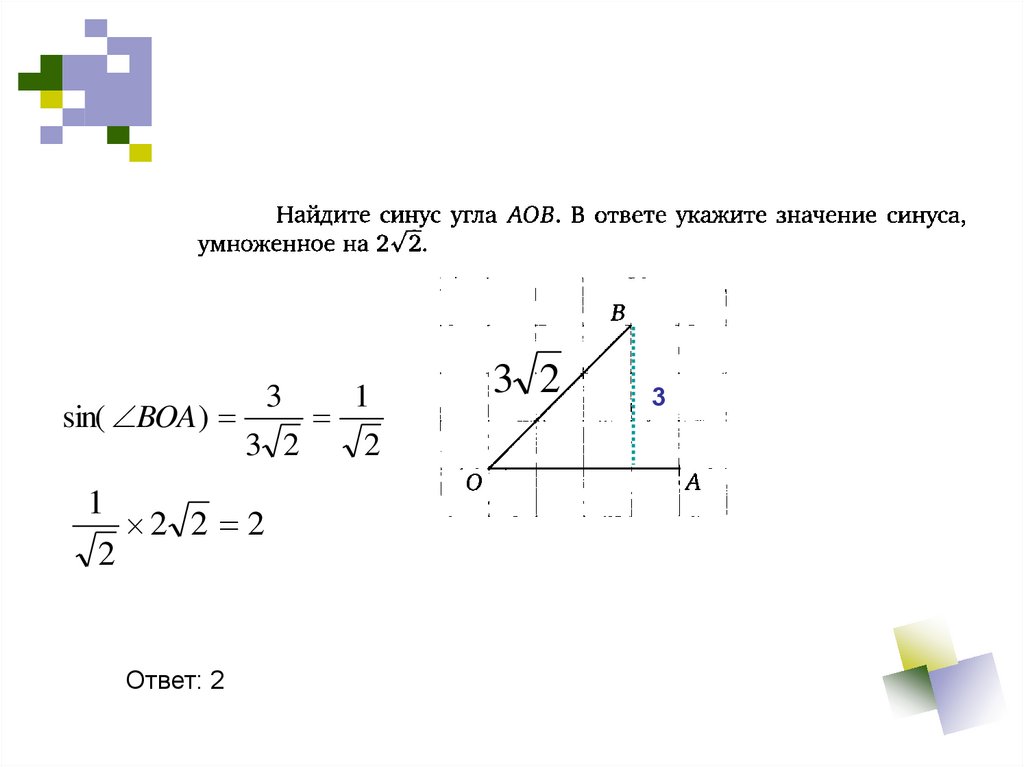

 02.2022?
02.2022? Choose the right form:
Choose the right form: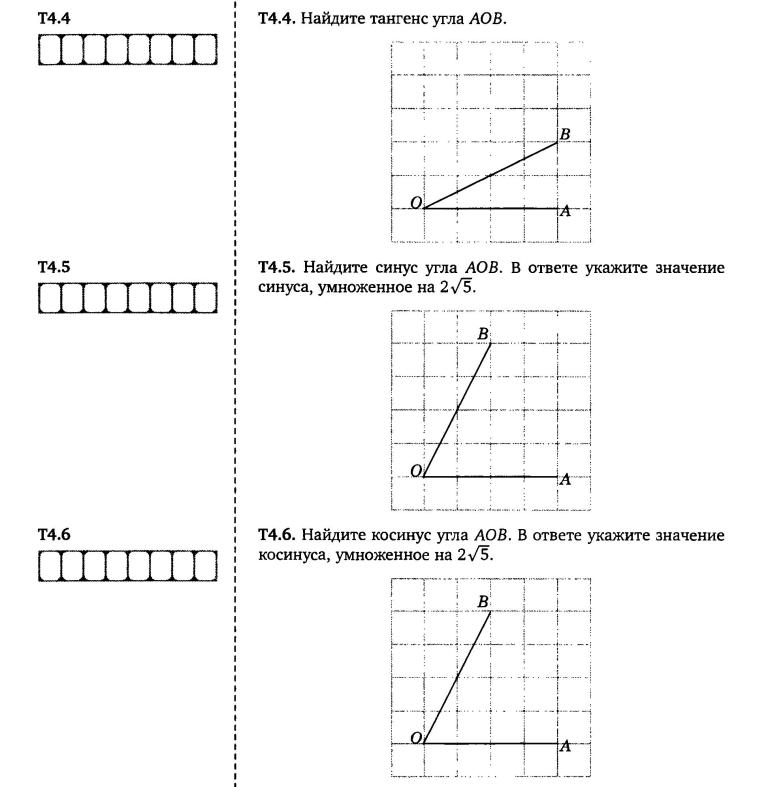
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
 Часть 1;
Часть 1; Выбор верного или неверного утверждения;
Выбор верного или неверного утверждения;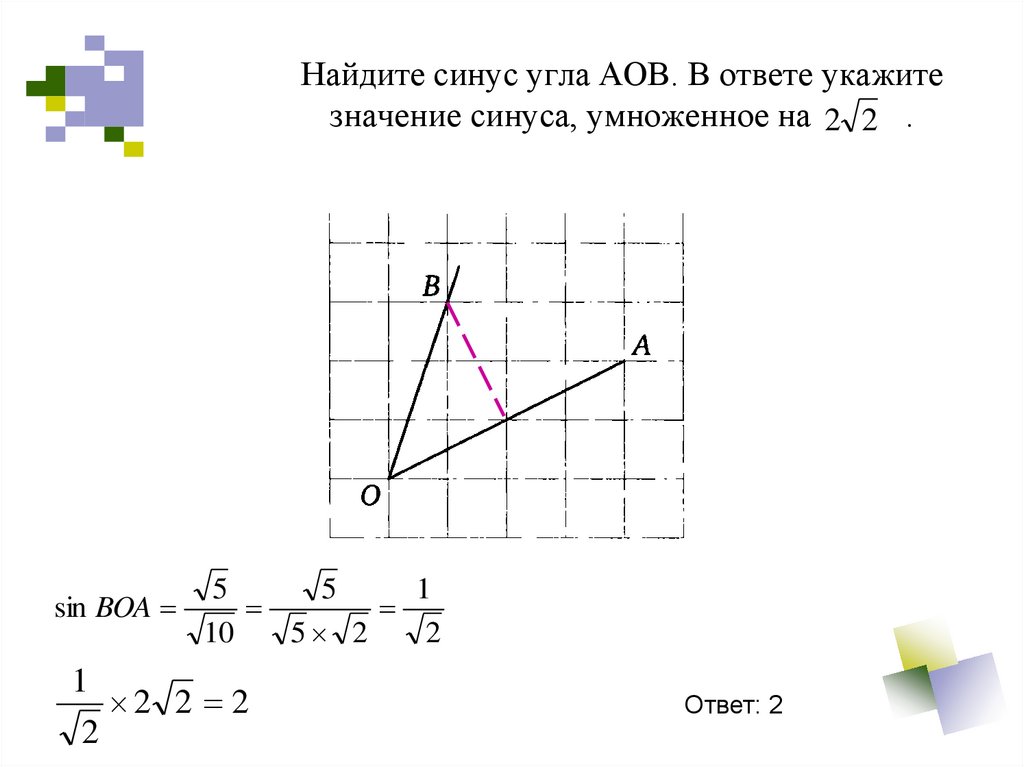 Формулы;
Формулы; Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.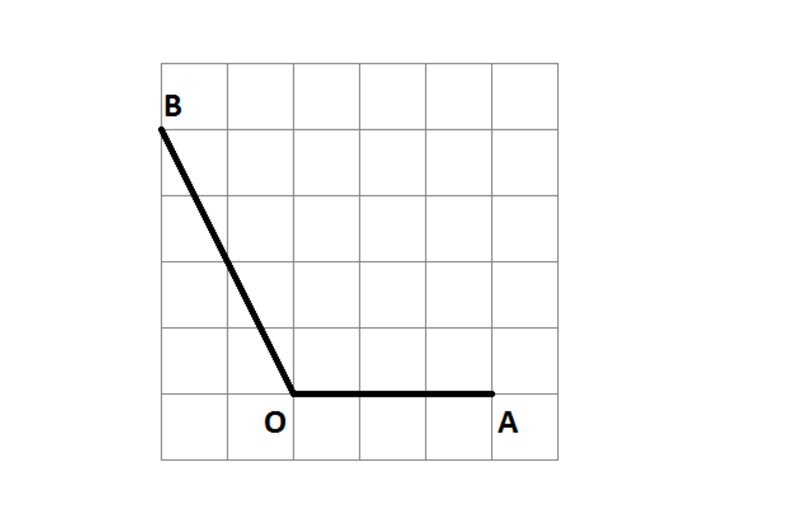 Найдите угол BAD. Ответ дайте в градусах.
Найдите угол BAD. Ответ дайте в градусах. Решить вариант с 1-19 задание
Решить вариант с 1-19 задание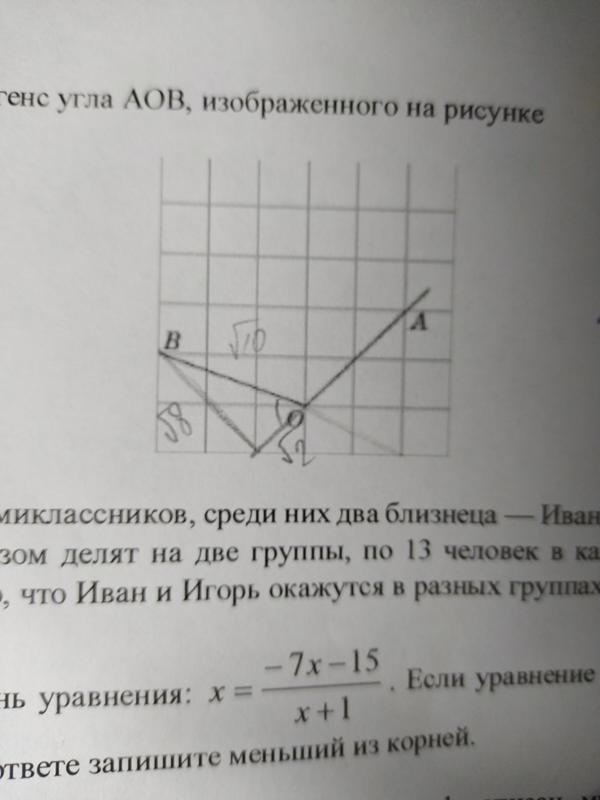 Таким образом,
Таким образом, Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1. Но координаты косинус и синус, так что делаем вывод
Поскольку точка B лежит на единичной окружности, ее координаты x и y удовлетворяют уравнению x 2 + y 2 =1. Но координаты косинус и синус, так что делаем вывод Любой полином с только сроками нечетной степени является нечетной функцией, например, F ( x ) = x 5 +8 x 3 2 x. (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 3 x 2 5. (Константа 5 равна 5 x 90 143 0 , а 0 — четное число.)
Любой полином с только сроками нечетной степени является нечетной функцией, например, F ( x ) = x 5 +8 x 3 2 x. (Обратите внимание, что все степени x являются нечетными числами.) Точно так же любой полином только с четными степенями является четной функцией. Например, f ( x ) = x 4 3 x 2 5. (Константа 5 равна 5 x 90 143 0 , а 0 — четное число.)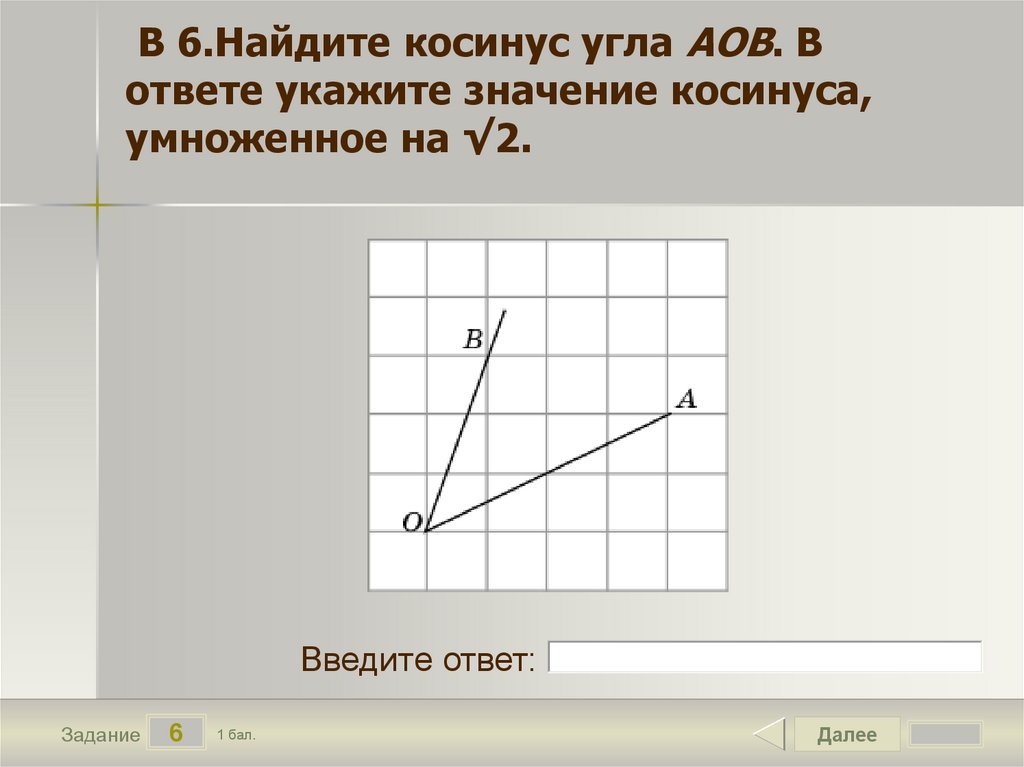
Leave A Comment