Как найти площадь прямоугольного треугольника? 🔺
Поможем понять и полюбить математику
Начать учиться
535.1K
О прямоугольном треугольнике, кажется, все уже сказано. Определения — даны, свойства — изучены. Осталось научиться находить его площадь. Давайте разберемся, какими способами это сделать.
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
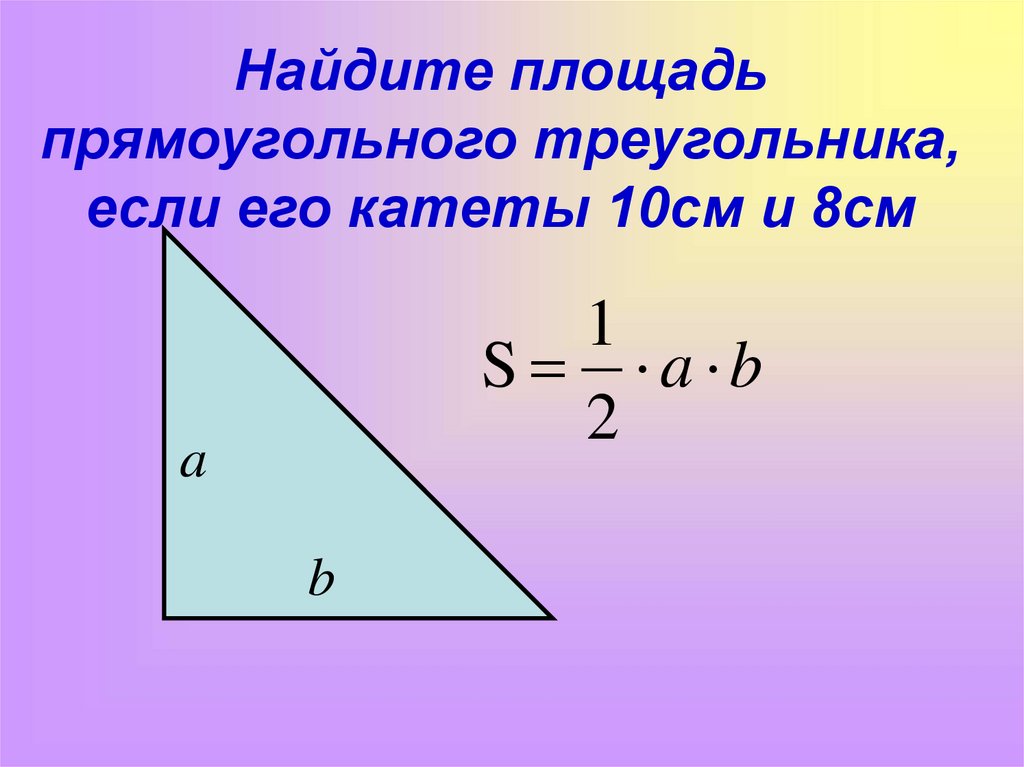
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. S = 1/2 (a × h) |
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе. S = 1/2 (c × h) где с — гипотенуза, h — высота. |
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
с — гипотенуза
a, b — катеты
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
a и b — катеты
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
r = (a + b − c) / 2
a и b — катеты
с — гипотенуза
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
с — гипотенуза
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Анастасия Белова
К предыдущей статье
213. 9K
9K
Прямая и обратная пропорциональность
К следующей статье
162.1K
Теория графов. Основные понятия и виды графов
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Найти площадь прямоугольного треугольника — онлайн калькулятор
- Главная
- /
- Математика
- /
- Геометрия
- /
- Найти площадь прямоугольного треугольника
Чтобы посчитать площадь прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- длины катетов a и b
- длину гипотенузы с и длину любого из катетов (a или b)
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- длину гипотенузы с и один из острых углов (α или β)
Найти площадь прямоугольного треугольника по двум катетам
Катет a =
Катет b =
S =
Просто введите длины двух катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
S = ½ ⋅ a ⋅ b
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Гипотенуза c =
Катет (a или b) =
S =
Введите длины гипотенузы и одного из катетов, и получите ответ.
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
S = ½ ⋅ a ⋅ √c² — a² = ½ ⋅ b ⋅ √c² — b²
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
S = 2 ⋅ √5² — 2² / 2 = √25 — 4 ≈ 4.58 см²
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Катет (a или b) =
Прилежащий угол (β или α) = °
S =

То есть к катету a прилежащий ∠β, а к катету b — ∠α
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Катет (a или b) =
Противолежащий угол (α или β) = °
S =
Введите длину одного из катетов и противолежащий к нему острый угол в градусах.
То есть к катету a противолежащий ∠α, а к катету b — ∠β
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(90 — α) = ½ ⋅ b² ⋅ tg(90 — β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Гипотенуза c =
Угол (α или β) = °
S =
Введите длину гипотенузы и один из острых угол в градусах.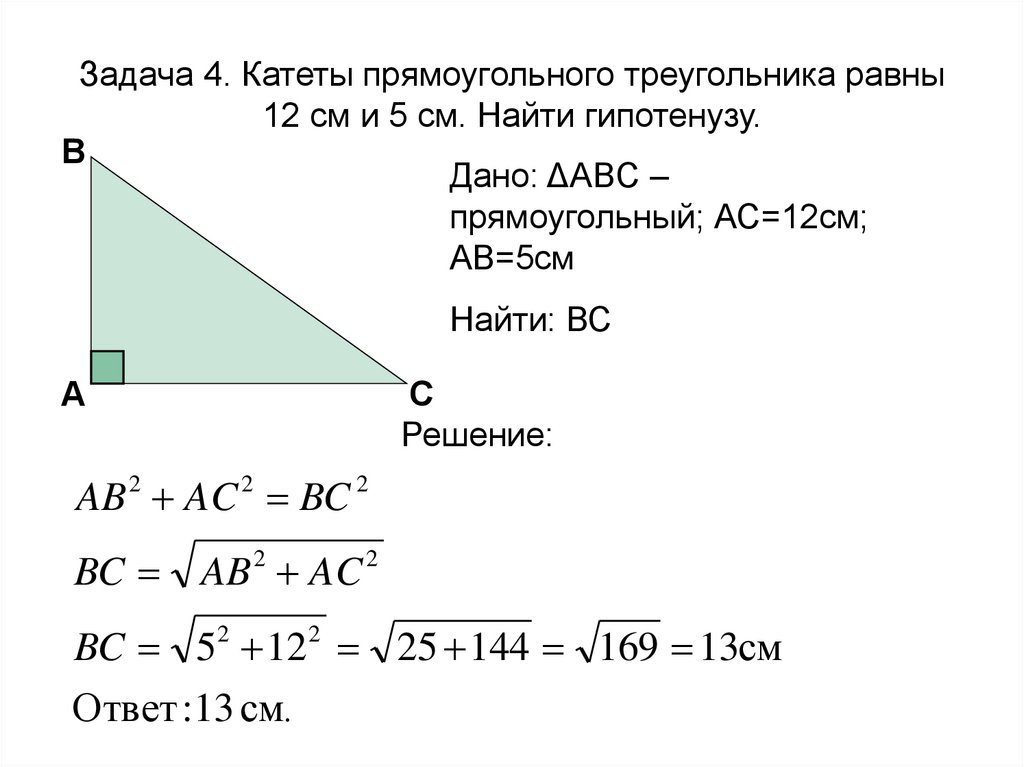
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Калькулятор площади прямоугольного треугольника
Если вам интересно как найти площадь прямоугольного треугольника , вы находитесь в нужном месте — этот калькулятор площади прямоугольного треугольника является инструментом для вас.
Ищете ли вы уравнение с катетом треугольника, катетом и гипотенузой или катетом и углом, вы не будете разочарованы — в этом калькуляторе все они реализованы.
Пожалуйста, прокрутите вниз, чтобы узнать больше о формулах площади прямоугольного треугольника, или просто попробуйте наш калькулятор!
Формулы площади прямоугольного треугольника
🙋 Если вы только что заметили, что ваш треугольник не является прямоугольным, проверьте этот общий калькулятор площади треугольника.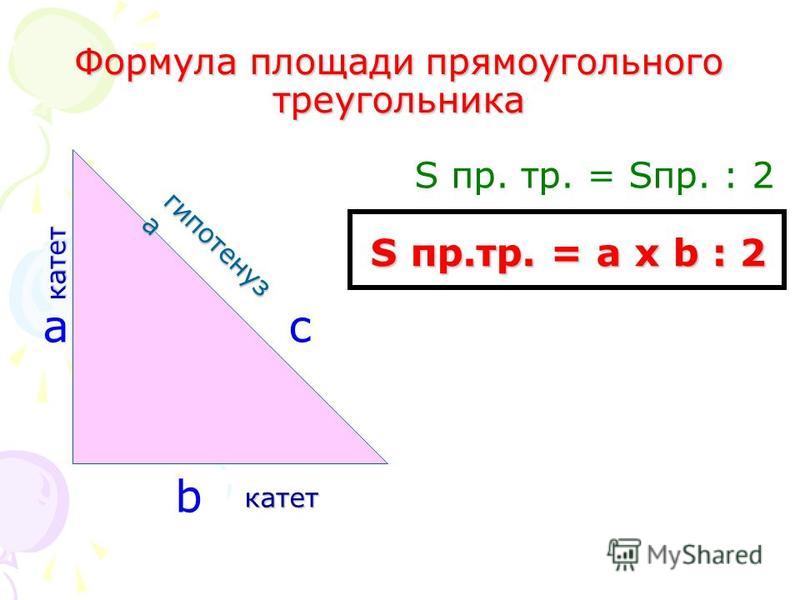
🙋 Хотите узнать больше о прямоугольных треугольниках? Посетите наш калькулятор прямоугольного треугольника!
Площадь равнобедренного прямоугольного треугольника
Равнобедренный прямоугольный треугольник — это особый прямоугольный треугольник, иногда называемый треугольником 45-45-90 (он настолько особенный, что мы создали специально для него инструмент — калькулятор треугольника 45 45 90). В таком треугольнике катеты равны по длине (поскольку гипотенуза всегда должна быть наибольшей из сторон прямоугольного треугольника): 92}{2}area=2a2
Как использовать калькулятор площади прямоугольного треугольника
Покажем пошаговый расчет:
Выберите один вариант в зависимости от того, что вы дали . Предположим, что мы знаем одну сторону и угол, поэтому мы меняем выделение на с учетом угла и одной стороны .

Введите значения . Например, мы знаем, что α=40°\alpha = 40\степеньα=40° и bbb равно 17 дюймам17\ \text{дюймам}17 дюймам.
92121,25 дюйма2.
Часто задаваемые вопросы
Как найти площадь прямоугольного треугольника по данным сторонам?
Метод зависит от того, какие стороны вам даны:
Если вы знаете две ноги , то используйте формулу
площадь = a × b / 2, гдеa, аbэто ноги.Если вы знаете один катет
aи гипотенузуc, используйте формулу:площадь = a × √(c² - a²) / 2
Какова площадь прямоугольного треугольника с гипотенузой 5 см и углом 45°?
Площадь 6.25 . Мы получаем этот ответ, применяя формулу площадь = c² × sin(α) × cos(α) / 2 , где c = 5 и α = 45° . Математическая теорема, используемая для вывода этой формулы, называется законом синусов .
Математическая теорема, используемая для вывода этой формулы, называется законом синусов .
Как узнать, прямоугольный ли это треугольник?
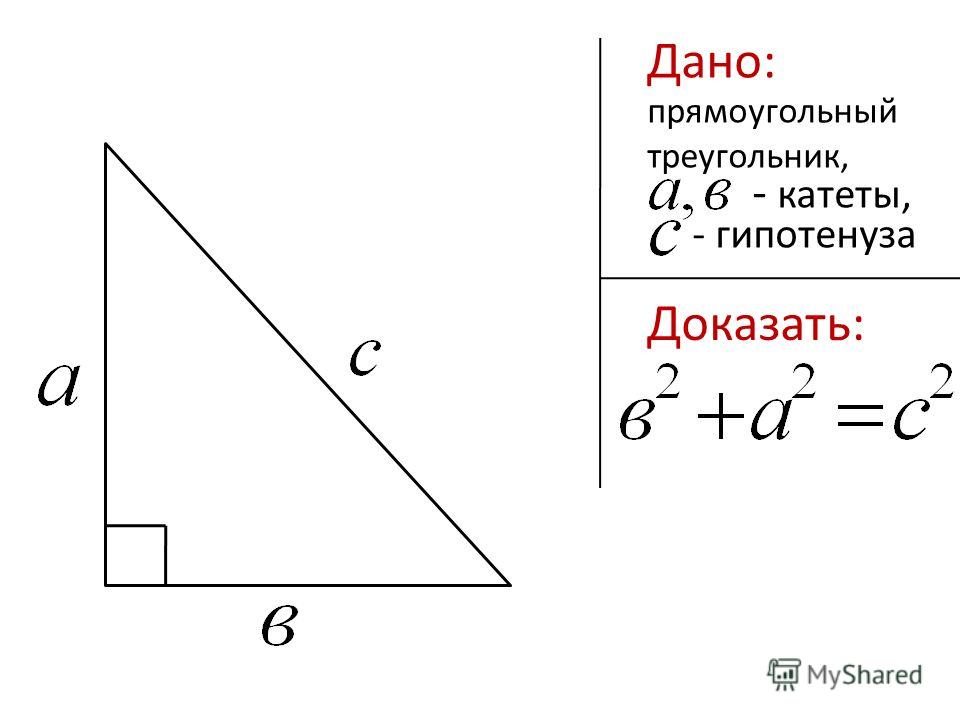
Если вам даны три стороны треугольника и вы хотите узнать, правильный ли этот треугольник, проверьте, верна ли формула Пифагора: a² + b² = c² , где c — самая длинная сторона, a и b — две другие стороны.
Что мы называем сторонами прямоугольного треугольника?
Две стороны, перпендикулярные друг другу, называются ножками . Сторона, противоположная прямому углу (другими словами, самая длинная сторона), равна гипотенузе .
Площадь прямоугольного треугольника
Площадь прямоугольного треугольника — это часть, которая находится внутри границы треугольника. Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90 градусов). Он просто известен как прямоугольный треугольник. В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой, а две другие стороны называются катетами.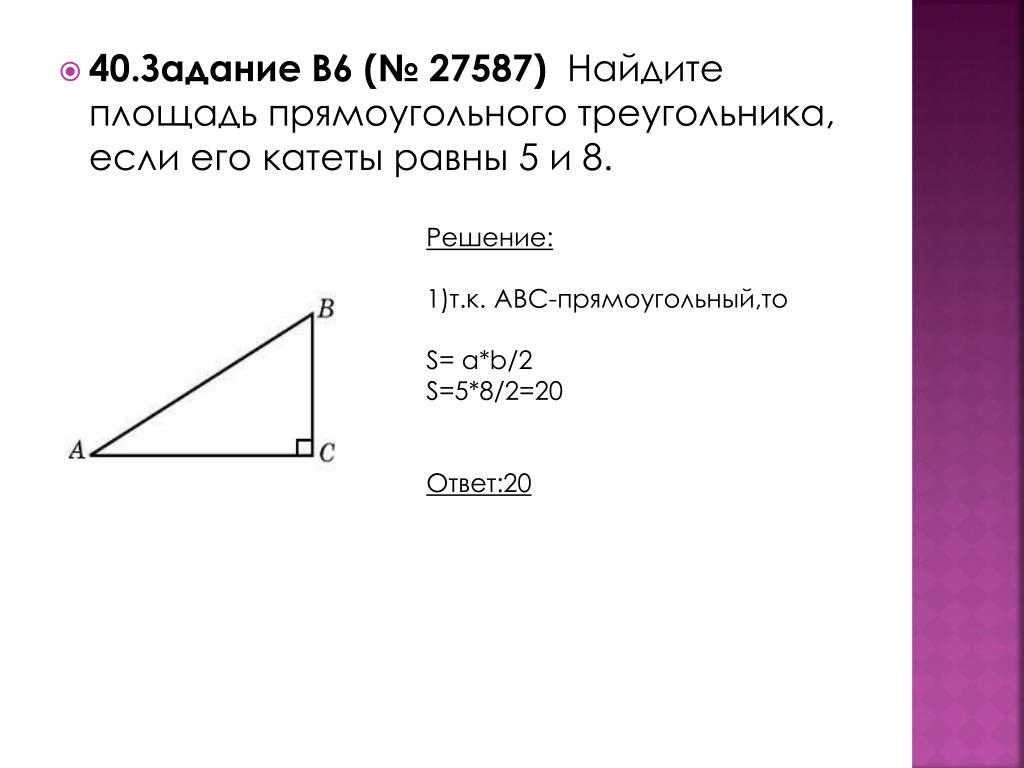 Две ножки взаимозаменяемо называются основанием и высотой. Формула площади прямоугольного треугольника представлена на изображении ниже.
Две ножки взаимозаменяемо называются основанием и высотой. Формула площади прямоугольного треугольника представлена на изображении ниже.
| Что такое площадь прямоугольного треугольника? | |
| 2. | Площадь прямоугольного треугольника Формула |
| 3. | Как вывести формулу площади прямоугольного треугольника? |
| 4. | Площадь прямоугольного треугольника с гипотенузой |
| 5. | Часто задаваемые вопросы о площади прямоугольного треугольника |
Что такое площадь прямоугольного треугольника?
Площадь прямоугольного треугольника, как мы обсуждали ранее, это пространство внутри него. Это пространство разделено на квадраты единичной длины, и количество единичных квадратов, находящихся внутри прямоугольного треугольника, является его площадью.
Можете ли вы попробовать посчитать количество единичных квадратов внутри этого треугольника? Всего 6 единичных квадратов. Таким образом, площадь треугольника выше равна 6 квадратных единиц. Но не всегда можно вычислить площадь прямоугольного треугольника, подсчитав количество квадратов. Для этого должна быть формула. Посмотрим, по какой формуле находится площадь прямоугольного треугольника.
Формула площади прямоугольного треугольника
В приведенном выше примере, если мы умножим основание и высоту, мы получим 3 × 4 = 12, а если мы разделим это на 2, мы получим 6. Таким образом, площадь прямоугольного треугольника получается путем умножения его основания и высоты и затем сделать продукт наполовину.
Площадь прямоугольного треугольника = 1/2 × основание × высота
Примеры:
- Площадь прямоугольного треугольника с основанием 6 футов и высотой 4 фута равна 1/2 × 6 × 4 = 12 футов 2 .

- Площадь прямоугольного треугольника с основанием 10 м и высотой 5 м равна 1/2 × 10 × 5 = 25 м 2 .
- Площадь прямоугольного треугольника с основанием 11 дюймов и высотой 5 дюймов равна 1/2 × 11 × 5 = 27,5 дюйма 2 .
Как вывести формулу площади прямоугольного треугольника?
Рассмотрим прямоугольник длины l и ширины w. Также проведите диагональ. Вы можете видеть, что прямоугольник разделен на два прямоугольных треугольника.
Мы знаем, что площадь прямоугольника равна длине × ширине. Таким образом, площадь указанного выше прямоугольника равна l × w. Мы видим, что два прямоугольных треугольника конгруэнтны, поскольку их можно расположить так, чтобы один накладывался на другой. Таким образом, площадь прямоугольника в два раза больше площади одного из указанных выше прямоугольных треугольников. то есть
Площадь прямоугольника = l × w = 2 × (площадь одного прямоугольного треугольника)
Это дает:
Площадь одного прямоугольного треугольника = 1/2 × l × w.
Мы обычно представляем катеты прямоугольного треугольника как основание и высоту.
Таким образом, формула площади прямоугольного треугольника: Площадь прямоугольного треугольника = 1/2 × основание × высота.
Площадь прямоугольного треугольника с гипотенузой
Вспомним теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. т. е. (гипотенуза) 2 = (основание) 2 + (высота) 2 .
Хотя невозможно найти площадь прямоугольного треугольника только с гипотенузой, можно найти его площадь, если мы знаем одно из основания и высоты вместе с гипотенузой. Давайте посмотрим пример.
Пример: Найдите площадь прямоугольного треугольника, основание которого равно 6 дюймам, а гипотенуза равна 10 дюймам.0005
(гипотенуза) 2 = (основание) 2 + (высота) 2
10 2 = 6 2 + (высота) 2 9000
9000 29000 29000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 29000 2 9000 2 9000 2 9000 29000 2 9000 2 + (высота) 2 2 + (высота) 2 2 + (высота) 2(высота) 2 = 64
высота = √(64) = 8 дюймов
Итак, площадь данного треугольника = 1/2 × основание × высота = 1/2 × 6 × 8 = 24 в 2 .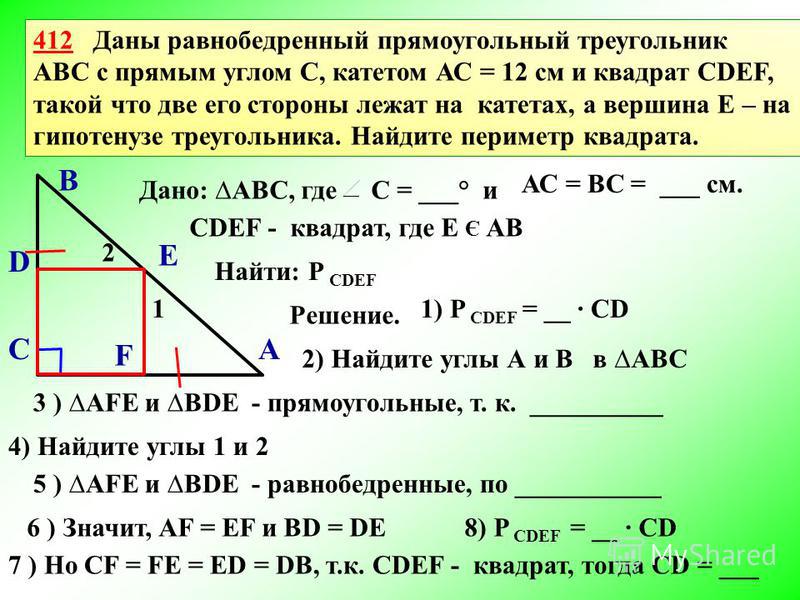
Примеры площади прямоугольного треугольника
Пример 1: Самая длинная сторона ломтика хлеба, напоминающего прямоугольный треугольник, равна 13 единицам. Если его высота равна 12 единицам, найдите его площадь по формуле площади прямоугольного треугольника.
Решение:
Мы знаем, что самая длинная сторона прямоугольного треугольника называется гипотенузой.
Итак, дано, что гипотенуза = 13 единиц, а высота = 12 единиц.
Подставить данные значения в теорему Пифагора,
(гипотенуза) 2 = (основание) 2 + (высота) 2
13 2 = (базу) 2 + (12) 2
169 = (базу) 2 + 144
(База) 2 2 + 144
(база) 2 2 2 2 2 2 + 144
(База) 2 2 + 144
(База) 2 + 144
(База) 2 + 144
(базу)
основание = √(25) = 5 единиц.

Площадь ломтика хлеба = 1/2 × основание × высота = 1/2 × 5 × 12 = 30 квадратных единиц.
Следовательно, площадь данного куска хлеба = 30 квадратных единиц.
Пример 2: Бассейн имеет форму прямоугольного треугольника. Его стороны находятся в соотношении 3:4:5. Его периметр составляет 720 единиц. Найдите его площадь.
Решение:
Предположим, что стороны бассейна равны 3x, 4x и 5x.
Дано, что его периметр = 720 единиц.
3x + 4x + 5x = 720
12x = 720
x = 60
Итак, стороны треугольника: единицы
5x = 5(60) = 300 единиц
Так как 300 единиц — самая длинная сторона бассейна (который имеет форму прямоугольного треугольника), это гипотенуза.
Итак, 180 единиц и 240 единиц должны быть основанием и высотой бассейна взаимозаменяемо.
Используя формулу площади прямоугольного треугольника,
Площадь бассейна = 1/2 × основание × высота = 1/2 × 180 × 240 = 21 600 единиц 2 .

Следовательно, площадь данного бассейна = 21 600 единиц 2 .
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по площади прямоугольного треугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади прямоугольного треугольника
Какова площадь прямоугольного треугольника?
Площадь прямоугольного треугольника определяется как общее пространство или область, покрытая прямоугольным треугольником. Выражается в квадратных единицах. Некоторые общие единицы, используемые для представления площади, м 2 , см 2 , дюймы 2 , ярды 2 и т. д.
Какая формула для нахождения площади прямоугольного треугольника?
Площадь прямоугольного треугольника с основанием b и высотой h равна 1/2 × основание × высота (или) 1/2 × b × h квадратных единиц.
Как найти периметр и площадь прямоугольного треугольника?
Площадь прямоугольного треугольника с основанием b и высотой h находится по формуле 1/2 × b × h, а его периметр получается простым сложением всех сторон. Если даны только две его стороны, то по теореме Пифагора находим третью сторону.
Как найти площадь прямоугольного треугольника без основания?
Если даны только высота и гипотенуза прямоугольного треугольника, то прежде чем найти площадь треугольника, надо сначала найти основание по теореме Пифагора. Тогда мы можем использовать формулу 1/2 × основание × высота, чтобы найти его площадь. Например, чтобы найти площадь прямоугольного треугольника с высотой 4 см и гипотенузой 5 см, мы сначала находим его основание, используя теорему Пифагора. Тогда мы получаем,
основание = √[(гипотенуза) 2 — (высота) 2 ] = √(5 2 — 4 2 ) = √9 = 3 см.
Площадь прямоугольного треугольника = 1/2 × 3 × 4 = 6 см 2 .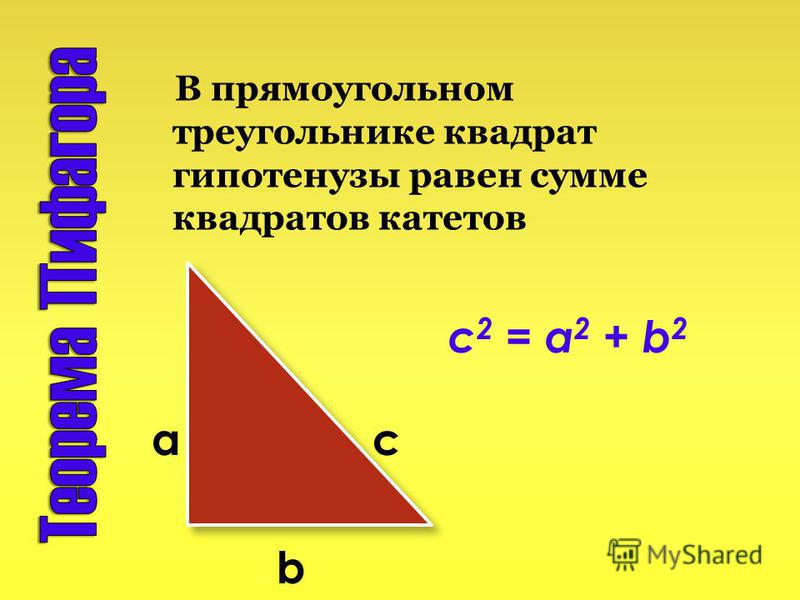



Leave A Comment