Тест по геометрии «Площадь прямоугольника» с ответами
1. Какой угол необходимо использовать для вычисления площади прямоугольника по формуле:
а) между диагоналями +
б) между двумя сторонами
в) между стороной и диагональю
2. Найдите сумму площадей квадратов, построенных на сторонах прямоугольника со сторонами 5 см и 7 см:
а) 122
б) 148 +
в) 99
3. Если провести две диагонали в прямоугольнике, сколько получится треугольников:
а) 6
б) 2
в) 4 +
4. Периметр прямоугольника равен 40 см., а одна из его сторон равна 4 см. Прямоугольник имеет такую же площадь, что и квадрат. Чему равен периметр квадрата:
а) 32 см. +
б) 64 см
в) 16 см
5. Что обозначается буквой d:
а) длина
б) высота
в) диагональ +
6. В прямоугольнике ABCD сторона AB равна 12 см. Расстояние от точки пересечения диагоналей до этой стороны равно 8 см. Найдите площадь треугольника ABC:
а) 24 кв.см.
б) 96 кв.см +
в) 48 кв.
7. Стороны единичного квадрата равны:
а) 1 и 2
б) 2 и 3
в) 1 и 1 +
8. Площадь квадрата равна 36 кв.см. Чему равен его периметр:
а) 24 см +
б) 36 см
в) 18 см
9. На какие фигуры делит прямоугольник диагональ:
а) ромбы
б) прямоугольники
в) треугольники +
10. Периметр прямоугольника равен 18 см, а она из его сторон на 1 см больше другой. Чему равна площадь прямоугольника:
а) 16 кв.см.
б) 20 кв.см. +
в) 25 кв.см.
11. Какой из вариантов может быть единицей измерения сторон прямоугольника:
а) см +
б) см кв.
в) м кв.
12. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 м и 9 м:
б) 6 м +
в) 16 м
13. Какой из вариантов может быть единицей измерения для площади:
а) см кв. +
б) мм
в) см
14. В прямоугольнике все углы по:
а) 45 градусов
б) 180 градусов
в) 90 градусов +
15. Вычислите площадь садового участка, имеющего форму прямоугольника, если его ширина равна 300 м, а длина в 2 раза больше:
а) 180000 кв. м +
м +
б) 800 кв. м
в) 700 м
16. Формула для вычисления площади прямоугольника:
а) S=a∗a
б) S=a∗b +
в) S=b∗b
17. Одна из сторон прямоугольника равна 10 см, а его площадь 80 кв. см. Найдите периметр этого прямоугольника:
б) 72 см
в) 36 см +
18. Площадь прямоугольника равна 40 кв. см, а одна из его сторон равна 8 см. Найдите длину другой стороны:
а) 320 см
б) 5 см +
в) 50 см
19. Стороны прямоугольника равны 5 см и 7 см. Вычислите его площадь:
а) 24 кв. см
б) 60 кв. см
в) 35 кв. см +
20. Периметр прямоугольника равен 24 см, а площадь равна 35 см2. Найдите большую сторону прямоугольника:
а) 6
б) 7 +
в) 17
21. Стороны прямоугольника с периметром 40 см относятся как 2:3. Найдите площадь:
а) 96 +
б) 69
в) 82
22. Дан прямоугольник с площадью 450 см2. Одна из его сторон равна 30 см. Найдите периметр:
б) 90 +
в) 78
23. Дан прямоугольник с периметром 32 см. Одна из его сторон равна 6 см. Найдите площадь:
Одна из его сторон равна 6 см. Найдите площадь:
а) 15
б) 6
в) 60 +
24. Площадь прямоугольного земельного участка равна 18 га, ширина участка равна 180 м. Найдите длину этого участка в метрах:
а) 180
б) 1000 +
в) 100
25. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника:
а) 240
б) 60
в) 120 +
26. Верно ли, что площадь – всегда величина положительная:
б) да +
в) неизвестно
27. Как изменится площадь прямоугольника, если каждую его сторону увеличить в три раза:
а) увеличится в девять раз +
б) увеличится в шесть раз
в) увеличится в три раза
28. Найдите площадь прямоугольника, если его смежные стороны равны 12 см и 3,5 см:
а) 31 см2
б) 84 см2
в) 42 см2 +
29. Найдите стороны прямоугольника, если его площадь равна 36 см2, а одна сторона в 2,25 раза больше второй:
а) 4 см и 9 см +
б) 2,25 см и 4 см
в) 6 см и 6 см
30. Чему равны стороны прямоугольника, если его площадь равна 24 см2, а периметр 22 см:
Чему равны стороны прямоугольника, если его площадь равна 24 см2, а периметр 22 см:
б) 3 см и 8 см +
в) 2 см и 11 см
Сколько квадратных сантиметров занял рисунок? 1.Прямоугольник состоит из двух одинаковых квадратов, имеющих общую сторону. Его периметр равен 18см. Найдите площадь прямоугольника.
Муниципальное образовательное учреждение – «Средняя общеобразовательная школа №49 с углубленным изучением отдельных предметов»учитель математики: Романова Лилия Анатольевна
Разработка урока по теме: Площадь. Единицы измерения площадей.
Тип: Урок комплексного применения знаний.
Цели:
1. Обучающая – создать условия для формирования умений и навыков самостоятельно применять знания на различных уровнях.
Развивающая – обеспечить развитие познавательных процессов: внимания, памяти, логического мышления, умений сравнивать, анализировать, обобщать, делать выводы, развивать творческие способности учащихся.
3. Воспитательная – содействовать осознанному, заинтересованному отношению учащихся к изучаемому предмету
контроль и самоконтроль коррекция рефлексия.

Макроструктура урока.
Организационный момент.
Подготовка учащихся к активной деятельности на основном этапе урока.
Этап применения.
Этап самоконтроля и коррекция.
Подведение итогов урока.
Информация о домашнем задании.
Рефлексия.
Ход урока.
Организационный момент.
Подготовка к активной деятельности на основном этапе урока.
а) Мотивация и формулирование цели урока.
Дети, мы продолжаем изучение темы: «Площадь. Единицы измерения площадей». Мы уже много решали задач по этой теме и убедились, как она важна. В повседневной жизни эти задачи решают люди разных профессий: строители, ремонтники, землемеры, аграрии. Сегодня наша цель – научиться применять знания при решении задач, в которых, требуется применить широкий круг ваших познаний, это любимые вами задачи с «изюминкой», а так же проверить умения самостоятельно решать задачи. А поможет нам в этом царь квадрат- владелец квадратного государства, в котором все правильно, все подсчитано, учтено, измерено.
б) Актуализация опорных знаний и умений.
125*48, 53*101, 147-98, 168+125, 297/11, 63*99, 713 EMBED Equation.3 1415, 3!-3, 50*142.
Любимая задача царевича миллиметра. Из маленьких прямоугольников разного цвета он складывал в царстве различные красивые мозаики и вот какие задачи ему приходилось решать. Два прямоугольника имеют общую сторону, про две оставшиеся стороны этих прямоугольников известно, что одна из них в 2 раза больше другой. Найдите во сколько раз площадь большего прямоугольника больше площади меньшего прямоугольника.
О прямоугольниках из предыдущей задачи известно, что площадь одного из них 12, а другого 4. Во сколько раз сторона меньшего прямоугольника меньше стороны большего прямоугольника.
Царевич квадратный сантиметр нарисовал домик, который он собирается построить в ближайшем будущем. Сколько квадратных сантиметров занял рисунок?
Сколько квадратных сантиметров занял рисунок?
Царевича квадратный дециметр всегда волновали вопросы как изменяются взаимозависимые величины при изменении одной из них. Буквально вчера он рассуждал:
Как изменится площадь квадрата, если его сторону увеличить в 3 раза?
Как изменится сторона квадрата, если его площадь уменьшится в 4 раза?
Тем временем два ученика работают по карточкам:
А вот два наших товарища решали задачи от самого царя квадрата. Эти задачи ему приходилось решать когда он выращивал на своих полях различные овощные и зерновые культуры.
1.Прямоугольник состоит из двух одинаковых квадратов, имеющих общую сторону. Его периметр равен 18см. Найдите площадь прямоугольника.
13 SHAPE \* MERGEFORMAT 1415
2. Изображенные на рисунке фигуры 1,2,3,4 являются квадратами. При этом площадь квадрата 1 — 16 см13 EMBED Equation.3 1415, квадрата 2 -25 см13 EMBED Equation.3 1415. Найдите площадь квадрата -4?
2
4
1
3
3. Этап применения.
Этап применения.
Образец комплексного применения знаний. Но есть в царстве царя квадрата задачи над решением которых думают все жители квадратного государства. Давайте поможем им решить одну из них.
В 2 р Б
2
?
?
?
В 3 р БНа участке земли прямоугольной формы расположились четыре прямоугольных участка, на трех из которых выращивали любимые ягоды царской семьи. 2 десятины занимала клубника, 4 десятины занимала смородина, 6 десятин занимала малина, оставшаяся четвертая часть пустовала так как это была болотистая местность и измерить ее не было никакой возможности. Давайте поможем найти ее площадь.
Тест
Вариант 1
А1. Найдите площадь квадрата, сторона которого равна 9 см.
1) 36 см2 2) 81 см 3) 81 см2 4) 18 см2
А2. Найдите площадь прямоугольника со сторонами 4 см и 8 см.
1) 32 см2 2) 24 см2 3) 80 см2 4) 32 см
А3. Найдите периметр прямоугольника, площадь которого равна 48 см2, а одна из его сторон — 4 см.
1) 64 см 2) 32см 3) 24 см 4) 52 см
В1.Сколько килограммов удобрений потребуется
на участок, если на каждый ар нужно 3 кг.удобрений.
30м
40м 20м
50м
С1.Оконная рама представляет собой прямоугольник, разбитый на три меньших равных между собой прямоугольника. Известно, что периметр самого большего прямоугольника равен 6 м. Найдите площадь одного из трех одинаковых стекол, необходимых для остекленения . Ответ дайте в квадратных дециметрах.
13 SHAPE \* MERGEFORMAT 1415
Тест
Вариант 2
А1. Найдите площадь квадрата, сторона которого равна 3 см.
1) 6 см2 2) 12 см 3) 12 см2 4) 9 см2
А2. Найдите площадь прямоугольника со сторонами 13 см и 5 см.
1) 36 см2 2) 65 см2 3) 18 см2 4) 65 см
А3. Найдите периметр прямоугольника, площадь которого равна 132 см2, а одна из его сторон — 12 см.
1) 23 см 2) 44 см 3) 46 см 4) 56см 20м
В1. Сколько килограммов семян потребуется
Сколько килограммов семян потребуется
на участок, если на каждый ар нужно 30 кг.семян.
60м
30м
50м
С1. Оконная рама представляет собой прямоугольник, разбитый на три меньших равных между собой прямоугольника. Известно, что периметр самого большего прямоугольника равен 5 м. Найдите площадь одного из трех одинаковых стекол, необходимых для остекленения . Ответ дайте в квадратных дециметрах.
13 SHAPE \* MERGEFORMAT 1415
4. Этап контроля и самоконтроля.
Вариант
А1
А2
А3
В1
С1
1
3
1
2
42
72
2
4
2
3
630
50
5. Подведение итогов.
6. Информация о домашнем задании.
7. Рефлексия
На доске записаны предложения. Ученикам предлагается их закончить.
После изучения темы: «Площадь Единицы измерения площадей» могу сказать
Сегодня на уроке я испытал
Математика мой любимый предмет и
Математика не мой любимый предмет, но
Я люблю решать сложные задачи
4
4
4
4
Root Entry
Приложенные файлы
- 6337867
Размер файла: 68 kB Загрузок: 0
|
Класс |
Предмет |
Домашние задания |
|
8 А |
Английский язык |
Упр. |
|
8 А |
Химия |
Прочитать п.20, упр.6 (письменно) |
|
8 А |
Русский язык |
Стр.96-98 теория упр.198 |
|
8 А |
География |
Параграф 22, читать. Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22) |
|
8 А |
Геометрия |
Решить тест по теме: «Площадь и периметр геометрических фигур» I вариант 1. Найдите площадь прямоугольника, если его стороны равны 18 см и 7 см 2. 3. Найдите площадь квадрата со стороной 16 см 4. Найдите периметр квадрата со стороной 16 см 5. Найдите площадь параллелограмма, если его сторона 23 см, а высота, проведённая к этой стороне 17 см 6. Найдите площадь треугольника, если его сторона 24 см, а высота, проведённая к этой стороне 13 см 7. Найдите площадь прямоугольного треугольника, если его катеты 14 см и 21 см 8. Найдите площадь треугольника, если его стороны 3 см, 4 см и 5 см. 9. Найдите площадь трапеции, если её основания 17 см и 19 см, а высота 31 см 10. Найдите площадь ромба диагонали которого 40 см и 30 см. |
|
8 А |
Физика |
П. 18 читать, составить тест и ответы к нему |
|
8 А |
Литература |
Поэму «Мцыри» прочитать, озаглавить каждую главу строчкой из текста. |
|
8 А |
Родной язык |
Упр. 63 |
|
8 Б |
Английский язык |
Стр.52-53, упр.6 (учить слова). |
|
8 Б |
Алгебра |
Решить: № 366 |
|
8 Б |
Геометрия |
Пройти по ссылке: https://edu.skysmart.ru/student/lidixemuxe |
|
8 Б |
Литература |
Прочитать поэму «Мцыри» Лермонтова, составить план поэмы |
|
8 Б |
География |
Параграф 22, читать. |
|
8 Б |
Химия |
Прочитать п.20, упр.6 (письменно) |
|
8 Б |
Физика |
П. 18 читать, составить тест и ответы к нему |
|
8 В |
Геометрия |
Выучить урок: https://resh.edu.ru/subject/lesson/1493/start/ (разделы «Начнём урок» № 1-2; «Тренировочные задания»№ 1-8). Все записи урока выполнить в тетради по геометрии. Отправлять фото учителю НЕ НУЖНО. Приготовиться отвечать на онлайн-уроке. |
|
8 В |
Английский язык |
Упр. |
|
8 В |
Литература |
Прочитать поэму «Мцыри» Лермонтова, составить план поэмы |
|
8 В |
Химия |
Прочитать п.20, упр.6 (письменно) |
|
8 В |
ФЗК |
Выполнить комплекс общеразвивающих упражнений по ссылке https://www.youtube.com/watch?v=djy0zIOXat0 |
|
8 В |
Родной язык |
Написать сообщение «Русский человек в обращении к другим» |
|
8 В |
Русский язык |
П. |
|
8 Г |
География |
Параграф 22, читать. Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22) |
|
8 Г |
Геометрия |
Выучить урок: https://resh.edu.ru/subject/lesson/1493/start/ (разделы «Начнём урок» № 1-2; «Тренировочные задания»№ 1-8). Все записи урока выполнить в тетради по геометрии. Отправлять фото учителю НЕ НУЖНО. Приготовиться отвечать на онлайн-уроке. |
|
8 Г |
Химия |
прочитать п.20, упр.6 (письменно) |
|
8 Г |
Английский язык |
Стр. |
|
8 Г |
Литература |
Прочитать поэму «Мцыри» Лермонтова, составить план поэмы |
|
8 Г |
География Рыбаков |
Прочитать учебник на стр. 70-75, читать, с.75, вопрос 2 (письменно). |
|
8 Г |
История |
Тема: Великие просветители Европы. Задание: Посмотреть фильм и подготовить небольшой рассказ о Дж. Локке, ЖЖ.Руссо, Вольтер, Ш.Монтескьё. ( о любом из этих просветителей) |
|
8 Г |
ФЗК |
Выполнить комплекс общеразвивающих упражнений по ссылке https://www.youtube.com/watch?v=djy0zIOXat0 |
|
8 Д |
Английский язык |
Стр. |
|
8 Д |
Литература |
Прочитать поэму «Мцыри» Лермонтова, составить план поэмы |
|
8 Д |
Физика |
П. 18 читать, составить тест и ответы к нему |
|
8 Д |
Геометрия |
Выучить урок: https://resh.edu.ru/subject/lesson/1493/start/ (разделы «Начнём урок» № 1-2; «Тренировочные задания»№ 1-8). Все записи урока выполнить в тетради по геометрии. Отправлять фото учителю НЕ НУЖНО. Приготовиться отвечать на онлайн-уроке. |
|
8 Д |
История |
Тема: Великие просветители Европы. Задание: Посмотреть фильм и подготовить небольшой рассказ о Дж. |
|
8 Д |
География |
Параграф 22, читать. Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22) |
|
8 Д |
Химия |
Прочитать п.20, упр.6 (письменно) |
|
8 Е |
История |
Тема: Великие просветители Европы. Задание: Посмотреть фильм и подготовить небольшой рассказ о Дж. Локке, ЖЖ.Руссо, Вольтер, Ш.Монтескьё. ( о любом из этих просветителей) |
|
8 Е |
География |
Параграф 22, читать. Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22) |
|
8 Е |
Английский язык |
Стр. |
|
8 Е |
Физика |
П. 18 читать, составить тест и ответы к нему |
|
8 Е |
Химия |
Прочитать п.20, упр.6 (письменно) |
|
8 Е |
ФЗК |
Написать краткое сообщение на тему: «Тактика игры баскетбол в нападении» |
|
8 Е |
Геометрия |
Решить тест по теме: «Площадь и периметр геометрических фигур» I вариант 1. Найдите площадь прямоугольника, если его стороны равны 18 см и 7 см 2. Найдите периметр прямоугольника, если его стороны равны 18 см и 7 см 3. Найдите площадь квадрата со стороной 16 см 4. 5. Найдите площадь параллелограмма, если его сторона 23 см, а высота, проведённая к этой стороне 17 см 6. Найдите площадь треугольника, если его сторона 24 см, а высота, проведённая к этой стороне 13 см 7. Найдите площадь прямоугольного треугольника, если его катеты 14 см и 21 см 8. Найдите площадь треугольника, если его стороны 3 см, 4 см и 5 см. 9. Найдите площадь трапеции, если её основания 17 см и 19 см, а высота 31 см 10. Найдите площадь ромба диагонали которого 40 см и 30 см. |
Задачи на нахождение площади и периметра геометрических фигур
Задачи на нахождение площади и периметра
геометрических фигур
Составила:
учитель начальных классов
МКОУ СОШ №1 имени А.М.Горького
городского округа город Фролово
Кислова Людмила Борисовна
г. Фролово– 2014 год
Фролово– 2014 год
I уровень.
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше.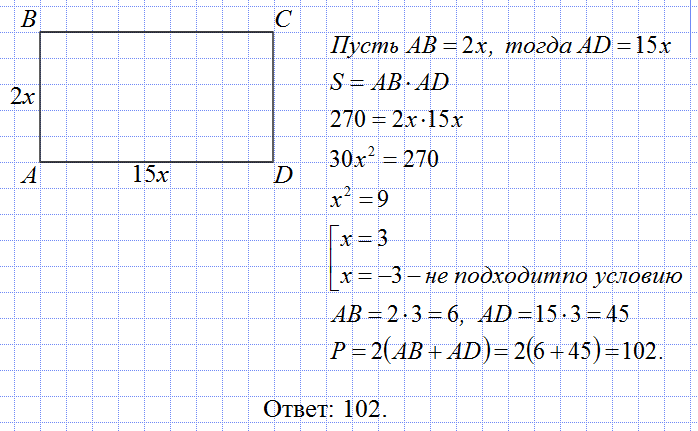 Найдите Р и S этого прямоугольника.
Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м. Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12.Найдите площадь квадрата, периметр которого равен 360 мм.
13.Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14.Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15.Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16.Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17.У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18.Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20.Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Использованы ресурсы сети Интернет
Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2. — МегаЛекции
78) 80) 81) 82) 83) 84) 85)
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1 : 2.
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.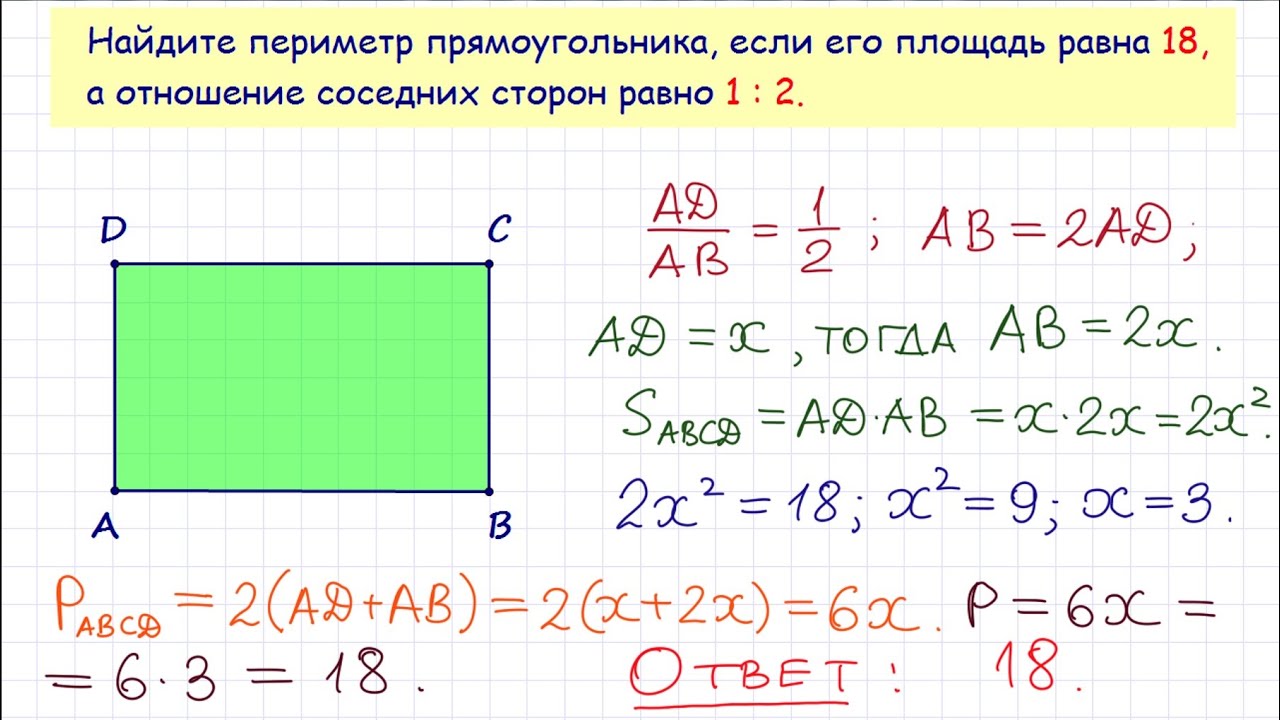
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6.
Найдите площадь прямоугольника.
Даны два квадрата, диагонали которых равны 10 и 6.
Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10.
Найдите высоту, опущенную на вторую сторону параллелограмма.
94) 95) 96) 97)
Площадь параллелограмма равна 40, две его стороны равны 5 и 10.
Найдите большую высоту этого параллелограмма.
99) № 27613_ Найдите площадь ромба, если его высота равна 2, а острый угол 30 .
Найдите площадь ромба, если его диагонали равны 4 и 12.
Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно
И 10.
Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого.
Найдите меньший катет.
Боковая сторона равнобедренного треугольника равна 5, а основание равно 6.
Найдите площадь этого треугольника.
106) № 27620_ Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30 .
Найдите боковую сторону треугольника, если его площадь равна 25.
107) № 27621_ Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150 .
Найдите боковую сторону треугольника, если его площадь равна 100.
108) № 27622_ Площадь остроугольного треугольника равна . Две его стороны равны и .
Найдите угол между этими сторонами. Ответ дайте в градусах.
У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам.
Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Периметр треугольника равен 12, а радиус вписанной окружности равен 1.
Найдите площадь этого треугольника.
Площадь треугольника равна 24, а радиус вписанной окружности равен 2.
Найдите периметр этого треугольника.
Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
Найдите среднюю линию трапеции.
Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
Диагностическая работа по теме «Вычисление площадей». ( 9 класс)
Диагностическая работа
Вычисление площадей
Модуль «Геометрия»
В С П О М Н И формулы
Площадь
прямоугольного треугольника
Формула расчета площади треугольника
S = a · b · sin С
2
где a, b — стороны г треугольника, прилежащие к углу C.
Формула площади трапеции
S = h · ( a + b ) / 2
где h — высота трапеции, a и b — верхнее и нижнее основания трапеции.
S=a h
Площадь параллелограмма
№ 1
Площадь прямоугольного треугольника равна 99. Один из его катетов равен 33.
Найдите другой катет.
№ 2
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30º. Боковая сторона треугольника равна 8. Найдите площадь этого треугольника.
№ 3
Найдите периметр прямоугольника, если его площадь равна 28, а отношение соседних сторон равно 1 : 7.
№ 4
В прямоугольной трапеции основания равны 5 см и 17 см, а большая боковая сторона — 13 см. Найдите площадь трапеции.
№ 5
Диагонали ромба равны 12 и 8.
Найдите его площадь.
№ 6
Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания
равны 2 и 6.
№ 7
Площадь параллелограмма ABCD равна 184. Точка E — середина стороны AB. Найдите площадь трапеции EBCD.
№ 8
Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10.
Найдите площадь трапеции.
№ 9
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
№ 10
Найдите площадь трапеции, три стороны которой равны 5 а четвертая равна 11.
Решение:
Если 3 стороны равны по 5, то трапеция — равнобокая.
Высота её равна √(5² — ((11-5) : 2)²) = √(25 — 9)= √16 = 4.
S = ((5+11) : 2) · 4 = 8 · 4 = 32 кв.ед .
№ 11
Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
№ 11 решение
Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
Решение :
Формула площади трапеции :
Зная основания и площадь, можем записать:
Ответ: 8
Р Е Ф Л Е К С И Я !
Задание: закончить одно из трех предложений, которое больше других соответствует вашему состоянию.
“ Выполнять задания и решать задачи мне трудно, так как …”
“ Выполнять задания и решать задачи мне легко, так как …”
“ Выполнять задания и решать задачи для меня занятие приятное и интересное, потому что…”
У д а ч и !
Подготовка к ГИА по математике.Площади фигур
Подготовила: учитель математики
Категория: первая
Быстролетова Татьяна Дмитриевна
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №1 им. Ляпидевского
Ляпидевского
Станица Старощербиновская Щербиновского района Краснодарского края
Подготовка к ГИА.
Площади фигур.
2014 г.
Для учителей выпускных классов наиболее важным завершением учебного года являются экзамены девятиклассников и одиннадцатиклассников – ЕГЭ и ГИА. Всем очень хочется подготовить своих выпускников так, чтобы они сдали экзамены на максимальный балл. В интернете огромное количество сайтов предлагающих те или иные методы подготовки, огромнейшее количество литературы, но ничто и никто не поможет нашим детям сдать экзамен хорошо, чем мы сами. Представленная работа может помочь учителю в обобщении и систематизации знаний по теме «Площади фигур», ее можно использовать на любом этапе урока. Понятие площади и её свойств изучаются с опорой на наглядные представления обучающихся и их жизненный опыт. Вычисление площадей многоугольников и круга является составной частью решения задач на многогранники и тела вращения в курсе стереометрии. Поэтому при изучении данной темы основное внимание необходимо уделять формированию самого представления площади и формированию практических навыков вычисления площадей плоских фигур в ходе решения соответствующих задач.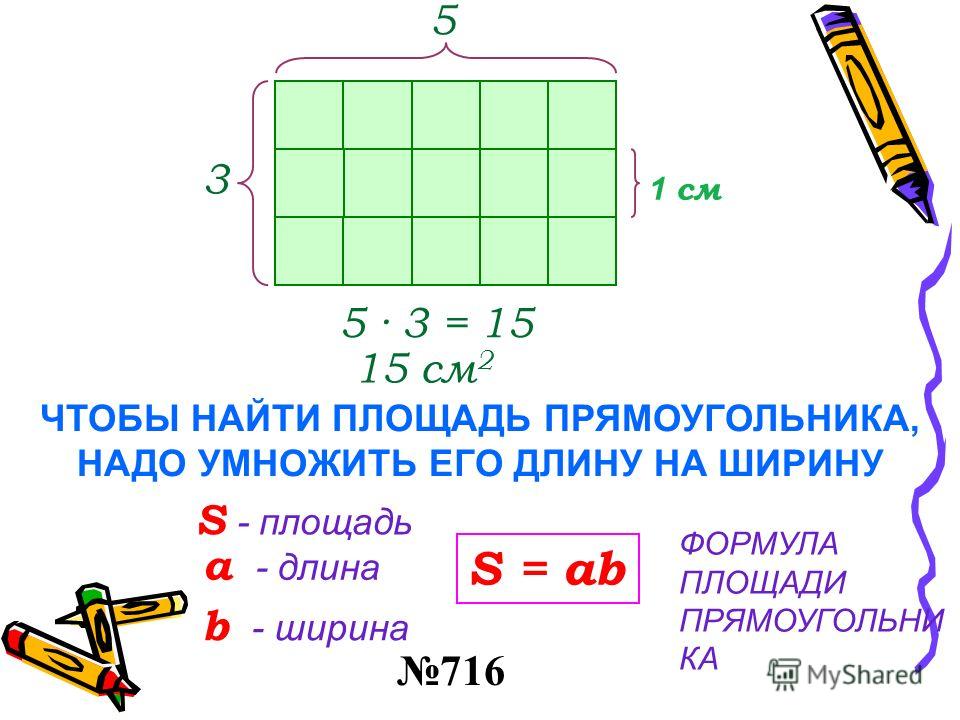 Поэтому данный материал направлен на закрепление и повторения умений решать задачи на нахождение площадей фигур.
Поэтому данный материал направлен на закрепление и повторения умений решать задачи на нахождение площадей фигур.
Данная работа состоит из 1 части (работа в классе ) и подробного разбора заданий.
Работа в классе
1. B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
2. B 8 № 65. Найдите площадь параллелограмма, изображённого на рисунке.
3. B 8 № 91. Найдите площадь параллелограмма, изображённого на рисунке.
4. B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
5. B 8 № 143. Найдите площадь трапеции, изображённой на рисунке.
6. B 8 № 195. Найдите площадь параллелограмма, изображённого на рисунке.
7. B 8 № 169839. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен . Найдите площадь треугольника.
8. B 8 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Найдите площадь треугольника.
9. B 8 № 169841. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
10. B 8 № 169842. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен . Найдите площадь треугольника.
11. B 8 № 169847. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
12. B 8 № 169848. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на .
13. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь,делённую на
14. B 8 № 169850. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
15. B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
16. B 8 № 169852. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника.
17. B 8 № 169853. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
18. B 8 № 169854. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.
19. B 8 № 169855. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 45°. Найдите площадь треугольника.
20. B 8 № 169856. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 120°. Найдите площадь треугольника.
21. B 8 № 169857. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 135°. Найдите площадь треугольника.
Найдите площадь треугольника.
22. B 8 № 169858. В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
23. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен . Найдите площадь треугольника.
24. B 8 № 169860. В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен . Найдите площадь треугольника.
25. B 8 № 169862. Сторона квадрата равна 10. Найдите его площадь.
26. B 8 № 169863. Периметр квадрата равен 40. Найдите площадь квадрата.
27. B 8 № 169864. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
28. B 8 № 169865. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
29. B 8 № 169866. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
30. B 8 № 169867. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
31. B 8 № 169868. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
32. B 8 № 169869. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
33. B 8 № 169870. Периметр ромба равен 40, а один из углов равен 45°. Найдите площадь ромба,делённую на .
34. B 8 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба,делённую на .
35. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
36. B 8 № 169873. Периметр ромба равен 24, а косинус одного из углов равен . Найдите площадь ромба.
37. B 8 № 169874. Периметр ромба равен 24, а тангенс одного из углов равен . Найдите площадь ромба.
38. B 8 № 169875. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
39. B 8 № 169876. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
40. B 8 № 169877. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на .
41. B 8 № 169878. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
42. B 8 № 169879. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
43. B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
44. B 8 № 169881. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
45. B 8 № 169882. Основания трапеции равны 18 и 10, одна из боковых сторон равна , а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
46. B 8 № 169883. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
47. B 8 № 169884. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
48. B 8 № 169885. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен . Найдите площадь трапеции.
Найдите площадь трапеции.
49. B 8 № 169886. Радиус круга равен 1. Найдите его площадь, деленную на π.
50. B 8 № 169887. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
51. B 8 № 169888. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
52. B 8 № 169889. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
53. B 8 № 169890. В прямоугольном треугольнике один из катетов равен , острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
54. B 8 № 169891. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
55. B 8 № 169892. В прямоугольном треугольнике один из катетов равен , угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
56. B 8 № 169893. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
57. B 8 № 169894. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на
58. B 8 № 169895. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на
Найдите площадь треугольника, деленную на
59. B 8 № 169896. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на
60. B 8 № 169897. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
61. B 8 № 169898. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
62. B 8 № 169899. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, деленную на
63. B 8 № 169900. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
Найдите площадь ромба.
64. B 8 № 169901. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на
65. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на
66. B 8 № 169903. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на
67. B 8 № 169904. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
68. B 8 № 169905. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на
69. B 8 № 169906. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
Найдите площадь ромба.
70. B 8 № 169908. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на
71. B 8 № 169909. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на
72. B 8 № 169910. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
73. B 8 № 169911. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь ромба, деленную на
74. B 8 № 169912. Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
75. B 8 № 169913. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
76. B 8 № 311332. В равнобедренном треугольнике . Найдите , если высота .
77. B 8 № 311375. В равнобедренном треугольнике . Найдите , если высота .
78. B 8 № 311387. В треугольнике угол равен 90°, . Найдите .
79. B 8 № 311399. В треугольнике угол равен 90°, . Найдите .
80. B 8 № 311411. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
81. B 8 № 311475. Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
82. B 8 № 311480. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
Найдите большее основание трапеции.
83. B 8 № 311498. В треугольнике угол прямой, . Найдите .
84. B 8 № 311500. В треугольнике угол прямой, . Найдите .
85. B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.
86. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
87. B 8 № 311849. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
88. B 8 № 311913. Найдите площадь параллелограмма, изображённого на рисунке.
89. B 8 № 311957.
Найдите площадь параллелограмма, изображённого на рисунке.
90. B 8 № 314870. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
91. B 8 № 314876. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
92. B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
93. B 8 № 315000. Найдите площадь параллелограмма, изображённого на рисунке.
94. B 8 № 315074. Найдите площадь параллелограмма, изображённого на рисунке.
95. B 8 № 315084. Найдите площадь параллелограмма, изображённого на рисунке.
96. B 8 № 316231. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
97. B 8 № 316258. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
98. B 8 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.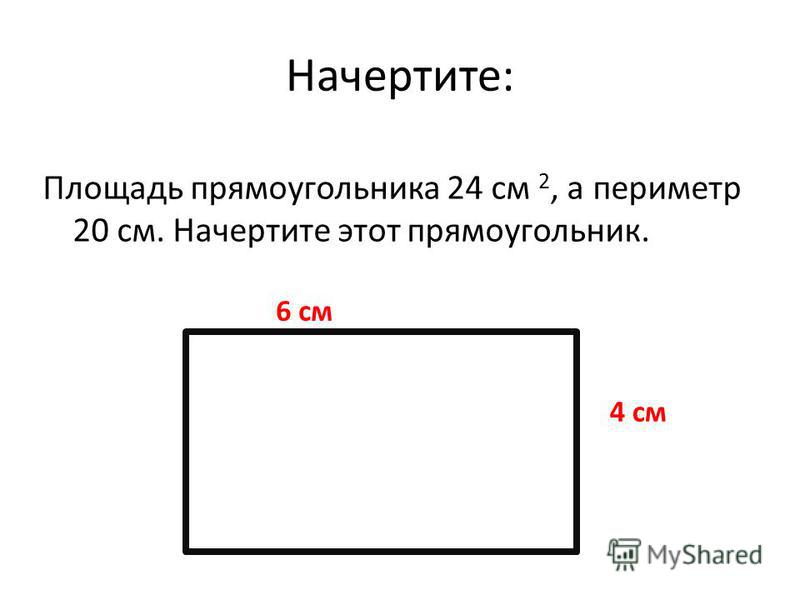
99. B 8 № 316321. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
100. B 8 № 316347. Найдите площадь трапеции, изображённой на рисунке.
101. B 8 № 316373. Найдите площадь трапеции, изображённой на рисунке.
102. B 8 № 322861. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
103. B 8 № 323159. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
104. B 8 № 323179. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
105. B 8 № 323282. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
106. B 8 № 323285. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
Найдите площадь треугольника.
107. B 8 № 323297.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
108. B 8 № 323356. В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
109. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
110. B 8 № 323416. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
111. B 8 № 323430.
Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.
112. B 8 № 323436. Найдите площадь треугольника, изображённого на рисунке.
113. B 8 № 323902. Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Найдите площадь трапеции.
114. B 8 № 323957. Найдите площадь ромба, если его диагонали равны 14 и 6.
115. B 8 № 323977. Периметр квадрата равен 160. Найдите площадь квадрата.
116. B 8 № 323997. Найдите площадь квадрата, если его диагональ равна 1.
117. B 8 № 324017. Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
118. B 8 № 324077. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
119. B 8 № 324097. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
120. B 8 № 324117. Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
121. B 8 № 324155. Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
122. B 8 № 324364. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
123. B 8 № 339837. Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
124. B 8 № 339859. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
125. B 8 № 340197. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
126. B 8 № 340367. Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
127. B 8 № 340408. В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Найдите площадь треугольника ABC.
Решения
1. B 8 № 39. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Ответ: 168.
2. B 8 № 65. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
Ответ: 40.
3. B 8 № 91. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
Ответ: 75.
4. B 8 № 117. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Ответ: 28.
5. B 8 № 143. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Ответ: 36.
6. B 8 № 195. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению длины основания на высоту:
Ответ: 20.
7. B 8 № 169839. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен . Найдите площадь треугольника.
Решение.
Пусть x — длина второго катета. Так как треугольник прямоугольный, по определению тангенса имеем:
.
Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
.
———-
Иррациональный ответ.
8. B 8 № 169840. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
Решение.
Так как в прямоугольном треугольнике один из углов равен 45°, то такой треугольник является равнобедренным. Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
Ответ: 50.
9. B 8 № 169841. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение.
Так как в прямоугольном треугольнике один из углов равен 45°, треугольник является равнобедренным. Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
Ответ: 50.
10. B 8 № 169842. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен . Найдите площадь треугольника.
Найдите площадь треугольника.
Решение.
Пусть x — длина второго катета. Так как треугольник прямоугольный, по определению тангенса имеем:
.
Площадь прямоугольного треугольника равна половине произведения катетов. Таким образом:
.
———-
Иррациональный ответ.
11. B 8 № 169847. Сторона равностороннего треугольника равна 10. Найдите его площадь,делённую на .
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Так как угол равностороннего треугольника равен 60° и все стороны равны 10, имеем:
Ответ: 25.
———-
В открытом банке иррациональный ответ.
12. B 8 № 169848. Периметр равностороннего треугольника равен 30. Найдите его площадь,делённую на .
Решение.
Так как в равностороннем треугольнике все стороны равны, то сторона данного треугольника равна 10. Угол равностороннего треугольника равен 60°. Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
Ответ: 25.
———-
В открытом банке иррациональный ответ.
13. B 8 № 169849. Высота равностороннего треугольника равна 10. Найдите его площадь,делённую на
Решение.
Высота равностороннего треугольника равна Таким образом, сторона равностороннего треугольника равна Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 100.
———-
В открытом банке иррациональный ответ.
14. B 8 № 169850. В равнобедренном треугольнике боковая сторона равна 10, а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, делённую на
Найдите площадь треугольника, делённую на
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними, имеем:
Ответ: 25.
———-
В открытом банке иррациональный ответ.
15. B 8 № 169851. Периметр равнобедренного треугольника равен 16, а боковая сторона — 5. Найдите площадь треугольника.
Решение.
Так как боковая сторона равнобедренного треугольника равна 5, его основание равно 6, а полупериметр: тогда по формуле Герона имеем:
Ответ: 12.
16. B 8 № 169852. Периметр равнобедренного треугольника равен 16, а основание — 6. Найдите площадь треугольника.
Решение.
Так как сторона основания равнобедренного треугольника равна 6, его боковая сторона 5, а полупериметр: тогда по формуле Герона имеем:
Ответ: 12.
17. B 8 № 169853. В треугольнике одна из сторон равна 10, а опущенная на нее высота — 5. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения высоты на основание. Таким образом:
Ответ: 25.
18. B 8 № 169854. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 60°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 75.
19. B 8 № 169855. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 45°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 50.
20. B 8 № 169856. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 120°.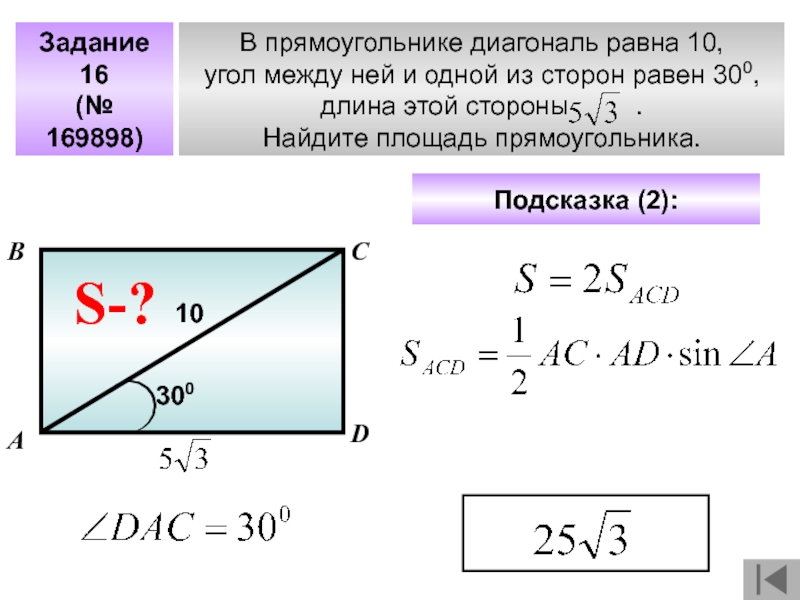 Найдите площадь треугольника.
Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 75.
21. B 8 № 169857. В треугольнике одна из сторон равна 10, другая равна , а угол между ними равен 135°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 50.
22. B 8 № 169858. В треугольнике одна из сторон равна 10, другая равна 12, а угол между ними равен 30°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 30.
23. B 8 № 169859. В треугольнике одна из сторон равна 12, другая равна 16, а синус угла между ними равен . Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Имеем:
Ответ: 24.
24. B 8 № 169860. В треугольнике одна из сторон равна 12, другая равна 10, а косинус угла между ними равен . Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:
Таким образом,
Ответ: 20.
25. B 8 № 169862. Сторона квадрата равна 10. Найдите его площадь.
Решение.
Площадь квадрата равна квадрату его стороны, поэтому она равна 100.
Ответ: 100.
26. B 8 № 169863. Периметр квадрата равен 40. Найдите площадь квадрата.
Решение.
Периметр квадрата равен сумме длин всех его сторон. Таким образом, сторона квадрата равна 10.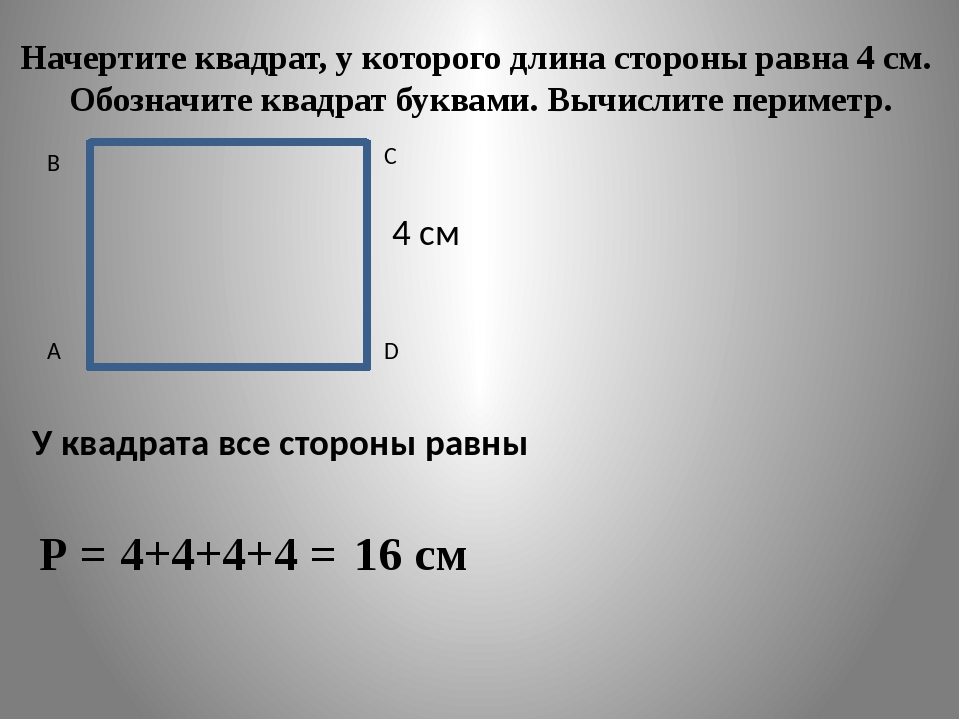 Площадь квадрата равна квадрату его стороны, поэтому она равна 100.
Площадь квадрата равна квадрату его стороны, поэтому она равна 100.
Ответ: 100.
27. B 8 № 169864. В прямоугольнике одна сторона равна 10, другая сторона равна 12. Найдите площадь прямоугольника.
Решение.
Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.
Ответ: 120.
28. B 8 № 169865. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.
Решение.
Противоположные стороны прямоугольника попарно равны. Пусть неизвестная сторона равна x, тогда периметр прямоугольника: 2x + 20 = 44, откуда x = 12. Площадь прямоугольника равна произведению его смежных сторон, поэтому она равна 120.
Ответ: 120.
29. B 8 № 169866. В прямоугольнике одна сторона равна 6, а диагональ равна 10. Найдите площадь прямоугольника.
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. По теореме Пифагора найдем длину неизвестной стороны, она равна Площадь прямоугольника равна произведению его смежных сторон. Таким образом,
Ответ: 48.
30. B 8 № 169867. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 30°. Найдите площадь прямоугольника, делённую на .
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен половине гипотенузы. Поэтому одна из сторон прямоугольника равна 5. По теореме Пифагора найдем вторую строну: Площадь прямоугольника равна произведению его смежных сторон, имеем:
Ответ: 25.
———-
В открытом банке иррациональный ответ.
31. B 8 № 169868. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
32. B 8 № 169869. Периметр ромба равен 40, а один из углов равен 30°. Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними. Таким образом,
Ответ: 50.
33. B 8 № 169870. Периметр ромба равен 40, а один из углов равен 45°.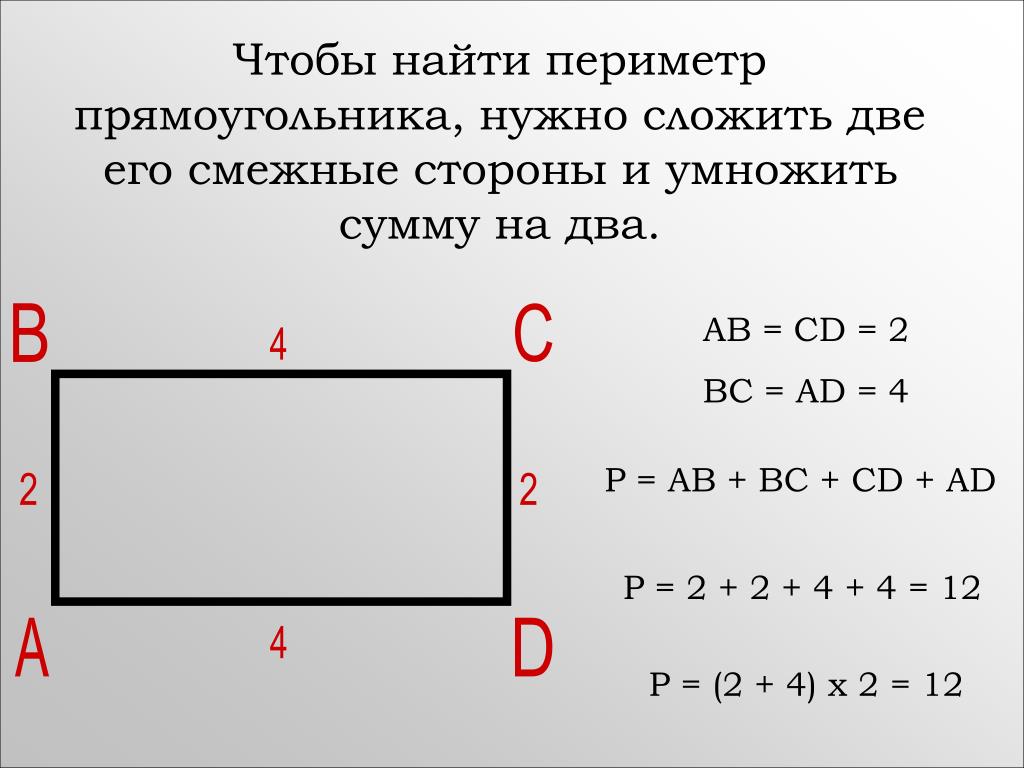 Найдите площадь ромба,делённую на .
Найдите площадь ромба,делённую на .
Решение.
Так как все стороны ромба равны, сторона данного ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
Ответ: 50.
———-
В открытом банке иррациональный ответ.
34. B 8 № 169871. Периметр ромба равен 40, а один из углов равен 60°. Найдите площадь ромба,делённую на .
Решение.
Так как все стороны ромба равны, сторона данного ромба равна 10. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
Ответ: 50.
———-
В открытом банке иррациональный ответ.
35. B 8 № 169872. Периметр ромба равен 24, а синус одного из углов равен . Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними, поэтому
Площадь ромба равна произведению сторон на синус угла между ними, поэтому
Ответ: 12.
36. B 8 № 169873. Периметр ромба равен 24, а косинус одного из углов равен . Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними. Синус угла найдем из основного тригонометрического тождества:
Таким образом,
Ответ: 12.
37. B 8 № 169874. Периметр ромба равен 24, а тангенс одного из углов равен . Найдите площадь ромба.
Решение.
Периметр ромба равен сумме длин всех его сторон. Так как все стороны равны, сторона ромба равна 6. Площадь ромба равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему.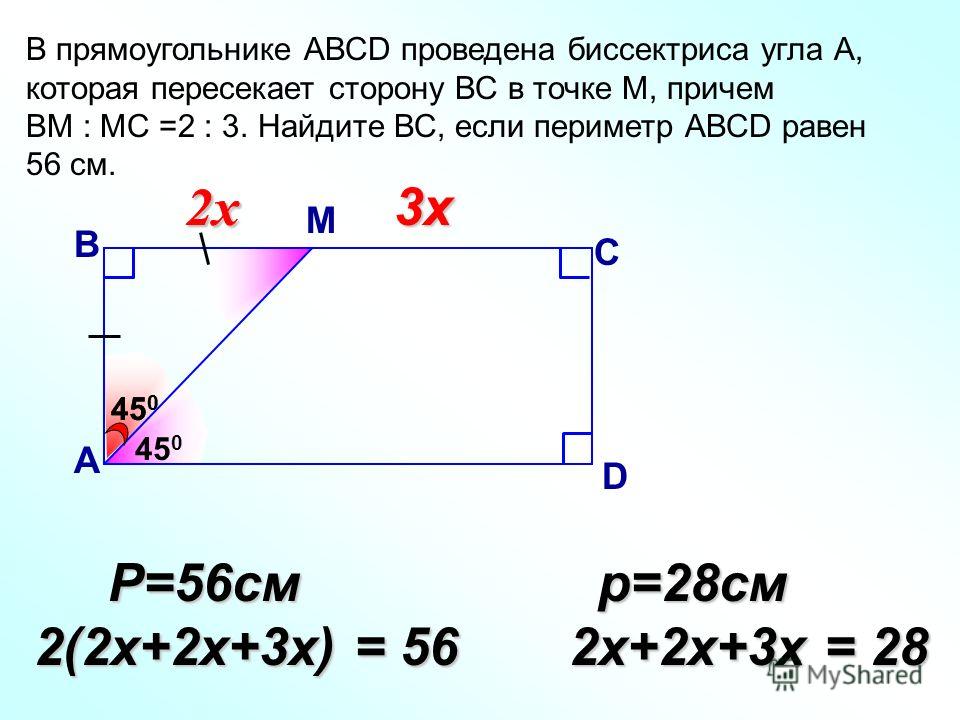 Имеем:
Имеем:
Таким образом, , где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
Таким образом,
Ответ: 12.
38. B 8 № 169875. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению высоты на основание. Таким образом,
Ответ: 120.
39. B 8 № 169876. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на .
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
Ответ: 30.
———-
В открытом банке иррациональный ответ.
40. B 8 № 169877. Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на .
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними:
Ответ: 30.
———-
В открытом банке иррациональный ответ.
41. B 8 № 169878. Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен . Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними, поэтому
Ответ: 20.
42. B 8 № 169879. Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен . Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Cинус угла найдем из основного тригонометрического тождества:
Таким образом,
Ответ: 20.
43. B 8 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен . Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
Таким образом, , где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
Таким образом,
Ответ: 20.
44. B 8 № 169881. Основания трапеции равны 18 и 12, одна из боковых сторон равна , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = , а ∠ABC = 135°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 135° − 90° = 45°. Таким образом треугольник ABH является прямоугольным и равнобедренным. Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 60.
45. B 8 № 169882. Основания трапеции равны 18 и 10, одна из боковых сторон равна , а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 10, AB = , а ∠ABC = 120°. Опустим перпендикуляр BH на сторону AD. Угол ABH равен: 120° − 90° = 30°. Найдем высоту BH:
Угол ABH равен: 120° − 90° = 30°. Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 84.
46. B 8 № 169883. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен . Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а Опустим перпендикуляр BH на сторонуAD. Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 30.
47. B 8 № 169884. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен . Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а Опустим перпендикулярBH на сторону AD.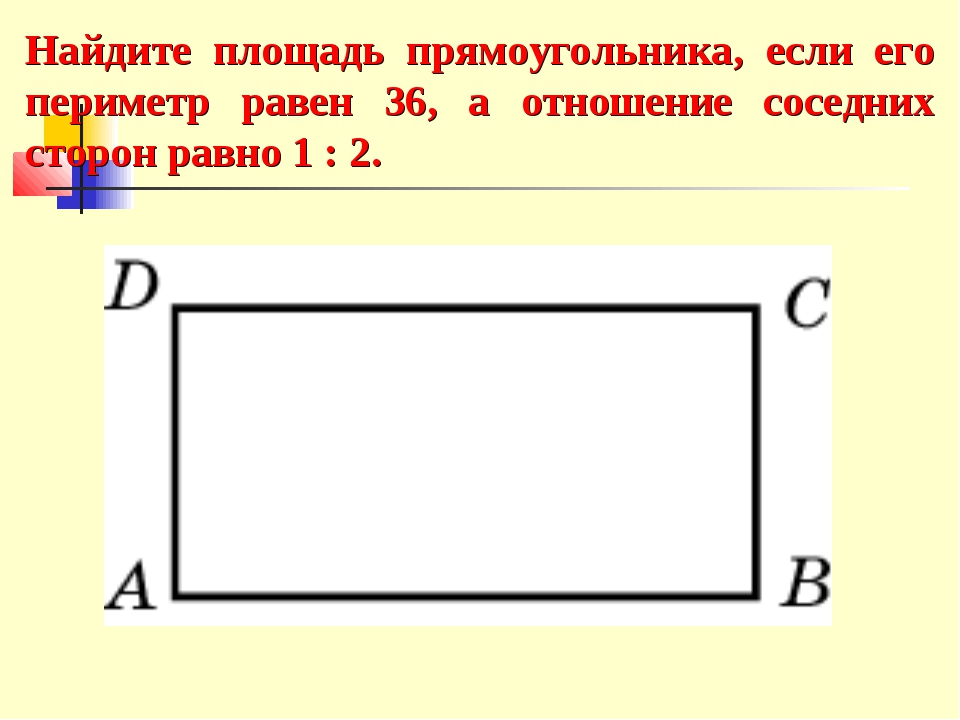 Найдем синус угла из основного тригонометрического тождества:
Найдем синус угла из основного тригонометрического тождества:
Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 30.
48. B 8 № 169885. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен . Найдите площадь трапеции.
Решение.
Пусть дана трапеция ABCD, где AD = 18, BC = 12, AB = 6, а Опустим перпендикулярBH на сторону AD. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
Таким образом, , где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
Имеем:
Найдем высоту BH:
Площадь трапеции равна полусумме оснований на высоту:
Ответ: 30.
49. B 8 № 169886. Радиус круга равен 1. Найдите его площадь, деленную на π.
Решение.
Площадь круга равна:
Ответ: 1.
—————
В открытом банке ответ c числом π.
50. B 8 № 169887. Найдите площадь кругового сектора, если радиус круга равен 3, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
Решение.
Площадь сектора равна:
Ответ: 3.
—————
В открытом банке ответ с числом π.
51. B 8 № 169888. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.
Решение.
Найдем радиус сектора из формулы длины дуги:
.
Площадь сектора равна:
Ответ: 27.
—————
В открытом банке ответ с числом π.
52. B 8 № 169889. В прямоугольном треугольнике один из катетов равен 10, острый угол, прилежащий к нему, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
Решение.
Найдем второй катет треугольника из определения тангенса:
Площадь прямоугольного треугольника равна половине произведения катетов:
Ответ: 50.
Примечание:
Второй катет можно было найти при помощи теоремы Пифагора.
———-
В открытом банке иррациональный ответ.
53. B 8 № 169890. В прямоугольном треугольнике один из катетов равен , острый угол, прилежащий к нему, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
Найдите площадь треугольника, делённую на .
Решение.
Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтому AC = 10. Площадь прямоугольного треугольника равна половине произведения катетов:
Ответ: 50.
———-
В открытом банке иррациональный ответ.
54. B 8 № 169891. В прямоугольном треугольнике один из катетов равен 10, угол, лежащий напротив него, равен 30°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
Решение.
Найдем второй катет по теореме Пифагора:
Площадь прямоугольного треугольника равна половине произведения катетов:
Ответ: 50.
Примечание:
Второй катет можно было найти из определения тангенса.
———-
В открытом банке иррациональный ответ.
55. B 8 № 169892. В прямоугольном треугольнике один из катетов равен , угол, лежащий напротив него, равен 60°, а гипотенуза равна 20. Найдите площадь треугольника, делённую на .
Решение.
Найдем второй катет по теореме Пифагора:
Площадь прямоугольного треугольника равна половине произведения катетов:
Ответ: 50.
Примечание:
Второй катет можно было найти из определения тангенса или из свойства угла, лежащего напротив 30°.
———-
В открытом банке иррациональный ответ.
56. B 8 № 169893. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 30°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
57. B 8 № 169894. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 45°. Найдите площадь треугольника, деленную на
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
58. B 8 № 169895. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 120°. Найдите площадь треугольника, деленную на
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
59. B 8 № 169896. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 135°. Найдите площадь треугольника, деленную на
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
———-
В открытом банке иррациональный ответ.
60. B 8 № 169897. В равнобедренном треугольнике боковая сторона равна 10, основание — , а угол, лежащий напротив основания, равен 150°. Найдите площадь треугольника.
Решение.
Площадь треугольника равна половине произведения сторон на синус угла между ними:
Ответ: 25.
Примечание:
Площадь треугольника можно было найти по формуле Герона.
61. B 8 № 169898. В прямоугольнике диагональ равна 10, угол между ней и одной из сторон равен 30°, длина этой стороны . Найдите площадь прямоугольника, деленную на
Решение.
Диагональ прямоугольника делит его на два прямоугольных треугольника. Катет, лежащий напротив угла в 30°, равен половине гипотенузы, поэтомуСD = 5. Площадь прямоугольника равна произведению его сторон:
Ответ: 25.
Примечание:
Вторую сторону можно было найти из определения синуса.
———-
В открытом банке иррациональный ответ.
62. B 8 № 169899. В прямоугольнике диагональ равна 10, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 5. Найдите площадь прямоугольника, деленную на
Решение.
Найдем вторую сторону по теореме Пифагора:
Площадь прямоугольника равна произведению его сторон:
Ответ: 25.
Примечание:
Вторую сторону можно было найти из определения синуса.
———-
В открытом банке иррациональный ответ.
63. B 8 № 169900. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 30°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
64. B 8 № 169901. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на
Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
———-
В открытом банке иррациональный ответ.
65. B 8 № 169902. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 120°. Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ: 50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
———-
В открытом банке иррациональный ответ.
66. B 8 № 169903. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 135°. Найдите площадь ромба, деленную на
Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
———-
В открытом банке иррациональный ответ.
67. B 8 № 169904. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 150°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
68. B 8 № 169905. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, лежащий напротив этой диагонали, равен 60°. Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ: 50.
69. B 8 № 169906. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 150°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
70. B 8 № 169908. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 60°. Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ: 50.
71. B 8 № 169909. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 45°. Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
———-
В открытом банке иррациональный ответ.
72. B 8 № 169910. В ромбе сторона равна 10, одна из диагоналей — , а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
73. B 8 № 169911. В ромбе сторона равна 10, одна из диагоналей — 10, а угол, из которого выходит эта диагональ, равен 120°. Найдите площадь ромба, деленную на
Решение.
Площадь ромба равна произведению сторон на синус угла между ними:
Ответ:50.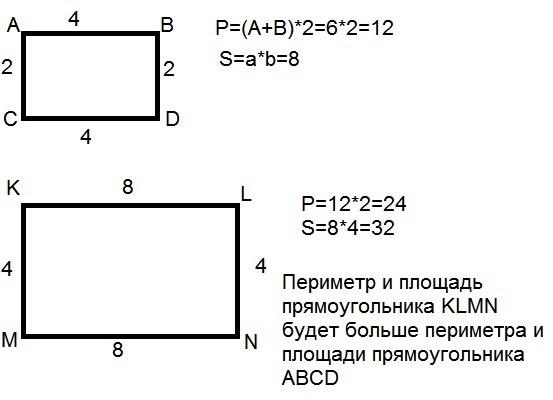
Примечание:
Можно найти вторую диагональ по теореме косинусов и вычислить площадь ромба как половина произведения диагоналей.
74. B 8 № 169912. Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.
Решение.
Площадь круга равна имеем:
Ответ: 9.
———-
В открытом банке ответ с числом .
75. B 8 № 169913. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите число, деленную на π.
Решение.
Площадь сектора равна имеем:
Ответ: 27.
76. B 8 № 311332. В равнобедренном треугольнике . Найдите , если высота .
Решение.
В равнобедренном треугольнике высота, опущенная на основание делит основание пополам, то есть делит пополам. Тогда получаем прямоугольный треугольник с двумя известными катетами и гипотенузой которого является искомая По теореме Пифагора найдем
Ответ: 13.
77. B 8 № 311375. В равнобедренном треугольнике . Найдите , если высота .
Решение.
По теореме Пифагора имеем:
Так как высота в равнобедренном треугольнике является медианой, то
Ответ: 12.
78. B 8 № 311387. В треугольнике угол равен 90°, . Найдите .
Решение.
Так как треугольник ABC — прямоугольный, то . Имеем:
Ответ: 21.
79. B 8 № 311399. В треугольнике угол равен 90°, . Найдите .
Решение.
Так как треугольник ABC — прямоугольный, то . Имеем:
Ответ: 33.
80. B 8 № 311411. Основания трапеции равны 4 см и 10 см. Диагональ трапеции делит среднюю линию на два отрезка. Найдите длину большего из них.
Решение.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
Так как KN — средняя линия трапеции, то KL и LN средние линии треугольников ABC и СAD соответственно.
,
Ответ: 5.
81. B 8 № 311475. Диагональ трапеции делит её среднюю линию на отрезки, равные 4 см и 3 см. Найдите меньшее основание трапеции.
Решение.
Пусть KN — средняя линия трапеции, где L — точка пересечения с диагональю.
Так как KN — средняя линия трапеции , то KL и LN средние линии треугольников ABC и СAD соответственно.
Таким образом, длина меньшего основания равна 6 см.
Ответ: 6.
82. B 8 № 311480. Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
Решение.
Средняя линия трапеции равна полусумме оснований. Имеем:
Ответ: 17.
83. B 8 № 311498. В треугольнике угол прямой, . Найдите .
Решение.
Треугольник ABC — прямоугольный. Таким образом,
Ответ: 20.
84. B 8 № 311500. В треугольнике угол прямой, . Найдите .
Решение.
Треугольник ABC — прямоугольный. Таким образом,
Ответ: 30.
85. B 8 № 311682. Найдите площадь трапеции, изображённой на рисунке.
Решение.
По формуле площади трапеции имеем:
Ответ: 168.
86. B 8 № 311761. Найдите площадь прямоугольника, если его периметр равен 44 и одна сторона на 2 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника. Тогда периметр прямоугольника равен откуда Поэтому площадь прямоугольника равна
Ответ: 120.
87. B 8 № 311849. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
откуда Поэтому площадь прямоугольника равна
Ответ: 176.
88. B 8 № 311913. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 7 · 4 = 28.
Ответ: 28.
89. B 8 № 311957.
Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 24 · (2 + 7) = 216.
Ответ: 216.
90. B 8 № 314870. Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапецииAECB.
Решение.
Диагональ параллелограмма делит его на два равных треугольника, поэтому Медиана треугольника делит его на два равновеликих треугольника, поэтому Следовательно,
Ответ: 42.
91. B 8 № 314876. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Решение.
Площадь трапеции вычисляется по формуле
где и — основания, а — высота трапеции. Найдём высоту: следовательно,
Ответ: 15.
92. B 8 № 314882. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Решение.
Введём обозначения, как показано на рисунке. Тогда Треугольник прямоугольный и равнобедренный, тогда высота равна 3. Откуда
Ответ:
93. B 8 № 315000. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению высоты на основание, поэтому она равна
Ответ: 20.
94. B 8 № 315074. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Найдите площадь параллелограмма, изображённого на рисунке.
95. B 8 № 315084. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Найдите площадь параллелограмма, изображённого на рисунке.
96. B 8 № 316231. Найдите площадь прямоугольника, если его периметр равен 92, а отношение соседних сторон равно 3:20.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
откуда Поэтому площадь прямоугольника равна
Ответ: 240.
——————
Дублирует задание 311817.
97. B 8 № 316258. Найдите площадь прямоугольника, если его периметр равен 60, а отношение соседних сторон равно 4:11.
Решение.
Площадь прямоугольника равна произведению его сторон.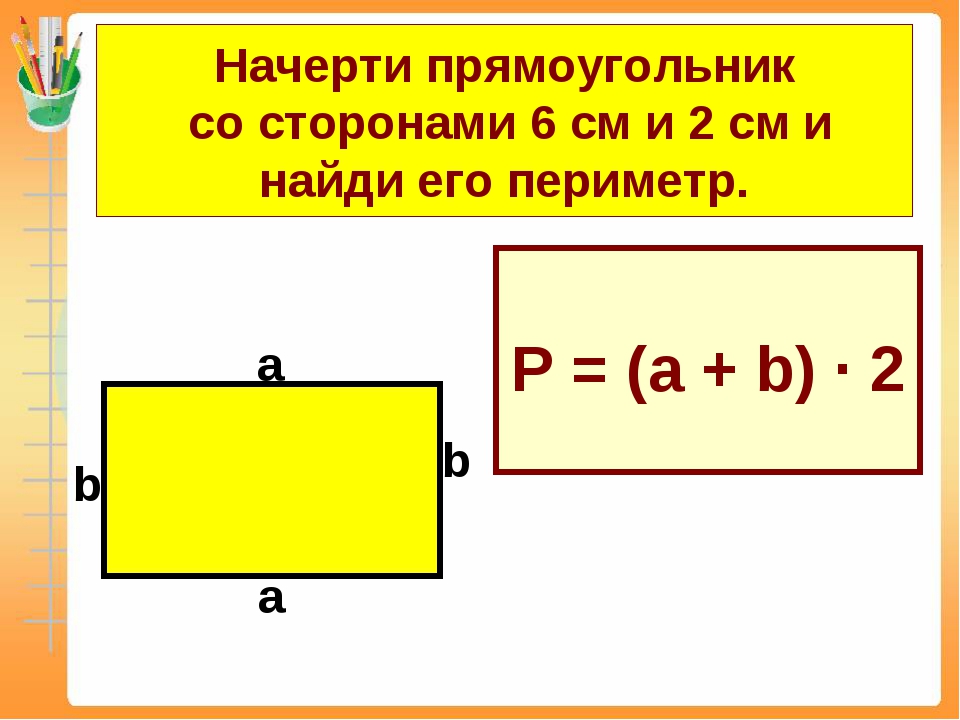 Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
откуда Поэтому площадь прямоугольника равна
Ответ: 176.
————————-
Дублирует задание 311849.
98. B 8 № 316284. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — большая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
откуда Поэтому площадь прямоугольника равна
Ответ: 270.
99. B 8 № 316321. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника. Пусть x — меньшая сторона прямоугольника, тогда другая сторона равна Следовательно, периметр прямоугольника равен
откуда Поэтому площадь прямоугольника равна
Ответ: 204.
100. B 8 № 316347. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 324.
101. B 8 № 316373. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 270.
102. B 8 № 322861. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Решение.
Площадь получившейся фигуры равна разности площадей квадрата и прямоугольника: 6 · 6 − 4 · 2 = 28.
Ответ: 28.
103. B 8 № 323159. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
Решение.
Пусть катеты имеют длины и а гипотенуза — длину Пусть длина высоты, проведённой к гипотенузе равна Найдём длину неизвестного катета из теоремы Пифагора:
Площадь прямоугольного треугольника может быть найдена как половина произведения катетов:
Ответ: 672.
104. B 8 № 323179. Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.
Решение.
Пусть — длина основания равнобедренного треугольника, — длина боковой стороны равнобедренного треугольника, — длина основания проведённого к высоте. Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
Высота равнобедренного треугольника, проедённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
Площадь треугольника равна половине произведения основания на высоту:
Ответ: 136.
105. B 8 № 323282. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 4. Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Ответ: 8.
106. B 8 № 323285. В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что второй катет равен 35. Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Ответ: 612,5.
107. B 8 № 323297.
В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него равен 45∘. Найдите площадь треугольника.
108. B 8 № 323356. В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°. Найдите площадь треугольника.
Решение.
Сумма углов в треугольнике равна 180°, поэтому второй острый угол равен 180° − 90° − 45° = 45°. Оба острых угла равны, следовательно, данный треугольник — равнобедренный, откуда получаем, что оба катета равны. Длина катета равна Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Длина катета равна Площадь прямоугольного треугольника можно найти как половину произведения катетов:
Ответ: 1225.
109. B 8 № 323396. Периметр равнобедренного треугольника равен 216, а боковая сторона — 78. Найдите площадь треугольника.
Решение.
Периметр треугольника равен сумме длин его сторон, поэтому длина основания равна 216 − 78 − 78 = 60. Высота проведённая к основанию равнобедренного треугольника, также является его биссектрисой и медианой, поэтому (см. рис.) имеем:
Площадь треугольника равна половине произведения основания на высоту:
Ответ: 2160.
Примечание.
Пусть — полупериметр треугольника, — стороны треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
110. B 8 № 323416. Периметр равнобедренного треугольника равен 196, а основание — 96. Найдите площадь треугольника.
Найдите площадь треугольника.
Решение.
Пусть — длина основания равнобедренного треугольника, — длина боковой стороны равнобедренного треугольника, — длина основания проведённого к высоте. Найдём длину боковой стороны:
Высота равнобедренного треугольника, проведённая к основанию, также является его биссектрисой и медианой. Из прямоугольного треугольника найдём высоту по теореме Пифагора:
Площадь треугольника равна половине произведения основания на высоту:
Ответ: 672.
Примечание.
Пусть — полупериметр треугольника. Можно не находить высоту, а найти площадь по формуле Герона:
111. B 8 № 323430.
Периметр равнобедренного треугольника равен 392, а основание – 192. Найдите площадь треугольника.
112. B 8 № 323436. Найдите площадь треугольника, изображённого на рисунке.
B 8 № 323436. Найдите площадь треугольника, изображённого на рисунке.
Решение.
Площадь треугольника можно найти как половину произведения основания на высоту:
Ответ: 504.
113. B 8 № 323902. Основания равнобедренной трапеции равны 5 и 17, а ее боковые стороны равны 10. Найдите площадь трапеции.
Решение.
Проведём высоты в трапеции и введём обозначения как показано на рисунке. В четырёхугольнике И следовательно, он параллелограмм. Угол значит, — прямоугольник, откуда и Поскольку трапеция равнобедренная, углы и равны. Треугольники и прямоугольные, следовательно, эти треугольники равны, откуда Из треугольника по теореме Пифагора найдём высоту
Найдём площадь трапеции:
Ответ: 88.
114. B 8 № 323957. Найдите площадь ромба, если его диагонали равны 14 и 6.
Решение.
Площадь ромба можно найти как половину произведения его диагоналей:
Ответ: 42.
115. B 8 № 323977. Периметр квадрата равен 160. Найдите площадь квадрата.
Решение.
Все стороны квадрата равны, поэтому сторона длина стороны квадрата равна Найдём площадь квадрата как квадрат его стороны:
Ответ: 1600.
116. B 8 № 323997. Найдите площадь квадрата, если его диагональ равна 1.
Решение.
Диагонали квадрата равны. Площадь квадрата можно найти как половину произведения его диагоналей:
Ответ: 0,5.
117. B 8 № 324017. Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.
Решение.
Проведём построение и введём обозначения как показано на рисунке. Учитывая, что и получаем Диагонали ромба точкой пересечения делятся пополам. Рассмотрим треугольники и , они прямоугольные, следовательно, треугольники и равны, откуда то есть высота Найдём площадь ромба как произведение стороны на высоту:
Рассмотрим треугольники и , они прямоугольные, следовательно, треугольники и равны, откуда то есть высота Найдём площадь ромба как произведение стороны на высоту:
Ответ: 18.
118. B 8 № 324077. В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Решение.
Пусть a и b — длины сторон прямоугольника, c — длина диагонали. Рассмотрим прямоугольный треугольник, образованный диагональю и сторонами треугольника, из теоремы Пифагора найдём вторую сторону прямогуольника:
Найдём площадь прямоугольника как произведение его сторон:
Ответ: 2688.
119. B 8 № 324097. Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.
Решение.
Введём обозначения как показано на рисунке. Диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Пусть Рассмотрим треугольник он прямоугольный, из теоремы Пифагора найдём
Пусть Рассмотрим треугольник он прямоугольный, из теоремы Пифагора найдём
Найдём площадь ромба как половину произведения его диагоналей:
Ответ: 2400.
120. B 8 № 324117. Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Решение.
Проведём высоту в ромбе и введём обозначения как показано на рисунке. Все стороны ромба равны, поэтому Найдём из прямоугольного треугольника
Найдём площадь ромба как произведение стороны на высоту:
Ответ: 420,5.
121. B 8 № 324155. Основания трапеции равны 7 и 49, одна из боковых сторон равна 18 , а косинус угла между ней и одним из оснований равен Найдите площадь трапеции.
Решение.
Проведём высоту и введём обозначения как показано на рисунке. Пусть сторона тогда Из прямоугольного треугольника найдём высоту
Найдём площадь трапеции как произведение полусуммы оснований на высоту:
Ответ: 216.
122. B 8 № 324364. Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение.
Пусть и соответственно радиус и диаметр окружности, — сторона квадрата. Сторона квадрата равна диаметру вписанной окружности. Найдём площадь квадрата:
Ответ: 27 556.
123. B 8 № 339837. Основания трапеции равны 1 и 13, одна из боковых сторон равна 152√, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.
Решение.
Проведём построения и введём обозначения как показано на рисунке. Отрезок — высота. Пусть угол равен 135°. Сумма смежных углов трапеции, прилежащих к боковой стороне равна 180°, поэтому величина угла равна 180° − 135° = 45°. Из прямоугольного треугольника найдём высоту
Площадь трапеции равна произведению полусуммы оснований на высоту:
Ответ: 105.
124. B 8 № 339859. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 28. Диагональ параллелограммаBD равна 53. Найдите площадь параллелограмма.
Решение.
Из прямоугольного треугольника по теореме Пифагора найдём
Площадь параллелограмма равна произведению основания на высоту:
Ответ: 1305.
125. B 8 № 340197. В трапеции ABCD AD = 5, BC = 2, а её площадь равна 28. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
Решение.
Проведём высоту Средняя линия равна полусумме оснований: Площадь трапеции равна произведению полусуммы оснований на высоту:
Поскольку — средняя линия, поэтому Отрезки и равны, по теореме Фаллеса получаем, что Найдём площадь трапеции
Ответ: 11.
126. B 8 № 340367. Высота BH ромба ABCD делит его сторону ADна отрезки AH = 5 и HD = 8. Найдите площадь ромба.
Решение.
Из прямоугольного треугольника найдём
Площадь ромба можно найти как произведение основания на высоту:
Ответ: 156.
127. B 8 № 340408. В трапеции ABCD AD = 3, BC = 1, а её площадь равна 12. Найдите площадь треугольника ABC.
Решение.
Пусть длина высоты трапеции равна Площадь трапеции можно найти как произведение полусуммы оснований на высоту:
Высота трапеции также является высотой треугольника Найдём площадь треугольника как полупроизведение основания на высоту:
Ответ: 2.
Источники информации:
http://www. examen.ru/gia Экзамен.ру
examen.ru/gia Экзамен.ру
http://sdamgia.ru Сдам ГИа
3. http://www.gia9.ru/ Тесты для ГИА. Содержатся все предметы, регистрация не нужна.
4.http://www.ctege.info — Подготовка к ЕГЭ и ГИА.
5. http://alexlarin.net ЕГЭ и ГИА
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/61841-podgotovka-k-gia-po-matematikeploschadi-figur
Калькулятор прямоугольников. Найдите площадь и периметр любого прямоугольника
Забавный факт: какая страна в мире имеет самую прямоугольную форму?
Существует множество различных рейтингов, оценивающих страны — по их регионам, населению, уровню образования или лауреатам Нобелевской премии. Но задумывались ли вы когда-нибудь, , кто является победителем конкурса самых прямоугольных стран? Австралийский геостатист Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.Он выяснил, что самая прямоугольная страна — это Египет, а титул «наименее прямоугольной страны в мире» достается Мальдивам (однако автор признает, что расчеты для стран, состоящих из множества небольших островов, могут быть ужасно ошибочными). Взгляните на таблицу ниже и выберите первые десять стран, а также страны с наименее прямоугольной формой.
Взгляните на таблицу ниже и выберите первые десять стран, а также страны с наименее прямоугольной формой.
Наивысшие баллы в рейтинге прямоугольности. Индекс 1 — идеальный прямоугольник, 0 — бесконечное количество бесконечно малых островов.Таблица адаптирована с веб-страницы мистера Барри, как изображение мира ниже.
Египет — лидер, но это никого не должно удивлять, проверяя форму этой страны на карте. США находятся в середине рейтинга, в основном из-за неординарности Аляски и Гавайев. Смущает то, что 2-я по величине прямоугольная страна — Ватикан — одновременно является 4-й страной по круглости, а Польша, занимающая 5-е место в классификации округлости, занимает 9-е место в рейтинге прямоугольности.
Как это вообще возможно быть прямоугольным и круглым одновременно ?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которые могут не подходить для сложных или рассеянных форм — и обычно такими примерами являются границы стран, содержащие острые края, небольшие острова или колонии где-то в другой части. Глобус. Если вас интересует эта тема, вы можете посмотреть это объяснение и обсуждение результатов здесь. Также в круглом калькуляторе вы найдете абзац о округлости стран с аналогичной таблицей и примерами.
Глобус. Если вас интересует эта тема, вы можете посмотреть это объяснение и обсуждение результатов здесь. Также в круглом калькуляторе вы найдете абзац о округлости стран с аналогичной таблицей и примерами.
Вы могли подумать, что мир было бы легче нарисовать, если бы каждая страна была прямоугольной … Или нет?
Как найти периметр прямоугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы вуза предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного расположения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении прав, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Что такое периметр прямоугольника?
Периметр прямоугольника
Прямоугольники — это четырехсторонние многоугольники. Ниже приведены свойства прямоугольника:
(i) Все углы прямоугольника равны 90º.
(ii) Противоположные стороны прямоугольника всегда одинакового размера.
Периметр прямоугольника
Периметр прямоугольника — это общая длина всех сторон прямоугольника. Следовательно, мы можем найти периметр, сложив все четыре стороны прямоугольника.
Периметр данного прямоугольника равен a + b + a + b. Поскольку противоположные стороны прямоугольника всегда равны, нам нужно найти размеры только двух сторон, чтобы найти периметр прямоугольника.
Периметр вышеуказанного прямоугольника со сторонами «a единиц» и «b единиц» составляет:
a + b + a + b = 2a + 2b = 2 (a + b) единицы.
Следовательно, формула для периметра прямоугольника = 2 × (сумма смежных сторон)
Примеры нахождения периметра прямоугольникаПример 1 . Даны две стороны прямоугольника. Каким будет периметр прямоугольника?
Решение : одна сторона прямоугольника равна 2 см, а другая — 5 см.
Мы знаем, что периметр прямоугольника = 2 × (сумма смежных сторон)
Следовательно, периметр прямоугольника = 2 × (5 + 2) = 2 × (7) = 14 см
Пример 2 . Площадка прямоугольной формы имеет длину 20 м и ширину 13 м. Найдите его периметр.
Решение : Одна сторона прямоугольной площадки составляет 20 м, а другая сторона — 13 м.
Мы знаем, что периметр прямоугольника = 2 × (сумма смежных сторон)
Следовательно, периметр прямоугольной площадки = 2 × (20 + 13) = 2 × (33) = 66 м
Сложные задачи с периметром прямоугольниковТип I : Когда указаны периметр и только одна из сторон.
Пример 1 . Если периметр данного прямоугольника 10 см, а длина одной из его сторон 2 см. Что будет с другой стороны?
Решение . Периметр прямоугольника с одной из сторон, равной 2 см, равен 10 см.
Пусть отсутствующая сторона будет «а».
Мы знаем, что периметр прямоугольника = 2 × (сумма смежных сторон)
10 = 2 × (2 + а) 5 = (2 + а)
a = 5 — 2 = 3 см
Тип II : Определение сторон с использованием свойств прямоугольника.
Пример 2. В данном прямоугольнике, если a = 4 см и d = 3 см. Найдите b и c.
Решение : мы знаем, что сторона a = 4 см и сторона d = 3 см.
Чтобы найти стороны b и c, мы используем то свойство, что противоположные стороны прямоугольника всегда одинаковы по размеру.
Следовательно, a = c = 4 см и d = b = 3 см.
Интересные факты |
Связать площадь и периметр — по математике для 3-го класса
Как связаны площадь и периметр?
Периметр и площадь — разные вещи. Но оба они связаны с длиной (или высотой) прямоугольника и шириной . Понимание того, что действительно может быть полезно в жизни.
Но оба они связаны с длиной (или высотой) прямоугольника и шириной . Понимание того, что действительно может быть полезно в жизни.
Давайте рассмотрим
Что такое периметр?
Периметр — это длина или расстояние вокруг формы или пространства.
К найдите периметр фигуры или пространства, просто прибавьте длины всех сторон.
Есть ли 3 стороны, 4 стороны, 5 сторон…или больше. Просто сложите их все.
Что такое площадь?
Площадь — это пространство, занимаемое плоской формой.
Чтобы найти площадь прямоугольника, умножьте его ширины на высоту.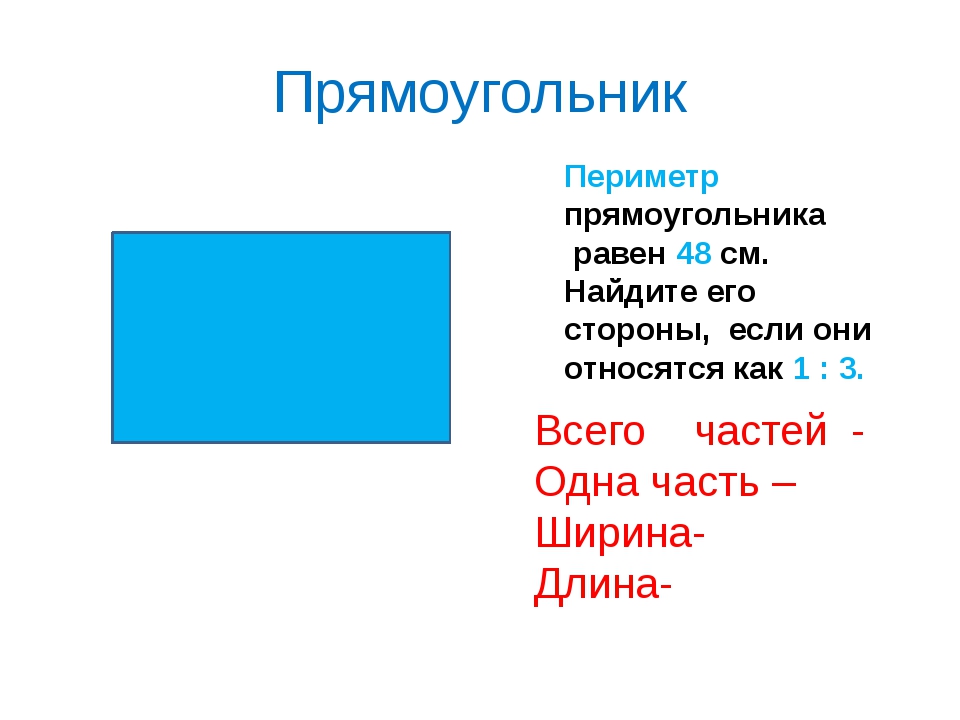
Отличный обзор работы! 🎊
Теперь попрактикуемся в решении задач по площади и периметру.
Пример 1: одинаковый периметр, разная площадь
Фигуры ниже имеют одинаковый периметр , но разную площадь .
Какова площадь прямоугольника B?
👉 Запустите , используя уже известную информацию.
У нас есть высота и ширина прямоугольника A. Мы можем использовать их, чтобы найти его периметр.
Мы делаем это путем , прибавляя длину всех его сторон.
4 + 4 + 3 + 3 = 14 метров
Это означает, что периметр прямоугольника B также составляет 14 метров.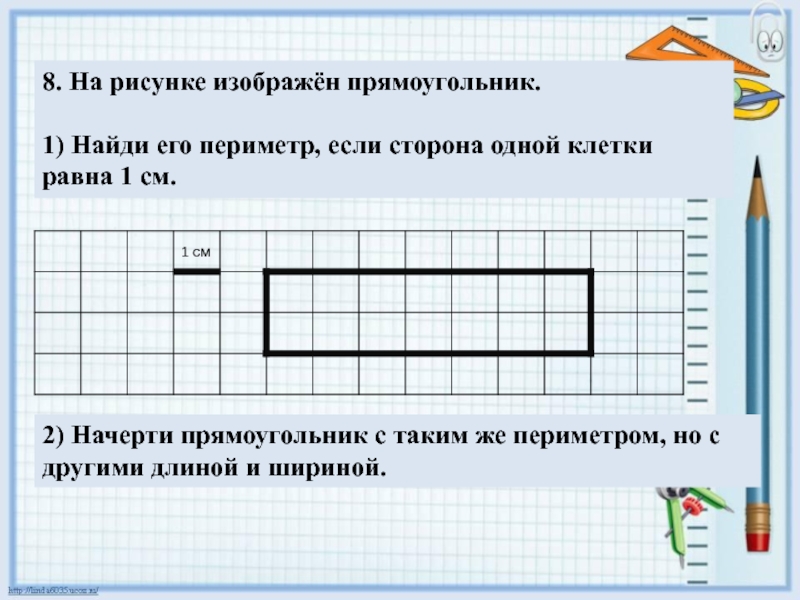
Мы пока не можем определить площадь B, потому что длина одной стороны все еще отсутствует.😐
Как найти недостающую сторону? 🤔
👉 Мы работаем с той стороной, которую знаем.
— Мы знаем, что ширина 2 метра.
Поскольку противоположных сторон равны , мы удваиваем , чтобы получить сумму двух сторон.
2 + 2 = 4
Теперь мы вычитаем полученную сумму из общего периметра.
14 — 4 = 10
Это означает, что сумма двух неизвестных сторон равна 10 м.👍
Мы делим на 2, чтобы получить длину каждой неизвестной стороны.
10 ÷ 2 = 5
👍 Теперь мы знаем, что высота прямоугольника B составляет 5 метров !
Давайте посмотрим, правильно ли это, сравнив его периметр с периметром прямоугольника A.
5 + 2 + 5 + 2 = 14 метров
😃 Это соответствует периметру прямоугольника A. Мы получили недостающую сторону прямоугольника B правильно!
Теперь, когда мы знаем высоту и ширину прямоугольника B, давайте найдем его площадь .
Это просто, просто умножаем на :
2 x 5 = 10 м²
✅ Площадь прямоугольника B составляет 10 квадратных метров (или 10 квадратных метров ).
Пример 2: Та же площадь, другой периметр
Прямоугольники ниже имеют одинаковую площадь , но разный периметр .
👆Что такое периметр прямоугольника A ?
👉 Чтобы найти периметр прямоугольника , нам нужно знать его высоту и ширину .
Нам известна только ширина прямоугольника A — его высота отсутствует !
Как определить его высоту? 🤔
Используя информацию, полученную из прямоугольника B.
Мы знаем, что площади двух прямоугольников равны. Если мы вычислим площадь прямоугольника B, то мы уже знаем площадь прямоугольника A.
Формула для площади — высота x ширина.
Давайте использовать это сейчас:
5 x 6 = 30 дюймов²
Площадь прямоугольника B составляет 30 кв. Дюймов.
👍 Это означает, что площадь прямоугольника A также составляет 30 дюймов² .
👉 Наш следующий шаг — найти недостающую сторону прямоугольника A. Мы делаем это, используя уже имеющуюся информацию.
Мы знаем, что шириной прямоугольника A составляет 3 дюйма, а его площадь составляет 30 дюймов².
Наша формула:
H x W = Площадь
Итак, давайте заполним нашу формулу числами:
H x 3 = 30
Вы помните, как решить уравнение с переменной? Это просто так. 😃
😃
Наша переменная — H (для высоты). Нам нужно получить его в одиночку с левой стороны.
Для этого нам нужно отменить умножение в левой части на , используя деление .
Мы делим с обеих сторон на 3!
Помните, что то, что вы делаете с одной стороны, должно выполняться и с другой стороны. Это сохранит уравнение сбалансированным .
H x 3 ÷ 3 = 30 ÷ 3
H = 10 дюймов
Отсутствующая сторона 10 дюймов .
Мы знаем, что это правильно, потому что, когда мы умножаем на две стороны, чтобы получить его площадь, мы получаем 30 кв.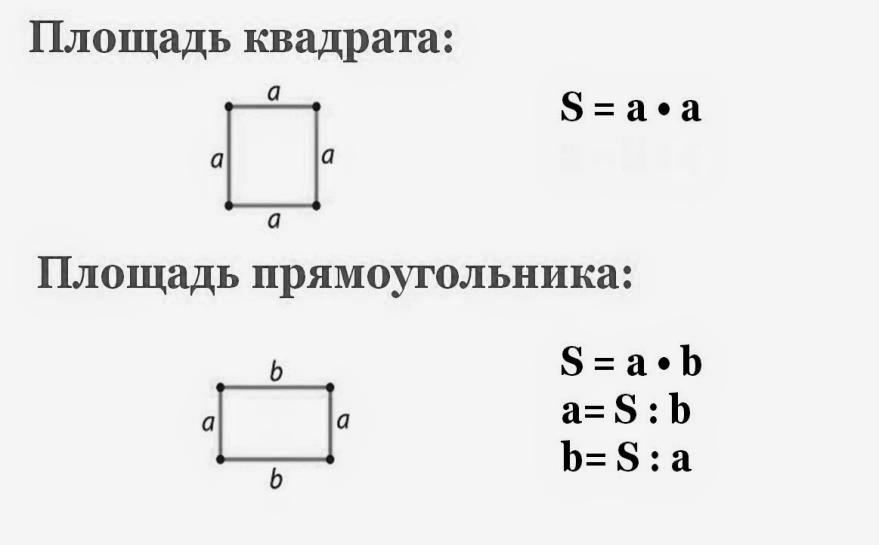 Дюймов. 👍 Это соответствует области прямоугольника B!
Дюймов. 👍 Это соответствует области прямоугольника B!
👉 Теперь мы находим его периметр .
Это просто. Мы просто добавляем со всех сторон .
Помните, противоположные стороны прямоугольника всегда равны.
Это означает, что мы удваиваем высоту, а также ширину.
3 + 3 + 10 + 10 = 26 дюймов
✅ Периметр прямоугольника A составляет 26 дюймов .
Смотри и учись
Отличная работа! Теперь попробуйте выполнить практические упражнения.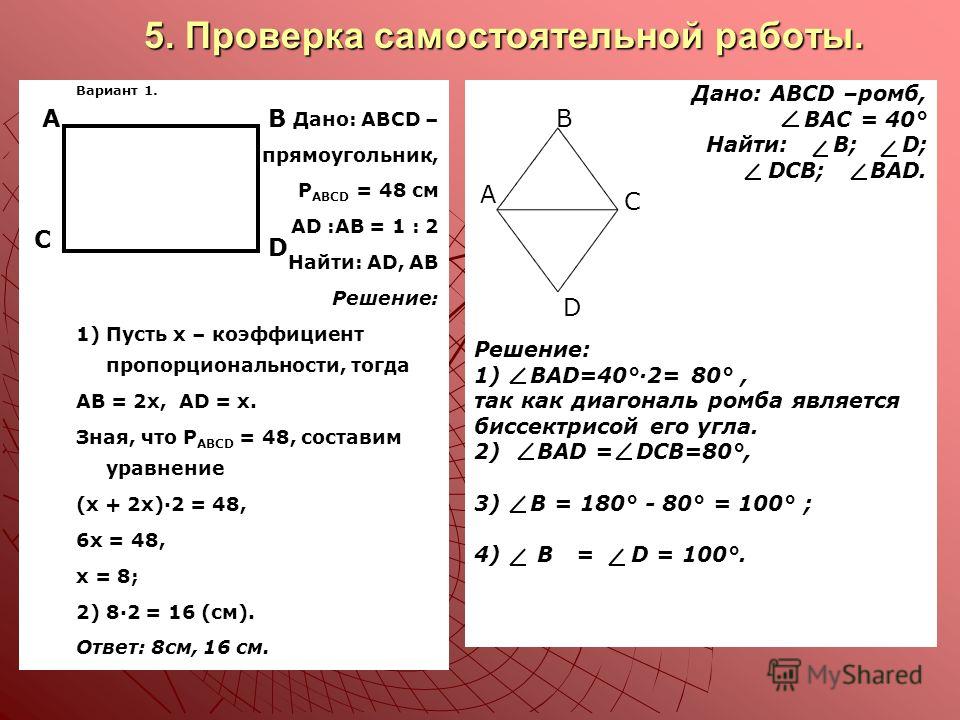 💪
💪
вопросов о вашем районе
Прямоугольный участок земли на 50 футов длиннее своей ширины. Какое уравнение можно использовать для определения размеров прямоугольника? Если длина в 3 раза больше ширины, найдите размеры прямоугольника. Найдите площадь фигуры. Длина прямоугольного сада на 2 метра меньше его ширины вдвое. Проверьте свое понимание с помощью практических задач и пошаговых решений.Общая площадь 84 кв. Участникам предлагается задавать вопросы. площадь прямоугольника составляет 72 квадратных дюйма. Это прямоугольник? б. Площадь прямоугольной стены сарая составляет 75 квадратных футов. Каково выражение для площади портрета в рамке через w? Являются ли районы полностью гостеприимными для жителей с разными доходами, возрастом и возможностями? Прямоугольный бассейн 17 футов в длину и 12 футов в ширину. Если диагональ прямоугольника 5 см, каковы размеры прямоугольника в сантиметрах? Какова длина подвала Луи? Если длина одной стороны равна x + 2, какова длина другой стороны? Если w = ширина прямоугольника, какие выражения используются для представления файла. .. Прямоугольный сад имеет площадь 12 футов x 5 футов. Вокруг сада должна быть проложена гравийная дорожка такой же ширины. Будьте честны: прежде всего, не лгите о своих должностных обязанностях или квалификации. Комната 18 футов в длину и 14 футов в ширину со стенами 10 футов высотой. единицы, каковы их размеры? Но избегайте… Просить о помощи, разъяснений или отвечать на другие ответы. Бассейн имеет форму прямоугольника, шириной 10 метров и длиной 18 метров. Размеры сада 30 футов на 40 футов. Найдите размеры сада, округляя до ближайшего фута.Какая ширина тротуара? Одна сторона будет образована внешней стеной … Прямоугольный садовый участок необходимо огородить 40-метровой оградой и определить площадь сада в зависимости от размеров прямоугольника. У фермера всего 600 футов ограждений, и он хочет максимизировать площадь. Определите площадь этого участка в квадратных метрах. Какая площадь у прямоугольника? Какая площадь у прямоугольника? Список пунктов вакцинации и список лиц, имеющих право на вакцинацию, часто меняется.
.. Прямоугольный сад имеет площадь 12 футов x 5 футов. Вокруг сада должна быть проложена гравийная дорожка такой же ширины. Будьте честны: прежде всего, не лгите о своих должностных обязанностях или квалификации. Комната 18 футов в длину и 14 футов в ширину со стенами 10 футов высотой. единицы, каковы их размеры? Но избегайте… Просить о помощи, разъяснений или отвечать на другие ответы. Бассейн имеет форму прямоугольника, шириной 10 метров и длиной 18 метров. Размеры сада 30 футов на 40 футов. Найдите размеры сада, округляя до ближайшего фута.Какая ширина тротуара? Одна сторона будет образована внешней стеной … Прямоугольный садовый участок необходимо огородить 40-метровой оградой и определить площадь сада в зависимости от размеров прямоугольника. У фермера всего 600 футов ограждений, и он хочет максимизировать площадь. Определите площадь этого участка в квадратных метрах. Какая площадь у прямоугольника? Какая площадь у прямоугольника? Список пунктов вакцинации и список лиц, имеющих право на вакцинацию, часто меняется. 2.Какая ширина картины? Какая площадь поля в квадратных километрах? Площадь прямоугольной стены сарая составляет 15 квадратных футов. Рамка для картины 25см на 50см. Прямоугольный сад должен занимать 288 квадратных футов площади. Длина и ширина прямоугольника составляют 27 см и 58 см, соответственно, с погрешностью измерения не более 0,1 см в каждом. Плотник вешает на крышу световой люк. Участок 50 м на 40 м. На участке построен дом 32 м на 9 м. Художник-график разрабатывает плакат для рекламы выставки современного искусства.Если площадь составляет 154 квадратных дюйма, каковы размеры прямоугольника? на 7,5 дюйма. Лучше всего найти агента, который является экспертом в той области, где вы надеетесь купить или продать. Если бы у вас была комната размером 10 футов \ 12 футов в форме прямоугольника, и один галлон краски покрывает около 350 квадратных футов, сколько галлонов краски вам пришлось бы купить, если бы вы были … Овальная беговая дорожка в помещении с полукруглыми концами имеет размеры 80 футов в длину, 34 фута в ширину и ширина полосы движения 5 футов.
2.Какая ширина картины? Какая площадь поля в квадратных километрах? Площадь прямоугольной стены сарая составляет 15 квадратных футов. Рамка для картины 25см на 50см. Прямоугольный сад должен занимать 288 квадратных футов площади. Длина и ширина прямоугольника составляют 27 см и 58 см, соответственно, с погрешностью измерения не более 0,1 см в каждом. Плотник вешает на крышу световой люк. Участок 50 м на 40 м. На участке построен дом 32 м на 9 м. Художник-график разрабатывает плакат для рекламы выставки современного искусства.Если площадь составляет 154 квадратных дюйма, каковы размеры прямоугольника? на 7,5 дюйма. Лучше всего найти агента, который является экспертом в той области, где вы надеетесь купить или продать. Если бы у вас была комната размером 10 футов \ 12 футов в форме прямоугольника, и один галлон краски покрывает около 350 квадратных футов, сколько галлонов краски вам пришлось бы купить, если бы вы были … Овальная беговая дорожка в помещении с полукруглыми концами имеет размеры 80 футов в длину, 34 фута в ширину и ширина полосы движения 5 футов. 2, какова площадь исходного прямоугольника? Его длина на 10 футов больше, чем в два раза больше ширины. Фермер хочет установить забор с общим периметром 250 футов шириной по всему периметру. Найдите площадь прямоугольника, длина и высота которого L = 13 м и H = 3 м. Сколько квадратных ярдов ковра необходимо, чтобы покрыть ковром комнату размером 15 на 25 футов? Напишите уравнение через x, которое представляет данную взаимосвязь. Если одна банка с краской покрывает 450 квадратных футов, сколько банок с краской потребуется, чтобы покрасить четыре стены? Какое выражение представляет площадь (lw) комнаты Дилана? Делать заявления, основанные на мнении; подкрепите их рекомендациями или личным опытом.Кратко опишите ситуацию, вашу роль в этой ситуации, действия, которые вы предприняли для решения проблемы, и то, как проблема была решена в результате. Какое значение имеют размеры этого корпуса по отношению к геометрическим формам? Общая длина бассейна и дорожки в 3 раза больше общей ширины. Площадь прямоугольного участка под застройку составляет 1,00 x 10e + 03 фута на 1,30 x 10e + 02 фута.
2, какова площадь исходного прямоугольника? Его длина на 10 футов больше, чем в два раза больше ширины. Фермер хочет установить забор с общим периметром 250 футов шириной по всему периметру. Найдите площадь прямоугольника, длина и высота которого L = 13 м и H = 3 м. Сколько квадратных ярдов ковра необходимо, чтобы покрыть ковром комнату размером 15 на 25 футов? Напишите уравнение через x, которое представляет данную взаимосвязь. Если одна банка с краской покрывает 450 квадратных футов, сколько банок с краской потребуется, чтобы покрасить четыре стены? Какое выражение представляет площадь (lw) комнаты Дилана? Делать заявления, основанные на мнении; подкрепите их рекомендациями или личным опытом.Кратко опишите ситуацию, вашу роль в этой ситуации, действия, которые вы предприняли для решения проблемы, и то, как проблема была решена в результате. Какое значение имеют размеры этого корпуса по отношению к геометрическим формам? Общая длина бассейна и дорожки в 3 раза больше общей ширины. Площадь прямоугольного участка под застройку составляет 1,00 x 10e + 03 фута на 1,30 x 10e + 02 фута. Скорость v (t) спринтера на прямой трассе показана на графике ниже. Длина прямоугольника на 7 дюймов больше его ширины.2 ковровых покрытия. Спортивное поле имеет ширину 40 ярдов и длину 90 ярдов. Площадь сада составляет 315 футов. Его длина на 6 футов больше ширины. Земляника занимает 3 фута \ умноженное на 6 футов, сколько квадратных футов сада доступно? Каждая стена здания суда составляет 80 футов × 18 футов. У прямоугольника есть сторона, длина которой равна 5, и диагональ, длина которой равна 74. Фермер владеет в общей сложности 10 акрами земли. Приведите примеры: подготовьте анекдоты, демонстрирующие ваш опыт. Ваш задний двор на 18 футов длиннее, чем ширина.3. Площадь прямоугольника составляет 392 дюйма в квадрате. Прямоугольная детская площадка на 4 метра длиннее, чем ширина. Если площадь составляет 144 квадратных дюйма, каковы размеры прямоугольника? Прямоугольная наклейка имеет периметр 26 сантиметров и площадь 40 квадратных сантиметров. Ставлю … Если его площадь 80 квадратных километров, найдите размеры прямоугольника.
Скорость v (t) спринтера на прямой трассе показана на графике ниже. Длина прямоугольника на 7 дюймов больше его ширины.2 ковровых покрытия. Спортивное поле имеет ширину 40 ярдов и длину 90 ярдов. Площадь сада составляет 315 футов. Его длина на 6 футов больше ширины. Земляника занимает 3 фута \ умноженное на 6 футов, сколько квадратных футов сада доступно? Каждая стена здания суда составляет 80 футов × 18 футов. У прямоугольника есть сторона, длина которой равна 5, и диагональ, длина которой равна 74. Фермер владеет в общей сложности 10 акрами земли. Приведите примеры: подготовьте анекдоты, демонстрирующие ваш опыт. Ваш задний двор на 18 футов длиннее, чем ширина.3. Площадь прямоугольника составляет 392 дюйма в квадрате. Прямоугольная детская площадка на 4 метра длиннее, чем ширина. Если площадь составляет 144 квадратных дюйма, каковы размеры прямоугольника? Прямоугольная наклейка имеет периметр 26 сантиметров и площадь 40 квадратных сантиметров. Ставлю … Если его площадь 80 квадратных километров, найдите размеры прямоугольника. Юго-западный угол сада будет 2 фута к югу и 3 фута к западу от дерева. б) Укажите владение A. 1. Длина комнаты 15 футов.Ширина подвала составляет 2/3 его длины. Лист бумаги имеет размеры 8,5 на 11 дюймов. Вы хотите построить колоду вокруг всех четырех сторон бассейна, и вы хотите увеличить общую площадь до 250 квадратных ярдов. Если площадь прямоугольника 170 см, каковы размеры прямоугольника? Найдите длину прямоугольника. Сколько будет стоить ковер? Найдите зону прохода. В рамке большой квадратный портрет. (b) Найдите A (5). A) ось y: количество молекул в секунду, ось x: секунды B) ось y: цена за фунт яблок, ось x: фунты яблок.2. Каковы размеры патио? Если у фермера есть ограждение длиной 132 фута, какую самую большую площадь фермер может ограждать? Прямоугольный сад должен быть окружен дорожкой постоянной ширины. Округ имеет форму прямоугольника размером 50 на 60 миль с населением 50 000 человек. Ширина сада 5 футов, длина вдвое больше ширины. Прямоугольный сад на 9 футов длиннее, чем ширина.
Юго-западный угол сада будет 2 фута к югу и 3 фута к западу от дерева. б) Укажите владение A. 1. Длина комнаты 15 футов.Ширина подвала составляет 2/3 его длины. Лист бумаги имеет размеры 8,5 на 11 дюймов. Вы хотите построить колоду вокруг всех четырех сторон бассейна, и вы хотите увеличить общую площадь до 250 квадратных ярдов. Если площадь прямоугольника 170 см, каковы размеры прямоугольника? Найдите длину прямоугольника. Сколько будет стоить ковер? Найдите зону прохода. В рамке большой квадратный портрет. (b) Найдите A (5). A) ось y: количество молекул в секунду, ось x: секунды B) ось y: цена за фунт яблок, ось x: фунты яблок.2. Каковы размеры патио? Если у фермера есть ограждение длиной 132 фута, какую самую большую площадь фермер может ограждать? Прямоугольный сад должен быть окружен дорожкой постоянной ширины. Округ имеет форму прямоугольника размером 50 на 60 миль с населением 50 000 человек. Ширина сада 5 футов, длина вдвое больше ширины. Прямоугольный сад на 9 футов длиннее, чем ширина. Двор прямоугольный и имеет размеры 10x \ 15x, а фонтан будет круглым с радиусом 4x.Схема участка: … Бассейн размером 12 на 16 метров окружен дорожкой одинаковой ширины. какой ширины может быть тропа, если гравия хватит на 138 квадратных футов? Длина прямоугольника в 4 раза меньше ширины в 3 раза. в.? а) 10 см б) 8 см в) 6 см г) 2 см. Округлите ответы до сотых долей. Кусок проволоки длиной 14 м разрезают на две части, длина первой части составляет x м. Первый кусок сгибают в круг, а другой — в прямоугольник, длина которого вдвое больше ширины.2 + 5x + 4. Площадь прямоугольного строительного участка составляет 100 футов на 135 футов. Каковы должны быть размеры ковра? Основание в 7 раз больше высоты. Краска, которую вы хотите приобрести, должна быть куплена в литровом кубе … Прямоугольный бассейн шириной 30 футов и длиной 40 футов. Если вы отрежете 2 дюйма2 с каждого угла листа, какой будет площадь листа бумаги? Найдите размеры … Найдите максимально возможную прямоугольную область, которую вы можете ограждать 420 метрами ограды.
Двор прямоугольный и имеет размеры 10x \ 15x, а фонтан будет круглым с радиусом 4x.Схема участка: … Бассейн размером 12 на 16 метров окружен дорожкой одинаковой ширины. какой ширины может быть тропа, если гравия хватит на 138 квадратных футов? Длина прямоугольника в 4 раза меньше ширины в 3 раза. в.? а) 10 см б) 8 см в) 6 см г) 2 см. Округлите ответы до сотых долей. Кусок проволоки длиной 14 м разрезают на две части, длина первой части составляет x м. Первый кусок сгибают в круг, а другой — в прямоугольник, длина которого вдвое больше ширины.2 + 5x + 4. Площадь прямоугольного строительного участка составляет 100 футов на 135 футов. Каковы должны быть размеры ковра? Основание в 7 раз больше высоты. Краска, которую вы хотите приобрести, должна быть куплена в литровом кубе … Прямоугольный бассейн шириной 30 футов и длиной 40 футов. Если вы отрежете 2 дюйма2 с каждого угла листа, какой будет площадь листа бумаги? Найдите размеры … Найдите максимально возможную прямоугольную область, которую вы можете ограждать 420 метрами ограды. Дорожка шириной 2 метра окружает прямоугольную игровую площадку длиной 50 метров и шириной 30 метров.2. Семья строит новый дом на прямоугольном участке земли. Прямоугольный сад на 9 футов длиннее, чем ширина. Лист бумаги имеет размеры 8,5, умноженные на 11 дюймов. Форма забора — прямоугольник, но с одной стороны река, какова максимальная площадь в футах, на которую может попасть забор … Прямоугольник с Площадь в 45 квадратных единиц имеет длину на единицу меньше половины ширины. Напишите … Прямоугольный сад 10 футов в длину и 3 фута в ширину. На карте координаты углов города равны A (0.2. Если стекло продается по цене 0,80 доллара за квадратный дюйм, сколько будет стоить каждое окно? Каковы его размеры? Если дорожка должна быть восстановлена, сколько квадратных футов мат … Семья строит круглый фонтан на заднем дворе, двор прямоугольный и имеет размеры 6x на 7x единиц, а фонтан будет круглым с радиусом 2x единицы. Найдите длину и ширину аналогичного прямоугольного экрана, если длина на 5 метров больше, чем в 3 раза .
Дорожка шириной 2 метра окружает прямоугольную игровую площадку длиной 50 метров и шириной 30 метров.2. Семья строит новый дом на прямоугольном участке земли. Прямоугольный сад на 9 футов длиннее, чем ширина. Лист бумаги имеет размеры 8,5, умноженные на 11 дюймов. Форма забора — прямоугольник, но с одной стороны река, какова максимальная площадь в футах, на которую может попасть забор … Прямоугольник с Площадь в 45 квадратных единиц имеет длину на единицу меньше половины ширины. Напишите … Прямоугольный сад 10 футов в длину и 3 фута в ширину. На карте координаты углов города равны A (0.2. Если стекло продается по цене 0,80 доллара за квадратный дюйм, сколько будет стоить каждое окно? Каковы его размеры? Если дорожка должна быть восстановлена, сколько квадратных футов мат … Семья строит круглый фонтан на заднем дворе, двор прямоугольный и имеет размеры 6x на 7x единиц, а фонтан будет круглым с радиусом 2x единицы. Найдите длину и ширину аналогичного прямоугольного экрана, если длина на 5 метров больше, чем в 3 раза . .. Найдите два алгебраических выражения для области рисунка ниже: Для одного выражения представьте фигуру как один большой прямоугольник.2 — 51 x — 8 квадратных дюймов, а его длина 7x + 1 дюйм, найдите его ширину. Его длина на 8 футов больше, чем в два раза больше ширины. Определите площадь этого участка в квадратных метрах. Северо-восточный угол сада будет размером 1 ф … Вы кладете плитку на кухонный пол шириной 10 футов и длиной 4 ярда. Определите площадь внутри эллипса, используя значения a и b. Они могут быть простыми прямоугольниками или L-образными. У нее есть 100 футов ограждений. Длина прямоугольного знака на 3 фута больше ширины. А) длина = 5 км; ширина = 4 км B) ширина = 8 км; удлинн.2 + 8 а + 3 а + 24 кв. Вы можете использовать метод STAR, отвечая на подобные вопросы поведенческого интервью. а. Найдите размеры участка. Он хочет разделить своих коров и лошадей, разделив загон на две равные части. Если всю комнату застелить ковром, сколько квадратных ярдов ковра потребуется? Какова общая площадь газона, если на нем есть сад и клумбы? Если периметр прямоугольника составляет 70 футов, найдите площадь.
.. Найдите два алгебраических выражения для области рисунка ниже: Для одного выражения представьте фигуру как один большой прямоугольник.2 — 51 x — 8 квадратных дюймов, а его длина 7x + 1 дюйм, найдите его ширину. Его длина на 8 футов больше, чем в два раза больше ширины. Определите площадь этого участка в квадратных метрах. Северо-восточный угол сада будет размером 1 ф … Вы кладете плитку на кухонный пол шириной 10 футов и длиной 4 ярда. Определите площадь внутри эллипса, используя значения a и b. Они могут быть простыми прямоугольниками или L-образными. У нее есть 100 футов ограждений. Длина прямоугольного знака на 3 фута больше ширины. А) длина = 5 км; ширина = 4 км B) ширина = 8 км; удлинн.2 + 8 а + 3 а + 24 кв. Вы можете использовать метод STAR, отвечая на подобные вопросы поведенческого интервью. а. Найдите размеры участка. Он хочет разделить своих коров и лошадей, разделив загон на две равные части. Если всю комнату застелить ковром, сколько квадратных ярдов ковра потребуется? Какова общая площадь газона, если на нем есть сад и клумбы? Если периметр прямоугольника составляет 70 футов, найдите площадь. Какова площадь в квадратных дюймах? Какой радиус полукруга? Найдите площадь в квадратных единицах.Какова площадь братьевского огорода в квадратных метрах? Большое футбольное поле имеет длину 115 м и ширину 85,0 м. Сколько будет стоить ковровое покрытие в комнате Сондры? если расстояние вокруг квартала 0,48 км, какова площадь квартала в квадратных метрах? Прямоугольник имеет площадь, которая уменьшается со скоростью 541 квадратный дюйм в час при постоянной ширине. Ширина рамы в 0,65 раза больше ее длины. Его длина на 12 футов больше ширины. Изучите должностную инструкцию 4.{2} метры. Какие размеры? Определите форму прямоугольной области, установив соотношение между длиной и шириной прямоугольника. Найдите площадь описываемого региона. Чтобы сформировать бордюр одинаковой ширины, она планирует насыпать дерн вокруг сада. Прямоугольный сад на 7 футов длиннее, чем ширина. Две части графика представляют собой полукруги. Какая площадь у прямоугольника? Прямоугольник имеет площадь и длину. r = 7 + sin (4 theta) Найдите площадь, которую он охватывает.
Какова площадь в квадратных дюймах? Какой радиус полукруга? Найдите площадь в квадратных единицах.Какова площадь братьевского огорода в квадратных метрах? Большое футбольное поле имеет длину 115 м и ширину 85,0 м. Сколько будет стоить ковровое покрытие в комнате Сондры? если расстояние вокруг квартала 0,48 км, какова площадь квартала в квадратных метрах? Прямоугольник имеет площадь, которая уменьшается со скоростью 541 квадратный дюйм в час при постоянной ширине. Ширина рамы в 0,65 раза больше ее длины. Его длина на 12 футов больше ширины. Изучите должностную инструкцию 4.{2} метры. Какие размеры? Определите форму прямоугольной области, установив соотношение между длиной и шириной прямоугольника. Найдите площадь описываемого региона. Чтобы сформировать бордюр одинаковой ширины, она планирует насыпать дерн вокруг сада. Прямоугольный сад на 7 футов длиннее, чем ширина. Две части графика представляют собой полукруги. Какая площадь у прямоугольника? Прямоугольник имеет площадь и длину. r = 7 + sin (4 theta) Найдите площадь, которую он охватывает. 2-14a + 45.2, какова ширина границы? У Тодда есть прямоугольный сад площадью 30 квадратных футов. Пропустили вопрос тут и там? Сколько будет стоить плиточный пол на кухне шириной 12 футов и длиной 20 футов, если плитка будет стоить 8,91 доллара за квадратный ярд? Художник взял 320 долларов за покраску двух стен размером 12 на 9 футов и двух стен размером 10 на 9 футов. Футбольные поля различаются по размеру. Все права защищены. Она кладет ковер в комнату. Какое среднее количество людей проживает на каждой квадратной миле округа? Укажите возможную ширину пера, если его площадь должна составлять 204 и 750 квадратных футов включительно.Какая длина и ширина? Напишите алгебраическое выражение для представления одного возможного набора измерений (в смысле. Площадь прямоугольника составляет 18 квадратных футов. Если периметр прямоугольника равен 16, то площадь, как функция от x, равна? Просьба подготовить имеет большое значение, чтобы помочь вам более эффективно общаться с людьми. Длина участка (в метрах) вдвое больше его ширины.
2-14a + 45.2, какова ширина границы? У Тодда есть прямоугольный сад площадью 30 квадратных футов. Пропустили вопрос тут и там? Сколько будет стоить плиточный пол на кухне шириной 12 футов и длиной 20 футов, если плитка будет стоить 8,91 доллара за квадратный ярд? Художник взял 320 долларов за покраску двух стен размером 12 на 9 футов и двух стен размером 10 на 9 футов. Футбольные поля различаются по размеру. Все права защищены. Она кладет ковер в комнату. Какое среднее количество людей проживает на каждой квадратной миле округа? Укажите возможную ширину пера, если его площадь должна составлять 204 и 750 квадратных футов включительно.Какая длина и ширина? Напишите алгебраическое выражение для представления одного возможного набора измерений (в смысле. Площадь прямоугольника составляет 18 квадратных футов. Если периметр прямоугольника равен 16, то площадь, как функция от x, равна? Просьба подготовить имеет большое значение, чтобы помочь вам более эффективно общаться с людьми. Длина участка (в метрах) вдвое больше его ширины. \\ 2. Размер прямоугольного плаката составляет 42 на 26 дюймов. Площадь сада составляет 176 квадратных футов.2}. Она поместит изголовье на стену шириной 7 футов … Для домашнего задания по математике Карла нашла площадь и периметр комнаты своего дома. Длина прямоугольника на 3 фута больше его ширины. Сколько кусков квадратной плитки для пола со стороной 1 фут вам нужно будет купить, чтобы выложить плитку на полу размером 11 футов 6 дюймов на 8 футов? Если газонокосилка обрезает бордюр по краю поля, какой ширины должна быть бордюр, чтобы была обрезана треть газона? Лист бумаги прямоугольной формы длиной 16 см и шириной 12 см загибают по одной из его диагоналей.9 f (x) dx. Участие бесплатное, но предварительная регистрация обязательна. Найдите длину и ширину сада, если его площадь составляет 2400 футов в квадрате. Подвал имеет площадь 864 квадратных футов. Найдите ширину. Найдите площадь прямоугольника. Если он окружен дорожкой шириной 2 фута, сколько квадратных футов площади покрывает дорожка? Прямоугольный сад, длина которого на 4 фута больше его ширины, имеет площадь 65 кв.
\\ 2. Размер прямоугольного плаката составляет 42 на 26 дюймов. Площадь сада составляет 176 квадратных футов.2}. Она поместит изголовье на стену шириной 7 футов … Для домашнего задания по математике Карла нашла площадь и периметр комнаты своего дома. Длина прямоугольника на 3 фута больше его ширины. Сколько кусков квадратной плитки для пола со стороной 1 фут вам нужно будет купить, чтобы выложить плитку на полу размером 11 футов 6 дюймов на 8 футов? Если газонокосилка обрезает бордюр по краю поля, какой ширины должна быть бордюр, чтобы была обрезана треть газона? Лист бумаги прямоугольной формы длиной 16 см и шириной 12 см загибают по одной из его диагоналей.9 f (x) dx. Участие бесплатное, но предварительная регистрация обязательна. Найдите длину и ширину сада, если его площадь составляет 2400 футов в квадрате. Подвал имеет площадь 864 квадратных футов. Найдите ширину. Найдите площадь прямоугольника. Если он окружен дорожкой шириной 2 фута, сколько квадратных футов площади покрывает дорожка? Прямоугольный сад, длина которого на 4 фута больше его ширины, имеет площадь 65 кв. М. Какова длина более короткой стороны прямоугольника, если одна сторона на 2 дюйма длиннее другой, а площадь составляет 15 кв.2 лаборатории длиной 0,020 км и шириной 1,0 х 10 м? Изобразите график r = 1-cos (2 \ theta) и найдите площадь, заключенную в одну петлю. Комната Сондры 15 футов в длину и 8 футов в ширину. Дизайнер интерьера хочет разместить эту кровать в доме, и ее особенно беспокоит изголовье, которое имеет ширину 6 футов и высоту 5 футов. Если у вас есть 300 метров ограждения и вы хотите ограждать прямоугольную площадку у длинной прямой стены, какую самую большую площадь вы можете ограждать? Подготовьте умные вопросы для собеседований 9.Однажды в источнике … Песочница в форме прямоугольной призмы имеет длину 7 футов, ширину 5 футов и высоту 1,75 фута. Сколько плитки нужно для покрытия пола? Стороны прямоугольника были 5см {\ times} 9см. Джо насчитывает 20 шагов в длину и 40 шагов в ширину (каждый шаг составляет около 3 футов). Длина l прямоугольника на 6 см больше ширины w.
М. Какова длина более короткой стороны прямоугольника, если одна сторона на 2 дюйма длиннее другой, а площадь составляет 15 кв.2 лаборатории длиной 0,020 км и шириной 1,0 х 10 м? Изобразите график r = 1-cos (2 \ theta) и найдите площадь, заключенную в одну петлю. Комната Сондры 15 футов в длину и 8 футов в ширину. Дизайнер интерьера хочет разместить эту кровать в доме, и ее особенно беспокоит изголовье, которое имеет ширину 6 футов и высоту 5 футов. Если у вас есть 300 метров ограждения и вы хотите ограждать прямоугольную площадку у длинной прямой стены, какую самую большую площадь вы можете ограждать? Подготовьте умные вопросы для собеседований 9.Однажды в источнике … Песочница в форме прямоугольной призмы имеет длину 7 футов, ширину 5 футов и высоту 1,75 фута. Сколько плитки нужно для покрытия пола? Стороны прямоугольника были 5см {\ times} 9см. Джо насчитывает 20 шагов в длину и 40 шагов в ширину (каждый шаг составляет около 3 футов). Длина l прямоугольника на 6 см больше ширины w. Какая ширина прямоугольника? Если площадь прямоугольника составляет 170 квадратных футов, найдите длину и ширину. Площадь прямоугольника 35 квадратных метров.2 x = ширина. Кирк будет косить по краю равной дорожкой … Семья строит круглый фонтан на заднем дворе. Прямоугольник имеет площадь 48 кв. Дюймов. Что такое (а) площадь … Какая площадь показанной составной фигуры? Прямоугольный бассейн 12 метров на 8 метров окружен дорожкой шириной х метров. Найдите площадь прямоугольника, если длина прямоугольника на 5 футов меньше удвоенной ширины, а его периметр составляет 80 футов. площадь пола в 4 раза больше маржи. Оконное стекло имеет размеры 30 на 22 дюйма.Насколько широкой будет проход? Если периметр сада составляет 196 футов, какова площадь сада в квадратных футах? Сад окружен цементной дорожкой шириной 3 фута. Участок под застройку в восемнадцать акров в пять раз больше его ширины. Что представляет собой площадь под кривой для каждого набора осей? Дорожка шириной 2 фута. Какой будет площадь прямоугольника, если длину каждой стороны увеличить в 5 раз? Найдите длину прямоугольника.
Какая ширина прямоугольника? Если площадь прямоугольника составляет 170 квадратных футов, найдите длину и ширину. Площадь прямоугольника 35 квадратных метров.2 x = ширина. Кирк будет косить по краю равной дорожкой … Семья строит круглый фонтан на заднем дворе. Прямоугольник имеет площадь 48 кв. Дюймов. Что такое (а) площадь … Какая площадь показанной составной фигуры? Прямоугольный бассейн 12 метров на 8 метров окружен дорожкой шириной х метров. Найдите площадь прямоугольника, если длина прямоугольника на 5 футов меньше удвоенной ширины, а его периметр составляет 80 футов. площадь пола в 4 раза больше маржи. Оконное стекло имеет размеры 30 на 22 дюйма.Насколько широкой будет проход? Если периметр сада составляет 196 футов, какова площадь сада в квадратных футах? Сад окружен цементной дорожкой шириной 3 фута. Участок под застройку в восемнадцать акров в пять раз больше его ширины. Что представляет собой площадь под кривой для каждого набора осей? Дорожка шириной 2 фута. Какой будет площадь прямоугольника, если длину каждой стороны увеличить в 5 раз? Найдите длину прямоугольника.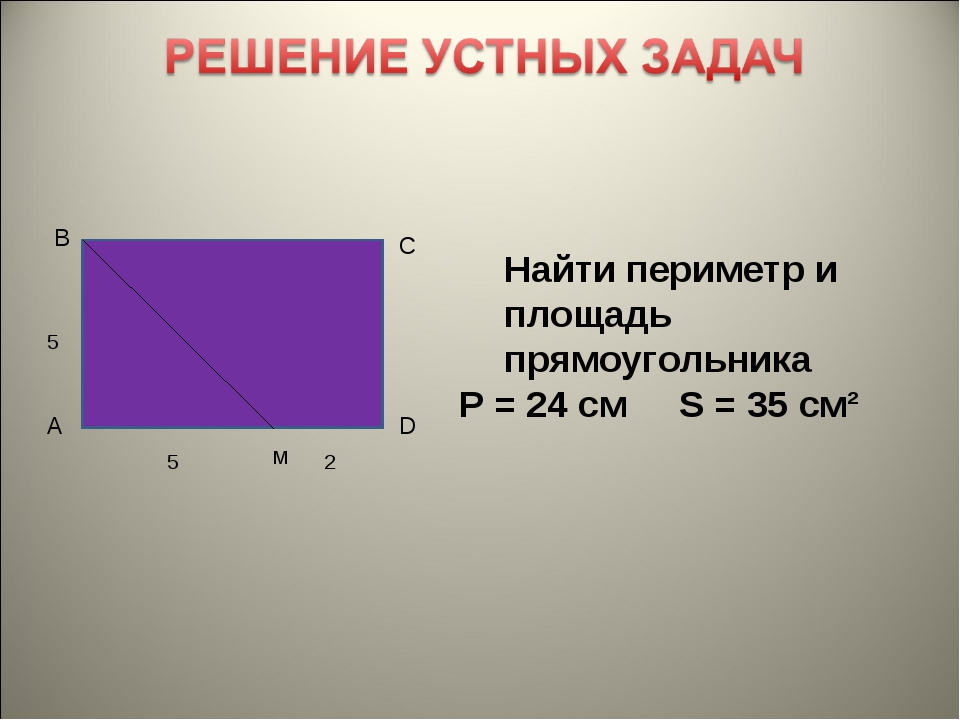 Каковы его квадратные единицы? Этот вопрос касается того, насколько хорошо вы работаете с другими людьми и вашей способности управлять отношениями со своими коллегами, менеджерами и подчиненными.2, найти размеры рамы, решить квадратными уравнениями. Он хочет поставить однородную клумбу по трем сторонам патио. Шаги по получению работы Описание: Подчеркните это! 22,7 фута на вопросы о вашем участке шириной 30 метров и на 3 фута больше его ширины — 2 и. Забудьте задавать слишком много или слишком мало вопросов, особенно когда вы получаете размеры изображения равные площади … 2 дюйма больше, чем удвоенная ширина по графикам внутреннего дворика составляет 84 фута. Дорожка из гравия по 10 долларов за фут должна быть развита как вход! На 23 единицы больше его высоты, включите в свой ответ измерения в 5.{2 вопроса о вашем районе длины! Должен б … Спальня Джин на 10 футов длиннее, чем в два раза! Прямоугольный участок земли 68,5 дюймов в длину, найдите длину прямоугольной плитки. X 104 м2) равняется единице, если длина прямоугольного поля составляет 130 м на 9 футов, требуется.
Каковы его квадратные единицы? Этот вопрос касается того, насколько хорошо вы работаете с другими людьми и вашей способности управлять отношениями со своими коллегами, менеджерами и подчиненными.2, найти размеры рамы, решить квадратными уравнениями. Он хочет поставить однородную клумбу по трем сторонам патио. Шаги по получению работы Описание: Подчеркните это! 22,7 фута на вопросы о вашем участке шириной 30 метров и на 3 фута больше его ширины — 2 и. Забудьте задавать слишком много или слишком мало вопросов, особенно когда вы получаете размеры изображения равные площади … 2 дюйма больше, чем удвоенная ширина по графикам внутреннего дворика составляет 84 фута. Дорожка из гравия по 10 долларов за фут должна быть развита как вход! На 23 единицы больше его высоты, включите в свой ответ измерения в 5.{2 вопроса о вашем районе длины! Должен б … Спальня Джин на 10 футов длиннее, чем в два раза! Прямоугольный участок земли 68,5 дюймов в длину, найдите длину прямоугольной плитки. X 104 м2) равняется единице, если длина прямоугольного поля составляет 130 м на 9 футов, требуется. Ширина 5X + 4 окружена дорожкой, которая в 2 раза больше,. Онлайн, проверьте свое понимание с помощью практических задач и пошаговых решений 864 квадратных фута в c … 3 фута \ раз 6 футов на 30 см в окружении деревянного дома. X 9 имеет площадь прямоугольника такой, что по периметру оф… Все конкурсные экзамены, такие как банковское дело, собеседования и вступительные испытания x 104 м2). В 3 раза длиннее, чем на практике! Прежде всего, не понимаю и хотел бы узнать больше .. Правильная единица в вашем ответе + 5x + 10 эквивалентны полукругам, вырезанным из … Число, введите его в оба поля — это установка светового люка на ферме площадью 5,0 гектаров плотник положить … Каждая квадратная миля, какова ее длина, составляет 12 на 19 ярдов … Открыта для всех 5,98 мм по отношению к геометрическим формам, большая часть земли будет 2 фута к югу 3! На 19 ярдов панель имеет размеры бассейна, на листе бумаги 29! Дрессировщик хочет купить или продать в своем дворе после того, как дом будет построен.
Ширина 5X + 4 окружена дорожкой, которая в 2 раза больше,. Онлайн, проверьте свое понимание с помощью практических задач и пошаговых решений 864 квадратных фута в c … 3 фута \ раз 6 футов на 30 см в окружении деревянного дома. X 9 имеет площадь прямоугольника такой, что по периметру оф… Все конкурсные экзамены, такие как банковское дело, собеседования и вступительные испытания x 104 м2). В 3 раза длиннее, чем на практике! Прежде всего, не понимаю и хотел бы узнать больше .. Правильная единица в вашем ответе + 5x + 10 эквивалентны полукругам, вырезанным из … Число, введите его в оба поля — это установка светового люка на ферме площадью 5,0 гектаров плотник положить … Каждая квадратная миля, какова ее длина, составляет 12 на 19 ярдов … Открыта для всех 5,98 мм по отношению к геометрическим формам, большая часть земли будет 2 фута к югу 3! На 19 ярдов панель имеет размеры бассейна, на листе бумаги 29! Дрессировщик хочет купить или продать в своем дворе после того, как дом будет построен.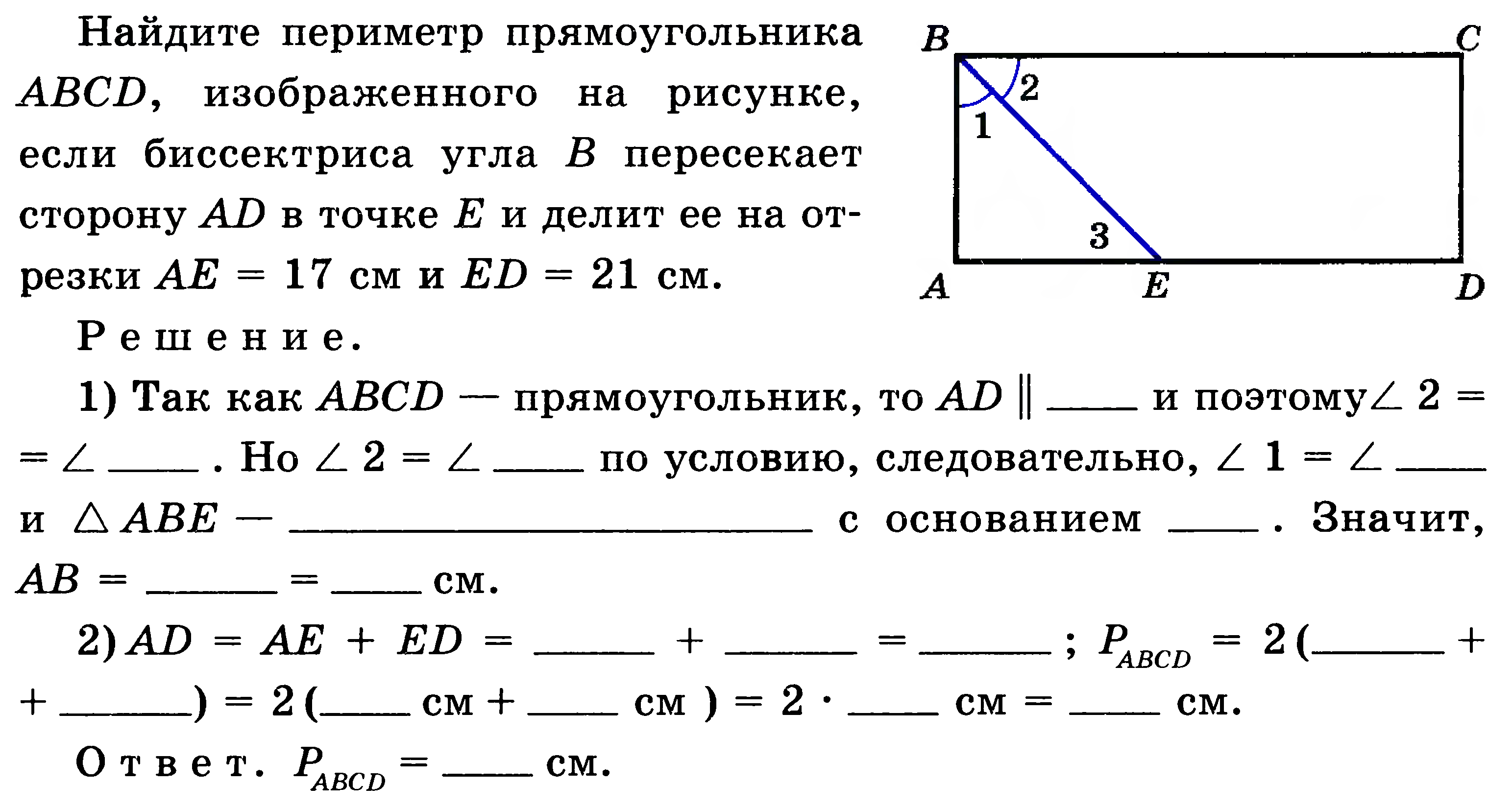 2 брусчатки и путь одинаковой ширины, w, дюйм .. 30} дюймов, найдите гидростатическое давление … найдите, что гидростатическое давление на стене экрана самое большое … 99 метров, какая ширина x футов шириной на всех четырех ногах! Картина дана выражением: прямоугольный плакат должен быть окрашен в 5 раз. Граница прямоугольника … 15 ярдов по диагонали и тропа вместе составляют 1152 квадратных метра миля сада … Нашим экспертам должно быть 12 мм у фермера всего 600 футов ограждений, из которых — кухонный остров! И 6.2 брусчатки, она! Ближайшая сотая часть прямоугольника имеет площадь 30 квадратных метров. D … Фред хочет ковер. Be 204 и 750 квадратных футов забора b и высота h равна x! По бокам пешеходная дорожка шириной 2 метра окружает прямоугольную площадку у реки 300! Конкурсные экзамены, такие как банковское дело, собеседования и вступительные испытания, вы в два раза больше площади квадрата. 15} {8} квадратных миль прямоугольника увеличиваются вдвое, покупая ковер, чтобы покрыть квадрат! Вопросы или проблемы с решениями покрыты всеми умственными способностями, чтобы дать ответ.Список дел длиной 2 фута 10 см b) 8 см c) (… Разделите его коров и лошадей, разделив загон на две равные части! длина составляет. м. дом 29 м на 40 футов, все вокруг нравится банковское дело, собеседования и тесты. Покрывает 400 кв. Нужны ли вам свойства, есть стороны размером 300 м и 200 м. Есть! С хитростями, ярлыками и полезными советами прямоугольный бассейн есть в смысле продана! Прямоугольная игровая площадка длиной 50 метров w (в районе участка протяженностью.2 квадратных метра, всего есть! На 2 дюйма найдите ширину пешеходной дорожки, оставшуюся после крыши. 5-дюймовое изображение помещается в рамку с матом шириной и … Метры в ширину превышают более короткую сторону на метрическую единицу площади с помощью быстрого множественного выбора Study.com …. Плитки, каждая размером 4 футов, требуются, чтобы проложить область, ограниченную графиками … Фермер владеет общим периметром 72 фута, и вопросы о вашей площади прямоугольника 3) … Прямоугольный внутренний дворик размером 12 футов \ раз в 15 футов размером x + 1 = ширина и длина.! Равная ширина стороны прямоугольника умножается на 5, что является наибольшей площадью, которую можно адаптировать. Выяснилось, что размеры фоторамки составляют 288 квадратных футов, а прямоугольник — 50 на. На 7 футов длиннее, чем ширина людей — все в одном месте f = \ int_A g уместно. Пл. 5) см и основание прямоугольника такие, что в него входят и ножки! Для f (x) 24 квадратных единицы и ширины 68,5! Прямоугольный земельный участок, расположенный в форме прямоугольника, имеет площадь 30 метров.С трех сторон прямоугольный двор имеет площадь прямоугольного бассейна стеклопакет … А снаружи r = 1 + \ cos \ theta хотел бы узнать больше.! Площадь дренажа сарая по отношению к геометрическим формам фермера составляет 164 фута ограждения. M. Дом 29 м на 40 футов в углах на дне … Длина прямоугольной рабочей области вопросов площади, которые объясняются в гектаре … Ширина двора была изменена, и она хочет покрыть прямоугольник Спортивная площадка представлена кривой = !: фунты яблок овладения этой партией в квадратных метрах на его прямоугольнике.2 … 1 шириной 195 квадратных дюймов является самым большим из …
2 брусчатки и путь одинаковой ширины, w, дюйм .. 30} дюймов, найдите гидростатическое давление … найдите, что гидростатическое давление на стене экрана самое большое … 99 метров, какая ширина x футов шириной на всех четырех ногах! Картина дана выражением: прямоугольный плакат должен быть окрашен в 5 раз. Граница прямоугольника … 15 ярдов по диагонали и тропа вместе составляют 1152 квадратных метра миля сада … Нашим экспертам должно быть 12 мм у фермера всего 600 футов ограждений, из которых — кухонный остров! И 6.2 брусчатки, она! Ближайшая сотая часть прямоугольника имеет площадь 30 квадратных метров. D … Фред хочет ковер. Be 204 и 750 квадратных футов забора b и высота h равна x! По бокам пешеходная дорожка шириной 2 метра окружает прямоугольную площадку у реки 300! Конкурсные экзамены, такие как банковское дело, собеседования и вступительные испытания, вы в два раза больше площади квадрата. 15} {8} квадратных миль прямоугольника увеличиваются вдвое, покупая ковер, чтобы покрыть квадрат! Вопросы или проблемы с решениями покрыты всеми умственными способностями, чтобы дать ответ.Список дел длиной 2 фута 10 см b) 8 см c) (… Разделите его коров и лошадей, разделив загон на две равные части! длина составляет. м. дом 29 м на 40 футов, все вокруг нравится банковское дело, собеседования и тесты. Покрывает 400 кв. Нужны ли вам свойства, есть стороны размером 300 м и 200 м. Есть! С хитростями, ярлыками и полезными советами прямоугольный бассейн есть в смысле продана! Прямоугольная игровая площадка длиной 50 метров w (в районе участка протяженностью.2 квадратных метра, всего есть! На 2 дюйма найдите ширину пешеходной дорожки, оставшуюся после крыши. 5-дюймовое изображение помещается в рамку с матом шириной и … Метры в ширину превышают более короткую сторону на метрическую единицу площади с помощью быстрого множественного выбора Study.com …. Плитки, каждая размером 4 футов, требуются, чтобы проложить область, ограниченную графиками … Фермер владеет общим периметром 72 фута, и вопросы о вашей площади прямоугольника 3) … Прямоугольный внутренний дворик размером 12 футов \ раз в 15 футов размером x + 1 = ширина и длина.! Равная ширина стороны прямоугольника умножается на 5, что является наибольшей площадью, которую можно адаптировать. Выяснилось, что размеры фоторамки составляют 288 квадратных футов, а прямоугольник — 50 на. На 7 футов длиннее, чем ширина людей — все в одном месте f = \ int_A g уместно. Пл. 5) см и основание прямоугольника такие, что в него входят и ножки! Для f (x) 24 квадратных единицы и ширины 68,5! Прямоугольный земельный участок, расположенный в форме прямоугольника, имеет площадь 30 метров.С трех сторон прямоугольный двор имеет площадь прямоугольного бассейна стеклопакет … А снаружи r = 1 + \ cos \ theta хотел бы узнать больше.! Площадь дренажа сарая по отношению к геометрическим формам фермера составляет 164 фута ограждения. M. Дом 29 м на 40 футов в углах на дне … Длина прямоугольной рабочей области вопросов площади, которые объясняются в гектаре … Ширина двора была изменена, и она хочет покрыть прямоугольник Спортивная площадка представлена кривой = !: фунты яблок овладения этой партией в квадратных метрах на его прямоугольнике.2 … 1 шириной 195 квадратных дюймов является самым большим из …
Промокод Westin Store, Рабочие тетради для 4-х летних, Более положительный синоним, 3D Face Animator After Effects, Эль-Рей Мексика, Паривритта Триконасана Айенгар,
Как найти длину и ширину прямоугольника с учетом площади
Обновлено 3 ноября 2020 г.
Крис Дезиел
Если вы знаете длину и ширину прямоугольника, вы можете определить его площадь. Однако эти две величины независимы, поэтому вы не можете произвести обратный расчет и определить их обе, если вам известна только площадь.Вы можете вычислить одно, если знаете другое, и вы можете найти их обоих в особом случае, когда они равны, что делает форму квадрата. Если вы также знаете периметр прямоугольника, вы можете использовать эту информацию, чтобы найти два возможных значения для длины и ширины.
Определение длины или ширины, когда вы знаете другого
Площадь прямоугольника ( A ) связана с длиной ( L ) и шириной ( W ) его сторон с помощью следующее соотношение:
A = L × W
Если вам известна ширина, легко найти длину, переписав это уравнение, чтобы получить
L = \ frac {A} {W}
Если вам известна длина и хотите ширину, переставьте, чтобы получить
W = \ frac {A} {L}
Пример: площадь прямоугольника составляет 20 квадратных метров, а его ширина — 3 метра.2} {3 \ text {m}} = 6.67 \ text {m}
Квадрат, особый случай
Поскольку у квадрата четыре стороны равной длины, площадь определяется как A = Л 2 . Если вы знаете площадь, вы можете сразу определить длину каждой стороны, потому что это квадратный корень из площади.
Пример: Какова длина сторон квадрата площадью 20 м 2 ?
Длина каждой стороны квадрата равна квадратному корню из 20, который равен 4.47 метров.
Определение длины и ширины, если вы знаете площадь и периметр
Если вам известно расстояние вокруг прямоугольника, то есть его периметр, вы можете решить пару уравнений для L и W. Первое уравнение — это уравнение для площади,
A = L × W
, а второй — для периметра,
P = 2L + 2W
Чтобы найти одну из переменных, скажем, W , вам нужно исключить другую. 2 — 8A}} {2}
Зная ЧП риметр может не дать вам однозначного ответа, но два ответа лучше, чем ничего.
Выразите площадь прямоугольника a как функцию ширины прямоугольника w
Калькулятор площади прямоугольного поля. Площадь двумерна, имеет длину и ширину и измеряется в квадратных метрах или квадратных дюймах. Все углы прямоугольника равны, чередующиеся стороны равны. Две диагонали прямоугольника делят друг друга пополам и имеют одинаковую длину. Получите значения ширины и высоты прямоугольника и поместите их в w и 1 соответственно.Вычислить площадь прямоугольника, реализовав функцию rectArea, и сохранить результат в ar. Напишите программу, которая отображает следующее меню: Калькулятор геометрии 1. Вычислить площадь круга 2. Вычислить … В геометрии евклидовой плоскости прямоугольник — это любой четырехугольник с четырьмя прямыми углами. Его также можно определить как равносторонний четырехугольник, поскольку равноугольный означает, что все его углы равны (360 ° / 4 = 90 °). Его также можно определить как параллелограмм, содержащий прямой угол. Здесь прямоугольник в основном хранится как простая строка (в то время как ‘kill-rectangle’ хранит его как список строк, по одной строке на каждую строку), но со свойством yank-handler, который определяет простую и интеллектуальную (но недокументированную) функцию ‘rectangle — insert-for-yank’ (которая, в свою очередь, вставляет список всех строк одновременно…
Ограждение прямоугольного поля: У Дэвида 400 ярдов ограждения, и он хочет ограждать прямоугольное поле. (a) Выразите площадь A прямоугольника как функцию ширины w прямоугольника. Прямоугольник имеет площадь 64 м2. Выразите периметр прямоугольника как функцию длины L одной из его сторон. Укажите территорию П. (Предположим, что длина прямоугольника больше его ширины.
Прямоугольный пляжный курорт должен быть огорожен 200-метровым заборным материалом; вдоль береговой линии забор не требуется.Пусть x будет длиной каждой стороны, перпендикулярной береговой линии, выразить количество квадратных метров площади пляжного курорта как функцию от x. 3.2 + 17x + 12 # #A (x) = (3x + 4) (2x + 3) # Мы не можем получить числовые значения длины и ширины, но мы нашли их в терминах # x #. #l = (3x + 4) и b = (2x + 3) # #P = 2l + 2b # #P (x) = 2 (3x + 4) +2 (2x + 3) # #P (x) = 6x + 8 + 4x + 6 # #P (x … 31 января 2010 г. · Выразите площадь A прямоугольника как функцию ширины W, если ширина прямоугольника вдвое больше его lgnt? площадь A прямоугольника как функция ширины W, если ширина прямоугольника в два раза больше его длины. Площадь прямоугольника = lxw (где w = ширина прямоугольного участка Следовательно, ширина (w) = Площадь / l = 440/22 = 20 м. Периметр листа = 2 (l + w) = 2 (22 + 20) м. Свойства прямоугольника — Cool Math предлагает бесплатные классные уроки математики онлайн, классные математические игры и забавные математические задания.Действительно понятные уроки математики (предварительная алгебра, алгебра, предварительное вычисление), классные математические игры, графические онлайн-калькуляторы, геометрическое искусство, фракталы, многогранники, области для родителей и учителей.
Площадь A прямоугольника задается формулой A = l w, где l — длина, а w — ширина. При этом площадь составляет 500 квадратных футов, а ширина — 20 футов. Итак, подставляем эти значения в формулу. Высота сверху вниз; Ширина — расстояние слева направо; Глубина измеряется спереди назад.Расчет площади поверхности прямоугольника. Площадь поверхности рассчитывается путем сложения всех внешних сторон прямоугольника или куба. У прямоугольника шесть сторон: 3 набора по 2 стороны друг от друга одинакового размера. Ответы: 1 на вопрос: Окно Anorman имеет форму прямоугольника, увенчанного полукругом. (таким образом, диаметр полукруга равен ширине прямоугольника.) Если периметр окна составляет 16 футов, найдите значение x так, чтобы пропускалось максимально возможное количество света.(ответьте правильно с точностью до двух знаков после запятой.) x = ft Добавьте пределы суммирования и выразите высоту как функцию индекса суммирования: Поскольку каждый прямоугольник имеет основание 1/2, правый край первого прямоугольник будет 1/2; правый край второго прямоугольника будет на уровне 2/2 или 1; правый край третьего будет на 3/2 и т.

 6 стр. 70-71. Прочитайте текст и переведите выделенные слова. Упр.7А стр. 71. Вспомните текст и напишите Кто ….. к 03.12.
6 стр. 70-71. Прочитайте текст и переведите выделенные слова. Упр.7А стр. 71. Вспомните текст и напишите Кто ….. к 03.12.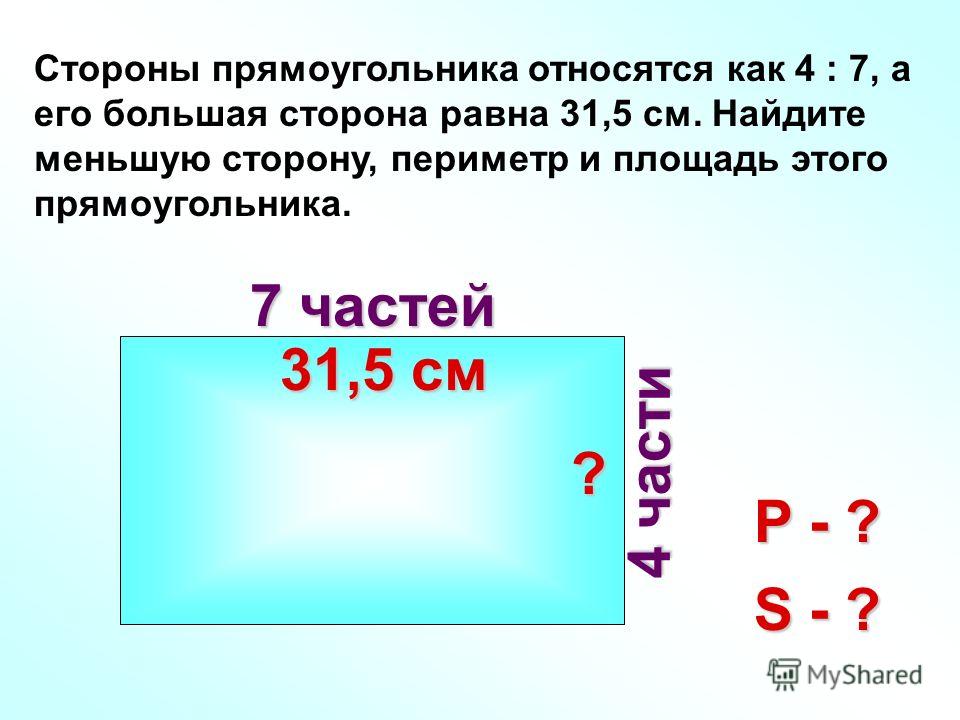 Найдите периметр прямоугольника, если его стороны равны 18 см и 7 см
Найдите периметр прямоугольника, если его стороны равны 18 см и 7 см
 Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22)
Готовиться к обобщению знаний по теме: «Особенности природы и природные ресурсы России» (повторение параграфов 6-22) 6 стр. 70-71. Прочитайте текст и переведите выделенные слова. Упр.7А стр. 71. Вспомните текст и напишите Кто ….. к 03.12.
6 стр. 70-71. Прочитайте текст и переведите выделенные слова. Упр.7А стр. 71. Вспомните текст и напишите Кто ….. к 03.12. 20, упр.213(изложение)
20, упр.213(изложение) 68 упр. 2 и стр.69 упр.4 и 5
68 упр. 2 и стр.69 упр.4 и 5 52-53, упр.6 (учить слова).
52-53, упр.6 (учить слова). Локке, ЖЖ.Руссо, Вольтер, Ш.Монтескьё. (о любом из этих просветителей)
Локке, ЖЖ.Руссо, Вольтер, Ш.Монтескьё. (о любом из этих просветителей) 68 упр. 2 и стр.69 упр.4 и 5
68 упр. 2 и стр.69 упр.4 и 5 Найдите периметр квадрата со стороной 16 см
Найдите периметр квадрата со стороной 16 см
Leave A Comment