Найдите корень уравнения корень из 16 4х 2: Найдите корень уравнение (все это под корнем )16 - 4х =2

Найдите корень уравнения — Задание 5 ЕГЭ

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 — это уравнение, а 3^.3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся — будем находить корень уравнения.

Задание 1 — найдите корень уравнения 2

^1-4x=32

Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2⁵

Таким образом, наше уравнение будет выглядеть так: 2^1-4х=2⁵

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

1-4х=5

Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:

-4х=5-1

-4х=4

х=-1.

Делаем проверку: 2^1-4(-1)=32

2⁵=32

32=32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

а) 2^5-х=64

б) 2^1-3х=128

Задание 2 — найдите корень уравнения 2

^5-x = 1/16

Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Тогда наше уравнение запишется в виде:

Если равны основания степени, значит, равны и показатели степени:

5-х=-4

-х=-4-5

х=9

Ответ: х=9.

Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.

2^5-9=1/16

2^-4=1/16

1/16=1/16

Мы нашли корень уравнения правильно.

Задание 3 — найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 — это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

3х-12=3

3х=15

х=5

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 — найдите корень уравнения log

₃(15-х)=log₃2

Это уравнение решается также как и показательное.

Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

15-х=2

-х=2-15

-х=-13

х=13

Ответ: х=13

Задание 5 — найдите корень уравнения log

₃(3-x)=3

Число 3 — это log₃27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

log₃(3-x)=log₃27

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

3-х=27

Получим,

-х=27-3

-х=24

х=-24

Сделаем проверку:

log₃(3-(-24))=log₃27

log₃(3+24)= log₃27

log₃27=log₃27

3=3

Ответ: x=-24.

Задание 6. Найдите корень уравнения log(x+3)=log

₂(3x-15).

log₂(x+3)=log₂(3x-15)

Решение:

x+3=3x-15

x-3x=-3-15

-2x=-18

x=9

Проверка: log₂(9+3)=log₂(27-15)

log₂12=log₂12

Ответ: x=9.

Задание 7. Найдите корень уравнения log

₂(14-2x)=2log₂3

log₂(14-2x)=2log₂3

log₂(14-2x)=log₂3²

14-2x=3²

14-2x=9

-2x=9-14

-2x=-5

x=2,5

Проверка: log₂(14-5)=2log₂3

log₂9=2log₂3

log₂3²=2log₂3

2log₂3=2log₂3

Ответ: x=2,5

Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .

15 Найдите корень уравнения log2(4-x)=7

15. Найдите корень уравнения log₂(4-x)=7

16. Найдите корень уравнения log₅(4+x)=2

17.Найдите корень уравнения log₅(5-x)=log₅3

18. Найдите корень уравнения log₂(15+x)=log₂3

19. Найдите корень уравнения 2^4-2x=64

20. Найдите корень уравнения 5^x-7=1/125

21.Найдите корень уравнения (1/3)^x-8=1/9

22. Найдите корень уравнения (1/2)^6-2x=4

23. Найдите корень уравнения 16^x-9=1/2

24. Найдите корень уравнения (1/9)^x-13=3

25. Найдите корень уравнения √(15-2x)=3

26. Найдите корень уравнения log₄(x+3)=log₄(4x-15)

27. Найдите корень уравнения log_1/7(7-x)=-2

28. Найдите корень уравнения log₅(5-x)=2log₅3

29. Найдите корень уравнения √(6/(4x-54))=1/7

30. Найдите корень уравнения √((2x+5)/3)=5

31. Найдите корень уравнения: (4/7)x=7 3/7

Пояснение: 7 3/7 (семь целых три седьмых)

32. Найдите корень уравнения: -(2/9)х=1 1/9

Пояснение: 1 1/9 (одна целая одна девятая)

33. Найдите корень уравнения: (х-119)/(х+7)=-5

Ответ: 14

34. Найдите корень уравнения: х=(6х-15)/(х-2)

Если уравнение имеет более одного корня, в ответе укажите больший из них.

35. Найдите корень уравнения: 9^-5+х=729

36. Найдите корень уравнения: х²-17х+72=0

Если уравнение имеет более одного корня, укажите меньший из них.

Тест на тему квадратное уравнение.

Квадратные уравнения 1 — вариант

1. Какое из данных уравнений является квадратным? 1) х 3 + 2х = 0; 2) 3х — 9 = 0; 3) 5х 2 — 4х = 0; 4) — 9 = 0. 2 . Укажите старший коэффициент квадратного уравнения -х 2 -5х + 1 = 0. 1) 5; 2) -1; 3) 1; 4) -5. 3 . Какое из следующих квадратных уравнений является приведённым? 1) 2х 2 — 5х +6 = 0; 2) 10 — 5х + х 2 = 0; 3) 6 — х 2 + 7х = 0; 4) 12х 2 + х — 1 = 0. 4 . Какие из данных квадратных уравнений являются полными? 1) х 2 +2х =0; 2) 8х 2 -5 = 0; 3) х 2 +14х — 23 = 0; 4) 5х — х 2 +7 = 0. 5 . Решить уравнение: 2х 2 — 5х = 0. 1) 0 ; 2,5. 2) 2; -5. 3) 0; 5. 4) -2,5; 0. 6 . Найдите дискриминант квадратного уравнения: -2х 2 +5х + 3 = 0. 1) 49; 2) 1; 3)- 49; 4) 25.

7. Определить число корней квадратного уравнения: 4х 2 +х + 66 = 0. 1) 2 различных корня; 2) 2 одинаковых корня; 3)корней нет. 8 . Решите уравнение: 10х 2 -13х -3 = 0. 1) 1; 0,3. 2) — 1; — 0,3. 3) 1,5; — 0,2.

4)1,5; 0,2. 9. У какого из данных уравнений сумма корней равна -7, а произведение — 12? 1) х 2 — 7х +12 = 0; 2) х 2 + 7х -12 = 0; 3) х 2 -12х -7 = 0; 4) х 2 +12х — 7 = 0. 1) 1; 2) 2; 3) 3; 4) 4. 10. Составьте квадратное уравнение, корнями которого являются числа 3 и 5. 1) х 2 +8х — 15 = 0; 2) х 2 +8х + 15 = 0; 3) х 2 -8х + 15 = 0; 4) х 2 +15х + 8 = 0;

Квадратные уравнения 2 — вариант

1. Какое из данных уравнений является квадратным? 1) х + 2х = 0; 2) 3х 2 — 9 = 0; 3) 5х 3 — х = 0; 4) — 5 = 0. 2 . Укажите старший коэффициент квадратного уравнения -х 2 +3х +11 = 0. 1) 3; 2) -1; 3) 11; 4) 1. 3. Какое из следующих квадратных уравнений является приведённым? 1) 2х 2 — 7х +6 = 0; 2) 12 — 5х — х 2 = 0; 3) 6 + х 2 + 7х = 0; 4) 12х 2 + х — 8 = 0. 4 . Какие из данных квадратных уравнений являются полными? 1) х 2 +3х =0; 2) 8х -5х +2х 2 = 0; 3) х 2 +14 = 0; 4) 5х — х 2 +7 = 0. 5. Решить уравнение: -2х 2 — 5х = 0. 1) 0 ; 2,5.

2) -2; -5. 3) -2,5; 5. 4) -2,5; 0. 6 . Найдите дискриминант квадратного уравнения: -3х 2 +2х + 1 = 0. 1) 4; 2) 8; 3)16; 4) -16. 7. Определить число корней квадратного уравнения: 3х 2 + х — 61 = 0. 1) 2 различных корня; 2) 2 одинаковых корня; 3)корней нет. 8 . Решите уравнение: 14х 2 +5х -1 = 0. 1) -2. 3)- 4) 9 . У какого из данных уравнений сумма корней равна -5, а произведение -14? 1) х 2 — 5х +14 = 0; 2) х 2 + 5х -14 = 0; 3) х 2 -14х -5 = 0; 4) х 2 +14х — 5 = 0. 1) 1; 2) 2; 3) 3; 4) 4. 10. Составьте квадратное уравнение, корнями которого являются числа 2 и 6. 1) х 2 + 8х — 12 = 0; 2) х 2 + 8х + 12 = 0; 3) х 2 — 8х + 12 = 0; 4) х 2 +12х — 8 = 0;

ТЕСТЫ по теме «Квадратные уравнения»

8 класс, 6 вариантов

Вариант № 1

(х + 1) 2 = х 2 – 4х

3) Решите уравнение 4х 2 + 3х. = 0

Корней нет

Х 2 + 3х + 4 = 0

4х 2 + 3х – 1 = 0

16х 2 – 3х = 0

2х 2 – 3х + 2 = 0

5) Решите уравнение: х 2 — 3х – 18 = 0.

6) Найдите сумму корней уравнения: 4х 2 + 17х + 4 = 0.

Другой ответ

7) Найдите произведение корней уравнения: 2х 2 + х +3 = 0.

Другой ответ

8) При каком d уравнение 8х 2 + d х + 8 = 0 имеет корень 2?

Вариант № 2

1) Какое из данных уравнений является квадратным?

(х – 3) 2 = 2х 2 + 3

(х – 2) 2 = х 2

2) Найдите коэффициенты a , b и c квадратного уравнения 5х + х 2 — 4 = 0.

3) Решите уравнение 5х 2 = 9х.

Корней нет

х 2 — 9х — 1 = 0

2х 2 — 7х + 4 = 0

4х 2 – 7х + 2 = 0

4х 2 + 7х + 2 = 0

5) Решите уравнение: х 2 + 2х – 24 = 0.

6) Найдите сумму корней уравнения: 2х 2 + 11х — 6 = 0.

Другой ответ

8) При каком c уравнение 4х 2 + c х — 16 = 0 имеет корень 4?

9) Выделите квадрат двучлена: х 2 — 6х + 7 = 0.

(х + 3 ) 2 + х

ТЕСТ «Квадратные уравнения» 8 класс

Вариант № 3

1) Какое из данных уравнений является квадратным?

х(х – 1) = х 2 – 2х

2/х 2 = 3/х + 4

2х 2 – 3х = х + 5

3) Решите уравнение: 17х = 10х 2 .

Корней нет

4) Дискриминант какого из уравнений равен 25?

4 х 2 — 3х + 1 = 0

2х 2 — 3х + 2 = 0

2х 2 + 3х -2 = 0

х 2 + 3х + 25 = 0

5) Решите уравнение: х 2 — 2х – 15 = 0.

6) Найдите сумму корней уравнения: 2х 2 — х + 7 = 0.

Другой ответ

8) При каком a уравнение 3х 2 + a х + 24 = 0 имеет корень 3?

(х – 3) 2 — 14

(х – 3) 2 + 4

ТЕСТ «Квадратные уравнения» 8 класс

Вариант № 4

1) Какое из данных уравнений является квадратным?

4/х + х 2 + 1 = 0

х 2 + 3х = 4х — 2

х 2 =(х – 2)(х + 1)

2) Найдите коэффициенты a , b и c квадратного уравнения.7 — 3х 2 + х = 0.

3) Решите уравнение 2х 2 — 7х. = 0

корней нет

5х 2 + 3х + 2 = 0

2х 2 — 3х – 5 = 0

3х 2 – 3х – 7 = 0

2х 2 – 3х + 5 = 0

5) Решите уравнение: х 2 + х — 20 = 0

6) Найдите сумму корней уравнения: 5х 2 — 9 х — 2 = 0.

другой ответ

7) Найдите произведение корней уравнения: 5х 2 — 3 х +2 = 0.

другой ответ

8) При каком b уравнение 2х 2 + b х — 10 = 0 имеет корень 5?

9) Выделите квадрат двучлена: х 2 + 4х + 3 = 0.

(х + 2) 2 – 1

ТЕСТ «Квадратные уравнения» 8 класс

Вариант № 5

1) Какое из данных уравнений является квадратным?

(х + 1) 2 = х 2 – 4х

3х 2 = 4х 2 + 8

2) Найдите коэффициенты a , b и c квадратного уравнения.3 – х 2 – 6х = 0.

3) Решите уравнение 5х 2 — 9х. = 0

корней нет

4) Дискриминант какого из уравнений равен 49?

5 х 2 + 3х + 2 = 0

2х 2 — 3х – 5 = 0

3х 2 – 3х — 7 = 0

2х 2 – 3х + 5= 0

5) Решите уравнение: х 2 — 3х – 18 = 0

6) Найдите сумму корней уравнения: 2х 2 + 11х – 6 = 0.

Другой ответ

7) Найдите произведение корней уравнения: 2х 2 — 13х -7 = 0.

Другой ответ

8) При каком b равнение 8х 2 + b х + 8 = 0 имеет корень 2?

9) Выделите квадрат двучлена: х 2 + 2х – 10 = 0.

ТЕСТ «Квадратные уравнения» 8 класс

Вариант № 6

1) Какое из данных уравнений является квадратным?

х(х – 1) = х 2 – 2х

2/х 2 = 3/х + 4

2х 2 – 3х = х + 5

2) Найдите коэффициенты a , b и c квадратного уравнения — х + 9. + 2х 2 = 0.

3) Решите уравнение: 18х = 10х 2 .

Корней нет

4) Дискриминант какого из уравнений равен 81?

х 2 – 9х– 1 = 0

2х 2 – 7х + 4 = 0.

4х 2 – 7х + 2 = 0.

4 х 2 + 7х + 2 = 0.

5) Решите уравнение: х 2 — 2х — 15 = 0.

6) Найдите сумму корней уравнения: 5х 2 — 9х + 2 = 0.

другой ответ

7) Найдите произведение корней уравнения: 2х 2 + 3х + 6 = 0.

другой ответ

8) При каком p уравнение 3х 2 + p х + 24 = 0 имеет корень 3?

9) Выделите квадрат двучлена: х 2 — 6х – 5 = 0.

(х – 3) 2 — 14

(х – 3) 2 + 4

ВАРИАНТ № 1










ВАРИАНТ № 2

В А Р И А Н Т № 3

В А Р И А Н Т № 4

В А Р И А Н Т № 5

В А Р И А Н Т № 6

Тест по алгебре

Квадратные уравнения 8 класс

А) 2 Б) 23 В) 4 Г) 0

А) 12 Б)3 В) -3 Г) -4

А) -3 Б) -13 В) 3 Г) 10

А) 4 Б) -1 В)2 Г) 1

А) 2 Б) -3 В) -2 Г) 3

ключи

№ задания

Кустова Людмила Анатольевна

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5.Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

6 . Найдите произведение корней уравнения: х2-4х+3=0 .

А) 12 Б)3 В) -3 Г) -4

7 . Найдите сумму корней уравнения: х2-3х-10=0.

А) -3 Б) -13 В) 3 Г) 10

8 . Найдите значение коэффициента а, если в уравнении ах2+3х-5=0:

один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

9. Найдите значение коэффициента b , если в уравнении х2+вх-15=0

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П. Орловка,Хохольского района,Воронежской области

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5.Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

А) 12 Б)3 В) -3 Г) -4

А) -3 Б) -13 В) 3 Г) 10

Один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания12345678910

АВ Б Б Г Б В В АБ

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П. Орловка,Хохольского района,Воронежской области

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5.Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

6. Найдите произведение корней уравнения: х2-4х+3=0 .

А) 12 Б)3 В) -3 Г) -4

7. Найдите сумму корней уравнения: х2-3х-10=0.

А) -3 Б) -13 В) 3 Г) 10

8. Найдите значение коэффициента а, если в уравнении ах2+3х-5=0:

Один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

9. Найдите значение коэффициента b, если в уравнении х2+вх-15=0

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания12345678910

АВ Б Б Г Б В В АБ

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П.Орловка,Хохольского района,Воронежской области

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5.Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

6 . Найдите произведение корней уравнения: х2-4х+3=0 .

А) 12 Б)3 В) -3 Г) -4

7 . Найдите сумму корней уравнения: х2-3х-10=0.

А) -3 Б) -13 В) 3 Г) 10

8 . Найдите значение коэффициента а, если в уравнении ах2+3х-5=0:

один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

9. Найдите значение коэффициента b , если в уравнении х2+вх-15=0

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П.Орловка,Хохольского района,Воронежской области

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5.Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

6 . Найдите произведение корней уравнения: х2-4х+3=0 .

А) 12 Б)3 В) -3 Г) -4

7 . Найдите сумму корней уравнения: х2-3х-10=0.

А) -3 Б) -13 В) 3 Г) 10

8 . Найдите значение коэффициента а, если в уравнении ах2+3х-5=0:

один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

9. Найдите значение коэффициента b , если в уравнении х2+вх-15=0

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П.Орловка,Хохольского района,Воронежской области

Тест по алгебре

Квадратные уравнения 8 класс

1. Какое из квадратных уравнений является полным:

А) 4х2-6х+8=0 Б) 9х+9х2=0 В) -6х2=0 Г) 9+х2=0

2. Дискриминант квадратного уравнения х2-4х+3=0 равен:

А) 2 Б) 23 В) 4 Г) 0

5. Выберите коэффициенты -х2-3х+7=0

А) 1,-3,7 Б) -1,-3,7 В) -1,-3,-7 Г) -1,-3,-7

4. Решите уравнение х2-3х-10=0

А) Корней нет Б) 2; -5 В) 6 Г) -5; -2

5. Решите уравнение 9х2-6х+1=0

А) 1,3 Б) 0; 3 В) корней нет Г) 1/3

6 . Найдите произведение корней уравнения: х2-4х+3=0 .

А) 12 Б)3 В) -3 Г) -4

7 . Найдите сумму корней уравнения: х2-3х-10=0.

А) -3 Б) -13 В) 3 Г) 10

8 . Найдите значение коэффициента а, если в уравнении ах2+3х-5=0:

один из корней уравнения равен 1.

А) 4 Б) -1 В)2 Г) 1

9. Найдите значение коэффициента b , если в уравнении х2+вх-15=0

Один из корней уравнения равен -5

А) 2 Б) -3 В) -2 Г) 3

10. Решите уравнение 3х(х-5)= 0

А) 1,5 Б) 0; 5 В) корней нет Г) 3,5

ключи

№ задания

Кустова Людмила Анатольевна

Учитель математики МКОУ «Орловская СОШ»

П.Орловка,Хохольского района,Воронежской области

Тест

«Квадратные уравнения»

8 класс

Составлен Митиной Т. В.

учителем математики

Лебяжьевского филиала

МБОУ Моисеево-Алабушской сош Уваровского района

Тамбовской области

2013 год

Пояснительная записка

Тематический тест составлен по теме «Квадратные уравнения» и предназначен для обучающихся 8 класса. Задания, которые содержатся в данном тесте, позволят не только отработать тему «Квадратные уравнения», но и помогут обучающимся научиться уверенно решать задания разного характера. Важность представленного теста обусловлена еще и тем, что задания, связанные с нахождением корней квадратных уравнений, встречаются в материалах ГИА. Тест может быть полезен как для обучающихся с повышенной мотивацией к изучению математики, так и для обучающихся, которые стремятся повысить уровень своих знаний по математике.

Цель: Контроль и проверка знаний, умений и навыков по решению квадратных уравнений.

Задачи: обобщить изученный по теме материал;

Формировать умения применять полученные математические знания на практике;

Формировать умения работать с тестами, что является очень актуальным для подготовки учащихся к экзаменам в виде ГИА;

Способствовать формированию умений применять приемы сравнения, обобщения выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти; развивать познавательную активность, творческие способности;

Воспитать интерес к математике;

Повышать уровень математической культуры.

Тест включает в себя пять вариантов. Задания разделены на два уровня: обязательный уровень (№1 — №6), в котором четыре задания с выбором ответа, одно задание с записью ответа и одно задание – указать верное утверждение. Дополнительный уровень (№7 — №10), в котором три задания с выбором ответа и одно задание на установление соответствия.

На выполнение теста отводится 45 минут.

Критерии оценивания

№ задания

6 баллов – оценка «3»

9 – 12 баллов – оценка «4»

16 – 20 баллов – оценка «5»

Планируемый результат

Обучающиеся должны знать:

Определения всех видов квадратных уравнений;

Формулы корней квадратного уравнения;

Теорему Виета;

Свойства коэффициентов квадратного уравнения.

Обучающиеся должны уметь:

Решать квадратные уравнения и уравнения, приводимые к квадратным;

определять знаки корней уравнения;

решать уравнения и неравенства.

Вариант I

1) Уравнение, приводимое к виду ах 2 +вх+с=0 , где а,в,с некоторые числа, х — переменная, причем а ≠0, называется линейным уравнением.

2) Уравнение, приводимое к виду ах 2 +вх+с=0 , где а,в,с некоторые числа, х — переменная, причем а ≠0, называется квадратным уравнением.

3) Уравнение, приводимое к виду ах 2 +вх+с=0 , где а,в,с некоторые числа, х — переменная, причем а ≠0, называется дробно-рациональным уравнением.

2. Какие из чисел являются корнями уравнения х 2 + 2х – 3 = 0.

1) 1; -3 2) –1; 3 3) нет таких чисел. 4) 0; 4

3. Найдите дискриминант квадратного уравнения 5х 2 – 4х – 1 = 0.

1) 16 2)- 20 3) 36 4)16

4. Найдите наибольший корень уравнения 2х 2 + 3х – 5 = 0.

1) –2,5 2) 1 3) –1 4) 2,5

5. При каких значениях m можно представить в виде квадрата двучлена выражение х 2 + mх + 9.Ответ:_______
6. Решите уравнение х 2 – х = 0.

1) 0; 1 2) –1; 1 3) 0 4) 0; -1

7. Найдите сумму корней уравнения: 10х 2 – 3х – 0,4 = 0.

1)нет корней 2) 0,3 3) 1 4) 0,6

8. Установите соответствие между данными уравнениями и знаками их корней: 1) х 2 — 5х + 3 = 0 А) Оба корня положительны 2) х 2 + 8х – 6 = 0 В) Оба корня отрицательны 3) 2х 2 + 7х + 1 = 0 С) Корни разных знаков
9. Один из корней квадратного уравнения х 2 + 5х + k = 0 равен –2. Найдите k.

1) –2 2) –5 3) 6 4) 0

1) – 0,7 2) 2 3) 0 4) 0,75

Вариант II

1. Укажите верное утверждение:

1) а =1, называется приведенным.

2) Квадратное уравнение, у которого коэффициент а =1, называется неприведенным.

3) Квадратное уравнение, у которого коэффициент а =1, называется неполным.

2.Какие из чисел являются корнями уравнения 2х 2 + 5х – 3 = 0.

1) 3; 0,5 2) –0,5; -3 3) 0,5; -3 4) 1; 0

3. Найдите дискриминант квадратного уравнения х 2 – 6х + 9 = 0.

1) 2 2) 9 3) 0 4) 36

4. Найдите наибольший корень уравнения 5х 2 – 7х + 2 = 0.

1) 0,4 2) 1 3) –1 4) 2

5. При каких значениях m можно представить в виде квадрата двучлена выражение х 2 – 2х – m.Ответ:_______
6. Решите уравнение 7х = 4 х 2 .

1) 0; — 1,75 2)1,4; 1,75 3) –3; 0 4) 0; 1,75

7. Найдите сумму корней уравнения: 7х 2 + 6х – 1 = 0.

1) 2) 1 3) – 0,5 4) –1

8. Установите соответствие между данными уравнениями и знаками их корней: 1) -3х 2 + 6х + 1 = 0 А) Оба корня положительны 2) -х 2 + 10х – 11 = 0 В) Оба корня отрицательны 3) 5х 2 + 17х + 5 = 0 С) Корни разных знаков9. Один из корней квадратного уравнения 5х 2 – 7х + k = 0 равен -2 .Найдите k.

1) – 47,6 2) –53 3) 54 4) 30

(5 + 4х) 2 = (9 – 21х)(4х + 5).

1) 2 2) – 0,2 3) 0,2 4) нет решений

Вариант III

1. Укажите верное утверждение:

1) Формула дискриминанта: D = в– 4ас

2) Формула дискриминанта: D= в 2 — 4а

3) Формула дискриминанта: D = в 2 — 4а c

2. Какие из чисел являются корнями уравнения 6х 2 + х = 0.

1) нет таких чисел 2) 0; 3) 0; 1 4) 2; 0

3. Найдите дискриминант квадратного уравнения 3х – х 2 + 10 = 0.

1) 49 2) — 49 3) 9 4) 25

4. Найдите наибольший корень уравнения 3х 2 + 5х – 2 = 0.

1) 2 2) 3) 4) 4

5. При каких значениях m можно представить в виде квадрата двучлена выражение mх 2 – 12х + 9.Ответ:_______
6. Решите уравнение х 2 + 5х + 6 = 0.

1) — 2; — 3 2) 2; 3 3) 3; 0 4) 2; -3

7. Найдите сумму корней уравнения х 2 + 12 = 7х.

1) 7 2) — 7 3) нет корней 4) — 5

8. Установите соответствие между данными уравнениями и знаками их корней: 1) х 2 — 7х + 4 = 0 А) Оба корня положительны 2) х 2 + 5х – 8 = 0 В) Оба корня отрицательны 3) 2х 2 + 9х + 1 = 0 С) Корни разных знаков
9.

Один из корней квадратного уравнения х 2 + kх – 16 = 0 равен -2. Найдите k.

1) 10 2) 16 3) — 6 4) — 10

10. Найдите произведение корней уравнения:

(1 – 2х)(4х 2 + 2х + 1) = 8(1 – х 2)(х + 2).

1) 3 2) 6,5 3) 0,76 4)

Вариант IV

1. Укажите верное утверждение:

1) Если D =0 , то уравнение имеет один корень.

2) Если D =0 , то уравнение имеетдва корня

3) Если D =0 , то уравнение не имеет корней

2. Какие из чисел являются корнями уравнения 6х 2 –5х – 1 = 0

1) –3; 2 2) 2; 4,2 3) 1; 4) — 2; 0

3. Найдите дискриминант квадратного уравнения 2х + 3 + 2х 2 = 0.

1) 20 2) 10 3) 15 4) — 20

4. Найдите наибольший корень уравнения 5х 2 – 8х + 3 = 0.

1) – 0,6 2) 0,5 3) 1 4) -1

5. При каких значениях m можно представить в виде квадрата двучлена выражение х 2 – 14х + m.Ответ:_______
6. Решите уравнение 5х 2 + 8х — 4 = 0.

1) 0,5; 2 2) 0,4; — 2 3) 0,5; 1 4) нет решений

Найдите сумму корней уравнения: 7х 2 + 5х = 2 1) – 1 2) 7 3) нет корней 4)
8. Установите соответствие между данными уравнениями и знаками их корней: 1) -2х 2 + 3х + 1 = 0 А) Оба корня положительны 2) -х 2 + 8х – 7 = 0 В) Оба корня отрицательны 3) 6х 2 + 13х + 4 = 0 С) Корни разных знаков9. Один из корней квадратного уравнения 3х 2 + kх + 10 = 0 равен -2. Найдите k.

1) 10 2) 12 3) 11 4) — 10

10. Найдите произведение корней уравнения:

8(х – 2)(х 2 – 1) = (4х 2 – 2х + 1)(2х + 1).

1) – 15 2) 16 3) 4) нет решений

Вариант V

1. Укажите верное утверждение:

1) По теореме Виета сумма корней уравнения х 2 +рх+q=0 равна – р.

2) По теореме Виета сумма корней уравнения х 2 +рх+q=0 равна q

3) По теореме Виета сумма корней уравнения х 2 +рх+q=0 равна р

2. Какие из чисел являются корнями уравнения 5х 2 – 8х + 3 = 0.

1) 0,6; 1 2) –1; 0,6 3) нет таких чисел. 4) 0; 0,6

3. Найдите дискриминант квадратного уравнения 2х 2 + 3х +1 = 0.

1) 4 2) 9 3) 3 4)1

4. Найдите сумму квадратов корней уравнения х 2 (х – 4) — (х – 4) = 0.

1) 18 2) 16 3) 4 4) 36

5. При каких значениях m можно представить в виде квадрата двучлена выражение х 2 + mх + 121.Ответ:_______
6. Решите уравнение -х 2 + 3 = 0.

1) 3; — 3 2) –√3; √3 3) 9; — 9 4) нет корней

7. Найдите сумму корней уравнения: 5х 2 + 3х – 8 = 0.

1) нет корней 2) 0,5 3) – 0,6 4) 1,6

8. Установите соответствие между данными уравнениями и знаками их корней: 1) х 2 — 5х + 6 = 0 А) Оба корня положительны 2) х 2 + 4х – 11 = 0 В) Оба корня отрицательны 3) 3х 2 + 7х + 1 = 0 С) Корни разных знаков9. Один из корней квадратного уравнения х 2 + k х — 35 = 0 равен 7. Найдите k.

1) –2 2) –5 3) 7 4) 0

10.Найдите произведение корней уравнения: (3 – 2х)(6х – 1) = (2х – 3) 2

1) – 0,7 2) 2 3) 0 4) 0,75

Ответы к заданиям по теме «Квадратные уравнения»

Тест

«Квадратное уравнение и его корни»

8 класс

(учебник «Алгебра» Ю. Н. Макарычев)

Составлен

Ветюковой Н.В.

учителем математики

МБОУ «Голузинская СОШ»

2018 год

Пояснительная записка

Цель: Контроль и проверка знаний, умений и навыков по решению квадратных уравнений.

Задачи: обобщить изученный по теме материал;

Формировать умения применять полученные математические знания на практике;

Воспитать интерес к математике;

Повышать уровень математической культуры.

Тест включает в себя два варианта. Задания разделены на два уровня: обязательный уровень – часть 1- (№1 — №6), в котором пять заданий с выбором ответа, одно задание с записью ответа и одно задание – на установление соответствия. Часть 2 — (№8 — №10), в котором три задания с подробной записью решения.

На выполнение теста отводится 45 минут.

Критерии оценивания

Планируемый результат

Обучающиеся должны знать:

Определения всех видов квадратных уравнений;

Формулы корней квадратного уравнения;

Теорему Виета;

Обучающиеся должны уметь:

Решать квадратные уравнения и уравнения, приводимые к квадратным;

Определять знаки корней уравнения;

Решать уравнения.

Вариант I

1. Какие из чисел являются корнями уравнения х 2 + 2х – 3 = 0.

1) 1; -3

2) –1; 3

3) нет таких чисел

4) 0; 4

Ответ:_____

2. Укажите число корней квадратного уравнения 5х 2 + 9х + 17 = 0.

нет корней

Ответ:_______

3. Решите уравнение 2х 2 + 3х – 5 = 0.

1) –2,5

2) 1

3) –1

4) 2,5

Ответ:_______

Ответ:________

А) х 2 — 5х + 3 = 0 1) Оба корня положительны

В) х 2 + 8х – 6 = 0 2) Оба корня отрицательны

С) 2х 2 + 7х + 1 = 0 3) Корни разных знаков

6. Один из корней квадратного уравнения х 2 + 5х + k = 0 равен –2. Найдите k.

1) –2

2) –5

3) 6

4) 0

Ответ:____________

7. Составьте квадратное уравнение по его корням х 1 = -8, х 2 = 7, используя теорему Виета.

Решение

Ответ: ________

Часть 2:

8. 2 – 3х + а + 4 =0 имеет один корень?

Решение:

Ответ:_________

9. На рисунке изображены графики функций у = 3 — и у = — 2х. Вычислите абциссу точки В.

Периметр прямоугольника равен 20 см. Найдите его стороны, если известно, что площадь прямоугольника равна 24

Вариант II .

1. Какие из чисел являются корнями уравнения 2х 2 + 5х – 3 = 0.

1) 3; 0,5

2) –0,5; -3

3) 0,5; -3

4) 1; 0

Ответ:_____________

2. Укажите число корней квадратного уравнения 4х 2 + 12х + 9 = 0.

нет корней

Ответ:______________

3. Решите уравнение 5х 2 – 7х + 2 = 0.

Если уравнение имеет несколько корней, то в ответе укажите наибольший корень.

1) 0,4

2) 1

3) –1

4) 2

Ответ:______________

4. Какое из следующих уравнений имеет корни — и 0?

Ответ:_____________

5. Установите соответствие между данными уравнениями и знаками их корней:

А) -3х 2 + 6х + 1 = 0 1) Оба корня положительны

В) -х 2 + 10х – 11 = 0 2) Оба корня отрицательны

С) 5х 2 + 17х + 5 = 0 3) Корни разных знаков

6. Один из корней квадратного уравнения 5х 2 – 7х + k = 0 равен -2 .Найдите k.

1) – 18

2) –10

3) 10

4) 18

Ответ:__________

7. Составьте квадратное уравнение по его корням х 1 =2, х 2 = , используя теорему Виета.

Решение

______________________________________________________________________

____________________________________________________________________

Ответ: _______

Часть 2:

8. При каком значении параметра а уравнение х 2 – 6х + 2а -1 = 0 имеет один корень?

Решение:

______________________________________________________________________________________________________________________________________________________

Ответ:_________

9. На рисунке изображены графики функций у = 6 — и у = — х. Вычислите абциссу точки В.

10. Решите задачу с помощью квадратного уравнения:

Периметр прямоугольника равен 30 см. Найдите его стороны, если известно, что площадь прямоугольника равна 56

Ответы к заданиям

Линейные и квадратные уравнения. | Образовательная социальная сеть

проверочный тест по теме: «Решение линейных уравнений» Вариант 1.

-6х – 4 = -9х + 11

1) 3 2) 12 3) 5 4) 1

6 – 5х = 2х +5

1) 8 2) 7 3) 4)

10(х – 9) = 7

1) 9,7 2) 0,87 3) 4) -0,97

5(2х + 4) = 6х – 10 Ответ: ______
7(-3 + х) – 2х = -6 Ответ: ______
2(х — 3) — 5 = 4х Ответ: ______
-5 (7 – х) + 2х = -7 Ответ: ______
Ответ: ______
Ответ: ______
9 + 3(1 – 2х) = 6х – 4 Ответ: ______
Ответ: ______
Ответ: ______
Ответ: ______

14) 3 – 3(х + 2) = 5 — 5х Ответ: ______

15) 1 + 8х +3(5 – х) = -4х – 2 Ответ: ______

16) -10х – 6(-1 + 6х) = -6х – 4 Ответ: ______

Проверочный тест по теме: «Решение линейных уравнений» Вариант 2.

10х + 4 = 7х + 19

1) 1 2) -5 3) 12 4) 5

9 – 6х = 8х + 7

1) 2) 3) 1 4) — 5

5(х + 2) = 1

1) 1,8 2) 3) -4 4) -1,8

7(2х + 3) = 12х + 11 Ответ: ______
7(-4 + х) + 3х = 4 Ответ: ______
2(х + 7) – 9 = -2х Ответ: ______
-3 (5 – х) = 11 + 2х Ответ: ______
Ответ: ______
Ответ: ______
Ответ: ______
Ответ: ______
Ответ: ______
Ответ: _____
-3 + 4( х – 1) = 5 – 2х Ответ: _____
2х – 3 + 2(х — 1) = 3х – 11 Ответ: _____
9х – 7(-10 — 3х) = х — 17 Ответ: ______

Ответы к проверочному тесту по теме: «Решение линейных уравнений».

Вариант 1.

1) 3

3) 1

4) – 7, 5

5) 3

6) – 5,5

7) 4

8) – 0,6

9) — 7

10) 1,75

11) – 1,5

12)

13) 7

14) 4

15) – 2

16) 0,25

Ответы к проверочному тесту по теме: «Решение линейных уравнений».

Вариант 2.

1) 4

2) 2

3) 4

4) – 5

5) 3,2

6) – 1,25

7) 26

8) – 3

9) 1,8

10) 3

11) 2

12)

13)

14) 2

15) – 6

16) – 3

Проверочный тест по теме: «Решение квадратных уравнений»

Вариант 1.

1) Решите уравнение: х2 + 4х = 0

1) 0; 4 2) 4 3) 0; -4 4) 1; -4

2) Решите уравнение: 1 – 9у2= 0

Ответ: ________

3) Решите уравнение: –у2 + 3 = 0

Ответ: ________

4) Решите уравнение: х2 – 7х + 12 = 0

1) -3; 4 2) -3; -4 3) 3; -4 4) 3; 4

5) Найдите наименьший корень уравнения:

у2 + 8у + 15 = 0

Ответ: _______

6) Решите уравнение: 2х2 – 7х + 5 = 0

Ответ: _______

7) Найдите сумму корней уравнения:

х2 – 13х + 40 = 0

Ответ: ________

8) Найдите наибольший корень уравнения:

х2 = -15х – 56

Ответ: ________

9) Найдите произведение корней уравнения:

х2 + 16х = — 63

Ответ: ________

10) Соотнесите квадратные уравнения и их корни:

а) х2 + 3х -4 = 0 б) х2 – 9 = 0 в) х2 — 10х + 25 =0

1) х1=-3, х2 = 3 2) х = 5

3) х1=-4, х2= 1 4) нет корней

Ответ:

11) Найдите корни уравнения: 4х +1= — 4х2

Ответ: ________

12) Решите уравнение:

Ответ: ________

13) Решите уравнение: 5(х – 2) = (3х +2)(х – 2)

Ответ: ________

14) Решите уравнение:

Ответ: ________

Проверочный тест по теме: «Решение квадратных уравнений»

Вариант 2.

1) Решите уравнение: 3х2 — х = 0

1) — 2) 0; 3 3) 0; 1 4)

2) Решите уравнение: 1 – 16у2= 0

Ответ: ____

3) Решите уравнение: –у2 + 8 = 0

Ответ:_______

4) Решите уравнение: х2 — 8х + 15 = 0

1) 3; 5 2) -3; -5 3) -3; 5 4) 3; -5

5) Найдите наибольший корень уравнения:

2х2 + 3х + 1 = 0

Ответ: ________

6)Решите уравнение: 4х2 — 7х + 3 = 0

Ответ: ________

7) Найдите сумму корней уравнения:

х2 – 17х + 42 =0

Ответ: ________

8) Найдите наименьший корень уравнения:

х2 = 7х + 18

Ответ: ________

9) Найдите произведение корней уравнения:

х2 + 9х = — 14

Ответ: ________

10) Соотнесите квадратные уравнения и их корни:

а) х2 — х — 2 = 0 б) х2 – х = 0 в) х2 + 25 =0

1) х1=-1, х2 = 1 2) х1 = 0, х2 = 1

3) х1=-1, х2= 2 4) нет корней

Ответ:

11) Найдите корни уравнения: 1 +4у = 5у2

Ответ: ________

12) Решите уравнение:

Ответ: ________

13) Решите уравнение: (х + 3)2 – 16 = (1 – 2х)2

Ответ: ________

14) Решите уравнение:

Ответ: ________

Ответы к проверочному тесту по теме: «Решение квадратных уравнений».

Вариант 1.

1) 3

4) 4

5) -5

6) 1; 2,5

7) 13

8) -7

9) 63

10)

11) -0,5

12) -0,75; 2,5

13) 1; 2

14) -4,8; 2

Ответы к проверочному тесту по теме: «Решение квадратных уравнений».

Вариант 2.

1) 4

2) -0,25; 0,25

4) 1

5) -0,5

6) 0,75; 1

7) 17

8) -2

9) 14

10)

11) -0,2; 1

12) -0,25;

13)

14) -0,8; 3

— Большая перемена

Тест

«Квадратные уравнения»

8 класс

Составлен Митиной Т.В.
учителем математики
Лебяжьевского филиала
МБОУ Моисеево-Алабушской сош Уваровского района
Тамбовской области

2013 год

Пояснительная записка
Тематический тест составлен по теме «Квадратные уравнения» и предназначен для обучающихся 8 класса. Задания, которые содержатся в данном тесте, позволят не только отработать тему «Квадратные уравнения», но и помогут обучающимся научиться уверенно решать задания разного характера. Важность представленного теста обусловлена еще и тем, что задания, связанные с нахождением корней квадратных уравнений, встречаются в материалах ГИА. Тест может быть полезен как для обучающихся с повышенной мотивацией к изучению математики, так и для обучающихся, которые стремятся повысить уровень своих знаний по математике.
Цель: Контроль и проверка знаний, умений и навыков по решению квадратных уравнений.
Задачи: обобщить изученный по теме материал;
— формировать умения применять полученные математические знания на практике;
— формировать умения работать с тестами, что является очень актуальным для подготовки учащихся к экзаменам в виде ГИА;
— способствовать формированию умений применять приемы сравнения, обобщения выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти; развивать познавательную активность, творческие способности;
— воспитать интерес к математике;
— повышать уровень математической культуры.
Тест включает в себя пять вариантов. Задания разделены на два уровня: обязательный уровень (№1 — №6), в котором четыре задания с выбором ответа, одно задание с записью ответа и одно задание – указать верное утверждение. Дополнительный уровень (№7 — №10), в котором три задания с выбором ответа и одно задание на установление соответствия.
На выполнение теста отводится 45 минут.

Критерии оценивания

№ задания 1 2 3 4 5 6 7 8 9 10
балл 1 1 1 1 1 1 3 3 4 4

6 баллов – оценка «3»
9 – 12 баллов – оценка «4»
16 – 20 баллов – оценка «5»

Планируемый результат

Обучающиеся должны знать:
— определения всех видов квадратных уравнений;
— формулы корней квадратного уравнения;
— теорему Виета;
— свойства коэффициентов квадратного уравнения.

Обучающиеся должны уметь:
— решать квадратные уравнения и уравнения, приводимые к квадратным;
определять знаки корней уравнения;
решать уравнения и неравенства.

Вариант I

1. Укажите верное утверждение:
1) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется линейным уравнением.
2) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется квадратным уравнением.
3) Уравнение, приводимое к виду ах2+вх+с=0, где а,в,с некоторые числа, х- переменная, причем а≠0, называется дробно-рациональным уравнением.

2. Какие из чисел являются корнями уравнения х2 + 2х – 3 = 0.
1) 1; -3 2) –1; 3 3) нет таких чисел. 4) 0; 4

3. Найдите дискриминант квадратного уравнения 5х2 – 4х – 1 = 0.
1) 16 2)- 20 3) 36 4)16

4. Найдите наибольший корень уравнения 2х2 + 3х – 5 = 0.
1) –2,5 2) 1 3) –1 4) 2,5

5. При каких значениях m можно представить в виде квадрата двучлена выражение х2 + mх + 9.
Ответ:_______

6. Решите уравнение х2 – х = 0.
1) 0; 1 2) –1; 1 3) 0 4) 0; -1

7. Найдите сумму корней уравнения: 10х2 – 3х – 0,4 = 0.
1)нет корней 2) 0,3 3) 1 4) 0,6

8. Установите соответствие между данными уравнениями и знаками их корней:
1) х2 — 5х + 3 = 0 А) Оба корня положительны
2) х2 + 8х – 6 = 0 В) Оба корня отрицательны
3) 2х2 + 7х + 1 = 0 С) Корни разных знаков

9. Один из корней квадратного уравнения х2 + 5х + k = 0 равен –2. Найдите k.
1) –2 2) –5 3) 6 4) 0

10.Найдите произведение корней уравнения: (3 – 2х)(6х – 1) = (2х – 3)2
1) – 0,7 2) 2 3) 0 4) 0,75

Вариант II

1. Укажите верное утверждение:
1) Квадратное уравнение, у которого коэффициент а=1, называется приведенным.
2) Квадратное уравнение, у которого коэффициент а=1, называется неприведенным.
3) Квадратное уравнение, у которого коэффициент а=1, называется неполным.

2. Какие из чисел являются корнями уравнения 2х2 + 5х – 3 = 0.
1) 3; 0,5 2) –0,5; -3 3) 0,5; -3 4) 1; 0

3. Найдите дискриминант квадратного уравнения х2 – 6х + 9 = 0.
1) 2 2) 9 3) 0 4) 36

4. Найдите наибольший корень уравнения 5х2 – 7х + 2 = 0.
1) 0,4 2) 1 3) –1 4) 2

5. При каких значениях m можно представить в виде квадрата двучлена выражение х2 – 2х – m.
Ответ:_______

6. Решите уравнение 7х = 4 х2.
1) 0; — 1,75 2)1,4; 1,75 3) –3; 0 4) 0; 1,75

7. Найдите сумму корней уравнения : 7х2 + 6х – 1 = 0.
1) 2) 1 3) – 0,5 4) –1

8. Установите соответствие между данными уравнениями и знаками их корней:
1) -3х2 + 6х + 1 = 0 А) Оба корня положительны
2) -х2 + 10х – 11 = 0 В) Оба корня отрицательны
3) 5х2 + 17х + 5 = 0 С) Корни разных знаков

9. Один из корней квадратного уравнения 5х2 – 7х + k = 0 равен -2 .Найдите k.
1) – 47,6 2) –53 3) 54 4) 30

10. Найдите произведение корней уравнения: (5 + 4х)2 = (9 – 21х)(4х + 5).

1) 2 2) – 0,2 3) 0,2 4) нет решений

Вариант III

1. Укажите верное утверждение:
1) Формула дискриминанта: D= в– 4ас
2) Формула дискриминанта: D= в2- 4а
3) Формула дискриминанта: D= в2- 4аc

2. Какие из чисел являются корнями уравнения 6х2 + х = 0.
1) нет таких чисел 2) 0; 3) 0; 1 4) 2; 0

3. Найдите дискриминант квадратного уравнения 3х – х2 + 10 = 0.
1) 49 2) — 49 3) 9 4) 25

4. Найдите наибольший корень уравнения 3х2 + 5х – 2 = 0.
1) 2 2) 3) 4) 4

5. При каких значениях m можно представить в виде квадрата двучлена выражение mх2 – 12х + 9.
Ответ:_______

6. Решите уравнение х2 + 5х + 6 = 0.
1) — 2; — 3 2) 2; 3 3) 3; 0 4) 2; -3

7. Найдите сумму корней уравнения х2 + 12 = 7х.
1) 7 2) — 7 3) нет корней 4) — 5

8. Установите соответствие между данными уравнениями и знаками их корней:
1) х2 — 7х + 4 = 0 А) Оба корня положительны
2) х2 + 5х – 8 = 0 В) Оба корня отрицательны
3) 2х2 + 9х + 1 = 0 С) Корни разных знаков

9. Один из корней квадратного уравнения х2 + kх – 16 = 0 равен -2. Найдите k.
1) 10 2) 16 3) — 6 4) — 10

10. Найдите произведение корней уравнения:
(1 – 2х)(4х2 + 2х + 1) = 8(1 – х2)(х + 2).

1) 3 2) 6,5 3) 0,76 4)

Вариант IV

1. Укажите верное утверждение:
1) Если D=0, то уравнение имеет один корень.
2) Если D=0, то уравнение имеет два корня
3) Если D=0, то уравнение не имеет корней

2. Какие из чисел являются корнями уравнения 6х2 –5х – 1 = 0
1) –3; 2 2) 2; 4,2 3) 1; 4) — 2; 0

3. Найдите дискриминант квадратного уравнения 2х + 3 + 2х2 = 0.
1) 20 2) 10 3) 15 4) — 20

4. Найдите наибольший корень уравнения 5х2 – 8х + 3 = 0.
1) – 0,6 2) 0,5 3) 1 4) -1

5. При каких значениях m можно представить в виде квадрата двучлена выражение х2 – 14х + m.
Ответ:_______

6. Решите уравнение 5х2 + 8х — 4 = 0.
1) 0,5; 2 2) 0,4; — 2 3) 0,5; 1 4) нет решений

7. Найдите сумму корней уравнения: 7х2 + 5х = 2
1) – 1 2) 7 3) нет корней 4)

8. Установите соответствие между данными уравнениями и знаками их корней:
1) -2х2 + 3х + 1 = 0 А) Оба корня положительны
2) -х2 + 8х – 7 = 0 В) Оба корня отрицательны
3) 6х2 + 13х + 4 = 0 С) Корни разных знаков

9. Один из корней квадратного уравнения 3х2 + kх + 10 = 0 равен -2. Найдите k.
1) 10 2) 12 3) 11 4) — 10

10. Найдите произведение корней уравнения:
8(х – 2)(х2 – 1) = (4х2 – 2х + 1)(2х + 1).
1) – 15 2) 16 3) 4) нет решений

Вариант V

1. Укажите верное утверждение:
1) По теореме Виета сумма корней уравнения х2+рх+q=0 равна – р.
2) По теореме Виета сумма корней уравнения х2+рх+q=0 равна q
3) По теореме Виета сумма корней уравнения х2+рх+q=0 равна р

2. Какие из чисел являются корнями уравнения 5х2 – 8х + 3 = 0.
1) 0,6; 1 2) –1; 0,6 3) нет таких чисел. 4) 0; 0,6

3. Найдите дискриминант квадратного уравнения 2х2 + 3х +1 = 0.
1) 4 2) 9 3) 3 4)1

4. Найдите сумму квадратов корней уравнения х2(х – 4) — (х – 4) = 0.
1) 18 2) 16 3) 4 4) 36

5. При каких значениях m можно представить в виде квадрата двучлена выражение х2 + mх + 121.
Ответ:_______

6. Решите уравнение -х2 + 3 = 0.
1) 3; — 3 2) –√3; √3 3) 9; — 9 4) нет корней

7. Найдите сумму корней уравнения: 5х2 + 3х – 8 = 0.
1) нет корней 2) 0,5 3) – 0,6 4) 1,6

8. Установите соответствие между данными уравнениями и знаками их корней:
1) х2 — 5х + 6 = 0 А) Оба корня положительны
2) х2 + 4х – 11 = 0 В) Оба корня отрицательны
3) 3х2 + 7х + 1 = 0 С) Корни разных знаков

9. Один из корней квадратного уравнения х2 + k х — 35 = 0 равен 7. Найдите k.
1) –2 2) –5 3) 7 4) 0

10.Найдите произведение корней уравнения: (3 – 2х)(6х – 1) = (2х – 3)2
1) – 0,7 2) 2 3) 0 4) 0,75

Ответы к заданиям по теме «Квадратные уравнения»

Вариант Задания
1 2 3 4 5 6 7 8 9 10
1 2 1 3 2 6 1 2 1 – А
2 – С
3 – В 3 4
2 1 3 3 2 -1 4 1 1 – С
2 – А
3 – В 1 2
3 3 2 1 3 2 1 1 1 – А
2 – С
3 – В 3 4
4 1 3 4 3 49 2 4 1 – С
2 – А
3 – В 3 3
5 1 1 4 1 22 2 3 1 – А
2 – С
3 – В 1 2

Тест №7 ЕГЭ по математике (база) 🐲 СПАДИЛО.РУ

Лимит времени: 0

Информация

Тестовые задания №7 ЕГЭ по математике.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

С ответом
С отметкой о просмотре

Задание 1 из 10
1. Решите уравнение х² = –2х + 24.
Если уравнение имеет больше одного корня, в ответе укажите больший из них.
Правильно
х² = –2х +24
х² +2х – 24 = 0
По т.Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.
Поскольку требуется указать больший из корней, то ответом будет 4.
Неправильно
х² = –2х +24
х² +2х – 24 = 0
По т. Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.
Поскольку требуется указать больший из корней, то ответом будет 4.
Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
Записываем в качестве ответа большее из полученных 2 чисел.
Задание 2 из 10
2. Найдите корни уравнения 4^х^–6 = 64.
Правильно
4^х^–6 = 64
4^х^–6 = 4³
х – 6 = 3
х = 9
Неправильно
4^х^–6 = 64
4^х^–6 = 4³
х – 6 = 3
х = 9
Представляем 64 как степень с основанием 4, т. е. приводим выражения справа и слева к степеням с одинаковым основанием.
Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
Находим корень ур-ния.
Задание 3 из 10
3. Найдите корень уравнения log₃ (2x – 5) = 2.
Правильно
log₃ (2x – 5) = 2
log₃ (2x – 5) = 2 · log₃3
log₃ (2x – 5) = log₃3²
2x – 5 = 3²
2x – 5 = 9
2x = 14
x=7
Неправильно
log₃ (2x – 5) = 2
log₃ (2x – 5) = 2 · log₃3
log₃ (2x – 5) = log₃3²
2x – 5 = 3²
2x – 5 = 9
2x = 14
x=7
Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xyⁿ=nlog_xy.
Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
Решаем полученное линейное ур-ние.
Задание 4 из 10
4. Найдите корень уравнения
Правильно
Неправильно
Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)^х=а^–х.
Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
Решаем полученное линейное ур-ние.
Задание 5 из 10
5. Найдите корень уравнения (х – 8)² = (х – 2)².
Правильно
(х – 8)² = (х – 2)²
х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²
х² – 16х + 64 = х² – 4х + 4
х² – 16х +64 – х² + 4х – 4 = 0
–12х + 60 = 0
–12х = –60
х = 5
Неправильно
(х – 8)² = (х – 2)²
х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²
х² – 16х + 64 = х² – 4х + 4
х² – 16х +64 – х² + 4х – 4 = 0
–12х + 60 = 0
–12х = –60
х = 5
Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)²=х²–2ху–у².
Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
Приводим подобные слагаемые. В результате уравнение стало линейным.
Решаем полученное уравнение.
Задание 6 из 10
6. Найдите корень уравнения
Правильно
Неправильно
Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)^х=а^–х.
Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
Решаем его.
Задание 7 из 10
7. Решите уравнение х² – 25 = 0
Правильно
х² – 25 = 0
х² = 25
х = ±√25
х₁ = –5, х₂ = 5
Для ответа берем 5.
Неправильно
х² – 25 = 0
х² = 25
х = ±√25
х₁ = –5, х₂ = 5
Для ответа берем 5.
Переносим 25 в правую часть ур-ния.
Выражаем из ур-ния х путем извлечения корня из 25.
Определяем корни, сравниваем их, определяем больший.
Задание 8 из 10
8. Найдите корень уравнения
Правильно
log₅ (24 – 7x) = log₅ 3
24 – 7x = 3
–7x = 3 – 24
7x = 21
x = 3
Неправильно
log₅ (24 – 7x) = log₅ 3
24 – 7x = 3
–7x = 3 – 24
7x = 21
x = 3
Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
Решаем полученное линейное ур-ние.
Задание 9 из 10
9. Найдите корень уравнения
Правильно
2^–(^x^–8) = 2³
–x+8 = 3
–x = 3–8
x = 5
Неправильно
2^–(^x^–8) = 2³
–x+8 = 3
–x = 3–8
x = 5
Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)^х=а^–х.
Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
Решаем его.
Задание 10 из 10
10. Найдите корень уравнения
Правильно
log₃ (2x + 4) – log₃ 2 = log₃ 5
log₃ (2x + 4)/2 = log₃ 5
log₃ (x + 2) = log₃ 5
x + 2 = 5
x = 3
Неправильно
log₃ (2x + 4) – log₃ 2 = log₃ 5
log₃ (2x + 4)/2 = log₃ 5
log₃ (x + 2) = log₃ 5
x + 2 = 5
x = 3
К левой части уравнения применяем св-во логарифмов log_a(x/y)=log_ax–log_ay.
Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
Решаем его.

2 — (- 16) = 0

Пошаговое решение:

Шаг 1:

Уравнение в конце шага 1:

 2 ² x ² - -16 = 0

Шаг 2:

Шаг 3:

Вытягивание как термины:

3.1 Вытягивающие факторы:

4x ² + 16 = 4 • (x ² + 4)

Калькулятор полиномиальных корней :

3.2 Найдите корни (нули): F (x) = x ² + 4
Калькулятор полиномиальных корней — это набор методов, направленных на поиск значений x, для которых F (x) = 0

Rational Roots Test является одним из вышеупомянутых инструментов.Он мог бы найти только рациональные корни, то есть числа x, которые можно выразить как частное двух целых чисел

Теорема рационального корня утверждает, что если полином обнуляется для рационального числа P / Q, то P является множителем конечной константы и Q является фактором ведущего коэффициента

В этом случае ведущий коэффициент равен 1, а конечная константа — 4.

Факторы:

ведущего коэффициента: 1
конечной постоянной: 1, 2, 4

Проверим….

P	Q	P / Q	F (P / Q)
-1	1	-1,00	5,00
-2	1	-2,00	8.00
-4	1	-4,00	20,00
1	1	1,00	5,00
2	1	2.00	8,00
4	1	4,00	20,00

Калькулятор полиномиальных корней не найден12 рациональных корней

в конце шага 3:

 4 • (x ² + 4) = 0

Шаг 4:

Уравнения, которые никогда не верны:

4. 1 Решить: 4 = 0

Это уравнение не имеет решения.
Ненулевая константа никогда не равна нулю.

Решение уравнения с одной переменной:

4.2 Решите: x ² +4 = 0

Вычтем 4 из обеих частей уравнения:
x ² = -4

Когда две вещи равны, их квадратные корни равны. Извлекая квадратный корень из двух частей уравнения, мы получаем:
x = ± √ -4

В математике i называется мнимой единицей.Это удовлетворяет i ² = -1. Оба i и -i являются квадратными корнями из -1

Соответственно, √ -4 =
√ -1 • 4 =
√ -1 • √ 4 =
i • √ 4

Можно ли упростить √ 4?

Да! Разложение на простые множители 4 равно
2 • 2
Чтобы удалить что-то из-под корня, должно быть 2 экземпляра этого числа (потому что мы берем квадрат, то есть второй корень).

√ 4 = √ 2 • 2 =
± 2 • √ 1 =
± 2

Уравнение не имеет реальных решений.2-x-16 = 0 Tiger Algebra Solver

Пошаговое решение:

Шаг 1:

Уравнение в конце шага 1:

 (2 ² x ² - x) - 16 = 0

Шаг 2:

Попытка разложить на множители путем разделения среднего члена

2. 1 Факторинг 4x ² -x-16

Первый член равен 4x ², его коэффициент равен 4.
Средний член, -x, его коэффициент -1.
Последний член, «константа», равен -16

Шаг-1: Умножьте коэффициент первого члена на константу 4 • -16 = -64

Шаг-2: Найдите два множителя -64, сумма которых равен коэффициенту среднего члена, который равен -1.

-64	+	1	=	-63
-32	+	2	=	-30
-16	+	4	=	-12
-8	+	8	=	0
-4	+	16	=	12
-2	+	32	=	30
-1	+	64	=	63

Наблюдение: таких факторов нет. можно найти !!
Вывод: Трехчлен не может быть разложен на множители

Уравнение в конце шага 2:

 4x ² - x - 16 = 0

Шаг 3:

Парабола, поиск вершины:

3.1 Найдите вершину y = 4x ² -x-16

Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (АКА абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент при первом члене, 4, положительный (больше нуля).

Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения.

Параболы могут моделировать многие реальные жизненные ситуации, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.

Для любой параболы Ax ² + Bx + C координата x вершины задается как -B / (2A).В нашем случае координата x равна 0,1250

Подставив в формулу параболы 0,1250 для x, мы можем вычислить координату y:
y = 4,0 * 0,12 * 0,12 — 1,0 * 0,12 — 16,0
или y = -16,062

Парабола, Графики вершин и пересечений X:

Корневой график для: y = 4x ² -x-16
Ось симметрии (пунктирная линия) {x} = {0.12}
Вершина в {x, y} = {0,12, — 16.06}
x -Перехват (корни):
Корень 1 при {x, y} = {-1,88, 0,00}
Корень 2 при {x, y} = {2.13, 0.00}

Решите квадратное уравнение, заполнив квадрат.

3.2 Решение 4x ² -x-16 = 0, заполнив квадрат.

Разделите обе части уравнения на 4, чтобы получить 1 в качестве коэффициента перед первым членом:
x ² — (1/4) x-4 = 0

Добавьте 4 к обеим сторонам уравнения:
x ² — (1/4) x = 4

А теперь умный бит: возьмите коэффициент при x, равный 1/4, разделите на два, получив 1/8, и возведите его в квадрат, получив 1/64

Добавьте 1/64 к обеим частям уравнения:
В правой части мы имеем:
4 + 1/64 или, (4/1) + (1/64)
Общий знаменатель двух дробей равен 64. (256/64) + (1/64) дает 257/64
Таким образом, прибавляя к обеим сторонам, мы окончательно получаем:
x ² — (1/4) x + (1/64) = 257/64

Добавление 1 / 64 превратил левую часть в полный квадрат:
x ² — (1/4) x + (1/64) =
(x- (1/8)) • (x- (1/8) ) =
(x- (1/8)) ²
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x ² — (1/4) x + (1/64) = 257/64 и
x ² — (1/4) x + (1/64) = (x- (1/8)) ²
тогда, в соответствии с законом транзитивности,
(x- (1/8)) ² = 257/64

Мы будем называть это уравнение уравнением. # 3.2.1

Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.

Обратите внимание, что квадратный корень из
(x- (1/8)) ² равен
(x- (1/8)) ^2/2 =
(x- (1/8)) ¹ =
x- (1/8)

Теперь, применяя принцип квадратного корня к уравнению. # 3.2.1 получаем:
x- (1/8) = √ 257/64

Добавьте 1/8 к обеим сторонам, чтобы получить:
x = 1/8 + √ 257/64

Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x ² — (1/4) x — 4 = 0
имеет два решения:
x = 1/8 + √ 257/64
или
x = 1/8 — √ 257/64

Обратите внимание, что √ 257/64 можно записать как
√ 257 / √ 64, что равно √ 257/8

Решите квадратное уравнение с помощью квадратичной формулы

3.3 Решение 4x ² -x-16 = 0 по квадратичной формуле.

Согласно квадратичной формуле, x, решение для Ax ² + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как:

— B ± √ B ² -4AC
x = ————————
2A

В нашем случае A = 4
B = -1
C = -16

Соответственно B ² — 4AC =
1 — (-256) =
257

Применяя квадратную формулу:

1 ± √ 257
x = —————
8

√ 257, округленное до 4 десятичных цифр, равно 16. 0312
Итак, теперь мы смотрим на:
x = (1 ± 16,031) / 8

Два реальных решения:

x = (1 + √257) / 8 = 2,129

или:

x = (1- √257) /8=-1,879

Были найдены два решения:

x = (1-√257) /8=-1,879
x = (1 + √257) / 8 = 2,129

Извлечение квадрата Корни

Извлечение квадратного корня

Напомним, что квадратное уравнение имеет стандартную форму Любое квадратное уравнение в форме ax2 + bx + c = 0, где a , b и c — действительные числа и a 0.если он равен 0:

, где a , b и c — действительные числа и a 0. Решение такого уравнения называется корневым решением квадратного уравнения в стандартной форме. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Если квадратное выражение слева множители, то мы можем решить его путем факторизации. Обзор шагов, используемых для решения с помощью факторинга, следующий:

Шаг 1: Выразите квадратное уравнение в стандартной форме.

Шаг 2: Факторизуйте квадратичное выражение.

Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным 0.

Шаг 4: Решите полученные линейные уравнения.

Например, мы можем решить x2−4 = 0, разложив на множители следующим образом:

Двумя решениями являются −2 и 2. Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, давая форму

Уравнение x2−4 = 0 находится в этой форме и может быть решено путем выделения x2.

Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее:

Здесь мы видим, что x = −2 и x = 2 являются решениями полученного уравнения. В общем, это описывает свойство квадратного корня для любого действительного числа k , если x2 = k, то x = ± k .; для любого действительного числа k ,

Обозначение «±» читается как «плюс или минус» и используется как компактное обозначение, обозначающее два решения.Следовательно, утверждение x = ± k указывает, что x = −k или x = k. Применение свойства квадратного корня как средства решения квадратного уравнения называется извлечением корней Применение свойства квадратного корня как средства решения квадратного уравнения.

Пример 1: Решите: x2−25 = 0.

Решение: Начните с выделения квадрата.

Затем примените свойство квадратного корня.

Ответ: Решения — 5 и 5.Чек предоставляется читателю.

Конечно, предыдущий пример можно было бы так же легко решить с помощью факторинга. Тем не менее, он демонстрирует метод, который можно использовать для решения уравнений в этой форме, которые не учитывают факторы.

Пример 2: Решить: x2−5 = 0.

Решение: Обратите внимание, что квадратичное выражение слева не множится. Мы можем извлечь корни, если сначала выделим главный член x2.

Примените свойство квадратного корня.

Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение. Как правило, проверка не является обязательной.

Ответ: Решения — 5 и 5.

Пример 3: Решить: 4×2-45 = 0.

Решение: Начните с изоляции x2.

Примените свойство квадратного корня, а затем упростите.

Ответ: Решения — 352 и 352.

Иногда квадратные уравнения не имеют реального решения.

Пример 4: Решить: x2 + 9 = 0.

Решение: Начните с изоляции x2.

После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения.

Ответ: Реального решения нет

Обратитесь к этому процессу, чтобы найти уравнения с заданными решениями вида ± k .

Пример 5: Найдите уравнение с решениями −23 и 23.

Решение: Начните с возведения в квадрат обеих частей следующего уравнения:

Наконец, вычтите 12 из обеих частей и представьте уравнение в стандартной форме.

Ответ: x2−12 = 0

Попробуй! Решите: 9×2−8 = 0.

Ответ: x = −223 или x = 223

Рассмотрите возможность решения следующего уравнения:

Чтобы решить это уравнение путем факторизации, сначала возведите в квадрат x + 2, а затем представьте его в стандартной форме, равной нулю, путем вычитания 25 из обеих частей.

Коэффициент

, а затем применить свойство нулевого произведения.

Два решения: −7 и 3.

Когда уравнение имеет такую форму, мы можем получить решения за меньшее количество шагов, извлекая корни.

Пример 6: Решите: (x + 2) 2 = 25.

Решение: Решите, извлекая корни.

На этом этапе разделите «плюс или минус» на два уравнения и упростите каждое по отдельности.

Ответ: Решения -7 и 3.

В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, которые не учитывают множители.

Пример 7: Решите: (3x + 3) 2−27 = 0.

Решение: Начните с выделения квадрата.

Затем извлеките корни и упростите.

Решите для x .

Ответ: Решения: −1−3 и −1 + 3.

Пример 8: Решите: 9 (2x − 1) 2−8 = 0.

Решение: Начните с выделения квадратного множителя.

Примените свойство квадратного корня и решите.

Ответ: Решения 3−226 и 3 + 226.

Попробуй! Решите: 3 (x − 5) 2−2 = 0.

Ответ: 15 ± 63

Пример 9: Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.

Решение:

Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы:

Решить.

Здесь мы получаем два решения, w = −25 и w = 25. Поскольку в задаче требовалась длина прямоугольника, мы игнорируем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.

Обратно подставить, чтобы найти длину.

Ответ: Длина прямоугольника составляет 455 футов, а ширина — 255 футов.

Ключевые выводы

Решите уравнения вида ax2 + c = 0, извлекая корни.
Извлечение корней включает в себя выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все радикальные выражения и при необходимости рационализируйте знаменатель.

Тематические упражнения

Часть A: извлечение квадратного корня

Решите с помощью факторизации, а затем извлеките корни.Проверить ответы.

1. x2−36 = 0

2. x2−81 = 0

3. 4y2−9 = 0

4. 9y2−25 = 0

5. (x − 2) 2−1 = 0

6. (x + 1) 2−4 = 0

7. 4 (y − 2) 2−9 = 0

8. 9 (y + 1) 2−4 = 0

9. −3 (t − 1) 2 + 12 = 0

10. −2 (t + 1) 2 + 8 = 0

11. (x − 5) 2−25 = 0

12. (x + 2) 2−4 = 0

Решите, извлекая корни.

13. x2 = 16

14. x2 = 1

15. y2 = 9

16. y2 = 64

17. x2 = 14

18. x2 = 19

19. y2 = 0,25

20. y2 = 0,04

21. x2 = 12

22. x2 = 18

23. 16×2 = 9

24. 4×2 = 25

25. 2t2 = 1

26.3t2 = 2

27. x2−100 = 0

28. x2−121 = 0

29. y2 + 4 = 0

30. y2 + 1 = 0

31. x2−49 = 0

32. x2−925 = 0

33. y2−0.09 = 0

34. y2−0,81 = 0

35. x2−7 = 0

36. x2−2 = 0

37. x2−8 = 0

38. t2−18 = 0

39. х2 + 8 = 0

40.х2 + 125 = 0

41. 16×2−27 = 0

42. 9×2-8 = 0

43. 2y2−3 = 0

44. 5y2−2 = 0

45. 3×2−1 = 0

46. 6×2−3 = 0

47. (x + 7) 2−4 = 0

48. (x + 9) 2−36 = 0

49. (2y − 3) 2-81 = 0

50. (2у + 1) 2−25 = 0

51. (x − 5) 2−20 = 0

52. (x + 1) 2−28 = 0

53.(3t + 2) 2−6 = 0

54. (3т − 5) 2−10 = 0

55,4 (у + 2) 2−3 = 0

56. 9 (y − 7) 2−5 = 0

57,4 (3x + 1) 2−27 = 0

58. 9 (2x − 3) 2−8 = 0

59. 2 (3x − 1) 2 + 3 = 0

60,5 (2x − 1) 2−3 = 0

61,3 (y − 23) 2−32 = 0

62. 2 (3y − 13) 2−52 = 0

Найдите квадратное уравнение стандартной формы со следующими решениями.

63. ± 7

64. ± 13

65. ± 7

66. ± 3

67. ± 35

68. ± 52

69. 1 ± 2

70,2 ± 3

Решите и округлите решения до сотых.

71. 9x (x + 2) = 18x + 1

72. x2 = 10 (x2−2) −5

73. (x + 3) (x − 7) = 11−4x

74.(x − 4) (x − 3) = 66−7x

75. (x − 2) 2 = 67−4x

76. (x + 3) 2 = 6x + 59

77. (2x + 1) (x + 3) — (x + 7) = (x + 3) 2

78. (3x − 1) (x + 4) = 2x (x + 6) — (x − 3)

Составьте алгебраическое уравнение и используйте его для решения следующих задач.

79. Если 9 вычесть из четырех квадратов числа, то результат будет 3. Найдите число.

80. Если из квадрата числа вычесть 20, то получится 4.Найдите номер.

81. Если 1 прибавить к троекратному квадрату числа, то получится 2. Найдите число.

82. Если 3 прибавить к двукратному квадрату числа, получится 12. Найдите число.

83. Если квадрат имеет площадь 8 квадратных сантиметров, найдите длину каждой стороны.

84. Если круг имеет площадь 32π квадратных сантиметра, найдите длину радиуса.

85.Объем правого кругового конуса составляет 36π кубических сантиметров при высоте 6 сантиметров. Найдите радиус конуса. (Объем правого кругового конуса равен V = 13πr2h.)

86. Площадь поверхности сферы составляет 75π квадратных сантиметров. Найдите радиус сферы. (Площадь поверхности сферы определяется как SA = 4πr2.)

87. Длина прямоугольника в 6 раз больше его ширины. Если площадь составляет 96 квадратных дюймов, то найдите размеры прямоугольника.

88. Основание треугольника вдвое больше его высоты. Если площадь составляет 16 квадратных сантиметров, то найдите длину его основания.

89. Квадрат имеет площадь 36 квадратных единиц. На какую равную величину необходимо увеличить стороны, чтобы получить квадрат с удвоенной заданной площадью?

90. Круг имеет площадь 25π квадратных единиц. На какую величину нужно увеличить радиус, чтобы создать круг с удвоенной заданной площадью?

91.Если стороны квадрата равны 1 единице, то найдите длину диагонали.

92. Если стороны квадрата равны 2 единицам, то найдите длину диагонали.

93. Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны.

94. Диагональ квадрата составляет 3 дюйма. Найдите длину каждой стороны.

95. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 10 футов, найдите размеры прямоугольника.

96. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 8 футов, найдите размеры прямоугольника.

97. Длина прямоугольника в 3 раза больше его ширины. Если диагональ 5 метров, то найдите размеры прямоугольника.

98. Длина прямоугольника в 3 раза больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.

99. Высота в футах объекта, падающего с 9-футовой лестницы, определяется выражением h (t) = — 16t2 + 9, где t представляет время в секундах после того, как объект был сброшен.Сколько времени нужно, чтобы объект упал на землю? (Подсказка: когда объект падает на землю, высота равна 0.)

100. Высота в футах объекта, сброшенного с 20-футовой платформы, определяется выражением h (t) = — 16t2 + 20, где t представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю?

101. Высота в футах объекта, упавшего с вершины 144-футового здания, определяется выражением h (t) = — 16t2 + 144, где t измеряется в секундах.

а. Сколько времени потребуется, чтобы добраться до половины расстояния до земли, 72 фута?

г. Сколько времени потребуется, чтобы добраться до земли?

Округлите до сотых долей секунды.

102. Высота в футах объекта, сброшенного с самолета на высоте 1600 футов, определяется выражением h (t) = — 16t2 + 1,600, где t — в секундах.

а. Сколько времени потребуется, чтобы добраться до земли на половину расстояния?

г.Сколько времени потребуется, чтобы добраться до земли?

Округлить до сотых долей секунды .

Часть B: Обсуждение

103. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им и решением на доске обсуждений.

104. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.

105. Объясните своими словами, как решить, извлекая корни.

106. Выведите формулу диагонали квадрата через его стороны.

ответы

1: −6, 6

3: −3/2, 3/2

5: 1, 3

7: 1/2, 7/2

9: -1, 3

11: 0, 10

13: ± 4

15: ± 3

17: ± 1/2

19: ± 0.5

21: ± 23

23: ± 3/4

25: ± 22

27: ± 10

29: Реального решения нет

31: ± 2/3

33: ± 0,3

35: ± 7

37: ± 22

39: Реального решения нет

41: ± 334

43: ± 62

45: ± 33

47: −9, −5

49: −3, 6

51: 5 ± 25

53: −2 ± 63

55: −4 ± 32

57: −2 ± 336

59: Реального решения нет

61: 4 ± 326

63: x2−49 = 0

65: x2−7 = 0

67: x2-45 = 0

69: x2−2x − 1 = 0

71: ± 0. 33

73: ± 5,66

75: ± 7,94

77: ± 3.61

79: −3 или 3

81: −33 или 33

83:22 сантиметра

85:32 сантиметра

87: Длина: 24 дюйма; ширина: 4 дюйма

89: −6 + 62≈2,49 ед.

91: 2 шт.

93: 522 дюйма

95: Длина: 45 футов; ширина: 25 футов

97: Длина: 3102 метра; ширина: 102 метра

99: 3/4 секунды

101: а.2,12 секунды; б. 0,88 секунды

Решение радикальных уравнений

Как решать уравнения с квадратными корнями, кубическими корнями и т. Д.

Радикальные уравнения

Решение радикальных уравнений

Мы можем избавиться от квадратного корня возведением в квадрат. (Или кубические корни кубиками и т. Д.)

Но предупреждение: иногда это может создавать «решения», которые на самом деле не работают, когда мы помещаем их в исходное уравнение. Итак, нам нужно проверить!

Выполните следующие действия:

изолируйте квадратный корень с одной стороны уравнения
возвести в квадрат обе части уравнения

Тогда продолжайте наше решение!

Пример: решить √ (2x + 9) — 5 = 0

вычлените квадратный корень: √ (2x + 9) = 5

квадрат с обеих сторон: 2x + 9 = 25

Теперь решать должно быть проще!

Переместите 9 вправо: 2x = 25 — 9 = 16

Разделить на 2: x = 16/2 = 8

Ответ: x = 8

Проверка: √ (2 · 8 + 9) — 5 = √ (25) — 5 = 5 — 5 = 0

Тот работал отлично.

Более одного квадратного корня

Что делать, если есть два или более квадратных корня? Легко! Просто повторите процесс для каждого.

Это займет больше времени (намного больше шагов) … но ничего особенного.

Пример: решить √ (2x − 5) — √ (x − 1) = 1

выделить один из квадратных корней: √ (2x − 5) = 1 + √ (x − 1)

квадрат с обеих сторон: 2x − 5 = (1 + √ (x − 1)) ²

Мы удалили один квадратный корень.

развернуть правую часть: 2x − 5 = 1 + 2√ (x − 1) + (x − 1)

упростить: 2x − 5 = 2√ (x − 1) + x

вычтем x из обеих частей: x − 5 = 2√ (x − 1)

Теперь снова вычислим квадратный корень:

выделите квадратный корень: √ (x − 1) = (x − 5) / 2

квадрат с обеих сторон: x − 1 = ((x − 5) / 2) ²

Мы успешно удалили оба квадратных корня.

Давайте продолжим решение.

Разверните правую часть: x − 1 = (x ² — 10x + 25) / 4

Это квадратное уравнение! Так что давайте представим это в стандартной форме.

Умножьте на 4, чтобы удалить деление: 4x − 4 = x ² — 10x + 25

Переместите все налево: 4x — 4 — x ² + 10x — 25 = 0

Объедините похожие термины: −x ² + 14x — 29 = 0

Поменять местами все знаки: x ² — 14x + 29 = 0

Использование квадратичной формулы (a = 1, b = −14, c = 29) дает решения:

2. 53 и 11,47 (до 2 знаков после запятой)

Проверим решения:

2,53: √ (2 × 2,53−5) — √ (2,53−1) ≈ −1 Ой! Должно быть плюс 1.

11,47: √ (2 × 11,47−5) — √ (11,47−1) ≈ 1 Да, это работает.

Есть реально только одно решение :

Ответ: 11,47 (с точностью до 2 знаков после запятой)

Видите? Этот метод может иногда давать решения, которые действительно не работают!

Корень, который казался работоспособным, но был неправильным, когда мы его проверили, называется «Посторонний корень»

Итак: Проверка важна.

Нахождение квадратного корня многочлена методом длинного деления

Метод деления в столбик при нахождении квадратного корня из многочлена полезен, когда степень многочлена выше.

Здесь мы увидим, как найти квадратный корень из многочлена четвертой степени, используя метод деления в долгую.

Вопрос 1:

Найдите квадратный корень из следующих многочленов методом деления

(i) x ⁴ −12x ³ + 42x ² −36x + 9

Шаг 1:

x ⁴ разложено на две равные части x ² и x ².

Шаг 2:

Умножив частное (x ²) на 2, мы получим 2x ². Теперь уменьшите следующие два члена -12x ³ и 42x ².

Разделив -12x ³ на 2x ², мы получим -6x. Продолжая таким образом, мы получаем следующие шаги.

Следовательно, квадратный корень из x ⁴ −12x ³ + 42x ² −36x + 9 равен x ² — 6x + 3

(ii) 37x ² −28x ³ + 4x ⁴ + 42x + 9

Решение:

Сначала расположим данный многочлен от наибольшего к наименьшему порядку.

4x ⁴ −28x ³ + 37x ² + 42x + 9

Следовательно, квадратный корень из 37x ² −28x ³ + 4x ⁴ + 42x + 9 равен 2x ² — 7x — 3.

(iii) 16x ⁴ + 8x ² + 1

Решение:

Следовательно, квадратный корень из 37x ² −28x ³ + 4x ⁴ + 42x + 9 равен 4x ² + 0x + 1.

(iv) 121x ⁴ — 198x ³ — 183x ² + 216x + 144

Решение:

Следовательно, квадратный корень из 121x ⁴ — 198x ³ — 183x ² + 216x + 144 составляет 11x ² + 9x + 12.

Вопрос 2:

Найдите квадратный корень из выражения

(x ² / y ²) — 10x / y + 27 — (10y / x) + (y ² / x ²)

Решение:

Взяв LCM, мы получаем

(x ⁴ — 10x ³ y + 27x ² y ² — 10xy ³ + y ⁴) / x ² y ²

= √ (x ⁴ — 10x ³ y + 27x ² y ² — 10xy ³ + y ⁴) / √x ² г ²

= (x ² — 5xy + y ²) / xy

= (x / y) — 5 + (y / x)

Следовательно, квадратный корень из полинома (x ² / y ²) — 10x / y + 27 — (10y / x) + (y ² / x ²) равно (x / y) — 5 + (y / x).

Давайте рассмотрим следующий пример «Нахождение квадратного корня многочлена методом длинного деления».

Поиск недостающего значения в многочлене

Вопрос 1:
Найдите значения a и b, если следующие многочлены являются полными квадратами
(i) 4x ⁴ −12x ³ + 37x ² + bx + a
Решение:
Приравнивая коэффициенты при x, получаем
b = -42
Приравнивая постоянные члены, получаем
a = 49
Следовательно, значения a и b равны -49 и 42 соответственно.
(ii) ax ⁴ + bx ³ + 361x ² + 220x + 100
Решение:
Приравнивая коэффициенты при x ³, получаем
b = 264
Приравнивая коэффициенты при x ⁴, получаем
a = 144
Следовательно, значения a и b равны 144 и 264 соответственно. .
Вопрос 2:
Найдите значения m и n, если следующие выражения являются точными sqaures
(i) (1 / x ⁴) — (6 / x ³) + (13 / x ²) + (m / x) + n
Решение:
Взяв L. C.M получаем
(1 — 6x + 13x ² + mx ³ + nx ⁴) / x ⁴
Приравнивая коэффициенты при x ³, получаем
m = -12
Приравнивая коэффициенты при x ⁴, получаем
n = 4
Следовательно, значения m и n равны 6 и 4 соответственно.
(ii) x ⁴ — 8x ³ + mx ² + nx + 16
Решение:
Приравнивая постоянный член, получаем
[(м — 16) / 2] ² = 16
(м — 16) / 2 = 4
м — 16 = 8
м = 8 + 16 = 24
Приравнивая коэффициенты при x, получаем
n = -4 (m — 16)
n = -4 (24-16)
n = -4 (8) = -32
Следовательно значения m и n равны 24 и -32.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть отзывы о наших математических материалах, напишите нам:
v4formath@gmail. com
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях 25
Задачи на слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямому и обратному изменению
Проблемы со словами по цене за единицу
Проблемы со словами по скорости за единицу
задачи по сравнению ставок
Преобразование обычных единиц словесные задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word задачи по сложным процентам
ngles
Проблемы с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
5 Задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами с линейными неравенствами
60 9125 59 Задачи
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Проблемы со словами для возрастов
Теорема Пифагора задачи со словами
Процент числового слова проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибыли и убытков
Сокращение в процентах
Сокращение в таблице времен
Сокращение времени, скорости и расстояния
Сокращение соотношения и пропорции
Домен и диапазон 912 рациональных функций 4 Область и диапазон 912 рациональных функций 4 функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных знаков в дроби
Десятичное представление рациональных чисел
Поиск корня из длинного квадрата видение
Л. Метод CM для решения задач времени и работы
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении в степени 17 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Графические радикальные функции: больше примеров
Purplemath
Первые два графа квадратного корня на предыдущей странице имели обычную форму дуги квадратного корня. Однако последний график на предыдущей странице больше походил на букву «V», но с закругленным дном (а не с острым изгибом дна, ожидаемым на графике абсолютных значений). Хотя большинство функций извлечения квадратного корня, которые вам будут даны, будут отображаться в виде дуг, некоторые — нет, и эти графики другой формы станут более распространенными, если вы перейдете к исчислению.
MathHelp.com
Однако основной процесс все тот же; а именно, сначала найдите область, а затем нанесите на нее достаточно точек, чтобы у вас было хорошее представление о том, куда должна идти графическая линия. (И, конечно, если у вас есть графический калькулятор, проверьте свою работу!)
График
В последнем примере на предыдущей странице аргумент квадратного корня, как и здесь, был квадратичным.
Сначала найду домен. Чтобы сделать это алгебраически, я начну с того, что установлю аргумент квадратного корня равным нулю.
16 — 9060 5 x ² = 0
x ² — 16 = 0
( x — 4) ( x + 4) = 0
x = –4, 4
Но мне нужно знать, где аргумент равен или больше нуля.Что мне теперь делать? Если я изучал, как решать квадратичные неравенства, я могу использовать эту методологию. Но что, если я еще не узнал об этом?
В этих двух найденных выше решениях аргумент квадратного корня пересекает ось x ; то есть мне говорят, где 16 — x ² — ноль. Эти решения, или нули, разделяют числовую прямую (то есть ось x ) на три интервала: (–∞, –4), (–4, 4) и (4, ∞).Мне нужен интервал (ы), на котором 16 — x ² находится выше оси x .
Поскольку я знаю, что исходный аргумент представляет собой параболу, которая находится выше оси x посередине, я знаю, что нужно выбрать средний интервал для области определения этой функции извлечения квадратного корня.
(Если вы не уверены в этом, то сделайте быстрый график y = 16 — x ² и посмотрите, где график находится выше и ниже горизонтальной оси.Интервал, в котором значения y положительны, равен (–4, 4), как показано ниже.)
Таким образом, интервал между x = –4 и x = 4 будет областью определения этой конкретной радикальной функции. Ни до, ни после этого интервала не будет никаких графиков.
Теперь мне нужно найти некоторые точки графика в дополнение к двум нулям, которые у меня уже есть.Поскольку значения для этой функции не подходят, я использовал калькулятор, чтобы приблизить значения и для моей Т-диаграммы:
Наконец, сделаю свой график:
Если вы думаете, что мой график выше очень похож на верхнюю половину круга, то вы совершенно правы. На самом деле, это верхняя половина круга с центром в начале координат и значением радиуса r = 4.(Отрицательный результат этой функции квадратного корня дал бы мне нижнюю половину того же круга.
График
Сначала найду домен. Поскольку аргумент радикала является квадратичным «плюсом», я знаю, что этот аргумент будет положительным, если соответствующая парабола находится выше оси x . Я ожидаю, что это будет по обе стороны от перехватов x , но не посередине между перехватами.
Перехваты находятся путем установки аргумента равным нулю и решения:
x ²-4 x = 0
x ( x — 4) = 0
х = 0, 4
Эти два нуля аргумента разделяют числовую строку на три интервала: (–∞, 0), (0, 4) и (4, ∞).Я ожидаю, что аргумент будет положительным (то есть выше оси x ) на первом и третьем интервалах, но отрицательным (то есть ниже оси x ) в середине. Чтобы убедиться, я посмотрю на график параболы y = x ²-4 x :
Как я и ожидал, квадратичный аргумент положительный (то есть его график выше оси x ) до первого пересечения при x = 0 и после второго пересечения при x = 4.
Аргумент радикала положителен на двух несвязанных интервалах на обоих концах графа параболы. Другими словами, область радикала разбита на ДВЕ части, которые не связаны друг с другом.
Это означает, что график радикальной функции также будет состоять из двух частей: одна часть слева, с остановкой на x = 0, а другая часть справа, начиная с x = 4.Между этими двумя частями не будет ничего, кроме , кроме пробела .
Помня об этом ограничении домена, я тщательно найду некоторые точки графика, используя свой калькулятор, чтобы получить десятичные приближения для значений и :
Наконец, сделаю свой график:
Партнер
Большинство графиков радикальных функций, которые вы будете делать, будут включать квадратные корни. Но можно изобразить и другие корни. Вот пример функции кубического корня:
График
Нет ограничений домена с кубическим корнем (или действительно для любого другого корня с нечетным индексом), потому что может иметь «минус» внутри кубического корня, поэтому я могу построить график кубического корня отрицательного числа. Итак, в отличие от случая, когда я работаю с квадратным корнем (или любым другим корнем с четным индексом), мне не нужно начинать с поиска домена; домен будет «все x ».
Итак, я сразу перейду к поиску некоторых точек на графике, используя свой калькулятор для вычисления десятичных приближений:
Мне удалось найти несколько значений x , которые дали мне хорошие значения y , установив аргумент корня куба равным идеальному кубу, например –8 или 1, и решив для x . Но, чтобы получить достаточно точек на графике, чтобы быть уверенным в том, что должна делать изображенная на графике линия, мне также пришлось использовать некоторые беспорядочные значения.
Мой график выглядит так:
Предупреждение: радикалы изображены изогнутыми линиями. Не поддавайтесь искушению провести прямую линию через нанесенные точки. Вместо этого используйте достаточное количество точек графика, чтобы четко показать форму графика, а затем нарисуйте график вместе с его кривыми . Вы должны ожидать, что графики большинства радикальных функций будут шире, чем высокие, но не думайте, что так будет всегда.Не торопитесь и помните, что сложно ошибиться с большим количеством сюжетов!
URL: https://www.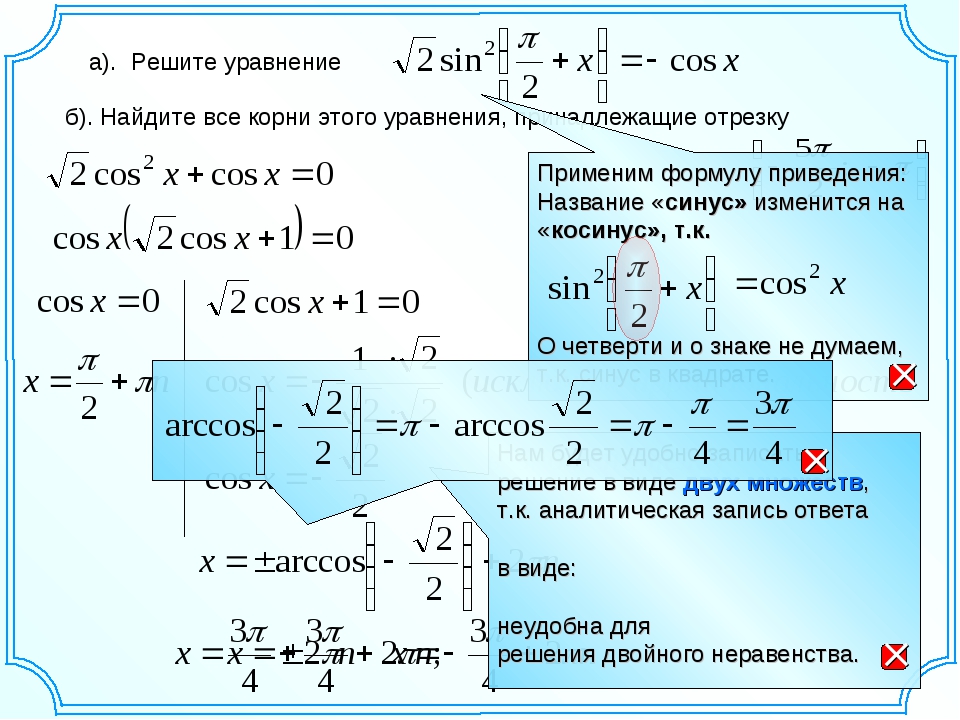 {2} + 25 & = 0 \\ 25 (- 1) + 25 & = 0 \\ — 25 + 25 & = 0 \\ 0 & = 0 \: \: \ color {Cerulean} {✓} \ end {align} \) Таблица \ (\ PageIndex {2} \)
Ответ :
Два комплексных решения, \ (\ pm 5 i \).{2} & = 9 \ quad \ quad \ quad \ color {Cerulean} {} Применить \: свойство \: square \: root \:. \\ x + 5 & = \ pm \ sqrt {9} \ quad \: \: \ color {Cerulean} {Упростить.} \\ x + 5 & = \ pm \ sqrt {9} \\ x & = — 5 \ pm 3 \ end {align} \)
На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.
\ (\ begin {array} {l} {x = — 5 + 3 \ quad \ text {или} \ quad x = — 5 — 3} \\ {x = — 2 \ quad \ quad \ quad \ quad \ quad x = — 8} \ end {array} \)
Ответ :
Решения: \ (- 2 \) и \ (- 8 \).{2} & = \ frac {5} {2} \ end {align} \)
Затем извлеките корни, решите относительно \ (x \) и затем упростите.
\ (\ begin {align} x — 2 & = \ pm \ sqrt {\ frac {5} {2}} \ quad \ quad \ quad \ quad \ color {Cerulean} {Рационализируйте \: знаменатель \:. } \\ x & = 2 \ pm \ frac {\ sqrt {5}} {\ sqrt {2}} \ cdot \ color {Cerulean} {\ frac {\ sqrt {2}} {\ sqrt {2}}} \ \ x & = 2 \ pm \ frac {\ sqrt {10}} {2} \\ x & = \ frac {4 \ pm \ sqrt {10}} {2} \ end {align} \)
Ответ :
Решения: \ (\ frac {4 — \ sqrt {10}} {2} \) и \ (\ frac {4 + \ sqrt {10}} {2} \).{2} & = 49 \ quad \ quad \ quad \ color {Cerulean} {Извлечь \: \: корни.} \\ x + 1 & = \ pm \ sqrt {49} \\ x + 1 & = \ pm 7 \\ x & = — 1 \ pm 7 \ end {align} \)
На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно.
\ (\ begin {array} {l} {x = — 1-7 \ text {or} x = — 1 + 7} \\ {x = — 8 \ quad \ quad \ quad x = 6} \ end { массив} \)
Ответ :
Решения: \ (- 8 \) и \ (6 \).
Примечание
В предыдущем примере решения — целые числа.{2} & = — \ frac {7} {4} \\ x + \ frac {3} {2} & = \ pm \ sqrt {\ frac {- 1 \ cdot 7} {4}} \\ x + \ frac {3} {2} & = \ pm \ frac {i \ sqrt {7}} {2} \\ x & = — \ frac {3} {2} \ pm \ frac {\ sqrt {7}} {2} i \ end {align} \)
Ответ :
Решения: \ (- \ frac {3} {2} \ pm \ frac {\ sqrt {7}} {2} i \).